② 浙江大学地球科学学院, 浙江杭州 310027
② School of Earth Sciences, Zhejiang University, Hangzhou, Zhejiang 310027, China
地震数据偏移成像是当前油气勘探开发中获取地下三维地质结构的主要方法[1-2]。自20世纪70年代初期,Claerbout[3-4]提出基于波动方程的现代偏移成像概念以来,有关偏移成像的研究与应用一直是地震数据处理技术的热点之一。在Claerbout波动方程偏移成像概念的基础上,Berkhout[5]提出适用于地震数据偏移成像的“WRW”地震反射波传播模型。经过40余年的发展,地震数据偏移已从叠后走向了叠前,从二维走向了三维,从时间域走向了深度域,从各向同性介质走向了各向异性介质,从主要关注相位信息的构造成像走向了相位和振幅并举的保幅成像[6-21]。
当前的地震数据偏移不区分散射和反射[22],在偏移中主要用反射的概念,而在最小二乘偏移中主要应用散射的概念[23]。偏移的目标是对地下非均匀体边界位置进行成像,即对产生散射的散射体位置和产生反射的反射面位置进行成像[24-31]。根据Berkhout的“WRW”概念模型,共炮道集地震数据偏移分两步实现,一是基于波动方程的震源波场正向传播和记录波场反向传播;二是利用正向传播得到的入射波场和反向传播得到的散射波场或反射波场实现对非均匀体空间位置的成像,即实现对非均匀体的构造成像。常规波动方程偏移成像中,没有考虑散射波与反射波在传播上的不同,散射波或反射波成像结果存在相位(极性)偏差。
本文首先讨论了常规波动方程偏移方法存在的不足,然后从波动方程的扰动形式出发,根据地下非均匀体大小与波长之间的关系定义产生散射波的散射体和产生反射波的反射体,在具有地震波运动学特征准确的偏移速度模型下,建立一次散射波数据的线性正演方程,再利用线性反演理论推导出对散射体空间位置进行成像的地震散射数据偏移计算公式,最后应用国际上常用的Sigbee2A模型数值模拟数据验证本文所提出的散射数据偏移方法。
1 常规波动方程偏移的主要不足共炮集地震数据的逆时偏移,具体计算步骤概括如下:
(1) 利用偏移速度模型计算入射波场
| $ \left[ {\frac{1}{{v_{\rm{m}}^2(\mathit{\boldsymbol{x}})}}\frac{{{\partial ^2}}}{{\partial {t^2}}} - {\nabla ^2}} \right]{u_{\rm{i}}}(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}) = f(t)\delta (\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_{\rm{s}}}) $ | (1) |
(2) 利用逆时外推重建地下反射波场(或散射波场)
| $ \left\{ {\begin{array}{*{20}{l}} {\left[ {\frac{1}{{v_{\rm{m}}^2(\mathit{\boldsymbol{x}})}}\frac{{{\partial ^2}}}{{\partial {t^2}}} - {\nabla ^2}} \right]{u_{\rm{r}}}(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}) = 0}\\ {{u_{\rm{r}}}(\mathit{\boldsymbol{x}} = {\mathit{\boldsymbol{x}}_{\rm{g}}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}) = {\rm{d}}({\mathit{\boldsymbol{x}}_{\rm{g}}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}})} \end{array}} \right. $ | (2) |
(3) 利用成像条件(反射系数成像条件)进行波场成像
| $ \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} I(\mathit{\boldsymbol{x}}) = \int_0^T {\frac{{{u_{\rm{r}}}(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}})}}{{{u_i}(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}})}}} {\rm{d}}t\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 或 \end{array}\\ {I(\mathit{\boldsymbol{x}}) = \int_0^T {{u_{\rm{r}}}} (\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}){u_{\rm{i}}}(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}){\rm{d}}t} \end{array}} \right. $ | (3) |
式中:
在地震波运动学特征(旅行时)准确的偏移速度模型下,利用式(1)和式(2)可得到入射波波场和重建的反射波场(或散射波场),但反射系数成像公式(式(3))仅适用于无穷大平边界和临界角下平面波的反射,要求ur(x, t; xs)与ui(x, t; xs)具有相同的波形。在弯曲边界或非平面波的情况下,反射系数与频率有关[32],即此时ur(x, t; xs)与ui(x, t; xs)的波形不同,会存在相位差异。由于产生散射波的非均匀体和无特定传播方向的散射波场不满足成像公式(式(3))所要求的“无穷大平反射边界和临界角下的平面波”条件,因此式(1)~式(3)构成的逆时偏移方法应用于散射数据是不合适的,得到的偏移成像结果会存在相位误差。
为了构建适合散射数据的偏移成像计算公式,首先必须建立适合偏移成像的散射数据正演方程。
2 散射波正演方程为了推导的简便和不失一般性,本文仅考虑常密度声波方程,即标量波动方程
| $ \left[ {\frac{1}{{{v^2}(\mathit{\boldsymbol{x}})}}\frac{{{\partial ^2}}}{{\partial {t^2}}} - {\nabla ^2}} \right]u(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}) = f(t)\delta (\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_{\rm{s}}}) $ | (4) |
式中:u为地震波场;v为速度。根据扰动理论,将速度表示为背景速度与速度扰动之和,即
| $ v(\mathit{\boldsymbol{x}}) = {v_{\rm{b}}}(\mathit{\boldsymbol{x}}) + \Delta v(\mathit{\boldsymbol{x}}) $ | (5) |
波场表示为背景波场与扰动波场之和,即
| $ u(\mathit{\boldsymbol{x}},t) = {u_{\rm{b}}}(\mathit{\boldsymbol{x}},t) + \Delta u(\mathit{\boldsymbol{x}},t) $ | (6) |
式(4)可写为扰动形式的波动方程形式
| $ \begin{array}{*{20}{l}} {\left[ {\frac{1}{{v_{\rm{b}}^2(\mathit{\boldsymbol{x}})}}\frac{{{\partial ^2}}}{{\partial {t^2}}} - {\nabla ^2}} \right]\Delta {u_r}(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}})}\\ {\quad = \frac{{2\Delta v(\mathit{\boldsymbol{x}})}}{{v_{\rm{b}}^3(\mathit{\boldsymbol{x}})}}\frac{{{\partial ^2}[{u_{\rm{b}}}(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}) + \Delta u(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}})]}}{{\partial {t^2}}}} \end{array} $ | (7) |
对于背景波场ub(x, t),有
| $ \left[ {\frac{1}{{v_{\rm{b}}^2(\mathit{\boldsymbol{x}})}}\frac{{{\partial ^2}}}{{\partial {t^2}}} - {\nabla ^2}} \right]{u_{\rm{b}}}(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}) = f(t)\delta (\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_{\rm{s}}}) $ | (8) |
如果把式(7)的右端项视为产生扰动场的虚源项,是由波场与速度扰动相互作用产生的,因此与速度扰动体的尺寸和速度扰动量有关。为了合理地描述速度扰动体尺寸对扰动波场的作用,以地震波场主频对应的波长度量速度扰动体尺度。
如果速度扰动Δv(x)的尺寸或者其空间变化的特征尺度a相对于波长λ较小,即a/λ≤1,则本文把该情况下的速度扰动体视为局部散射体,相应地式(7)的右端项可近似为点源项,产生的扰动波场可视为散射波场。如果速度扰动Δv(x)的尺寸或者其空间变化的特征尺度a相对于波长λ较大,即a/λ>1,则速度扰动体是一种在空间具有一定延续度的非均匀体,本文称之为反射体,相应地式(7)的右端项可视为一种集成源项,产生具有特定方向性的反射波场,本文不考虑这种情况。上述的“速度扰动Δv(x)的尺寸或者其空间变化的特征尺度相对于波场的波长比较小”,在物理实质上是一种局部近似条件,本文称为局部散射近似条件。
在局部散射近似条件下,扰动波场Δu(x,t)转化为散射波场us(x,t),即Δu(x,t)→us(x,t),相应地把波场扰动方程(式(7))改写为散射波正演方程
| $ \begin{array}{*{20}{l}} {\left[ {\frac{1}{{v_{\rm{b}}^2(\mathit{\boldsymbol{x}})}}\frac{{{\partial ^2}}}{{\partial {t^2}}} - {\nabla ^2}} \right]{u_{\rm{s}}}(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}})}\\ {\quad = \frac{{2\Delta v(\mathit{\boldsymbol{x}})}}{{v_{\rm{b}}^3(\mathit{\boldsymbol{x}})}}\frac{{{\partial ^2}[{u_{\rm{b}}}(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}) + {u_s}(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}})]}}{{\partial {t^2}}}} \end{array} $ | (9) |
再利用散射波场相对于背景波场的小扰动近似(一阶Born近似),式(9)退化为描述散射波场与速度扰动Δv(x)成线性关系的一次散射波正演方程,即
| $ \begin{array}{*{20}{l}} {\left[ {\frac{1}{{v_{\rm{b}}^2(\mathit{\boldsymbol{x}})}}\frac{{{\partial ^2}}}{{\partial {t^2}}} - {\nabla ^2}} \right]u_{\rm{s}}^1(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}})}\\ {\quad = \frac{{2\Delta v(\mathit{\boldsymbol{x}})}}{{v_{\rm{b}}^3(\mathit{\boldsymbol{x}})}}\frac{{{\partial ^2}{u_{\rm{b}}}(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}})}}{{\partial {t^2}}}} \end{array} $ | (10) |
式(10)中的散射波场us1(x, t)为局部速度扰动体产生的一次散射波场。相应地,式(10)为一阶Born近似下的一次散射波正演方程,即给定背景速度和速度扰动以及震源子波的条件下散射波的正演表达方程。式(10)是式(9)的线性化版本。
由于现有的偏移方法不区分散射和反射,因此在波动方程的最小二乘偏移和常规偏移方法的正演表达推导中会出现与上述散射波正演方程类似的推导[23],并把速度相对扰动Δv(x)/vb(x)定义为反射系数。由于反射系数在数学上是一个Dirac函数,而速度相对扰动在数学上是一个阶跃函数。因此本文认为在偏移中不区分散射与反射,并直接用Born近似下的散射波正演方程作为波动方程的最小二乘偏移和常规偏移方法的正演表达,在数学和物理意义上欠严谨。
3 散射数据偏移在局部散射近似和一阶Born近似条件下推导出的一次散射波正演方程式(10)是进行一次散射波模拟和一次散射波反演成像的基础方程,也是本文散射数据偏移的基础方程。
为便于推导,利用式(8)所对应的Green函数将式(10)转化为积分形式,即
| $ \begin{array}{*{20}{l}} {u_{\rm{s}}^1(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}) = \int_\mathit{\Omega } {\rm{d}} \mathit{\boldsymbol{y}}g(\mathit{\boldsymbol{x}},t;\mathit{\boldsymbol{y}}){*_t}}\\ {\frac{{2\Delta v(\mathit{\boldsymbol{y}})}}{{v_{\rm{b}}^3(\mathit{\boldsymbol{y}})}}\frac{{{\partial ^2}{u_{\rm{b}}}(\mathit{\boldsymbol{y}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}})}}{{\partial {t^2}}}} \end{array} $ | (11) |
式中:Ω表示速度扰动体的分布范围;“*t”表示时间方向的褶积。Green函数满足
| $ \left[ {\frac{1}{{v_{\rm{b}}^2(\mathit{\boldsymbol{x}})}}\frac{{{\partial ^2}}}{{\partial {t^2}}} - {\nabla ^2}} \right]g(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}) = \delta (t)\delta (\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_{\rm{s}}}) $ | (12) |
利用已知的一次散射数据us1(x, t; xs)和背景速度vb(y)反演速度扰动Δv(y),需要求解线性积分方程式(11)。令式(10)的虚源项为s,有
| $ s(\mathit{\boldsymbol{y}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}) = \frac{{2\Delta v(\mathit{\boldsymbol{y}})}}{{v_{\rm{b}}^3(\mathit{\boldsymbol{y}})}}\frac{{{\partial ^2}{u_{\rm{b}}}(\mathit{\boldsymbol{y}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}})}}{{\partial {t^2}}} $ | (13) |
线性积分方程(式(11))可写为
| $ u_{\rm{s}}^1(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}) = \int_\mathit{\Omega } {\rm{d}} \mathit{\boldsymbol{y}}g(\mathit{\boldsymbol{x}},t;y){*_t}s(\mathit{\boldsymbol{y}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}) $ | (14) |
因此求解式(11)对应为一个线性反演源问题(Inverse Source Problem)[33]。把式(14)写为矩阵方程形式,有
| $ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{Gm}} $ | (15) |
式中:d为一次散射数据组成的矩阵;G为由Green函数构成的矩阵;m为虚源项形成的矩阵。利用最小二乘反演,可得到m的解
| $ \mathit{\boldsymbol{m}} = {({\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{G}})^{ - 1}}{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{d}} $ | (16) |
由于(GTG)-1的数值计算难度问题,把式(16)近似为
| $ \mathit{\boldsymbol{m}} = {\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{d}} $ | (17) |
利用式(17)得到的近似m,是对式(13)的虚源s(y, t; xs)的近似求解。再利用由式(8)得到的背景波场ub(y, t; xs),就可得到对速度扰动Δv(y)的近似估计
| $ \Delta v(\mathit{\boldsymbol{y}}) = \frac{{v_{\rm{b}}^3(\mathit{\boldsymbol{y}})s(\mathit{\boldsymbol{y}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}})}}{{2\frac{{{\partial ^2}{u_{\rm{b}}}(\mathit{\boldsymbol{y}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}})}}{{\partial {t^2}}}}} $ | (18) |
考虑到式(18)除法运算的稳定性问题,根据常规偏移中把反褶积成像条件转化为互相关成像条件的处理办法,把式(18)中的分母项转化到分子项,得到散射波互相关成像条件公式,即
| $ \Delta v(\mathit{\boldsymbol{y}}) = \frac{{v_{\rm{b}}^3(\mathit{\boldsymbol{y}})}}{2}s(\mathit{\boldsymbol{y}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}})\frac{{{\partial ^2}{u_{\rm{b}}}(\mathit{\boldsymbol{y}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}})}}{{\partial {t^2}}} $ | (19) |
由于式(19)与式(17)近似,利用上述公式得到的速度扰动反演结果虽然只是真实速度扰动的近似,但由于速度扰动体的局部假定,该反演结果还是能清楚反映速度扰动体(散射体)的空间位置,即实现对散射体空间位置的成像。
式(17)是利用Green函数矩阵的转置,把散射波场反向传播到产生散射波的虚源处,在数值计算中可利用地震波的逆时外推方法,把记录的散射波场逆时外推到入射波场(背景波场)作用于散射体产生散射虚源时刻的波场。式(19)中的s(y, t; xs)与背景波场ub(y, t; xs)具有相同的时间(即入射波作用于散射体时的时间)。
综上所述,可以得到下述对散射体空间位置进行成像的计算公式,即散射数据的偏移计算公式。
(1) 根据式(17),得到散射数据的逆时传播近似反演散射虚源的计算公式
| $ \left[ {\frac{1}{{v_{\rm{b}}^2(\mathit{\boldsymbol{x}})}}\frac{{{\partial ^2}}}{{\partial {t^2}}} - {\nabla ^2}} \right]s(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}) = d(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}){|_{\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_{\rm{g}}}}} $ | (20) |
(2) 根据式(8)可得地下背景波场计算公式
| $ \left[ {\frac{1}{{v_{\rm{b}}^2(\mathit{\boldsymbol{x}})}}\frac{{{\partial ^2}}}{{\partial {t^2}}} - {\nabla ^2}} \right]{u_{\rm{b}}}(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}) = f(t)\delta (\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_{\rm{s}}}) $ | (21) |
(3) 根据式(19),得到对散射体空间位置进行成像的计算公式
| $ \Delta v(\mathit{\boldsymbol{x}}) = \sum\limits_{{\mathit{\boldsymbol{x}}_{\rm{s}}}} {\frac{{v_{\rm{b}}^3(\mathit{\boldsymbol{x}})}}{2}} \int_0^{{T_{ {\rm{max}} }}} s (\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}})\frac{{{\partial ^2}{u_{\rm{b}}}(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}})}}{{\partial {t^2}}}dt $ | (22) |
式(20)是散射数据从Tmax到零时刻的反向传播,式(21)是地震波场从零时刻到Tmax的正向传播。
对比本文推导的散射数据偏移方法与常规反射波偏移方法,可见两者的主要差异是成像条件不同(式(22)与式(3))。式(22)是基于一次散射波方程式(10)推导得到的,而式(3)是基于无穷大平边界和平面波的反射波传播理论推导得到的。散射数据偏移方法是对速度扰动的近似成像,由于速度扰动体在地震波长尺度下的空间局部性,速度扰动Δv(x)在空间上可近似为一个Dirac函数,因此通过对速度扰动的近似成像实现对速度扰动体的位置成像[29],而常规逆时偏移方法是对反射面的反射系数成像。其次是散射数据的逆时传播方程(式(20)与式(2))不同,式(20)是非齐次波动方程(有源项)的波场逆时传播,式(2)是齐次波动方程(无源项)边值条件的波场逆时传播。本文利用局部散射近似条件推导出的散射数据逆时偏移方法,与当前不区分散射和反射而直接把常规逆时偏移方法作为散射数据偏移方法相比,更严谨合理。
由于式(22)较式(3)增加了对入射波场的时间二阶导数算子(该算子不仅可以提高成像的分辨率,相位也会发生180°旋转),因此本文的散射数据偏移方法较常规散射数据偏移方法在理论上会有更高的分辨率和准确的相位。对比本文提出的散射数据偏移方法的计算公式(式(20)~式(22))与常规逆时偏移方法的计算公式(式(1)~式(3))可知,本文算法的运算成本与常规方法相当。
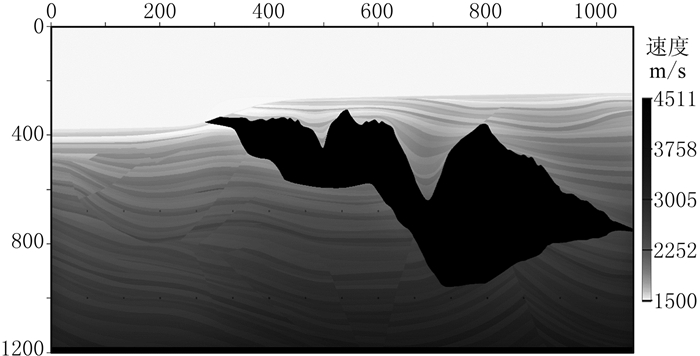
4 数值试验为了验证本文基于散射波方程推导出的散射偏移方法的正确性与有效性,应用Sigbee2A模型进行偏移成像试验。该模型(图 1)在沉积地层中包含高速盐体和许多高速散射体(图 1深层中分布的黑色孤立体),非常适合对本文散射偏移方法的验证。图 2为用于偏移成像试验的背景速度模型。模型大小为1067×1201个网格点,水平和垂直方向的网格间距分别为22.86m和7.62m,观测方式为海上拖缆观测系统。共模拟500炮,炮间距为45.72m,拖缆长度为7932.42m,检波点间距为22.86m,每炮道数不等,最少为57道,最多为348道,时间采样间隔为8ms,时间采样点数为1500。

|
图 2 Sigbee2A偏移速度模型 |
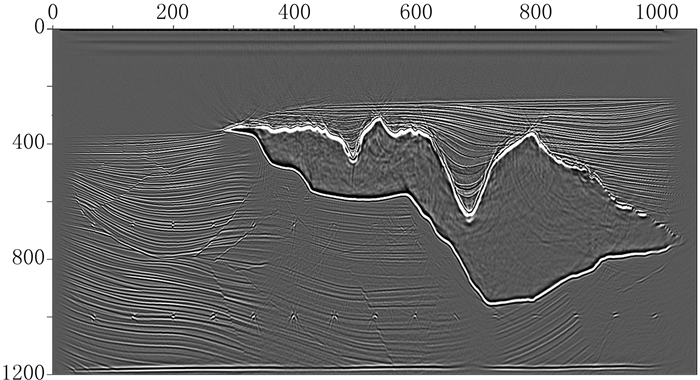
分别应用常规逆时偏移成像方法和本文提出的散射地震偏移成像方法对Sigbee2A模型数据进行偏移成像(图 3、图 4)。
|
图 3 Sigbee2A模型的常规逆时偏移结果 |

|
图 4 Sigbee2A模型的散射偏移结果 |
对比图 1、图 3和图 4可以看出,不论常规逆时偏移方法还是本文的散射偏移方法都能对Sigbee2A模型中的高速盐体、反射层和高速散射体进行清晰成像,相对于常规逆时偏移方法的成像结果(图 3),散射波偏移方法的成像结果(图 4)中同相轴较细、分辨率较高。由图 3、图 4中的盐体边界成像结果可以看出,两者是反相的,存在180°的相位差异,这与本文的理论是一致的,但两者的相位都是错的[34],都存在90°的相位误差。对于反射体边界的偏移成像需要使用针对反射数据的偏移成像方法[18, 34],才能获得正确相位的反射面偏移成像结果(图 3相位旋转90°,图 4相位旋转-90°)。对于散射体的成像,散射偏移成像方法得到的散射体的偏移成像结果要好于常规偏移成像方法。
为了仔细对比散射偏移方法和常规逆时偏移方法的成像效果,截取图 1速度模型和图 3、图 4两种偏移成像结果的左边部分进行局部放大,如图 5~图 7所示。常规逆时偏移对散射体的成像出现了反极性,高速散射体成像为低速散射体(图 6);在图 7的散射偏移结果中,散射体极性正确,高速散射体成像为高速散射体。与图 6所示的常规逆时偏移成像结果相比,散射偏移结果中高速散射体不仅分辨率高,而且位置准确、相位(极性)正确。这一结果证明了本文提出的散射偏移方法对散射体成像的有效性。

|
图 5 速度模型的局部放大 |

|
图 6 常规逆时偏移成像结果的局部放大 |

|
图 7 散射偏移成像结果的局部放大 |
地震散射波是地下相对于地震波长较小的局部非均匀体产生的,而地震反射波是地下相对于地震波长在空间上具有一定延续度的非均匀体产生的。不考虑散射波场与反射波场之间的特征差异,直接把基于反射波概念的逆时偏移方法应用于散射数据的偏移成像,缺乏理论上的严谨性。本文利用波动方程的扰动形式,通过地下非均匀体与地震波长之间的相对关系,得到了描述一次散射波的非齐次波动方程,并把该方程作为散射数据偏移成像的线性正演方程;然后再利用反源问题的求解方法反演散射波的地下散射虚源,推导出散射数据的逆时偏移公式。对于散射体产生的散射数据,本文提出的散射偏移方法相对于当前的常规逆时偏移方法,可以得到更高分辨率的散射体成像结果和准确的相位(极性),并在Sigbee2A模型高速散射体的成像中取得理想效果。
| [1] |
Gray S, Etgen J, Dellinger J, et al. Seismic migration problems and solutions[J]. Geophysics, 2001, 66(5): 1622-1640. |
| [2] |
Yilmaz O.Seismic Data Analysis[M].SEG, Tulsa, 2001.
|
| [3] |
Claerbout J. Toward a unified theory of reflector mapping[J]. Geophysics, 1971, 36(3): 467-481. |
| [4] |
Claerbout J.Fundamentals of Geophysical Data Processing[M].McGraw-Hill Book Co Inc, New York, 1976.
|
| [5] |
Berkhout A.Seismic Migration: Imaging of Acoustic Energy by Wavefield Extrapolation, Part A: Theoretical Aspects(2nd Edition)[M]. Elsevier, Amsterdam, 1982.
|
| [6] |
Du Q, Zhu Y, Ba J. Polarity reversal correction for elastic reverse time migration[J]. Geophysics, 2012, 77(2): S31-S41. |
| [7] |
Chang W, McMechan G. A 3-D elastic prestack re-verse-time depth migration[J]. Geophysics, 1994, 59(4): 597-609. |
| [8] |
Zhang Y, Duan L, Xie Y. A stable and practical implementation of least-squares reverse time migration[J]. Geophysics, 2015, 80(1): V23-V31. |
| [9] |
Yao G, Jakubowicz H.Least-squares reverse time migration[C].SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [10] |
Yao G, Jakubowicz H.Non-linear least-squares reverse time migration[C].SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [11] |
Dong S, Cai J, Guo M, et al.Least-squares reverse time migration: towards true amplitude imaging and improving the resolution[C].SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [12] |
Gray S. True-amplitude seismic migration:A comparison of three approaches[J]. Geophysics, 1997, 62(3): 926-936. |
| [13] |
郭振波, 李振春. 最小平方逆时偏移真振幅成像[J]. 石油地球物理勘探, 2014, 49(1): 113-120. GUO Zhenbo, LI Zhenchun. True amplitude imaging based on least-squares reverse time migration[J]. Oil Geophysical Prospecting, 2014, 49(1): 113-120. |
| [14] |
黄建平, 孙陨松, 李振春, 等. 一种基于分频编码的最小二乘裂步偏移方法[J]. 石油地球物理勘探, 2014, 49(4): 702-707. HUANG Jianping, SUN Yunsong, LI Zhenchun, et al. Least-squares split step migration based on frequency division encoding[J]. Oil Geophysical Prospecting, 2014, 49(4): 702-709. |
| [15] |
周华敏, 陈生昌, 任浩然, 等. 基于照明补偿的单程波最小二乘偏移[J]. 地球物理学报, 2014, 57(8): 2644-2655. ZHOU Huamin, CHEN Shengchang, REN Haoran, et al. One way wave equation least squares migration based on illumination compensation[J]. Chinese Journal of Geophysics, 2014, 57(8): 2644-2655. |
| [16] |
Zhang Y, Ratcliffe A, Duan L.Velocity and impedance inversion based on true amplitude reverse time migration[C].SEG Technical Program Expanded Abstracts, 2013, 32: 949-953.
|
| [17] |
Duan L, Zhang Y and Peng L.Band-limited impedance perturbation inversion using cross-correlative least-squares RTM[C].SEG Technical Program Expanded Abstracts, 2014, 33: 3720-3725.
|
| [18] |
陈生昌. 基于反射波动方程的地震反射数据波形成像[J]. 石油地球物理勘探, 2018, 53(3): 487-501. CHEN Shengchang. Waveform imaging of seismic reflection data based on reflection wave equation[J]. Oil Geophysical Prospecting, 2018, 53(3): 487-501. |
| [19] |
段沛然, 谷丙洛, 李振春. 基于优化算子边界存储策略的高效逆时偏移方法[J]. 石油地球物理勘探, 2019, 54(1): 93-101. DUAN Peiran, GU Bingluo, LI Zhenchun. An efficient reverse time migration in the vertical time domain based on optimal operator boundary storage strategy[J]. Oil Geophysical Prospecting, 2019, 54(1): 93-101. |
| [20] |
李闯, 黄建平, 李振春, 等. 基于混合随机共轭梯度的最小二乘逆时偏移[J]. 石油地球物理勘探, 2018, 53(6): 1188-1197. LI Chuang, HUANG Jianping, LI Zhenchun, et al. Least-squares reverse time migration with a hybrid stochastic conjugate gradient[J]. Oil Geophysical Prospecting, 2018, 53(6): 1188-1197. |
| [21] |
陈可洋, 王建民, 关昕, 等. 逆时偏移技术在VSP数据成像中的应用[J]. 石油地球物理勘探, 2018, 53(增刊1): 89-93. CHEN Keyang, WANG Jianmin, GUAN Xin, et al. VSP data imaging with reverse time migration[J]. Oil Geophysical Prospecting, 2018, 53(S1): 89-93. |
| [22] |
Leveille J, Jones I, Zhou Z, et al. Subsalt imaging for exploration, production, and development:A review[J]. Geophysics, 2011, 76(5): WB3-WB20. |
| [23] |
Schuster G.Seismic Inversion[M].SEG, Tulsa, 2017.
|
| [24] |
马在田. 地震成像技术——有限差分偏移[M]. 北京: 石油工业出版社, 1989.
|
| [25] |
Robein E.Seismic Imaging: A Review of the Tech-niques, Their Principles, Merits and Limitations[M].EAGE, Houten, 2010.
|
| [26] |
Stolt R, Benson A. Seismic Migration:Theory and Practice[M]. London: Geophysical Press, 1986.
|
| [27] |
Beylkin G. Imaging of discontinuities in the inverse scattering problem by the inversion of a causal Radon transform[J]. Journal of Mathematics Physics, 1985, 26(1): 99-108. |
| [28] |
Bleistein N. On the imaging of reflectors in the earth[J]. Geophysics, 1987, 52(7): 931-942. |
| [29] |
Bleistein N, Cohen J, Stockwell J. Mathematics of Multidimensional Seismic Imaging, Migration, and Inversion[M]. New York: Springer, 2001.
|
| [30] |
李振春, 等. 地震叠前成像理论与方法[M]. 山东东营: 中国石油大学出版社, 2011.
|
| [31] |
李振春. 地震偏移成像技术研究现状与发展趋势[J]. 石油地球物理勘探, 2014, 49(1): 1-21. LI Zhenchun. Research status and development trends for seismic migration technology[J]. Oil Geophysical Prospecting, 2014, 49(1): 1-21. |
| [32] |
Aki K, Richards P. Quantitative Seismology(2nd edition)[M]. Sausalito: University Science Books, 2002.
|
| [33] |
Devaney A. Mathematical Foundations of Imaging, Tomography and Wavefield Inversion[M]. New York: Cambridge University Press, 2012.
|
| [34] |
陈生昌, 周华敏. 再论地震数据偏移成像[J]. 地球物理学报, 2016, 59(2): 643-654. CHEN Shengchang, ZHOU Huamin. Re-exploration to migration of seismic data[J]. Chinese Journal of Geophysics, 2016, 59(2): 643-654. |



 陈生昌, 浙江省杭州市浙大路38号浙江大学地球科学学院, 310027。Email:
陈生昌, 浙江省杭州市浙大路38号浙江大学地球科学学院, 310027。Email: