基于VSP数据的波形反演[1]的实质是,在一定条件约束下,通过多次迭代,最小化模型参数的正演模拟合成数据与观测数据的残差[2-4],因而波动方程正演模拟的数值计算效率和计算精度是制约全波形反演应用于实际的重要因素[5]。针对高精度的VSP正演数值模拟问题,国内外学者展开了一系列研究。邹延延等[6]比较完整地总结了VSP正演方法,包括射线追踪法、高斯射线束法[7]、反射率法[8]和有限差分法。其中,有限差分法[9-10]由于计算效率高而成为VSP波形反演中最常用的正演模拟方法,但该方法受限于频散条件及稳定性条件,需要严格的子波主频和网格比匹配。另外,人工边界[11]吸收不完全也会引入多余的干扰。
基于体积分方程的正演模拟方法则很好地克服了以上有限差分算法存在的问题,不受正演子波频率的限制,且正演过程不会引入人工边界导致的干扰。Fokkema等[12]介绍了声波互易性原理在地震勘探中的应用,在均匀介质假设下,把二维一阶应力—速度声波方程组转化为边界积分和体积积分形式,将该正演问题转化为求解第二类Fredholm积分方程,至此拉开了研究波动方程积分数值解法的序幕。Lam等[13]将WKBJ近似方法引入背景介质格林函数的求解中,利用Neumann级数迭代方法求解一维声波方程的近似解,但是数值计算方法忽略了地下介质和波场之间严格的非线性特征,并且计算效率较低。Yang等[14]提出了一种共轭梯度—傅里叶变换(CG-FFT)法求解三维弹性波动方程散射问题,该方法在高频情况下仍具有较高的计算效率和计算精度,不足之处在于该方法选定均匀介质作为背景介质,模型较复杂时,格林函数不能满足计算精度要求。Haffinger等[15]在求解声波方程散射问题时采用了一种介于Neumann级数迭代法和共轭梯度迭代方法之间的一种数值求解方法,计算过程比较复杂。
针对体积分声波方程,在前人的研究基础上,本文提出了一种提高积分方程计算效率的数值计算方法,求解零井源距VSP波场。首先将积分方程转化为矩阵相乘的形式,给出了在常背景介质假设下的格林函数以及正演算子的矩阵表达格式,并给出了均匀变化的背景介质假设下的格林函数表达式;通过预条件最小二乘方法实现了波场的直接快速精确求解;最后,以阶梯状模型和根据实际声波测井数据建立的模型验证本文数值计算方法的可行性和有效性。
1 理论及方法本文从三个方面阐述基于散射理论的声波方程正演问题的快速、稳定数值求解方法。首先,详细介绍了由散射理论将声波方程微分方程转换为Lippman-Schwinger积分方程的过程以及求解该积分方程的迭代计算方法;然后,将该第二类Fredholm积分方程通过简化的正演算子转化为大型线性方程组的求解问题;最后,介绍了求解该问题的预条件最小二乘数值计算方法。
1.1 声波方程散射问题在常密度假设下,频率—空间域声波在地下各向同性介质中传播满足Helmholtz方程
| $ \left[ {\frac{{{\partial ^2}}}{{\partial {\mathit{\boldsymbol{x}}^2}}} + {k^2}(\mathit{\boldsymbol{x}})} \right]u(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega ) = f(\omega )\delta (\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_{\rm{s}}}) $ | (1) |
式中:k(x)=ω/c(x)为波数,其中c(x)为介质的真实纵波速度场;u(x,xs, ω)为频率—空间域的声波全波场;xs(xs,ys,zs)为源点坐标;f(ω)为震源子波,ω=2πf为角频率。
根据声波散射理论,全波场u(x,xs,ω)可描述为在背景介质中传播的入射波场u0(x,xs,ω)和由速度扰动产生的散射波场us(x,xs,ω)的叠加,即
| $ u(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega ) = {u_0}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega ) + {u_{\rm{s}}}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega ) $ | (2) |
入射波场u0满足
| $ \left[ {\frac{{{\partial ^2}}}{{\partial {\mathit{\boldsymbol{x}}^2}}} + k_0^2(\mathit{\boldsymbol{x}})} \right]{u_0}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega ) = f(\omega )\delta (\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_{\rm{s}}}) $ | (3) |
式中k0(x)=ω/c0(x),其中c0(x)为背景速度,一般通过对真实纵波速度场c(x)做低通滤波获得。引入背景介质对应的格林函数G(x,xs,ω),可得入射波场的解析解为
| $ {u_0}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega ) = f(\omega )G(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega ) $ | (4) |
引入对比函数
| $ \chi (\mathit{\boldsymbol{x}}) = 1 - \frac{{c_0^2(\mathit{\boldsymbol{x}})}}{{{c^2}(\mathit{\boldsymbol{x}})}} $ | (5) |
根据式(1)~式(3),散射波场us(x,xs,ω)满足
| $ \left[ {\frac{{{\partial ^2}}}{{\partial {\mathit{\boldsymbol{x}}^2}}} + k_0^2} \right]{u_{\rm{s}}}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega ) = k_0^2\chi (\mathit{\boldsymbol{x}})u(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega ) $ | (6) |
在Sommerfeld辐射边界条件假设下,利用互易定理,式(6)所示的声波散射波场的微分方程等价于如下的积分方程
| $ {u_{\rm{s}}}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega ) = k_0^2\int G (\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}^\prime },\omega )\chi ({\mathit{\boldsymbol{x}}^\prime })u({\mathit{\boldsymbol{x}}^\prime },{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega ){\rm{d}}{\mathit{\boldsymbol{x}}^\prime } $ | (7) |
上式也称数据方程,描述了散射场与对比函数和全波场之间的非线性关系。式(7)两边同时加上入射波场u0(x,xs,ω),则全波场可表示为
| $ \begin{array}{*{20}{l}} {u(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega ) = {u_0}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega ) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k_0^2\int G (\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}^\prime },\omega )\chi ({\mathit{\boldsymbol{x}}^\prime })u({\mathit{\boldsymbol{x}}^\prime },{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega ){\rm d}{\mathit{\boldsymbol{x}}^\prime }} \end{array} $ | (8) |
式(8)即为求解Helmholtz方程空间全波场的Lippman-Schwinger积分方程,对应于数据方程,被称为目标方程,描述了全波场与对比函数之间的非线性关系,被广泛应用于积分方程对比源反演[16-17]。从物理意义上看,通过散射理论,该积分方程将声波全波场分解为在背景介质中传播的入射波场以及将真实介质中异于背景介质的散射体看作二次震源所产生的散射波场之和;从数学形式上看,该积分方程是典型的第二类Fredholm积分方程,格林函数和对比函数的乘积构成了积分核,通常采用迭代方法[18]求解。
1.2 数值迭代求解方法简单起见,将式(8)写为
| $ u = {u_0} + L(\chi )u $ | (9) |
式中L(χ)是正演算子,它是一个关于对比函数的函数。对于式(9)所示的第二类Fredholm积分方程,通常使用Neumann级数迭代方法、超松弛迭代方法等迭代方法[19]求解。以Neumann级数迭代方法为例,其迭代流程如下:
(1) 给定迭代次数,迭代误差限;
(2) 选定入射波场u0为全波场u的零级近似;
(3) 利用迭代公式un=un+L(χ)un-1,逐步得到全波场u的Neumann级数解;
(4) 定义迭代误差rn=u0-un+L(χ)un,如果误差大于误差限,返回步骤(3),否则终止迭代。
由上述迭代公式可得
为实现基于声波体积分方程的零井源距VSP波场快速数值模拟方法,将式(9)写为矩阵形式
| $ \mathit{\boldsymbol{Au}} = \mathit{\boldsymbol{g}} $ | (10) |
式中
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{Au}} = [\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{L}}(\chi )]\mathit{\boldsymbol{u}} = \mathit{\boldsymbol{u}}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega ) - }\\ {\quad \quad {\kern 1pt} {\kern 1pt} k_0^2\int \mathit{\boldsymbol{G}} (\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}^\prime },\omega )\chi ({\mathit{\boldsymbol{x}}^\prime })\mathit{\boldsymbol{u}}({\mathit{\boldsymbol{x}}^\prime },{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega ){\rm{d}}{\mathit{\boldsymbol{x}}^\prime }} \end{array} $ | (11) |
I为单位矩阵;A为线性方程组的系数矩阵;
| $ \mathit{\boldsymbol{g}} = {\mathit{\boldsymbol{u}}_0} $ | (12) |
假设震源点坐标为zs,根据留数定理[21]可得常速度背景介质假设下一维频率域格林函数G的解析解
| $ G(z,{z_{\rm{s}}},\omega ) = \frac{{ - {\rm{i}}}}{{2{k_0}}} {\rm{exp}} ( - {\rm{i}}{k_0}|z - {z_{\rm{s}}}|) $ | (13) |
将空间网格离散为z1,z2,…,zn,可得格林函数的离散格式
| $ \mathit{\boldsymbol{G}} = \frac{{ - {\rm{i}}}}{{2{k_0}}}\left[ {\begin{array}{*{20}{c}} { {\rm{exp}} ( - {\rm{i}}{k_0}|{z_1} - {z_{\rm{s}}}|)}\\ { {\rm{exp}} ( - {\rm{i}}{k_0}|{z_2} - {z_{\rm{s}}}|)}\\ \vdots \\ { {\rm{exp}} ( - {\rm{i}}{k_0}|{z_n} - {z_{\rm{s}}}|)} \end{array}} \right] $ | (14) |
同样将空间z′离散为z′1,z′2,…,z′n,利用计算积分的矩形公式[22],可得正演算子L(χ)u的离散格式为
| $ \begin{array}{l} \mathit{\boldsymbol{L}}(\chi )\mathit{\boldsymbol{u}} = \frac{{ - {\rm{i}}{k_0}{\rm d}{z^\prime }}}{2}\left[ {\begin{array}{*{20}{l}} { {\rm{exp}} ( - {\rm{i}}{k_0}|{z_1} - z_1^\prime |)}&{ {\rm{exp}} ( - {\rm{i}}{k_0}|{z_1} - z_2^\prime |)}& \cdots &{ {\rm{exp}} ( - {\rm{i}}{k_0}|{z_1} - z_n^\prime |)}\\ { {\rm{exp}} ( - {\rm{i}}{k_0}|{z_2} - z_1^\prime |)}&{ {\rm{exp}} ( - {\rm{i}}{k_0}|{z_2} - z_2^\prime |)}& \cdots &{ {\rm{exp}} ( - {\rm{i}}{k_0}|{z_2} - z_n^\prime |)}\\ {}&{}& \vdots &{}\\ { {\rm{exp}} ( - {\rm{i}}{k_0}|{z_n} - z_1^\prime |)}&{ {\rm{exp}} ( - {\rm{i}}{k_0}|{z_n} - z_2^\prime |)}& \cdots &{ {\rm{exp}} ( - {\rm{i}}{k_0}|{z_n} - z_n^\prime |)} \end{array}} \right] \times \\ \quad \quad \quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {\chi (z_1^\prime )}&{}&{}&{}\\ {}&{\chi (z_2^\prime )}&{}&{}\\ {}&{}& \ddots &{}\\ {}&{}&{}&{\chi (z_n^\prime )} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {u(z_1^\prime )}\\ {u(z_2^\prime )}\\ \vdots \\ {u(z_n^\prime )} \end{array}} \right] \end{array} $ | (15) |
另外,数值积分具有可以对网格进行非等间距剖分的特点,因此可以根据速度的复杂情况更加合理地进行网格剖分,因此本文方法能更好地适应较复杂的速度模型。
常速度背景介质假设往往会导致波场旅行时的畸变。在均匀变化的速度背景介质假设下,基于WKBJ近似,格林函数G解析解为
| $ \begin{array}{*{20}{l}} {G(z,{z_{\rm{s}}},\omega )}\\ {\quad = \frac{1}{{2{\rm{i}}\sqrt {{k_0}(z){k_0}({z_{\rm{s}}})} }} {\rm{exp}} ( - {\rm{i}})\smallint _{{z_s}}^z|{k_0}({z^\prime })|{\rm{d}}{z^\prime })} \end{array} $ | (16) |
类似于常速度背景介质假设,可以得到均匀变化的速度背景介质下的离散形式格林函数G以及正演算子L。
至此,将式(8)的声波方程散射问题转化为如式(10)的大型线性方程组的求解问题。
由于离散的格林函数矩阵G是对称正定的,因此,考虑到系数矩阵A的对称性和正定性,引入稳定高效的最小二乘数值解法求解式(10),实现全波场的直接求解。最小二乘法通过最小化误差的平方和,寻找解的最佳函数匹配。引入目标函数
| $ \varphi (\mathit{\boldsymbol{u}}) = \left\| {\mathit{\boldsymbol{Au}} = \mathit{\boldsymbol{g}}} \right\|_2^2 $ | (17) |
当
| $ \mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{A}}^{ - 1}}\mathit{\boldsymbol{g}}{\rm{ 或 }}\mathit{\boldsymbol{u}} = {({\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}})^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{g}} $ | (18) |
由上式可知,进行声波方程正演时,在每个频率点处,基于数值积分的方法只需做一次矩阵的求逆运算。相比于Neumann级数迭代法,上述求解方法比较简洁,数值测试表明本文方法计算效率较高。
另外,当频率较高时,格林函数矩阵G的条件数往往较大,会造成数值计算的不稳定[23]。引入对角矩阵D=diag(A)作为预条件算子,求解DAu=Dg,而不是直接求解Au=g。则式(10)的最小二乘解为
| $ \mathit{\boldsymbol{u}} = {(\mathit{\boldsymbol{DA}})^{ - 1}}\mathit{\boldsymbol{Dg}} $ | (19) |
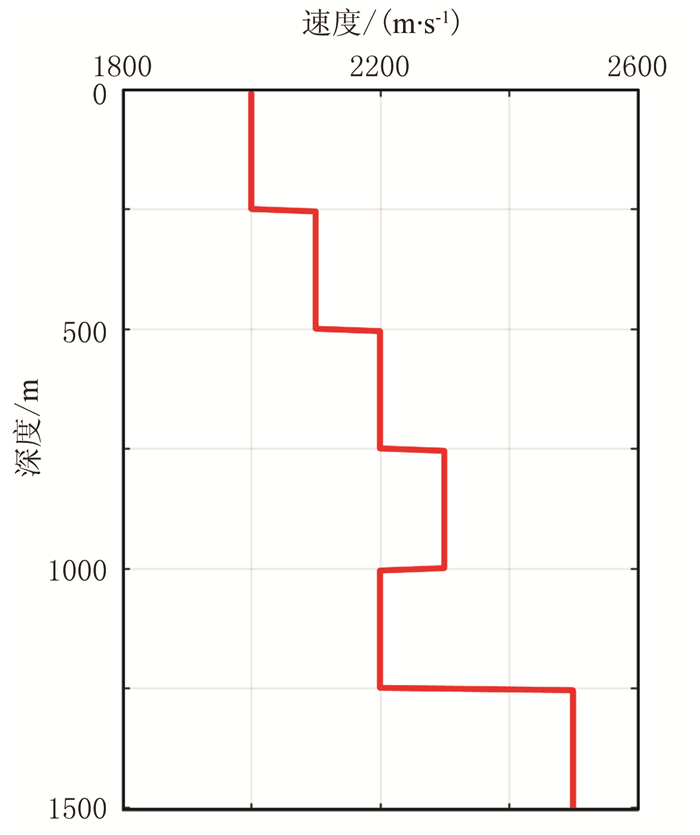
为了验证本文方法的有效性、可行性以及解的精确性,设计了一个如图 1所示的阶梯状速度模型。模型的深度采样间隔为5m,深度采样点数为301,正演采用主频为35Hz的零相位Ricker子波。记录长度为2.5s,时间采样间隔为2ms。在频率域,由背景速度计算格林函数G以及正演算子L。对0~250Hz的频率范围采用0.4Hz的频率间隔,分别利用上述预条件最小二乘方法和Neumann级数迭代方法求解,进行626次正演,得到频率域的全波场u,对其进行傅里叶反变换得到时间域的VSP全波场记录如图 2a所示(两种方法的计算结果相差无几,仅展示一个)。图中可见清晰的直达波和反射波,其后可见明显的多次波,说明该方法可以有效地模拟包括直达波、一次反射波以及多次波在内的完整的全波场信息。在同等软硬件配置条件下,表 1列出了本文的数值积分方法、Neumann级数迭代方法计算该阶梯状模型波场时的运算时间,可见本文的数值积分法在计算声波积分方程时具有相对较高的计算效率。
|
图 1 层状速度模型 |
|
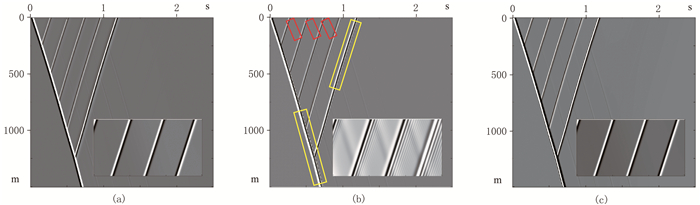
图 2 层状模型不同方法正演的零井源距VSP记录 (a)本文方法;(b)时间2阶、空间2阶有限差分法;(c)时间2阶、空间8阶有限差分法 |
|
|
表 1 不同方法的计算时间对比 |
为了说明本文方法计算精度的优势,与时间2阶、空间2阶差分法进行对比。采用10层完全匹配层吸收边界和相同的模拟参数,时间2阶、空间2阶交错网格有差分法正演的零井源距VSP全波场记录如图 2b所示。与图 2a相比,二者的旅行时信息和波形信息基本一致。但是,声波方程交错网格有限差分方法需要满足数值计算的稳定性条件
| $ \frac{{{v_{ {\rm{max}} }}\Delta t}}{{\Delta z}} \le \frac{1}{{\sum\limits_{m = 1}^M | {a_m}|}} $ | (20) |
式中:vmax为最大速度;am为2M阶空间差分算子系数[24]。
在相同的网格参数情况下,本文方法的计算结果不受数值频散以及人工边界反射的干扰,而有限差分方法正演受到选取的正演子波主频和网格参数的限制,计算的波场中存在严重的数值频散假象(图 2b中矩形黄框所示)。另外,由于PML吸收边界不能完全吸收到达边界的波场,因此波场中存在人工边界反射(图 2b中矩形红框所示); 而吸收效果更好的边界条件往往会导致计算量的增加[11]。对于图 1速度模型,保持空间采样间隔和时间总记录长度不变,减小时间采样间隔为0.5ms,采用300层完全匹配层吸收边界,时间2阶、空间8阶交错网格有限差分法正演结果如图 2c所示,可以较好地压制数值频散和边界反射。从VSP记录0.25~1.00s、0~250m范围的放大显示(图 2中小图)可见,图 2b中存在边界反射干扰和数值频散假象,而图 2a中则不见这些干扰,图 2c中的干扰得到了有效压制。
抽取图 2切除直达波后的第一个接收点的记录,如图 3所示,有5个(4个正相和1个负相)明显的反射波形。可以看出:三种方法正演结果的波峰到达时刻一致,但时间2阶、空间2阶有限差分法(红色实线)受到空间采样间隔和子波频率的限制,在每一个反射界面处,由于数值频散产生能量较强的续至波形;时间2阶、空间8阶有限差分方法(蓝色虚线)的结果能够有效压制频散现象。作为声波微分方程的解析解,对式(9)进行数值求解比用差分法对微分方程直接求解精度更高,但当空间采样点数相对较多时,数值计算相对耗时,可以根据不同的需求选用不同的数值求解方法。

|
图 3 层状模型不同方法正演结果的单道对比 黑色实线、红色实线和蓝色虚线分别为本文方法、声波方程时间2阶空间2阶有限差分法和时间2阶空间8阶有限差分法正演结果 |
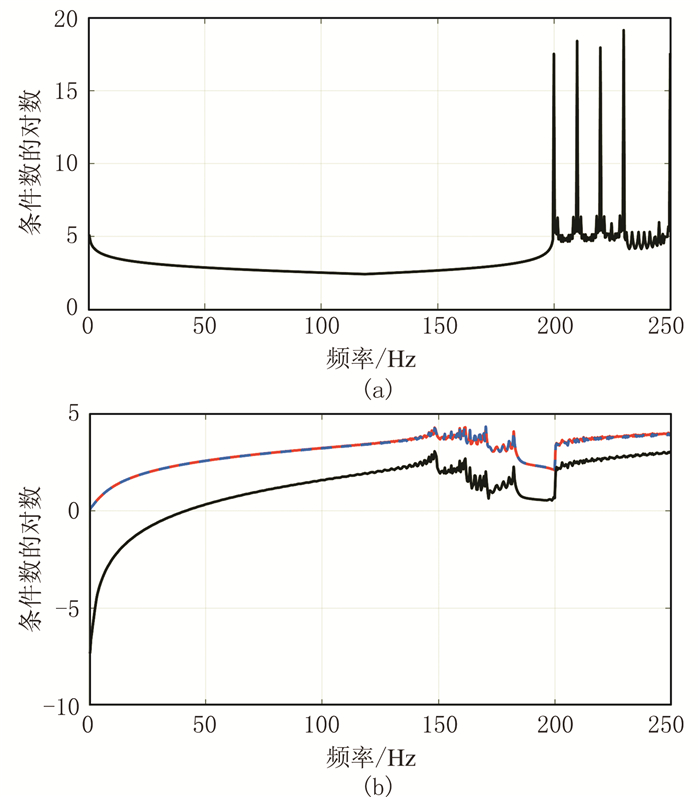
不同频率下格林函数矩阵G的条件数如图 4a所示,可见当正演频率较高时,格林函数矩阵G的条件数会存在一些异常大的值以及振荡。图 4b展示了矩阵A(红色虚线)和DA(蓝色实线)条件数的对数及二者之差的对数(黑色实线)随频率的变化情况。由图可知,在150Hz范围以内,随着频率的增加,条件数逐渐增大;在频率范围150~200Hz条件数变化比较剧烈;频率超过200Hz时,条件数逐渐增加,同时,二者条件数之差也有相似的规律。值得注意的是,频率较高时,矩阵DA比矩阵A的条件数大约减小了10%,亦即在理论上,引入预条件算子D小幅度提高了计算的稳定性。另外,在每个频率下,矩阵DA的条件数都大于0,根据条件数的定义
|
图 4 不同频率下三个矩阵的条件数 (a)格林函数矩阵G;(b)系数矩阵A(红色虚线)和系数矩阵DA(蓝色实线)及其差(黑色实线) |
| $ K(\mathit{\boldsymbol{A}}) \buildrel \Delta \over = \left\| \mathit{\boldsymbol{A}} \right\|\left\| {{\mathit{\boldsymbol{A}}^{ - 1}}} \right\| $ | (21) |
可知矩阵DA是满秩的。由矩阵论可知,应用D=Diag(A)作为预条件算子后,可以较好地保证解的一致性。
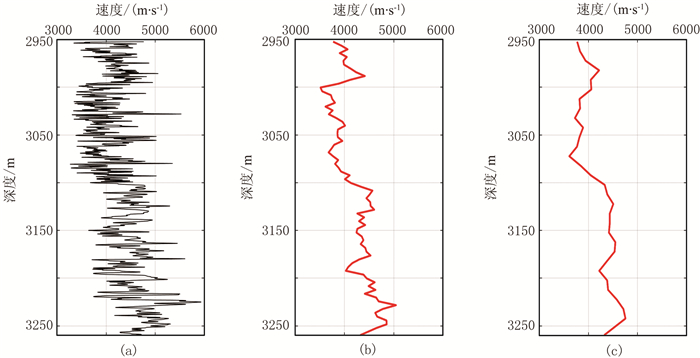
2.2 声波测井数据模型实际声波测井资料(图 5a)采样间隔为0.125m,井位处的地层倾角接近0°。应用Backus平均方法[25-26]获得间隔为4、10m重采样速度曲线(图 5b和图 5c)。
|
图 5 实际声波测井(a)及其4m(b)和10m(c)间隔重采样曲线 |
为了测试不同深度采样间隔对地震响应的影响,利用本文提出的预条件最小二乘方法求解两种采样间隔模型对应的波场。设置地震记录的时间长度为0.5s,采样间隔为2ms;正演采用主频为35Hz的零相位Ricker子波。在频率域,对0~250Hz的频率范围采用2Hz的频率间隔,进行126次正演,得到频率域的全波场,对其进行傅里叶反变换,得到时间域的零井源距VSP波场记录(图 6a和6b)。如果采用如上的网格参数,则有限差分法计算不稳定。减小时间采样间隔到0.5ms,记录长度为0.5s,采用50层的完全匹配层吸收边界,时间2阶、空间8阶有限差分法模拟的零井源距VSP波场记录如图 6c和6d所示。由图 6可见,如采用适当的有限差分网格参数以及适当层数的PML吸收边界,两种方法计算的波场基本一致,都很好地模拟了声波在实际介质中的传播,但较小深度采样间隔的速度模型对应的波场细节更加丰富。表 2展示了不同方法实现数值模拟波场时所需要的计算时间,可见,当空间采样点数比较小时,本文的数值积分法和有限差分法的计算效率非常接近。同时,本文的数值积分法的理论计算效率与网格参数的关系还有待进一步深入地研究。

|
图 6 实际测井数据速度模型两种方法计算的零井源距VSP记录 (a)采样间隔为4m,本文方法;(b)采样间隔为10m,本文方法;(c)采样间隔为4m,有限差分法;(d)采样间隔为10m,有限差分法 |
|
|
表 2 不同空间采用间隔两种方法模拟用时 |
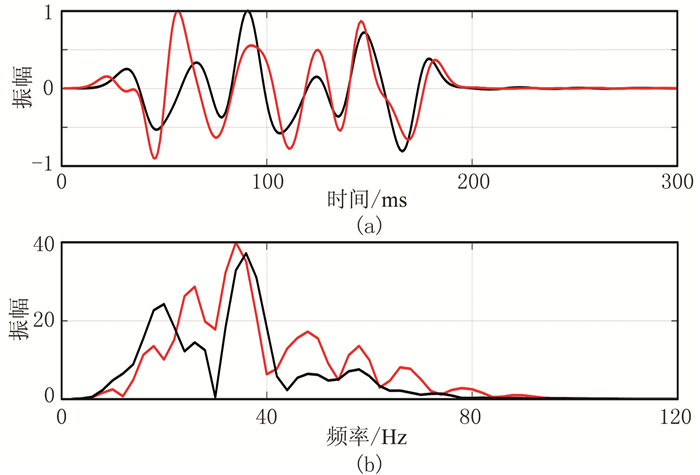
切除直达波之后,从图 6a与图 6b中分别抽取第一个接收点的记录并归一化,其波形、频谱分别如图 7所示。由图可见,当空间采样间隔为10m时,在地震有效频段内存在严重的陷频现象,并且缺少有效的中高频段信息;当空间采样间隔为4m时,在有效地震频段内,该频谱在中高频率段的信息更加完整和丰富。因此,对于相同的测井速度,重采样间隔较小的速度模型对应的地震记录具有更强的分辨能力。
|
图 7 空间采样间隔为10m(黑线)和4m(红线)本文方法模拟记录的单道波形(a)及其频谱(b)对比 |
基于声波散射理论,本文提出了一种精确求解声波方程得到零井源距VSP波场记录的数值计算方法。将声波微分方程推导为Lippman-Schwinger积分方程,再基于矩形积分公式,将其改写为矩阵相乘的形式,将Fredholm第二类积分方程的声波散射正问题转化为凸函数的最优化问题,借助预条件最小二乘方法实现了声波波场的稳定求解。
本文方法将Sommerfeld辐射边界条件引入积分公式推导中,因此不会在零井源距VSP波场中引入边界反射。同时不受子波频率和空间采样间隔的影响而产生数值频散,为后续进行高精度零井源距VSP波形反演奠定了较好的基础。
通过阶梯状速度模型和实际声波测井数据建立的速度模型,验证了方法的可行性和有效性。模型正演结果表明,本文提出的方法克服了有限差分方法求解声波微分方程时受限于频散条件和稳定性条件,以及人工边界吸收不完全的固有缺陷,具有明显的优势。
另外,其他可以增强计算稳定性或者提高解的精度以及计算效率的预条件算子值得进一步深入研究。将本文的方法推广到二维声波方程和弹性波方程,模拟非零井源距VSP波场,也是下一步的研究方向。
| [1] |
赵邦六, 董世泰, 曾忠. 井中地震技术的昨天、今天和明天——井中地震技术发展及应用展望[J]. 石油地球物理勘探, 2017, 52(5): 1112-1123. ZHAO Bangliu, DONG Shitai, ZENG Zhong. Borehole seismic deveplement, status quo and future:Application prospect of borehole seismic[J]. Oil Geophysical Prospecting, 2017, 52(5): 1112-1123. |
| [2] |
侯爱源, 李庆忠, 张文波. 复杂区深井VSP层析求速度场的方法[J]. 石油地球物理勘探, 2017, 52(6): 1150-1155. HOU Aiyuan, LI Qingzhong, ZHANG Wenbo. A method for velocity field with deep-well VSP tomography in complex areas[J]. Oil Geophysical Prospecting, 2017, 52(6): 1150-1155. |
| [3] |
高静怀, 汪超, 赵伟. 用于零偏移距VSP资料的自适应波形反演方法研究[J]. 地球物理学报, 2009, 52(12): 3091-3100. GAO Jinghuai, WANG Chao, ZHAO Wei. On the method of adaptive waveform inversion with zero-offset VSP data[J]. Chinese Journal of Geophysics, 2009, 52(12): 3091-3100. DOI:10.3969/j.issn.0001-5733.2009.12.018 |
| [4] |
Egorov A, Pevzner R, Bóna A, et al. Time-lapse full waveform inversion of vertical seismic profile data:Workflow and application to the CO2 CRC Otway project[J]. Geophysical Research Letters, 2017, 44(14): 7211-7218. DOI:10.1002/2017GL074122 |
| [5] |
韩璇颖, 印兴耀, 曹丹平, 等. 基于分段快速模拟退火的零偏VSP全波形反演[J]. 石油物探, 2019, 58(1): 103-111. HAN Xuanying, YIN Xingyao, CAO Danping, et al. Zero-offset VSP velocity inversion with FWI using segmented fast simulated annealing[J]. Geophysical Prospecting for Petroleum, 2019, 58(1): 103-111. DOI:10.3969/j.issn.1000-1441.2019.01.012 |
| [6] |
邹延延, 徐义贤, 沙椿. VSP正反演综述[J]. 地球物理学进展, 2009, 24(1): 145-153. ZOU Yanyan, XU Yixian, SHA Chun. Review on the forward modeling and inversion of vertical seismic profile[J]. Progress in Geophysics, 2009, 24(1): 145-153. |
| [7] |
杨飞龙, 孙渊, 李绪宣, 等. 基于高斯射线束的斜井VSP正演方法[J]. 地球物理学进展, 2014, 29(6): 2791-2799. YANG Feilong, SUN Yuan, LI Xuxuan, et al. Devia-ted hole VSP forward method based on the Gaussian beam[J]. Progress in Geophysics, 2014, 29(6): 2791-2799. |
| [8] |
金超, 曹丹平, 梁锴, 等.基于反射率法的VSP波场正演模拟[C].中国地球科学联合学术年会, 2017, 47-47.
|
| [9] |
Virieux J. P-SV wave propagation in heterogeneous media:Velocity-stress finite-difference method[J]. Geophysics, 1986, 51(4): 889-901. DOI:10.1190/1.1442147 |
| [10] |
陈可洋. 标量声波波动方程高阶交错网格有限差分法[J]. 中国海上油气, 2009, 21(4): 232-236. CHEN Keyang. High-order staggered-grid finite diffe-rence scheme for scalar acoustic wave equation[J]. China Offshore Oil and Gas, 2009, 21(4): 232-236. DOI:10.3969/j.issn.1673-1506.2009.04.004 |
| [11] |
蔡晓慧, 刘洋, 王建民, 等. 基于自适应优化有限差分方法的全波VSP逆时偏移[J]. 地球物理学报, 2015, 58(9): 3317-3334. CAI Xiaohui, LIU Yang, WANG Jianmin, et al. Full-wavefield VSP reverse-time migration based on the adaptive optimal finite-difference scheme[J]. Chinese Journal of Geophysics, 2015, 58(9): 3317-3334. |
| [12] |
Fokkema J T, van den Berg P M.Seismic Applica-tions of Acoustic Reciprocity[M].Elsevier, Amsterdam, 1993.
|
| [13] |
Lam C, Bakrac S, van den Berg P M, et al.On the background model for non-linear inversion of seismic data[C].SEG Technical Program Expanded Abstracts, 2006, 25: 2012-2016. https://www.researchgate.net/publication/240736722_On_the_background_model_for_non-linear_inversion_of_seismic_data
|
| [14] |
Yang J, Abubakar A, van den Berg P M, et al. A CG-FFT approach to the solution of a stress-velocity formulation of three-dimensional elastic scattering problems[J]. Journal of Computational Physics, 2008, 227(24): 10018-10039. DOI:10.1016/j.jcp.2008.07.027 |
| [15] |
Haffinger P, Gisolf A, van den Berg P M. Towards high resolution quantitative subsurface models by full waveform inversion[J]. Geophysical Journal International, 2013, 193(2): 788-797. DOI:10.1093/gji/ggt021 |
| [16] |
Abubakar A, van den Berg P M. Iterative forward and inverse algorithms based on domain integral equations for three-dimensional electric and magnetic objects[J]. Journal of Computational Physics, 2004, 195(1): 236-262. DOI:10.1016/j.jcp.2003.10.009 |
| [17] |
李杰, 缪竟鸿. 对比源反演算法在二维弹性波成像中的应用[J]. 系统工程与电子技术, 2012, 34(8): 1560-1564. LI Jie, MIAO Jinghong. Application of the contrast source inversion algorithm on 2-D elastic wave imaging[J]. Systems Engineering and Electronics, 2012, 34(8): 1560-1564. |
| [18] |
Kleinman R E, van den Berg P M. Iterative methods for solving integral equations[J]. Radio Science, 1991, 26(1): 175-181. DOI:10.1029/90RS00934 |
| [19] |
秦博.多维第二类Fredholm积分方程高精度数值算法研究[D].四川成都: 电子科技大学, 2015. QIN Bo.Research on High Precision Numerical Algorithm for Multidimensional Fredholm Integral Equation of the Second Kind[D].University of Electronic Science and Technology of China, Chengdu, Sichuan, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10614-1015707217.htm |
| [20] |
Fokkema J T, Van Den Berg P M. Stretched back-grounds for acoustic scattering models[J]. Journal of Computational Physics, 2012, 231(4): 1728-1742. DOI:10.1016/j.jcp.2011.11.002 |
| [21] |
陆晓. 一维Lippmann-Schwinger方程及其应用[J]. 大学物理, 2001, 20(2): 14-16. LU Xiao. One-dimensional Lippmann-Schwinger equation and its applications[J]. College Physics, 2001, 20(2): 14-16. |
| [22] |
张明. 应用数值分析[M]. 北京: 石油工业出版社, 2012. ZHANG Ming. Applied Numerical Analysis[M]. Beijing: Petroleum Industry Press, 2012. |
| [23] |
Saad Y.Iterative Methods for Sparse Linear Systems[M].SIAM, Philadelphia, 2003.
|
| [24] |
杨庆节, 刘财, 耿美霞, 等. 交错网格任意阶导数有限差分格式及差分系数推导[J]. 吉林大学学报(地球科学版), 2014, 44(1): 375-385. YANG Qingjie, LIU Cai, GENG Meixia, et al. Staggered grid finite difference scheme and coefficients deduction of any number of derivatives[J]. Journal of Jilin University(Earth Science Edition), 2014, 44(1): 375-385. |
| [25] |
Backus G E. Long-wave elastic anisotropy produced by horizontal layering[J]. Journal of Geophysical Research, 1962, 67(11): 4427-4440. DOI:10.1029/JZ067i011p04427 |
| [26] |
曹丹平. 基于Backus等效平均的测井资料尺度粗化方法研究[J]. 石油物探, 2015, 54(1): 105-111. CAO Danping. The upscaling method of the well logging data based on Backus equivalence average me-thod[J]. Geophysical Prospecting for Petroleum, 2015, 54(1): 105-111. DOI:10.3969/j.issn.1000-1441.2015.01.015 |



 颜红芹, 湖南省娄底市娄星区新星中路娄底职业技术学院, 417000。Email:
颜红芹, 湖南省娄底市娄星区新星中路娄底职业技术学院, 417000。Email: