② 大地测量与地球动力学国家重点实验室, 湖北武汉 430077;
③ 中国科学院大学, 北京 100049;
④ 东方地球物理公司物探技术研究中心, 河北涿州 072751
② State Key Laboratory of Geodesy and Earth's Dynamics, Wuhan, Hubei 430077, China;
③ University of Chinese Academy of Sciences, Beijing 100049, China;
④ Research & Development Center, BGP, CNPC, Zhuozhou, Hebei 072751, China
地震偏移成像技术是现今地震数据处理的核心技术之一,在油气资源探测中起重要作用[1]。勘探风险和勘探难度的不断加大使偏移成像的振幅保真受到重视[2-5],真振幅叠前深度偏移能获得更准确的地下介质物性参数信息,提高油气勘探精度。地震波真振幅偏移成像旨在得出能更准确地反映地下反射系数或介质参数扰动的成像振幅[6-7],从而能进行高精度储层反演。
研究表明,基于线性化反演理论的最小二乘偏移是实现真振幅成像的有效方法[8],也是今后保幅成像方法的发展趋势[9]。但因当前计算机硬件条件难以承受Hessian矩阵数量庞大的元素、迭代更新求解反问题的极高计算成本、Hessian算子难以精确求逆等,极大地限制了最小二乘偏移方法在此领域的推广应用[9]。作为最小二乘偏移成像特例的常规一次成像(即Hessian矩阵为单位阵)在实际数据成像处理中仍具现实意义。对于常规一次成像,真振幅偏移成像的本质是波场传播的准确模拟。
射线理论真振幅偏移成像的基本思想[1, 3, 6]是通过加权绕射叠加抵消波的传播引起的振幅变化,提高成像结果的准确性。射线理论中,基于射线雅可比计算输运方程解的方法给出了地震波沿射线的格林函数振幅表达式[3, 6, 10],该格林函数普遍存在于射线[11-19]及高斯束类偏移中[20-23]。因此,射线雅可比对于积分法真振幅偏移成像意义重大。
通常利用射线追踪计算射线雅可比。传统射线追踪方法旨在实现走时和射线路径的快速计算[24-27],较少涉及雅可比的计算,主要应用于块状构造模型的快速正演模拟。为适应叠前偏移成像的需求,新型网格类射线追踪方法不断涌现[28-31],按其基本原理可分为最短路径法[32-33]、有限差分法[34-35]和波前构建法[28, 36]等三种。最短路径法和有限差分法侧重于快速计算网格模型中单次波至走时。在保幅偏移成像处理中,需依赖走时场在空间上的二阶偏导数信息计算所涉及的波前几何扩散[37-40]。
Vanelle等[40]从计算效率和数据存储的角度对基于走时场计算波前几何扩散的方法做了系统研究,即从走时场平方的泰勒展开式出发,提出了基于双曲线走时插值计算波前几何扩散的方法。对于此双曲线走时插值方法,在存在多波至的复杂区域,走时场在空间的一阶偏导数和二阶偏导数均不连续(泰勒展开的条件不满足),通过插值系数得出的波前几何扩散因子与动力学射线追踪所得结果存在较大差异[40]。提高用双曲线走时插值方法计算波前扩散的精度需考虑多波至。然而,在用网格差分计算走时空间二阶偏导数时,多波至走时的利用十分复杂。基于走时场计算波前几何扩散的方法涉及走时场的空间二阶偏导数的计算[10],该二阶偏导数需根据网格节点上的走时进行差分数值计算而获得。网格节点上的走时精度通常不高,差分计算走时场的二阶偏导数不很准确,且难以较好地处理复杂区域多波至问题,因此这种依赖走时场空间二阶偏导数的方法不适合波前几何扩散的高精度计算[10]。
Popov等[41]最早提出计算波前几何扩散的动力学射线追踪系统,并将其广泛应用于波前构建法射线追踪的振幅计算和各种射线类保幅叠前深度偏移[12, 36, 41-42],在高斯束偏移中尤为常见[20-23]。动力学射线追踪通过求解动力学常微分方程组实现射线雅可比的计算[10, 41]。该方法基于射线一阶扰动理论[43]。在速度扰动较小的变速介质中,通过动力学射线追踪能快速有效地计算射线雅可比;但当速度扰动较大时,其空间上二阶导数很不稳定,这时动力学射线追踪求得的射线雅可比难以准确反映波前的实际变化,导致得到伪焦散点,遗漏真焦散点。
为实现更准确的射线雅可比计算以提高GRT逆散射偏移成像[6, 7, 44-45]精度,本文从射线雅可比定义出发[10],提出利用射线管横截面元直接数值计算的方法求取射线雅可比。即通过数值计算射线管横截面元与初始角面元二者的面积比得出射线雅可比,所得结果具有明确的物理意义,能准确识别射线上的真实焦散点。在逆散射保幅偏移成像条件中,权函数的分母项存在两个射线雅可比[6-7],射线的焦散会导致权函数奇异。为此,文中绘出一种合理的雅可比平滑阈值方法,避免了焦散引起的奇异问题。基于不同的速度模型,对动力学射线追踪和直接数值计算两种方法计算的射线雅可比进行了测试和比较。结果表明:在速度扰动较小的介质中,上述两种方法得出的射线雅可比一致;在速度扰动较大的介质中,动力学射线追踪难以获得较准确的射线雅可比,直接数值计算的射线雅可比则能准确地反映波前实际变化。最后将两种射线雅可比计算方法分别应用于盐丘模型的逆散射保幅偏移成像,直接数值计算法获得的成像剖面更清晰,进一步验证了射线雅可比直接数值计算法的有效性和适用性。
1 射线雅可比的定义与计算射线雅可比是射线的参数坐标与直角坐标之间转换的雅可比矩阵行列式,具有与射线管面元相关的物理定义[10],通常用J表示射线雅可比。在速度场具有连续的一阶和二阶偏导数的假设下,Popov等[41]基于扰动理论导出了计算射线雅可比的动力学射线追踪方程组,该方程组涉及两个传输矩阵P和Q的求解,其中以Q表示与波前几何扩散有关的射线雅可比矩阵、detQ表示射线雅可比。理论上,detQ=J,但速度模型复杂时,动力学射线追踪法计算的射线雅可比与物理定义的直接数值计算方法求得结果的差异不可忽略。这里讨论两种射线雅可比计算方法的原理,并分析各自的特点。
1.1 动力学射线追踪动力学射线追踪是计算射线雅可比、得出波前几何扩散和射线振幅的一种常用途径,它在射线及高斯束类保幅偏移成像中的应用十分普遍。动力学射线追踪满足以下微分方程组[41]
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}\mathit{\boldsymbol{P}}}}{{{\rm{d}}t}} = - \frac{1}{v}\mathit{\boldsymbol{VQ}}}\\ {\frac{{{\rm{d}}\mathit{\boldsymbol{Q}}}}{{{\rm{d}}t}} = {v^2}\mathit{\boldsymbol{Q}}} \end{array}} \right. $ | (1) |
式中:v为介质的波速;t为时间;P和Q是与波前几何扩散有关的传输矩阵,其中P的初值通常取为v0-1I(I为单位矩阵),Q的初值为0;V是射线中心坐标系下速度的二阶偏导数构成的矩阵
| $ \mathit{\boldsymbol{V}} = \left( {\begin{array}{*{20}{l}} {{v_{,nn}}}&{{v_{,nm}}}\\ {{v_{,nm}}}&{{v_{,mm}}} \end{array}} \right) $ | (2) |
式中m和n表示与中心射线垂直的平面坐标。
设et、em和en为构成射线中心坐标系的一组正交基向量,且这三个基向量依次表示中心射线的单位切向量(倾角和方位角分别为θ和φ)、m坐标的单位切向量和n坐标的单位切向量,则这组正交基向量可由θ和φ表示为
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{e}}_t} = {{( {\rm{sin}} \theta {\rm{cos}} \varphi , {\rm{sin}} \theta {\rm{sin}} \varphi , {\rm{cos}} \theta )}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{e}}_n} = {{( {\rm{cos}} \theta {\rm{cos}} \varphi , {\rm{cos}} \theta {\rm{sin}} \varphi , - {\rm{sin}} \theta )}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{e}}_m} = {{( - {\rm{sin}} \varphi , {\rm{cos}} \varphi ,0)}^{\rm{T}}}} \end{array}} \right. $ | (3) |
进而可得式(2)的矩阵V中各个二阶偏导数的具体表达式为
| $ \left\{ \begin{array}{l} {v_{,nn}} = \frac{{{\partial ^2}v}}{{\partial {x^2}}}{( {\rm{cos}} \theta {\rm{cos}} \varphi )^2} + \frac{{{\partial ^2}v}}{{\partial {y^2}}}{( {\rm{cos}} \theta {\rm{sin}} \varphi )^2} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\partial ^2}v}}{{\partial {z^2}}} {\rm{sin}}{ ^2}\theta + 2\frac{{{\partial ^2}v}}{{\partial x\partial y}} {\rm{cos}}{ ^2}\theta {\rm{sin}} \varphi {\rm{cos}} \varphi - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2 {\rm{sin}} \theta {\rm{cos}} \theta (\frac{{{\partial ^2}v}}{{\partial x\partial z}} {\rm{cos}} \varphi + \frac{{{\partial ^2}v}}{{\partial y\partial z}} {\rm{sin}} \varphi )\\ {v_{,mm}} = \frac{{{\partial ^2}v}}{{\partial {x^2}}} {\rm{sin}}{ ^2}\varphi + \frac{{{\partial ^2}v}}{{\partial {y^2}}} {\rm{cos}}{ ^2}\varphi - 2 {\rm{sin}} \varphi {\rm{cos}} \varphi \frac{{{\partial ^2}v}}{{\partial x\partial y}}\\ {v_{,mn}} = cos \theta {\rm{sin}} \varphi {\rm{cos}} \varphi (\frac{{{\partial ^2}v}}{{\partial {y^2}}} - \frac{{{\partial ^2}v}}{{\partial {x^2}}}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{cos}} \theta ( {\rm{cos}}{ ^2}\varphi - {\rm{sin}}{ ^2}\varphi )\frac{{{\partial ^2}v}}{{\partial x\partial y}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} sin \theta ( sin \varphi \frac{{{\partial ^2}v}}{{\partial x\partial z}} - cos \varphi \frac{{{\partial ^2}v}}{{\partial y\partial z}}) \end{array} \right. $ | (4) |
二维介质中,P和Q分别退化为标量p(初值为v0-1)和标量q (初值为0),式(1)蜕变为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}p}}{{{\rm{d}}t}} = - \frac{{{v_{,nn}}}}{v}q}\\ {\frac{{{\rm{d}}q}}{{{\rm{d}}t}} = {v^2}p} \end{array}} \right. $ | (5) |
此时
| $ {v_{,nn}} = \frac{{{\partial ^2}v}}{{\partial {x^2}}} {\rm{cos}}{ ^2}\theta - {\rm{sin}} 2\theta \frac{{{\partial ^2}v}}{{\partial x\partial z}} + \frac{{{\partial ^2}v}}{{\partial {z^2}}} {\rm{sin}}{ ^2}\theta $ |
Q反映波前的几何扩散情况。式(1)基于射线的一阶扰动理论,介质的速度扰动较小时,根据该式进行动力学射线追踪能够较准确地得出波场的动力学信息;当介质的速度场复杂时,二阶导数矩阵V变化较大,得出的动力学参数也会不稳定和不准确。在保幅叠前深度偏移成像中,为了使计算的射线振幅更稳定,通常会将速度场的二阶导数进行一定的限制,比如直接将其设置为零,但这样的处理不利于成像振幅保真。
1.2 射线雅可比的直接数值计算射线雅可比是表示射线上点的射线参数坐标γ1,γ2,u与广义笛卡尔坐标x,y,z之间转换的行列式。γ1和γ2为决定射线初始入射角的射线参数,u为沿着射线的单调参数,u通常为射线长度s或时间T。从射线参数坐标到笛卡尔坐标转换的雅可比行列式为[10]
| $ \begin{array}{l} {J^{(u)}} = \frac{{\partial (x,y,z)}}{{\partial ({\gamma _1},{\gamma _2},u)}} = \left| {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial {\gamma _1}}}}&{\frac{{\partial x}}{{\partial {\gamma _2}}}}&{\frac{{\partial x}}{{\partial u}}}\\ {\frac{{\partial y}}{{\partial {\gamma _1}}}}&{\frac{{\partial y}}{{\partial {\gamma _2}}}}&{\frac{{\partial y}}{{\partial u}}}\\ {\frac{{\partial z}}{{\partial {\gamma _1}}}}&{\frac{{\partial z}}{{\partial {\gamma _2}}}}&{\frac{{\partial z}}{{\partial u}}} \end{array}} \right|\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{1}{{{g_u}}}\left| {\begin{array}{*{20}{l}} {{{(\frac{{\partial x}}{{\partial {\gamma _1}}})}_u}}&{{{(\frac{{\partial x}}{{\partial {\gamma _2}}})}_u}}&{{e_x}}\\ {{{(\frac{{\partial y}}{{\partial {\gamma _1}}})}_u}}&{{{(\frac{{\partial y}}{{\partial {\gamma _2}}})}_u}}&{{e_y}}\\ {{{(\frac{{\partial z}}{{\partial {\gamma _1}}})}_u}}&{{{(\frac{{\partial z}}{{\partial {\gamma _2}}})}_u}}&{{e_z}} \end{array}} \right| \end{array} $ | (6) |
式中:J(u)表示关于参数u的雅可比;ex、ey和ez为射线的单位切向量e在笛卡尔坐标系下的三个分量。令
| $ {J^{(u)}} = \frac{1}{{{g_u}}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^{(u)}} \cdot \mathit{\boldsymbol{e}} $ | (7) |
式中:
| $ J = {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^{(u)}} \cdot \mathit{\boldsymbol{e}} $ | (8) |
于是,可根据
| $ J = {g_u}{J^{(u)}} = {J^{(s)}} = {g_T}{J^{(T)}} $ | (9) |
计算关于任意参数u的雅可比J(u)(u = T,s)。
根据矢量微分可得
| $ {\rm{d}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^{(u)}} = {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^{(u)}}{\rm{d}}{\gamma _1}{\rm{d}}{\gamma _2} $ | (10) |
式中:dΩ(u)表示射线管截等u面的矢量微元面;dγ1、dγ2为初始入射角微元面。当u=T时,矢量微元面有着明确的物理意义,这时dΩ(u)=dΩ(T)表示射线管截波前面的矢量微元面。dΩ(T)在射线雅可比J的计算中起着关键作用。
联合式(7)、式(9)和式(10),可得
| $ J = {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^{(T)}} \cdot \mathit{\boldsymbol{e}} = \frac{{{\rm{d}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^{(T)}} \cdot \mathit{\boldsymbol{e}}}}{{{\rm{d}}{\gamma _1}{\rm{d}}{\gamma _2}}} = \frac{{(\mathit{\boldsymbol{e}} \cdot \mathit{\boldsymbol{N}}){\rm{d}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^{(T)}}}}{{{\rm{d}}{\gamma _1}{\rm{d}}{\gamma _2}}} $ | (11) |
式中:N是垂直于波前面的单位法向量;dΩ(T)的单位向量为±N,且有dΩ(T)=dΩ(T)·N。
由于e为射线的单位切向量,N为波前面单位法向量,因此e·N=vp/vg,其中vp为相速度,vg为群速度。以有限差分代替式(11)中微分,得到基于射线管面元的射线雅可比直接数值计算方法
| $ J = \frac{{{v_{\rm{p}}}\Delta {S^{(T)}}}}{{{v_{\rm{g}}}\Delta \varOmega }} $ | (12) |
式中:ΔS(T)表示T时刻射线管截波前面的横截面元;ΔΩ表示射线管初始角面元,该初始角面元是射线管初始切线构成的圆锥侧面截单位球面所得面元。
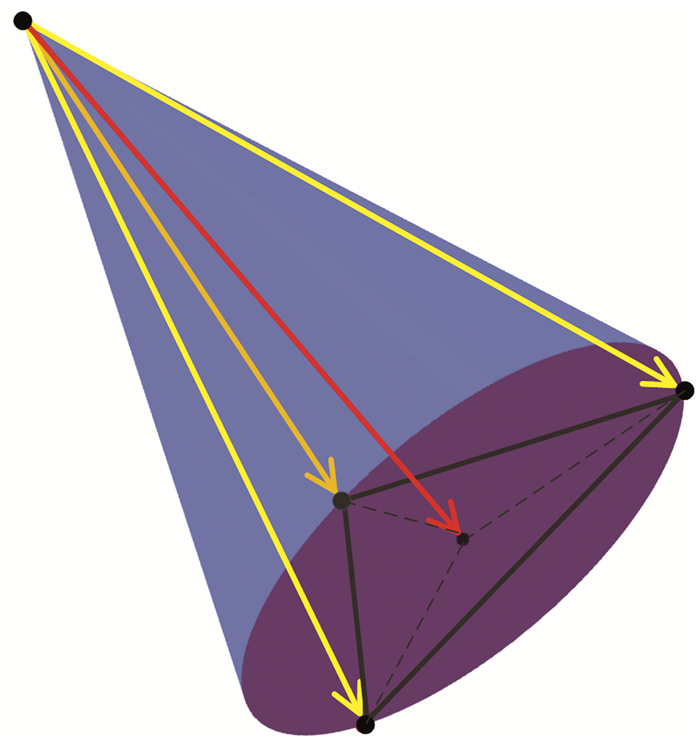
式(12)中初始角面元的数值计算可通过计算一个侧棱长为一个单位的正三棱锥的底面面积实现,图 1是初始角面元面积数值计算示意图。设中心射线的初始切向量与辅助射线的初始切向量夹角(图 1中红色向量与黄色向量夹角)为θless(为小量),由空间几何知识易得中心射线对应的射线管初始角面元面积(圆锥底面上的正三角形面积)为
|
图 1 初始角面元计算示意图 圆锥顶点代表炮点;红色向量(所在直线为圆锥轴)代表中心射线的初始入射切向量;三个黄色的单位向量(终点构成正三角形)代表三条辅助射线的初始入射切向量 |
| $ \Delta \varOmega = \frac{{3\sqrt 3 }}{4} {\rm{sin}}{ ^2}{\theta _{{\rm{less}}}} $ | (13) |
基于上式,式(12)中ΔS(T)表示图 1中以黄色的向量为初始切向量的三条辅助的射线在T时刻的三个端点构成的三角形面积。在二维介质情况下,需要计算两条辅助的射线路径,式(12)中的面元ΔS(T)和角面元ΔΩ分别退化为线元和初始角元(两条辅助射线的初始切线截单位圆所得的弧长)。
式(12)很好地避免了动力学射线追踪(式(1))计算波前几何扩散涉及到的速度场二阶偏导数不稳定问题,是具有明确物理意义的射线雅可比数值计算方法,求得的结果具有很好的准确性和稳定性。式(12)不仅能够较好地应用于各向同性介质背景下射线雅可比的计算,而且还能够很好地适应各向异性介质背景下波前几何扩散和振幅的计算,可有效避免求解复杂的各向异性动力学射线追踪方程组中存在的简化计算和不准确问题。
2 两种射线雅可比计算方法的比较射线雅可比既可为正,也可为负,还可以为零。雅可比为零表示射线族产生交叉,局部波前面汇聚成一点,这样的点称为焦散点。对相同的射线,分别应用动力学射线追踪方法和直接数值计算方法计算射线雅可比,通过得出的雅可比曲线及其射线族展开,比较两种方法的准确性。
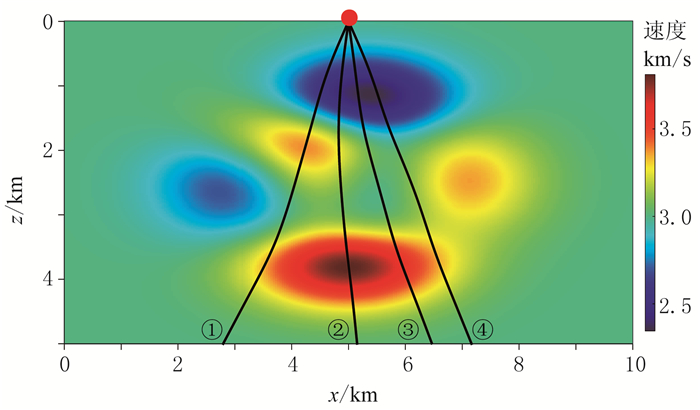
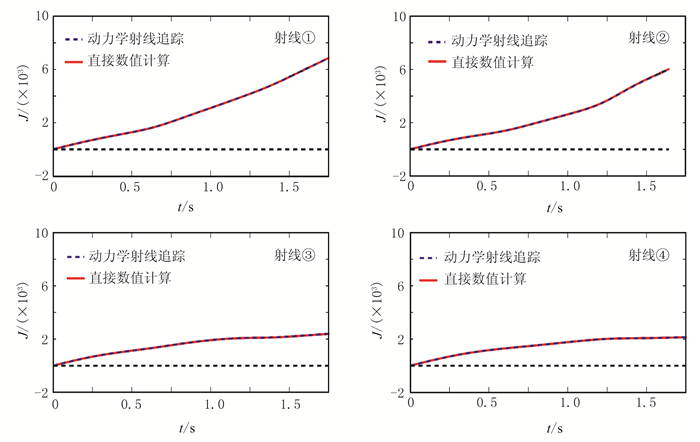
图 2为设计的变化较平缓的速度模型及以该模型背景计算的4条射线,模型的横向和深度方向均有251个采样点,横向采样间隔为40m,深度方向采样间隔为20m,炮点在地表横向第126个采样点上,从左到右四条射线的入射角分别为-27°、-9°、9°、27°。图 3给出了两种方法求得的4条射线随时间变化的雅可比曲线。在图 3的4个子图中,蓝色虚线是基于动力学射线追踪方法计算的结果,红色实线是基于直接数值计算方法计算的结果,二者重合。可见对于每条射线,动力学射线追踪与直接数值计算两种方法得出的射线雅可比相同。
|
图 2 速度分布及对应的4条射线(标号为①~④) |
|
图 3 对应图 2中的4条射线两种方法计算的雅可比曲线 |
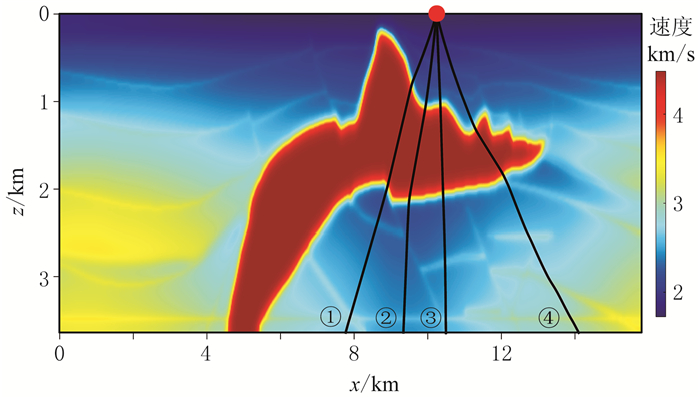
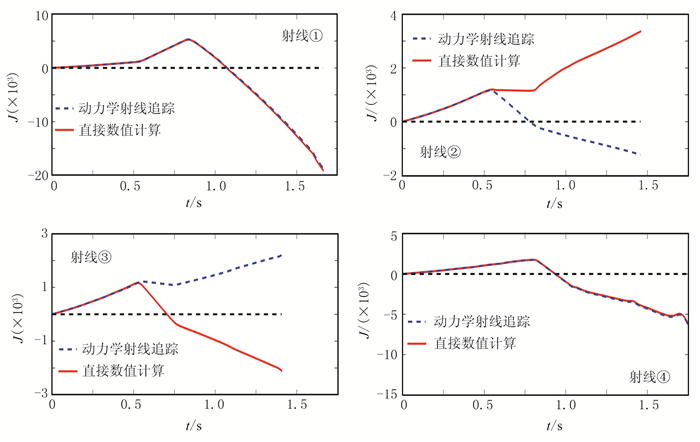
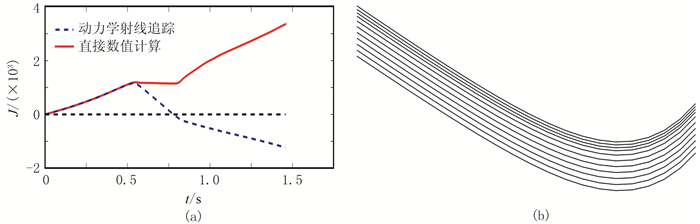
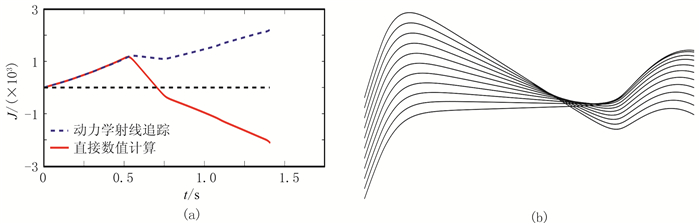
图 4给出了盐丘速度模型和以该模型为背景计算的4条射线,模型横向有649个采样点,采样间隔为24.384m(80ft),深度方向有300个采样点,采样间隔为12.192m(40ft)。射线追踪的炮点位于地表横向第421个采样点上,从左到右4条射线的入射角分别为-36°、-13.5°、5.2°、31.5°。图 5给出了应用两种方法求得的4条射线的雅可比曲线。在图 5的4个子图中,蓝色的虚线是动力学射线追踪方法计算的结果,红色的实线是直接数值计算方法计算的结果。可见射线①的两条雅可比曲线与射线④的两条雅可比曲线仍具有较好的一致性,射线②和射线③的各两条雅可比曲线均呈现出较大的偏差。对于射线②,动力学射线追踪方法计算的雅可比曲线经过了原点以外的零点,直接数值计算方法计算的雅可比曲线没有经过原点以外的零点。为更好地分析射线②两种方法计算的雅可比的差异,以这条射线为中心进行射线族展开,图 6为两种方法计算的雅可比曲线(图 6a)及其射线族(图 6b)。在[-13.7°,-13.3°]内以0.04°的采样间隔给定了11个入射角计算得出的射线族(射线族所在的时间段包括0.75s以后图 6a中蓝色曲线的零点所在时刻),从图 6b中的射线族可以看出,这个射线族中的射线没有产生交叉,表明射线上实际并不存在焦散点。因此,图 6a中正确的雅可比曲线不应该经过原点以外的零点,动力学射线追踪方法计算的雅可比得出了伪焦散点,与实际不符,直接数值计算方法计算的结果更准确。与图 6相反,图 7为图 4中射线③两种方法计算的雅可比曲线(图 7a)及其射线族展开(图 7b),射线族中产生的交叉现象是射线上存在焦散点的典型特征。因此,图 7a中正确的雅可比曲线应该经过原点以外的零点,图中可见动力学射线追踪方法计算的雅可比曲线未能经过原点以外的零点,直接数值计算方法计算的雅可比则准确识别出了焦散点。
|
图 4 速度分布及4条射线(标号为①~④)位置 |
|
图 5 对应图 4中的4条射线两种方法计算的雅可比曲线 |
|
图 6 中心射线②的雅可比曲线(a)及其射线族展开(b,射线族上不存在焦散点) |
|
图 7 中心射线③的雅可比曲线(a)及其射线族展开(b,射线族上存在焦散点) |
由以上测试结果可知,对于介质速度扰动较小的情况,两种射线雅可比计算方法获得的雅可比曲线能很好地符合。当介质速度变化较大时,速度场的二阶偏导数不稳定,动力学射线追踪计算的射线雅可比难以保证准确性;这时基于物理定义的射线雅可比直接数值计算方法无需计算速度场的二阶偏导数,求得的雅可比具有更好的稳定性和准确性。
由于射线雅可比的直接数值计算方法需要额外计算辅助的射线路径(二维介质需要计算两条辅助射线,三维介质需要计算三条辅助射线),因此,计算效率较动力学射线追踪稍有降低,但在可接受的范围内。表 1给出了图 2的二维介质中相同的参数下两种射线雅可比计算方法的耗时,可见,两种方法的计算效率在同一个数量级。
|
|
表 1 二维介质中两种射线雅可比计算方法的耗时 |
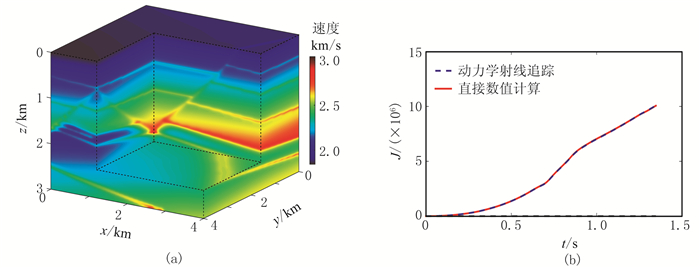
图 8为三维介质的速度剖面显示(左)及其中一条射线基于两种方法计算的雅可比曲线(右),表 2给出了该图中相同的参数下两种射线雅可比计算方法的耗时,可见,三维情况下两种方法的计算效率也在同一个数量级。
|
图 8 三维速度剖面(a)与其中的一条射线基于两种方法计算的射线雅可比曲线(b) |
|
|
表 2 三维介质中两种射线雅可比计算方法的耗时 |
无论是动力学射线追踪还是直接数值计算,求取射线追踪表的计算耗时相对整个偏移成像的耗时来说是很小的,两种雅可比计算方法在计算效率上的差异可以忽略。对于基于物理定义的直接数值计算方法,控制中心射线初始切向量与辅助射线的初始切向量夹角θless充分小(通常可设为0.001°~0.005°),能够很好地保证中心射线与辅助射线的一致性。在一些较极端的情况下,即使对于很小的θless,辅助射线可能也会出现较大的偏折,导致射线族失去一致性,这是介质复杂时运动学射线追踪计算的射线场存在固有的“阴影区”引起的,不是直接数值计算方法本身的问题;对于这种很极端的情况,射线雅可比的较准确计算涉及更加复杂的射线理论。
基于射线雅可比的直接数值计算方法具有明确的物理意义,避免了动力学射线追踪涉及的不稳定的速度场空间二阶偏导数的计算。直接数值计算方法求得的射线雅可比能够更好地反映波前的变化,准确识别出真正的焦散点,通过对雅可比进行合理的阈值能够有效避免保幅叠前深度偏移中焦散引起的奇异问题。
3 逆散射保幅偏移成像射线雅可比的计算对于GRT逆散射保幅偏移成像非常重要,该雅可比是其真振幅成像条件的组成部分[6-7, 44-45],复杂介质中射线雅可比计算的准确性会影响成像。将射线雅可比的直接数值计算方法应用到逆散射保幅偏移成像,对比根据动力学射线追踪得到的成像结果,进一步说明雅可比直接数值计算方法的有效性与适用性。
3.1 GRT逆散射保幅偏移成像基本原理根据散射理论,地下介质被分解成背景介质和扰动介质,地表记录的散射波场是入射波场作用于扰动介质的产物。在一阶Born近似的条件下,用波场振幅的射线理论解代替格林函数,地表的声波散射场满足以下积分方程[6]
| $ \begin{array}{*{20}{l}} {{U_\rm s}(\mathit{\boldsymbol{s}},\mathit{\boldsymbol{r}},t) = - {\partial _t}\int_D {\rm{d}} \mathit{\boldsymbol{x}}f(\mathit{\boldsymbol{x}})A(\mathit{\boldsymbol{s}},\mathit{\boldsymbol{x}},\mathit{\boldsymbol{r}}) \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta [t - \phi (\mathit{\boldsymbol{s}},\mathit{\boldsymbol{x}},\mathit{\boldsymbol{r}})]} \end{array} $ | (14) |
式中:Us是散射波场;f(x)=[c(x)/c0(x)]-2-1是表征平方慢度扰动的散射位,其中c0-2(x)是背景平方慢度,c-2(x)是真实平方慢度;A(s,x,r)是射线总振幅与背景平方慢度的乘积;ф(s,x,r)是射线总旅行时, 其中s是炮点,r是检波点,x是成像点;D表示地表。将广义Radon反变换算子R*作用于地表散射波场记录,可得到以下成像条件[6]
| $ \begin{array}{*{20}{l}} {I(\mathit{\boldsymbol{x}}) = ({\mathit{\boldsymbol{R}}^*}{U_\rm s})(\mathit{\boldsymbol{x}})}\\ {\quad = \frac{1}{{{\mathsf{π} ^2}}}\int {\rm{d}} \mathit{\boldsymbol{s}}\int {\rm{d}} \mathit{\boldsymbol{r}}B(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}},\mathit{\boldsymbol{r}}){U_\rm s}[\mathit{\boldsymbol{s}},\mathit{\boldsymbol{r}},\phi (\mathit{\boldsymbol{s}},\mathit{\boldsymbol{x}},\mathit{\boldsymbol{r}})]} \end{array} $ | (15) |
| $ B(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}},\mathit{\boldsymbol{r}}) = \frac{{ {\rm{co}}{{\rm{s}}^3} \frac{{{\theta _{ {\rm{mig}} }}}}{2} {\rm{cos}} {\theta _{\rm{s}}} {\rm{cos}} {\theta _{\rm{r}}}}}{{{c_0}(\mathit{\boldsymbol{x}})\sqrt {J(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}})J(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{r}})} }} $ | (16) |
式中:B为权函数;J(x, s)与J(x, r)分别为炮点到成像点的射线雅可比与检波点到成像点的射线雅可比;θmig为成像点的偏移张角;θs为炮点的射线倾角;θr为检波点的射线倾角;c0(x)为成像点的声波速度。权函数B的分母中存在两个射线雅可比,在焦散点处雅可比为零,权函数奇异。为避免焦散引起的奇异值问题,给出以下雅可比平滑阈值处理方案
| $ \left\{ {\begin{array}{*{20}{l}} {{J^\prime }(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{r}}) = J(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{r}}) + \varepsilon {J_{{\rm{d}}t}}(\mathit{\boldsymbol{r}})}\\ {{J^\prime }(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}}) = J(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}}) + \varepsilon {J_{{\rm{d}}t}}(\mathit{\boldsymbol{s}})} \end{array}} \right. $ | (17) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {{J_{{\rm{d}}t}}(\mathit{\boldsymbol{r}}) = {v_0}(\mathit{\boldsymbol{r}}){\rm{d}}t}\\ {{J_{{\rm{d}}t}}(\mathit{\boldsymbol{s}}) = {v_0}(\mathit{\boldsymbol{s}}){\rm{d}}t} \end{array}} \right. $ | (18) |
式中:v0(s)与v0(r)分别为炮点与检波点的波速;dt为射线追踪的时间采样间隔;Jdt(s)和Jdt(r)分别为关于炮点与检波点的基准雅可比;ε为雅可比阈值参数(通常设为0.1%~1.0%);J′为平滑阈值处理后的雅可比。以J′代替J,则式(16)变为
| $ B(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}},\mathit{\boldsymbol{r}}) = \frac{{ {\rm{co}}{{\rm{s}}^3} \frac{{{\theta _{{\rm{mig}}}}}}{2} {\rm{cos}} {\theta _{\rm{s}}} {\rm{cos}} {\theta _{\rm{r}}}}}{{{c_0}(\mathit{\boldsymbol{x}})\sqrt {{J^\prime }(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}}){J^\prime }(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{r}})} }} $ | (19) |
式(19)能够克服在焦散点附近过小的J引起的奇异问题。另外,当J较大时,J′→J,保证了非焦散区域计算结果的准确性。
3.2 偏移成像数值试验分别将基于动力学射线追踪和直接数值计算方法求取的射线雅可比
应用于SEG/EAGE盐丘模型(其各种参数均与图 4对应参数相同)的偏移成像。总计模拟了325炮的地震数据,炮间距为48.768m(160ft),每炮2593道接收,道间距为6.096m(20ft)。从基于动力学射线追踪方法计算射线雅可比获得的成像剖面(图 9a)可看出,在盐丘的内部和下方出现了一些离散的随机噪声。将基于直接数值计算方法计算射线雅可比获得的成像剖面(图 9b)与图 9a对比,可见随机噪声得到了很好的压制,获得了更清晰的成像剖面。因此,直接数值计算方法在复杂介质中的射线雅可比计算具有更强适应性。

|
图 9 基于动力学射线追踪(a)和直接数值计算(b)两种射线雅可比求取方法所得逆散射保幅偏移成像剖面(左)及局部放大(右) |
射线雅可比在计算波前几何扩散因子和射线格林函数振幅的过程中起到了关键的作用。该雅可比对于基于射线理论的真振幅偏移成像意义重大,是GRT逆散射偏移真振幅成像条件权函数的组成部分。在复杂介质中,速度场的二阶偏导数变化较大,动力学射线追踪计算的雅可比不准确,难以识别真正的焦散点,会导致形成伪焦散点。为更好地实现GRT逆散射保幅偏移成像,本文研究了更准确的射线雅可比计算方法,从其物理定义出发,利用射线管的横截面元直接数值计算的方法求取射线雅可比。直接数值计算方法避免了速度场二阶偏导数的计算,得出的雅可比更稳定,能够准确地识别出真正的焦散点。同时,给出了一种合理的雅可比平滑阈值方法,避免了叠前深度保幅偏移中焦散点处的奇异问题。将两种计算射线雅可比的方法分别应用到逆散射保幅偏移成像,直接数值计算获得了更清晰的成像剖面,进一步验证了射线雅可比直接数值计算方法的有效性与适用性。
| [1] |
李振春. 地震偏移成像技术研究现状与发展趋势[J]. 石油地球物理勘探, 2014, 49(1): 1-21. LI Zhenchun. Research status and development trends for seismic migration technology[J]. Oil Geophysical Prospecting, 2014, 49(1): 1-21. |
| [2] |
岳玉波, 李振春, 钱忠平, 等. 复杂地表条件下保幅高斯束偏移[J]. 地球物理学报, 2012, 55(4): 1376-1383. YUE Yubo, LI Zhenchun, QIAN Zhongping, et al. Amplitude-preserved Gaussian beam migration under complex topographic conditions[J]. Chinese Journal of Geophysics, 2012, 55(4): 1376-1383. DOI:10.6038/j.issn.0001-5733.2012.04.033 |
| [3] |
徐升, Lambaré G. 复杂介质下保真振幅Kirchhoff深度偏移[J]. 地球物理学报, 2006, 49(5): 1431-1444. XU Sheng, Lambaré G. True amplitude Kirchhoff prestack depth migration in complex media[J]. Chinese Journal of Geophysics, 2006, 49(5): 1431-1444. DOI:10.3321/j.issn:0001-5733.2006.05.022 |
| [4] |
李斐, 吕彬, 王宇超, 等. 裂步傅里叶真振幅叠前深度偏移[J]. 石油地球物理勘探, 2008, 43(4): 387-390. LI Fei, LYU Bin, WANG Yuchao, et al. Split-step Fourier true amplitude prestack depth migration[J]. Oil Geophysical Prospecting, 2008, 43(4): 387-390. DOI:10.3321/j.issn:1000-7210.2008.04.005 |
| [5] |
Thierry P, Lambaré G, Podvin P, et al. 3-D preserved amplitude prestack depth migration on a workstation[J]. Geophysics, 1999, 64(1): 222-229. |
| [6] |
Beylkin G, Burridge R. Linearized inverse scatte-ring problems in acoustic and elasticity[J]. Wave Motion, 1990, 12(1): 15-52. DOI:10.1016/0165-2125(90)90017-X |
| [7] |
Li W Q, Mao W J, Li X L, et al. Angle-domain inverse scattering migration/inversion in isotropic media[J]. Journal of Applied Geophysics, 2018, 154: 196-209. DOI:10.1016/j.jappgeo.2018.05.006 |
| [8] |
陈云峰, 王华忠, 任浩然, 等. 线性反演最小二乘叠前偏移的矩阵形式解析[J]. 石油地球物理勘探, 2014, 49(6): 1091-1096. CHEN Yunfeng, WANG Huazhong, REN Haoran, et al. Matrix representation of least square prestack migration based on linearization[J]. Oil Geophysical Prospecting, 2014, 49(6): 1091-1096. |
| [9] |
李江, 李庆春, 张向辉. 最小二乘偏移方法研究进展综述[J]. 地球物理学进展, 2016, 31(4): 1601-1607. LI Jiang, LI Qingchun, ZHANG Xianghui. Overview of progress in least squares migration studying[J]. Progress in Geophysics, 2016, 31(4): 1601-1607. |
| [10] |
Červený V. Seismic Ray Theory[J]. Cambridge University Press, 2001. |
| [11] |
Operto M S, Xu S, Lambaré G. Can we quantitatively image complex structures with rays?[J]. Geophysics, 2000, 65(4): 1223-1238. |
| [12] |
Keho T H, Beydoun W B. Paraxial ray Kirchhoff migration[J]. Geophysics, 1988, 53(12): 1540-1546. DOI:10.1190/1.1442435 |
| [13] |
Cohen J K, Hagin F G, Bleistein N. Three-dimensional Born inversion with an arbitrary reference[J]. Geophysics, 1986, 51(8): 1552-1558. DOI:10.1190/1.1442205 |
| [14] |
Forgues E, Lambaré G. Parameterization study for acoustic and elastic ray plus born inversion[J]. Journal of Seismic Exploration, 1997, 6(2-3): 253-277. |
| [15] |
Xu S, Chauris H, Lambaré G, et al. Common angle migration:A strategy for imaging complex media[J]. Geophysics, 2001, 66(6): 1877-1894. DOI:10.1190/1.1487131 |
| [16] |
Jin S, Madariaga R, Virieux J, et al. Two-dimensional asymptotic iterative elastic inversion[J]. Geophysical Journal International, 1992, 108(2): 575-588. DOI:10.1111/j.1365-246X.1992.tb04637.x |
| [17] |
Lambare G, Virieux J, Madariaga R, et al. Iterative asymptotic inversion in the acoustic approximation[J]. Geophysics, 1992, 57(9): 1138. DOI:10.1190/1.1443328 |
| [18] |
Thierry P, Operto S, Lambaré G. Fast 2-D ray+Born migration/inversion in complex media[J]. Geophy-sics, 1999, 64(1): 162-181. |
| [19] |
De Hoop M V, Bleistein N. Generalized Radon transform inversions for reflectivity in anisotropic elastic media[J]. Inverse problems, 1997, 13(3): 669-690. |
| [20] |
Hill N R. Gaussian beam migration[J]. Geophysics, 1990, 55(11): 1416-1428. DOI:10.1190/1.1442788 |
| [21] |
Hill N R. Prestack Gaussian-beam depth migration[J]. Geophysics, 2001, 66(4): 1240-1250. DOI:10.1190/1.1487071 |
| [22] |
Gray S H, Bleistein N. True-amplitude Gaussian-beam migration[J]. Geophysics, 2009, 74(2): S11-S23. |
| [23] |
栗学磊, 毛伟建. 多波多分量高斯束叠前深度偏移[J]. 地球物理学报, 2016, 59(8): 2989-3005. LI Xuelei, MAO Weijian. Multimode and multi-component Gaussian beam prestack depth migration[J]. Chinese Journal of Geophysics, 2016, 59(8): 2989-3005. |
| [24] |
Mao W J, Stuart G W. Rapid multi-wave-type ray tracing in complex 2-D and 3-D isotropic media[J]. Geophysics, 1997, 62(1): 298-308. |
| [25] |
Um J, Thurber C. A fast algorithm for two-point ray tracing[J]. Bulletin of the Seismological Society of America, 1987, 77(3): 972-986. |
| [26] |
徐涛, 徐果明, 高尔根, 等. 三维复杂介质的块状建模和试射射线追踪[J]. 地球物理学报, 2004, 47(6): 1118-1126. XU Tao, XU Guoming, GAO Ergen, et al. Block mo-deling and shooting ray tracing in complex 3-D media[J]. Chinese Journal of Geophysics, 2004, 47(6): 1118-1126. DOI:10.3321/j.issn:0001-5733.2004.06.027 |
| [27] |
Xu Q R, Mao W J. An efficient ray-tracing method and its application to Gaussian beam migration in complex multilayered anisotropic media[J]. Geophy-sics, 2018, 83(5): T281-T289. |
| [28] |
白海军, 孙赞东, 王学军. 基于波前构建法的TTI介质射线追踪[J]. 石油地球物理勘探, 2011, 46(增刊1): 1-6. BAI Haijun, SUN Zandong, WANG Xuejun. Raytracing in TTI media using wavefront construction[J]. Oil Geophysical Prospecting, 2011, 46(S1): 1-6. |
| [29] |
张凯, 陈军屹, 祝佰航, 等. 基于程函方程的VTI介质初至波走时层析反演[J]. 石油地球物理勘探, 2018, 53(6): 1218-1226. ZHANG Kai, CHEN Junyi, ZHU Baihang, et al. First break traveltime tomographic imaging based on the eikonal equation in VTI medium[J]. Oil Geophysical Prospecting, 2018, 53(6): 1218-1226. |
| [30] |
李同宇, 张建中. 地震射线追踪的线性走时扰动插值法[J]. 石油地球物理勘探, 2018, 53(6): 1165-1174. LI Tongyu, ZHANG Jianzhong. A linear traveltime perturbation interpolation method for seismic ray tracing[J]. Oil Geophysical Prospecting, 2018, 53(6): 1165-1174. |
| [31] |
魏脯力, 孙建国, 孟祥羽. 应用网格走时的射线路径计算方法[J]. 石油地球物理勘探, 2018, 53(4): 722-729. WEI Puli, SUN Jianguo, MENG Xiangyu. A ray path calculation method based on grid traveltime[J]. Oil Geophysical Prospecting, 2018, 53(4): 722-729. |
| [32] |
Moser T J. Shortest path calculation of seismic rays[J]. Geophysics, 1991, 56(1): 59-67. |
| [33] |
Fisher R, Lees J M. Shortest path ray tracing with sparse graphs[J]. Geophysics, 1993, 58(7): 987-996. DOI:10.1190/1.1443489 |
| [34] |
Vidale J E. Finite-difference calculation of travel times[J]. Bulletin of the Seismological Society of America, 1988, 78(6): 2062-2076. |
| [35] |
张霖斌, 刘迎曦, 赵振峰, 等. 有限差分法射线追踪[J]. 石油地球物理勘探, 1993, 28(6): 673-677. ZHANG Linbin, LIU Yingyi, ZHAO Zhenfeng, et al. Finite-difference ray tracing[J]. Oil Geophysical Prospecting, 1993, 28(6): 673-677. |
| [36] |
Vinje V, Iversen E, Gjøystdal H. Traveltime and am-plitude estimation using wavefront construction[J]. Geophysics, 1993, 58(8): 1157-1166. DOI:10.1190/1.1443499 |
| [37] |
Vidale J E, Houston H. Rapid calculation of seismic amplitudes[J]. Geophysics, 1990, 55(11): 1504-1507. DOI:10.1190/1.1442798 |
| [38] |
Buske S. Finite-difference solution of the transport equation:First results[J]. Pure and Applied Geophy-sics, 1996, 148(3-4): 565-581. DOI:10.1007/BF00874579 |
| [39] |
Schleicher J, Tygel M, Hubral P. 3-D true-amplitude finite-offset migration[J]. Geophysics, 1993, 58(8): 1112-1126. DOI:10.1190/1.1443495 |
| [40] |
Vanelle C, Gajewski D. Determination of geometrical spreading from traveltimes[J]. Journal of Applied Geophysics, 2003, 54(3-4): 391-400. DOI:10.1016/j.jappgeo.2003.02.002 |
| [41] |
Popov M M, Pšeník I, ervený V. Computation of ray amplitudes in inhomogeneous media with curved interfaces[J]. Studia Geophysica et Geodaetica, 1978, 22(3): 248-258. DOI:10.1007/BF01627902 |
| [42] |
Červený V, Klimeš L, Pšeník I. Applications of dy-namic ray tracing[J]. Physics of the Earth and Planetary Interiors, 1988, 51(1-3): 25-35. DOI:10.1016/0031-9201(88)90019-2 |
| [43] |
Chapman C. Fundamentals of Seismic Wave Propagation[M]. Cambridge University Press, 2004.
|
| [44] |
Ouyang W, Mao W J, Li X L. Approximate solution of nonlinear double-scattering inversion for true amplitude imaging[J]. Geophysics, 2015, 80(1): R43-R55. |
| [45] |
Ouyang W, Mao W J, Li W Q, et al. Approximate non-linear multiparameter inversion with single and double scattering seismic wavefields in acoustic media[J]. Geophysical Journal International, 2017, 208(2): 767-789. DOI:10.1093/gji/ggw422 |



 毛伟建, 湖北省武汉市武昌区徐东大街340号中国科学院测量与地球物理研究所计算与勘探地球物理中心, 430077。Email:
毛伟建, 湖北省武汉市武昌区徐东大街340号中国科学院测量与地球物理研究所计算与勘探地球物理中心, 430077。Email: