② 东方地球物理公司研究院, 河北涿州 072751;
③ 东方地球物理公司海洋物探处, 天津 300450
② Geophysical Research Institute, BGP, CNPC, Zhuozhou, Hebei 072751, China;
③ Division of Marine Geophysical Exploration, BGP, CNPC, Tianjin 300450, China
多项式拟合回归被广泛用于地震数据随机噪声衰减、多次波压制、品质因子估计及初至拾取静校正等方面[1-7]。早在1988年俞寿朋等[8]利用信号横向相干性,提出了多项式拟合加强有效信号的方法,并在叠后地震资料处理中获得较好应用效果。田小平等[9]提出利用多项式拟合模板法消除地震信号的低频干扰,分析了模板性质并给出了模板与低频随机干扰最高频率之间的关系,实验证明了方法的有效性。Johansen等[10]利用正交多项式提取AVO特征,很好地保护了剖面特征。李鲲鹏等[11]提出了小波变换过零点匹配和基于奇异值分解总体最小二乘(SVD-TLS)算法的多项式拟合去噪方法,提高了地震资料分辨率和信噪比。夏洪瑞等[12]提出了二次多项式拟合与中值约束的矢量分解方法,解决了常规正交多项式拟合过程中出现的断点模糊问题。Lu等[1]利用滑动窗多项式拟合压制局部线性噪声,并用于衰减随机噪声以保护边缘信息[13]。多项式拟合不仅用于叠后去噪,也可应用于叠前CMP去噪。薛亚茹等[14]利用多项式变换压制动校正后CMP道集的随机噪声,既提高了信号和噪声的分离效果,又有效地保护了地震信号的AVO信息。结合时频变换的多项式拟合也被用于地震数据处理。李向云等[15]提出了改进的正交多项式变换,利用奇异值分解确定有效信号正交多项式系数谱的阶数,结合小波变换减弱了有效信号和噪声在低阶的混叠,改善了随机噪声压制效果。陆文凯[16]沿多次波旅行时轨迹,利用L1范数多项式拟合技术估计多次波,有效地消除了一次波和随机噪声对预测多次波的影响。在初至拾取静校正方面,王辉等[17]针对常规静校正方法的不足,提出利用多项式拟合单炮记录初至时间进行地表静校正,取得了较好效果。
Fomel[18-19]利用整形正则化技术研究非平稳回归,针对非平稳信号给出了时变非平稳回归系数估计方法。非平稳回归已被用于多次波自适应相减[19]、随机噪声压制[20]和时频分析[21-22]等领域,应用效果较好。在非平稳回归基础上,Liu等[23]提出了基于非平稳多项式拟合的地震随机噪声压制方法,通过自适应估计非平稳信号的相干分量,在压制噪声的同时更好地保护了有效信号。
非平稳多项式拟合是L2范数下的优化问题,尽管考虑了信号的时变特征,但是仍然假设残差呈随机分布,当地震数据中存在较强非随机噪声时,常规的基于L2范数的非平稳多项式拟合不再适用。因此,本文针对复杂稀疏分布残差问题,在反问题正则化理论框架下,结合非平稳多项式回归和L1范数约束,研究了稀疏约束非平稳多项式回归理论与方法。首先,回顾了非平稳多项式回归的基本原理;然后提出了L1范数约束的估计时变光滑多项式回归系数和稀疏分布回归残差的方法,给出了算法基本流程和参数分析;最后,应用稀疏约束非平稳多项式回归衰减噪声及拾取初至,获得了较好效果。
1 方法原理 1.1 非平稳多项式回归假设信号d(p)可以通过M阶多项式近似,有
| $ d(p) = \sum\limits_{i = 0}^M {{b_i}} {p^i} + n $ | (1) |
式中:pi为多项式自变量;bi为多项式系数;n为拟合误差。如果n为随机噪声,通过拟合误差能量最小的方法得到bi,即其为L2范数约束的最小二乘优化问题
| $ {\rm{min}} :\left\| {d(p) - \sum\limits_{i = 0}^M {{b_i}} {p^i}} \right\|_2^2 $ | (2) |
式中‖·‖2表示L2范数。在L2范数约束下可以将多项式拟合问题改进为非平稳形式,非平稳多项式回归假设多项式系数是时变的,则式(2)变为
| $ {\rm{min}} :\left\| {d(p) - \sum\limits_{i = 0}^M {{b_i}} (p){p^i}} \right\|_2^2 $ | (3) |
可以看出,由于待估计的bi变为bi(p)后未知数个数变多,因此式(3)为欠定反问题,需要对其强加约束限制才能求解。在反问题研究领域,存在多种正则化形式实现反问题约束求解。若考虑经典的Tikhonov正则化,则式(3)在正则化约束条件下的最小平方优化问题为
| $ {\rm{min}} :\left\| {d(p) - \sum\limits_{i = 0}^M {{b_i}} (p){p^i}} \right\|_2^2 + {\sigma ^2}\sum\limits_{i = 0}^M {\left\| {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{b_i}(p)} \right\|_2^2} $ | (4) |
式中:σ为正则化参数;Γ为Tikhonov正则化算子。为了方便起见,采用矩阵或算子的形式描述式(4),即式(4)变为联立最小平方问题
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{min}} :{{\left\| {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Pb}}} \right\|}_2}}\\ {{\rm{min}} :{{\left\| {\mathit{\boldsymbol{ \boldsymbol{\varGamma} b}}} \right\|}_2}} \end{array}} \right. $ | (5) |
式中d、P和b分别为式(4)中的d、p和b对应的矩阵形式。式(5)为线性优化问题,通过共轭梯度法求解。本文选取整形正则化作为正则化方式,其类似于反问题预条件方法,在计算效率和参数选取方面具有一定优势[19]。
1.2 稀疏约束非平稳多项式回归在常规非平稳多项式拟合中,假设噪声呈随机分布,采用L2范数约束能够得到较好的结果。在噪声复杂情况下,如存在强野值噪声、涌浪噪声等非随机分布的噪声,L2范数约束不再适合。在存在非随机噪声情况下,式(5)修正为
| $ {{\rm{min}} :{{\left\| {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Pb}}} \right\|}_1}} $ | (6a) |
| $ {{\rm{min}} :{{\left\| {\mathit{\boldsymbol{ \boldsymbol{\varGamma} b}}} \right\|}_2}} $ | (6b) |
式中‖·‖1表示L1范数,表明拟合噪声误差是稀疏的。为更好地求解式(6),在式(6a)中将残差稀疏噪声作为变量,即
| $ {{\rm{min}} :{{\left\| {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Pb}} - \mathit{\boldsymbol{n}}} \right\|}_2}} $ | (7a) |
| $ {{\rm{min}} :{{\left\| {\mathit{\boldsymbol{ \boldsymbol{\varGamma} b}}} \right\|}_2}} $ | (7b) |
| $ {\rm{min}} :{\left\| \mathit{\boldsymbol{n}} \right\|_1} $ | (7c) |
式中n为稀疏分布非随机噪声。式(7a)表示经多项式拟合后稀疏分布噪声的误差在最小平方意义下最小;式(7b)表示对多项式系数的约束项,是对多项式系数的假设;式(7c)表示噪声的L1范数最小,表明噪声满足稀疏约束。在不同的情况下,式(7)可以具有不同的含义:
(1) 只考虑式(7a)和式(7b),可以估计L2范数约束的非平稳多项式系数,此时假设噪声n满足L2范数下最小。则式(7a)和式(7b)退化为式(5),在理论上具有最小平方解,即
| $ \mathit{\boldsymbol{\hat b}} = {({\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{P}} + {\sigma ^2}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }})^{ - 1}}{\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{d}} $ | (8) |
σ控制估计解
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\hat b}} = {{({\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{P}} + {\mathit{\boldsymbol{S}}^{ - 1}} - \mathit{\boldsymbol{I}})}^{ - 1}}{\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{d}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {{[\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{S}}({\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{P}} - \mathit{\boldsymbol{I}})]}^{ - 1}}\mathit{\boldsymbol{S}}{\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{d}}} \end{array} $ | (9) |
式中:S为整形算子,一般取三角平滑或者高斯平滑算子;I为单位矩阵。需要注意的是,式(9)是式(7a)和式(7b)的正则化约束理论解,采用共轭梯度类算法求解。为了简便,将式(9)记为
| $ \mathit{\boldsymbol{\hat b}} = {\mathit{\boldsymbol{G}}^{ - 1}}\mathit{\boldsymbol{d}} $ | (10) |
式中G代表综合线性算子,包含整形正则化的形式。
(2) 综合考虑式(7a)~式(7c),可以估计L1范数约束的非平稳多项式拟合。此时式(7)变为
| $ {{\rm{min}} :{{\left\| {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Gb}} - \mathit{\boldsymbol{n}}} \right\|}_2}} $ | (11a) |
| $ {\rm{min}} :{\left\| \mathit{\boldsymbol{n}} \right\|_1} $ | (11b) |
算子G包含在L2范数约束下对b的平滑约束。式中未知量为b和n,为了求解非线性优化问题,将式(11a)写为
| $ \mathit{\boldsymbol{d}} - \left( {\begin{array}{*{20}{l}} \mathit{\boldsymbol{I}}&\mathit{\boldsymbol{G}} \end{array}} \right)\left( {\begin{array}{*{20}{l}} \mathit{\boldsymbol{n}}\\ \mathit{\boldsymbol{b}} \end{array}} \right) \approx {0} $ | (12) |
此时未知量变为(n b)T。假设噪声n服从稀疏分布、b沿着时间方向是平滑的,则式(12)简化为
| $ \mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Fx}} \approx 0 $ | (13) |
式中:F=(I G);x=(n b)T。采用Daubechies迭代[24]求解式(13),即
| $ {\mathit{\boldsymbol{x}}_{k + 1}} = {\mathit{\boldsymbol{T}}_{{\lambda _k}}}[{\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{d}} + (\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{F}}){\mathit{\boldsymbol{x}}_k}] $ | (14) |
式中Tλk为噪声n的阈值算子,k为迭代次数。
将式(14)展开,得
| $ \begin{array}{*{20}{l}} {\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{n}}_{k + 1}}}\\ {{\mathit{\boldsymbol{b}}_{k + 1}}} \end{array}} \right) = {\mathit{\boldsymbol{T}}_{{\lambda _k}}}\left[ {\left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{Id}}}\\ {{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{d}}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{n}}_k}}\\ {{\mathit{\boldsymbol{b}}_k}} \end{array}} \right) - \left( {\begin{array}{*{20}{c}} \mathit{\boldsymbol{I}}\\ {{G^{\rm{T}}}} \end{array}} \right)(\mathit{\boldsymbol{IG}})\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{n}}_k}}\\ {{\mathit{\boldsymbol{b}}_k}} \end{array}} \right)} \right]}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {{\rm{T}}_{{{\dot \lambda }_k}}}\left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{b}}_k}}\\ {{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{d}} - {\mathit{\boldsymbol{G}}^{\rm{T}}}{\mathit{\boldsymbol{n}}_k}} \end{array}} \right)} \end{array} $ | (15) |
由于Tλk仅仅对噪声n进行阈值约束,而不对多项式系数b约束,则式(15)变为
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{n}}_{k + 1}} = {\mathit{\boldsymbol{T}}_{{\lambda _k}}}(\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{b}}_k})}\\ {{\mathit{\boldsymbol{b}}_{k + 1}} = {\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{d}} - {\mathit{\boldsymbol{G}}^{\rm{T}}}{\mathit{\boldsymbol{n}}_k}} \end{array}} \right. $ | (16) |
式(16)为最终的L1范数约束的非平稳多项式回归迭代公式。由于采用共轭梯度类算法求解L2范数整形正则化约束的非平稳多项式回归公式(式(9)),因此在式(16)中可以直接用线性共轭梯度迭代几次后的结果代替GT,即
| $ {\mathit{\boldsymbol{b}}_{k + 1}} = {\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{d}} - {\mathit{\boldsymbol{G}}^{\rm{T}}}{\mathit{\boldsymbol{n}}_k} = {\mathit{\boldsymbol{G}}^{\rm{T}}}(\mathit{\boldsymbol{d}} - {\mathit{\boldsymbol{n}}_k}) \approx {\mathit{\boldsymbol{G}}^{ - 1}}(\mathit{\boldsymbol{d}} - {\mathit{\boldsymbol{n}}_k}) $ | (17) |
通过上述分析,可以得到稀疏约束非平稳多项式回归的具体实现算法。
(1) 设置迭代初始值。设初始噪声n0=0,初始系数b0=0,P为多项式,非线性最大迭代次数为K,共轭梯度线性迭代次数为L。
(2) 设非线性迭代次数k为1~K,计算bk+1=G-1(d-nk)。值得注意的是,具体实现是利用整形正则化约束共轭梯度算法实现的[19],其求解为线性算法,最大线性共轭梯度迭代次数为L。
(3) 计算nk+1=Tλi(d-Gbk)。即将残差做阈值处理,以满足残差噪声服从稀疏分布,解决拟合残差中含有强稀疏分布噪声的问题。
(4) 重复步骤(2)、步骤(3)。迭代终止条件可以通过最大迭代次数K控制,也可以通过约束残差的能量控制,在实际应用中前者更方便。
1.4 稀疏约束非平稳多项式回归关键参数分析在稀疏约束非平稳多项式回归算法流程中,整形正则化平滑参数和阈值参数是较重要的2个参数。正则化平滑参数控制多项式系数的平滑性,它是非平稳系数估计的重要度量。平滑参数设置越大,求取的多项式系数越平滑,则多项式回归系数随自变量变化不大、越平稳;平滑参数设置越小,说明多项式系数时变性强、非平稳性越强。
阈值参数是稀疏约束反演的重要参数之一,阈值一般分为软阈值和硬阈值。软阈值的形式为
| $ {{\boldsymbol{T}}_{{{ \lambda }_k}}}[{n_i}] = \left\{ {\begin{array}{*{20}{l}} {{n_i} - {\lambda _k}}&{\left\| {{n_i}} \right\| > {\lambda _k}}\\ 0&{\left\| {{n_i}} \right\| < {\lambda _k}} \end{array}} \right. $ | (18) |
硬阈值的形式为[22]
| $ {{\boldsymbol{T}}_{{{ \lambda }_k}}}[{n_i}] = \left\{ {\begin{array}{*{20}{l}} {{n_i}}&{\left\| {{n_i}} \right\| > {\lambda _k}}\\ 0&{\left\| {{n_i}} \right\| < {\lambda _k}} \end{array}} \right. $ | (19) |
阈值参数λk有不同的选取方式,如常数阈值、线性下降阈值、指数下降阈值等[25-26],本文采用容易实现且收敛较快的百分比阈值[27]。
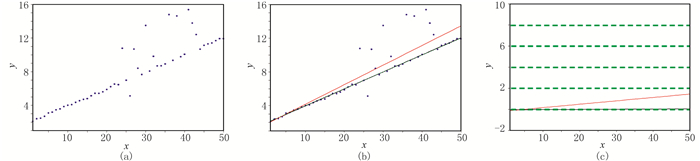
2 理论模型算例图 1为含非随机噪声数据的平稳、非平稳多项式回归结果。由图可见:①含有非高斯分布噪声的散点(图 1a)是在直线y=b0+b1x上加随机噪声和稀疏分布的野值得到的,基本符合直线y=b0+b1x分布,但是在x∈[25, 40]时存在强野值噪声,这些噪声偏离了直线,且不符合随机分布。②由于L2范数约束的平稳多项式回归结果(图 1b红线)存在野值,导致回归直线向上方偏离,这是因为在回归过程中引入了远离真解的采样点所致;采用L1范数稀疏约束的平稳多项式回归结果较理想(图 1b黑线),这是由于在L1范数约束下假设回归残差符合稀疏分布。③对比L2范数和L1范数回归结果表明,L1范数更好地处理了含有稀疏分布噪声的情况(图 1c黑线)。
|
图 1 含非随机噪声数据的平稳多项式(y=b0+b1x)回归结果 (a)含有非高斯分布噪声的散点;(b)回归结果;(c)回归曲线与真实曲线(不含噪声)的绝对误差红线代表L2范数约束,黑线代表L1范数稀疏约束 |
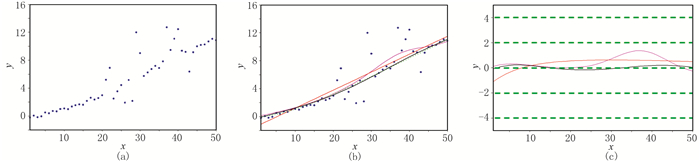
为了测试非平稳多项式回归效果,设计了一条曲线,并在该曲线上加随机噪声和稀疏分布的噪声(图 2a)。图 2为含非随机噪声数据的非平稳多项式回归结果。由图可见:①平稳回归(即直线)考虑了所有点的影响,并且呈直线分布(图 2b红线);L2范数约束非平稳回归(图 2b粉线)考虑了曲线的时变特征,在x∈[0, 20]时由于不存在稀疏分布的噪声,回归效果较好,但是在x∈[20, 45]时存在稀疏分布的噪声,回归效果变差,表明异常值干扰了回归结果。②对比不同回归方法结果的绝对误差发现,对于含有稀疏分布噪声的情况,L1范数约束非平稳回归拟合的曲线绝对误差最小(图 2c黑线)。
|
图 2 含非随机噪声数据的非平稳多项式(y=b0(x)+b1(x)x)回归结果 (a)含有非高斯分布噪声的散点;(b)回归结果;(c)回归曲线与真实曲线(不含噪声)的绝对误差 红线代表L2范数约束平稳回归,粉线代表L2范数约束非平稳回归,黑线代表L1范数稀疏约束非平稳回归 |
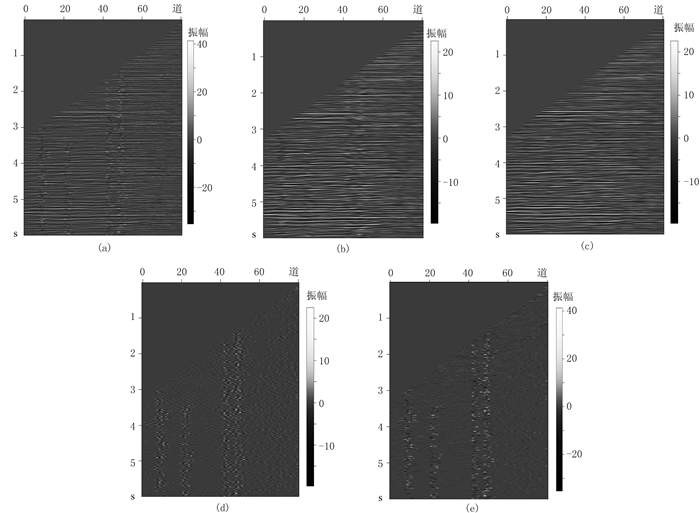
动校正后CMP道集上某一反射点的反射系数曲线(AVO曲线)可以通过多项式近似表示[28]。薛亚茹等[14]探讨了多项式变换压制CMP道集随机噪声的方法;Liu等[23]将其扩展到非平稳多项式的情形,研究了非平稳多项式回归CMP道集去噪方法。上述方法在噪声呈随机分布时去噪效果较好,但如果存在稀疏分布的噪声,如陆地地震数据的强野值噪声、海洋地震数据的涌浪噪声等,L2范数约束的非平稳多项式回归不再适用。图 3为含强稀疏分布噪声的CMP道集非平稳多项式回归去噪结果。由图可见:①动校正后的CMP道集中存在强稀疏分布噪声及随机噪声(图 3a);②L2范数约束去噪效果欠佳(图 3b),L1范数约束去噪效果很好(图 3c);③L2范数约束去除的噪声呈随机分布(图 3d),强噪声“平均”影响了周围信号,L1范数约束去除的噪声中强噪声基本呈稀疏分布(图 3e)。
|
图 3 含强稀疏分布噪声的CMP道集非平稳多项式回归去噪效果 (a)含噪CMP道集;(b)L2范数约束去噪结果;(c)L1范数稀疏约束去噪结果;(d)L2范数约束去除的噪声;(e)L1范数约束去除的噪声 |
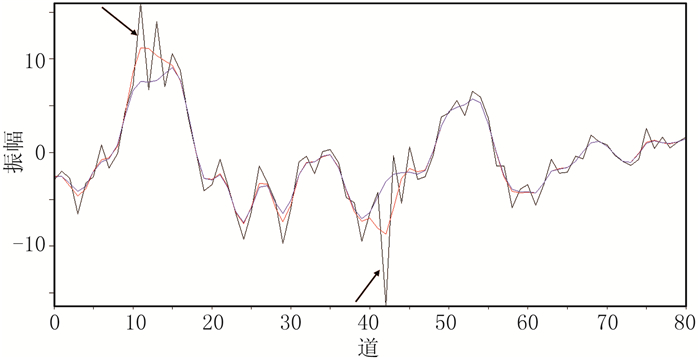
图 4为不同方法去噪结果在旅行时为4.5s时刻的振幅。由图可见:在强稀疏噪声处(箭头处),L2范数约束方法去噪结果的振幅与原始数据不一致,L1范数约束方法去噪结果几乎摒弃了强振幅的影响;在没有强噪声处(如50~80道处),L1范数约束和L2范数约束的去噪结果几乎一致,这是由于在回归过程中充分考虑了非平稳特征所致。
|
图 4 不同方法去噪结果在旅行时为4.5s时刻的振幅 黑线为原始数据,红线为L2范数约束去噪结果,蓝线为L1范数约束去噪结果 |
地震初至拾取对建立近地表地震速度模型和静校正非常重要,当前有很多初至拾取方法,其中能量比法是较常用的方法之一[29-32],该方法计算滑动窗口内能量与累计能量的比值
| $ {R_j} = \frac{{\sum\limits_{i = j}^{j + l} {A_i^2} }}{{\sum\limits_{i = 1}^{j + l} {A_i^2} }} $ | (20) |
式中:Ai为地震振幅;l为滑动窗口长度。可以看出,能量比值Rj的第1个峰值在前几个采样点,因为在前几个采样点累计能量与滑动窗口内能量差别不大。能量比值的第2个峰值一般对应初至[29],但是当存在噪声时,较难拾取第2个峰值,尤其存在强野值噪声时拾取更不准确。因此,考虑采用稀疏约束多项式回归方法处理强野值噪声。
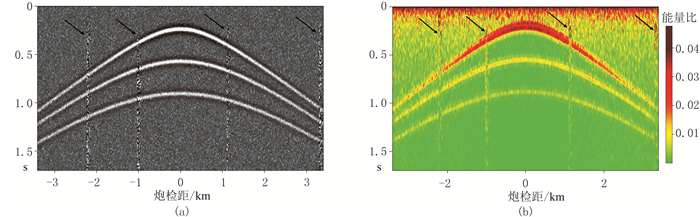
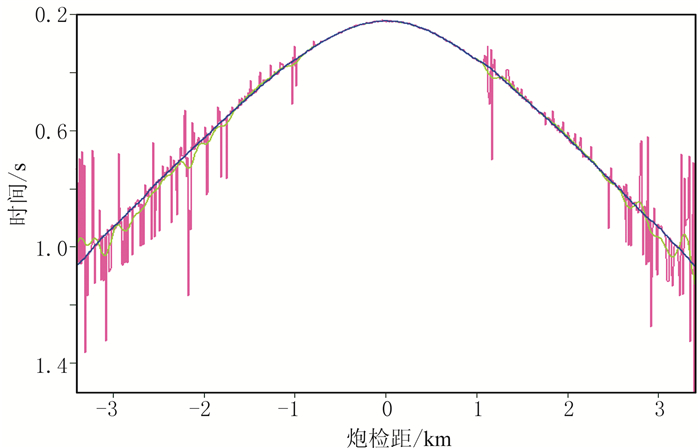
图 5为模拟的炮记录及能量比。由图可见:假设炮点和检波点不在一条直线上,因此模拟的炮记录的初至是一条双曲线(图 5a);为了测试方法的有效性,在模拟炮记录上加随机噪声和强稀疏分布噪声(箭头所示),强稀疏分布噪声导致能量比第2个峰值与初至时刻差距较大(图 5b),因此难以自动拾取初至。图 6为不同方法自动拾取的初至对比。由图可见,噪声的存在使自动拾取的第2个峰值(粉色线)与真实初至时刻有一定误差,尤其对于稀疏噪声存在的位置,获得的初至结果不精确。分别利用自动拾取的初至位置进行L2范数和L1范数约束的非平稳多项式回归发现:前者的初至更平滑,但是异常抖动也严重影响了L2范数回归结果;后者通过稀疏约束减小了稀疏分布野值噪声的影响,提高了初至拾取精度。
|
图 5 模拟的炮记录(a)及能量比(b) |
|
图 6 不同方法自动拾取的初至对比 粉线为自动拾取能量比的第2个峰值得到的初至,绿线为L2范数非平稳回归得到的初至,蓝线为L1范数非平稳回归得到的初至 |
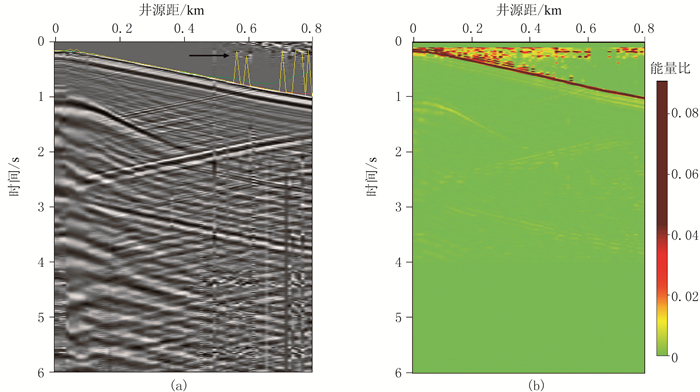
在VSP数据处理中,初至拾取是非常重要的一步,利用初至信息可以直接求取速度、衰减参数及进行静校正等处理。图 7为VSP数据及能量比。由图可见:在井源距大于0.5km处存在一些噪声,导致能量比法初至拾取效果不好(图 7b);通过非平稳回归可以改善初至拾取精度,尤其采用L1范数约束的非平稳回归(图 7a的红线)基本可以消除噪声影响,可以获得较可靠的初至。
|
图 7 VSP数据(a)及能量比(b) 黄线为能量比直接拾取的初至,绿线为L2范数拾取的初至,红线为L1范数拾取的初至 |
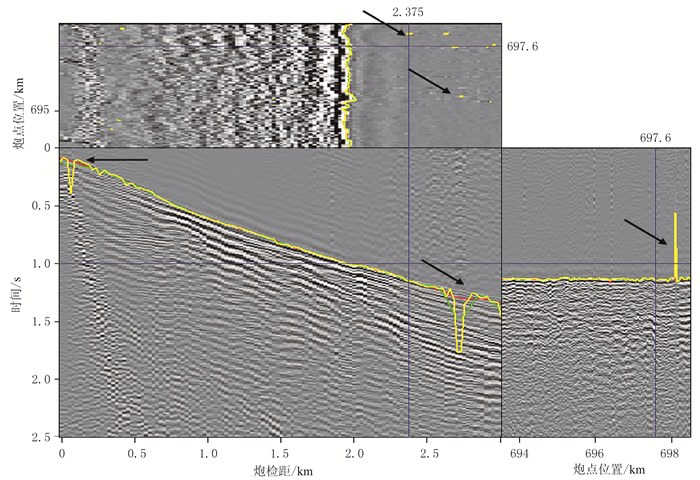
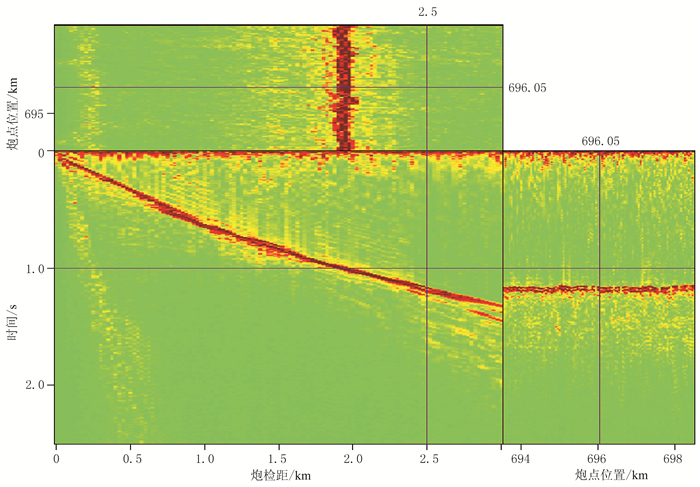
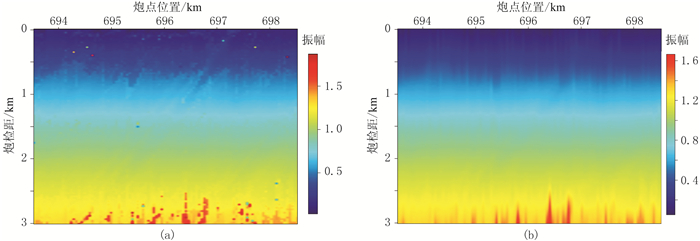
图 8、图 9分别为陆地地震数据及其滑动时窗能量比剖面。由图可见,由于实际数据的复杂性,自动拾取的初至效果不理想(图 8箭头处),经L1范数约束的非平稳回归改善了初至拾取效果(图 8红线)。图 10为常规初至拾取结果、稀疏约束非平稳多项式回归初至拾取结果。由图可见:①远炮检距处由于信号较弱,信噪比低,两种方法拾取的初至均存在异常点,但稀疏约束非平稳多项式回归拾取的初至更平滑(图 10b)。②近炮检距处由于存在野值等噪声导致常规初至拾取结果存在异常值,效果较差(图 10a);稀疏约束非平稳多项式回归摒弃了稀疏分布噪声的影响,初至拾取结果稳定、可靠(图 10b)。
|
图 8 陆地地震数据 最大炮检距为3km,共100炮。黄线为能量比直接拾取的初至,绿线为L2范数拾取的初至,红线为L1范数拾取的初至。上为时间切片,左下为共炮点道集,右下为共炮检距剖面 |
|
图 9 对应图 8的滑动时窗能量比剖面 |
|
图 10 常规初至拾取结果(a)、稀疏约束非平稳多项式回归初至拾取结果(b) |
需要说明的是,稀疏约束非平稳多项式回归的初至拾取误差由不规则稀疏分布噪声引起,对地表高程变化剧烈或采样不规则引起的初至剧烈抖动,初至拾取效果会受到影响。
4 讨论与结论(1) 针对地震数据非平稳特征及噪声稀疏分布问题,在稀疏约束反问题正则化理论框架下,提出了稀疏约束非平稳多项式回归方法,并用于地震噪声压制和初至拾取。该方法采用整形正则化和L1范数联合约束策略,利用共轭梯度和投影算法求解联合约束反问题,同时估计具有时变光滑特征的多项式回归系数和具有稀疏分布特征的回归残差,克服了稀疏分布强噪声对反演的影响。
(2) 整形正则化平滑参数和阈值参数是稀疏约束非平稳多项式回归方法的两个重要参数。正则化平滑参数控制多项式系数的平滑性,参数越小表明参数非平稳特征越强;阈值参数选取与噪声的稀疏特征有关,本文采用容易实现且收敛较快的百分比阈值参数。
(3) 与常规的多项式回归相比,稀疏约束非平稳多项式回归方法计算量略大,但由于数据处理过程中一般采用一维多项式回归,因此计算量在可接受范围内。
| [1] |
Lu W K, Zhang W, Liu D. Local linear coherent noise attenuation based on local polynomial approximation[J]. Geophysics, 2006, 71(6): V163-V169. DOI:10.1190/1.2335873 |
| [2] |
曹鹏涛, 张敏, 李振春. 基于广义S变换及高斯平滑的自适应滤波去噪方法[J]. 石油地球物理勘探, 2018, 53(6): 1128-1136. CAO Pengtao, ZHANG Min, LI Zhenchun. An adaptive filtering denoising method based on generalized S-transform and Gaussian smoothing[J]. Oil Geophysical Prospecting, 2018, 53(6): 1128-1136. |
| [3] |
Zhen Z, Yun L, Jun W, et al.Multiple suppression based on polynomial fitting[C].SEG Technical Program Expanded Abstracts, 2012, 31: 1-4. https://www.researchgate.net/publication/268454866_Multiple_suppression_based_on_polynomial_fitting
|
| [4] |
薛亚茹, 陈小宏, 马继涛. 多方向正交多项式变换压制多次波[J]. 地球物理学报, 2012, 55(10): 3450-3458. XUE Yaru, CHEN Xiaohong, MA Jitao. Multiples attenuation based on directional orthogonal polynomial transform[J]. Chinese Journal of Geophysics, 2012, 55(10): 3450-3458. DOI:10.6038/j.issn.0001-5733.2012.10.028 |
| [5] |
刘宏杰, 毛海波, 杨晓海, 等. 基于三维各向异性拉普拉斯滤波的随机噪声压制方法及应用[J]. 石油地球物理勘探, 2019, 54(3): 522-528. LIU Hongjie, MAO Haibo, YANG Xiaohai, et al. 3D anisotropic Laplacian filtering based random seismic noise suppression[J]. Oil Geophysical Prospecting, 2019, 54(3): 522-528. |
| [6] |
Zhou H, Wang C, Marfurt K, et al.Enhancing the re-solution of seismic data using improved time-frequency spectral modeling[C].SEG Technical Program Expanded Abstracts, 2014, 33: 2656-2660.
|
| [7] |
徐彦凯, 曹思远, 潘晓, 等. 随机噪声的局部正交压制方法[J]. 石油地球物理勘探, 2019, 54(2): 280-287. XU Yankai, CAO Siyuan, PAN Xiao, et al. A local orthogonalization for seismic random noise suppression[J]. Oil Geophysical Prospecting, 2019, 54(2): 280-287. |
| [8] |
俞寿朋, 蔡希玲, 苏永昌. 用地震信号多项式拟合提高叠加剖面信噪比[J]. 石油地球物理勘探, 1988, 23(2): 131-139. YU Shouming, CAI Xiling, SU Yongchang. Improvement of signal-to-noise ratio of stack section using polynomial fitting of seismic signals[J]. Oil Geophysical Prospecting, 1988, 23(2): 131-139. |
| [9] |
田小平, 丁玉美. 利用多项式拟合模板法消除地震数据中的低频随机干扰[J]. 地球物理学报, 1996, 39(增刊): 309-315. TIAN Xiaoping, DING Yumei. Removing low-frequency disturb in the seismic data by polynomial approach pattern method[J]. Chinese Journal of Geophysics, 1996, 39(S): 309-315. |
| [10] |
Johansen T, Bruland L, Lutro J. Tracking the amplitude versus offset (AVO) by using orthogonal polynomials[J]. Geophysical Prospecting, 1995, 43(2): 245-261. DOI:10.1111/j.1365-2478.1995.tb00134.x |
| [11] |
李鲲鹏, 刘业新, 李衍达, 等. 小波变换的过零点特性与地震勘探信号的信噪比和分辨率[J]. 地球物理学报, 1997, 40(4): 561-568. LI Kunpeng, LIU Yexin, LI Yanda, et al. Zero crossing property of wavelet transform and improvement of both seismic signal noise ratio and resolution[J]. Chinese Journal of Geophysics, 1997, 40(4): 561-568. DOI:10.3321/j.issn:0001-5733.1997.04.014 |
| [12] |
夏洪瑞, 董江伟, 邹少峰, 等. 常规二次多项式拟合地震数据[J]. 石油物探, 2006, 45(2): 492-496. XIA Hongrui, DONG Jiangwei, ZOU Shaofeng, et al. Normal quadratic polynomials fitting seismic data[J]. Geophysical Prospecting for Petroleum, 2006, 45(2): 492-496. |
| [13] |
Lu Y H, Lu W K. Edge-preserving polynomial fitting method to suppress random seismic noise[J]. Geophysics, 2009. DOI:10.1190/1.3129907 |
| [14] |
薛亚茹, 陆文凯, 陈小宏, 等. 基于正交多项式变换的CMP动校正道集随机噪声压制[J]. 地球物理学进展, 2009, 24(1): 159-163. XUE Yaru, LU Wenkai, CHEN Xiaohong, et al. Random noise attenuation based on orthogonal polynomials transform for CMP gathers[J]. Progress in Geophysics, 2009, 24(1): 159-163. |
| [15] |
李向云, 曹思远, 杨燕, 等. 改进的正交多项式变换在地震资料去噪中的应用[J]. 地球物理学进展, 2013, 28(4): 2085-2093. LI Xiangyun, CAO Siyuan, YANG Yan, et al. The application of improved orthogonal polynomials transform in seismic data process[J]. Progress in Geophy-sics, 2013, 28(4): 2085-2093. |
| [16] |
陆文凯. 基于L1范数多项式拟合的多次波消除方法[J]. 石油地球物理勘探, 2011, 46(3): 386-389. LU Wenkai. Multiples suppression using L1-norm based on polynomial approximation[J]. Oil Geophysical Prospecting, 2011, 46(3): 386-389. |
| [17] |
王辉, 崔若飞. 利用多项式拟合单炮初至作地表静校正[J]. 中国矿业大学学报, 2001, 30(1): 87-90. WANG Hui, CUI Ruofei. Static correction by fitting first breaks of direct waves using polynomial[J]. Journal of China University of Mining & Technology, 2001, 30(1): 87-90. DOI:10.3321/j.issn:1000-1964.2001.01.021 |
| [18] |
Fomel S. Adaptive multiple subtraction using regula-rized nonstationary regression[J]. Geophysics, 2009, 74(1): V25-V33. |
| [19] |
Fomel S. Shaping regularization in geophysical-esti-mation problems[J]. Geophysics, 2007. DOI:10.1190/1.2433716 |
| [20] |
Liu G, Chen X, Du J, et al. Random noise attenuation using f-x nonstationary autoregression[J]. Geophy-sics, 2012, 77(2): V61-V69. |
| [21] |
Liu G, Fomel S, Chen X. Time-frequency analysis of seismic data using local attributes[J]. Geophysics, 2011, 76(6): P23-P34. DOI:10.1190/geo2010-0185.1 |
| [22] |
Liu Y, Fomel S. Seismic data interpolation beyond aliasing using regularized nonstationary autoregre-ssion[J]. Geophysics, 2011, 76(5): V69-V77. DOI:10.1190/geo2010-0231.1 |
| [23] |
Liu G, Chen X, Li J, et al. Seismic noise attenuation using nonstationary polynomial fitting[J]. Applied Geo-physics, 2011, 8(1): 18-26. |
| [24] |
Daubechies I, Defrise M, Mol C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on Pure and Applied Mathematics, 2003. DOI:10.1002/cpa.20042 |
| [25] |
Wang B, Chen X, Li J, et al. An improved weighted projection onto convex sets method for seismic data interpolation and denoising[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(1): 228-235. DOI:10.1109/JSTARS.2015.2496374 |
| [26] |
Gao J J, Chen X H, Liu J Y, et al. Irregular seismic data reconstruction based on exponentional threshold model of POCS method[J]. Applied Geophysics, 2010. DOI:10.1007/s11770-010-0246-5 |
| [27] |
Yang P L, Gao J H, Chen W C.Improved POCS interpolation using a percentage thresholding strategy and excessively zero-padded FFT[C].SEG Technical Program Expanded Abstracts, 2012, 31: 1-6. https://www.researchgate.net/publication/268455155_Improved_POCS_interpolation_using_a_percentage_thresholding_strategy_and_excessively_zero-padded_FFT
|
| [28] |
Ursin B, Dahl T.Least-square estimation of reflectivity polynomials[C].SEG Technical Program Expanded Abstracts, 1990, 9: 1069-1071. https://www.researchgate.net/publication/259018843_Least-squares_estimation_of_reflectivity_polynomials
|
| [29] |
Coppens F. First arrival picking on common-offset trace collections for automatic estimation of static corrections[J]. Geophysical Prospecting, 1985. DOI:10.1111/j.1365-2478.1985.tb01360.x |
| [30] |
Al-Ghamdi A.Automatic First Arrival Picking Using Energy Ratios[D].King Fahd University of Petroleum & Minerals, 2007. https://www.researchgate.net/publication/265573284_Automatic_First_Arrival_Picking_Using_Energy_Ratios
|
| [31] |
Sabbione J, Velis D. Automatic first-breaks picking:New strategies and algorithms[J]. Geophysics, 2010, 75(4): V67-V76. DOI:10.1190/1.3463703 |
| [32] |
Mousa W, Al-Shuhail A. Enhancement of first arrivals using the τ-p transform on energy-ratio seismic shot records[J]. Geophysics, 2012, 77(3): V101-V111. DOI:10.1190/geo2010-0331.1 |



 刘国昌, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院, 102249。Email:
刘国昌, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院, 102249。Email: