② 中国石油大学CNPC物探重点实验室, 北京 102249
② CNPC Key Laboratory of Geophysical Exploration, China University of Petroleum(Beijing), Beijing 102249, China
现今地震数据处理的目标主要集中于“三高”方向,即高信噪比、高保真度和高分辨率。为了提高信噪比,各种去噪方法[1-6]应运而生,成效显著;基于高保真度要求,保幅处理技术[7-9]也迅速发展,使得对与沉积相有关的综合地质分析更为准确;在高分辨率数据处理方面,谱白化[10]、反褶积[11]、反Q滤波[12]等提高分辨率方法也均取得较好效果,其中谱白化作为可直接“操控”频谱形态的高分辨率处理方法,在地震子波整形处理领域倍受青睐。
地震数据处理中,受复杂地表、环境等因素的影响,无法做到准确地提取地震子波。因此,在一定程度上可认为由震源产生的尖脉冲经过大地滤波作用,等效于对δ函数进行了带通滤波,该子波被称为带限子波。由于带限子波的旁瓣较大且振荡严重,不利于实际的高分辨率处理;同时,广泛应用的Ricker子波本身存在旁瓣过大、保真度较弱等缺点。因此,俞寿朋[13]提出了宽带Ricker子波,即俞氏子波。
该子波具有保真性强、旁瓣能量弱、相同主瓣宽度下的分辨率较Ricker子波高等优点,已被更广泛地应用于地震数据(尤其是高分辨率)处理中,并取得了较好应用效果。李英才等[14]将宽带Ricker子波作为反褶积的期望输出,成功地开发出地表一致性俞氏子波反褶积处理软件;曹思远[15]将宽带Ricker子波与小波变换相结合进行时频分析,得到不同尺度下地震数据子波整形记录;栾颖[16]使用基于宽带Ricker子波合成的地震记录进行递推反演,避免了递推反演过程中误差随深度递增的缺点;苏世龙等[17]论证了宽带Ricker子波统计反褶积的保真性优于预测反褶积;Hou等[18]首次将宽带Ricker子波同谱反演方法相结合,获得更适用于储层描述的地震资料。
综观以上研究成果,目前对于宽带Ricker子波的研究大部分聚焦于应用方面,而对该子波的性质并未做更深入讨论。本文从宽带Ricker子波的数学表达式入手,全面分析了宽带Ricker子波的构造参数对子波和振幅谱形态的影响,定量给出子波分辨率和保真度的综合衡量标准;同时基于宽带Ricker子波提出兼顾分辨率和保真度的均衡子波;依托模型测试了不同参数的宽带Ricker子波对地震分辨率的影响;针对实际数据,进行了不同参数宽带Ricker子波的频谱整形处理,结果充分展示了本文所提均衡子波在高分辨率处理中的优越性。
1 基本原理 1.1 宽带Ricker子波宽带Ricker子波的时域表达式为
| $ y(t)=\frac{1}{q-p} \int_{p}^{q}\left[1-2(\mathsf{π} g t)^{2}\right] \mathrm{e}^{-(\mathsf{π} g t)^{2}} \mathrm{d} g $ | (1) |
式中:g为积分内部Ricker子波的峰值频率;t为时间;q、p分别为Ricker子波主频的上、下限。其相应的振幅谱表达式为
| $ Y(f)=\frac{1}{(q-p) \sqrt{\mathsf{π}}}\left[\mathrm{e}^{-(f / q)^{2}}-\mathrm{e}^{-(f / p)^{2}}\right] $ | (2) |
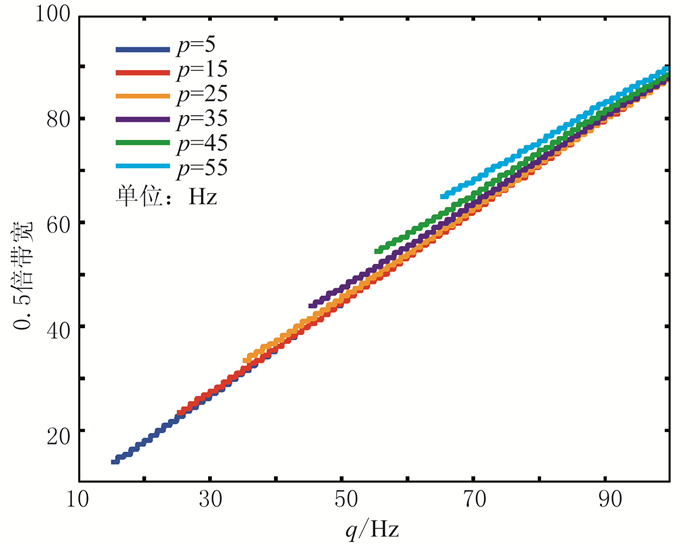
宽带Ricker子波由p、q两个参数控制,其本质是在一定频率范围内对Ricker子波的积分。当p逐渐增至p=q时,宽带Ricker子波退化为主频fm=q的经典Ricker子波。研究分析p和q对子波和振幅谱形态的影响(表 1)可知:当固定p值时,q值与宽带Ricker子波的频带宽度近似为线性关系(图 1),因此可通过目标频谱的频带宽度确定宽带Ricker子波的参数q。
|
|
表 1 宽带Ricker子波参数对子波和振幅谱形态的影响 |
|
图 1 不同p值时q与频带宽度的关系 |
由图 1可知,固定频带宽度相当于确定了宽带Ricker子波的参数q。同时,从表 1可知,当参数q固定不变时,p越大,则主瓣宽度越窄,旁瓣振幅越大,对应的时间分辨率越高,而由于旁瓣过大,子波保真度变差;p越小,主瓣宽度越宽,旁瓣振幅越小,对应的时间分辨率变低,但因旁瓣能量减弱,使得子波保真度变好,调谐现象减弱。
1.2 均衡子波基于以上对宽带Ricker子波参数的讨论,易知宽带Ricker子波的分辨率和保真度难以同时达到最佳。因此,本文尝试在子波保真度和分辨率之间寻找出一均衡点,在该点处得到的子波称为均衡子波,该子波的分辨率和保真度均达到最佳相对均衡。定义无量纲参数
| $ R=\frac{T}{T_{\mathrm{rk}}} \cdot \frac{A}{A_{\mathrm{rk}}} $ | (3) |
式中:T、Trk分别为宽带Ricker子波和经典Ricker子波的主瓣宽度;A、Ark分别表示宽带Ricker子波和经典Ricker子波的旁瓣振幅。
如图 2所示,兼顾分辨率与保真度的均衡性,定义所设计参数R的极大值位置为均衡点。以该均衡点为中心,保持参数q不变、参数p减小,则子波保真度提高,相应的时间分辨率降低;当参数p等于起始频率时,子波的保真度最好,此时的子波称为保真子波;若参数p增大,则子波的时间分辨率提高,对应的保真度降低;当p=q时,子波的时间分辨率达到最高,即为经典Ricker子波。同时,极值点p值位置与q值呈近似线性变化。因此,实际应用中可通过搜寻极值点位置来选取p值,以达到子波保真度和分辨率两者的相对最优。

|
图 2 宽带Ricker子波参数p和q对设计参数R的影响 (a)不同q下p与R的关系曲线;(b)均衡点位置与参数p和q的关系曲线 |
对地震信号处理的过程本质上是对子波进行整形的过程,处理的目的是得到高分辨率、高信噪比、高保真度的地震记录。本文采用基于时频谱的点谱白化,即通过求取地震记录每一时刻频谱包络,得到若干个“子波”,然后做谱白化处理,最后应用期望的目标频谱形态再对白化后的“子波谱”做整形处理。
曹思远等[19]指出,高分辨率地震处理的本质是压缩子波,增强弱信号。因此,拓展频谱时需确定目标频谱形态,在提高分辨率的同时要兼顾信噪比和保真度,这就要求对目标频谱的形态进行分析,以便找到能兼顾这三方面处理目标的频谱形态。
1.4 处理过程分析在噪声较弱的情况下,地震记录s(t)可看作是地震子波w(t)同反射系数r(t)的褶积
| $ s(t)=w(t)*r(t) $ | (4) |
相应的时频域表达式为
| $ S(f, t)=W(f, t)R(f, t) $ | (5) |
式中S(f, t)、W(f, t)和R(f, t)分别是地震记录、地震子波、反射系数对应的小波变换结果。
陈双全等[20]考虑到地震反射系数序列是尖脉冲序列,认为地震记录的频谱特征主要来源于地震子波的频谱形态。据此,可假设若得到高分辨率地震资料,其对应子波为
| $ \hat s(t)= \hat w(t)*r(t) $ | (6) |
相应地在时频域有
| $ \hat S(f, t)= \hat W(f, t)R(f, t) $ | (7) |
结合式(5)和式(7)可得
| $ \hat S(f, t)= \frac{{\hat W (f, t)}}{{W(f, t)}}S(f, t) $ | (8) |
由于非稳态地震子波w(t)提取难度较大,故此应用时频分析工具求取每一时刻的“点谱”,并对这些点谱进行平滑,以得到近似每一时刻的“子波谱”W(f,t)。然后应用谱白化方法将频谱补偿成白谱,因地震记录频带宽度有限,这样得到的整个地震记录的时间域子波形态即是带限子波形态。
将谱白化后每一时刻子波的频谱记为
| $ \hat {\hat W}(f, t)=W(f, t)G(f, t) $ | (9) |
式中G(f, t)为谱白化因子,相当于将原“子波”处理为白谱的时频滤波器。
综合式(8)与式(9)可得
| $ \begin{aligned} \hat{W}(f, t) &=\hat{\hat W}(f, t) \hat{W}_{0}(f, t) \\ &=W(f, t) G(f, t) \hat{W}_{0}(f, t) \\ &=W(f, t) H(f, t) \end{aligned} $ | (10) |
式中
将式(10)代入式(8),得到
| $ \hat S(f, t)=H(f, t)S(f, t) $ | (11) |
式中H(f, t)为所构造的滤波器,用于将地震频谱S(f, t)整形为
综上所述,应用宽带Ricker子波做频谱整形的步骤可归结如下:
(1) 对地震记录进行频谱分析,综合考虑其信噪比等因素确定可拓展频带范围;
(2) 据选定的频带宽度确定宽带Ricker子波的参数q,再通过对分辨率和保真度的不同要求调节参数p;
(3) 对地震记录做时频域谱白化处理,得到谱白化因子,再应用由步骤(2)得到的宽带Ricker子波频谱构造滤波器H(f, t);
(4) 应用该滤波器对地震记录做频谱整形处理。
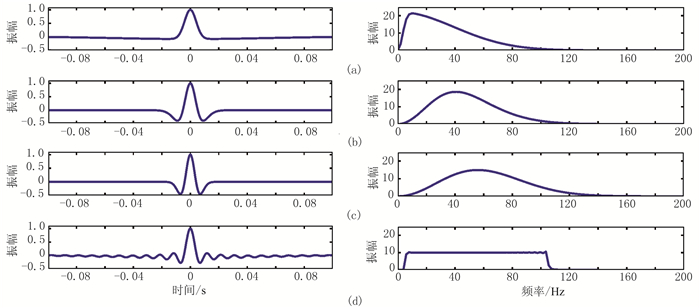
2 模型试算使用模型进行子波分辨率和保真效果的综合测试。选取频率范围是5~105Hz的带限子波;计算其均衡点位置,得到均衡子波的参数p=31.85Hz、q=55.86Hz;取主频fm=q=55.86Hz的Ricker子波;同时调整参数p,使之等于带限子波的下限频率,得到保真子波(理论上保真度最好,调谐现象最弱)参数p=5.00Hz、q=55.86Hz。图 3为上述四种子波的时域图像和频谱图,分别使用同极性和反极性的反射系数测试子波的性能。
|
图 3 模型所测试的四种子波的波形(左)及其振幅谱(右) (a)保真子波;(b)均衡子波;(c)Ricker子波;(d)带限子波 |
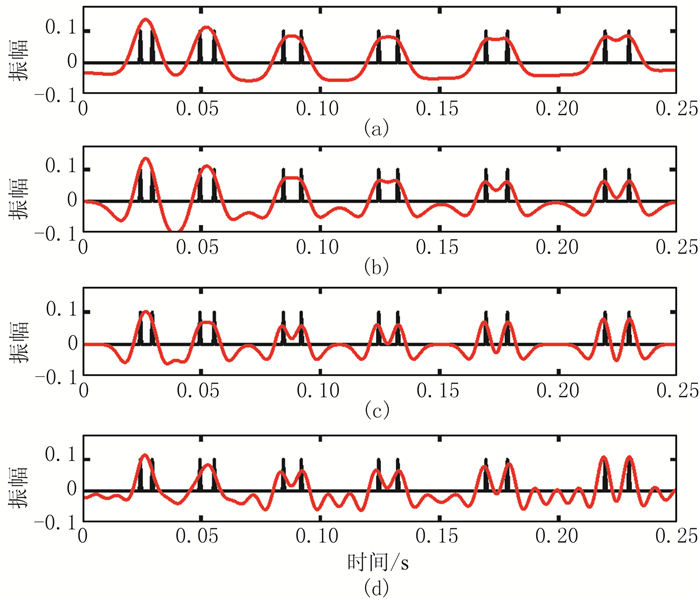
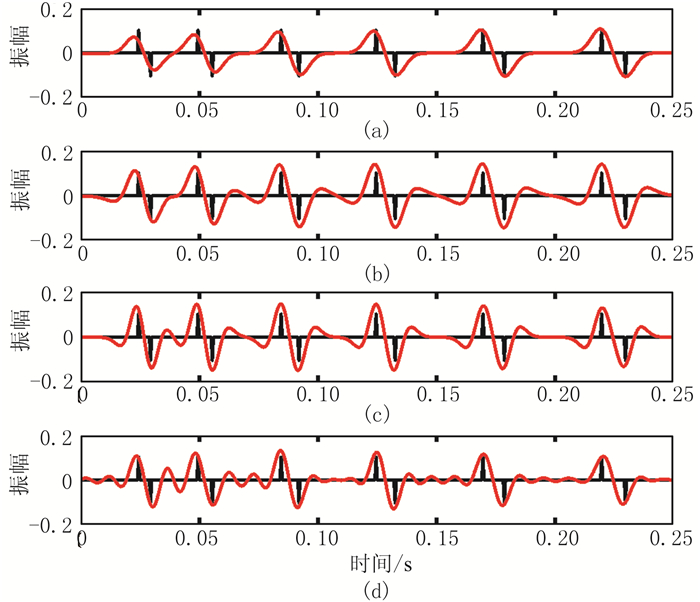
图 4和图 5分别是同极性和反极性反射系数合成的地震记录,同极性地震记录主要测试子波的分辨率,反极性地震记录考察子波旁瓣的干涉作用,偏向于测试子波的保真度。
|
图 4 同极性反射系数合成地震记录 (a)保真子波;(b)均衡子波;(c)Ricker子波;(d)带限子波 |
|
图 5 反极性反射系数合成地震记录 (a)保真子波;(b)均衡子波;(c)Ricker子波;(d)带限子波 |
为了进一步量化这两个参数,本文使用“子波极值均方根误差”参数,定义为:合成地震记录极值处的位置和振幅序列与真实反射系数的均方根误差。显然,当子波主瓣较窄时,调谐现象较弱,与真实反射系数对应较好,参数值变小;同时,当子波旁瓣幅值较弱时,极值处的振幅变小,参数值变小。
子波极值均方根误差的测试结果如表 2所示。由于带限子波震荡较严重(图 4d、图 5d),可不列入比较范围。Ricker子波在同极性的反射系数测试中,其分辨率较高;均衡子波次之,但仍具有较高的保真度;而保真子波在反极性的地震记录中显示出较为优异的保真效果。因此,在实际资料处理时,若强调保真性,则将p值从均衡点向下限频率减小,等于下限频率时,子波旁瓣最小,地震剖面的振幅最接近于反射系数的大小。
|
|
表 2 合成地震记录子波极值均方根误差测试 |
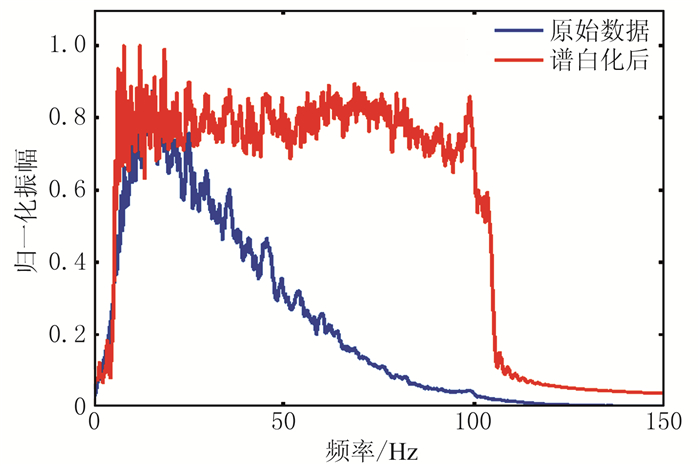
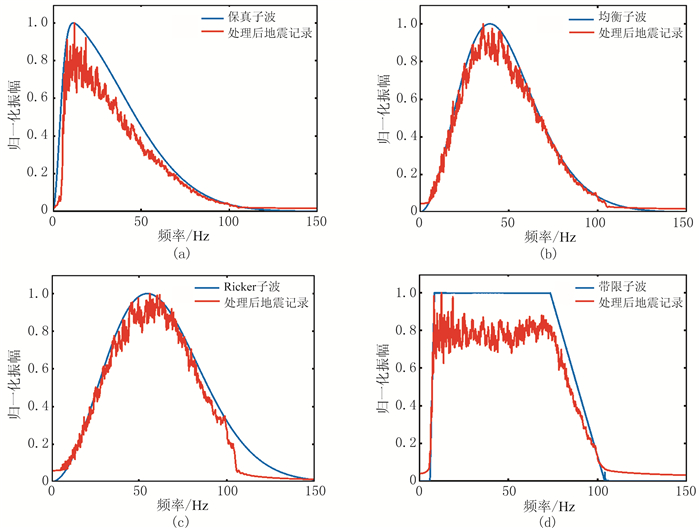
选取A地区的实际地震数据进行处理。如图 6所示,首先应用谱白化方法将该数据频谱(蓝线)补偿为带限子波所对应的白谱(红线),得到白谱的频带宽度后,计算宽带Ricker子波的参数,分别得到保真子波、均衡子波和Ricker子波;然后分别使用上述三种子波和梯形窗带限子波对该地区的地震数据振幅谱进行整形,得到的理论振幅谱与实际振幅谱对比如图 7所示。为了便于显示,在绘图时做了归一化处理。
|
图 6 原始频谱和谱白化后频谱 |
|
图 7 归一化后四种子波的振幅谱与整形后振幅谱对比 (a)保真子波;(b)均衡子波;(c) Ricker子波;(d)梯形窗的带限子波 |
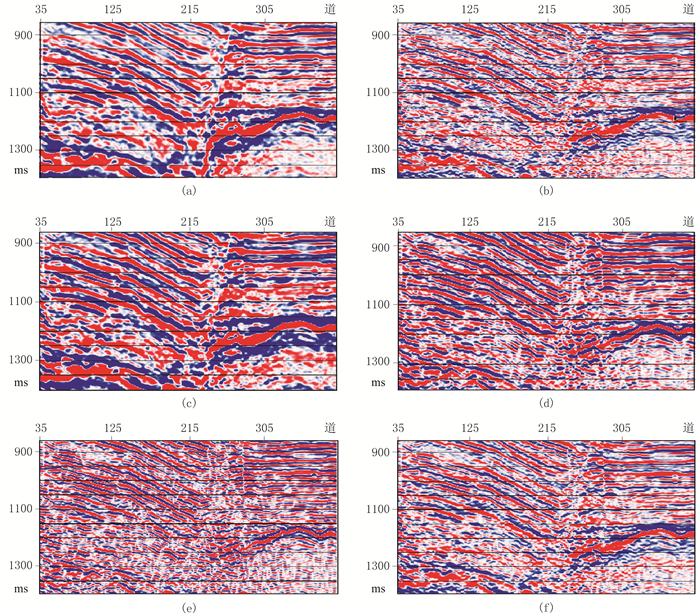
图 8是子波振幅谱整形前后的对比。视觉上,图 8b、图 8d、图 8e和图 8f的分辨率较高。从前文可知图 8b所使用的带限子波振荡严重,会在记录上出现假轴,故无法反映地下真实情况。图 8f所使用的梯形窗带限子波,其第一旁瓣值较高,在剖面上也会形成假轴,但实际上图 8f的假轴成分较图 8b的假轴要少一些。图 8e是Ricker子波整形的结果,其时间分辨率最高。而图 8c是保真子波振幅谱整形结果,其分辨率较低,经过数据验证,其保真度最好。均衡子波(图 8d)正是介于图 8c与图 8e这两者之间的结果,在考虑了分辨率的同时又兼顾了保真度(图 8d)。以均衡点为中心,增大参数p,分辨率提高,整形处理效果逐渐趋近于图 8e;减小参数p,保真度提高,整形处理效果逐渐趋向于图 8c。在实际地震数据处理中,可根据不同的处理目的进行各参数的选择。
|
图 8 实际数据应用子波振幅谱整形前、后对比 (a)原始地震剖面;(b)谱白化后剖面;(c)保真子波频谱整形剖面;(d)均衡子波频谱整形剖面;(e)Ricker子波频谱整形剖面;(f)梯形窗带限子波频谱整形剖面 |
地震数据的频谱形态是反映地震分辨率的一个重要因素,在以往的地震数据处理中,往往忽略频谱形态对分辨率、信噪比、保真度的影响,导致处理结果难如人意。本文基于宽带Ricker子波对地震记录进行频谱整形,得到以下认识和结论。
(1) 谱白化处理中,目标频谱形态的选择是处理中的难点,通过测试不同频谱形态的子波选取最优频谱形态,从而得到均衡子波,在此基础上针对保真度、分辨率的不同要求做进一步调整。
(2) 实际地震数据处理时,根据频带宽度确定均衡子波的参数p和q,再通过对处理目标保真度和分辨率的不同侧重点,调整所需的参数p值。
(3) 将带限子波整形为宽带Ricker子波的过程实际上就是旁瓣由多到少、振幅由大到小的过程。
(4) 保真度也是高分辨率处理的标准之一,旁瓣干扰越小,越能突出剖面弱能量同相轴的显示,越有利于后续的地震解释、反演等。
| [1] |
王进海, 朱敏. 高分辨率资料处理与高信噪比资料[J]. 石油地球物理勘探, 1996, 31(4): 587-596. WANG Jinhai, ZHU Min. High-resolution data processing and high signal/noise ratio data[J]. Oil Geophysical Prospecting, 1996, 31(4): 587-596. |
| [2] |
Xue Y, Man M, Zu S, et al. Amplitude-preserving ite-rative deblending of simultaneous source seismic data using high-order radon transform[J]. Journal of Applied Geophysics, 2017, 139: 79-90. |
| [3] |
Zhang D, Chen Y, Huang W, et al. Multi-step damped multichannel singular spectrum analysis for simultaneous reconstruction and denoising of 3D seismic data[J]. Journal of Geophysics and Engineering, 2016, 13(5): 704-720. |
| [4] |
张华, 陈小宏, 李红星, 等. 曲波变换三维地震数据去噪技术[J]. 石油地球物理勘探, 2017, 52(2): 226-232. ZHANG Hua, CHEN Xiaohong, LI Hongxing, et al. 3D seismic data de-noising approach based on Curvelet transform[J]. Oil Geophysical Prospecting, 2017, 52(2): 226-232. |
| [5] |
张岩, 任伟建, 唐国维. 应用结构聚类字典学习压制地震数据随机噪声[J]. 石油地球物理勘探, 2018, 53(6): 1119-1127. ZHANG Yan, REN Weijian, TANG Guowei. Random noise suppressing on seismic data based on structured-clustering dictionary learning[J]. Oil Geophysical Prospecting, 2018, 53(6): 1119-1127. |
| [6] |
陈颖频, 彭真明, 李美惠, 等. 基于交叠组稀疏广义全变分的地震信号随机噪声衰减[J]. 石油地球物理勘探, 2019, 54(1): 24-35. CHEN Yingpin, PENG Zhenming, LI Meihui, et al. Random noise suppression based on the improved total generalized variation with overlapping group sparsity[J]. Oil Geophysical Prospecting, 2019, 54(1): 24-35. |
| [7] |
Hanitzsch C. Comparison of weights in prestack amplitude-preserving Kirchhoff depth migration[J]. Geo-physics, 1997, 62(6): 1812-1816. |
| [8] |
Plessix R E, Mulder W A. Frequency-domain finite-difference amplitude-preserving migration[J]. Geophysical Journal International, 2004, 157(3): 975-987. |
| [9] |
王者顺, 樊佳芳, 高鸿, 等. 塔河油田叠后地震资料高保真处理技术[J]. 物探与化探, 2004, 28(5): 436-438, 442. WANG Zheshun, FAN Jiafang, GAO Hong, et al. A study on post-stacked seismic data high fidelity processing in Tahe oilfield[J]. Geophysical and Geochemical Exploration, 2004, 28(5): 436-438, 442. |
| [10] |
高静怀, 朱光明, 汪文秉, 等. 小波变换与地震资料谱白化[J]. 煤田地质与勘探, 1997, 25(3): 44-49. GAO Jinghuai, ZHU Guangming, WANG Wenbing, et al. Wavelet transform and spectrum whitening of seismogram[J]. Coal Geology and Exploration, 1997, 25(3): 44-49. |
| [11] |
张晶. 子波整形处理方法研究[J]. 内蒙古石油化工, 2009, 35(11): 17-19. ZHANG Jing. Study on wavelet shaping processing[J]. Inner Mongolia Petrochemical Industry, 2009, 35(11): 17-19. |
| [12] |
陈增保, 陈小宏, 李景叶, 等. 一种带限稳定的反Q滤波算法[J]. 石油地球物理勘探, 2014, 49(1): 68-75. CHEN Zengbao, CHEN Xiaohong, LI Jingye, et al. A band-limited and robust inverse Q filtering algorithm[J]. Oil Geophysical Prospecting, 2014, 49(1): 68-75. |
| [13] |
俞寿朋. 宽带Ricker子波[J]. 石油地球物理勘探, 1996, 31(5): 605-615. YU Shoupeng. Wide-band Ricker wavelet[J]. Oil Geo-physical Prospecting, 1996, 31(5): 605-615. |
| [14] |
李英才, 王艳仓, 李旭, 等. 地表一致性俞氏子波反褶积[J]. 石油物探, 1997, 36(增刊1): 56-62. LI Yingcai, WANG Yancang, LI Xu, et al. Surface consistent deconvolution of Yu's wavelet[J]. Geophysical Prospecting for Petroleum, 1997, 36(S1): 56-62. |
| [15] |
曹思远.基于俞氏子波的时频分解[C].中国地球物理学会第22届年会论文集, 四川成都, 2006, 126. CAO Siyuan.Time-frequency decomposition based on Yu's wavelet[C].The 22nd Annual Meeting Symposium of the Chinese Geophysical Society, Chengdu, Sichuan, 2006, 126. |
| [16] |
栾颖.约束稀疏脉冲波阻抗反演方法在煤层识别中的应用[D].吉林长春: 吉林大学, 2010. LUAN Ying.The Application of Constrained Sparse Spike Inversion in the Coal Bed Identification[D].Jilin University, Changchun, Jilin, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10183-2010110050.htm |
| [17] |
苏世龙, 贺振华, 戴晓云, 等. 岩性油气藏地震保幅处理技术及其应用——以东部某油田岩性气藏为例[J]. 物探与化探, 2015, 39(1): 54-59. SU Shilong, HE Zhenhua, DAI Xiaoyun, et al. The application of relative amplitude compensation technology to lithologic reservoir exploration:A case study of lithologicgas reservoir in an oilfield of eastern China[J]. Geophysical and Geochemical Exploration, 2015, 39(1): 54-59. |
| [18] |
Hou D J, Zhou D H, Zhang Z J, et al.The application of broadband Ricker wavelet in thin reservoir description[C].Extended Abstracts of 79th EAGE Confe-rence & Exhibition, 2017, 1-5.
|
| [19] |
曹思远, 袁殿. 高分辨率地震资料处理技术综述[J]. 新疆石油地质, 2016, 37(1): 112-119. CAO Siyuan, YUAN dian. A review of high-resolution seismic data processing approaches[J]. Xinjiang Petroleum Geology, 2016, 37(1): 112-119. |
| [20] |
陈双全, 李向阳. 应用傅里叶尺度变换提高地震资料分辨率[J]. 石油地球物理勘探, 2015, 50(2): 213-218. CHEN Shuangquan, LI Xiangyang. Seismic resolution enhancement based on the scale characteristics of Fourier transform[J]. Oil Geophysical Prospecting, 2015, 50(2): 213-218. |



 陈思远, 北京市昌平区府学路18号中国石油大学(北京)CNPC物探重点实验室, 102249。Email:
陈思远, 北京市昌平区府学路18号中国石油大学(北京)CNPC物探重点实验室, 102249。Email: