② 中国石油大学(华东)地球科学与技术学院, 山东青岛 266580
② School of Geosciences, China University of Petroleum(East China), Qingdao, Shandong 266580, China
多次波自适应相减是预测减去法压制多次波的重要步骤[1-5],主要包含基于匹配滤波器方法[4-8]、基于模式方法[9-10]和基于盲信号分离的独立成分分析法[11-12]等。基于匹配滤波器方法是一种常用的多次波自适应相减方法。业界通常采用2D匹配滤波器实现多次波自适应相减,该方法将预测多次波与原始数据逐个道集匹配估计一次波[13]。然而,当预测多次波与真实多次波之间存在较大的时间、空间和振幅差异时,2D匹配滤波器会残留多次波或损伤一次波[7-8, 13]。
本文引入3D匹配滤波器实现多次波自适应相减,即3D匹配滤波器可将多个预测多次波道集与原始数据进行匹配。由于3D匹配滤波器利用了多个道集的预测多次波信息,与2D匹配滤波器相比可以更好地去除残余多次波。为避免3D匹配滤波器可能造成的一次波损伤,文中采用相同3D匹配滤波器同时拟合多个原始数据道集的方式。
多次波自适应相减可归结为一个滤波器求解的优化问题[13-14]。根据对一次波施加的约束不同,可将多次波自适应相减分为基于一次波能量最小化方法[15]和基于一次波稀疏约束方法[4, 7-8, 14]。前者需要一次波与多次波正交的假设。当一次波与多次波相互重叠或强一次波周围存在弱多次波时,该类方法不能有效均衡一次波的保护与多次波的压制。而基于一次波稀疏约束的方法不需要一次波与多次波正交的假设,能有效避免产生残余多次波或损伤一次波。
通过构建基于一次波Huber范数最小化约束的优化问题求解3D匹配滤波器[16-18]。对一次波施加Huber范数最小化约束,等价于对强一次波施加L1范数最小化约束和对弱一次波施加L2范数最小化约束。通过将Huber范数最小化优化问题转化为L2范数最小化问题,伪地震数据算法已成功应用于图像去水印[19]、地震数据插值[20]及去噪[21]等方面。为了高效地求解3D匹配滤波器,本文引入伪地震数据算法[19-21]求解Huber范数最小化优化问题。伪地震数据算法在整个迭代过程中,只需利用Cholesky分解算法[22]进行一次矩阵分解,计算效率较高。
文中首先介绍基于3D匹配滤波器的数学模型;然后在构建Huber范数最小化优化问题基础上,推导伪地震数据算法的迭代步骤;根据模型数据和实际资料处理效果,给出了认识和结论。
1 基于3D匹配滤波器的数学模型基于2D匹配滤波器的方法[13-14]在相互重叠的2D数据窗口中实现多次波自适应相减, 其数学模型可表示为[13-14]
| $ \mathit{\boldsymbol{p}} = \mathit{\boldsymbol{s}} - \mathit{\boldsymbol{\tilde Mf}} $ | (1) |
式中:p表示一次波;s表示原始数据;
本文引入3D匹配滤波器,同时利用多个道集的预测信息实现多次波自适应相减。基于3D匹配滤波器的数学模型可表示为
| $ \mathit{\boldsymbol{v}} = \mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Hx}} $ | (2) |
其中
| $ \mathit{\boldsymbol{v}} = {\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{p}}_1}}&{{\mathit{\boldsymbol{p}}_2}}& \cdots &{{\mathit{\boldsymbol{p}}_k}} \end{array}} \right]^{\rm{T}}} $ | (3) |
| $ \mathit{\boldsymbol{d}} = {\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{s}}_1}}&{{\mathit{\boldsymbol{s}}_2}}& \cdots &{{\mathit{\boldsymbol{s}}_k}} \end{array}} \right]^{\rm{T}}} $ | (4) |
| $ \mathit{\boldsymbol{x}} = {\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{f}}_1}}&{{\mathit{\boldsymbol{f}}_2}}& \cdots &{{\mathit{\boldsymbol{f}}_r}} \end{array}} \right]^{\rm{T}}} $ | (5) |
| $ \mathit{\boldsymbol{H}} = {\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\tilde M}}}_1}}&{{{\mathit{\boldsymbol{\tilde M}}}_2}}& \cdots &{{{\mathit{\boldsymbol{\tilde M}}}_r}}\\ {{{\mathit{\boldsymbol{\tilde M}}}_2}}&{{{\mathit{\boldsymbol{\tilde M}}}_3}}& \ldots &{{{\mathit{\boldsymbol{\tilde M}}}_{r + 1}}}\\ \ldots & \ldots & \ldots & \ldots \\ {{{\mathit{\boldsymbol{\tilde M}}}_k}}&{{{\mathit{\boldsymbol{\tilde M}}}_{k + 1}}}& \ldots &{{{\mathit{\boldsymbol{\tilde M}}}_{k + r - 1}}} \end{array}} \right]^{\rm{T}}} $ | (6) |
式中:k为原始数据的道集个数;r为表征匹配滤波器长度的道集个数;v表示估计的一次波;d表示3D原始数据;x表示3D匹配滤波器;H表示多个道集的预测多次波构建的褶积矩阵。
由于利用了多个道集的预测多次波信息,3D匹配滤波器能更好地去除残余多次波。然而,3D匹配滤波器易导致一次波损伤,特别是在一次波与多次波相互交叉重叠处[13]。为此本文利用相同的3D匹配滤波器同时拟合k个原始数据道集。基于3D匹配滤波器的方法是将多个预测多次波道集同时与多个原始数据道集进行匹配,在相互重叠的3D数据窗口中通过估计3D匹配滤波器实现多次波自适应相减。此时k与r的相对大小不做限定。当k变大时,3D数据窗口变大,预测多次波需拟合更多原始数据,故一次波能被更好地保护,但可能会造成残余多次波。可见,基于3D匹配滤波器的方法能有效均衡一次波的保护与多次波的压制。
2 优化问题通常,可假设一次波满足能量最小化约束估计匹配滤波器。相应的优化问题可表达为[13-15]
| $ {\rm{arg}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {{\rm{min}}}\limits_x \left[ {\left\| {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Hx}}} \right\|_2^2 + \lambda \left\| \mathit{\boldsymbol{x}} \right\|_2^2} \right] $ | (7) |
式中λ为正则化参数。当一次波与多次波相互重叠或强一次波周围存在弱多次波时,通过求解优化问题(式(7))所估计的3D匹配滤波器会产生残余多次波或损伤一次波。为有效均衡一次波的保护与多次波的压制,本文构建如下基于一次波Huber范数最小化约束的优化问题
| $ {\rm{arg}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {{\rm{min}}}\limits_x \left\{ {\sum\limits_{i = 1}^N \rho [{{(\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Hx}})}_i}] + \lambda \left\| \mathit{\boldsymbol{x}} \right\|_2^2} \right\} $ | (8) |
式中N表示一次波总的采样点个数。Huber范数ρ(·)作用在标量上,定义如下[16-18]
| $ \rho ({a_i}) = \left\{ {\begin{array}{*{20}{l}} {a_i^2}&{|{a_i}| \le \varepsilon }\\ {\varepsilon (2|{a_i}| - \varepsilon )}&{|{a_i}| > \varepsilon } \end{array}} \right. $ | (9) |
式中:ai=(d-Hx)i,表示所估计一次波的采样点;ε为区分L1范数与L2范数的阈值。在本文中,阈值ε可取为ε=s×max (|d-Hx|),其中s为反复试错后选取的权重参数,用于均衡一次波保护与多次波压制的效果。
对一次波施加Huber范数最小化约束,等价于对强一次波施加L1范数最小化约束和对弱一次波施加L2范数最小化约束。基于一次波Huber范数最小化的方法不需要一次波与多次波的正交性假设,能在保护一次波的同时有效减少残余多次波。
3 伪地震数据算法对优化问题(式(7))中的3D匹配滤波器,求解如下[13-15]
| $ \mathit{\boldsymbol{x}} = {({\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H}} + \lambda \mathit{\boldsymbol{I}})^{ - 1}}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{d}} $ | (10) |
式中I为单位矩阵。
为求解优化问题(式(8))中的3D匹配滤波器,本文构建如下的伪地震数据
| $ {{\mathit{\boldsymbol{\tilde d}}}^{(i)}} = \left\{ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{d}}&{m = 0}\\ {\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{x}}^{(i)}} + \frac{1}{2}\varPsi ({\mathit{\boldsymbol{v}}^{(i)}})}&{m > 0} \end{array}} \right. $ | (11) |
式中:i表示迭代次数;Huber模ρ(·)的导数Ψ(·)定义如下
| $ \varPsi (a) = \left\{ {\begin{array}{*{20}{c}} {2a}&{|a| \le \varepsilon }\\ {2\varepsilon {\rm{sgn}} (a)}&{|a| > \varepsilon } \end{array}} \right. $ | (12) |
式中
| $ {\rm{sgn}} (a) = \left\{ {\begin{array}{*{20}{c}} 1&{a > 0}\\ 0&{a = 0}\\ { - 1}&{a < 0} \end{array}} \right. $ |
用来定义变量a的正、负号。
然后,用伪地震数据算法求解如下的最优化问题以估计3D匹配滤波器
| $ \mathop {{\rm{arg}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{min}}}\limits_{{x^{(m + 1)}}} (\left\| {{{\mathit{\boldsymbol{\tilde d}}}^{(i)}} - \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{x}}^{(i + 1)}}} \right\|_2^2 + \gamma \left\| {{\mathit{\boldsymbol{x}}^{(i + 1)}}} \right\|_2^2) $ | (13) |
式中γ为正则化因子。求解最优化问题(式(13))等价于求解如下的线性方程
| $ \mathit{\boldsymbol{\bar H}}{\mathit{\boldsymbol{x}}^{(i + 1)}} = {\mathit{\boldsymbol{c}}^{(i)}} $ | (14) |
式中:
因此,可将伪地震数据算法总结如下:
输入:H、d、阈值权重参数s、正则化因子γ、最大迭代次数Mγ。计算矩阵H=HTH+γI,并利用Cholesky分解算法将矩阵H分解为H=LLT,其中L表示下三角矩阵。
对于迭代次数i=0, 1, …, Mγ-1:
(1) 利用式(11)计算伪地震数据
(2) 计算向量
(3) 用式(2)估计一次波v(i+1)=d-Hx(i+1);
(4) i=i+1,若i未达到最大迭代次数Mγ,返回步骤(1);否则,停止迭代。
输出:一次波估计结果v(i+1)。
在伪地震数据算法的每一步迭代中,通过构建伪地震数据
将本文方法应用于模型数据和实际数据;并将测试结果与基于伪地震数据算法的2D匹配滤波器方法和基于一次波能量最小化的3D匹配滤波器方法的测试结果进行对比。
4.1 模型数据模型数据的每个道集包含49道,每道包含600个采样点,道间距为20m,采样点间距为4ms。图 1a和图 1b分别是原始数据和2D SRME(Surface Related Multiple Elimination)方法[23-25]预测的多次波。为验证所提方法保护一次波的有效性,在原始数据中人为添加了一个倾斜的一次波同相轴,得到图 1c;而图 1d则为真实一次波。

|
图 1 合成数据的共炮点道集 (a)原始地震数据;(b)预测多次波;(c)对图a添加了倾斜一次波;(d)真实一次波 |
设定m和p(p <m)为采样点个数,分别表示2D数据窗口的时间长度和2D匹配滤波器的时间长度;n和q(q <n)为道数,分别表示2D数据窗口的空间长度和2D匹配滤波器的空间长度。针对本文方法,选择3D数据窗口m=23、n=45、k=3;3D匹配滤波器长度p=9、q=7、r=3。因此,用3个预测多次波道集匹配3个原始数据道集,并可同时输出3个道集的一次波估计结果。另外,选取阈值权重s=0.06、正则化因子γ=0.001、最大迭代次数Mγ=20。
为了定量评价所提方法的性能,计算信噪比为
|
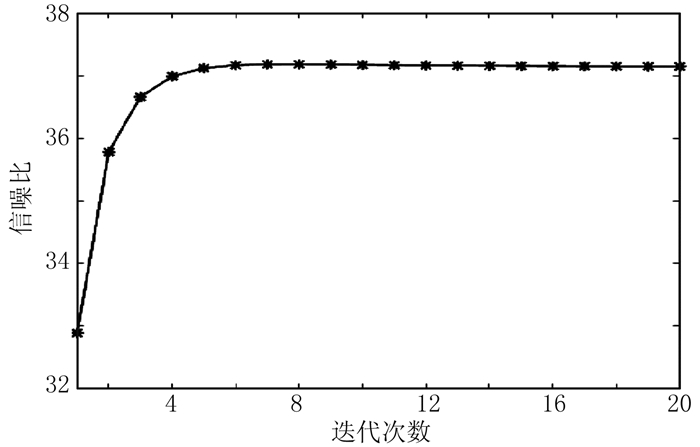
图 2 合成数据信噪比随迭代次数的变化曲线 对应于应用本文方法对图 3a估计的一次波 |
|
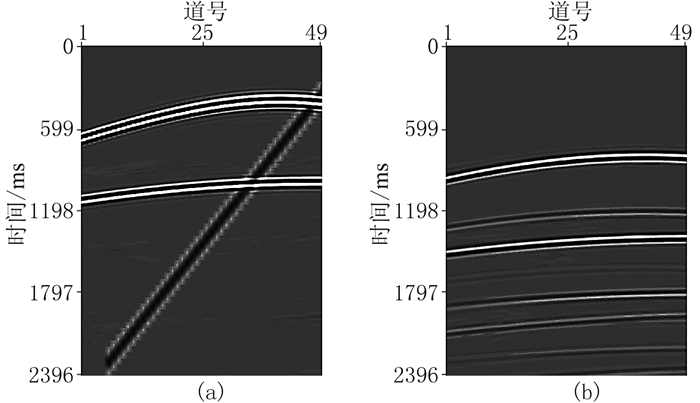
图 3 基于本文方法第6次迭代估计的一次波(a)及去除的多次波(b)的共炮点道集 |
从图 2可见,当迭代次数小于6时,一次波估计精度会随着迭代次数增加而明显提升;当迭代次数大于6后,一次波估计精度随迭代次数不会有明显提升。将基于本文方法的最大迭代次数设置为1,可得到基于一次波能量最小化的3D匹配滤波器方法的多次波自适应相减结果,此时信噪比曲线的取值为32.89。因此,本文方法比基于一次波能量最小化的3D匹配滤波器方法具有更高的一次波估计精度。
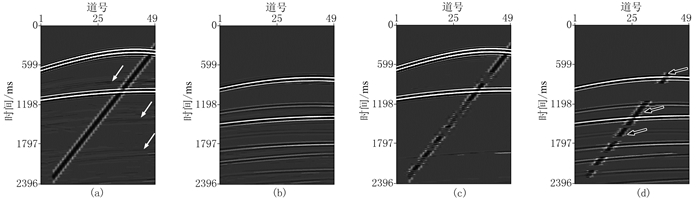
图 3a显示了用本文方法第6次迭代后的一次波估计结果,图 3b是所减去的多次波。图 4a显示基于一次波能量最小化的3D匹配滤波器方法的一次波估计结果,图 4b是所减去的多次波。图 4a中白色箭头表明,基于一次波能量最小化的3D匹配滤波器方法在有强一次波同相轴存在的地方,会残留多次波。图 4b中黑色箭头表明,基于一次波能量最小化的3D匹配滤波器方法会造成一次波损伤。因此,本文方法比基于一次波能量最小化的3D匹配滤波器方法能更好地均衡一次波保护与多次波压制。

|
图 4 基于一次波能量最小化的3D匹配滤波器方法估计的一次波(a)及去除的多次波(b)的共炮点道集 |
针对基于伪地震数据算法的2D匹配滤波器方法,选择数据窗口m=23、n=45;滤波器长度p=9、q=7。图 5a显示了基于伪地震数据算法的2D匹配滤波器方法的一次波估计结果,图 5b是所减去的多次波。图 5a中一次波估计所采用的阈值权重s=0.06、正则化因子γ=0.001、最大迭代次数Mγ=6,与图 3a对应参数的取值相同。图 5a中一次波的信噪比为31.40,其中白色箭头指示残留的多次波。可见基于伪地震数据算法的2D匹配滤波器方法不能有效均衡一次波保护与多次波分离。因此,本文方法比基于伪地震数据算法的2D匹配滤波器方法能更彻底地分离一次波与多次波,并得到更高的信噪比。

|
图 5 基于伪地震数据算法的2D匹配滤波器方法估计的一次波(a)及去除的多次波(b)的共炮点道集 |
为了分析所提方法中可选参数对一次波与多次波分离效果的影响,做了进一步的实验。
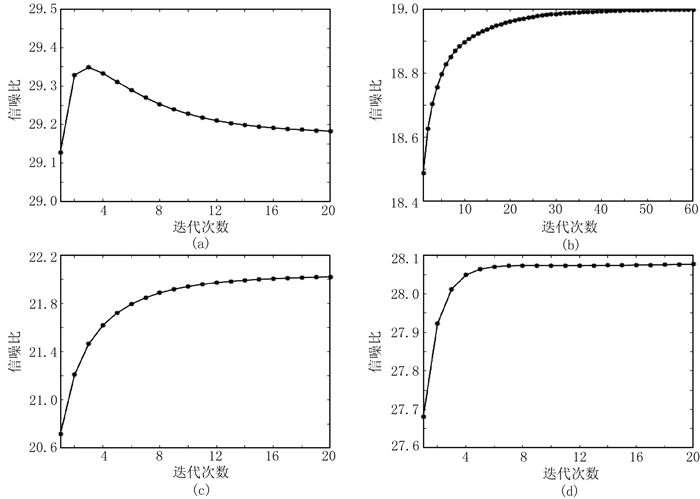
选择较大的3D数据窗口(m=60、n=47、k=3),其他参数(3D滤波器长度、阈值权重、正则化因子)与图 3a中的对应参数取值相同。图 6a给出信噪比随迭代次数的变化曲线,可见在第3次迭代时得到最高信噪比29.35。图 7a和图 7b给出在第3次迭代时一次波估计结果及去除的多次波。图 7a中白色箭头表明,当数据窗口变大时,本文方法会产生残余多次波,所得信噪比低于图 3a。
|
图 6 本文方法选取不同数据窗口和匹配滤波器长度合成数据的信噪比随迭代次数的变化曲线 (a)大窗口;(b)小窗口;(c)大匹配滤波器长度;(d)小匹配滤波器长度 |
|
图 7 本文方法不同数据窗口时合成数据的共炮点道集 (a)估计的一次波(大窗口);(b)去除的多次波(大窗口);(c)估计的一次波(小窗口);(d)去除的多次波(小窗口) |
选择较小数据窗口(m=11、n=11、k=3),其他参数(滤波器长度、阈值权重、正则化因子)取值与图 3a一次波对应参数相同。从图 6b的信噪比随迭代次数变化曲线易见,约在第50次时收敛,其信噪比为19.00。图 7c和图 7d给出第50次迭代时的一次波估计结果及去除的多次波。图 7d中黑色箭头表明,当数据窗口变小时,迭代结果会造成一次波损伤,其信噪比低于图 3a。
选择较大的3D匹配滤波器长度(p=15、q=11、r=3),其他参数(3D数据窗口、阈值权重、正则化因子)与图 3a中一次波对应的参数取值相同,图 6c给出信噪比随迭代次数的变化曲线,该曲线在第20次迭代时达到收敛,得到最高的信噪比22.02。图 8a和图 8b为在第20次迭代时的一次波估计和去除的多次波。图 8b中的黑色箭头表明,当匹配滤波器长度变大时,本文方法会造成一次波损伤现象,所得信噪比低于图 3a。
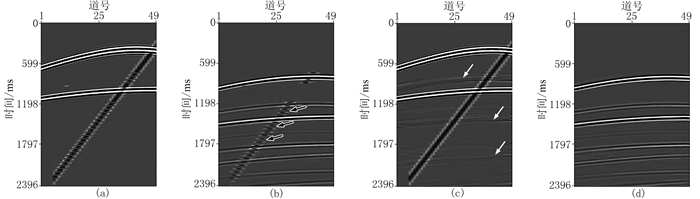
|
图 8 本文方法不同匹配滤波器长度时合成数据的共炮点道集 (a)估计的一次波(大匹配滤波器);(b)去除的多次波(大匹配滤波器);(c)估计的一次波(小匹配滤波器);(d)去除的多次波(小匹配滤波器) |
选择较小的3D匹配滤波器长度(p=q=r=3),其他参数(3D数据窗口大小、阈值权重、正则化因子)与图 3a中一次波所对应的参数取值相同,图 6d给出信噪比随迭代次数的变化曲线,该曲线在第7次迭代时达到收敛,信噪比为28.07。图 8c和图 8d为在第7次迭代时的一次波估计结果和去除的多次波。图 8c中的白色箭头表明,当匹配滤波器长度变小时,所提方法会残留多次波,得到的信噪比低于图 3a。
选择较大的阈值权重(s=0.99),其他参数(3D数据窗口大小、3D匹配滤波器长度、正则化因子)与图 3a中一次波所对应的参数取值相同。图 9a给出信噪比随迭代次数的变化曲线,在整个迭代过程中,信噪比大约为32.89。第3步迭代得到的信噪比(32.89)与基于一次波能量最小化的3D匹配滤波器方法得到的信噪比相同。图 10a和图 10b为在第3次迭代时的一次波估计结果和去除的多次波。图 10a中的白色箭头表明,当阈值权重变大时,所提方法会产生残余多次波,图 10b中的黑色箭头表明,当阈值权重变大时,所提方法会造成一次波损伤,得到的信噪比低于图 3a。
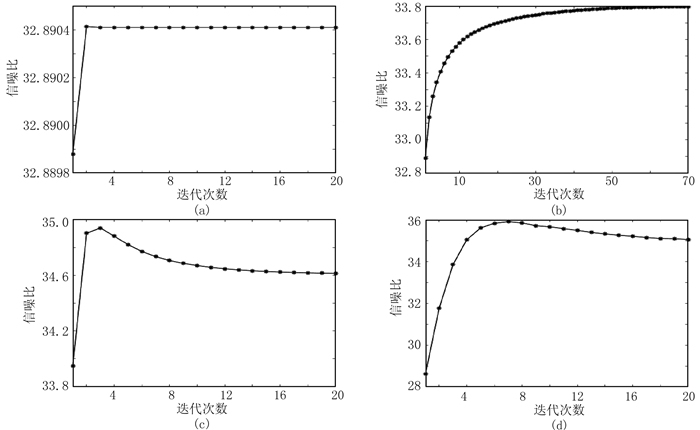
|
图 9 本文方法选取不同阈值权重和正则化因子时合成数据的信噪比随迭代次数的变化曲线 (a)大阈值权重;(b)小阈值权重;(c)大正则化因子;(d)小正则化因子 |
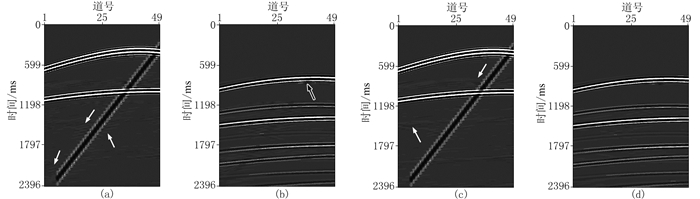
|
图 10 本文方法不同阈值权重时的合成数据的共炮点道集 (a)一次波(大阈值权重);(b)去除的多次波(大阈值权重);(c)一次波(小阈值权重);(d)去除的多次波(小阈值权重) |
选择较小的阈值权重(s=0.00001),其他参数(3D数据窗口、3D匹配滤波器长度、正则化因子)与图 3a中一次波所对应的参数取值相同,图 9b给出信噪比随迭代次数的变化曲线,该曲线在第60次迭代时达到收敛,信噪比为33.79。图 10c和图 10d为在第60步迭代时的一次波估计结果和去除的多次波。图 10c中的白色箭头表明,当阈值权重变小时,所提方法会产生残余多次波,所得信噪比低于图 3a。
选择较大的正则化因子(γ=0.1),其他参数(3D数据窗口大小、3D匹配滤波器长度、阈值权重)与图 3a中一次波所对应的参数取值相同。图 9c给出信噪比随迭代次数的变化曲线,该曲线在第3步迭代时收敛,信噪比为34.94。图 11a和图 11b为在3次迭代时的一次波估计结果和去除的多次波。图 11a中的白色箭头表明,当正则化因子变大时,所提方法会残留多次波,得到的信噪比低于图 3a。
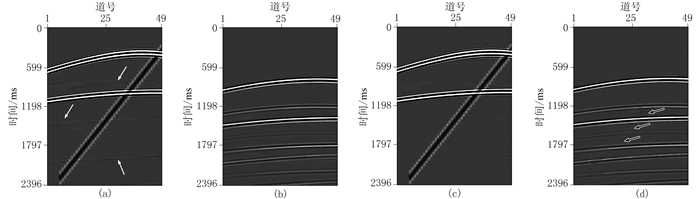
|
图 11 本文方法不同正则化因子时的合成数据的共炮点道集 (a)一次波(大正则化因子);(b)去除的多次波(大正则化因子);(c)一次波(小正则化因子);(d)去除的多次波(小正则化因子) |
选择较小的正则化因子(γ=0.0000001),其他参数(3D数据窗口大小、3D匹配滤波器长度、阈值权重)与图 3a中一次波所对应的参数取值相同。图 9d给出信噪比随迭代次数的变化曲线,该曲线在第7步迭代时收敛,信噪比为35.91。图 11c和图 11d为在7次迭代时的一次波估计结果和去除的多次波。图 11d中的黑色箭头表明,当正则化因子变小时,所提方法会造成一次波损伤,得到的信噪比低于图 3a。
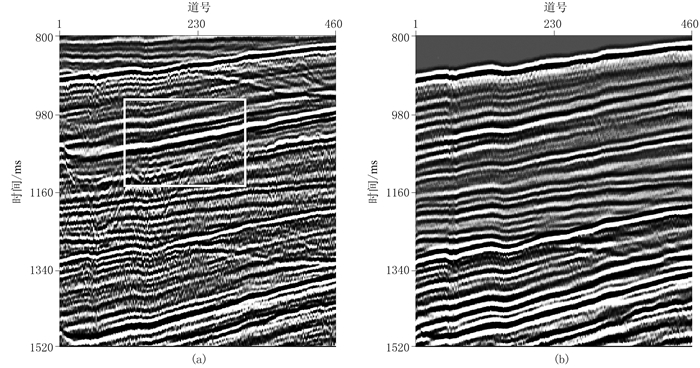
4.2 实际数据选取361个采样点(800~1520ms)、道数为460道的共炮检距道集展示多次波自适应相减的效果。图 12a显示了原始数据,图 12b为2D SRME方法预测的多次波。
|
图 12 共炮检距道集显示的原始实际地震数据(a)及2D SRME方法预测的多次波(b) |
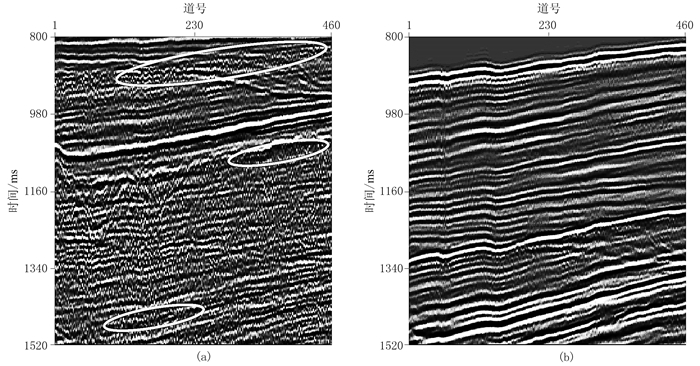
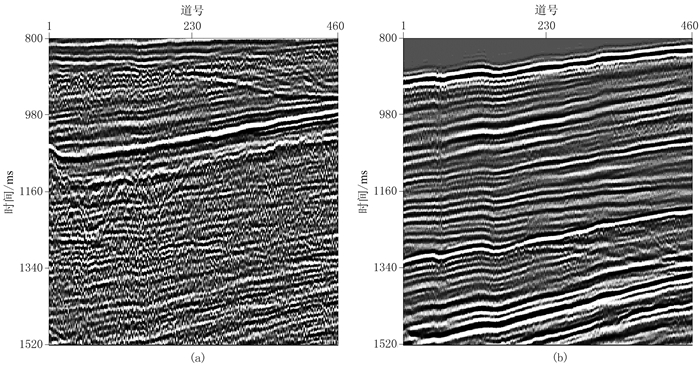
采用本文所提方法,选取3D数据窗口m=70、n=70、k=3,3D匹配滤波器长度p=3、q=5、r=3,阈值权重s=0.05,正则化因子γ=0.001,迭代次数Mγ=10。图 13a和图 13b分别为基于本文方法的一次波估计结果和减去的多次波。将基于本文方法的最大迭代次数设置为1,可以得到基于一次波能量最小化的3D匹配滤波器方法的多次波自适应相减结果。图 14a和图 14b分别为基于一次波能量最小化的3D匹配滤波器方法的一次波估计结果和减去的多次波。
|
图 13 本文方法估计的实际数据的一次波(a)及去除的多次波(b) |
|
图 14 基于一次波能量最小化的3D匹配滤波器方法估计的实际数据的一次波(a)及去除的多次波(b) |
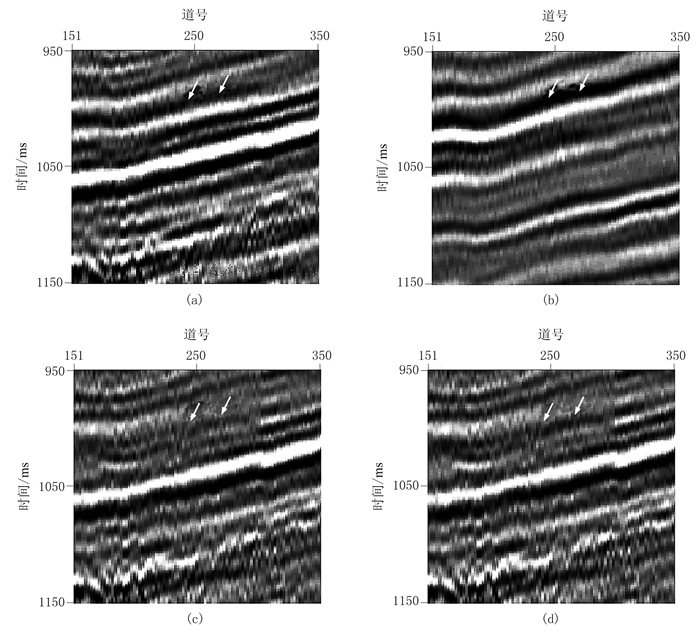
图 15a为图 12a中白色方框内数据的放大显示结果;图 15b为2D SRME方法预测多次波的放大显示结果;图 15c为基于本文方法估计一次波的放大显示结果;图 15d为基于一次波能量最小化的3D匹配滤波器方法估计一次波的放大显示结果。图 15d中的白色箭头表明,在有强一次波同相轴存在的地方,由于基于一次波能量最小化的3D匹配滤波器方法的正交性假设不满足,所以会残留多次波。对比图 15c与图 15d中的白色箭头处可见,基于本文方法比基于一次波能量最小化的3D匹配滤波器方法能更彻底地去除多次波。
|
图 15 实际数据的共炮检距道集放大显示 (a)原始数据;(b)预测多次波;(c)本文方法估计一次波;(d)基于一次波能量最小化的3D匹配滤波器方法估计的一次波 |
对于基于伪地震数据算法的2D匹配滤波器方法,选取2D数据窗口m=70、n=70,2D匹配滤波器长度p=3、q=5,阈值权重s=0.05,正则化因子γ=0.001,迭代次数Mγ=10。图 16a和图 16b分别为基于伪地震数据算法的2D匹配滤波器方法的一次波估计结果及去除的多次波。对比图 13a与图 16a中白色椭圆,可知本文方法能更彻底地去除残余多次波。
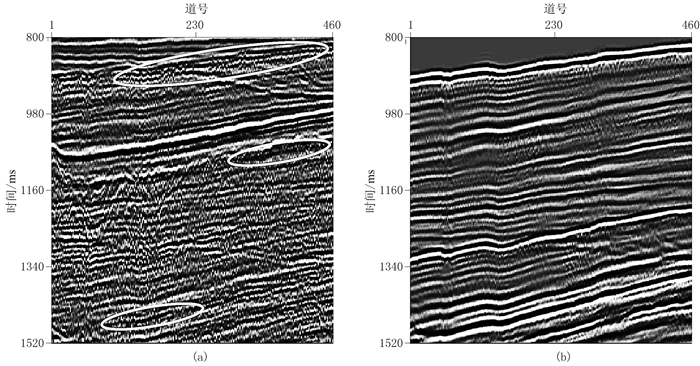
|
图 16 基于伪地震数据算法的2D匹配滤波器方法估计的一次波(a)及去除的多次波(b)的共炮检距道集 |
本文提出基于伪地震数据算法的3D匹配滤波器方法用于多次波自适应相减,即引入3D匹配滤波器,同时利用多个预测多次波道集匹配原始数据减少残余多次波;为避免3D匹配滤波器可能造成的一次波损伤现象,采用相同的3D匹配滤波器同时拟合多个原始数据道集;另外,对估计一次波施加Huber范数最小化约束,等价于对强一次波施加L1范数最小化约束和对弱一次波施加L2范数最小化约束。因此,所提方法不需满足一次波与多次波正交的假设。同时,所提方法引入伪地震数据算法将Huber范数最小化优化问题转化为L2范数最小化问题。在整个迭代过程中,伪地震数据算法只需利用Cholesky分解算法进行一次矩阵分解,计算效率比较高。模型和实际数据的处理结果表明,本文方法比基于伪地震数据算法的2D匹配滤波器方法和基于一次波能量最小化的3D匹配滤波器方法,能更好地均衡一次波的保护与多次波的压制。
| [1] |
戴晓峰, 徐右平, 甘利灯, 等. 川中深层-超深层多次波识别和压制技术——以高石梯-磨溪连片三维区为例[J]. 石油地球物理勘探, 2019, 54(1): 54-64. DAI Xiaofeng, XU Youping, GAN Lideng, et al. Deep & ultra-deep multiple suppression in Central Sichuan:an example of Gaoshiti-Moxi[J]. Oil Geophysical Prospecting, 2019, 54(1): 54-64. |
| [2] |
董烈乾, 李培明, 张奎, 等. 利用曲波变换预测多次波模型[J]. 石油地球物理勘探, 2015, 50(6): 1098-1104. DONG Lieqian, LI Peiming, ZHANG Kui, et al. Multiple model prediction based on Curvelet transform[J]. Oil Geophysical Prospecting, 2015, 50(6): 1098-1104. |
| [3] |
崔永福, 刘嘉辉, 陈猛, 等. 虚同相轴方法及其在陆上地震层间多次波压制中的应用[J]. 石油地球物理勘探, 2019, 54(6): 1228-1236. CUI Yongfu, LIU Jiahui, CHEN Meng, et al. Land seismic peg-leg multiple attenuation with the virtual event method[J]. Oil Geophysical Prospecting, 2019, 54(6): 1228-1236. |
| [4] |
Guitton A, Verschuur D J. Adaptive subtraction of multiples using the L1-norm[J]. Geophysical Prospecting, 2004, 52(1): 27-38. |
| [5] |
Wang Y H. Multiple subtraction using an expanded multichannel matching filter[J]. Geophysics, 2003, 68(1): 346-354. |
| [6] |
李鹏, 刘伊克, 常旭, 等. 均衡拟多道匹配滤波法在波动方程法压制多次波中的应用[J]. 地球物理学报, 2007, 50(6): 1844-1853. LI Peng, LIU Yike, CHANG Xu, et al. Application of the equipoise pseudo multichannel matching filter in multiple elimination using wave equation method[J]. Chinese Journal of Geophysics, 2007, 50(6): 1844-1853. |
| [7] |
Li Z X, Li Z C. Accelerated 3D blind separation of convolved mixtures based on the fast iterative shrinkage thresholding algorithm for adaptive multiple subtraction[J]. Geophysics, 2018, 83(2): V99-V113. |
| [8] |
Li Z X, Lu W K. Adaptive multiple subtraction based on 3D blind separation of convolved mixtures[J]. Geophysics, 2013, 78(6): V251-V266. |
| [9] |
Guitton A. Multiple attenuation in complex geology with a pattern-based approach[J]. Geophysics, 2005, 70(4): V97-V107. |
| [10] |
Manin M and Spitz S.3D attenuation of targeted multiples with a pattern recognition technique[C].Extended Abstracts of 57th EAGE Conference & Exhibition, 1995, B046. https://www.researchgate.net/publication/301469457_3D_Attenuation_of_Targeted_Multiples_with_a_Pattern_Recognition_Technique
|
| [11] |
Lu W K. Adaptive multiple subtraction using inde-pendent component analysis[J]. Geophysics, 2006, 71(5): S179-S184. |
| [12] |
Lu W K, Liu L. Adaptive multiple subtraction based on constrained independent component analysis[J]. Geophysics, 2009, 74(1): V1-V7. |
| [13] |
Verschuur D J.Seismic Multiple Removal Techniques: Past, Present and Future[M].EAGE Publications BV, 2006.
|
| [14] |
李钟晓, 陆文凯, 庞廷华, 等. 基于多道卷积信号盲分离的多次波自适应相减方法[J]. 地球物理学报, 2012, 55(4): 1325-1334. LI Zhongxiao, LU Wenkai, PANG Tinghua, et al. Adaptive multiple subtraction based on multi-traces convolutional signal blind separation[J]. Chinese Journal of Geophysics, 2012, 55(4): 1325-1334. |
| [15] |
Verschuur D J, Berkhout A J, Wapenaar C P A. Adaptive surface-related multiple elimination[J]. Geophy-sics, 1992, 57(9): 1166-1177. |
| [16] |
Guitton A, Symes W W. Robust inversion of seismic data using the Huber norm[J]. Geophysics, 2003, 68(4): 1310-1319. |
| [17] |
Huber P J and Ronchetti E M.Robust Statistics (2nd Edition)[M].John Wiley & Sons, New Jersey, 2011, 693.
|
| [18] |
李娜. 基于Huber范数的多震源最小二乘逆时偏移[J]. 石油地球物理勘探, 2017, 52(5): 941-947. LI Na. Multi-source least-squares reverse time migration based on Huber norm[J]. Oil Geophysical Pro-specting, 2017, 52(5): 941-947. |
| [19] |
Wong R K and Lee T. Matrix Completion with Noisy Entries and Outliers[M].arXiv, 1503.00214, 2015.
|
| [20] |
Li Z, Zhao Q, Zhang J. Robust POCS method for interpolation of seismic data[J]. Journal of Applied Geophysics, 2019, 170: 1-15. |
| [21] |
Zhao Q, Du Q, Gong X, et al. Signal-preserving erratic noise attenuation via iterative robust sparsity-promoting filter[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(6): 3547-3560. |
| [22] |
Higham N J. Cholesky factorization[J]. Wiley Interdisciplinary Reviews:Computational Statistics, 2009, 1: 251-254. |
| [23] |
Berkhout A J, Verschuur D J. Estimation of multiples scattering by iterative inversion.Part Ⅰ:Theore-tical consideration[J]. Geophysics, 1997, 62(5): 1586-1595. |
| [24] |
石颖, 王维红. 基于波动方程预测和双曲Radon变换联合压制表面多次波[J]. 地球物理学报, 2012, 55(9): 3115-3125. SHI Ying, WANG Weihong. Surface-related multiple suppression approach by combining wave equation prediction and hyperbolic Radon transform[J]. Chinese Journal of Geophysics, 2012, 55(9): 3115-3125. |
| [25] |
黄新武, 孙春岩, 牛滨华, 等. 基于数据一致性预测与压制自由表面多次波——理论研究与试处理[J]. 地球物理学报, 2005, 48(1): 173-180. HUANG Xinwu, SUN Chunyan, NIU Binhua, et al. Surface-related multiple prediction and suppression based on data-consistence:A theoretical study and test[J]. Chinese Journal of Geophysics, 2005, 48(1): 173-180. |



 李钟晓, 山东省青岛市市南区宁夏路308号青岛大学电子信息学院, 266071。Email:
李钟晓, 山东省青岛市市南区宁夏路308号青岛大学电子信息学院, 266071。Email: