2 青岛大学电子信息学院, 山东青岛 266071;
3 中国石油大学(华东)地球科学与技术学院, 山东青岛 266580;
4 中海油湛江分公司研究院, 广东湛江 524057
2 College of Electronic Information, Qingdao University, Qingdao, Shandong 266071, China;
3 School of Geosciences, China University of Petroleum(East China), Qingdao, Shandong 266580, China;
4 Research Institute of CNOOC Zhanjiang Branch, Zhanjiang, Guangdong 524057, China
多次波在地震剖面上会产生虚假反射同相轴,甚至会与一次波相互混叠,降低地震资料的信噪比和分辨率,影响一次波的成像精度[1]。目前,自由表面多次波的压制方法比较成熟,但随着勘探开发的不断深入,特别是陆地勘探逐渐转向高分辨率地震反演和成像,层间多次波的问题日益凸显。因此,如何有效压制层间多次波,是地震勘探的一个重要问题[1-3]。
与自由表面多次波的压制方法类似,层间多次波的压制方法可以分为两大类:滤波方法和基于波动方程理论的预测相减方法。后者主要包括两步,第一步是从速度模型或地震记录中预测出层间多次波,第二步是将预测的多次波从原始地震数据中自适应减去。目前层间多次波预测方法主要有两种:一种是基于物理界面的共聚焦点波场延拓方法[4];另一种是基于点散射物理模型的逆散射级数方法[5]。共聚焦点方法需要依赖速度模型,计算过程繁杂,且一次只能预测与一个界面相关的层间多次波,不适合预测复杂介质中的层间多次波。逆散射级数方法是基于散射理论[6]的多维直接反演方法。Carvalho等[7]利用T矩阵散射理论推导了层间多次波压制的非线性反演公式;Araújo等[8]利用点散射模型构建自由表面多次波和层间多次波的预测模型,并给出先压制自由表面多次波后压制层间多次波的处理流程;Coates等[9]在叠前1D/2D声波和弹性波合成数据中利用逆散射级数方法压制层间多次波;Weglein等[10]系统阐述了逆散射理论与地震勘探的关系,并将逆散射理论应用于自由表面多次波去除、层间多次波去除和地震成像中;Malcolm[11]在地震成像的共成像点道集中利用逆散射理论去除层间多次波;金德刚等[12]对基于逆散射级数的层间多次波预测方法进行优化改进,以进一步提高预测精度和效率;杨金龙等[13]通过去除和补偿子波提高逆散射级数层间多次波预测的精度。
逆散射级数法压制多次波,是将散射级数分离成与鬼波、自由表面多次波和层间多次波相关的不同子级数,以实现多次波的预测,是个完全数据驱动的过程,不需要地下介质的先验信息,并且可以从逆散射子序列中一次性地预测出与所有层界面相关的同阶次多次波。实现层间多次波预测后,由于预测多次波与真实多次波之间存在空间、时间以及振幅等差异,因此需要将预测多次波和原始数据进行匹配,再从原始数据中减去,这个过程称为多次波自适应相减[14-16]。设计匹配滤波器是常用的多次波自适应相减方法,首先要建立与一次波相关的目标函数,通过优化目标函数求取合适的匹配滤波器,使预测多次波逼近真实多次波,进而估计一次波。依据不同的假设建立目标函数就可以实现不同的滤波方法。将L2范数最小化作为目标函数是最常用的一种方法,但它有两个假设条件:一是地震记录中的一次波与多次波具有正交性;二是压制多次波后的地震记录剩余能量最小[15]。当多次波周围有强一次波或者多次波与一次波相交时,不满足上述两个假设条件。因此,在这种情况下,基于一次波L2范数最小化的方法难以实现预测多次波与真实多次波的正确匹配。为了消除这些限制,L1范数匹配滤波[16]、独立成分分析(ICA)[17-18]以及盲信号分离[19-21]等方法相继被提出,这些方法在分离一次波和多次波的过程中利用了地震信号的非高斯分布特性,对一次波施加稀疏约束,能够在压制多次波的同时,更好地保护一次波。
本文首先推导了简化的逆散射级数公式以实现层间多次波的准确预测,然后阐述了2D卷积盲分离方法实现层间多次波的自适应相减。模型试算和实际资料应用结果表明,本文的层间多次波自适应压制方法是数据驱动的,不需要多次波和一次波的正交性假设条件,在消除多次波的同时能更好地保护一次波。
1 方法原理 1.1 逆散射级数层间多次波预测方法根据Weglein等[5]和Araújo等[8]提出的基于逆散射级数的2D层间多次波预测公式,并结合金德刚等[12, 22]给出的逆散射级数波场预测的改进策略,首先对基于逆散射级数的1D和1.5D层间多次波预测公式进行推导。
假设炮点和检波点的深度相等且为零,可以得到1D层间多次波预测公式
| $ \begin{array}{*{20}{l}} {{b_{\rm{p}}}(\omega ) = \int_{ - \infty }^{ + \infty } {{{\rm{e}}^{ - {\rm{i}}\omega {t_1}}}} b({t_1}){\rm{d}}{t_1}\int_{ - \infty }^{{t_1} - \varepsilon } {{{\rm{e}}^{{\rm{i}}\omega {t_2}}}} b({t_2}){\rm{d}}{t_2} \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_{{t_2} + \varepsilon }^{ + \infty } {{{\rm{e}}^{ - {\rm{i}}\omega {t_3}}}} b({t_3}){\rm{d}}{t_3}} \end{array} $ | (1) |
式中:b(t)是1D地震记录;bp(ω)是频率域的1D层间多次波预测结果;ε是子波长度;ω是角频率;t1、t2和t3是多重积分的不同时间区间。由式(1)积分上下限的关系可知,t2≤t1-ε, t3≥t2+ε。
在近似水平的层状介质条件下,通过引入阶跃函数,式(1)可以写为
| $ \begin{array}{*{20}{l}} {{b_{\rm{p}}}(\omega ) = \int_{ - \infty }^{ + \infty } {{\rm{e}}_1^{ - {\rm{i}}\omega t}} b({t_1}){\rm{d}}{t_1} \times }\\ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_{ - \infty }^{ + \infty } H ({t_1} - \varepsilon - {t_2}){{\rm{e}}^{{\rm{i}}\omega {t_2}}}b({t_2}){\rm{d}}{t_2} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_{ - \infty }^{ + \infty } H ({t_3} - \varepsilon - {t_2}){{\rm{e}}^{ - {\rm{i}}\omega {t_3}}}b({t_3}){\rm{d}}{t_3} \end{array} \end{array} $ | (2) |
交换积分次序可得
| $ \begin{array}{*{20}{l}} {{b_{\rm{p}}}(\omega ) = \int_{ - \infty }^{ + \infty } {{{\rm{e}}^{{\rm{i}}\omega {t_2}}}} b({t_2}){\rm{d}}{t_2}\int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } b } ({t_1}) \times }\\ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} H({t_1} - \varepsilon - {t_2})H({t_3} - \varepsilon - {t_2}) \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} b({t_3}){{\rm{e}}^{ - {\rm{i}}\omega ({t_3} + {t_1})}}{\rm{d}}{t_3}{\rm{d}}{t_1} \end{array} \end{array} $ | (3) |
利用阶跃函数的性质可得
| $ \begin{array}{*{20}{l}} {{b_{\rm{p}}}(\omega ) = \int_{ - \infty }^{ + \infty } {{\rm{e}}_2^{{\rm{i}}\omega t}} b({t_2}){\rm{d}}{t_2}\int_{{t_2} + \varepsilon }^{ + \infty } {{{\rm{e}}^{ - {\rm{i}}\omega {t_1}}}} b({t_1}){\rm{d}}{t_1} \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_{{t_2} + \varepsilon }^{ + \infty } {{{\rm{e}}^{ - {\rm{i}}\omega {t_3}}}} b({t_3}){\rm{d}}{t_3}} \end{array} $ | (4) |
式中
对频率域预测结果做反傅里叶变换,可得时间域的1D层间多次波预测结果
| $ {b_{\rm{p}}}(t) = \int_{ - \infty }^{ + \infty } {{{\rm{e}}^{{\rm{i}}\omega t}}} {b_{\rm{p}}}(\omega ){\rm{d}}\omega $ | (5) |
对比式(1)与式(4)可知,对层间多次波预测公式简化之前,对b(t3)的积分与t1、t2均有关。简化之后,对b(t3)的积分仅与t2有关,因此,简化公式可以有效降低层间多次波预测的计算复杂度。
同样地,通过引入阶跃函数可以推导出如下的叠前层间多次波预测公式
| $ \begin{array}{l} {b_{\rm{p}}}({x_{\rm{s}}},{x_{\rm{g}}},\omega )\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \int_{ - \infty }^{ + \infty } {\rm{d}} {x_{{\rm{s}}1}}\int_{ - \infty }^{ + \infty } {\rm{d}} {x_{{\rm{g}}1}}\int_{ - \infty }^{ + \infty } b ({x_{{\rm{s1}}}},{x_{{\rm{g}}1}},{t_2}){{\rm{e}}^{{\rm{i}}\omega {t_2}}}{\rm{d}}{t_2} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_{{t_{{\rm{m2}}}}}^{ + \infty } b ({x_{\rm{s}}},{x_{{\rm{g}}1}},{t_1}){{\rm{e}}^{ - {\rm{i}}\omega {t_1}}}{\rm{d}}{t_1}\int_{{t_{{\rm{m}}1}}}^{ + \infty } b ({x_{{\rm{s}}1}},\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_{\rm{g}}},{t_3}){{\rm{e}}^{ - {\rm{i}}\omega {t_3}}}{\rm{d}}{t_3} \end{array} $ | (6) |
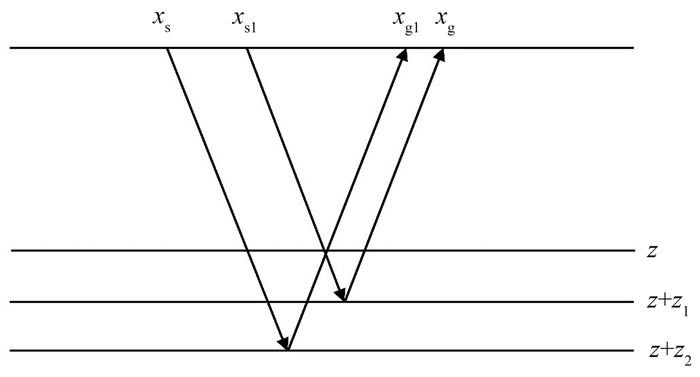
式中:bp(xs, xg, ω)为频率域的层间多次波预测结果;b(xs, xg, t)为时间域的叠前道集;tm1、tm2为时间积分区间的下限。其他变量结合图 1说明:xs、xg分别表示预测层间多次波的炮点位置和检波点位置;xs1、xg1为式(6)中的积分参数,分别表示积分炮点位置和检波点位置,选取的xs1和xg1通常位于xs与xg中间,即利用xs与xg之间采集的道进行层间多次波预测。
|
图 1 层间多次波预测原理示意图 |
在2D情况下,tm1、tm2与层间多次波下行反射的位置、地震子波长度、xs、xs1和xg、xg1有关。在1.5D的共中心点道集中,b(xs, xg, t)表示时间域的共中心点道集,假设xs=-xg, xs1=-xg1,则tm1、tm2可以表示为
| $ \left\{ {\begin{array}{*{20}{l}} {{t_{{\rm{m1}}}} = {t_1} + \frac{{\sqrt {{{({x_{\rm{g}}} - {x_{{\rm{g1}}}})}^2} + 4z_1^2} }}{v}}\\ {{t_{{\rm{m2}}}} = {t_2} + \frac{{\sqrt {{{({x_{\rm{s}}} - {x_{{\rm{s1}}}})}^2} + 4z_2^2} }}{v}} \end{array}} \right. $ | (7) |
式中:v表示参考速度;z1、z2表示发生层间多次波反射的地层深度间隔(图 1)。进一步地,可以限定xs1、xg1分别位于有限积分区间[x1,x2]、[x3,x4],则1.5D层间多次波预测公式为
| $ \begin{array}{*{20}{l}} {{b_{\rm{p}}}({x_{\rm{s}}},{x_{\rm{g}}},\omega )}\\ { = \int_{{x_1}}^{{x_2}} d {x_{{\rm{s1}}}}\int_{{x_3}}^{{x_4}} d {x_{{\rm{g1}}}}\int_{ - \infty }^{ + \infty } b ({x_{{\rm{s1}}}},{x_{{\rm{g1}}}},{t_2}){{\rm{e}}^{{\rm{i}}\omega {t_2}}}{\rm{d}}{t_2} \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_{{t_{{\rm{m2}}}}}^{ + \infty } b ({x_{\rm{s}}},{x_{{\rm{g1}}}},{t_1}){{\rm{e}}^{ - {\rm{i}}\omega t}}{\rm{d}}{t_1}\int_{{t_{m1}}}^{ + \infty } b ({x_{{\rm{s1}}}},{x_{\rm{g}}},{t_3}){{\rm{e}}^{ - {\rm{i}}\omega {t_3}}}{\rm{d}}{t_3}} \end{array} $ | (8) |
对频率域的1.5D层间多次波预测结果进行反傅里叶变换,可以得到时间域1.5D层间多次波预测结果
| $ {b_{\rm{p}}}({x_{\rm{s}}},{x_{\rm{g}}},t) = \int_{ - \infty }^{ + \infty } {{{\rm{e}}^{{\rm{i}}\omega t}}} {b_{\rm{p}}}({x_{\rm{s}}},{x_{\rm{g}}},\omega ){\rm{d}}\omega $ | (9) |
式(8)中,通过选取的适当积分区间[x1,x2]、[x3,x4],并根据式(7)计算tm1、tm2,可以有效降低1.5D层间多次波预测的计算量。
与在伪深度波数域实现逆散射级数波场预测的方法[5, 8]不同,上述推导的逆散射级数波场预测方法不需要做偏移和反偏移,不会引入偏移噪声,计算量比较小[12, 22]。而且,在上述的层间多次波预测公式推导中,没有破坏逆散射级数方法预测层间多次波的单调性条件[12, 22]。
预测的层间多次波与真实多次波存在时间、空间、振幅等差异,因此需要将预测多次波从原始数据中自适应减去[1, 15]。
1.2 2D卷积盲分离方法假设s是原始地震记录,由真实一次波p0和真实多次波m两部分[16, 21]构成
| $ \mathit{\boldsymbol{s}} = {\mathit{\boldsymbol{p}}_0} + \mathit{\boldsymbol{m}} $ | (10) |
考虑地震数据的非稳态特性,2D卷积盲分离方法是将地震数据进行分窗处理,在每一个处理窗口中用一个2D卷积核表示预测多次波与真实多次波之间的时间和空间等差异。因此,真实多次波与预测多次波的关系可以表示为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\tilde m}} = \mathit{\boldsymbol{m}}*\mathit{\boldsymbol{h}}}\\ {\mathit{\boldsymbol{m}} = \mathit{\boldsymbol{\tilde m}}*{\mathit{\boldsymbol{h}}^{ - 1}}} \end{array}} \right. $ | (11) |
式中:
| $ \mathit{\boldsymbol{p}} = \mathit{\boldsymbol{s}} - \mathit{\boldsymbol{\tilde m}}*\mathit{\boldsymbol{f}} = \mathit{\boldsymbol{s}} - \mathit{\boldsymbol{\tilde Mf}} $ | (12) |
式中:p为估计的一次波;
如何选取目标函数来设计滤波器f,使预测多次波经过滤波后与真实多次波之间的差异最小是至关重要的。常用的基于L2范数的多次波自适应相减方法[1, 15]将分离出的一次波L2范数最小化作为目标函数。然而,地震数据满足超高斯分布[23]。根据中心极限定理,多个独立随机变量之和的分布比其中任何一个随机变量的分布更接近于高斯分布[24]。这就意味着,在每一处理窗口中原始地震数据减去多次波后,所得到的一次波具有最大的超高斯性。为了更加吻合地震信号的统计特性,本文选用卷积信号盲分离中的非高斯性最大化准则作为目标函数求取滤波器f。不同的非高斯性度量准则的选取对实际地震数据的处理结果有比较大的影响。负熵是常用的非高斯性度量准则,但它的多项式阶数高,对大值敏感,所以需要寻找合适的负熵近似公式,削弱其对噪声的敏感性[21, 24]。对于具有零均值和单位方差的随机信号,可以利用近似公式建立目标函数
| $ {\rm{max}}J(\mathit{\boldsymbol{f}}) = {\{ E[G(\mathit{\boldsymbol{\bar p}})] - E[G(\mathit{\boldsymbol{u}})]\} ^2} $ | (13) |
式中:p为对一次波p进行零均值和方差归一化后的结果;u是满足零均值和单位方差高斯分布的随机信号;E(·)表示求均值;G(·)为非线性函数
| $ G(x) = - {\rm{exp}} ( - \frac{{{x^2}}}{2}) $ | (14) |
另外,已经证明对一次波施加非高斯最大化约束等同于对一次波施加L1范数最小化约束[20]。为了确保滤波器估计的稳定性,对滤波器系数施加能量最小化约束,相应的优化问题可以表示为
| $ \arg {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {{\rm{min}}}\limits_f \left[ {{{\left\| {\mathit{\boldsymbol{s}} - \mathit{\boldsymbol{\tilde Mf}}} \right\|}_1} + \alpha \left\| \mathit{\boldsymbol{f}} \right\|_2^2} \right] $ | (15) |
式中加权因子α是用于均衡一次波的稀疏约束项与滤波器系数的能量最小化约束项。
迭代重加权最小二乘算法[16, 21]可用于求解2D卷积盲分离方法中的稀疏优化问题。然而,该算法在每一步迭代需要求解一个重加权最小二乘问题,加权矩阵与所估计一次波的振幅值有关,所以每一步迭代中的加权矩阵均不同,且需要在每一步迭代进行一次矩阵求逆,计算量比较大。本文引入快速迭代收缩阈值算法[25-26]求解2D卷积盲分离中的稀疏优化问题,该算法利用收缩阈值算子求解L1范数最小化优化问题,提高所估计一次波的稀疏性,且在整个迭代过程中只需要进行一次矩阵求逆,计算量比较小。利用快速迭代收缩阈值算法求解式(15)中优化问题得到匹配滤波器f后,再利用式(12)估计一次波。
为了定量评价自适应相减方法的性能,定义信噪比(SNR)参数
| $ {\rm{SNR}} = 10 \times {\rm{lg }}\frac{{\left\| {{\mathit{\boldsymbol{p}}_0}} \right\|_2^2}}{{\left\| {\mathit{\boldsymbol{p}} - {\mathit{\boldsymbol{p}}_0}} \right\|_2^2}} $ | (16) |
SNR越大,说明方法精度越高。
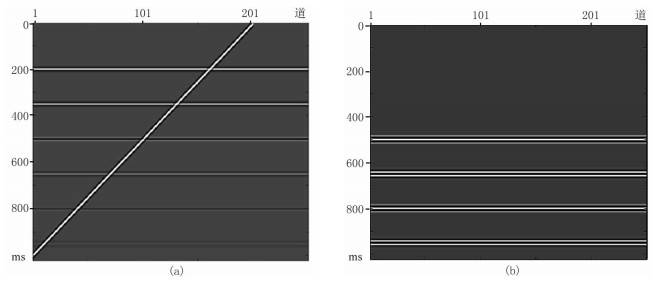
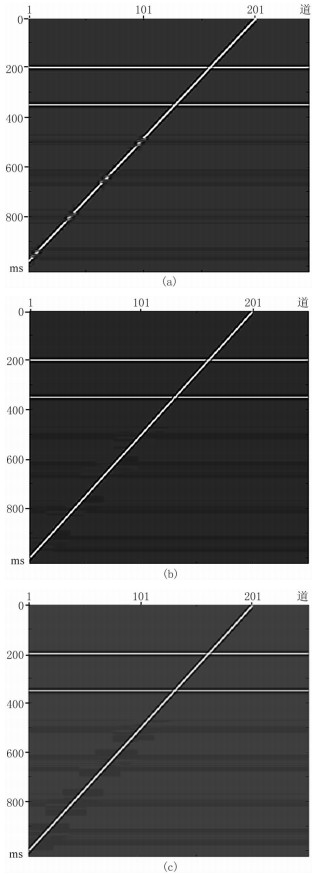
2 模型试算与应用实例 2.1 简单层状模型首先利用简单层状模型数据进行方法验证。图 2a是用褶积模型合成的含层间多次波的简单模型,假定最上面两个水平同相轴以及倾斜同相轴是一次波,下面四个水平同相轴是层间多次波。图 2b是用1D逆散射级数法预测的层间多次波。分别利用单道卷积盲分离、多道卷积盲分离以及多道L2范数最小化方法压制多次波,结果如图 3所示。由图可见:当有效波与多次波相交时,单道卷积盲分离方法会对有效波造成严重的损伤,而多道卷积盲分离方法则能在减去多次波的同时保护有效波;并且,在有效波与多次波的相交处,多道卷积盲分离方法残余的多次波少,压制效果优于多道L2范数最小化方法。针对不同方法所得的压制效果,利用式(16)求取其信噪比(表 1)。表 1中的多道卷积盲分离方法结果信噪比最高,进一步验证了多道卷积盲分离方法的优势。
|
图 2 简单层状模型数据 (a)含有层间多次波的模型;(b)预测的层间多次波 |
|
图 3 层状模型数据不同方法的层间多次波压制结果 (a)单道卷积盲分离方法;(b)多道卷积盲分离方法;(c)多道L2范数最小化方法 |
|
|
表 1 简单层状模型数据不同方法压制结果的信噪比 |
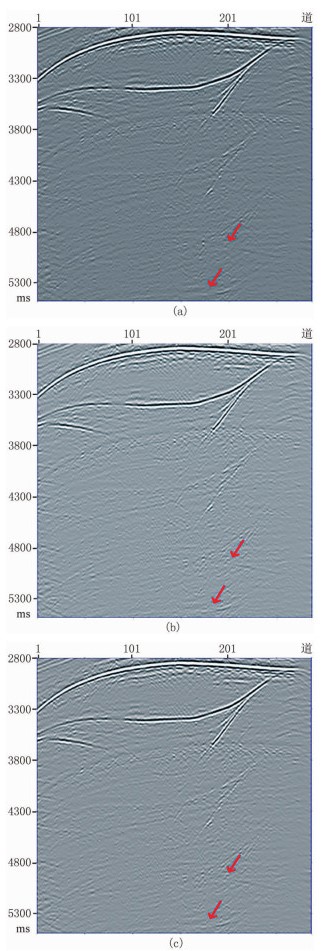
SMARRT模型数据中包含明显的自由表面多次波和层间多次波,在利用逆散射级数预测层间多次波前,首先要去除数据中的自由表面多次波。图 4a是去除自由表面多次波后的共炮检距道集。针对单一的共炮检距道集,可以采用1D逆散射级数方法预测层间多次波(图 4b)。图 5是利用单道卷积盲分离、多道卷积盲分离以及多道L2范数最小化方法对预测多次波进行自适应相减后得到的结果。对比红色箭头所示位置可以发现:三种方法都可以实现层间多次波的压制,但由于地层并非完全满足水平假设条件,1D逆散射级数方法预测的层间多次波与真实多次波存在比较大的相位差异,导致自适应相减后存在部分残余多次波。图 6为三种方法的差值剖面(即去除的多次波)。对比图 6中的红红色箭头所示位置,单道卷积盲分离比多道卷积盲分离对多次波的压制力度更大。当层间多次波周围没有强振幅有效波时,多道卷积盲分离与多道L2范数最小化方法具有相近的压制效果。
|
图 4 SMARRT模型数据 (a)去除自由表面多次波后的共炮检距道集;(b)预测的层间多次波 |
|
图 5 SMARRT模型数据不同方法的层间多次波压制结果 (a)单道卷积盲分离方法;(b)多道卷积盲分离方法;(c)多道L2范数最小化方法 |

|
图 6 SMARRT模型数据不同压制方法的差值剖面 (a)单道卷积盲分离方法;(b)多道卷积盲分离方法;(c)多道L2范数最小化方法 |
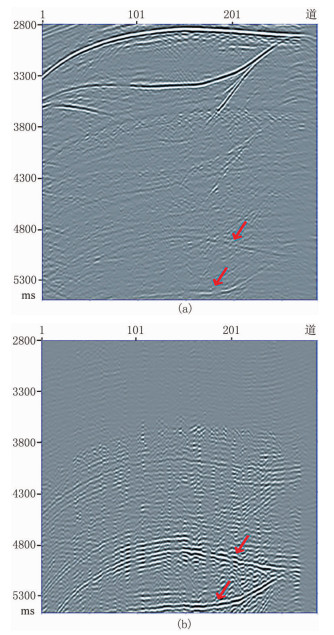
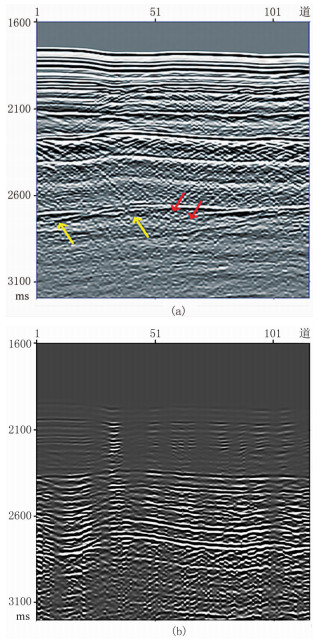
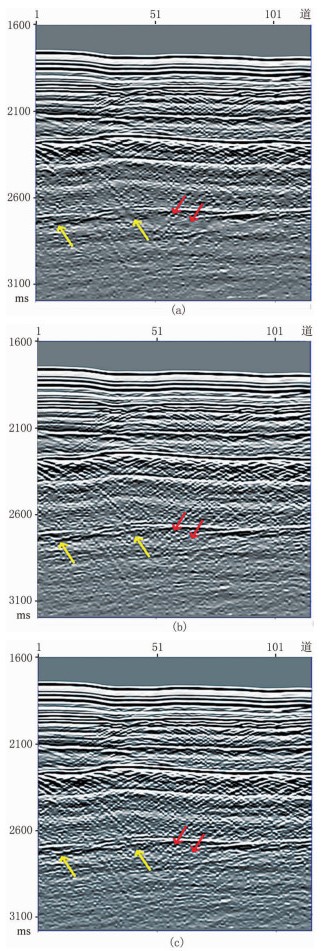
利用陆上实际数据验证本文方法的有效性。对实际共炮检距道集(图 7a),利用1.5D逆散射级数方法预测其层间多次波(图 7b)。相对于1D逆散射级数方法,1.5D逆散射级数方法计算量大,但对层间多次波的预测精度较高。分别用单道卷积盲分离、多道卷积盲分离和多道L2范数最小化方法压制多次波,其结果如图 8所示。对比可以发现:1.5D逆散射级数方法可以有效地预测层间多次波的旅行时;利用单道和多道卷积盲分离方法都可以实现层间多次波压制(图 8a和图 8b中红色箭头所示),但使用单道相减方法时,会对有效波造成损伤(图 8a中黄色箭头所示)。图 9是图 8a和图 8b中2600~2800ms的局部放大,黄色箭头处更加清晰地显示了单道相减方法会造成一次波损伤,并证明了多道相减方法的优势。图 10对多道卷积盲分离与L2范数最小化两种方法的差值剖面进行比较,多道L2范数最小化方法的差值剖面中含有较强的有效波,而本文采用的多道卷积盲分离方法在有效压制多次波的同时,能更好地保护有效波(图 10中红色箭头所示)。
|
图 7 实际数据共炮检距道集(a)及预测的层间多次波(b) |
|
图 8 实际资料不同方法的层间多次波压制结果 (a)单道卷积盲分离方法;(b)多道卷积盲分离方法;(c)多道L2范数最小化方法 |

|
图 9 单道(a)和多道(b)自适应相减法压制结果的局部放大对比 |

|
图 10 实际资料不同方法去除多次波前后差值剖面对比 (a)多道卷积盲分离方法;(b)多道L2范数最小化方法 |
本文研究了逆散射级数方法进行层间多次波预测,并利用2D卷积盲分离方法将预测多次波从原始数据中自适应减去以实现层间多次波的压制。通过理论公式推导、模型试算以及实际资料应用,可以得到以下结论:
(1) 本文方法不依赖速度模型,能有效实现层间多次波的预测和自适应相减;
(2) 同常规的多道L2范数最小化方法相比,本文方法可以在资料不满足一次波与多次波正交假设的情况下更好地保护有效波;
(3) 在对预测层间多次波进行自适应相减时,采用多道相减方法优于单道相减方法,多道相减方法能有效避免对有效波造成损伤。
下一步将深化研究高维(2D/3D)逆散射级数公式的简化策略,以进一步提高层间多次波预测的效率和精度。
| [1] |
Verschuur D J. Seismic Multiple Removal Techniques:Past, Present and Future[M]. Netherlands: EAGE Publications BV, 2006.
|
| [2] |
陈泓竹, 王彦春. 频率域拉动变换加权约束反演压制层间多次波[J]. 石油地球物理勘探, 2018, 53(4): 666-673. CHEN Hongzhu, WANG Yanchun. Peg-leg multiple suppression with the weight-constrain inversion of Radon transform in the frequency domain in Songliao Basin[J]. Oil Geophysical Prospecting, 2018, 53(4): 666-673. |
| [3] |
崔永福, 刘嘉辉, 陈猛, 等. 虚同相轴方法及其在陆上地震层间多次波压制中的应用[J]. 石油地球物理勘探, 2019, 54(6): 1228-1236. CUI Yongfu, LIU Jiahui, CHEN Meng, et al. Land seismic peg-leg multiple attenuation with the virtual event method[J]. Oil Geophysical Prospecting, 2019, 54(6): 1228-1236. |
| [4] |
Berkout A J, Verschuur D J. Removal of internal multiples with the common-focus-point(CFP) approach, Part Ⅰ:Explanation of the theory[J]. Geophysics, 2005, 70(3): V45-V60. |
| [5] |
Weglein A B, Gasparotto F A, Carvalho P M, et al. An inverse scattering series method for attenuating multiples in seismic reflection data[J]. Geophysics, 1997, 62(6): 1975-1989. DOI:10.1190/1.1444298 |
| [6] |
Norton S J. Iterative seismic inversion[J]. Geophysical Journal International, 1988, 94(3): 457-468. DOI:10.1111/j.1365-246X.1988.tb02268.x |
| [7] |
Carvalho F M, Weglein A B, Stolt R H.Examples of a nonlinear inversion method based on the T matrix of scattering theory: application to multiple suppression[C].SEG Technical Program Expanded Abstracts, 1991, 10: 1319-1322.
|
| [8] |
Araújo F V, Weglein A B, Carvalho P M, et al.Inverse scattering series for multiple attenuation: An example with surface and internal multiples[C].SEG Technical Program Expanded Abstracts, 1994, 13: 1039-1041.
|
| [9] |
Coates R T and Weglein A B.Internal multiple atte-nuation using inverse scattering: Results from pre-stack 1 & 2D acoustic and elastic synthetics[C].SEG Technical Program Expanded Abstracts, 1996, 15: 1522-1525.
|
| [10] |
Weglein A B, Araujo F V, Carvalho P M, et al. Inverse scattering series and seismic exploration[J]. Inverse Problems, 2003, 19(6): R27-R83. DOI:10.1088/0266-5611/19/6/R01 |
| [11] |
Malcolm A E.Inverse multiple scattering in the downward continuation approach[C].SEG Technical Program Expanded Abstracts, 2004, 23: 456-459.
|
| [12] |
金德刚, 常旭, 刘伊克. 逆散射级数法预测层间多次波的算法改进及其策略[J]. 地球物理学报, 2008, 51(4): 1209-1217. JIN Degang, CHANG Xu, LIU Yike. Algorithm improvement and strategy of internal multiples prediction based on inverse scattering series method[J]. Chinese Journal of Geophysics, 2008, 51(4): 1209-1217. DOI:10.3321/j.issn:0001-5733.2008.04.032 |
| [13] |
杨金龙, 朱立华. 逆散射级数层间多次波压制方法及应用[J]. 石油物探, 2018, 57(6): 853-861. YANG Jinlong, ZHU Lihua. Inverse scattering series internal multiple attenuation method and its application[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 853-861. DOI:10.3969/j.issn.1000-1441.2018.06.007 |
| [14] |
陆文凯. 基于L1范数多项式拟合的多次波消除方法[J]. 石油地球物理勘探, 2011, 46(3): 386-389. LU Wenkai. Multiples suppression using L1-norm based polynomial approximation[J]. Oil Geophysical Prospecting, 2011, 46(3): 386-389. |
| [15] |
井洪亮, 石颖, 李莹. 基于L1/L2范数的表面多次波自适应相减方法[J]. 石油地球物理勘探, 2015, 50(4): 619-625. JING Hongliang, SHI Ying, LI Ying. Surface-related multiple adaptive subtraction method based on L1/L2 norm[J]. Oil Geophysical Prospecting, 2015, 50(4): 619-625. |
| [16] |
Guitton A, Verschuur D J. Adaptive subtraction of multiples using the L1-norm[J]. Geophysical Pros-pecting, 2004, 52(1): 27-38. DOI:10.1046/j.1365-2478.2004.00401.x |
| [17] |
Kaplan S T, Innanen K A. Adaptive separation of free-surface multiples through independent component analysis[J]. Geophysics, 2008, 73(3): V29-V36. |
| [18] |
Lu W K, Liu L. Adaptive multiple subtraction based on constrained independent component analysis[J]. Geophysics, 2009, 74(1): V1-V7. |
| [19] |
Li Z X, Lu W K. Adaptive multiple subtraction based on 3D blind separation of convolved mixtures[J]. Geophysics, 2013, 78(6): V251-V266. DOI:10.1190/geo2012-0455.1 |
| [20] |
Li Z X, Li Z C. Accelerated 3D blind separation of convolved mixtures based on the fast iterative shrin-kage thresholding algorithm for adaptive multiple subtraction[J]. Geophysics, 2018, 83(2): V99-V113. |
| [21] |
李钟晓, 陆文凯, 庞廷华, 等. 基于多道卷积信号盲分离的多次波自适应相减方法[J]. 地球物理学报, 2012, 55(4): 1325-1334. LI Zhongxiao, LU Wenkai, PANG Tinghua, et al. Adaptive multiple subtraction based on multi-traces convolutional signal blind separation[J]. Chinese Journal of Geophysics, 2012, 55(4): 1325-1334. DOI:10.6038/j.issn.0001-5733.2012.04.028 |
| [22] |
金德刚.基于波动方程的层间多次波预测方法研究[D].北京: 中国科学院地质与地球物理研究所, 2007. JIN Degang.Internal Multiples Prediction Methods Based on Wave-equation[D].Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing, 2007. |
| [23] |
Walden A T. Non-Gaussian reflectivity, entropy, and deconvolution[J]. Geophysics, 1985, 50(12): 2862-2888. DOI:10.1190/1.1441905 |
| [24] |
Hyvarinen A. Fast and robust fixed-point algorithms for independent componet analysis[J]. IEEE Transctions on Netural Networks, 1999, 10(3): 626-634. DOI:10.1109/72.761722 |
| [25] |
Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Science, 2009, 2(1): 183-202. DOI:10.1137/080716542 |
| [26] |
Li Z X, Li Z C, Lu W K. Multichannel predictive deconvolution based on the fast iterative shrinkage-thresholding algorithm[J]. Geophysics, 2016, 81(1): V17-V30. |



 秦宁, 山东省东营市东营区北一路210号中国石化胜利油田物探研究院, 257022。Email:
秦宁, 山东省东营市东营区北一路210号中国石化胜利油田物探研究院, 257022。Email: