地震资料往往含有严重的随机噪声,给后续的数据处理、解释及储层预测等工作带来十分不利的影响[1]。由于随机噪声是由各种因素综合作用形成的,没有固定的频率和传播方向,分布于全时、全频段,因此很难将其从地震记录中有效地分离出来。针对随机噪声压制问题,学者们开展了大量相关研究并根据有效信号和随机噪声各自的特征提出了不同的压制方法,典型的有K-L变换滤波[2]、f-x域预测滤波[3]、自适应滤波[4]、Radon变换[5]、径向预测滤波[6]、小波变换[7-8]、奇异值分解[9]、多项式拟合[10]、S变换[11]、Curvelet变换[12-13]、Seislet变换[14]、倾角导向中值滤波[15-16]、径向时频峰值滤波[17]、稀疏字典学习[18]、局部正交压制[19]等方法。尽管这些方法都取得较好的实际应用效果,但每种方法都受到某种假设或条件限制[20],去噪性能在不同工区差别较大,适应能力和保真能力有待进一步提高;此外,去噪效果较好的方法通常计算复杂度较高、计算效率较低,需要较多的参数调试,不能充分应对宽频、宽方位、单点高密度采集时代大数据量处理的挑战。因此,研究保真且高效的去噪方法是人们不懈的追求。
深度学习[21]是近年来引起广泛关注的机器学习的一个分支,该概念由Hinton等[22]提出。深度学习实质上是一种人工神经网络,但比以往的人工神经网络具有更深的神经元层,通过组合低层特征形成更加抽象的高层特征,以发现数据的分布式特征表示,减少了人工提取特征的巨量工作。目前,深度学习已经发展出多种模型,如生成式/无监督模型(受限玻尔兹曼机、深度置信网络、正则化的自编码器等)和判别式模型(递归神经网络、深度神经网络、卷积神经网络(Convolutional Neural Network,CNN)等)。CNN通过用卷积代替规则神经元的矩阵乘法运算,大大减少每层中需要训练的未知权重系数的数量,能够从输入中学习到高度复杂的非线性关系。
由于存在诸多优点,CNN已被逐渐应用于地震勘探领域中。如:Lewis等[23]将CNN用于全波形反演中的正则化先验信息提取;Itan等[24]将CNN用于反射和绕射波场分离;Huang等[25]将CNN用于断裂特征的自动检测。以上研究都取得了较好的应用效果,展现出CNN在地震勘探领域中的巨大优势和广阔的应用前景。
考虑到CNN具有自动学习高度复杂的非线性特征的能力,本文将其应用于叠前地震数据随机噪声的压制中,通过对叠前地震数据中随机噪声特征的自动学习,实现自动且高效的随机噪声分离。
1 深度残差网络去噪原理 1.1 深度残差网络目前卷积神经网络领域已取得许多令人瞩目的研究成果,并且不断有新的CNN模型被提出,其中最著名的有LeNet[26]、AlexNet[27]、Google-Net[28]、VGGNet[29]和深度残差网络(ResNet)[30]等。目前在图像分类方面,ResNet的准确度是最高的。鉴于ResNet的优异性能,Zhang等[31]将ResNet应用于图像数据去噪。研究表明,在随机噪声压制中应用ResNet并不依赖于数据的信噪比,其对不同信噪比的数据都能够达到较好的去噪效果。
深度残差网络是针对更深层的网络模型难以训练的问题而提出的一个网络架构,很好地克服了因深度增加而出现的网络退化问题,能够通过增加网络深度提高网络性能。图 1说明了深度残差网络与常规网络的差别。假定某段神经网络的输入是y,期望输出是N(y),即N(y)是期望的复杂潜在映射,但学习难度较大;如果通过图 1所示的越层连接直接把输入y传到输出作为初始结果,则此时需要学习的目标变为R(y)=y-N(y),即ResNet相当于学习恒等映射y与最优解N(y)的残差。在极端情况下,将残差R(y)置为零比通过非线性层拟合恒等映射y更容易。

|
图 1 残差网络与常规网络的差别 (a)常规网络;(b)残差网络 |
如果地震数据中包含随机噪声,则地震数据可以表示为
| $ \boldsymbol{y}=\boldsymbol{x}+\boldsymbol{n} $ | (1) |
式中:x为有效信号;y为含随机噪声地震记录;n为随机噪声。深度学习的基本思想是通过下面的公式建立x和y之间的映射关系
| $ \mathit{\boldsymbol{x}} = {\mathop{\rm Net}\nolimits} (\mathit{\boldsymbol{y}};{\mathit{\pmb{\Theta}}}) $ | (2) |
式中:Net表示深度学习网络;Θ={W, b}为网络参数,其中W为权重,b为偏置。根据深度残差网络原理,可以将随机噪声作为网络输出
| $ \mathit{\boldsymbol{n}} = \mathit{\boldsymbol{y}} - \mathit{\boldsymbol{x}} = {\mathop{\rm Res}\nolimits} (\mathit{\boldsymbol{y}};\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}) $ | (3) |
式中:Res表示残差学习网络。为了最优化式(3)中的网络,定义如下的代价函数[30]
| $ L(\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}) = \frac{1}{{2N}}\sum\limits_{i = 1}^N {\left\| {{\mathop{\rm Res}\nolimits} (\mathit{\boldsymbol{y}};\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}) - \left( {{\mathit{\boldsymbol{y}}_i} - {\mathit{\boldsymbol{x}}_i}} \right)} \right\|_{\rm{F}}^2} $ | (4) |
式中:{yi-xi)}i=1N表示包含N对训练样本的训练集;‖·‖F代表Frobenious范数。由于N非常大,直接将训练集用于计算L(Θ)的梯度是不现实的,因此本文采用小批次随机梯度下降(Stochastic Gradient Descent,SGD)法[32]最小化L(Θ),即在每次迭代过程中,只有小部分训练样本被用来计算梯度,利用局部梯度来代替全局梯度,这样既可以提高效率又可以降低复杂度。
为衡量深度残差网络的去噪性能,将峰值信噪比(Peak Signal to Noise Ratio,PSNR)作为评价指标,其计算公式为
| $ {\mathop{\rm PSNR}\nolimits} (\mathit{\boldsymbol{\hat x}}, \mathit{\boldsymbol{x}}) = 10 \times \lg \frac{{N\max [{\mathop{\rm abs}\nolimits} (\mathit{\boldsymbol{x}})]}}{{{{\left[ {\sum\limits_{j = 1}^M {{{\left( {{x_j} - {{\hat x}_j}} \right)}^2}} } \right]}^{\frac{1}{2}}}}}{\rm{ }} $ | (5) |
式中:
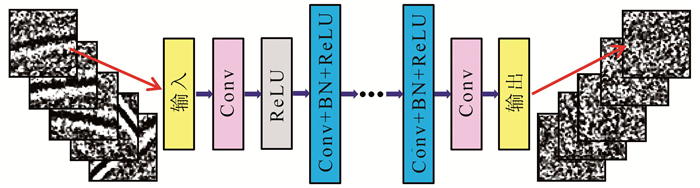
针对随机噪声压制问题,设计了一个由多层依次连接构成的去噪网络Res(y; Θ),如图 2所示,图中不同层的定义如表 1所示。在去噪网络的第二层和最后一层之间为多个构建块,每个构建块由一个卷积层(Conv)、一个批标准化层(Batch Normalization,BN)和一个修正线性单元层(Rectified Linear Unit,ReLU)依次连接组成。去噪网络中除第一个卷积层的尺寸为3×3×1×64 (64个卷积核为3×3的卷积滤波器,通道数为1)和最后一个卷积层的尺寸为3×3×64×1(1个卷积核为3×3的卷积滤波器,通道数为64)之外,其他卷积层的尺寸均为3×3×64×64 (64个卷积核为3×3的卷积滤波器,通道数为64)。去噪网络中修正线性单元层之前加入批标准化层[31],用于固定每层输入信号的均值和方差,使每一层的输入均有一个稳定的分布,在有效避免梯度弥散的同时可以提高去噪网络的泛化能力和收敛速度。
|
图 2 深度残差网络的架构示意图 |
|
|
表 1 深度残差网络不同层的定义 |
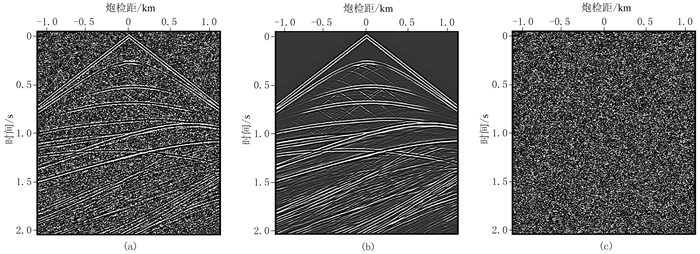
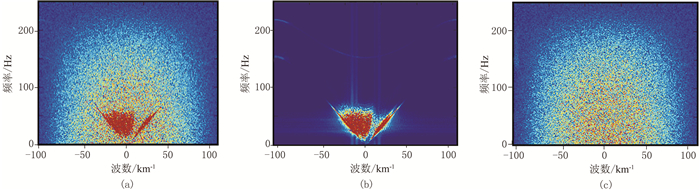
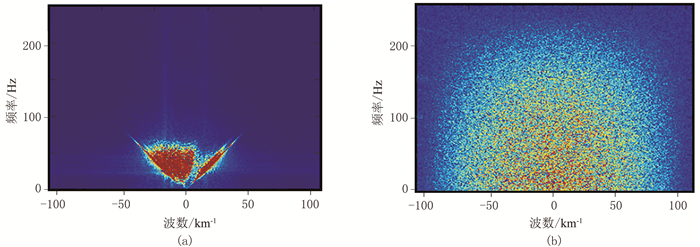
为验证基于深度残差网络的随机噪声压制方法的有效性,设计了一个二维合成数据模型构建训练集及去噪测试。图 3a给出了合成的含随机噪声记录,其峰值信噪比为9.08dB,是图 3b所示有效信号和图 3c所示随机噪声的叠加,共512道,每道1000个采样点,空间采样间隔为5m,时间采样间隔为2ms。图 4为图 3各记录的f-k谱,由图 4a可见随机噪声分布在整个时频空间,与有效信号的分布区域重叠。
|
图 3 含随机噪声数据模型 (a)含随机噪声记录;(b)有效信号;(c)随机噪声 |
|
图 4 含随机噪声数据模型的f-k谱 (a)含随机噪声记录;(b)有效信号;(c)随机噪声 |
为了训练去噪网络,通过将含随机噪声记录作为输入、将随机噪声模型作为标签,构建了包括输入数据集和标签数据集的训练集。为测试样本大小对网络去噪性能的影响,固定网络深度为18层、训练周期[31]为20、批次规模[31]为128,利用构建的不同训练样本大小的训练集对去噪网络进行训练。表 2为不同样本大小对应的峰值信噪比和训练时间,可见随着样本的变大训练时间也逐渐增大,但峰值信噪比在样本大小为30×30时达到最大,此后随着样本的变大反而变小了,因此在随机噪声压制应用中训练样本不是越大越好(图 2的两边给出了训练集中的5对训练样本)。大量的模型数据测试和实际资料应用表明,选取训练样本大小为30×30能够获得比较好的随机噪声压制效果,因此在本文的后续讨论中训练样本大小均设置为30×30。
|
|
表 2 训练样本大小对深度残差网络性能的影响 |
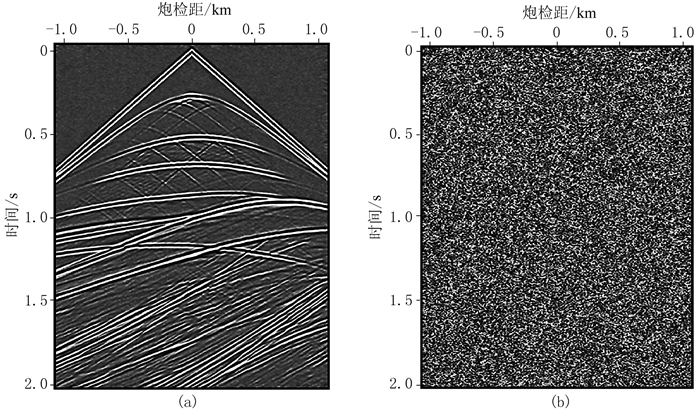
为测试网络深度对网络去噪性能的影响,固定训练样本的大小为30×30、训练周期为20、批次规模为128,对不同深度的去噪网络进行训练。表 3为不同网络深度对应的峰值信噪比、训练时间和去噪时间,可见:随着网络深度的增加峰值信噪比逐渐增大,网络越深去噪效果越好,这正是深度学习的本质所在;网络越深训练时间和去噪时间也越长,因此从时间成本考虑,本文在保证去噪效果的前提下选取网络深度为18层。此外,由表 3可见,尽管深度残差网络在训练阶段是比较耗时的,但训练好的网络在去噪阶段速度很快。利用固定好的参数训练得到去噪网络Ⅰ,并将其应用于图 3a所示的合成含随机噪声记录,结果如图 5所示。由图 5可见,去噪网络Ⅰ有效地学习到无规律随机噪声的特征,并成功地预测出随机噪声,随机噪声压制结果的PSNR为19.70dB,与含噪记录的PSNR相比得到显著的提升。对比图 4与图 6的f-k谱可见,在时频空间中有效信号和随机噪声得到了有效分离,选取网络深度为18层已足以满足去噪需求。
|
|
表 3 网络深度对深度残差网络性能的影响 |
|
图 5 网络Ⅰ去噪结果(a)及预测的随机噪声(b) |
|
图 6 网络Ⅰ去噪结果(a)及预测的随机噪声(b)的f-k谱 |
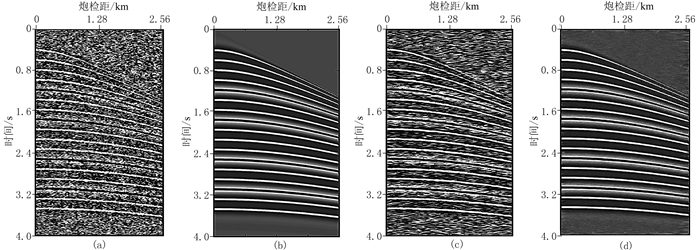
为进一步测试网络的去噪性能,将去噪网络Ⅰ应用于图 7a所示的合成含随机噪声记录。图 7a所示含随机噪声记录的峰值信噪比为4.32dB,是在图 7b所示有效信号中加入随机噪声得到的,共128道,每道1000个采样点,空间采样间隔为20m,时间采样间隔为4ms。图 7c给出了去噪网络Ⅰ的随机噪声压制结果,尽管其峰值信噪比提高到7.65dB,但随机噪声并未得到充分地压制。
|
图 7 含随机噪声记录及相应的去噪结果 (a)含随机噪声记录;(b)有效信号模型;(c)网络Ⅰ去噪结果;(d)网络Ⅱ去噪结果 |
针对该问题,将图 3a和图 7a所示的含随机噪声记录作为输入、将其相应的随机噪声模型作为标签,构建出新的训练集并对去噪网络进行训练,得到去噪网络Ⅱ。图 7d为去噪网络Ⅱ应用于图 7a数据的去噪结果,可见随机噪声得到了有效地压制,去噪后峰值信噪比达到17.15dB;同时将去噪网络Ⅱ应用于图 3a,也得到理想的去噪结果,去噪后峰值信噪比为19.46dB,与去噪网络Ⅰ的去噪能力基本相同。
可见,只要有足够完备的涵盖各种情况的高质量标签数据,训练后的去噪网络对于各种不同的数据都能得到较好的去噪结果,这也是在图像分类方面深度残差网络能够取得惊人准确度的主要原因之一。可以预见,在随机噪声去噪应用中,随着各工区不同类型标签数据的逐渐积累和网络的强化训练,本文去噪网络的泛化能力将会得到大幅度地提高。
5 实际资料应用深度残差网络是一种有监督的深度学习算法,要实现去噪首先得有高质量的标签数据。针对模型数据的去噪问题,由于随机噪声是已知的,因此能够获得较好的去噪效果,然而针对实际资料的去噪问题,随机噪声事先是未知的。针对实际资料随机噪声标签数据的获取问题,可以通过多种方法的去噪效果对比,选取最优的去噪方法获得标签数据。
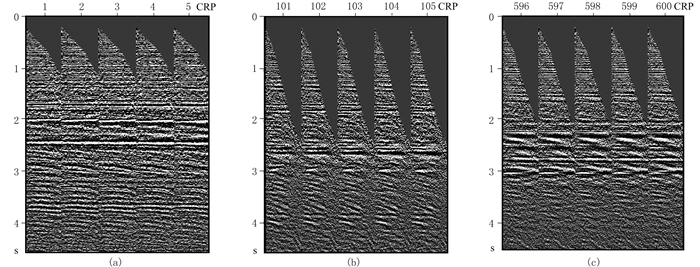
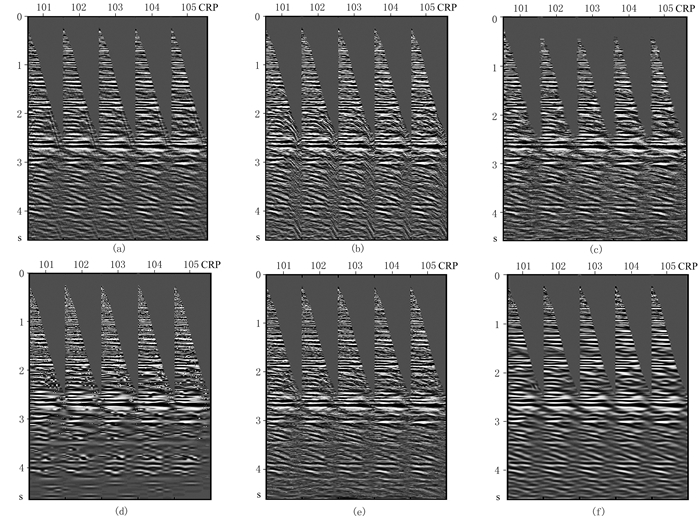
首先,将本文去噪方法应用于叠前CRP道集的随机噪声压制。图 8为三个不同位置的CRP道集,可见随机噪声干扰比较严重。分别利用f-x域预测滤波法、径向预测滤波法、倾角导向中值滤波法、小波迭代阈值法、Seislet变换法和曲波迭代阈值法对图 8b所示记录进行去噪处理,得到图 9和图 10所示的通过精细参数调试后的有效信号和随机噪声。通过对图 9和图 10中各方法去噪结果及相应的f-k谱和计算时间对比分析可知:f-x域预测滤波法的去噪效率是最高的,但其去噪能力和保幅性是最差的;径向预测滤波法、倾角导向中值滤波法和Seislet变换法的去噪效果依赖于局部倾角场的准确性,去噪结果的平滑性较差,且容易产生去噪假象;小波变换不能有效稀疏表示局部线状变化特征,因此小波迭代阈值法容易产生局部奇异性而破坏反射同相轴的连续性;曲波变换能够有效表示同相轴等局部线状变化特征,因此曲波迭代阈值法能够得到保幅且光滑的理想去噪结果,但效率最低。综合比较,针对图 8b所示记录,曲波迭代阈值法的随机噪声压制效果是最优的,因此利用该方法来获取随机噪声标签数据。
|
图 8 三个不同位置的含噪CRP道集 (a)CRP1~CRP5;(b)CRP101~CRP105;(c)CRP596~CRP600 |
|
图 9 图 8b数据不同方法的去噪结果 (a)f-x域预测滤波法;(b)径向预测滤波法;(c)倾角导向中值滤波法;(d)小波迭代阈值法;(e)Seislet变换法;(f)曲波迭代阈值法 |

|
图 10 图 8b数据不同方法的去除的随机噪声 (a)f-x域预测滤波法;(b)径向预测滤波法;(c)倾角导向中值滤波法;(d)小波迭代阈值法;(e)Seislet变换法;(f)曲波迭代阈值法 |
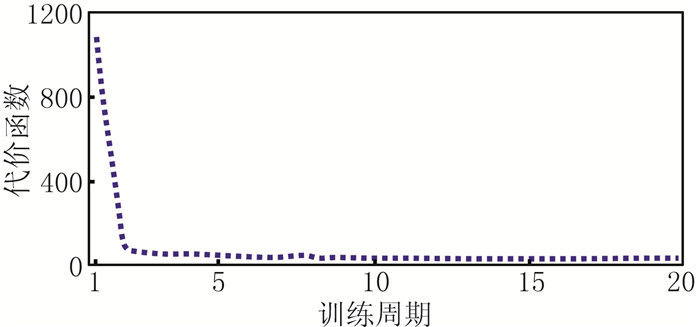
将图 8b所示CRP101~CRP105位置的含噪记录作为输入、将图 10f所示的相应随机噪声作为标签,构建了包含170000多个训练样本对的训练集,样本的大小为30×30。通过对本文设计的18层网络20个周期的训练,得到了最终的随机噪声去噪网络。图 11给出了代价函数随训练周期[31]的变化曲线,可以看出本文去噪网络在训练阶段非常稳定,网络的输出误差随着训练周期的增加迅速而单调地下降。
|
图 11 代价函数随训练周期的变化曲线 |
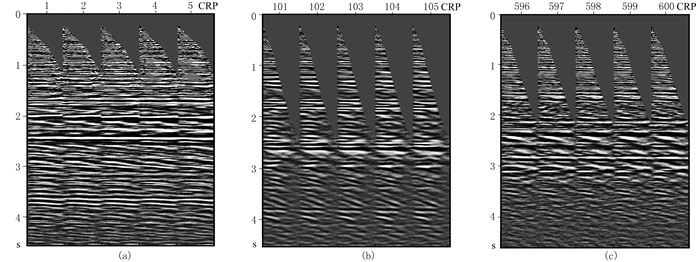
将训练好的随机噪声去噪网络应用于图 8所示的各含随机噪声记录,结果如图 12和图 13所示。图 9f所示曲波迭代阈值法得到的有效信号与图 12b所示深度残差网络得到的有效信号的峰值信噪比皆为21.87dB,可见二者的去噪能力相当,深度残差网络通过学习获得了曲波迭代阈值法的去噪能力。同时,通过比较可见,无论是在离获取标签位置CRP101~CRP105较近的CRP1~CRP5位置还是较远的CRP596~CRP600位置,去噪网络的随机噪声压制结果均较好,可见在局部构造相似区域,小样本训练获得的去噪网络也具有较强的泛化能力。
|
图 12 深度残差网络去噪结果 (a)CRP1~CRP5;(b)CRP101~CRP105;(c)CRP596~CRP600 |

|
图 13 深度残差网络预测的随机噪声 (a)CRP1~CRP5;(b)CRP101~CRP105;(c)CRP596~CRP600 |
此外,该去噪网络训练完成之后不仅与曲波迭代阈值法的去噪能力相同,同时还具有下述优点:①去噪效率高,与曲波迭代阈值法相比去噪效率提高了近200倍;②智能去噪,不需要复杂的参数调试,自动地识别并分离出噪声;③适应能力强、内存占用小;④保幅性好,只学习到了随机噪声的特征,在去噪过程中有效信息得到尽可能的保护。
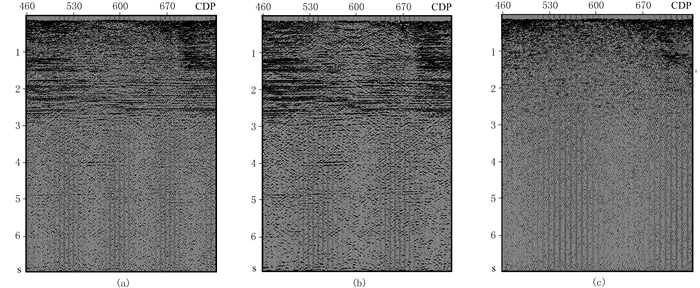
为进一步验证本文去噪方法对叠前炮记录的去噪性能,构建了新的训练集并进行了相应的网络训练。新的训练集中输入数据集和标签数据集的构建利用了不同来源的数据:一部分数据来源于加入了不同信噪比随机噪声的正演模拟炮记录及相应的随机噪声记录,另一部分数据来源于几个不同工区的实际含噪单炮记录及通过优选的去噪技术分离得到的随机噪声记录。将利用该训练集训练得到的去噪网络应用于实际二维测线数据,该数据为做完规则噪声压制之后的炮记录,共有802炮,图 14a为第320个单炮记录。图 14b和14c分别为图 14a数据的去噪结果及去除的随机噪声,可见该网络具有较好的泛化能力,对单炮记录中的随机噪声进行了较好的压制。图 15为该二维测线去噪前后的叠加剖面对比,可见预测出的随机噪声叠加剖面中基本无有效信息损失,网络的去噪性能得到进一步验证。

|
图 14 第320炮的深度残差网络去噪前(a)、后(b)记录及预测的噪声(c) |
|
图 15 深度残差网络去噪前(a)、后(b)的叠加剖面及去除的随机噪声叠加剖面(c) |
(1) 针对叠前地震记录中随机噪声的智能高效压制问题,根据深度残差网络原理设计了一种深层随机噪声压制网络,并引入批标准化策略和小批次随机梯度下降法来提高网络的综合性能,训练后的网络可以拟合出含噪声地震记录与随机噪声之间的非线性映射关系,实现对随机噪声的自动识别和分离。模型数据测试和实际资料应用,证明了本文方法的有效性。
(2) 深度残差网络是一种有监督的深度学习算法,去噪性能在很大程度上依赖于训练集的完备程度,如果有足够完备的涵盖各种情况的高质量标签数据,训练后的去噪网络将会具有很强的泛化能力,因此标签数据的获取和积累至关重要。
(3) 理论上深度残差网络越深去噪性能越好,但网络越深训练时间和去噪时间也越长;构建训练集时学习样本并不是越大越好,选择合适的尺寸能使网络获得最佳去噪性能。针对叠前随机噪声压制问题,网络深度选取18或者21层、样本大小设置为30×30就可以很好地满足去噪需求。
(4) 尽管深度残差网络在训练阶段比较耗时,但训练好之后具有较高的去噪效率。同时,从本文实际资料处理实例可见,该网络还具有智能去噪、适应能力强、保幅性好等优点,在局部构造相似区域,小样本训练也能够获得泛化能力较强的去噪网络。
| [1] |
Zhang B, Lin T and Marfurt K.Noise suppression of time migrated gathers using prestack structure oriented filtering[C].SEG Technical Program Expanded Abstracts, 2015, 34: 4678-4681.
|
| [2] |
Jones I F, Levy S. Signal-to-noise ratio enhancement in multichannel seismic data via the Karhunen-Loeve transform[J]. Geophysical Prospecting, 1987, 35(1): 12-32. |
| [3] |
Harris P E, White R E. Improving the perfor-mance of f-x prediction filtering at low signal-to-noise ratios[J]. Geophysical Prospecting, 1997, 45(2): 269-302. |
| [4] |
曹鹏涛, 张敏, 李振春. 基于广义S变换及高斯平滑的自适应滤波去噪方法[J]. 石油地球物理勘探, 2018, 53(6): 1128-1136. CAO Pengtao, ZHANG Min, LI Zhenchun. An adaptive filtering denoising method based on generalized S-transform and Gaussian smoothing[J]. Oil Geophysical Prospecting, 2018, 53(6): 1128-1136. |
| [5] |
Wang Y H. Antialiasing conditions in the delay-time Radon transform[J]. Geophysical Prospecting, 2002, 50(6): 665-672. |
| [6] |
夏洪瑞, 陈德刚, 周开明. 地震资料处理中随机干扰消除方法分析[J]. 石油物探, 2003, 42(1): 93-96. XIA Hongrui, CHEN Degang, ZHOU Kaiming. Random noise elimination in seismic data processing[J]. Geophysical Prospecting for Petroleum, 2003, 42(1): 93-96. |
| [7] |
Cao S Y, Chen X P. The second-generation wavelet transform and its application in denoising of seismic data[J]. Applied Geophysics, 2005, 2(2): 70-74. |
| [8] |
邵婕, 孙成禹, 唐杰, 等. 基于字典训练的小波域稀疏表示微地震去噪方法[J]. 石油地球物理勘探, 2016, 51(2): 254-260. SHAO Jie, SUN Chengyu, TANG Jie, et al. Micro-seismic data denoising based on sparse representations over learned dictionary in the wavelet domain[J]. Oil Geophysical Prospecting, 2016, 51(2): 254-260. |
| [9] |
桑雨, 高树生, 宋宏文, 等. 利用奇异值分解方法提高地震数据信噪比[J]. 石油地球物理勘探, 2014, 49(增刊1): 72-75. SANG Yu, GAO Shusheng, SONG Hongwen, et al. Signal to noise ratio improvement with the SVD method[J]. Oil Geophysical Prospecting, 2014, 49(S1): 72-75. |
| [10] |
Liu X W, Gou L M. Suppressing random noise to broaden the useful bandwidth of seismic reflection data[J]. Applied Geophysics, 2007, 4(1): 37-44. |
| [11] |
赵淑红, 朱光明. S变换时频滤波去噪方法[J]. 石油地球物理勘探, 2007, 42(4): 402-406. ZHAO Shuhong, ZHU Guangming. Time-frequency filtering to denoise by S transform[J]. Oil Geophysical Prospecting, 2007, 42(4): 402-406. |
| [12] |
齐少华, 刘启元, 陈九辉, 等. 接收函数的曲波变换去噪[J]. 地球物理学报, 2006, 59(3): 884-896. QI Shaohua, LIU Qiyuan, CHEN Jiuhui, et al. Atte-nuation of noise in receiver functions using curvelet transform[J]. Chinese Journal of Geophysics, 2006, 59(3): 884-896. |
| [13] |
张华, 刁塑, 温建亮, 等. 应用二维非均匀曲波变换压制地震随机噪声[J]. 石油地球物理勘探, 2019, 54(1): 16-23. ZHANG Hua, DIAO Su, WEN Jianliang, et al. A random noise suppression with 2D non-uniform curvelet transform[J]. Oil Geophysical Prospecting, 2019, 54(1): 16-23. |
| [14] |
刘洋, Fomel S, 刘财, 等. 高阶seislet变换及其在随机噪声消除中的应用[J]. 地球物理学报, 2009, 52(8): 2142-2151. LIU Yang, Fomel S, LIU Cai, et al. High-order seislet transform and its application of random noise attenuation[J]. Chinese Journal of Geophysics, 2009, 52(8): 2142-2151. |
| [15] |
王伟, 高静怀, 陈文超, 等. 基于结构自适应中值滤波器的随机噪声衰减方法[J]. 地球物理学报, 2012, 55(5): 1732-1741. WANG Wei, GAO Jinghuai, CHEN Wenchao, et al. Random seismic noise suppression via structure-adaptive median filter[J]. Chinese Journal of Geophysics, 2012, 55(5): 1732-1741. |
| [16] |
孙哲, 王建锋, 王静, 等. 基于时空变中值滤波的随机噪声压制方法[J]. 石油地球物理勘探, 2016, 51(6): 1094-1102. SUN Zhe, WANG Jianfeng, WANG Jing, et al. Random noise elimination based on the time-space variant median filtering[J]. Oil Geophysical Prospecting, 2016, 51(6): 1094-1102. |
| [17] |
林红波, 马海涛, 许丽萍. 压制空间非平稳地震勘探随机噪声的ROAD径向时频峰值滤波算法[J]. 地球物理学报, 2015, 58(7): 2546-2555. LIN Hongbo, MA Haitao, XU Liping. A radial time-frequency peak filtering based on ROAD for suppressing spatially nonstationary random noise in seismic data[J]. Chinese Journal of Geophysics, 2015, 58(7): 2546-2555. |
| [18] |
张岩, 任伟建, 唐国维. 应用结构聚类字典学习压制地震数据随机噪声[J]. 石油地球物理勘探, 2018, 53(6): 1119-1127. ZHANG Yan, REN Weijian, TANG Guowei. Random noise suppression on seismic data based on structured-clustering dictionary learning[J]. Oil Geophysical Prospecting, 2018, 53(6): 1119-1127. |
| [19] |
徐彦凯, 曹思远, 潘晓, 等. 随机噪声的局部正交压制方法[J]. 石油地球物理勘探, 2019, 54(2): 280-287. XU Yankai, CAO Siyuan, PAN Xiao, et al. A local orthogonalization for seismic random noise suppression[J]. Oil Geophysical Prospecting, 2019, 54(2): 280-287. |
| [20] |
钟铁, 李月, 杨宝俊, 等. 陆地地震勘探随机噪声统计特性[J]. 地球物理学报, 2017, 60(2): 655-664. ZHONG Tie, LI Yue, YANG Baojun, et al. Statistical features of the random noise in land seismic prospecting[J]. Chinese Journal of Geophysics, 2017, 60(2): 655-664. |
| [21] |
Lecun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015, 521(7553): 436-444. |
| [22] |
Hinton G, Osindero S, Teh Y. A fast learning algo-rithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527-1554. |
| [23] |
Lewis W and Vigh D.Deep learning prior models from seismic images for full-waveform inversion[C].SEG Technical Program Expanded Abstracts, 2017, 36: 1512-1516.
|
| [24] |
Itan L, Serfaty Y, Chase D, et al.Wavefield separation via PCA and deep learning in the local angle domain[C].SEG Technical Program Expanded Abstracts, 2017, 36: 991-995.
|
| [25] |
Huang L, Dong X, Clee T E. A scalable deep learning platform for identifying geologic features from seismic attributes[J]. The Leading Edge, 2017, 36(3): 249-256. |
| [26] |
Lecun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition[J]. Procee-dings of the IEEE, 1998, 86(11): 2278-2324. |
| [27] |
Krizhevsky A, Sutskever I and Hinton G.Image net classification with deep convolutional neural networks[C].International Conference on Neural Information Processing Systems, 2012, 1097-1105.
|
| [28] |
Szegedy C, Liu W, Jia Y, et al.Going deeper with convolutions[C].Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015, 1-9.
|
| [29] |
Simonyan K and Zisserman A.Very deep convolutio-nal networks for large-scale image recognition[C].International Conference on Learning Representations, 2015, 1-14.
|
| [30] |
He K, Zhang X, Ren S, et al.Deep residual learning for image recognition[C].Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, 770-778.
|
| [31] |
Zhang K, Zuo W, Chen Y, et al. Beyond a Gaussian denoiser:Residual learning of deep CNN for image denoising[J]. IEEE Transactions on Image Proce-ssing, 2017, 26(7): 3142-3155. |
| [32] |
Yann L. Efficient backprop//Neural Networks:Tricks of the Trade[M]. New York: Springer, 1998: 9-50.
|



 李海山, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院, 730020。Email:
李海山, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院, 730020。Email: