2 中国石油大学(北京)CNPC物探重点实验室, 北京昌平 102249;
3 中国石油大学(北京)克拉玛依校区, 新疆克拉玛依 834000
2 CNPC Key Laboratory of Geophysical Prospecting, China University of Petroleum(Beijing), Beijing 102249, China;
3 Karamay Campus, China University of Petroleum(Beijing), Karamay, Xinjiang 834000, China
纵、横波速度是地震勘探中的关键参数,在地下构造解释和油藏描述等工作中具有重要作用。通过常规声波测井可以得到纵波速度。横波测井(如偶极子声波测井)勘探成本太高,在一般情况下,实际地震资料中往往缺少横波速度信息。因此,有必要研究精确预测横波速度的方法。
横波速度预测方法主要分为经验公式法和岩石物理建模法。传统的经验公式法通过统计学分析纵、横波速度,拟合得到纵、横波速度关系式,由纵波速度预测横波速度。Pickett[1]通过分析大量测井数据,得到灰岩的纵、横波速度经验公式。Castagna等[2]基于碎屑岩中的纵、横波速度关系,提出了著名的“泥岩线”公式。此外,不同岩石存在不同的纵、横波速度拟合公式[3-4]。随着勘探技术的发展,传统的经验公式法已经不能满足横波速度预测的精度需求。因此,基于传统经验公式法,人们在拟合过程中加入密度、自然伽马和电阻率等参数,提出了多元回归法[5-7]。经验公式法容易实现,计算效率高,但拟合关系式反映了大量测井数据的统计规律,在实际应用时存在较大误差。
岩石物理建模法主要通过建立岩石物理模型精确地计算岩石的弹性参数,然后基于弹性参数和横波速度之间的关系计算横波速度。Xu等[8]基于砂岩和泥岩孔隙的几何形态,提出了砂泥岩储层的等效介质模型——“Xu-White模型”;随后Xu等[9]基于该模型估算了碳酸盐岩的孔隙形状,较为精确地预测了横波速度。刘欣欣等[10]采用自适应遗传算法计算岩石物理模型的弹性参数、预测横波速度并应用于体积模量反演,取得了较好效果。罗水亮等对Pride模型[11]和Lee模型[12]进行变形,提出了变形P-L模型,利用地震反演预测横波速度[13]。此外,郑旭桢等[14]、唐杰等[15]、熊晓军等[16]基于岩石物理建模预测横波速度,均取得了较好效果。利用岩石物理建模法预测横波速度精度较高,但是算法复杂、所需参数较多,导致计算效率较低。
经验公式法和岩石物理建模法都是基于横波速度和其他参数之间的关系,利用其他参数预测横波速度。经验公式法利用储层参数(密度和自然伽马等)预测横波速度,岩石物理建模法利用弹性参数(体积模量和剪切模量等)预测横波速度,相比而言,储层参数更容易获得。但是在一般情况下,横波速度和弹性参数的关系式较横波速度和储层参数的关系式更准确,因此提高横波速度预测精度和预测效率可以从两方面入手,即建立横波速度和储层参数之间的高精度关系式或提高提取弹性参数的效率,后者在目前较难实现。本文主要研究如何精确地建立横波速度和储层参数之间的关系式。
近年来,机器学习技术迅速发展,在不同领域取得了重大进展。机器学习方法主要分为分类、回归和聚类三种,其中回归主要处理和预测时序数列。GRU(gated recurrent unit)神经网络是基于回归思想提出的一种机器学习方法,并已经成功应用于时序数列的分析和预测。通过引入GRU神经网络,本文提出一种利用储层参数预测横波速度的方法,具体步骤包括神经网络构建、数据预处理、样本训练和数据预测等。选择D区测井数据测试,结果表明该方法具有较高精度和较好的适用性。
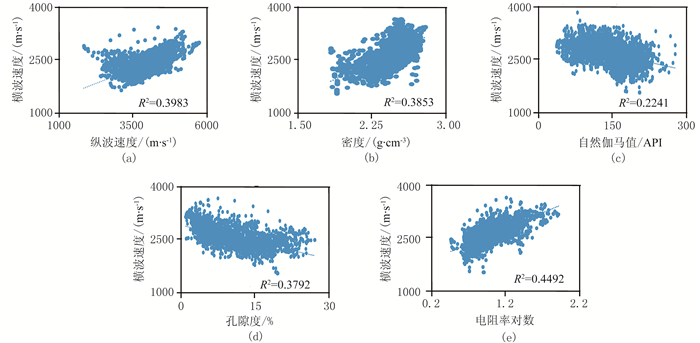
1 储层参数与横波速度的相关性储层参数反映了储层的具体特征,与横波速度之间存在着必然联系。通常通过测井方法得到储层参数,目前常用的测井方法包括声波时差测井、密度测井、自然伽马测井、中子测井和电阻率测井等。本文主要分析由这些测井方法得到的储层参数(纵波速度、密度、自然伽马值、孔隙度和电阻率)与横波速度之间的相关性。纵、横波速度同时受储层的岩石骨架和孔隙流体影响,因此纵、横波速度之间存在正相关关系;密度直接参与储层体积模量和剪切模量的计算,间接参与横波速度的计算,因此密度与横波速度具有一定相关性;自然伽马值反映了储层骨架中的泥质含量,与横波速度具有正相关关系;孔隙度值反映了储层的地质结构,直接影响横波速度;储层的岩石骨架通常不导电,电阻率主要反映储层的孔隙流体特征,因此也能反映横波速度变化。图 1为D区储层参数与横波速度交会图。由图可见:纵波速度(图 1a)、密度(图 1b)和电阻率对数(图 1e)均与横波速度呈正相关(R2约为0.40),其中电阻率对数与横波速度的正相关性最好(R2=0.4492);自然伽马值(图 1c,R2=0.2241)、孔隙度(图 1d,R2=0.3792)均与横波速度呈负相关,但前者与横波速度的负相关性较弱。
|
图 1 D区储层参数与横波速度交会图 (a)纵波速度—横波速度;(b)密度—横波速度;(c)自然伽马—横波速度;(d)孔隙度—横波速度;(e)电阻率对数—横波速度 R为两个变量之间的相关系数 |
储层参数与横波速度之间存在一定的相关关系,但是这种关系较复杂,很难得到解析解。为此,本文构建了GRU神经网络方法,通过训练神经网络逼近横波速度与储层参数之间的关系,然后预测横波速度。
2 基于GRU的横波速度预测方法 2.1 GRU神经网络理论GRU神经网络是LSTM神经网络(long short term memory network)的一种变体,LSTM神经网络是在RNN(recurrent neural network)的基础上发展起来的。RNN是一种成熟的机器学习方法,在处理时序数列方面具有着很大优势[17]。RNN中包含信号反馈结构,能将t时刻的输出信息与t时刻之前的信息相关联,具有动态特征和记忆功能。
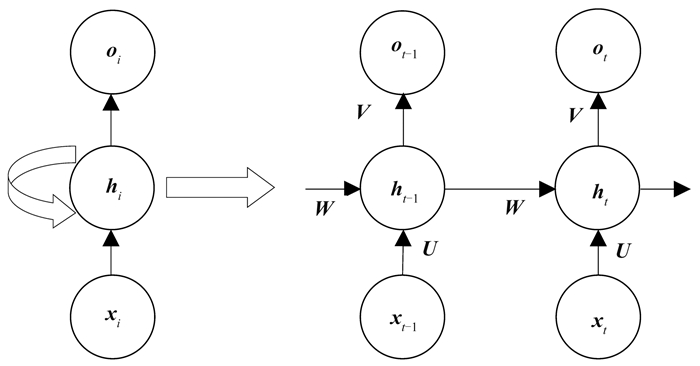
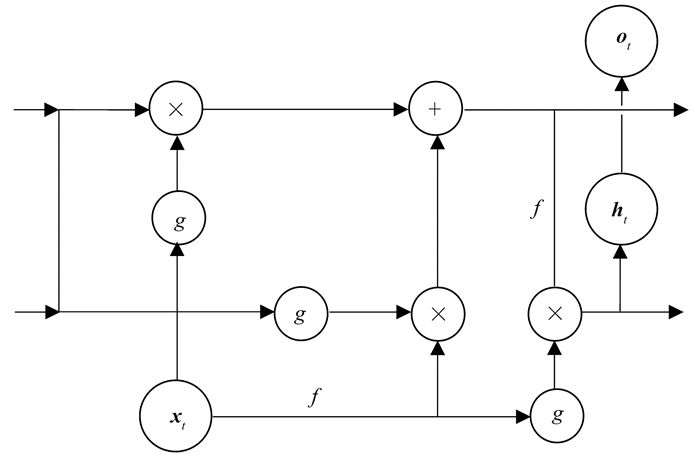
图 2为RNN结构示意图。由图可见:①RNN结构包括输入层、隐藏层和输出层,其中隐藏层包含反馈结构;②t时刻的输出值是该时刻及其之前时刻的输入信息共同作用的结果;③RNN能够有效地分析和处理较短的时序数列,但不能分析和处理维度过长的时序数列,否则会产生“梯度消失”或“梯度爆炸”的现象[18]。针对这一问题,Hocheriter等[19]提出了一种RNN改进结构LSTM神经网络,其隐藏层结构如图 3所示[20]。LSTM神经网络基于隐藏层中的记忆单元(遗忘门、输入门和输出门)实现时序上的记忆可控,改善了RNN长期记忆力不足的问题,但其隐藏层的结构过于复杂,样本训练需要花费大量的时间。基于LSTM神经网络,Cho等[21]提出了GRU神经网络,利用重置门和更新门代替LSTM神经网络中的遗忘门、输入门和输出门。LSTM神经网络和GRU神经网络在隐藏层内具有相似的数据流,但GRU神经网络中没有单独的存储单元,因此样本训练效率更高。
|
图 2 RNN结构示意图[17] ht为t时刻隐藏层的值,ht-1为t时刻之前隐藏层的值;ot为t时刻输出层的值,ot-1为t时刻之前输出层的值;U为输入层到隐藏层的权重矩阵;V为隐藏层到输出层的权重矩阵;W为隐藏层上一次的值作为这一次输入的权重矩阵;每一个圆圈代表一个神经元。对于常规的RNN隐藏层,当给定输入值xt(t=1, 2, …, n)时,t时刻输出层、隐藏层的输出值分别为ot=g(V·ht)、ht=f(U·xt+W·ht-1),其中 |
|
图 3 LSTM隐藏层结构示意图[20] “×”表示对两个向量做○运算(下文详细说明),“+”表示对两个向量做和运算 |
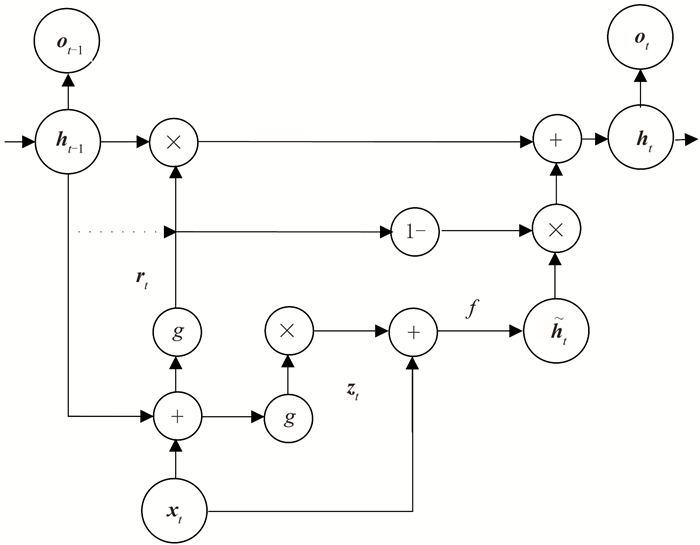
图 4为GRU神经网络的隐藏层结构示意图。由图可见:更新门控制前一时刻的信息对当前时刻的影响程度,更新门的值越大,前一时刻的信息对当前时刻的影响越小;重置门控制对前一时刻信息的接收百分比,重置门的值越大,对前一时刻的信息接收的越多。
|
图 4 GRU神经网络隐藏层结构示意图[20] “1-”表示用1减去该向量中的每一个元素。对于t时刻更新门的值zt,取值越大表示t时刻隐藏层的值ht受t-1时刻隐藏层的值ht-1影响越小,受t时刻的候选值 |
对于GRU神经网络的隐藏层,给定输入值xt(t=1, 2, …, n),则t时刻隐藏层的值为[20]
| $ \boldsymbol{z}_{t}=g\left(\boldsymbol{W}_{z} \cdot\left[\boldsymbol{h}_{t-1}, \boldsymbol{x}_{t}\right]\right) $ | (1) |
| $ \boldsymbol{r}_{t}=g\left(\boldsymbol{W}_{r} \cdot\left[\boldsymbol{h}_{t-1}, \boldsymbol{x}_{t}\right]\right) $ | (2) |
| $ {\mathit{\boldsymbol{\widetilde h}}_t} = f\left( {{\mathit{\boldsymbol{W}}_{\mathit{\boldsymbol{\tilde h}}}} \cdot \left[ {{\mathit{\boldsymbol{r}}_\mathit{t}} \circ {\mathit{\boldsymbol{h}}_{t - 1}}, {\mathit{\boldsymbol{x}}_t}} \right]} \right) $ | (3) |
| $ {\mathit{\boldsymbol{h}}_t} = \left( {1 - {\mathit{\boldsymbol{z}}_t}} \right) \circ {\mathit{\boldsymbol{h}}_{t - 1}} + {\mathit{\boldsymbol{z}}_t} \circ {\mathit{\boldsymbol{\widetilde h}}_t} $ | (4) |
式中:“[]”表示两个向量相连接;“○”是矩阵间的一种计算方法,表示按元素乘,当“○”作用于两个向量时,运算为
| $ \mathit{\boldsymbol{a}} \circ \mathit{\boldsymbol{b}} = \left[ {\begin{array}{*{20}{c}} {{a_1}}\\ {{a_2}}\\ {{a_3}}\\ \vdots \\ {{a_n}} \end{array}} \right]\circ \left[ {\begin{array}{*{20}{c}} {{b_1}}\\ {{b_2}}\\ {{b_3}}\\ \vdots \\ {{b_n}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{a_1}{b_1}}\\ {{a_2}{b_2}}\\ {{a_3}{b_3}}\\ \vdots \\ {{a_n}{b_n}} \end{array}} \right] $ | (5) |
由式(1)~式(4)可以看到,GRU神经网络需要训练的t时刻的权重矩阵为Wz、Wr和W
| $ {\mathit{\boldsymbol{W}}_z} = {\mathit{\boldsymbol{W}}_{zx}} + {\mathit{\boldsymbol{W}}_{z\mathit{\boldsymbol{\tilde h}}}} $ | (6) |
| $ {\mathit{\boldsymbol{W}}_r} = {\mathit{\boldsymbol{W}}_{rx}} + {\mathit{\boldsymbol{W}}_{r\mathit{\boldsymbol{\tilde h}}}} $ | (7) |
| $ {\mathit{\boldsymbol{W}}_{\mathit{\boldsymbol{\tilde h}}}} = {\mathit{\boldsymbol{W}}_{\mathit{\boldsymbol{\tilde h}}x}} + {\mathit{\boldsymbol{W}}_{\mathit{\boldsymbol{\tilde h\tilde h}}}} $ | (8) |
式中:Wzx、Wrx和W
GRU神经网络的训练方法基于反向传播理论,主要包括四个步骤。
(1) 前向计算每个神经元的输出值。
(2) 反向计算每个神经元的误差项。GRU神经网络误差项的反向传播包括两个方面:一个是沿时间的反向传播,即从当前时刻起,计算每个时刻的误差项;另一个是将误差项传递到上一层。
(3) 根据误差项,利用优化算法计算相应的权重梯度。
(4) 利用得到的梯度更新权重。本文采用随机梯度下降法(SGD,stochastic gradient descent)计算权重梯度。普通的批量梯度下降法(BGD,batch gradient descent)在每次迭代过程中把所有的样本都计算一遍,然后更新梯度;SGD算法是从样本中随机抽出一组进行计算然后更新梯度。相对于BGD算法,SGD算法既能够较好地避免在计算过程中陷入局部极值,又不需要在每次迭代过程中计算所有样本,能够兼顾计算效率和计算精度。
2.2 横波速度预测方法图 5为基于GRU神经网络的横波速度预测流程。由图可见,包括输入层、隐藏层和输出层,输入层对储层参数进行异常值处理和归一化处理,并将处理后数据输入到隐藏层。归一化是为了限定输入数据的最大值和最小值不超过隐藏层函数和输出层函数的限定范围。本文采用的归一化公式为

|
图 5 基于GRU神经网络的横波速度预测流程 |
| $ {\tilde x_i} = \frac{{{x_i} - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}}\;\;\;\;\;\;\;\;\;i = 1, 2, \cdots , n $ | (9) |
式中xmin和xmax分别为xi的最小值和最大值。
当训练神经网络时,隐藏层接收数据并利用构建好的GRU神经网络计算,将计算结果传递给输出层;输出层接收计算结果并进行反归一化,提供输出结果;将输出结果与样本值比较,迭代更新隐藏层的权重系数直至训练结束。进行神经网络预测时,隐藏层接收数据并利用训练好的GRU神经网络计算,将计算结果传递给输出层;输出层接收计算结果并进行反归一化,提供横波速度信息。
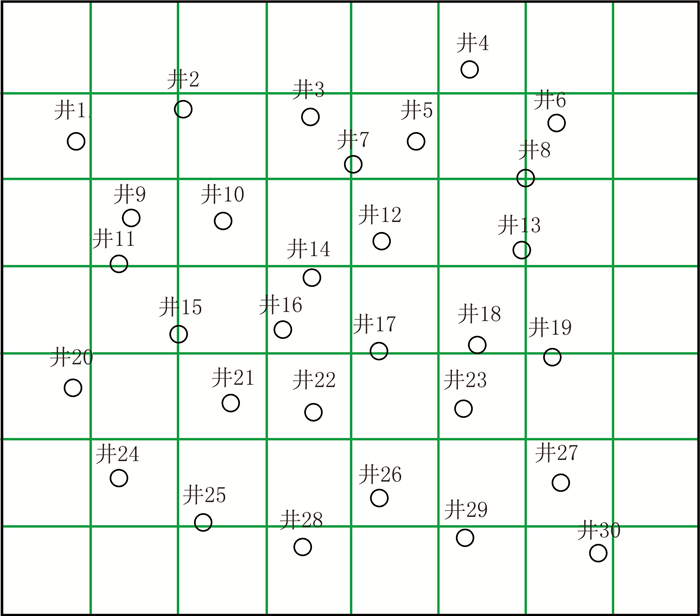
3 横波速度预测试算利用D区的30口井的测井数据预测横波速度,将这些井按顺序从1到30编号(图 6)。30口井的测井资料(共90000个实测样本点)包括纵波速度、密度、自然伽马值、孔隙度、电阻率和横波速度数据。对测井数据进行异常值处理和归一化处理,使这些数据的值域为(0,1),然后将其分为90000个二维数组,每个二维数组包括输入值和样本值两部分,其中输入值为xt=(纵波速度,密度,自然伽马值,孔隙度,电阻率),样本值=(横波速度)。每次迭代的输出结果为ot=(横波速度),其中井1包含3000个数据点(图 7)。本文采用Matlab编程语言构建模型,在构建GRU神经网络时,经过反复迭代、测试,在同时考虑计算效率和精度的情况下,选择具有一个输入层、三个隐藏层和一个输出层的神经网络结构。其中学习率为0.02,激活函数为sigmoid函数和tanh函数,利用SGD优化目标函数。为了检验预测效果,对比本文方法、经验公式法(下文简称公式法)和基于最小平方的横波速度拟合法[22](下文简称拟合法)的预测结果,以相对误差和相关系数作为评价标准。
|
图 6 D区井位分布示意图 |

|
图 7 井1的测井数据 |
为了验证本文方法的预测精度和泛化能力,分别做多数井训练、少数井验证和少数井训练、多数井验证的试算。
3.1 多数井训练、少数井验证试算利用24口井数据训练、6口井数据验证,并采用交叉验证的方法检验本文方法的预测精度和泛化能力。
(1) 选择井2、井5、井13、井15、井23和井24的测井数据作为测试样本,其他测井数据作为训练样本。
将训练样本对应的72000个二维数组依次输入到构建好的神经网络中,对神经网络训练。然后将测试样本对应的18000个二维数组依次输入到训练好的神经网络中,输出预测横波速度并与实际横波速度、基于“公式法”预测的横波速度和基于“拟合法”预测的横波速度对比。表 1为井2、井5、井13、井15、井23和井24的测井数据作为测试样本的横波速度预测相对误差。由表可见:对于训练数据,本文方法预测的横波速度相对误差约为3.00%,小于“拟合法”(4.09%)和“公式法”(4.81%);对于测试数据,本文方法预测的横波速度相对误差略有增大,约为3.19%,仍低于“公式法”和“拟合法”。表 2为井2、井5、井13、井15、井23和井24的测井数据作为测试样本的横波速度预测值与实际值的相关系数。由表可见:对于训练数据,本文方法的预测结果与实际值的相关系数平均值为0.9837,大于“拟合法”(0.9638)和“公式法”(0.9526);对于测试数据,本文方法的相关系数略有减小,平均值为0.9805,仍大于“公式法”和“拟合法”。
|
|
表 1 井2、井5、井13、井15、井23和井24的测井数据作为测试样本的横波速度预测相对误差 |
|
|
表 2 井2、井5、井13、井15、井23和井24的测井数据作为测试样本的横波速度预测值与实际值的相关系数 |
(2) 选择井3、井8、井11、井18、井21和井29的测井数据作为测试样本,其他测井数据作为训练样本。
将训练样本对应的72000个二维数组和测试样本对应的18000个二维数组按照上文的顺序依次输入,由相对误差(表 3)和相关系数(表 4)可以看出:①对于训练数据,本文方法预测的横波速度相对误差平均值为3.01%,小于“拟合法”(4.10%)和“公式法”(4.69%);本文方法的相关系数平均值为0.9839,大于“拟合法”(0.9655)和“公式法”(0.9499)。②对于测试数据,本文方法预测的横波速度相对误差略有增大,相关系数略有减小,平均值分别为3.20%和0.9797。
|
|
表 3 井3、井8、井11、井18、井21和井29的测井数据作为测试样本的横波速度预测相对误差 |
|
|
表 4 井3、井8、井11、井18、井21和井29的测井数据作为测试样本的横波速度预测值与实际值的相关系数 |
(3) 选择井4、井9、井12、井20、井22和井27的测井数据作为测试样本,其他测井数据作为训练样本。
将训练样本对应的72000个二维数组和测试样本对应的18000个二维数组依次输入,由相对误差(表 5)和相关系数(表 6)可见:无论是训练数据还是测试数据,本文方法预测的横波速度相对误差小于“拟合法”和“公式法”,本文方法的预测结果与实际值的相关系数大于“拟合法”和“公式法”。
|
|
表 5 井4、井9、井12、井20、井22和井27的测井数据作为测试样本的横波速度预测相对误差 |
|
|
表 6 井4、井9、井12、井20、井22和井27的测井数据作为测试样本的横波速度预测值与实际值的相关系数 |
通过以上交叉验证算例可以看出,本文方法预测的横波速度与真实横波速度的相对误差更小,相关系数更大,证明了该方法具有较高的预测精度和较强的泛化能力。
3.2 少数井训练、多数井验证试算为了进一步验证本文方法的泛化能力,利用10口井数据训练、20口井数据测试。选择井2、井4、井7、井8、井9、井14、井19、井20、井22和井29的测井数据作为训练样本,其他测井数据作为测试样本。
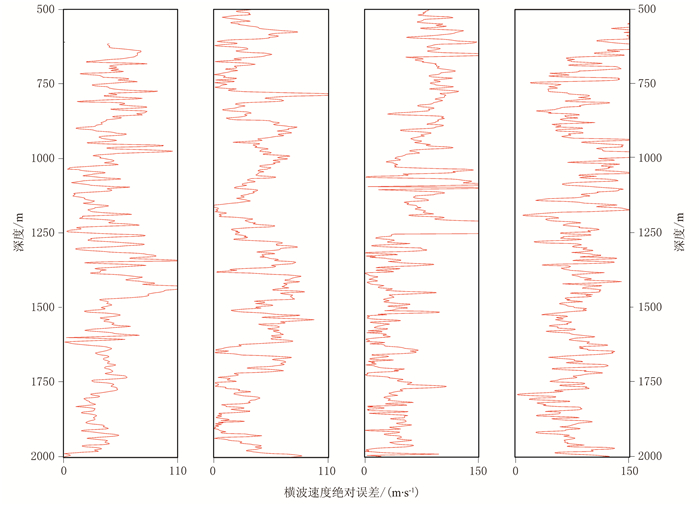
将训练样本对应的30000个二维数组依次输入构建好的神经网络中,对神经网络训练。然后将测试样本对应的60000个二维数组依次输入到训练好的神经网络中,输出预测横波速度并与实际横波速度、基于“公式法”预测的横波速度和基于“拟合法”预测的横波速度对比。表 7为井2、井4、井7、井8、井9、井14、井19、井20、井22和井29的测井数据作为训练样本的横波速度预测相对误差。由表可见:对于训练数据,本文方法预测的横波速度相对误差平均值为2.49%,小于多数井训练、少数井验证;对于测试数据,本文方法预测的横波速度相对误差平均值为3.91%,大于多数井训练、少数井验证。这是由于减少了训练样本的数量,增加了测试集的样本数量所致。但总体来说,本文方法预测的横波速度相对误差仍小于“拟合法”和“公式法”。表 8为井2、井4、井7、井8、井9、井14、井19、井20、井22和井29的测井数据作为训练样本的横波速度预测值与实际值的相关系数。由表可见:对于训练数据,本文方法预测的横波速度相对误差和相关系数分别为2.49%和0.9867,预测结果好于“拟合法”和“公式法”;对于测试数据,本文方法预测的横波速度相对误差和相关系数分别为3.92%和0.9686,预测结果与“拟合法”相当,好于“公式法”。图 8为横波速度预测值和真实值。由图可见,预测横波速度和实际横波速度曲线趋势一致,具有很好的匹配度。图 9为横波速度绝对误差曲线。由图可见,训练井的绝对误差值小于110m/s,测试井的绝对误差值小于150m/s,表明本文方法的实用性较好。
|
|
表 7 井2、井4、井7、井8、井9、井14、井19、井20、井22和井29的测井数据作为训练样本的横波速度预测相对误差 |
|
|
表 8 井2、井4、井7、井8、井9、井14、井19、井20、井22和井29的测井数据作为训练样本的横波速度预测值与实际值的相关系数 |

|
图 8 横波速度预测值和真实值 从左至右依次为训练井2、训练井29、测试井5和测试井25 |
|
图 9 横波速度绝对误差曲线 从左至右依次为训练井2、训练井29、测试井5和测试井25 |
本文提出了一种基于GRU神经网络的横波速度预测方法,利用D区的测井数据训练、测试,得到以下认识。
(1) 横波速度与纵波速度、密度和自然伽马等储层参数之间存在一定的相关性。纵波速度、密度和电阻率对数与横波速度呈较好的正相关关系。自然伽马值、孔隙度与横波速度呈负相关关系。
(2) 利用基于GRU神经网络的横波速度预测方法对实际测井数据的试算结果表明:对于多数井训练、少数井验证,训练数据预测的横波速度与真实值的相对误差和相关系数分别约为3.00%和0.9837,测试数据预测的横波速度与真实值的相对误差和相关系数分别约3.19%和0.9805;对于少数井训练、多数井验证,训练数据预测的横波速度与真实值的相对误差和相关系数分别约为2.49%和0.9867,测试数据预测的横波速度与真实值的相对误差和相关系数分别约3.92%和0.9686。因此本文提出的横波速度预测方法具有较高的预测精度和较强的泛化能力。
尚需指出,本文方法虽能较为准确地预测横波速度,但仍然存在两个主要问题:
(1) 本文提出的GRU神经网络方法是一种有监督的机器学习方法,其预测精度依赖于训练样本的精度,若训练样本的精度不够,则不能得到精确的预测结果。因此,有必要研究一种基于无监督思想的横波速度预测方法。
(2) 本文采用SGD算法更新梯度的速度相对较快,但由于单个样本的训练大多会带来很多噪声,因此SGD算法的每次迭代并不都是向着整体最优化的方向进行,易造成早期收敛快、晚期收敛慢的现象。
| [1] |
Pickett G R. Acoustic character logs and their application in formation evaluation[J]. Journal of Petroleum Technology, 1963, 15(6): 650-667. |
| [2] |
Castagna J P, Batzle M L, Eastwood R L. Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks[J]. Geophysics, 1985, 50(4): 571-581. DOI:10.1190/1.1441933 |
| [3] |
Han D, Nur A, Morgan D. Effect of porosity and clay content on wave velocity in sandstones[J]. Geophy-sics, 1986, 51(11): 2093-2107. |
| [4] |
Smith G C, Gidlow P M. Weighted stacking for rock property estimation and detection of gas[J]. Geophy-sical Prospecting, 1987, 35(9): 993-1014. DOI:10.1111/j.1365-2478.1987.tb00856.x |
| [5] |
Gal D, Dvorkin J, Nur A. A physical model for porosity reduction in sandstones[J]. Geophysics, 1998, 63(2): 454-459. |
| [6] |
Dvorkin J, Prasad M, Sakai A, et al. Elasticity of marine sediments:Rock physics modeling[J]. Geophysical Research Letters, 1999, 26(12): 1781-1784. DOI:10.1029/1999GL900332 |
| [7] |
李文成, 彭嫦姿, 杨鸿飞. 横波预测技术在YB地区的应用[J]. 地球物理学进展, 2014, 29(4): 1695-1700. LI Wencheng, PENG Changzi, YANG Hongfei. The application of S-wave predication technology in YB area[J]. Progress in Geophysics, 2014, 29(4): 1695-1700. |
| [8] |
Xu S, White R E. A physical model for shear-wave velocity prediction[J]. Geophysics, 1996, 44(4): 687-717. |
| [9] |
Xu S, Payne M A. Modeling elastic properties in carbonate rocks[J]. The Leading Edge, 2009, 28(1): 66-74. DOI:10.1190/1.3064148 |
| [10] |
刘欣欣, 印兴耀, 张峰. 一种碳酸盐岩储层横波速度估算方法[J]. 中国石油大学学报(自然科学版), 2013, 37(1): 42-49. LIU Xinxin, YIN Xingyao, ZHANG Feng. S-wave velocity estimation method in carbonate reservoir[J]. Journal of China University of Petroleum(Edition of Natural Sciences), 2013, 37(1): 42-49. DOI:10.3969/j.issn.1673-5005.2013.01.007 |
| [11] |
Pride S R, Berryman J G, Harris J M. Seismic attenua-tion due to wave-induced flow[J]. Journal of Geophysical Research Solid Earth, 2004, 109(B1): 247-278. |
| [12] |
Lee M W. A simple method of predicating S-wave velocity[J]. Geophysics, 2006, 71(6): F161-F164. DOI:10.1190/1.2357833 |
| [13] |
罗水亮, 杨培杰, 胡光明, 等. 基于变形P-L模型的矩阵方程迭代精细横波预测[J]. 地球物理学报, 2016, 59(5): 1839-1848. LUO Shuiliang, YANG Peijie, HU Guangming, et al. S-wave velocity predication based on the modified P-L model and matrix equation iteration[J]. Chinese Journal of Geophysics, 2016, 59(5): 1839-1848. |
| [14] |
郑旭桢, 王涛, 刘钊, 等. 泥岩基质弹性参数对Xu-White模型横波速度估算的影响[J]. 石油地球物理勘探, 2017, 52(5): 990-998. ZHENG Xuzhen, WANG Tao, LIU Zhao, et al. Inf-luence of clay elastic parameters on S-wave velocity estimation based on Xu-White model[J]. Oil Geophysical Prospecting, 2017, 52(5): 990-998. |
| [15] |
唐杰, 王浩, 姚振岸, 等. 基于岩石物理诊断的横波速度估算方法[J]. 石油地球物理勘探, 2016, 51(3): 537-543. TANG Jie, WANG Hao, YAO Zhen'an, et al. Shear wave velocity estimation based on rock physics diagnosis[J]. Oil Geophysical Prospecting, 2016, 51(3): 537-543. |
| [16] |
熊晓军, 林凯, 贺振华. 基于等效弹性模量反演的横波速度预测方法[J]. 石油地球物理勘探, 2012, 47(5): 723-727. XIONG Xiaojun, LIN Kai, HE Zhenhua. A method for S-wave velocity estimation based on equivalent elastic modulus inversion[J]. Oil Geophysical Prospecting, 2012, 47(5): 723-727. |
| [17] |
Lipton Z C, Berkowitz J, Elkan C.A critical review of recurrent neural networks for sequence learning[J].Computer Science, 2015, arXiv: 1506.00019.
|
| [18] |
张国豪, 刘波. 采用CNN和Bidirectional GRU的时间序列分类研究[J]. 计算机科学与探索, 2019, 13(6): 916-927. ZHANG Guohao, LIU Bo. Research on time series classification using CNN and Bidirectional GRU[J]. Journal of Frontiers of Computer Science and Technology, 2019, 13(6): 916-927. |
| [19] |
Hocheriter S, Schmidhuber J, Cummins F. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [20] |
Jozefowicz R, Zaremba W, Sutskever I.An empirical exploration of recurrent network architectures[C].International Conference on Machine Learning, 2015, 2342-2350.
|
| [21] |
Cho K, van Merrienboer B, Bahdanau D, et al. On the properties of neural machine translation: Encoder-decoder approaches[J]. Computer Science, 2014. DOI:10.3115/v1/W14-4012 |
| [22] |
王维红, 包培楠, 陈国飞, 等. 基于最小平方的横波速度拟合及应用[J]. 地球物理学进展, 2019, 34(5): 1924-1929. WANG Weihong, BAO Peinan, CHEN Guofei, et al. S-wave prediction and its application based on least square algorithm[J]. Progress in Geophysics, 2019, 34(5): 1924-1929. |



 刘洋, 新疆维吾尔自治区克拉玛依市中国石油大学(北京)克拉玛依校区, 834000。Email:
刘洋, 新疆维吾尔自治区克拉玛依市中国石油大学(北京)克拉玛依校区, 834000。Email: