② 中国自然资源航空物探遥感中心, 北京 100083
② Airborne Geophysical Prospecting and Remote Sensing Center, Ministry of Natural Resources, Beijing 100083, China
边界识别是位场(重磁)数据处理与解释的重要内容,其对圈定异常范围,划分断裂构造等具有重要意义。基于重磁异常的传统导数类边界识别方法,如垂向导数法[1-3]、总水平导数法[4-5]、解析信号法[6-9]等,均存在不能清晰识别深部地质体边界的缺点。为了提高对深部地质体边界的识别效果,地球物理学家提出了均衡边界识别方法。Miller等[10]提出了第一种均衡边界识别方法——倾斜角法,该方法分析垂向导数与总水平导数的比值,基于其零等值线推断地质体边界。倾斜角法能很好地均衡深、浅部地质体边界,但识别精度较低。Verduzco等[11]利用倾斜角的总水平导数进行地质体的边界识别,该方法对浅部地质体的边界识别效果较好,且其受地质体倾斜侧面的影响较小,但对边界的增强效果不明显。Wijns等[12]提出Theta法,该方法计算总水平导数与解析信号的比值,根据最大值的分布定义地质体边界。Theta法受场源埋深影响较小,但识别精度不高,且输出结果稳定性较差。Cooper等[13]提出了水平倾斜角法,根据水平倾斜角的极大值解释地质体边界。该方法能同时识别深、浅部异常体的边界,但也存在识别精度不高的问题,且对噪声极其敏感。马国庆等[14]提出了基于总水平导数与垂向导数的相关系数法,利用相关系数的极小值识别地质体边界。该方法具有一定的抗噪性,但识别效果受滑动窗口影响较大。Ma等[15]提出利用归一化总水平导数的极大值识别地质体边界。该方法有效提高了输出结果的稳定性,但识别结果同样依赖于滑动窗口的选择。马国庆等[16]提出增强型均衡滤波器,该滤波器利用不同阶导数之间的组合识别地质体边界。该方法能有效识别深、浅部地质体边界,但高阶导数的引入使噪声不可避免地被放大,从而影响整体边界识别的稳定性。总之,重磁异常的传统导数类边界识别方法大多存在识别精度低和输出结果稳定性差等缺点。
随着重磁勘探技术的不断发展,目前主要进行重磁梯度全张量测量。重磁梯度全张量数据具有高精度、高分辨率、多参量的优点[17],成为近年来位场数据处理与解释的研究热点[18-21]。大量学者对重磁梯度全张量的不变量[22-23]、特征值[24]以及总模值[25]进行了研究,并提出了相应的边界识别方法,一定程度上提高了地质体边界的识别效果,但还没有一种既能够提高识别精度、又能提高结果稳定性的边界识别方法。
基于磁力梯度全张量的最大特征值,提出了一种新的均衡边界识别方法。该方法不仅能够同时识别深浅模型体的边界,而且具有较高的识别精度、一定的抗倾斜磁化能力和较强的稳定性,是一种能够同时提高识别精度和输出结果稳定性的边界识别新方法。
1 基本理论 1.1 磁力梯度全张量特征值磁力梯度全张量G可表示为
| $ \begin{array}{l} \mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} {\frac{{{\partial ^2}U}}{{\partial {x^2}}}}&{\frac{{{\partial ^2}U}}{{\partial x\partial y}}}&{\frac{{{\partial ^2}U}}{{\partial x\partial z}}}\\ {\frac{{{\partial ^2}U}}{{\partial y\partial x}}}&{\frac{{{\partial ^2}U}}{{\partial {y^2}}}}&{\frac{{{\partial ^2}U}}{{\partial y\partial z}}}\\ {\frac{{{\partial ^2}U}}{{\partial z\partial x}}}&{\frac{{{\partial ^2}U}}{{\partial z\partial y}}}&{\frac{{{\partial ^2}U}}{{\partial {z^2}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {B_x}}}{{\partial x}}}&{\frac{{\partial {B_x}}}{{\partial y}}}&{\frac{{\partial {B_x}}}{{\partial z}}}\\ {\frac{{\partial {B_y}}}{{\partial x}}}&{\frac{{\partial {B_y}}}{{\partial y}}}&{\frac{{\partial {B_y}}}{{\partial z}}}\\ {\frac{{\partial {B_z}}}{{\partial x}}}&{\frac{{\partial {B_z}}}{{\partial y}}}&{\frac{{\partial {B_z}}}{{\partial z}}} \end{array}} \right]\\ \;\;\;\; = \left[ {\begin{array}{*{20}{l}} {{B_{xx}}}&{{B_{xy}}}&{{B_{xz}}}\\ {{B_{yx}}}&{{B_{yy}}}&{{B_{yz}}}\\ {{B_{zx}}}&{{B_{zy}}}&{{B_{zz}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{T_{11}}}&{{T_{12}}}&{{T_{13}}}\\ {{T_{21}}}&{{T_{22}}}&{{T_{23}}}\\ {{T_{31}}}&{{T_{32}}}&{{T_{33}}} \end{array}} \right] \end{array} $ | (1) |
式中:U表示磁位;Bx、By、Bz为磁场矢量的三个分量;Bmn(m, n=x, y, z)是磁场张量的9个分量;为了方便下文公式推导,将磁场张量的9个分量记为Tij(i, j=1, 2, 3)。
利用下式求取式(1)的特征值λ
| $ \begin{array}{l} \det \left( {\mathit{\boldsymbol{G}} - \lambda \mathit{\boldsymbol{E}}} \right) = \left| {\begin{array}{*{20}{c}} {{T_{11}} - \lambda }&{{T_{12}}}&{{T_{13}}}\\ {{T_{21}}}&{{T_{22}} - \lambda }&{{T_{23}}}\\ {{T_{31}}}&{{T_{32}}}&{{T_{33}} - \lambda } \end{array}} \right|\\ \;\;\;\;\; = \left( {{T_{11}} - \lambda } \right)\left[ {\left( {{T_{22}} - \lambda } \right)\left( {{T_{33}} - \lambda } \right) - {T_{23}}{T_{32}}} \right] - \\ \;\;\;\;\;\;\;{T_{12}}\left[ {{T_{21}}\left( {{T_{33}} - \lambda } \right) - {T_{23}}{T_{31}}} \right] + \\ \;\;\;\;\;\;\;{T_{13}}\left[ {{T_{21}}{T_{32}} - {T_{31}}\left( {{T_{22}} - \lambda } \right)} \right] = 0 \end{array} $ | (2) |
式中:det(·)表示求取矩阵行列式;E表示单位矩阵。
由磁力梯度全张量矩阵的对称性,即Tmn=Tnm(m, n=1, 2, 3, m≠n),以及在无源三维空间中磁位U满足拉普拉斯方程
| $ \begin{array}{l} \lambda + \lambda \left( {{T_{11}}{T_{22}} + {T_{11}}{T_{33}} + {T_{22}}{T_{33}} - T_{12}^2 - } \right.\\ \;\;\left. {T_{13}^2 - T_{23}^2} \right) + {T_{11}}T_{23}^2 + {T_{22}}T_{13}^2 + {T_{33}}T_{12}^2 - \\ \;\;{T_{11}}{T_{22}}{T_{33}} - {T_{12}}{T_{23}}{T_{31}} - {T_{13}}{T_{21}}{T_{32}} = 0 \end{array} $ | (3) |
式(3)可等效为如下形式的一元三次方程
| $ {\lambda ^3} + p\lambda + q = 0 $ | (4) |
式中
| $ p = {T_{11}}{T_{22}} + {T_{11}}{T_{33}} + {T_{22}}{T_{33}} - T_{12}^2 - T_{13}^2 - T_{23}^2 $ | (5) |
| $ \begin{array}{l} q = {T_{11}}T_{23}^2 + {T_{22}}T_{13}^2 + {T_{33}}T_{12}^2 - {T_{11}}{T_{22}}{T_{33}} - \\ \;\;\;\;\;{T_{12}}{T_{23}}{T_{31}} - {T_{13}}{T_{21}}{T_{32}} \end{array} $ | (6) |
利用卡尔丹公式,可得式(4)的三个解分别为
| $ {\lambda _1} = y_1^{\frac{1}{3}} + y_2^{\frac{1}{3}} $ | (7) |
| $ {\lambda _2} = y_1^{\frac{1}{3}}\omega + y_2^{\frac{1}{3}}{\omega ^2} $ | (8) |
| $ {\lambda _3} = y_1^{\frac{1}{3}}{\omega ^2} + y_2^{\frac{1}{3}}\omega $ | (9) |
式中
| $ {y_{1,2}} = - \frac{q}{2} \pm {\left[ {{{\left( {\frac{q}{2}} \right)}^2} + {{\left( {\frac{p}{3}} \right)}^3}} \right]^{\frac{1}{2}}} $ | (10) |
| $ \omega = \frac{{ - 1 + {\rm{i}}\sqrt 3 }}{2} $ | (11) |
磁力梯度全张量矩阵的最大特征值λ1对应地质体边界[24],但由于其主要构成元素为磁场张量,而张量信号随着地质体埋深的增加会急剧衰减,因此该方法对深部地质体的分辨率不高。
1.2 均衡边界识别方法磁力梯度全张量的总模值M为
| $ \begin{array}{l} M = \left( {B_{xx}^2 + B_{xy}^2 + B_{xz}^2 + B_{yx}^2 + B_{yy}^2 + B_{yz}^2 + } \right.\\ \;\;\;\;\;\;{\left. {B_{zx}^2 + B_{zy}^2 + B_{zz}^2} \right)^{\frac{1}{2}}} \end{array} $ | (12) |
M含有全部9个张量元素的信息,其最大值对应着地质体的边界[25],但是其识别精度较低。为了增强有用信号的幅值,本文提出将磁力梯度全张量矩阵的最大特征值与总模值相乘
| $ S = {\lambda _1}M $ | (13) |
相乘的优点是使浅部边界处异常幅值较大的有用信号增强,缺点是使深部边界处异常幅值较小的有用信号减弱,因此S能够提高对浅部地质体边界的识别精度,但无法有效识别深部地质体的边界,为此,对其进行了均衡处理
| $ {\rm{BS}} = \frac{S}{{\left| {{B_{zz}}} \right| + k\max \left( {\left| S \right|} \right)}} $ | (14) |
式中k是均衡深浅部异常的调节系数,一般取值为0~1,其大小与地质体异常信号的幅度有关,需要解释人员通过模型和实际数据调试。
1.3 对比边界识别方法为了说明本文提出的边界识别方法的有效性,选取三种基于磁力梯度全张量的边界识别方法进行对比,即不同分量组合法(HG)、总水平解析信号法(TA)和方向解析信号法(BDA),其参数分别定义如下
| $ {\rm{HG}} = \sqrt {B_{xy}^2 + {{\left( {{B_{xx}} - {B_{yy}}} \right)}^2} + B_{zx}^2 + B_{zy}^2} $ | (15) |
| $ {\rm{TA}} = \sqrt {{{\left( {\frac{{\partial {A_x}}}{{\partial z}}} \right)}^2} + {{\left( {\frac{{\partial {A_y}}}{{\partial z}}} \right)}^2}} $ | (16) |
| $ {\rm{BDA}} = {\tan ^{ - 1}}\left( {\frac{{\sqrt {{{\left( {\frac{{\partial {A_x}}}{{\partial z}}} \right)}^2} + {{\left( {\frac{{\partial {A_y}}}{{\partial z}}} \right)}^2}} }}{{\left| {\frac{{\partial {A_z}}}{{\partial z}}} \right|}}} \right) $ | (17) |
式中
| $ \left\{ {\begin{array}{*{20}{l}} {{A_x} = \sqrt {B_{xx}^2 + B_{xy}^2 + B_{xz}^2} }\\ {{A_y} = \sqrt {B_{yx}^2 + B_{yy}^2 + B_{yz}^2} }\\ {{A_z} = \sqrt {B_{zx}^2 + B_{zy}^2 + B_{zz}^2} } \end{array}} \right. $ | (18) |
分别为方向解析信号。
2 模型试验为了检验本文方法的边界识别效果,分别建立了简单模型和复杂模型进行计算分析。
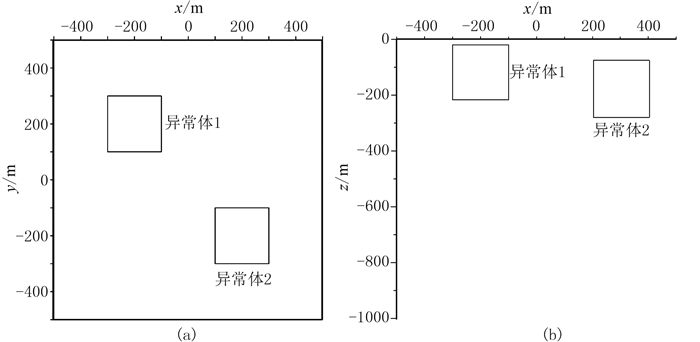
2.1 简单模型首先建立由两个立方体组成的简单模型(图 1)。两个立方体的边长均为200m,中心点坐标(x,y,z)分别为(-200m,200m,120m)和(200m,-200m,180m),顶面埋深分别为20、80m。
|
图 1 简单模型俯视图(a)和平视图(b) |
下面分别考虑垂直磁化、倾斜磁化和加噪垂直磁化三种情形分析本文方法对异常体边界的识别效果。
2.1.1 垂直磁化地质体产生的重磁异常会随着地质体埋深的增加而迅速衰减,对深部地质体产生的弱异常信号进行有效提取是边界识别的主要问题,因此埋深是影响边界识别效果的主要因素之一。
首先分析埋深对边界识别效果的影响。对图 1所示模型设置其地磁倾角为90°,地磁偏角为0°,磁化倾角为90°,磁化偏角为0°,磁化强度为1A/m。
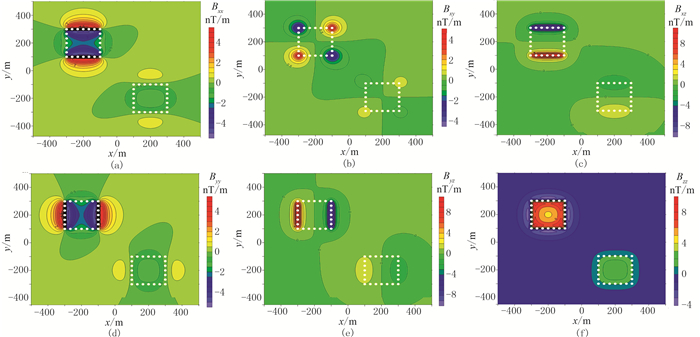
图 2是垂直磁化下磁力梯度全张量6个元素的平面等值线图(由于张量矩阵的对称性,有3组分量完全相同,因此只展示每组中的一个,下同)。可以看出,较浅的异常体的异常信息较丰富,所反映的模型体边界很清晰;反之,较深异常体的异常信息比较弱,所反映的异常体边界较模糊。
|
图 2 垂直磁化情况下磁力梯度全张量6个元素的平面等值线图
(a)Bxx;(b)Bxy;(c)Bxz;(d)Byy;(e)Byz;(f)Bzz
图中白色虚线框为异常体边界,下同 |
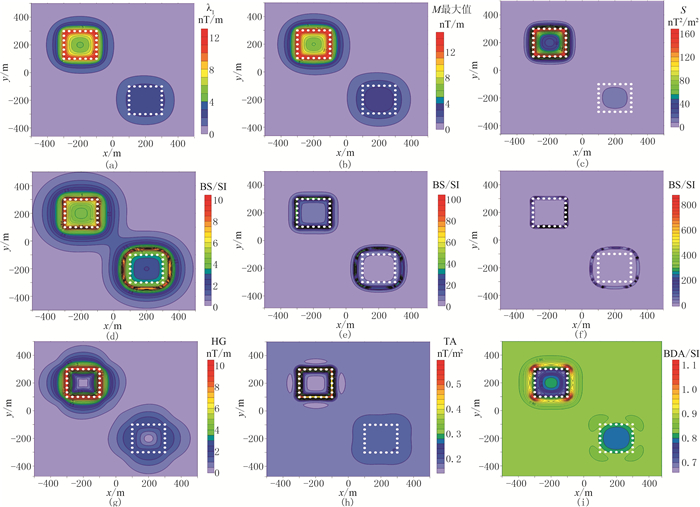
图 3是垂直磁化情况下各边界识别参数或识别方法计算结果。从图 3a~图 3c可以看出,λ1和M的最大值可以识别浅部异常体边界,但识别精度较低,且对深部异常体边界无法识别。相比于λ1和M,S对浅部异常体的识别精度更高,但仍无法有效识别深部异常体边界。从图 3d~图 3f可以看出,相比于参数S,均衡边界识别方法的参数BS能够识别深部异常体边界,调节系数k起到均衡深浅部异常的作用:大的k值对深部模型边界的识别均衡能力强,但识别精度低;小的k值对深部模型边界的均衡能力弱,但识别精度高。模型试验表明,k取0.001时可兼顾深部和浅部异常体的边界识别效果。从图 3g~图 3i可以看出:参数HG的总体识别效果一般,且边界处异常分布发散;参数TA对浅部模型的识别效果较好,但无法有效识别深部模型体的边界;参数BDA能够识别深部异常体边界,但总体识别精度不高。
|
图 3 垂直磁化情况下不同参数的平面分布图 (a)λ1;(b)M最大值;(c)S;(d)BS:k=0.100;(e)BS:k=0.010;(f)BS:k=0.001;(g)HG;(h)TA;(i)BDA |
由上分析可知,本文均衡边界识别方法在垂直磁化情况下,能够很好地识别深部和浅部异常体边界,调节系数k取0.001时,有着较高的识别精度,可兼顾深部和浅部异常体。
2.1.2 倾斜磁化实际情况中,地质体所处的磁场环境往往都是倾斜磁化的,而倾斜磁化会使地质体产生的异常形态变得复杂,不再具有对称性,因此倾斜磁化也是影响边界识别效果的因素之一。本节分析倾斜磁化对边界识别效果的影响。对图 1所示模型,设地磁倾角为60°,地磁偏角为5°,磁化倾角为60°,磁化偏角为5°,磁化强度为1A/m。
图 4是倾斜磁化情况下磁力梯度全张量6个元素的平面等值线图。相比于图 2,图 4中各张量元素所体现的异常形态不再具有对称性,与模型体边界的实际位置也存在一定的偏移。

|
图 4 倾斜磁化情况下磁力梯度全张量6个元素的平面等值线图 (a)Bxx;(b)Bxy;(c)Bxz;(d)Byy;(e)Byz;(f)Bzz |
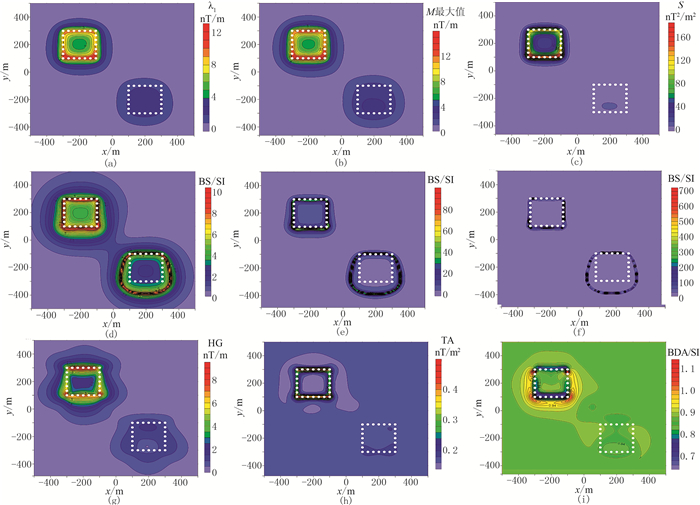
图 5是倾斜磁化情况下各边界识别参数或识别方法计算结果的平面等值线图。相比于图 3,图 5中λ1、M以及S受倾斜磁化影响较小,但总体来说识别的边界向南移动;均衡边界识别方法的参数BS也体现了相似特征,即具有一定的抗倾斜磁化能力;参数HG、TA及BDA受倾斜磁化的影响较大,对深部和浅部异常体边界均不能有效识别,尤其是BDA受倾斜磁化的影响最严重,产生了错误的边界信息。
|
图 5 倾斜磁化情况下不同参数的平面分布图 (a)λ1;(b)M最大值;(c)S;(d)BS:k=0.100;(e)BS:k=0.010;(f)BS:k=0.001;(g)HG;(h)TA;(i)BDA |
总体上看,本文提出的均衡边界识别方法在倾斜磁化情况下,具有一定的抗干扰能力,对倾斜磁化敏感度较低,可对深部和浅部异常体边界进行识别。
2.1.3 加噪垂直磁化除了异常体埋深和倾斜磁化会对边界识别产生影响,测量环境和测量仪器等带来的各种噪声也会对边界识别结果产生较大干扰,尤其是基于重磁异常的传统导数类边界识别方法会大幅度放大高频噪声,无法有效地识别边界。
因此,本节讨论噪声对边界识别效果的影响。对垂直磁化情况下的9个张量元素,分别加入各自异常最大幅值10%的高斯噪声。
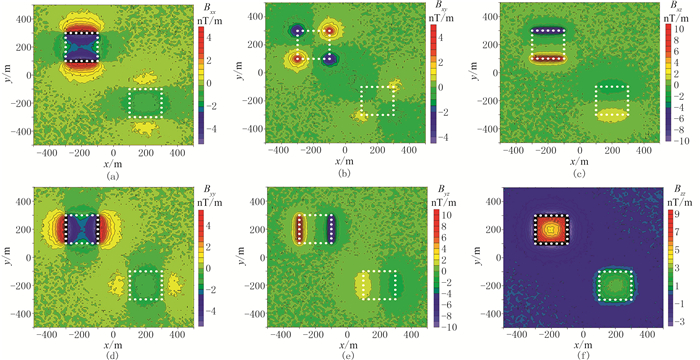
图 6是含噪垂直磁化情况下磁力梯度全张量6个元素的平面等值线图。相比于图 2,图 6中各张量元素的异常形态由于噪声的干扰变得十分紊乱,无法反映模型体的边界位置。
|
图 6 含噪垂直磁化情况下磁力梯度全张量6个元素的平面等值线图 (a)Bxx;(b)Bxy;(c)Bxz;(d)Byy;(e)Byz;(f)Bzz |
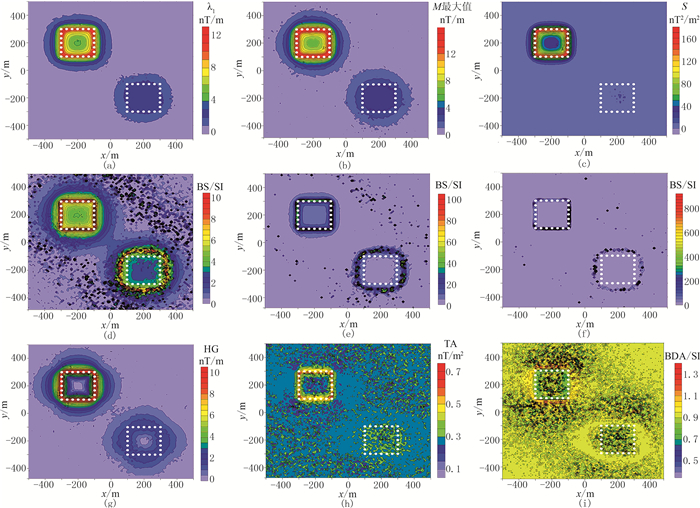
图 7是含噪垂直磁化情况下不同边界识别参数或识别方法计算结果。可以看出,参数λ1、M的识别效果受到了噪声的影响,但参数S受噪声的影响较小;参数BS对于调节系数k取值不同情况下受噪声影响的大小不同:k值越大,受噪声的影响越大,k值越小,受噪声的影响越小;基于磁力梯度全张量的边界识别方法中,参数HG具有一定的抗噪性,而参数TA和BDA对噪声极其敏感,尤其是BDA受噪声的影响最为严重。
|
图 7 含噪垂直磁化情况下不同参数的平面分布图 (a)λ1;(b)M最大值;(c)S;(d)BS:k=0.100;(e)BS:k=0.010;(f)BS:k=0.001;(g)HG;(h)TA;(i)BDA |
因此,总体上来看,本文提出的均衡边界识别方法在加噪垂直磁化情况下,当调节系数k取0.001时,受噪声的影响较小,具有较强的鲁棒性。
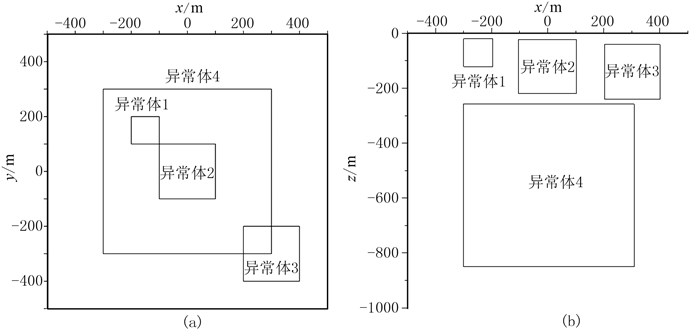
2.2 复杂模型为了进一步说明本文方法的有效性并分析如何选取恰当的k值,下面建立一个包括四个立方体的复杂模型(表 1和图 8)进行计算。
|
|
表 1 复杂模型参数表 |
|
图 8 复杂模型俯视图(a)和平视图(b) |
对复杂模型仅考虑垂直磁化不加噪的情况,并选取不同的k值,对比分析边界识别效果,从而得到最佳k值。
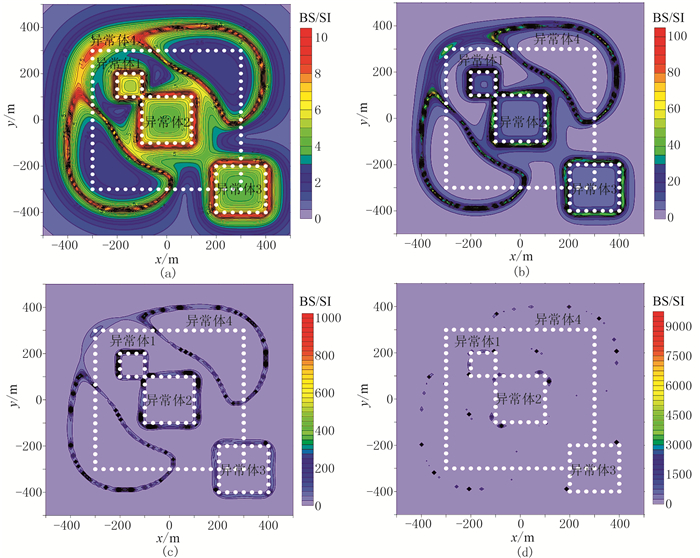
图 9是复杂模型垂直磁化情况下调节系数k不同取值时利用本文均衡边界识别方法得到的平面等值线图。可以看出,随着k取值由大到小,边界识别的效果也在变化:图 9a中k=0.1000,此时对异常体的边界识别精度不高;图 9b中k=0.0100,识别的边界精度较图 9a而有所提高;图 9c中k=0.0010时,边界识别精度较图 9b有所提高;图 9d中当k=0.0001时,几乎没有异常显示,即无法识别异常体边界。
|
图 9 复杂模型垂直磁化情况下的BS平面等值线图 (a)k=0.1000;(b)k=0.0100;(c)k=0.0010;(d)k=0.0001 |
综上,可以得出:利用本文提出的均衡边界识别方法能够完成对复杂模型体边界的识别,且当调节系数k取0.0010时,取得的边界识别效果最好。本文提出的方法理论及k值选取的合理性得到了进一步验证。
3 实际应用由于磁力梯度全张量测量对测量仪器的要求很高,目前很少能够在地面直接测量较高精度的磁力梯度全张量数据,但是航磁三分量的测量技术已发展成熟,国内以中国自然资源航空物探遥感中心为代表,已获得了高精度的航磁三分量数据,而对航磁三分量数据求取三维空间各方向上的一阶导数,便能获得航磁梯度全张量数据。
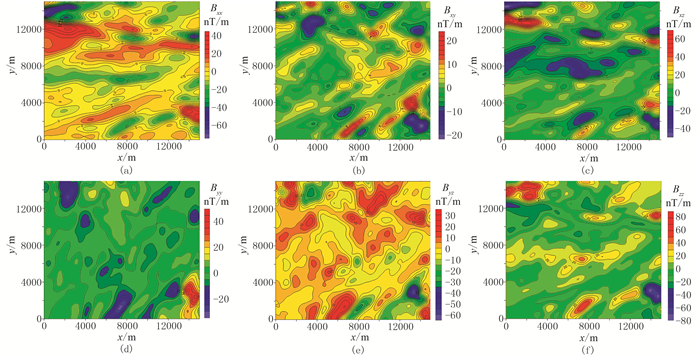
为了检验本文均衡边界识别方法的实际应用效果,截取了中国北部某地区的实测航磁三分量数据,并对其进行求导,进而得到航磁梯度全张量数据(图 10)。
|
图 10 研究区磁力梯度全张量6个元素的平面等值线图 (a)Bxx;(b)Bxy;(c)Bxz;(d)Byy;(e)Byz;(f)Bzz |
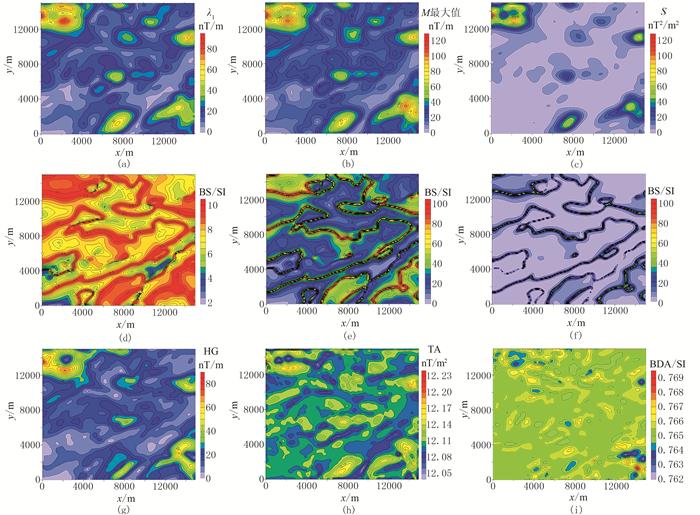
对转换后的航磁梯度全张量数据(图 10)进行了边界识别方法的计算,结果见图 11。可以看出,λ1识别的边界信息不够清晰;M识别出的边界只包含浅部地质体的信息;S识别结果精度有所提高,但仍无法显示深部地质体的边界信息;参数BS随着调节系数k取值的变化,识别结果越来越清晰,当k=0.001时识别出精度较高的地质体边界;而基于磁力梯度全张量的三种边界识别方法中,参数HG识别的地质体边界不清晰;TA和BDA识别出的边界十分模糊,对异常体的刻画不够清晰。
|
图 11 研究区不同参数的平面分布图 (a)λ1;(b)M最大值;(c)S;(d)BS:k=0.100;(e)BS:k=0.010;(f)BS:k=0.001;(g)HG;(h)TA;(i)BDA |
综上,本文提出的均衡边界识别方法对于实际航磁数据的应用具有良好的边界识别效果,能够获得较清晰的边界信息。
4 结论本文基于磁力梯度全张量的最大特征值和总模值,提出了一种新的均衡边界识别方法。模型试验和实际应用证明,利用本文提出的均衡边界识别方法,当调节系数k=0.0010时,能够有效识别地质体边界,并具一定的抗倾斜磁化能力和较强的抗噪性,是一种既能够提高识别精度、又能提高计算稳定性的磁场数据边界识别新方法。
| [1] |
Evjen H M. The place of vertical gradient gravitatio-nal interpretations[J]. Geophysics, 1936, 1(1): 127-136. DOI:10.1190/1.1437067 |
| [2] |
Hood P, McClure D J. Gradient measurements in ground magnetic prospecting[J]. Geophysics, 1965, 30(3): 403-410. DOI:10.1190/1.1439592 |
| [3] |
Hood P, Teskey D J. Aeromagnetic gradiometer pro-gram of the Geological Survey of Canada[J]. Geophysics, 1989, 54(8): 1012-1022. DOI:10.1190/1.1442726 |
| [4] |
Cordell L.Gravimetric expression of graben faulting in Santa Fe Country and the Espanola Basin, New Mexico[C]. New Mexico Geology Society Guidebook, 30th Annual Fall Field Conference, 1979, 59-64.
|
| [5] |
Codell L, Grauch V J S.Mapping basement magnetization zones from aeromagnetic data in the San Juan Basin, New Mexico[C]. SEG Technical Program Expanded Abstracts, 1985, 4: 181-185.
|
| [6] |
Nabighian M N. The analytic signal of two-dimensional magnetic bodies with polygonal cross-section:Its properties and use for automated anomaly interpretation[J]. Geophysics, 1972, 37(3): 507-517. DOI:10.1190/1.1440276 |
| [7] |
Nabighian M N. Toward a three-dimensional automa-tic interpretation of potential field data via generalized Hilbert transforms:Fundamental relations[J]. Geophysics, 1984, 49(6): 780-786. DOI:10.1190/1.1441706 |
| [8] |
Roest W R, Verhoef J, Pilkington M. Magnetic interpretation using the 3-D analytic signal[J]. Geophy-sics, 1992, 57(1): 116-125. |
| [9] |
Hsu S, Sibuet J C, Shyu C. High-resolution detection of geologic boundaries from potential field anomalies:an enhanced analytic signal technique[J]. Geophysics, 1996, 61(2): 373-386. DOI:10.1190/1.1443966 |
| [10] |
Miller H G, Singh V. Potential field tilt:a new concept for location of potential field sources[J]. Journal of Applied Geophysics, 1994, 32(2-3): 213-217. DOI:10.1016/0926-9851(94)90022-1 |
| [11] |
Verduzco B, Fairhead J D, Green C M, et al. New insights into magnetic derivatives for structural mapping[J]. The Leading Edge, 2004, 23(2): 116-119. DOI:10.1190/1.1651454 |
| [12] |
Wijns C, Perez C, Kowalczyk P. Theta map:Edge detection in magnetic data[J]. Geophysics, 2005, 70(4): L39-L43. DOI:10.1190/1.1988184 |
| [13] |
Cooper G R J, Cowan D R. Enhancing potential field data using filters based on the local phase[J]. Computers & Geosciences, 2006, 32(10): 1585-1591. |
| [14] |
马国庆, 杜晓娟, 李丽丽. 利用水平与垂直导数的相关系数进行位场数据的边界识别[J]. 吉林大学学报(地球科学版), 2011, 41(增刊1): 345-348. MA Guoqing, DU Xiaojuan, LI Lili. Edge detection of potential field data using correlation coefficients of horizontal and vertical derivatives[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(S1): 345-348. |
| [15] |
Ma G Q, Li L L. Edge detection in potential fields with the normalized total horizontal derivative[J]. Computer & Geosciences, 2012, 41(1): 83-87. |
| [16] |
马国庆, 黄大年, 于平, 等. 改进的均衡滤波器在位场数据边界识别中的应用[J]. 地球物理学报, 2012, 55(12): 4288-4295. MA Guoqing, HUANG Danian, YU Ping, et al. Application of improved balancing filters to edge identification of potential field data[J]. Chinese Journal of Geophysics, 2012, 55(12): 4288-4295. DOI:10.6038/j.issn.0001-5733.2012.12.040 |
| [17] |
舒晴, 马国庆, 刘财, 等. 全张量磁梯度数据解释的均衡边界识别及深度成像技术[J]. 地球物理学报, 2018, 61(4): 1539-1548. SHU Qing, MA Guoqing, LIU Cai, et al. Balanced edge detection and depth imaging technique for the interpretation of full-tensor magnetic gradient data[J]. Chinese Journal of Geophysics, 2018, 61(4): 1539-1548. |
| [18] |
马国庆, 李丽丽, 杜晓娟. 磁张量数据的边界识别和解释方法[J]. 石油地球物理勘探, 2012, 47(5): 815-821. MA Guoqing, LI Lili, DU Xiaojuan. Boundary detection and interpretation by magnetic gradient tensor data[J]. Oil Geophysical Prospecting, 2012, 47(5): 815-821. |
| [19] |
周文纳, 杜晓娟, 李吉焱. 重力数据的平面全张量梯度角度边界识别方法[J]. 石油地球物理勘探, 2013, 48(6): 1009-1015. ZHOU Wenna, DU Xiaojuan, LI Jiyan. Gravity data edge identification using plane full tensor gradient angle[J]. Oil Geophysical Prospecting, 2013, 48(6): 1009-1015. |
| [20] |
郑建拥, 范红波, 张琪, 等. 利用磁梯度张量识别地下小型目标体[J]. 石油地球物理勘探, 2019, 54(3): 692-699. ZHENG Jianyong, FAN Hongbo, ZHANG Qi, et al. Underground small target recognition using magnetic gradient tensor[J]. Oil Geophysical Prospecting, 2019, 54(3): 692-699. |
| [21] |
李青竹, 李志宁, 张英堂, 等. 基于二阶磁张量欧拉反褶积的磁源单点定位方法[J]. 石油地球物理勘探, 2019, 54(4): 915-924. LI Qingzhu, LI Zhining, ZHANG Yingtang, et al. Magnetic source single-point positioning based on se-cond-order magnetic tensor Euler deconvolution[J]. Oil Geophysical Prospecting, 2019, 54(4): 915-924. |
| [22] |
Beiki M, Perdersen L B. Eigenvector analysis of gravity gradient tensor to locate geologic bodies[J]. Geophysics, 2010, 75(6): 137-149. DOI:10.1190/1.3503577 |
| [23] |
Beiki M, Clark D A, Austin J R, et al. Estimating source location using normalized magnetic sourcestrength calculated from magnetic gradient tensordata[J]. Geophysics, 2012, 77(6): J23-J37. DOI:10.1190/geo2011-0437.1 |
| [24] |
Zuo B X, Hu X Y. Edge detection of gravity field using eigenvalue analysis of gravity gradient tensor[J]. Journal of Applied Geophysics, 2015, 114: 263-270. DOI:10.1016/j.jappgeo.2015.01.013 |
| [25] |
Wu H, Li L, Xing C C, et al. A new method of edge detection based on the total horizontal derivative and the modulus of full tensor gravity gradient[J]. Journal of Applied Geophysics, 2017, 139: 239-245. DOI:10.1016/j.jappgeo.2017.02.026 |



 郭华, 北京市海淀区学院路31号中国自然资源航空物探遥感中心, 100083。Email:
郭华, 北京市海淀区学院路31号中国自然资源航空物探遥感中心, 100083。Email: