② 东北大学资源与土木工程学院, 辽宁沈阳 110819;
③ 自然资源部第二海洋研究所国家海洋局海底科学重点实验室, 浙江杭州 310012
② College of Resources and Civil Engineering, Northeastern University, Shenyang, Liaoning 110819, China;
③ Key Laboratory of Submarine Geosciences, Se-cond Institute of Oceanography, Ministry of Natural Resources, Hangzhou, Zhejiang 310012, China
利用重力勘探数据反演地下物性、几何位置等参数是一种常用的数据处理解释方法[1-2]。对于计算地质体在水平方向上的分布范围,边界识别是一种快速、有效的手段。常用的边界识别方法包括总水平导数法[3]、解析信号法[4]、倾斜角法及其总水平导数法[5-6]、Theta图法[7]、结构张量特征值法[8]等。重力梯度数据与重力异常相比具有更高的信噪比,使用梯度数据识别边界效果较好[9]。
目前,边界识别方法还存在一些不足之处,如对深部地质体边界识别不清晰,结果中存在虚假边界等。因此,学者们提出了不同的改进方式,例如:方向总水平导数(Directional Total Horizontal Derivative, DTHD)法[10-11],改进结构张量法[12],均衡总水平导数法与正则化解析信号法[13],全张量梯度数据的特征值法[14],水平方向Theta图法[15],高阶导数法[16],全张量梯度角度法[17],伪总梯度余弦值法[18]等,这些研究在一定程度上改善了以上问题。其中,DTHD法比解析信号法具有更高的分辨率[19]。DTHD法可通过计算x、y等方向上的总水平导数,进一步提高检测能力,在实际应用中能够从这两个方向上较好地识别地质体边界。
相关系数在位场数据的处理解释中可用于快速成像[20-21]和反演[22-24]。相关系数不仅能够表示观测异常与地下空间几何函数的相关程度,还可以表示不同物理量的相似程度。根据这一性质,马国庆等[25]通过总水平导数与垂直导数的相关系数识别边界,该方法联合两种物理量增强了识别效果;徐梦龙等[26]还利用各方向均方差的相关系数实现了边界识别,通过联合多个方向窗口中的均方差数据增强了相关性特征。
本文利用重力梯度数据计算x和y方向总水平导数的相关系数识别边界,结合多方向窗口技术改善识别效果,并通过改进的二值化和阈值处理(Binarization and Threshold Processing, BTP)方法[27]突出解释结果中的边界位置,提高识别精度。
1 多方向窗口联合相关系数方法原理 1.1 x和y方向总水平导数的相关系数根据文献[10],x和y方向的总水平导数分别定义为
| $ \mathrm{THD}_{x}=\sqrt{V_{x y}^{2}+V_{x z}^{2}} $ | (1) |
| $ \mathrm{THD}_{y}=\sqrt{V_{y x}^{2}+V_{y z}^{2}} $ | (2) |
式中:V表示重力场;Vxy、Vxz、Vyx与Vyz表示重力场梯度,且Vxy=Vyx。THDx与THDy的相关系数定义为
| $C=\frac{\sum\limits_{i=1}^{N}\left(\mathrm{THD}_{x, i}-\frac{1}{N} \sum\limits_{i=1}^{N} \mathrm{THD}_{x, i}\right)\left(\mathrm{THD}_{y, i}-\frac{1}{N} \sum\limits_{i=1}^{N} \mathrm{THD}_{y, i}\right)}{\sqrt{\sum\limits_{i=1}^{N}\left(\mathrm{THD}_{x, i}-\frac{1}{N} \sum\limits_{i=1}^{N} \mathrm{THD}_{x, i}\right)^{2} \sum\limits_{i=1}^{N}\left(\mathrm{THD}_{y, i}-\frac{1}{N} \sum\limits_{i=1}^{N} \mathrm{THD}_{y, i}\right)^{2}}} $ | (3) |
式中:THDx, i和THDy, i分别表示窗口内第i个THDx和THDy数据;N表示窗口内的总点数。
式(3)中,-1≤C≤1,属无量纲的物理量。C的绝对值越接近于1,表示THDx与THDy的相关程度越高;越接近于0,表示相关程度越低。C值为正数表示正相关;若为负数,表示负相关;当C等于0,表示不相关。根据式(1)和式(2),地质体在x、y方向的边界可分别根据THDx和THDy的极大值分布特征进行解释。C越接近于-1,即THDx与THDy呈负相关时,该点为地质体边界的可能性越大。这种利用极小值分布特征解释地质体边界的方法即是相关系数边界识别(Correlation Coefficients Edge Detection, CCED)法。
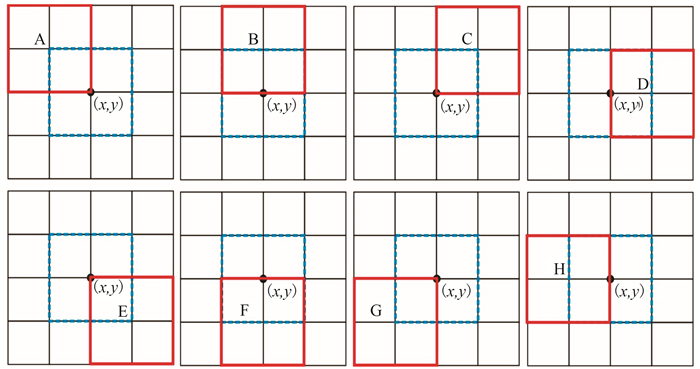
1.2 多方向窗口的联合方法式(3)的计算使用了滑动窗口,通常窗口的中心点就是测点位置。徐梦龙等[26]为获得测点与其邻近各方向上的数据在波动性方面的相关性,使用了8个方向的窗口,即测点分别在窗口的右下角、下方中心、左下角、左侧中心、左上角、上方中心、右上角、右侧中心,并分别定义测点位于中心和边缘的8个窗口为窗口0和A~H(图 1)。
|
图 1 多方向窗口示意图 图中蓝色虚线框表示窗口0,红色框分别表示窗口A~H,黑色实心圆点为测点(x, y)的位置 |
对于任意测点(x, y),使用窗口0、A~H计算相关系数能够得到9个Ck(k=0,A, B, C, D, E, F, G, H),这些值共同表征以该测点为中心的区域上THDx与THDy的相关度。利用不同观测场或不同计算条件下的相关系数可以计算联合相关系数[28],即多方向窗口联合相关系数(Multi-directional Window Joint Correlation-coefficient, MWJC)
| $ \begin{aligned} C_{\text {joint }}=& C_{0} \times C_{\mathrm{A}} \times C_{\mathrm{B}} \times C_{\mathrm{C}} \times C_{\mathrm{D}} \times C_{\mathrm{E}} \times \\ & C_{\mathrm{F}} \times C_{\mathrm{G}} \times C_{\mathrm{H}} \end{aligned} $ | (4) |
Cjoint可以增强THDx与THDy的相关性特征,进一步提高边界识别效果。
1.3 改进的二值化与阈值处理方法利用式(4)计算的Cjoint结果中可能存在干扰,影响地质体边界的识别和成图效果。根据数字图像处理中的BTP原理,设定一阈值α,并据其对数据划分区间,对不同区间内的数据赋值为0或1。这样整个数据被转化为只包含0或1的数据集,图像中的细节被弱化,边界将更清晰地显示出来。MWJC法是利用THDx与THDy的负相关性判断边界的,即相关系数的分布区间为[-1, 1]。为了不破坏结果的幅值分布规律并保留边界细节,本文提出改进的BTP(Improved BTP, IBTP)方法。具体步骤包括:
(1) 将Cjoint的取值区间[-1, 1]划分为若干个长度相等的子区间,并统计各子区间上的数量;
(2) 设定阈值α等于某个子区间的最小值,且α≤0(大于α的所有子区间中包含的结果数量占较大比例);
(3) 将大于α的子区间标注为1。这样既保留了具有负相关性特征的幅值的细节,也将非边界结果的正值全部转化为1,一定程度上增加了图像中边界显示的对比度。
2 理论模型试验为了验证本文提出的MWJC法在边界识别中的效果,设计了两个理论模型进行计算分析。模型的测点均匀分布在z=0平面上,x、y方向观测范围均为-1000~1000m。
2.1 模型一模型一包括两个大小相同的正方体,平面位置见图 2。异常体1和异常体2的边长均为400m,埋深分别为200m和300m,剩余密度均为1.0g/cm3。观测点距、线距均为10m,总计201×201个测点。
|
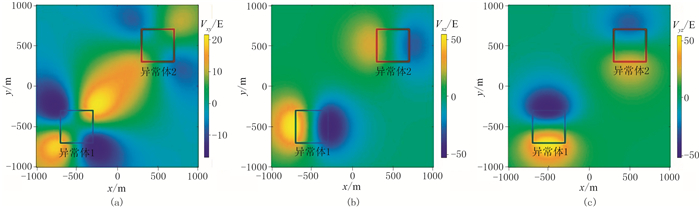
图 2 模型一重力梯度数据
(a)Vxy;(b)Vxz;(c)Vyz 图中矩形框表示异常体边界,下同 |
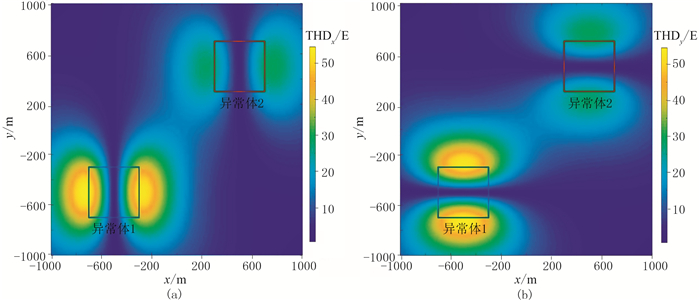
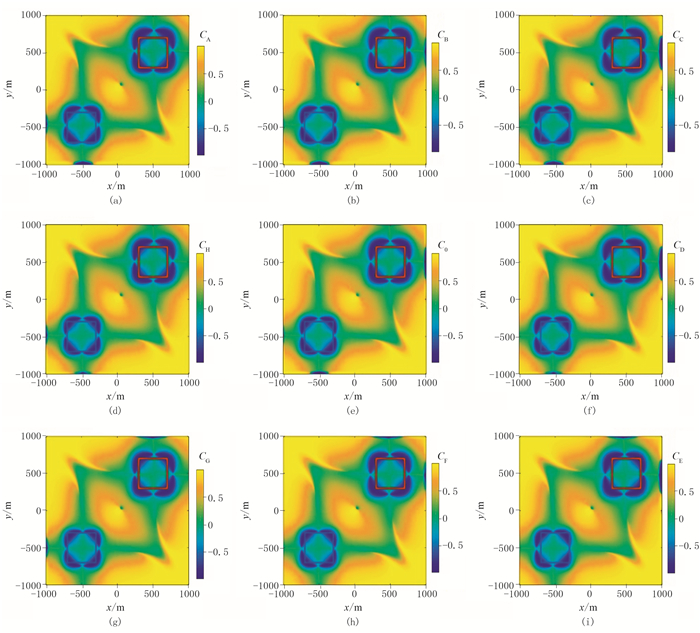
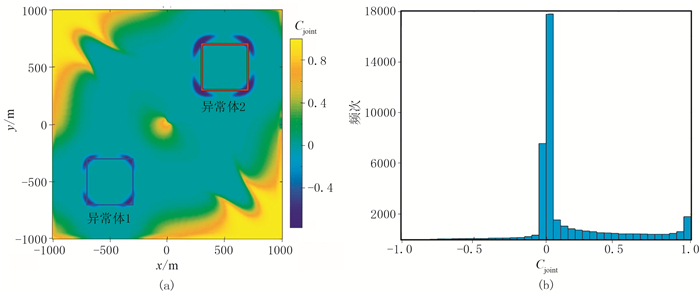
该模型正演模拟的Vxy、Vxz和Vyz如图 2所示,进而计算得到THDx与THDy(图 3)及不同窗口的CCED法识别结果(图 4)和MWJC分布(图 5)。这里CCED的计算窗口为5×5,即包含5×5个观测数据,尺寸为40m×40m。由图 3可见,THDx和THDy能够分别检测到两个异常体的x和y方向的边界,但检测不到另一个方向上的边界,且强异常所覆盖范围较大。由图 4可见,使用窗口0的CCED识别结果(图 4e)兼有THDx与THDy的优点,即均可很好地识别两个异常体的x和y方向的边界,其中,浅部异常体1的边界最准确,检测的深部异常体2的范围略大于实际范围。MWJC计算结果(图 5)进一步增强了异常体边界位置的负相关性,虽检测到的深部异常体2的边界虽仍然大于实际范围,但较图 4e的检测结果更接近于实际情况。需要注意的是,图 5中识别的深部地质体的范围比实际模型范围略大,且形态也略显发散;相对而言,对浅部异常体1的边界识别更准确。基于CCED及MWJC的识别结果均在一定程度上改善了由于异常体埋深增加而导致的边界识别分辨率下降问题;甚至从图 4和图 5还可见,深部地质体边界的负相关程度高于浅部地质体。
|
图 3 模型一的THDx(a)和THDy(b)分布 |
|
图 4 模型一的Ck分布 (a)k=A;(b)k=B;(c)k=C;(d)k=H;(e)k=0;(f)k=D;(g)k=G;(h)k=F;(i)k=E |
|
图 5 模型一的Cjoint分布(a)及Cjoint子区间数量统计柱状图(b) |
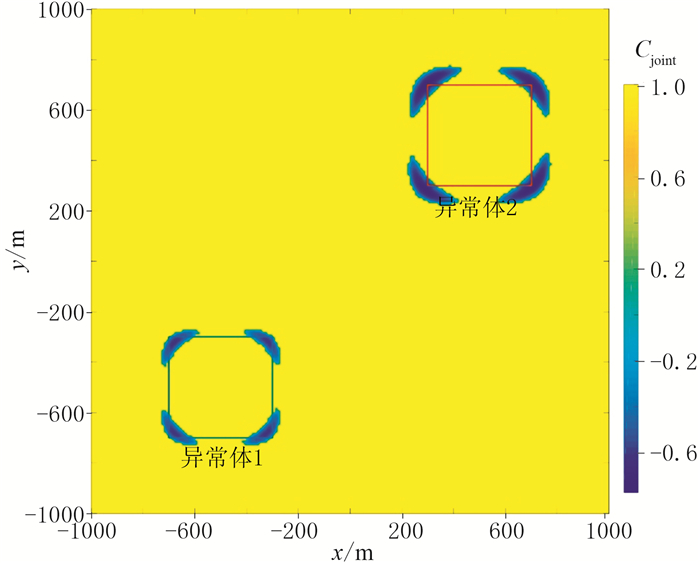
同一测点在不同窗口中的相对位置会不同,因此基于窗口A~H的CCED识别结果也有所不同:识别的地质体边界会随窗口方向的变化而移动。例如,在图 1中位于窗口A中的右下角的测点,在图 3a中则位于窗口A的右上角,即识别出的地质体边界向图中实际边界的右上方移动。基于MWJC的识别结果进一步突出了边界中四个顶点的位置,提高了识别的边界与背景的对比度。根据统计结果确定α=-0.2,经过IBTP处理的MWJC结果(图 6)完全消除了图 5a中的干扰,边界显示更清晰。从图 6可见,每个正方体的四个顶点位置均被准确地识别,结合图 4e,能够判断不同深度正方体的边界。
|
图 6 图 5a经IBTP处理的结果 |
由以上分析可见,基于MWJC的识别结果能够综合THDx与THDy在y和x方向的边界识别能力。与其他方法[8, 12, 16]相比,无需考虑矩阵的秩、归一化等问题,原理和计算方法都很简单,易于编程实现;通过IBTP处理后,MWJC的分布特征能够很好地突出地质体边界。
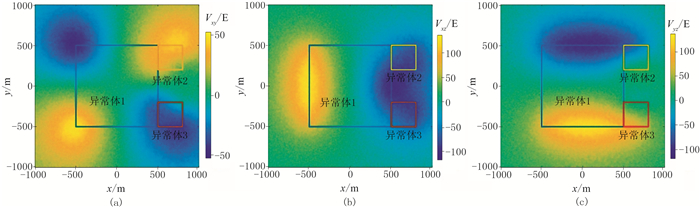
2.2 模型二该模型包含三个剩余密度均为1.0g/cm3的立方异常体,埋深均为200m,大小分别为1000m×1000m×5000m、300m×300m×300m和300m×300m×300m,在水平方向上三个异常体组呈“凹”形分布,相对位置见图 7。观测点距、线距均为10m,共201×201个测点。在理论数据中加入5%的高斯噪声。计算Cjoint的窗口大小为3×3,即尺寸为20m×20m,并采取高斯滤波的方法压制噪声。
|
图 7 模型二重力梯度数据(含5%噪声) (a)Vxy;(b)Vxz;(c)Vyz |
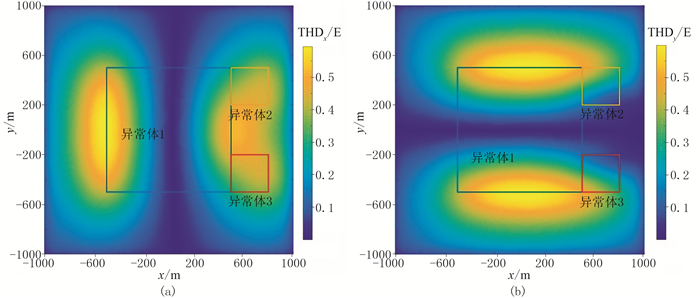
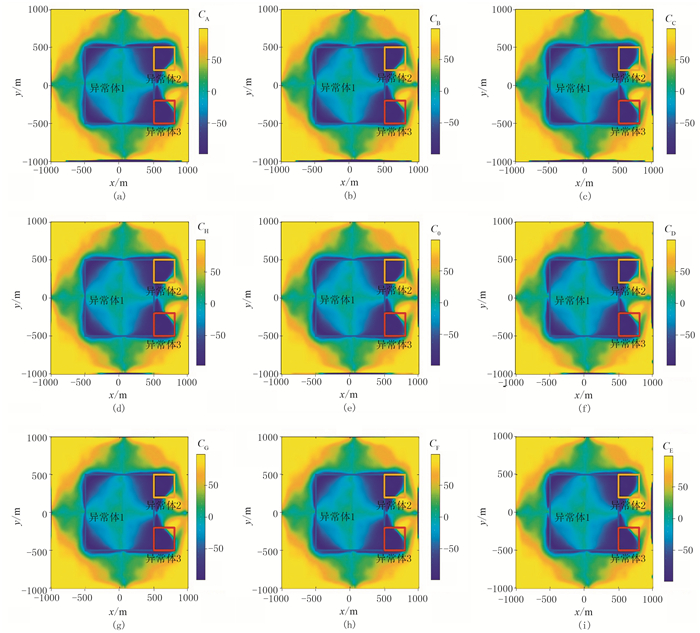
由于模型中的异常体2和异常体3的体积较小,所以不论是从观测数据(图 7)还是DTHD分布(图 8)都不易分辨;但是从图 9所示的C分布特征能够识别到异常体边界,图中的极小值揭示了异常体的边界位置。
|
图 8 模型二THDx(a)和THDy(b)分布 |
|
图 9 模型二的Ck分布 (a)k=A;(b)k=B;(c)k=C;(d)k=H;(e)k=0;(f)k=D;(g)k=G;(h)k=F;(i)k=E |
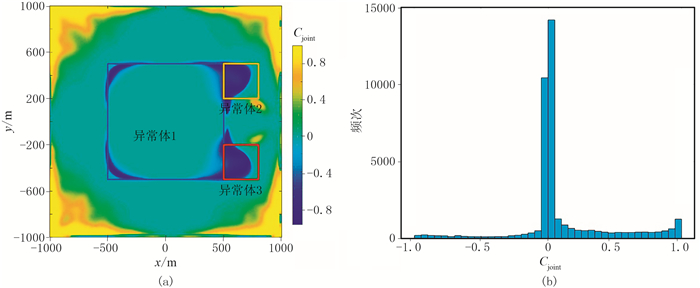
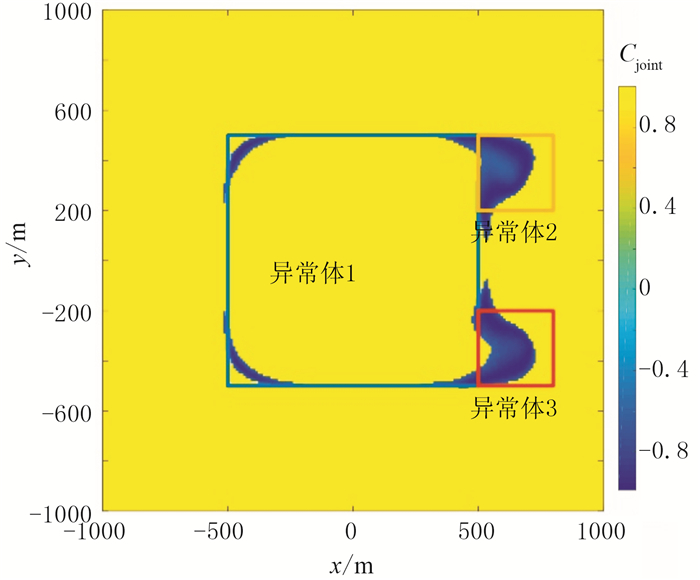
根据Cjoint分布(图 10)可以清晰地识别出三个异常体的边界拐点,与模型相符。通过统计Cjoint在各个子区间中的个数,设阈值α=-0.6对图 10a进行IBTP处理,结果如图 11所示。由图可见正值干扰被去除,结合模型一的计算结果,发现MWJC法对模型边界中拐角的识别结果较好,但对于模型边界中的锐角,只能识别分布趋势。即便如此,仍可认为该结果对于边界识别具有实际意义。
|
图 10 模型二的Cjoint分布(a)及Cjoint子区间数量统计柱状图(b) |
|
图 11 图 10a经IBTP处理的结果 |
为了进一步检验方法的实用性,以模型二为例,讨论算法中影响边界识别结果的因素。
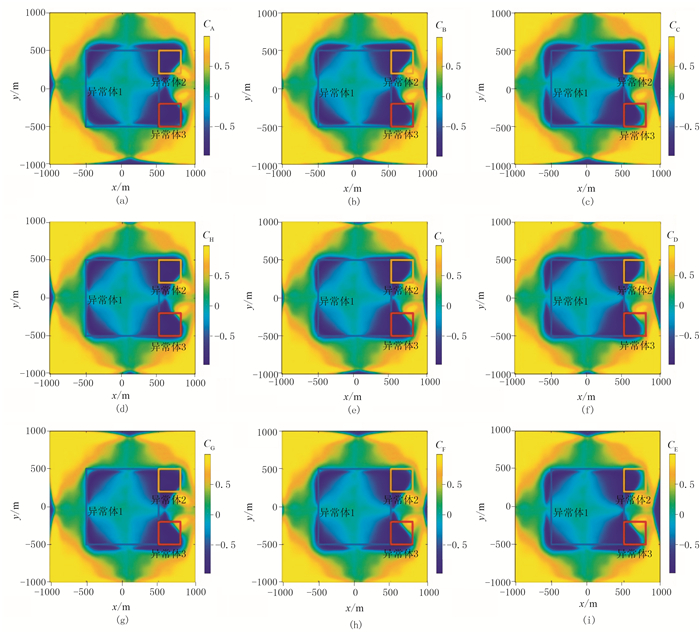
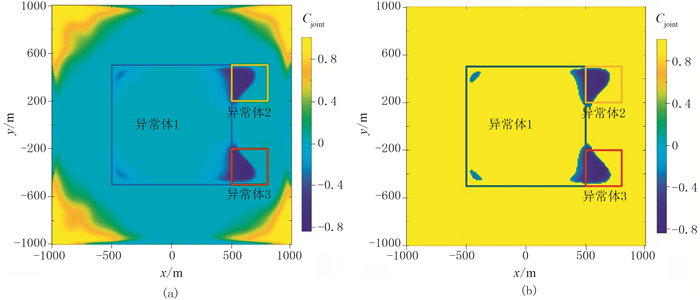
由于算法采用的是正方形窗,窗口边长为(n-1)×Δx,其中Δx表示点距或线距,n≥3且为奇数。当Δx为常数时,调节窗口中的测点数即可改变窗口尺寸。将窗口增大至11×11,即尺寸为100m×100m。参数C及Cjoint和经IBTP处理后的结果分别如图 12和图 13所示。与图 9~图 11对比可见,窗口尺寸增大时,CCED的识别效果无明显改善;经联合多窗口后,MWJC识别的边界信息减少;选取α=-0.2进行IBTP处理,同样不能识别出较准确的边界。这是由于增大窗口尺寸会使包含的测点数增大,改变方向时,更多对应方向的观测点汇入窗口,计算结果会有明显的方向性。联合多窗口的CCED结果降低了结果中的负相关信息量,故出现了部分边界缺失等问题。
|
图 12 窗口大小为11×11时模型二的Ck分布 (a)k=A;(b)k=B;(c)k=C;(d)k=H;(e)k=0;(f)k=D;(g)k=G;(h)k=F;(i)k=E |
|
图 13 窗口大小为11×11时模型二的Cjoint分布(a)及经IBTP处理的结果(b) |
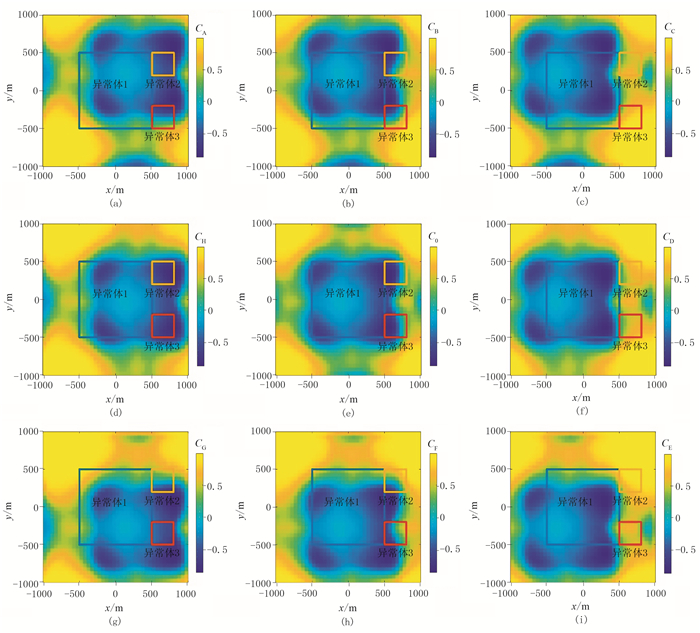
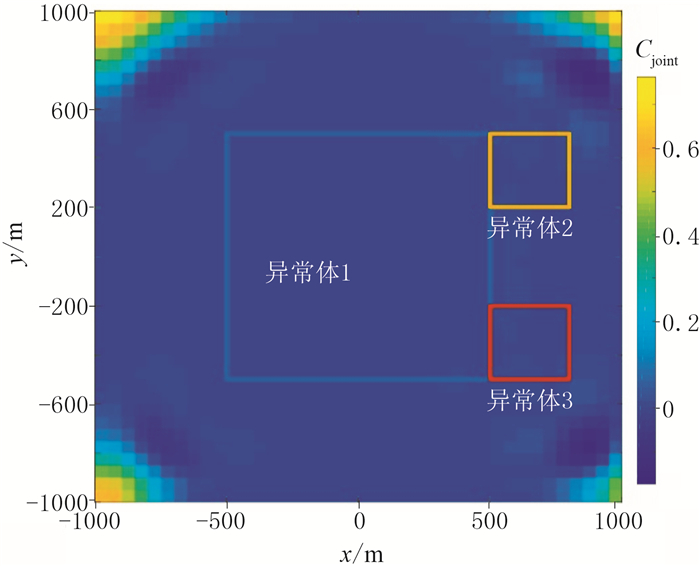
继续增加点距和线距至50m,其他条件不变,测点数减至41×41,处理结果如图 14和图 15所示。与图 9~图 11对比发现,尽管增加窗口大小至11×11降低了识别精度,但CCED结果仍能识别出模型在水平方向上的分布范围和形状;不同方向窗口CCED结果的方向性进一步增强,即结果中负值区域与真实位置在对应方向上的偏差更大,无法识别异常体的部分边界,即MWJC结果也无法增强负相关性,说明此时算法失效。
|
图 14 测点数为41×41时模型二的Ck分布 (a)k=A;(b)k=B;(c)k=C;(d)k=H;(e)k=0;(f)k=D;(g)k=G;(h)k=F;(i)k=E |
|
图 15 测点数为41×41时模型二的Cjoint分布图 |
上述分析说明:算法选用的窗口尺寸与观测数据的点距、线距均会对边界识别结果产生影响。较大的窗口尺寸会包含较多的观测信息,但不一定会提高分辨率,甚至会减少边界信息。对于本文算法,若观测数据的点距、线距过大,将导致MWJC及IBTP处理结果无法检测到异常体边界。因此,建议在实际工作中应用多方向窗口时,应保持窗口内尽量少的测点数,例如3×3,即选取待计算测点附近的窗,这样既减少了单个窗口内的计算量,也避免了大窗口带来的方向性影响。另外,观测数据的点距和线距一般是根据具体的勘探任务与工作标准制定的,无法通过数据处理来增加点距、线距。当数据量较大时(106量级以上),如考虑数据抽稀,建议数据量保持量级在104以上,避免重新网格化导致的点距、线距的增加。
3 实测数据试验为检验MWJC法在实际应用中的效果,将其应用于加拿大圣乔治湾地区的实测航空重力梯度数据(图 16),该地区位于纽芬兰西南海滨的圣劳伦斯海湾。

|
图 16 实测重力梯度数据 (a)Vxy;(b)Vxz;(c)Vyz |
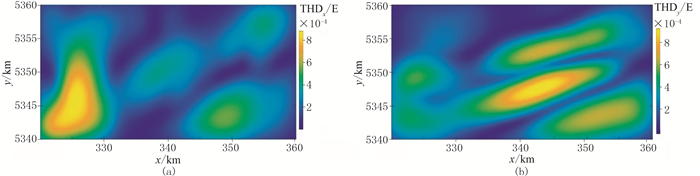
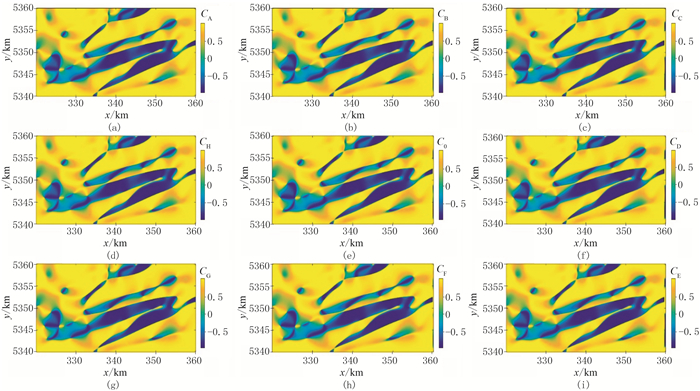
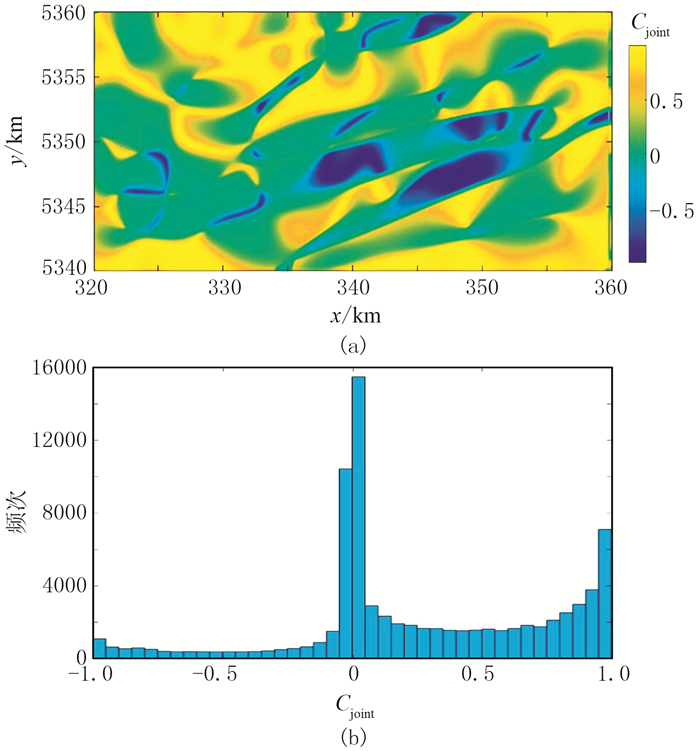
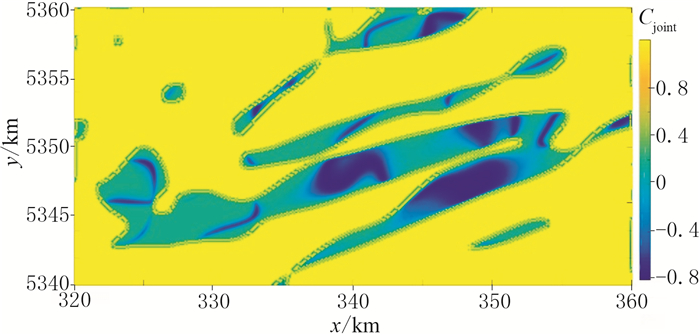
飞机的平均飞行高度为129m,经网格化后的点距、线距均为100m。根据3.3节的分析,MWJC计算时窗口设置为3×3,尺寸为200m×200m,即选取窗口的边界与待计算测点的距离不超过200m。利用高斯滤波进行去噪。图 17为DTHD分布,可见对地下构造边界识别效果较差,只能初步看出三个极大值区域,不能确定异常体或者构造的具体范围。通过计算相关系数C(图 18),可识别出四个南西—北东向条带状负值区;联合9窗口的C值计算Cjoint(图 19a),发现图 18中的部分极小值消失,结合模型试验结果,认为被保存下来的极小值分布区域即是被突出的构造边界的拐角位置或边界弯曲部分。根据统计结果(图 19b)设阈值α=0,经IBTP处理后的结果(图 20)中保留了图 18中极小值的条带状分布特征,且进一步突出了构造边界的拐角区域。与文献[11-12]中其他方法的处理结果对比,可见识别的边界分布特征基本一致,进一步说明MWJC法具有一定的实用性,适用于实测数据的边界识别,且效果良好。
|
图 17 实测数据的THDx(a)和THDy(b)分布 |
|
图 18 实测数据的Ck分布 (a)k=A;(b)k=B;(c)k=C;(d)k=H;(e)k=0;(f)k=D;(g)k=G;(h)k=F;(i)k=E |
|
图 19 实测数据的Cjoint分布(a)及Cjoint子区间数量统计柱状图(b) |
|
图 20 图 19a经IBTP处理的结果 |
本文通过x、y方向总水平导数的相关系数实现了基于多方向窗口联合相关系数的地质体边界识别。多方向窗口技术与改进二值化与阈值处理方法相结合,使地下结构的边界成像更加清晰,有助于识别边界中的拐角、增强边界显示效果。理论模型试验证明:过大的窗口尺寸、观测点距和线距会降低识别效果,甚至使算法失效,合理选择相关参数有助于更加准确地识别地质体边界;本文方法能够较准确地同时识别不同深度异常体的边界。将本文方法应用于圣乔治湾地区实测重力梯度数据,对该地区的地下构造边界得到较为准确的识别结果。
感谢加拿大自然资源部(Natural Resources Canada)为本项研究提供了实测重力梯度数据,允许本文使用此数据进行研究并发表研究成果。
| [1] |
商宇航, 邰振华, 秦涛. 基于双曲线密度模型的频率域界面反演[J]. 石油地球物理勘探, 2018, 53(4): 858-864. SHANG Yuhang, TAI Zhenhua, QIN Tao. Interface inversion in the frequency domain based on the hyperbolic density model[J]. Oil Geophysical Prospecting, 2018, 53(4): 858-864. |
| [2] |
林宝泽, 肖锋, 王明常. 二维重力数据径向反演及应用[J]. 石油地球物理勘探, 2018, 53(2): 403-409. LIN Baoze, XIAO Feng, WANG Mingchang. 2D gra-vity data radial inversion[J]. Oil Geophysical Prospecting, 2018, 53(2): 403-409. |
| [3] |
Cordell, L, Grauch V J S.Mapping basement magnetization zones from aeromagnetic data in the San Juan Basin, New Mexico[C]. SEG Technical Program Expanded Abstracts, 1982, 1: 246-247.
|
| [4] |
Roest W R, Verhoef J, Pilkington M. Magnetic interpretation using the 3-D analytic signal[J]. Geophy-sics, 1992, 57(1): 116-125. |
| [5] |
Miller H G, Singh V. Potential field tilt:a new concept for location of potential field sources[J]. Journal of Applied Geophysics, 1994, 32(2-3): 213-217. DOI:10.1016/0926-9851(94)90022-1 |
| [6] |
Verduzco B, Fairhead J D, Green C M, et al. New insights into magnetic derivatives for structural mapping[J]. The Leading Edge, 2004, 23(2): 116-119. DOI:10.1190/1.1651454 |
| [7] |
Wijns C, Perez C, Kowalczyk P. Theta map:edge detection in magnetic data[J]. Geophysics, 2005, 70(4): L39-L43. DOI:10.1190/1.1988184 |
| [8] |
Sertcelik I, Kafadar O. Application of edge detection to potential field data using eigenvalue analysis of structure tensor[J]. Journal of Applied Geophysics, 2012, 84: 86-94. DOI:10.1016/j.jappgeo.2012.06.005 |
| [9] |
朱自强, 曾思红, 鲁光银. 重力张量数据的目标体边缘检测方法探讨[J]. 石油地球物理勘探, 2011, 46(3): 482-488. ZHU Ziqiang, ZENG Sihong, LU Guangyin. Discussion on the edge detection technique for gravity gradient tensor data[J]. Oil Geophysical Prospecting, 2011, 46(3): 482-488. |
| [10] |
Yuan Y, Geng M.Directional total horizontal derivatives of gravity gradient tensor and their application to delineat the edges[C]. Extended Abstracts of 76th EAGE Conference and Exhibition, 2014, 1-3.
|
| [11] |
袁园, 黄大年, 余青露. 利用加强水平方向总水平导数对位场全张量数据进行边界识别[J]. 地球物理学报, 2015, 58(7): 2556-2565. YUAN Yuan, HUANG Danian, YU Qinglu. Using enhanced directional total horizontal derivatives to detect the edges of potential-field full tensor data[J]. Chinese Journal of Geophysics, 2015, 58(7): 2556-2565. |
| [12] |
Yuan Y, Huang D, Yu Q, et al. Edge detection of potential field data with improved structure tensor methods[J]. Journal of Applied Geophysics, 2014, 108: 35-42. DOI:10.1016/j.jappgeo.2014.06.013 |
| [13] |
M aG, Li uC, HuangD. Theremovalofadditional edges in the edge detection of potential field data[J]. Journal of Applied Geophysics, 2015, 114: 168-173. DOI:10.1016/j.jappgeo.2015.01.007 |
| [14] |
Zuo B, Hu X. Edge detection of gravity field using eigenvalue analysis of gravity gradient tensor[J]. Journal of Applied Geophysics, 2015, 114: 263-270. DOI:10.1016/j.jappgeo.2015.01.013 |
| [15] |
Yuan Y, Gao J Y, Chen L N. Advantages of horizontal directional theta method to detect the edges of full tensor gravity gradient data[J]. Journal of Applied Geophysics, 2016, 130: 53-61. DOI:10.1016/j.jappgeo.2016.04.009 |
| [16] |
Ma G, Huang D, Liu C. Step-edge detection filters for the interpretation of potential field data[J]. Pure and Applied Geophysics, 2016, 173(3): 795-803. DOI:10.1007/s00024-015-1053-6 |
| [17] |
周文纳, 杜晓娟, 李吉焱. 重力数据的平面全张量梯度角度边界识别方法[J]. 石油地球物理勘探, 2013, 48(6): 1009-1015. ZHOU Wenna, DU Xiaojuan, LI Jiyan. Gravity data edge identification using plane full tensor gradient angle[J]. Oil Geophysical Prospecting, 2013, 48(6): 1009-1015. |
| [18] |
邰振华, 张凤旭, 刘国兴, 等. 基于差分求导的伪总梯度余弦值法的位场边界检测[J]. 石油地球物理勘探, 2014, 49(4): 807-814. TAI Zhenhua, ZHANG Fengxu, LIU Guoxing, et al. Potential field edge detection based on difference derivative with cosine of pseudo total gradient[J]. Oil Geophysical Prospecting, 2014, 49(4): 807-814. |
| [19] |
Marson I, Klingele E E. Advantages of using the vertical gradient of gravity for 3-D interpretation[J]. Geo-physics, 1993, 58(11): 1588-1595. |
| [20] |
Guo L, Meng X, Shi L. 3D correlation imaging of the vertical gradient of gravity data[J]. Journal of Geophysics and Engineering, 2011, 8(1): 6-12. |
| [21] |
Guo L, Shi L, Meng X. 3D correlation imaging of magnetic total field anomaly and its vertical gradient[J]. Journal of Geophysics and Engineering, 2011, 8(2): 287-293. DOI:10.1088/1742-2132/8/2/013 |
| [22] |
孟小红, 刘国峰, 陈召曦, 等. 基于剩余异常相关成像的重磁物性反演方法[J]. 地球物理学报, 2012, 55(1): 304-309. MENG Xiaohong, LIU Guofeng, CHEN Zhaoxi, et al. 3-D gravity and magnetic inversion for physical pro-perties based on residual anomaly correlation[J]. Chinese Journal of Geophysics, 2012, 55(1): 304-309. DOI:10.6038/j.issn.0001-5733.2012.01.030 |
| [23] |
Hou Z, Huang D, Wei X. Fast inversion of probability tomography with gravity gradiometry data based on hybrid parallel programming[J]. Journal of Applied Geophysics, 2016, 124: 27-38. DOI:10.1016/j.jappgeo.2015.11.009 |
| [24] |
Hou Z, Huang D. Multi-GPU parallel algorithm design and analysis for improved inversion of probability tomography with gravity gradiometry data[J]. Journal of Applied Geophysics, 2017, 144: 18-27. DOI:10.1016/j.jappgeo.2017.06.009 |
| [25] |
马国庆, 杜晓娟, 李丽丽. 利用水平与垂直导数的相关系数进行位场数据的边界识别[J]. 吉林大学学报(地球科学版), 2011, 41(增刊1): 345-348. MA Guoqing, DU Xiaojuan, LI Lili. Edge detection of potential filed data using correlation coefficients of horizontal and vertical derivatives[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(S1): 345-348. |
| [26] |
徐梦龙, 杨长保, 吴燕冈, 等. 利用各方向均方差相关系数进行位场边界检测[J]. 应用地球物理, 2015, 12(1): 23-34. XU Menglong, YANG Changbao, WU Yangang, et al. Edge detection in the potential field using the correlation coefficients of multidirectional standard deviations[J]. Applied Geophysics, 2015, 12(1): 23-34. |
| [27] |
Rafael C, Gonzalez, Richard E W. 数字图像处理(第三版)[M]. 北京: 电子工业出版社, 2017.
|
| [28] |
侯振隆.重力全张量梯度数据的并行反演算法研究及应用[D].吉林长春: 吉林大学, 2016. HOU Zhenlong.Research and Application of the Pa-rallel Inversion Algorithms Based on the Full Tensor Gravity Gradiometry Data[D]. Jilin University, Changchun, Jilin, 2016. |



 侯振隆, 辽宁省沈阳市和平区文化路三巷11号东北大学, 110819。Email:
侯振隆, 辽宁省沈阳市和平区文化路三巷11号东北大学, 110819。Email: