② 中国石油新疆油田分公司采油二厂, 新疆克拉玛依 834008;
③ 中国石化河南油田分公司采油二厂, 河南南阳 473100;
④ 中国石化重庆涪陵页岩气勘探开发有限公司, 重庆 408014;
⑤ 中国石油长庆油田分公司油气工艺研究院, 陕西西安 710018
② The Second Oil Production Plant, Xinjiang Oilfield Company, CNPC, Karamay, Xinjiang 834008, China;
③ The Second Oil Production Plant, Henan Oilfield Company, SINOPEC, Nanyang, Henan 473100, China;
④ Chongqing Fuling Shale Gas Exploration and Development Company, SINOPEC, Chongqing 408014, China;
⑤ Oil and Gas Technology Research Institute, Changqing Oilfield Company, CNPC, Xi'an, Shaanxi 710018, China
随机模拟方法通常用于储层预测[1-6]。影响随机建模精度的关键因素是基础资料的质量、数量及方法的选择[7]。只有选择合适的建模方法,利用资料之间的相互约束关系,才能获得更为精确的地质模型[8]。
试井是油气勘探开发过程中认识储层的一个重要手段。试井资料可以反映地层的横向变化,对储层平面展布特征的认识有着重要的作用。但是,目前结合试井资料的储层建模方法[9-11]较少,并且大多采用的流程为:先利用压力恢复试井数据,反演井周围的渗透率;再利用渗透率数据求出渗透率的变差函数;然后在变差函数的约束下模拟生成渗透率模型。该方法存在一定局限性,主要是因为用压力恢复试井数据求得的渗透率数据有限,根据其计算的变差函数难以保证准确性和连续性。
本文将试井测试资料用于储层建模方法中,首先使用传统随机建模方法结合静态资料建立储层初始地质模型,再利用模拟退火算法结合试井动态资料对初始模型进行修正,建立同时符合静态资料和试井动态资料的地质模型。该方法可保证模型有更好的连续性,同时修正孔隙度和渗透率模型,应用范围更广。
1 方法原理首先利用静态资料和传统的随机地质建模方法[12-16](如序贯高斯模拟、序贯指示模拟等)建立储层的初始属性模型,包括孔隙度模型和渗透率模型等。初始模型建立后,结合试井动态资料(主要为试井压力数据),利用模拟退火算法[17-21]对属性模型进行修正。
模型修正方法为:在初始模型中产生随机扰动,在扰动后的参数场中,利用数值模拟计算单井井底压力;然后比较模型计算的压力与实际测试压力之间的误差,根据误差判断是否进行下一次扰动;如果计算的各单井的压力与实际测试压力之间误差满足要求,则结束扰动,从而得到修正后的模型。
1.1 目标函数模拟退火算法源于固体退火原理。固体退火是指先将固体加热至较高温度后,再让其缓慢冷却至常温。该过程中固体中粒子不断转移,由无序到有序,内能不断降低,故固体退火趋势可以由内能函数判断。同样,在模拟退火过程中,需要反复扰动参数场,并且需要目标函数[22]判断是否继续扰动。本文采用试井压力数据作为评判指标,目标函数为
| $ O=\sum\limits_{i=1}^{n_{\mathrm{w}}} \sum\limits_{j=1}^{n_{\mathrm{t}}}\left[E\left(P_{\mathrm{date}}^{i, j}, P_{\mathrm{cal}}^{i, j}\right)\right] $ | (1) |
式中:nw为井数;nt为时间步数;Pdatei, j、Pcali, j分别为第i口井在j时间步的地层压力、模拟压力;E为Pdatei, j与Pcali, j之间的函数差值。
每次扰动均需要重新计算目标函数、对比扰动前后的目标函数值。一般模拟退火算法使用Metropolis准则[17]判断是否继续扰动,但本文中的初始模型是利用静态资料根据传统随机建模方法建立的,能在一定程度上反映基本地质特征,因此将退火温度设置为接近0的状态,简化模拟退火优化过程。同时,引入MAP算法[23]判断是否接受扰动,当目标函数减少时接受扰动;而目标函数增大时拒绝扰动,这样会使算法较快达到收敛。其数学表达式为
| $ P_{\text {accept }}=\left\{\begin{array}{ll} 1 & O_{\text {new }}<O_{\text {old }} \\ 0 & O_{\text {new }} \geqslant O_{\text {old }} \end{array}\right. $ | (2) |
式中:Paccept为接受扰动的概率;Oold、Onew分别为扰动前、后的目标函数值。
1.2 算法优化目标函数中的模拟压力一般通过数值模拟计算得到,但由于模拟退火过程中需要对模型初始参数场进行多次扰动,如果每次扰动都利用数值模拟计算井底压力,则需要花费大量时间。为减少数值模拟次数,本文引入偏心井的两区复合油藏压力公式计算压力值[24-26]。
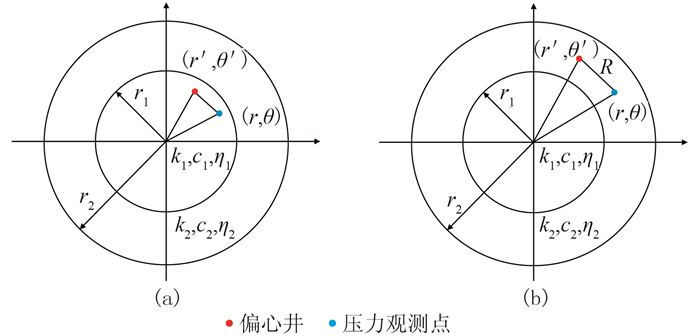
当油井位于油藏内区(图 1a)时,压力计算公式为
| $ \bar{P}_{\mathrm{D1}}\left(r_{\mathrm{D}}, s\right)=\frac{1}{s} \sum\limits_{n=0}^{\infty} \varepsilon_{n} I_{n}\left(r_{\mathrm{D}} \sqrt{s}\right) \times\\ \ \ \ \left[K_{n}\left(r_{\mathrm{D}}^{\prime} \sqrt{s}\right)-\frac{\mathit{\Omega}_{n}}{\mathit{\Psi}_{n}} I_{n}\left(r_{\mathrm{D}}^{\prime} \sqrt{s}\right)\right] \cos n\left(\theta-\theta^{\prime}\right)\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0 \leqslant r \leqslant r^{\prime} $ | (3) |
| $ \bar{P}_{\mathrm{D} 2}\left(r_{\mathrm{D}}, s\right)=\frac{M \eta_{\mathrm{D}}}{r_{\mathrm{D} 1}} \frac{1}{s} \sum\limits_{n=0}^{\infty}\left[\varepsilon_{n} \frac{1}{\mathit{\Psi}_{n \mathrm{D}}} I_{n}\left(r_{\mathrm{D}}^{\prime} \sqrt{s}\right)\right] \times\\ \left[K_{n}\left(r_{\mathrm{D}} \sqrt{\eta_{\mathrm{D}} s}\right)\right] \cos n\left(\theta-\theta^{\prime}\right) \quad\quad\quad r \geqslant r_{1} $ | (4) |
|
图 1 两区均质油藏偏心井模型示意图 (a)油井在内区; (b)油井在外区 |
当油井位于油藏外区(图 1b)时,压力计算公式为
| $ \bar{P}_{\mathrm{D} 1}\left(r_{\mathrm{D}}, s\right)=\frac{\eta_{\mathrm{D}}}{M} \frac{1}{s} \sum\limits_{n=0}^{\infty} \varepsilon_{n} \frac{K_{n}\left(r_{\mathrm{D}}^{\prime} \sqrt{s}\right)}{I_{n}\left(r_{\mathrm{D} 1} \sqrt{\frac{s}{\eta_{\mathrm{D}}}}\right)} \times\\ \left[I_{n}\left(r_{\mathrm{D} 1} \sqrt{s}\right)+\frac{\mathit{\Omega}_{n}}{\mathit{\Psi}_{n}} K_{n}\left(r_{\mathrm{D1}} \sqrt{s}\right)\right] \times\\ I_{n}\left(r_{\mathrm{D}} \sqrt{\frac{s}{\eta_{\mathrm{D}}}}\right) \cos n\left(\theta-\theta^{\prime}\right) \quad\quad\quad 0 \leqslant r \leqslant r_{1} $ | (5) |
| $ \bar{P}_{\mathrm{D} 2}\left(r_{\mathrm{D}}, s\right)=\frac{1}{s}\left[K_{0} s R_{\mathrm{D}}+\sum\limits_{n=0}^{\infty} \varepsilon_{n} \frac{\mathit{\Omega}_{n}}{\mathit{\Psi}_{n}} K_{n}\left(s r_{\mathrm{D}}^{\prime}\right) \times\right.\\ \left.K_{n}\left(s r_{\mathrm{D}}\right) \cos n\left(\theta-\theta^{\prime}\right)\right] \quad\quad\quad r_{1} \leqslant r \leqslant r^{\prime} $ | (6) |
| $\bar{P}_{\mathrm{D} 2}\left(r_{\mathrm{D}}, s\right)=\frac{1}{s}\left[K_{0} s R_{\mathrm{D}}+\sum\limits_{n=0}^{\infty} \varepsilon_{n} \frac{\mathit{\Omega}_{n}}{\mathit{\Psi}_{n}} K_{n}\left(s r_{\mathrm{D}}\right) \times\right.\\ \ \ \ \ \left.K_{n}\left(s r_{\mathrm{D}}^{\prime}\right) \cos n\left(\theta-\theta^{\prime}\right)\right] \quad\quad\quad r \geqslant r^{\prime} $ | (7) |
上述各式中:PD1、PD2分别为内区、外区的无因次压力分布;r、r′分别为观测点和偏心井到油藏中心的距离;r1、r2(图 1)分别为复合油藏中心至内区、外区边界的距离;s为拉氏变量;n为贝塞尔函数的阶数;In、Kn分别为第一、二类n阶修正贝塞尔函数;εn为计算参数,当n=0时,εn=1,当n≥1时,εn=2;rD为观测点到油藏中心的无因次距离,rD=r/rw,其中rw为井半径;r′D为无因次偏心距,r′D=rD/rw;Ωn、Ψn为压力解的n阶辅助变量,ΨnD为Ψn的无因次化数值;θ、θ′分别为观测点、偏心井关于地层中心的极角;M、ηD分别为内外区流度比、导压系数比;rD1为为无因次内区半径,rD1=r1/rw;R、RD分别为观测点到偏心井的距离、无因次距离。
由于油藏的非均质性,计算结果会有误差。但在扰动次数较少时,压力解析解与数值模拟计算结果误差不大。随着退火扰动次数增加,误差会不断增大。因此在扰动次数较多时,解析解不能满足计算精度,中间需要穿插数值模拟进行复算,修正计算误差。本文采取每扰动50次后利用数值模拟计算一次,即利用解析解和数值解相结合的方法计算单井的井底压力。这样既保证了计算的准确性,又节约了运算时间。
在目标函数中引入计算的压力值,优化后的模拟退火目标函数为
| $O=\frac{1}{O_\text{i}} \sum\limits_{i=1}^{n_{\mathrm{w}}} \omega_{\mathrm{w}}^{i}\left\{\sum\limits_{j=1}^{n_{\mathrm{t}}}\left[\omega_{\mathrm{P}}^{i} \frac{\left|\Delta P_{\mathrm{data}}^{i, j}-\Delta P_{\mathrm{cal}}^{i, j}\right|}{\Delta P_{\mathrm{data}}^{i, j}}+\right.\right.\\ \ \ \ \ \ \ \left.\left.\left(1-\omega_{\mathrm{P}}^{i}\right) \frac{\left|\Delta P_{\mathrm{data}}^{\prime i, j}-\Delta P_{\mathrm{cal}}^{\prime i, j}\right|}{\Delta P_{\mathrm{data}}^{\prime i, j}}\right]\right\} $ | (8) |
式中:Oi为初始目标函数;ωwi为第i口井所占的权重系数;ωPi为第i口井压力所占的权重系数;1-ωPi为第i口井压力导数所占的权重系数;ΔPcal=Pi-Pcal为计算压力降,其中Pi表示初始地层压力;ΔPdata=Pi-Pdata为实测压力降;ΔPdatai, ∞为第i口井试井记录中最后的压力降;ΔP′cal、ΔP′data、ΔP′datai, ∞为相应压力降的导数。
在式(8)的基础上加入调节因子αi得到
| $O=\frac{1}{O_\text{i}} \sum\limits_{i=1}^{n_\text{w}} \omega_\text{w}^{i}\left\{\sum\limits_{j=1}^{n_\text{t}}\left[\alpha_{i} \omega_{\mathrm{P}}^{i} \frac{\left|\Delta P_{\text {data }}^{i, j}-\Delta P_{\text {cal }}^{i, j}\right|}{\Delta P_{\text {data }}^{i, j}}+\right.\right.\\ \ \ \ \ \ \ \ \ \left.\left.\left(1-\alpha_{i} \omega_{\mathrm{P}}^{i}\right) \frac{\left|\Delta P_{\mathrm{data} }^{\prime i, j}-\Delta P_{\mathrm{cal}}^{\prime i j}\right|}{\Delta P_{\mathrm{data}}^{\prime i, j}}\right]\right\} $ | (9) |
式(9)可以加快计算速度[27]。
1.3 扰动改进在扰动阶段,模拟退火方法通常是先在模型中随机挑选一个网格,然后在数据集中随机挑选新的孔隙度和渗透率数据替换原有的数据,扰动过程中没有范围限制。这在退火温度较高的模型中有助于跳出局部最优而达到全局最优,但在退火温度很低时却有可能增加无效扰动次数。因此,需要对新数据的挑选做出一定限制,以减少扰动次数,更快达到全局最优。
本文扰动替换网格采用以目标网格为中心的7×7网格区域(根据模型的大小和精细程度可以适当调整区域范围),以其中数据的最大值和最小值作为扰动的上限和下限改进扰动过程。
2 计算步骤结合试井动态资料的随机模拟算法主要包含扰动、决策和更新三个过程。
扰动过程就是扰动储层的参数场,即随机改变储层中某位置孔隙度和渗透率,从而导致模型计算的井底压力产生变化,再利用解析方法计算扰动后参数场的目标函数。然后持续扰动,当达到退火温度下的最大扰动次数时,停止扰动。
决策过程就是判断扰动过程中参数场扰动前后目标函数值的大小,从而判断是否接受扰动;判断是否达到极限扰动值;决定是否利用数模模拟值修正目标函数;判断是否满足循环条件和停止条件。
更新过程就是更新网格扰动次数和接受网格扰动次数,更新储层的渗透率、孔隙度的网格分布。如果接受扰动,那么Oold将被Onew代替,而新的目标函数与网格扰动后的渗透率和孔隙度有关,目标函数的准确性将会影响到决策过程的可靠性。如果参数场改变了N次,那么利用解析解计算的目标函数就有N次误差(由于解析解采用储层参数平均值导致);因此,当达到一定的扰动次数后,引入数值模拟更新扰动后参数场的压力,重新计算目标函数,使目标函数更准确。
结合试井动态资料的随机模拟方法的具体步骤如下。
(1) 生成初始参数场并计算初始目标函数Oi,令Ncal=0,Nswap=0,ΔOmax=0,Ntry=0。
(2) 在模型中随机挑选一个网格,使用Gibbs采样[28-29]对参数场进行扰动,在扰动过程中,根据邻近网格属性值设定扰动范围,加快收敛速度,重新计算目标函数O,Ntry=Ntry+1。
(3) 内循环。判断ΔO与ΔOmax的大小,若ΔO≥ΔOmax,则拒绝扰动;再判断Ntry是否到达Nmax,若未达到则返回步骤(2),若达到则终止循环并重新开始步骤(1);若ΔO<ΔOmax,则接受扰动,转到步骤(4)。
(4) 根据新的参数场,利用压力公式计算目标函数O,则Ncal=Ncal+1,Nswap=Nswap+1。
(5) 判断Ncal是否等于Nsmax,若相等,则利用模拟器计算目标函数O,Ncal=0。判断O与Omin的大小,若O<Omin,则输出结果;若O≥Omin,则转到步骤(6)。
(6) 外循环。判断Nswap与Ntot的大小,若Nswap>Ntot,则输出结果;若Nswap<Ntot,则重复步骤(2)。
上述步骤中:Ncal为用解析解计算模拟压力次数;Nswap为互换网格次数;Ntry为当前退火温度下扰动次数;Nmax为当前退火温度下最大扰动次数;Nsmax为用解析解计算模拟压力的极限次数;Ntot为总的接受扰动的最大次数;ΔO为目标函数差值;Omin为最小目标函数值。
3 实例分析选择某注水开发油田的一反五点注采井网模型为实例,研究区范围为800m×800m,共四口采油井(A、B、C和D井)和一口注水井(I井),相关参数见表 1。
|
|
表 1 储层参数表 |
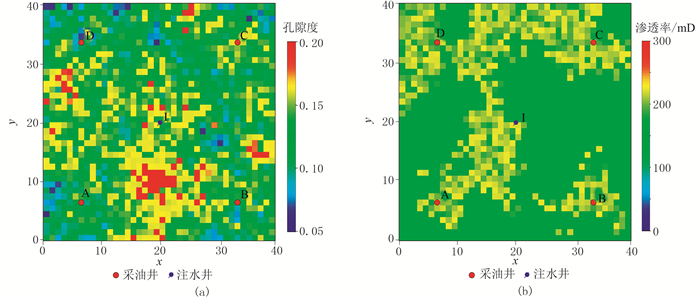
利用五口井测井解释的孔隙度、渗透率建立该井组的属性模型。为了简化研究,模型垂向上假设为1层,平面网格步长为20m,总网格数为1600(40×40×1)个,采用序贯高斯模拟方法建立初始孔隙度、渗透率模型如图 2所示。
|
图 2 初始孔隙度(a)和渗透率(b)模型 |
建立初始模型参数场后,需要利用试井测试的井底压力对模型的参数场进行修正。研究区四口采油井均有压力降落试井资料。利用A、B、C三口井的资料构建目标函数,采用前述模拟退火算法拟合压力数据,将D井作为后验井进行符合率分析、验证。
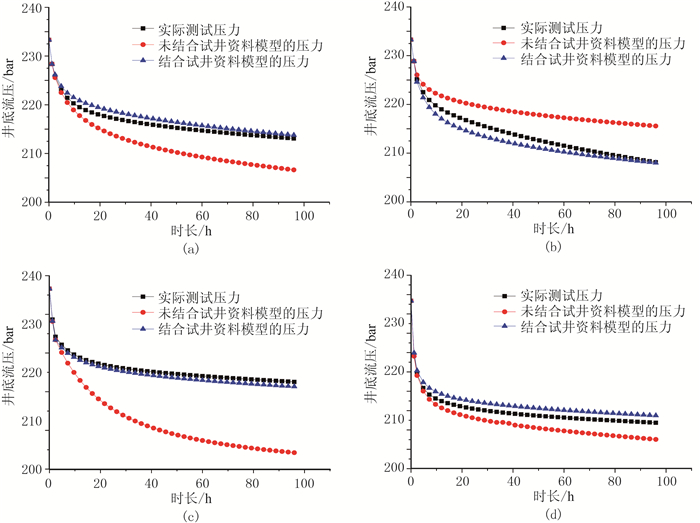
由图 3可以看出,初始模型计算的各井的井底压力与测试压力差别较大,因此有必要进行井底压力拟合。在井底压力拟合过程中,共经历675次扰动,接受扰动次数为352次。若扰动未经优化,则需扰动1000次以上,因此扰动接受效率约提高48%。
|
图 3 A井(a)、B井(b)、C井(c)和D井(d)的压力变化曲线 |
用Eclipse数模软件进行7次数值模拟计算,计算时间约为15.0min,其中每次扰动及判定需要1s,共用时11.5min,每次数值模拟需要30s,共用时3.5min;如不利用解析解对压力进行近似计算,数值模拟的计算次数将达到352次,增加345次的数模计算时间,共用时约为173min。
最终使模型计算的压力与试井测试的压力基本一致,其中A、B、C三口井平均误差在0.7%以内,后验井D井误差也在1%以内(表 2),满足精度要求。
|
|
表 2 优化前后实测值与计算值平均误差 |
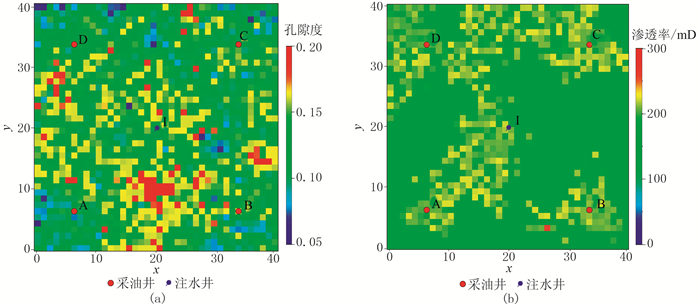
图 4为经过试井压力拟合后的渗透率和孔隙度模型,与拟合前的模型(图 2)相比,经过模拟退火的扰动后,储层参数的整体分布趋势基本一致。修正后的模型不仅能反映储层静态参数的分布特征,同时新模型很好地符合了试井的压力数据,比原模型更接近真实的地质模型。
|
图 4 经过试井压力拟合(本文方法)后的孔隙度(a)和渗透率(b)模型 |
在传统随机建模方法基础上,结合试井压力数据对初始模型加以修正,使模型符合动态资料,可以提高模型精度。
(1) 以试井压力数据作为评判标准建立目标函数可以使优化后的模型反映压力动态。
(2) 引入偏心井的两区复合油藏压力公式,交替使用解析公式和数值模拟,既可保证计算精度,又可减少数模次数,节约计算时间,提高了实用性。
(3) 对模拟退火中的扰动过程进行了改进,在每次扰动过程中,以邻近的网格作为参考,对扰动的范围进行了限制,扰动后被接受的效率提高了约48%,有效减少了扰动次数。
| [1] |
霍春亮, 刘松, 古莉, 等. 一种定量评价储集层地质模型不确定性的方法[J]. 石油勘探与开发, 2007, 34(5): 574-579. HUO Chunliang, LIU Song, GU Li, et al. A quantitative method for appraising reservoir geological model uncertainty[J]. Petroleum Exploration and Development, 2007, 34(5): 574-579. DOI:10.3321/j.issn:1000-0747.2007.05.010 |
| [2] |
Maschio C, de Carvalho C P V, Schiozer D J. A new methodology to reduce uncertainties in reservoir simu-lation models using observed data and sampling techniques[J]. Journal of Petroleum Science and Engineering, 2010, 72(1): 110-119. |
| [3] |
Zafari M, Reynolds A C.Assessing the uncertainty in reservoir description and performance predictions with the ensemble Kalman filter[C]. SPE Annual Technical Conference and Exhibition, Society of Petroleum Engineers, 2005.
|
| [4] |
杨懋新, 刘金平, 王允清, 等. 井震联合地质建模技术在扶杨油层油藏描述中的应用[J]. 石油地球物理勘探, 2010, 45(增刊1): 130-133. Yang Maoxin, Liu Jinping, Wang Yunqing, et al. Application of well-seismic joint geology modeling technique in reservoir characterization in Fuyang reservoir[J]. Oil Geophysical Prospecting, 2010, 45(S1): 130-133. |
| [5] |
叶迪, 程志国, 郑伟, 等. 复杂构造建模技术在地震反演中的应用[J]. 石油地球物理勘探, 2018, 53(增刊1): 270-275. YE Di, CHENG Zhiguo, ZHENG Wei, et al. Complex-structure modeling in seismic inversion[J]. Oil Geophysical Prospecting, 2018, 53(S1): 270-275. |
| [6] |
宋建国, 刘励云, 周廷全. 陡坡带复杂地质模型的建立[J]. 石油地球物理勘探, 2008, 43(4): 473-478. SONG Jianguo, LIU Liyun, ZHOU Tingquan. Buildup of complex geologic model of steep slope zone[J]. Oil Geophysical Prospecting, 2008, 43(4): 473-478. DOI:10.3321/j.issn:1000-7210.2008.04.022 |
| [7] |
宋力, 宋慧莹. 提高油藏地质建模精度的几点认识[J]. 石化技术, 2015, 22(2): 160-161. SONG Li, SONG Huiying. Some thoughts on improving the accuracy of reservoir geological modeling[J]. Petrochemical Technology, 2015, 22(2): 160-161. DOI:10.3969/j.issn.1006-0235.2015.02.103 |
| [8] |
吴胜和, 张一伟, 李恕军, 等. 提高储层随机建模精度的地质约束原则[J]. 石油大学学报(自然科学版), 2001, 25(1): 55-58. WU Shenghe, ZHANG Yiwei, LI Shujun, et al. Geological constraint principle for improving the accuracy of stochastic reservoir modeling[J]. Journal of China University of Petroleum (Natural Science Edition), 2001, 25(1): 55-58. |
| [9] |
Feitosa G S, Chu L, Thompson L G, et al.Determination of reservoir permeability distributions from pressure buildup data[C]. SPE Annual Technical Conference and Exhibition, Society of Petroleum Engineers, 1993.
|
| [10] |
李鸿英, 廖新维, 陈钦雷. 用模拟退火方法和试井资料确定渗透率分布状况[J]. 石油大学学报(自然科学版), 2001, 25(2): 34-37. LI Hongying, LIAO Xinwei, CHEN Qinlei. Determination of permeability distribution by simulated annealing method and well test data[J]. Journal of the University of Petroleum(Natural Science Edition), 2001, 25(2): 34-37. DOI:10.3321/j.issn:1000-5870.2001.02.012 |
| [11] |
廖新维, 沈平平, 杨永智. 利用试井信息确定储集层非均质性[J]. 石油勘探与开发, 2004, 31(7): 100-102. LIAO Xinwei, SHEN Pingping, YANG Yongzhi. Determination of reservoir heterogeneity utilizing well testing data[J]. Petroleum Exploration and Development, 2004, 31(7): 100-102. |
| [12] |
Ersoy A, Yünsel T Y. Assessment of lignite quality variables:a practical approach with sequential Gaussian simulation[J]. Energy Sources, 2008, 31(2): 175-190. DOI:10.1080/15567030701522260 |
| [13] |
杨勇, 孟海泉, 别爱芳, 等. 基于地震反演的储层建模及实例分析[J]. 江汉石油学院学报, 2003, 25(3): 49-50. YANG Yong, MENG Haiquan, BIE Aifang, et al. Reservoir modeling and case analysis based on seismic inversion[J]. Journal of Jianghan Petroleum Institute, 2003, 25(3): 49-50. DOI:10.3969/j.issn.1000-9752.2003.03.021 |
| [14] |
Monjezi M, Kashani M R, Ataei M. A comparative study between sequential Gaussian simulation and Kriging method grade modeling in open-pit mining[J]. Arabian Journal of Geosciences, 2013, 6(1): 123-128. DOI:10.1007/s12517-011-0293-8 |
| [15] |
Bakke N E, Ertresvag E T, Naess A, et al.Application of seismic data and sequence stratigraphy for constraining a stochastic model of calcite cementation[C]. European 3-D Reservoir Modelling Conference, Society of Petroleum Engineers, 1996.
|
| [16] |
王留奇, Wong P M, Shibli S, 等. 岩相骨架的地质统计模拟[J]. 石油勘探与开发, 1999, 26(3): 93-98, 103. WANG Liuqi, Wong P M, Shibli S, et al. Geological statistical simulation of lithofacies framework[J]. Petroleum Exploration and Development, 1999, 26(3): 93-98, 103. DOI:10.3321/j.issn:1000-0747.1999.03.025 |
| [17] |
Metropolis N, Rosenbluth A W, Rosenbluth M N, et al. Equation of state calculations by fast computing machines[J]. The Journal of Chemical Physics, 1953, 21(6): 1087-1092. DOI:10.1063/1.1699114 |
| [18] |
Deutsch C V.Annealing Techniques Applied to Re-servoir Modeling and the Integration of Geological and Engineering (Well Test) Data[D]. Stanford University, California, 1992.
|
| [19] |
Kainourgiakis M E, Kikkinides E S, Charalambopoulou G C, et al. Simulated annealing as a method for the determination of the spatial distribution of a condensable adsorbate in mesoporous materials[J]. Langmuir, 2003, 19(8): 3333-3337. DOI:10.1021/la026766p |
| [20] |
彭国民, 徐凯军, 杜润林, 等. MCSEM和地震AVA数据联合反演储层物性[J]. 石油地球物理勘探, 2018, 53(5): 1110-1116. Peng Guomin, Xu Kaijun, Du Runlin, et al. Reservoir petrophysical parameter estimation with joint inversion of MCSEM and seismic AVA data[J]. Oil Geophysical Prospecting, 2018, 53(5): 1110-1116. |
| [21] |
徐桂芬, 何展翔, 石艳玲, 等. 电磁-地震联合研究深层火山岩储层——以辽东凹陷火山岩勘探为例[J]. 石油地球物理勘探, 2019, 54(4): 937-946. XU Guifen, HE Zhanxiang, SHI Yanling, et al. Deep volcanic reservoir exploration with jointed electromagnetic and seismic data:an example of volcanic investigation in Liaodong Sag[J]. Oil Geophysical Prospecting, 2019, 54(4): 937-946. |
| [22] |
Tauzin E.Integration of Well Test Data into Stochastic Modeling[D]. Stanford University, California, 1995.
|
| [23] |
Groot D, Morris H.Optimal Statistical Decisions[M]. John Wiley & Sons, 2005.
|
| [24] |
Su H J著, 姜瑞忠等译.油藏模拟中建立偏心井模型的方法[J].世界石油科学, 1995, (5): 38-44.
|
| [25] |
Rosa A J, Magalhaes A, Carlos A, et al. Pressure transient behavior in reservoirs with an internal circular discontinuity[J]. SPE Journal, 1996, 1(1): 83-92. |
| [26] |
巨亚锋, 于九政, 郭方元, 等. 低渗两区复合油藏注水井试井解释模型[J]. 石油天然气学报, 2012, 34(7): 109-113. JU Yafeng, YU Jiuzheng, GUO Fangyuan, et al. A well test interpretation model for injection wells in low permeability two-zone composite reservoirs[J]. Journal of Oil and Gas Technology, 2012, 34(7): 109-113. DOI:10.3969/j.issn.1000-9752.2012.07.023 |
| [27] |
李振英, 冯国庆, 张烈辉. 神经网络方法在水淹层识别中的改进[J]. 大庆石油地质与开发, 2004, 23(3): 44-45. LI Zhenying, FENG Guoqing, ZHANG Liehui. Improvement of neural network method in water flooded layer identification[J]. Petroleum Geology and Deve-lopment in Daqing, 2004, 23(3): 44-45. DOI:10.3969/j.issn.1000-3754.2004.03.017 |
| [28] |
Kirkpatrick S, Gelatt C D, Vecchi M P. Optimization by simulated annealing[J]. Science, 1983, 220(4598): 671-680. DOI:10.1126/science.220.4598.671 |
| [29] |
路鹏飞, 杨长春, 郭爱华, 等. 改进的模拟退火算法及其在叠前储层参数反演中的应用[J]. 地球物理学进展, 2008, 23(1): 104-109. LU Pengfei, YANG Changchun, GUO Aihua, et al. Modified simulated annealing algorithm and its application in pre-stack inversion of reservoir parameters[J]. Progress in Geophysics, 2008, 23(1): 104-109. |



 何玉俊, 四川省成都市新都区新都大道8号西南石油大学石油与天然气工程学院, 610500。Email:
何玉俊, 四川省成都市新都区新都大道8号西南石油大学石油与天然气工程学院, 610500。Email: