② 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266580;
③ 中国石化胜利油田物探研究院, 山东东营 257022
② Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266580, China;
③ Shengli Geophysical Research Institute of SINO-PEC, Dongying, Shandong 257022, China
河流相薄储层是目前油气勘探的重点目标之一,该类储层弹性参数空间变化剧烈,常规地震反演方法难以刻画。为此,学者们在AVO理论的基础上发展了FAVO反演技术,以减少薄层反演的不确定性,提高薄层反演精度。
Chapman等[1-3]通过动态等效介质模型得到不同频率地震数据体所包含的储层信息;Wilson等[4]结合瞬时谱分解与Smith-Gidlow反射方程,提出了频变AVO反演理论;Wu等[5]利用伪Wigner-Ville分布算法实现了依赖频率的AVO反演;张世鑫等[6]在叠后反演的过程中基于Shuey近似公式提出了纵波速度频散梯度;吴国忱等[7]通过正演模拟分析发现,叠前道集的地震属性随炮检距和频率变化同样具有很大的差异性;杨千里等[8]提出了基于贝叶斯理论的多尺度地震反演方法;吴建鲁等[9]构建了一维虚岩石物理模型,证明了中观尺度不同流体间的相对流动是诱导地震波在地震频带衰减的主控因素;李坤等[10]推导了时频域FAVO直接反演目标方程,并提出了基于匹配追踪谱分解的时频域FAVO流体识别方法;张繁昌等[11]在频率域利用地震数据的正、余弦分量,研究了稀疏反射系数频率域正、余弦分量协同反演方法。
FAVO反演技术不断发展,频率信息的充分发掘、利用是关键,即如何获得高分辨率的频谱是保障FAVO反演精度的基础。傅里叶变换是频谱分解的基础,Gabor[12]利用可滑动的高斯窗提出了窗口傅里叶变换(STFT);Morlet等[13]提出了连续小波变换(CWT)使时频窗口可调;Stockwell等[14]省去了窗函数的选择,提出了S变换,改善了窗宽固定的缺陷。然而这些时频分解方法均属于线性时频分析技术,都会受到海森堡测不准原理的影响。为克服这种影响,学者们逐步建立了非线性的时频分析技术。Mallat等[15]提出了匹配追踪技术;Liu等[16]通过引入地震信号的瞬时信息,提出了动态匹配追踪的快速算法;张繁昌等[17]提出了双参数动态子波库匹配追踪快速算法,由于具自适应特征,在频谱分解时具有较好的时频分辨率,更适用于复杂的地震信号,可以更准确地刻画地震信号的时频特征,真实反映地下沉积体信息。
然而,尽管FAVO反演理论的不断发展促进了薄层反演、流体识别等问题的解决,但因道集叠加而导致的干涉效应往往并未消除,稀疏表示技术的应用也主要偏向于时频分析和地震属性分析,这些因素制约了薄层刻画的精度。因此,本文提出一种不叠加的思想,建立基于稀疏表示的增维叠前地震反演模式,有效削弱干涉调谐效应的影响,实现维度增加的高精度叠前地震反演。
需要说明的是,本文中增维既指反演输入数据是多维的信息,又指对叠前道集的信息进一步挖掘的过程。利用谱分解方法将地震信号从炮检距—时间剖面拓展为炮检距—时间—频率三维数据体,结合测网所组合的观测系统实现了信息量的增维,增强了反演解释描述能力。
1 方法原理基于稀疏表示的增维叠前地震反演方法:首先,以目的层为筛选条件对叠前道集进行角度优选,抽取有效的单角度地震资料;其次,基于稀疏表示理论,结合匹配追踪算法与时频分解方法对得到的单角度地震资料进行高分辨率的时频分解,完成炮检距—时间(O-T)域数据体向炮检距—频率—时间(O-F-T)域数据体的增维;再次,以每个角度的单频资料为基础,利用地震速度与Aki-Richard近似公式构建无井反演低频模型[18],基于贝叶斯理论直接建立波阻抗与地震数据之间的映射关系,利用非线性最优化算法对初始模型进行扰动,以前一个频率反演的结果作为后一个频率反演的约束,逐级反演,最终得到不同角度高分辨率增维反演结果;最后,通过联合储层的优势响应频带计算截至该频带的增维反演结果,实现对非均质薄储层的刻画。
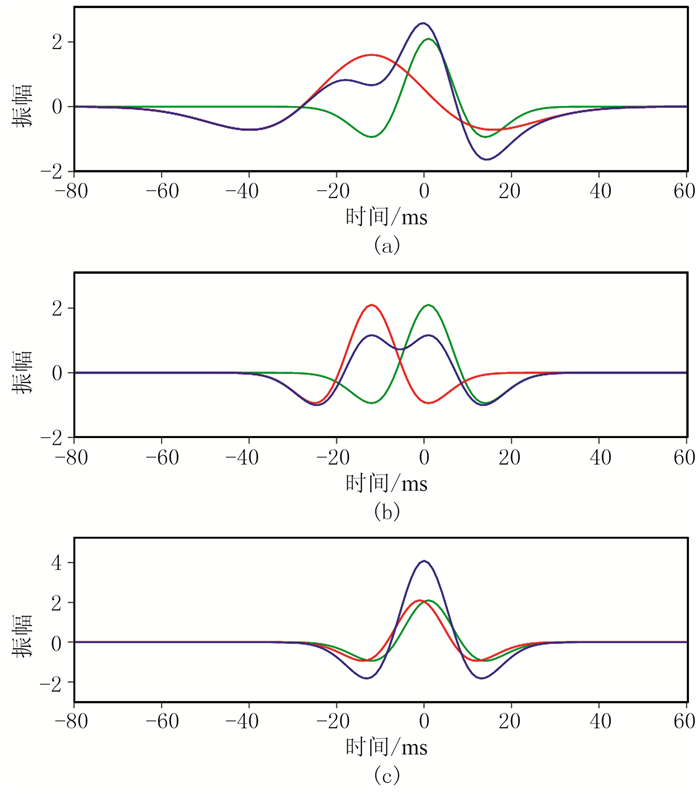
1.1 道集优选叠加产生的干涉效应影响着叠后和叠前(部分角道集叠加)地震反演精度。如图 1所示,振幅、频率均不相同的两列波叠加产生的混合帯限子波常见于地震信号(图 1a)。频率、振幅均相同的两列波,当时差较大时,波峰与波谷相遇叠加振幅被削弱(图 1b);当时差较小时,波峰与波峰叠加,振幅得到增强(图 1c)。因此利用叠加地震资料难以对目标准确描述。
|
图 1 两列波叠加效应 (a)振幅、频率均不相同;(b)振幅、频率均相同,时差大;(c)频率、振幅均相同,时差小。蓝色曲线所示地震波为绿色和红色曲线所示地震波的叠加 |
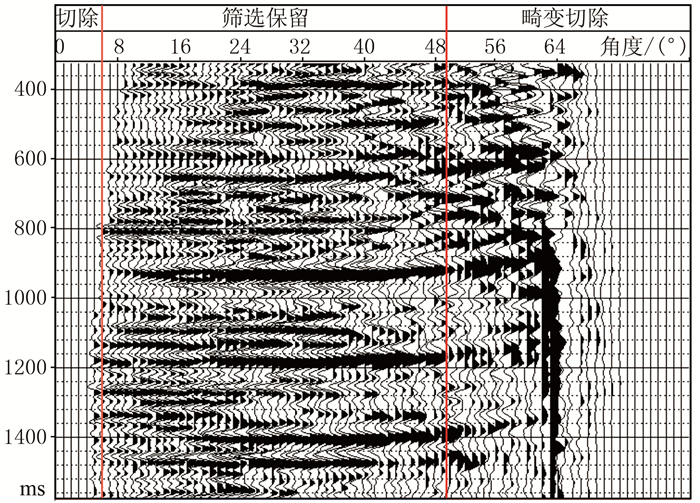
为了消除叠加效应,需对目的层段所包含的数据范围进行优选,如图 2所示,对存在畸变的角度道集进行切除,逐一提取有效炮检距或角度范围内的地震数据组成若干单角度地震数据体,作为下一步时频分解的资料基础。
|
图 2 道集优选 |
道集优选后所得的地震信号均为单角度的地震信号,避免了因为角度叠加而可能产生的干涉,但储层厚度变化所导致的调谐效应依然存在。为得到高分辨率的频谱分解结果,势必要消除波形叠加影响,将子波进行还原、分解。
在地震信号处理领域,稀疏表示理论能够有效促进反褶积、地震数据重建等线性反演问题的求解[19],得到信号稀疏表示的过程被称为稀疏分解。匹配追踪算法通过构造过完备匹配子波库、挑选与输入信号最匹配的原子,可以实现信号稀疏表示的自适应分解[20],所得的匹配子波相互独立,因而可以利用该算法分离混合帯限子波(图 1a)。
匹配追踪算法的核心之一是对过完备匹配子波库的构建。过完备匹配子波库可以理解为由一系列匹配子波所构成的子波矩阵,也可以描述为不同原子的集合。匹配子波实质上是通过对基本子波ω进行时移、调制和相位变化而产生的。经典的匹配追踪算法以Garbor字典构建过完备匹配子波库,为了适应信号的不同特征,可以选择Fourier字典描述频率;构造Dirac字典刻画位置[19];创建wavelet字典确定位置和尺度[21]。不同字典的选择可解决不同的问题,Ricker子波因波形简单、收敛较快、延迟时间短而在薄互层的时频分析中更具优势。并且Ricker子波具有三个控制参量,延迟时间可控,子波库波形丰富,与地震子波匹配较为灵活[22]。因此,本文以Ricker子波为母小波构建子波字典。
假设ω(t)为匹配子波库中满足条件的一个基本子波,令δ=(τ, f, φ)作为匹配子波的控制参数,则匹配子波表示为
| $ {\omega _\delta }\left( t \right) = \omega \left( {t - \tau } \right){{\rm{e}}^{{\rm{j}}\left[ {2{\rm{ \mathsf{ π} }}f\left( {t - \tau } \right) + \varphi } \right]}} $ | (1) |
式中:τ为时移;f为频率;φ为相位;j为虚数单位。通过控制参量τ、f、φ便可以完成对子波的匹配,其中时移因子固定匹配子波的位置;频率因子把基本子波的能量集中在少数的时频点附近。故过完备匹配子波库Φ可以表征为
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = {\left\{ {{\omega _\delta }\left( t \right)} \right\}_{\delta \in \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}}} $ | (2) |
式中Γ表示为δ=(τ, f, φ)的集合,则一道带宽有限的地震信号s(t)可描述为
| $ s\left( t \right) = \mathit{\boldsymbol{ \boldsymbol{\varPhi} \alpha }}\sum\limits_k {{\alpha _k}{\omega _{{\delta _k}}}\left( {t - {\tau _k},{f_k}{\varphi _k}} \right)} $ | (3) |
式中:α=[α1, …, αk]称为s(t)在完备匹配子波库Φ中的表示系数;ωδk表示第k次的匹配子波;αk、τk、fk、和φk分别为控制第k次匹配子波ω的振幅、中心时间、波峰频率和相位。
控制参量是通过扫描过完备匹配子波库、实现信号全局寻优自适应分解而确定的。构建过完备匹配子波库Φ后,从中选出与给定信号s最为匹配的匹配子波ω1,满足内积〈s, ωi〉为匹配子波库中所有原子与s内积中最大的一个
| $ \left\langle {s,{\omega _1}} \right\rangle > \left\langle {s,{\omega _i}} \right\rangle \;\;\;\;i \ne 1\;\;\;\;{\omega _i} \in \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} $ | (4) |
式中ωi为子波字典内的第i个子波原子。一次迭代后,信号s(t)被分解为
| $ s\left( t \right) = \left\langle {s,{\omega _1}} \right\rangle {\omega _1} + {R_{{s_1}}} $ | (5) |
式中Rs1是第一次迭代后的残差信号。〈s, ω1〉越大,代表子波匹配度越高。
对残差信号Rs1重复相同的匹配过程,即从Φ中筛选出与Rs1最为匹配的第二个原子。不断重复上述过程,则迭代第k次(k≥0)有
| $ {R_{{s_k}}} = \left\langle {s,{\omega _{k - 1}}} \right\rangle {\omega _{k - 1}} + {R_{{s_{k - 1}}}} $ | (6) |
| $ s\left( t \right) = \sum\limits_{k = 1}^M {\left\langle {{R_{{s_{k - 1}}}},{\omega _k}} \right\rangle {\omega _k} + {R_{{s_k}}}} $ | (7) |
式中:Rsk为第k次迭代后的残差信号;M为匹配子波的个数。
经过k次迭代分解后,原始信号s(t)可以用k个匹配子波的合成近似表示。当残差信号Rsk足够小,即信号的稀疏表示跟信号的近似程度足够好或残差信号满足设定的阈值时,迭代停止。
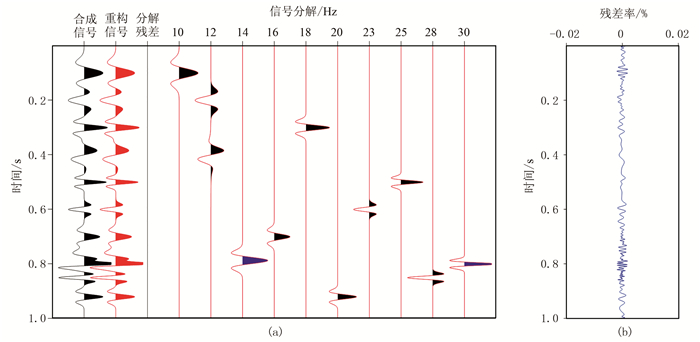
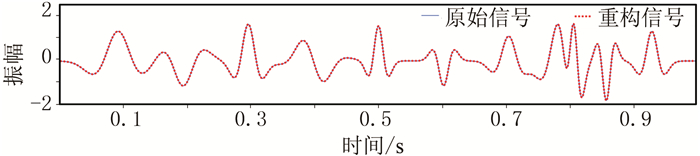
如图 3所示,设计11个Ricker子波叠加合成的单道信号,并在0.8s附近以两个相距小于λ/4的子波模拟出一个混合帯限子波。可以看出,合成信号被重新分解为11个主要的子波,而位于0.8s附近的混合带限子波也被重新分解为2个互相独立的子波,有效地还原了其所蕴含的真实信息。匹配追踪算法具有良好的稀疏分解效果,能够有效地保存信号的原始信息(图 4),保障后续时频分解的准确性。
|
图 3 基于匹配追踪算法的稀疏分解结果 (a)信号的分解与重构,前三道分别为输入的合成信号、利用匹配追踪算法重构后的信号以及分解残差,第四道起为利用匹配追踪算法分解出的匹配子波集;(b)分解残差率 |
|
图 4 基于匹配追踪算法的分解重构结果 |
在传统的信号分析和处理中,傅里叶变换得到的振幅谱或相位谱反映地震信号的平均信息,而不能得到局部信息[23]。短时傅里叶变换受时窗长度限制,不同的时窗参数对结果产生较大的影响,无法同时兼顾时间分辨率和频率分辨率。得益于匹配追踪算法的优势,在利用匹配追踪算法将信号s(t)稀疏分解后,由于匹配子波集中的每一个匹配子波ωδn(t)都具有独立性,因此可以对每一个匹配子波分别进行短时傅里叶变换。对低频子波选取大的时窗、高频子波选用较小的时窗,如此便可以克服常规短时傅里叶变换时窗固定不可调、分辨率单一的缺点,得到具有较高分辨率的时频分布。基于匹配追踪算法的STFT时频分布为
| $ {\rm{MPSTFT}}\left( {t,f} \right) = \sum\limits_{ - \infty }^{ + \infty } {{\omega _{\delta n}}} \left( \tau \right){g_n}\left( {\tau - t} \right){{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}f\tau }} $ | (8) |
式中gn(t)是与子波ωδn(t)对应的时窗。虽然在整体上短时傅里叶变换的时窗是不断改变的,但是仅对某一确定的主频时窗是固定的,因此可以极大地提升时频分辨率。进而利用匹配追踪算法得到的子波集,选择不同的时频分解方法就可以有效地提升分解精度,并且有效地避免干涉影响。
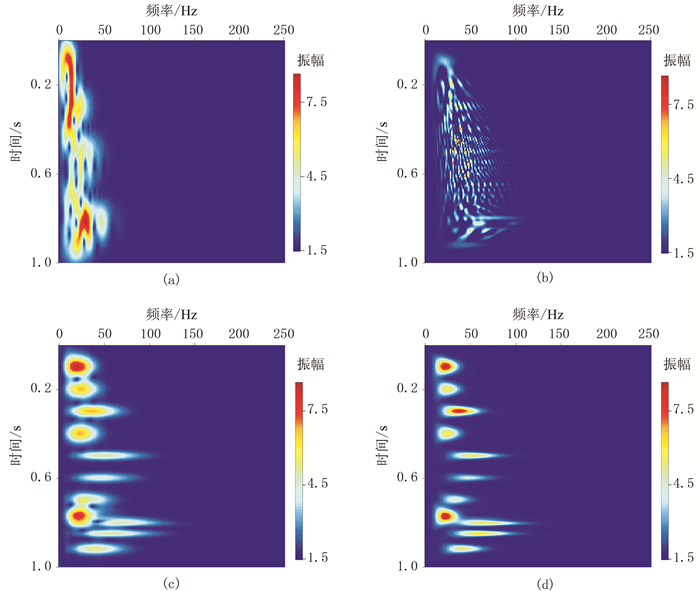
对图 3的合成信号选取不同方法进行时频表征,结果如图 5所示。可以看出,短时傅里叶变换过程中不会产生交叉项,但因为时窗不可调,时频表征的分辨率受到限制(图 5a);经过匹配追踪算法的改良,时频分辨率得到了有效提升(图 5c);相对于短时傅里叶变换,利用Wigner-Ville分布虽然分辨率有所提升,但产生了交叉干扰项,出现伪影(图 5b);利用匹配追踪算法的Wigner-Ville分布在保证时频分辨率的同时,消除了交叉项的干扰(图 5d)。因此,相比于对信号直接进行时频表征,基于匹配追踪稀疏分解子波集解析得到的时频分析结果能够保证更高的时频分辨率。
|
图 5 不同算法下的时频表征 (a)短时傅里叶变换频谱;(b)Wigner-Ville分布频谱;(c)基于匹配追踪算法的短时傅里叶变换频谱;(d)基于匹配追踪算法的Wigner-Ville分布频谱 |
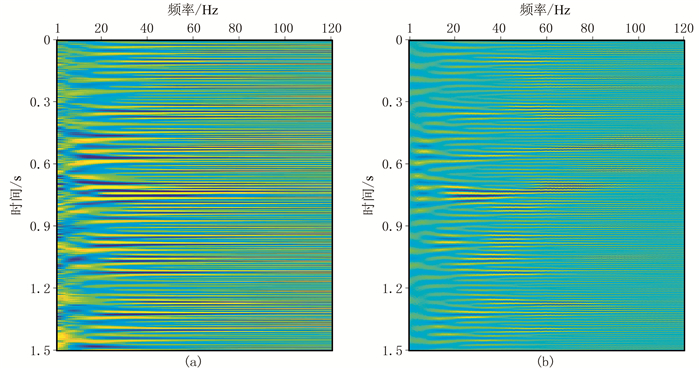
为了更好地验证频谱分解效果,进一步设计如图 6所示的复杂信号模型。对图 6b的复杂信号利用匹配追踪算法进行稀疏分解,并以此为基础在分解子波集内进行STFT变换。为更直观地对比分解效果,改用谱图形式进行对比,得到了如图 7b所示的频谱图,它与图 7a展示的原谱图基本一致,证明了该方法的有效性。

|
图 6 复杂信号模型 (a)120道主频分别为1~120Hz的单频波;(b)由图a中各单频波叠加合成的复杂信号 |
|
图 7 模型分解效果对比 (a)主频分别为1~120Hz的单频波;(b)基于匹配追踪算法处理后的合成信号时频分解图 |
谱分解技术拓宽了信号的维度,增加了所含的信息量。而基于稀疏表示理论(本文采用匹配追踪算法)的时频分解方法极大地提高了信号的时频分辨率,保障了频率信息的精确度,为后续道集多维分解与增维反演提供了基础。
1.3 叠前道集的多维分解叠前道集的地震属性随炮检距和频率变化,并且具有很大的差异性。因此,有别于传统的AVO分析,叠前反演除了要考虑炮检距,还应该考虑频率的选择。将上述的稀疏表示求解方法应用于叠前地震资料多维分解,能够有效克服干涉效应,提高地震数据的时频分辨率,且在分解过程中不会引入假频,为增维叠前反演提供可靠的数据支持。
在叠前地震反演过程中,对于地球物理反演问题,模型参数和数据是以某种方式联系起来的,数学上常构建为
| $ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{Px}} + \mathit{\boldsymbol{n}} $ | (9) |
式中:d∈RN为含噪声地震数据;P(RT→RN)为有界线性算子,T和N表示数据维度;x∈RT为待求解数据;n为噪声。
观测得到的地震数据d涵盖了不同尺度频率成分,可以表征为
| $ \mathit{\boldsymbol{d}} = \sum\limits_{{f_i} = 0}^{{f_{\rm{c}}}} {{\mathit{\boldsymbol{d}}_{{f_i}}}} $ | (10) |
式中:fi表示地震数据分解的频率为i Hz;fc为设定的分解截止频率;dfi是频率为fi的地震数据。
结合稀疏表示地震信号x=Φα以及稀疏正则化算法,不考虑噪声干扰,基于L1范数的稀疏约束反演问题可表示为以下泛函问题
| $ \mathop {\arg \min }\limits_{\mathit{\boldsymbol{\alpha }} \in {R^T}} \chi {\left\| \mathit{\boldsymbol{\alpha }} \right\|_1} + \frac{1}{2}\left\| {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{Px}}} \right\|_2^2 $ | (11) |
式中:χ为正则参数;d=Px=PΦα, α=[α1, …, αi],因此不同频率下的地震数据分量可描述为
| $ {\mathit{\boldsymbol{S}}_{\mathit{\boldsymbol{\delta }}\left( {{f_i}} \right)}} = \chi {\left\| {{\mathit{\boldsymbol{\alpha }}_i}} \right\|_1} + \frac{1}{2}\left\| {{\mathit{\boldsymbol{d}}_{{f_i}}} - \mathit{\boldsymbol{P}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\mathit{\boldsymbol{\delta }}\left( {{f_i}} \right)}}{\mathit{\boldsymbol{\alpha }}_i}} \right\|_2^2 $ | (12) |
式中:αi为字典的表示系数;Φδ(fi)={ωδ(fi)(t)}d(fi)∈Γ, 0<fi<fc为相应频率下子波字典。利用上述匹配追踪算法通过求解式(12)即可将地震数据分解为不同的频率分量。
图 8为A研究区a测线28°角道集地震数据按不同频率尺度分解图。可以看出:对于浅层(1.0~1.4s)河流相薄储层(红框所示),分解所得频率越高的单频剖面,信息越丰富(图 8b~图 8f);对于深部潜山(2.2~3.0s),分解所得频率越低的单频剖面,潜山内部的地震响应越清晰。

|
图 8 A研究区a测线稀疏时频域地震数据多频率分解图 (a)角度为28°的全频带剖面;角度为28°、主频为10Hz (b)、20Hz(c)、30Hz(d)、40Hz(e)、50Hz(f)的单频剖面。红框内为河流相薄储层 |
因此,不同深度的目标优势响应频段并不相同。对道集展开多维分解,在优势响应频段内可有效提升目标反演分辨率,进而提升储层识别能力。
1.4 增维叠前地震反演方法地震反演可分为叠后与叠前反演。叠后反演通过全角度叠加,虽然提高了资料品质,但弱化了储层岩性及流体性质信息[24]。叠前反演以佐普里兹方程及其近似式为基础[25],采用部分角度叠加的策略,考虑子波在反演过程中的影响,得到了分辨率更高的反演结果,因此被广泛应用。为消除干涉影响,提高对薄储层的刻画能力,发挥所拓展的频率分量优势,本文以贝叶斯数理统计理论为框架,开展增维叠前地震反演。
假定目标待反演的L组参数为m=[m1, m2, m3, …, mL],为避免干涉效应所处理得到的增维道集数据集合
| $ \mathit{\boldsymbol{d}} = \left[ {\begin{array}{*{20}{c}} {d\left( {{\theta _1},{f_1}} \right)}&{d\left( {{\theta _1},{f_2}} \right)}&{d\left( {{\theta _1},{f_3}} \right)}& \cdots &{d\left( {{\theta _1},{f_{\rm{c}}}} \right)}\\ {d\left( {{\theta _2},{f_1}} \right)}&{d\left( {{\theta _2},{f_2}} \right)}&{d\left( {{\theta _2},{f_3}} \right)}& \cdots &{d\left( {{\theta _2},{f_{\rm{c}}}} \right)}\\ {d\left( {{\theta _3},{f_1}} \right)}&{d\left( {{\theta _3},{f_2}} \right)}&{d\left( {{\theta _3},{f_3}} \right)}& \cdots &{d\left( {{\theta _3},{f_{\rm{c}}}} \right)}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {d\left( {{\theta _n},{f_1}} \right)}&{d\left( {{\theta _n},{f_2}} \right)}&{d\left( {{\theta _n},{f_3}} \right)}& \cdots &{d\left( {{\theta _n},{f_{\rm{c}}}} \right)} \end{array}} \right] $ | (13) |
式中:θ={θ1, θ2, θ3, …, θn}表示目的层段所涵盖的角度范围,θn为筛选的最大角度;f={f1, f2, …, fc}为目标层的优势响应频带。
根据贝叶斯理论,将数据—模型参数空间中的后验概率密度(PPDF)表示为
| $ p\left( {\mathit{\boldsymbol{m}}\left| {{\mathit{\boldsymbol{d}}_{{\theta _f}}}} \right.} \right) = \frac{{p\left( \mathit{\boldsymbol{m}} \right)p\left( {{\mathit{\boldsymbol{d}}_{{\theta _f}}}\left| \mathit{\boldsymbol{m}} \right.} \right)}}{{\int_L {p\left( \mathit{\boldsymbol{m}} \right)p\left( {{\mathit{\boldsymbol{d}}_{{\theta _f}}}\left| \mathit{\boldsymbol{m}} \right.} \right){\rm{d}}\mathit{\boldsymbol{m}}} }} $ | (14) |
式中dθf是入射角为θ、频率为f的地震数据。
假设地震数据中的噪声完全服从高斯分布,则似然函数可约定为
| $ p\left( {{\mathit{\boldsymbol{d}}_{{\theta _f}}}\left| \mathit{\boldsymbol{m}} \right.} \right) \propto \exp \left[ { - \frac{1}{2}{{\left( {\mathit{\boldsymbol{Gm}} - {\mathit{\boldsymbol{d}}_{{\theta _f}}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^{ - 1}}\left( {\mathit{\boldsymbol{Gm}} - {\mathit{\boldsymbol{d}}_{{\theta _f}}}} \right)} \right] $ | (15) |
式中:G为模型参数与观测数据间的正演算子;Ω=σns2I为不同角度、不同频率地震数据中噪声的协方差矩阵,I为单位矩阵,σns2为地震数据中噪声的方差。先验信息保障了待反演参数的约束范围,令模型参数服从柯西分布,模型参数与背景趋势拟合误差满足高斯分布,则得到先验信息概率分布
| $ \begin{array}{l} p\left( \mathit{\boldsymbol{m}} \right) = \frac{1}{{{{\left( {{\rm{ \mathsf{ π} }}{\sigma _m}} \right)}^L}}}\prod\limits_{i = 1}^L {\left( {\frac{1}{{1 + \frac{{m_i^2}}{{\sigma _m^2}}}}} \right)} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\exp \left[ { - \frac{1}{2}\frac{{{{\left( {\mathit{\boldsymbol{Gm}} - \mathit{\boldsymbol{\zeta }}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{Gm}} - \mathit{\boldsymbol{\zeta }}} \right)}}{{2\sigma _\zeta ^2}}} \right] \end{array} $ | (16) |
积分矩阵
| $ \mathit{\boldsymbol{C}} = \left( {\begin{array}{*{20}{c}} 1&0& \cdots &0\\ 1&1& \ddots & \vdots \\ \vdots & \vdots & \ddots &0\\ 1&1& \cdots &1 \end{array}} \right) $ | (17) |
上述式中:σm2为模型参数方差;mi是待反演参数;ζ为背景趋势数据;σζ2为反演参数与背景趋势的方差。结合式(15)与式(16),后验概率分布表征为
| $ \begin{array}{l} p\left( {\mathit{\boldsymbol{m}}\left| \mathit{\boldsymbol{d}} \right.} \right) = \frac{{ - 1}}{{{{\left( {{\rm{ \mathsf{ π} }}{\sigma _m}} \right)}^L}}}\prod\limits_{i = 1}^L {\left( {\frac{1}{{1 + \frac{{m_i^2}}{{\sigma _m^2}}}}} \right)} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left[ { - \frac{1}{2}{{\left( {\mathit{\boldsymbol{Gm}} - {\mathit{\boldsymbol{d}}_{{\theta _f}}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^{ - 1}}\left( {\mathit{\boldsymbol{Gm}} - {\mathit{\boldsymbol{d}}_{{\theta _f}}}} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{1}{2}\frac{{{{\left( {\mathit{\boldsymbol{Gm}} - \mathit{\boldsymbol{\zeta }}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{Gm}} - \mathit{\boldsymbol{\zeta }}} \right)}}{{2\sigma _\zeta ^2}}} \right] \end{array} $ | (18) |
对式(18)两边同取对数,得到目标泛函
| $ \begin{array}{l} J\left( \mathit{\boldsymbol{m}} \right) = {\left( {\mathit{\boldsymbol{Gm}} - {\mathit{\boldsymbol{d}}_{{\theta _f}}}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{Gm}} - {\mathit{\boldsymbol{d}}_{{\theta _f}}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\mu {\left( {\mathit{\boldsymbol{Cm}} - \mathit{\boldsymbol{\zeta }}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{Cm}} - \mathit{\boldsymbol{\zeta }}} \right) + \lambda \sum\limits_{i = 1}^L {\frac{{\frac{{m_i^2}}{{\sigma _m^2}}}}{{1 + \frac{{m_i^2}}{{\sigma _m^2}}}}} \end{array} $ | (19) |
式中μ和λ别为柯西约束项权值与趋势背景约束项权值
| $ \left\{ {\begin{array}{*{20}{l}} {\mu = \frac{{\sigma _{{n_s}}^2}}{{\sigma _\zeta ^2}}}\\ {\lambda = \frac{{2\sigma _{{n_s}}^2}}{{\sigma _m^2}}} \end{array}} \right. $ | (20) |
由贝叶斯理论中模型参数的后验概率分布构建反演目标函数,采用最大后验概率解求取模型参数的方法,对目标函数(式(18))求导,整理得到反演方程
| $ \left(\frac{1}{\sqrt{\boldsymbol{A}}} \boldsymbol{P}^{\mathrm{T}} \boldsymbol{P} \frac{1}{\sqrt{\boldsymbol{A}}}+\lambda \boldsymbol{I}\right) \boldsymbol{\hat m}=\frac{1}{\sqrt{\boldsymbol{A}}} \boldsymbol{P}^{\mathrm{T}} \boldsymbol{S} $ | (21) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{P}} = {{\left[ {\mathit{\boldsymbol{G}},\mathit{\boldsymbol{C}}} \right]}^{\rm{T}}}}\\ {\mathit{\boldsymbol{S}} = {{\left[ {{\mathit{\boldsymbol{d}}_{{\theta _f}}},\mathit{\boldsymbol{I}}} \right]}^{\rm{T}}}} \end{array}} \right. $ | (22) |
式中A为对角矩阵,对角线元素为
式(21)可表示为
|
|
表 1 求解m流程 |
增维叠前地震反演流程如图 9所示。首先,从角道集中筛选、抽取n个角度的单角度地震数据,并对每一个单角度地震数据结合匹配追踪算法按照fc个频率进行频率分解;其次,依托速度场与Aki-Richard近似公式构建不同角度的低频模型,以单角度地震数据所截取频带中的最低频率数据d(θ1, f1)作为初始输入,按照式(19)求解,得到该角度频率的弹性阻抗结果EI(θ1, f1);再次,以该角度第二个频率d(θ1, f2)的地震数据作为输入,以第一个频率d(θ1, f1)数据的弹性阻抗结果EI(θ1, f1)作为低频模型,继续按照式(19)求解,得到d(θ1, f2)的弹性阻抗结果EI(θ1, f2);依次循环,直到得到该角度截止频率处数据d(θ1, fc)的反演结果EI(θ1, fc),则该结果为此角度的分频逐级反演结果;最后,由此转入下一个角度数据体,重复上述步骤,直到所有截取角度反演完成,得到n个增维弹性阻抗反演结果。

|
图 9 增维叠前反演流程图 |
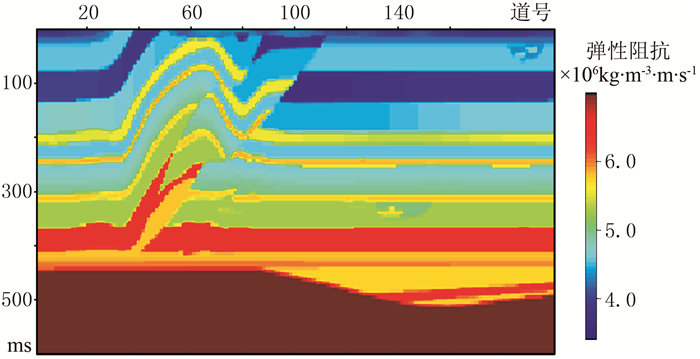
为了验证本文提出的增维叠前地震反演方法的有效性,采用经典的EAGE推覆体模型中的一条二维剖面(图 10)进行试算,以验证增维反演结果的精度。
|
图 10 弹性阻抗模型 |
首先,基于稀疏表示理论对相应的褶积模型进行分解,得到不同频率的地震数据;其次,依托模型速度场构建低频模型,以分解得到的5Hz地震数据为初始输入,得到如图 11a所示的弹性阻抗反演结果;再次,以图 11a所示的阻抗数据为模型输入,以10Hz的地震数据作为输入,得到10Hz的弹性阻抗反演结果;以此类推逐级反演,最终得到了各频率的逐级反演结果。因数据量过多,本文只截取了5、25、35、45Hz的反演结果进行展示。由模型增维叠前反演结果(图 11)可以看出,可由低频信息恢复模型的背景部分,高频信息恢复出薄层小目标细节,逐级进行更新刻画,可以有效地恢复局部薄层(200ms~300ms,黄色所示)细节。

|
图 11 不同频率增维叠前地震反演结果 (a)5Hz;(b) 25Hz;(c) 35Hz;(d) 45Hz |
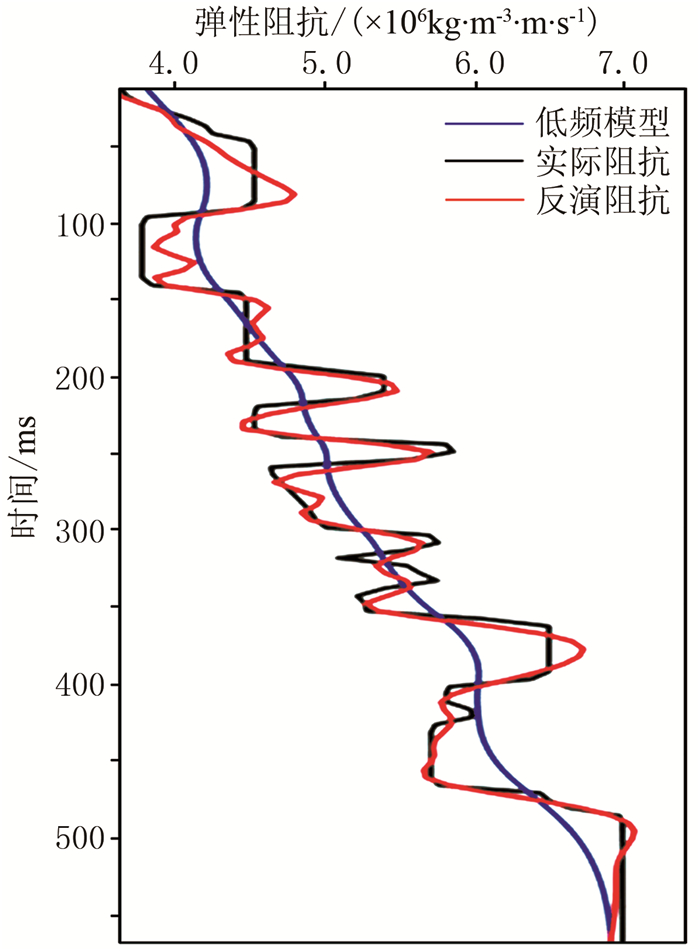
为了更直观地分析反演效果,抽取单道反演结果(图 12)。可见本文方法反演所得的弹性阻抗曲线与实际弹性阻抗曲线相比具有较高的吻合度。
|
图 12 抽取的单道反演结果 |
为了测试增维叠前地震反演方法的实际应用效果,选取A研究区进行实验,目的层段为馆陶组河流相薄储层。目前已有钻井63口,其中失利井30口。失利的主要原因之一为储层薄、反演精度不高。该区Well-1井钻遇厚度为7.18m与11.9m的两套油层。
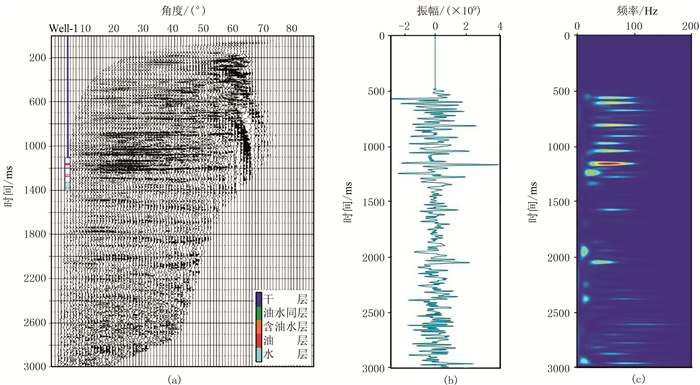
图 13为Well-1井井旁叠前角道集。首先对1200ms处目的层段按优势响应角度进行筛选,选择品质良好的角度范围;其次对目的层的优势频段进行评估,选取储层优势响应频带。如图 13b所示,抽选道集中的28°地震数据具体分析,可见本区目的层1200ms处薄储层段为高频响应。进一步通过时频分析(图 13c)处理,得出本区目的层段的优势响应频带为45~80Hz。
|
图 13 Well-1井井旁叠前道集及频谱 (a)Well-1井旁叠前道集;(b)Well-1井旁叠前道集28°地震数据;(c)Well-1井旁叠前道集28°地震时频分析结果 |
为验证增维叠前反演方法对于薄储层的识别精度,针对研究区过Well-1、Well-2井的b测线抽选6°~28°的地震记录作为观测数据,利用稀疏表示结合短时傅里叶变换对该范围内的单角度剖面以2Hz为间隔逐一进行高分辨率的谱分解。以此为基础,在每一个角度内对单频波从低到高重排,由低频向高频移动,在贝叶斯理论框架下,以前一个频率的反演结果作为后一个频率反演的约束,逐级反演,最终得到了增维叠前地震反演结果。
图 14为b测线利用不同反演方法所得结果。为了展示反演效果,选取测线所过Well-1、Well-2两井的测井解释结果进行比对。可以看出,由于受到叠加影响,常规叠后反演剖面上黑色圆圈处的两套油层(图 14a)混叠在一起难以区分。图 14b为16°~24°的叠加数据输入所得到的叠前反演结果,与叠后反演相比,叠前地震反演结果信噪比虽有所降低,但大套层组间的界面变得更加清晰(黑色圆圈所示),但黑色圆圈处的两套油层(图 14b)仍难以分辨。单角度地震数据直接反演(图 14c)避免了地震资料叠加时产生的干涉效应,反演结果分辨率更高,黑色圆圈处的两套油层已经隐约可见。而考虑了频率因素的增维叠前反演结果(图 14d)与测井解释结果吻合更好,有效地区分出了1250ms(图中黑色圆圈所示)处的两套薄层,对于储层的整体刻画也更加精细。以上结果证明在不叠加思想下考虑频率增维反演结果具有更高的描述精度,能够更准确地对薄储层进行识别和刻画。

|
图 14 A研究区b测线不同波阻抗反演方法剖面对比 (a)叠后弹性阻抗反演;(b)16°~24°地震数据叠前弹性阻抗反演;(c)28°单角度地震数据叠前弹性阻抗反演;(d)28°增维叠前弹性阻抗反演。底部色标为测井解释结果 |
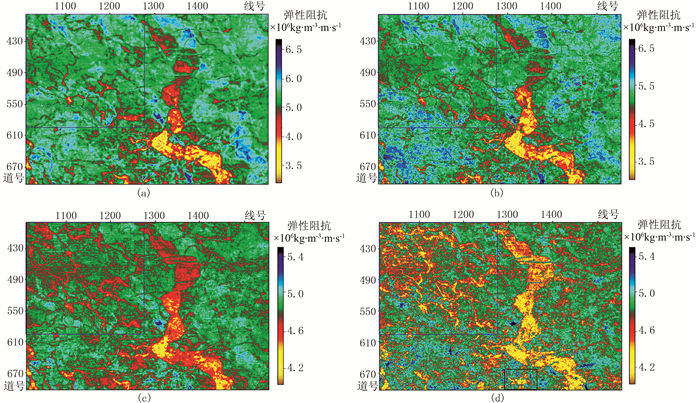
为了进一步验证增维叠前地震反演方法的应用效果,截取目的层1250ms馆陶组沿层切片(图 15),分别采用不同的反演方法对有利储层进行刻画。叠后反演方法得到的弹性阻抗(图 15a)能够大致刻画出主河道的轮廓,但无法分辨分支河道;以部分角度叠加的叠前弹性阻抗反演(图 15b)在一定程度上加强了对分支河道的识别能力,但主河道上游(主河道自北向南流动)与切片左上部分(蓝框内)分支河道的连续性仍较差;28°单角度地震数据反演结果(图 15c)不仅能够刻画主河道的轮廓,并且主河道上游轮廓更加清晰,能很好地识别分支河道;利用28°单角度地震数据按照增维策略分频逐级反演切片(图 15d)上,主河道、分支河道可清晰识别,还揭示出在主河道下游因干涉效应而被掩盖的一分支河道砂体(图 15d黑框处),这在勘探中得到证实。
|
图 15 A研究区馆陶组不同反演方法的沿层波阻抗切片 (a)叠后弹性阻抗反演;(b)叠前弹性阻抗反演;(c)28°的单角度地震数据叠前弹性阻抗反演;(d)28°地震数据的增维叠前弹性阻抗反演 |
本文引入不叠加的叠前反演理念,既不对角度进行叠加,同时又兼顾频率因素的影响进行频谱分解,有效地避免了干涉效应造成的信息畸变与缺失。基于贝叶斯反演理论,结合FAVO的反演思想,提出基于稀疏表示的增维叠前地震反演方法,得到了具有更高分辨率的反演结果,有效地提升了薄层识别能力。得到了以下认识。
(1) 叠加会使部分区域的信息产生畸变,弱化反演精度。不叠加思想能够有效地避免这种影响,并对真实信息进行还原。
(2) 考虑频率因素的反演可以有效地提升储层描述能力。
(3) 本文提出的增维高分辨叠前反演方法较传统反演方法具有更高的分辨能力,能够对河道砂体进行有效识别。
| [1] |
Chapman M, Maultzsch S, Liu E, et al. The effect of fluid saturation in an anisotropic multi-scale equant porosity model[J]. Journal of Applied Geophysics, 2003, 54(3-4): 191-202. DOI:10.1016/j.jappgeo.2003.01.003 |
| [2] |
Chapman M, Liu E, Li X Y. The influence of abnormally high reservoir attenuation on the AVO signature[J]. The Leading Edge, 2005, 24(11): 1120-1125. DOI:10.1190/1.2135103 |
| [3] |
Chapman M, Liu E, Li X Y. The influence of fluid-sensitive dispersion and attenuation on AVO analysis[J]. Geophysical Journal of the Royal Astronomical Society, 2006, 167(1): 89-105. DOI:10.1111/j.1365-246X.2006.02919.x |
| [4] |
Wilson A, Chapman M, Li X Y.Frequency-dependent AVO inversion[C]. SEG Technical Program Expanded, 2009, 28: 341-345.
|
| [5] |
Wu X Y, Chapman M, Li X. Estimating seismic dispersion from prestack data using frequency-dependent AVO analysis[J]. Journal of Seismic Exploration, 2014, 23(3): 425-429. |
| [6] |
张世鑫, 印兴耀, 张广智, 等. 纵波速度频散属性反演方法研究[J]. 石油物探, 2011, 50(3): 219-224. ZHANG Shixin, YIN Xingyao, ZHANG Guangzhi, et al. Inversion method for the velocity dispersion-dependent attribute of P-wave[J]. Geophysical Prospecting for Petroleum, 2011, 50(3): 219-224. DOI:10.3969/j.issn.1000-1441.2011.03.002 |
| [7] |
吴国忱, 田军. 基于尺度约束项的AVO反演方法[J]. 石油地球物理勘探, 2014, 49(6): 1157-1164. WU Guochen, TIAN Jun. AVO inversion based on scale constraints[J]. Oil Geophysical Prospecting, 2014, 49(6): 1157-1164. |
| [8] |
杨千里, 吴国忱. 基于贝叶斯理论的多尺度地震反演方法[J]. 地球物理学进展, 2016, 31(3): 1246-1256. YANG Qianli, WU Guochen. Multi-scale seismic inversion method based on Bayesian theory[J]. Progress in Geophysics, 2016, 31(3): 1246-1256. |
| [9] |
吴建鲁, 吴国忱. 一维频率域中观尺度虚岩石物理方法[J]. 石油地球物理勘探, 2018, 53(1): 105-112. WU Jianlu, WU Guochen. A method of 1D mesoscopic digital rock physics in the frequency domain[J]. Oil Geophysical Prospecting, 2018, 53(1): 105-112. |
| [10] |
李坤, 印兴耀, 宗兆云. 基于匹配追踪谱分解的时频域FAVO流体识别方法[J]. 石油学报, 2016, 37(6): 777-786. LI Kun, YIN Xingyao, ZONG Zhaoyun. Time-frequency-domain FAVO fluid discrimination method based on matching pursuit spectrum decomposition[J]. Acta Petrolei Sinica, 2016, 37(6): 777-786. |
| [11] |
张繁昌, 何晋越, 桑凯恒, 等. 稀疏反射系数频率域正余弦分量协同反演方法[J]. 石油地球物理勘探, 2018, 53(4): 778-783. ZHANG Fanchang, HE Jinyue, SANG Kaiheng, et al. A sparse reflectivity sine-cosine synergistic inversion method in the frequency domain[J]. Oil Geophysical Prospecting, 2018, 53(4): 778-783. |
| [12] |
Gabor D. Theory of communication, Part 1:The analy-sis of information[J]. Electrical Engineers Ⅲ, 1946, 93(26): 429-441. |
| [13] |
Morlet J, Arens G, Fourgeau E, et al. Wave propagation and sampling theory, Part Ⅰ:Complex signal and scattering in multilayered media[J]. Geophysics, 1982, 47(2): 203-221. DOI:10.1190/1.1441328 |
| [14] |
Stockwell R G, MansinhaL, Lowe R P. Localization of the complex spectrum:the S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. DOI:10.1109/78.492555 |
| [15] |
Mallat S G, Zhang Z. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415. DOI:10.1109/78.258082 |
| [16] |
Liu J, Wu Y, Han D, et al.Time-frequency decomposition based Ricker wavelet[C]. SEG Technical Program Expanded Abstract, 2004, 23: 1937-1940.
|
| [17] |
张繁昌, 李传辉. 地震信号复数域高效匹配追踪分解[J]. 石油地球物理勘探, 2013, 48(2): 171-175. ZHANG Fanchang, LI Chuanhui. Complex domain efficient matching pursuit decomposition of seismic signals[J]. Oil Geophysical Prospecting, 2013, 48(2): 171-175. |
| [18] |
何兵红, 方伍宝, 刘定进, 等. 基于波动方程转换的时间域多尺度全波形反演速度建模[J]. 石油物探, 2019, 58(2): 229-236. HE Binghong, FANG Wubao, LIU Dingjin. Velocity building by multi-scale full waveform inversion with time-domain wave equation transform[J]. Geophysical Prospecting for Petroleum, 2019, 58(2): 229-236. DOI:10.3969/j.issn.1000-1441.2019.02.008 |
| [19] |
李海山.基于稀疏表示理论的地震信号处理方法研究[D].山东青岛: 中国石油大学(华东), 2013. LI Haishan.Seismic Signal Processing Methods Based on Sparse Representation Theory[D]. China University of Petroleum(East China), Qingdao, Shandong, 2013. |
| [20] |
张繁昌, 李传辉, 印兴耀. 基于动态匹配子波库的地震数据快速匹配追踪[J]. 石油地球物理勘探, 2010, 45(5): 667-673. ZHANG Fanchang, LI Chuanhui, YIN Xingyao. Seismic data fast matching pursuit based on dynamic matching wavelet library[J]. Oil Geophysical Prospecting, 2010, 45(5): 667-673. |
| [21] |
Mallat S. A Wavelet Tour of Signal Processing:The Sparse Way[M]. New York: Academic Press, 2008.
|
| [22] |
宋新武, 郑浚茂, 范兴燕, 等. 基于Ricker子波匹配追踪算法在薄互层砂体储层预测中的应用[J]. 吉林大学学报(地球科学版), 2011, 41(增刊1): 387-392. SONG Xinwu, ZHENG Junmao, FAN Xingyan, et al. Application of the thin-interbedded reservoir prediction based on Ricker wavelet match tracing algorithm[J]. Journal of Jilin University(Earth Science Edition), 2011, 41(S1): 387-392. |
| [23] |
冯磊, 姜在兴. 基于匹配追踪的谱分解方法及其应用[J]. 勘探地球物理进展, 2009, 32(1): 33-36. FENG Lei, JIANG Zaixing. Spectral decomposition based on matching pursuit and its application[J]. Progress in Geophysics, 2009, 32(1): 33-36. |
| [24] |
杨千里.多尺度分级地震反演方法研究[D].山东青岛: 中国石油大学(华东), 2016. YANG Qianli.The Research of Multiscale Seismic Inversion[D]. China University of Petroleum(East China), Qingdao, Shandong, 2016. |
| [25] |
黄捍东, 王彦超, 郭飞. 基于佐普里兹方程的高精度叠前反演方法[J]. 石油地球物理勘探, 2013, 48(5): 740-749. HUANG Handong, WANG Yanchao, GUO Fei. High precision prestack inversion algorithm based on Zoeppritz equations[J]. Oil Geophysical Prospecting, 2013, 48(5): 740-749. |



 吴国忱, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
吴国忱, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: