② 东方地球物理公司物探技术研究中心, 河北涿州 072751;
③ 太原理工大学矿业工程学院, 山西太原 030024;
④ 中国石油勘探开发研究院, 北京 100083;
⑤ 中国石油大学(北京)地球物理学院, 北京 102249
② R&D Center, BGP, CNPC, Zhuozhou, Hebei 072751, China;
③ College of Mining Engineering, Taiyuan University of Technology, Taiyuan, Shanxi 030024, China;
④ Research Institute of Petroleum Exploration and Development, PetroChina, Beijing 100083, China;
⑤ College of Geophysics, China University of Petroleum(Beijing), Beijing 102249, China
地震波阻抗反演作为储层描述的工具之一,在储层预测方面具有重要作用[1-5]。地震波阻抗反演方法众多,可以分为确定性反演与统计学反演两大类[6-8]。确定性反演是一类成熟的方法,这类方法的共性是构建一个目标函数,求取使目标函数取得极小值的解作为反演结果[9-10]。确定性反演常见的方法包括模型法反演[11]和稀疏脉冲反演[12],在特定的解约束条件下,只能进行单一的最优解估计,无法评价反演结果的不确定性。实际上,地震反演是一个多解性问题,相比于确定性反演只给出一个某种范数意义下的最优解,统计学反演则尝试用概率语言完整地表达解空间及其每个解的可能性。因此,统计学反演给出的是一簇满足约束条件的解,而非一个唯一解[13]。对于统计学反演输出的多个结果,利用概率统计的手段评价反演结果的不确定性,是分析勘探风险的一个重要方面[14-15],这是统计学反演的优势之一。为了完全探索反演解空间的结构,统计学反演利用采样求解的策略,反演结果的分辨率高于确定性反演,在薄层刻画方面取得了很好的效果[16-18],这是统计学反演的优势之二。
作为统计学反演方法的一个分支,Haas等[19]首次将地质统计学应用于地震反演,将地震资料作为约束条件,控制测井资料序贯模拟结果的取舍,构成了传统地质统计学反演的基本思想。随着研究的深入,地质统计学由两点地质统计学向多点地质统计学发展,地质统计学反演相应地也由两点地质统计学反演转向多点地质统计学反演[20-22]。González等[22]首次将多点地质统计学算法与地震反演结合反演河道砂波阻抗,探讨了多点地质统计学反演的可行性与优越性。目前,多点地质统计学反演的难点在于如何合理建立训练图像以及提高计算效率,这两方面制约着多点地质统计学反演的实际应用效果[23-24]。
目前地质统计学反演主流算法均为地质统计学随机模拟方法与马尔科夫链—蒙特卡洛方法的某种结合[25-28],并没有将地震反演、测井数据约束、随机模拟方法统一在一个理论框架下。为此,本文首先在贝叶斯理论框架下,将地震反演理论、测井数据约束、地质统计信息统一在波阻抗求解这个问题中,推导了基于对数波阻抗的地震数据与测井数据联合方程,然后通过序贯高斯随机模拟算法对反演方程进行高效采样求解,最后通过理论模型试算和实际资料应用验证了方法的可行性和有效性。
1 方法原理 1.1 地震正演模型假设地层界面两侧为各向同性、弹性介质,当地震波垂直入射时,反射系数r(t)和波阻抗z(t)的关系可表达为[29]
| $ r\left( t \right) = \frac{1}{2}\frac{{{\rm{d}}\ln z\left( t \right)}}{{{\rm{d}}t}} $ | (1) |
式中t为时间。在小反射系数假设条件下,将式(1)改写为矩阵形式[30]
| $ \mathit{\boldsymbol{r}} = \frac{1}{2}\mathit{\boldsymbol{D}}\ln \mathit{\boldsymbol{z}} $ | (2) |
式中:r=[r1, r2, …, rN-1]T代表一道反射系数序列,下标N代表地震道的时间采样点数;z=[z1, z2, …, zN]T代表声波阻抗;而
| $ \mathit{\boldsymbol{D}} = {\left[ {\begin{array}{*{20}{c}} { - 1}&1&{}&{}&{}\\ {}&{ - 1}&1&{}&{}\\ {}&{}& \ddots & \ddots &{}\\ {}&{}&{}&{ - 1}&1 \end{array}} \right]_{\left( {N - 1} \right) \times N}} $ | (3) |
代表差分矩阵。根据褶积模型, 观测地震数据dobs为
| $ {\mathit{\boldsymbol{d}}_{{\rm{obs}}}} = \mathit{\boldsymbol{Wr}} + \mathit{\boldsymbol{e}} = \mathit{\boldsymbol{WDm}} + \mathit{\boldsymbol{e}} = \mathit{\boldsymbol{Gm}} + \mathit{\boldsymbol{e}} $ | (4) |
式中:W为N×(N-1)维子波褶积矩阵;e为误差项;m=(1/2)lnz为波阻抗中间变量(模型参数);而
| $ \mathit{\boldsymbol{G}} = \mathit{\boldsymbol{WD}} $ |
为N×N维正演算子矩阵。
1.2 贝叶斯空间结构约束后验模型地震反演的目的为从dobs中估计m,但由于地震资料的带限特征,存在无数解满足式(4)。传统确定性反演直接对解空间添加约束条件[31],如最小长度解、最光滑解、或者最稀疏解等,从而获得单一的解估计。在此类方法中,正则化参数的选择过于主观,反演结果受人为因素影响大,而且不能评估反演结果的不确定性。
贝叶斯反演方法能够综合观测数据中的多种先验信息,通过概率统计理论获得完备的后验解空间,并且能够表征反演结果的不确定性[9, 13, 32]。在贝叶斯反演中,反演结果由后验概率密度函数σ(m)表示,其为先验概率密度函数ρ(m)与地震似然函数L(m)的乘积,即
| $ \sigma \left( \mathit{\boldsymbol{m}} \right) = c\rho \left( \mathit{\boldsymbol{m}} \right)L\left( \mathit{\boldsymbol{m}} \right) $ | (5) |
式中c为归一化常数。
假设m服从多维高斯分布,即m~
| $ \rho \left( \mathit{\boldsymbol{m}} \right) = {c_1}\exp \left[ { - \frac{1}{2}{{\left( {\mathit{\boldsymbol{m}} - {\mathit{\boldsymbol{m}}_{{\rm{prior}}}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^{ - 1}\left( {\mathit{\boldsymbol{m}} - {\mathit{\boldsymbol{m}}_{{\rm{prior}}}}} \right)} \right] $ | (6) |
式中:mprior=lnz0为N维列向量,表示波阻抗的先验低频背景模型,z0为初始波阻抗模型;c1为归一化常数;Cm为N×N维模型先验协方差矩阵
| $ {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}}\left( {p,q} \right) = {\mathit{\boldsymbol{C}}_0}\left[ {1 - v\left( h \right)} \right] $ | (7) |
式中:v(h)为反映地质统计先验信息的变差函数,主要有高斯模型、球状模型、指数模型以及多种模型的套合结构,h为模型空间中任意两点p点和q点的距离;C0=σlnz02为初始对数域波阻抗模型方差。同时,假设地震误差项服从零均值高斯分布,即e~
| $ \begin{array}{*{20}{c}} {L\left( \mathit{\boldsymbol{m}} \right) = {c_2}\exp \left[ { - \frac{1}{2}{{\left( {{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} - \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{m}}_{{\rm{prior}}}}} \right)}^{\rm{T}}} \times } \right.}\\ {\left. {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{d}}^{ - 1}\left( {{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} - \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{m}}_{{\rm{prior}}}}} \right)} \right]} \end{array} $ | (8) |
式中:c2为归一化常数;Cd为N×N维地震数据协方差矩阵,通过测井合成记录与实际井旁地震道资料估算得到。
上述情形为典型的线性高斯求解问题,可知模型参数的后验概率同样服从高斯分布。将式(6)和式(8)代入式(5),可得全概率的后验解空间,其中后验期望
| $ \mathit{\boldsymbol{\tilde m}} = {\mathit{\boldsymbol{m}}_{{\rm{prior}}}} + {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}}{\mathit{\boldsymbol{G}}^{\rm{T}}}{\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}}{\mathit{\boldsymbol{G}}^{\rm{T}}} + {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{d}}}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{d}}_{{\rm{dos}}}} - \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{m}}_{{\rm{prior}}}}} \right) $ | (9) |
| $ {{\mathit{\boldsymbol{\tilde C}}}_\mathit{\boldsymbol{m}}} = {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}} - {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}}{\mathit{\boldsymbol{G}}^{\rm{T}}}{\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}}{\mathit{\boldsymbol{G}}^{\rm{T}}} + {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{d}}}} \right)^{ - 1}}\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}} $ | (10) |
在地质统计学理论范畴中,式(9)和式(10)为在观测资料约束下的简单克里金估计,其中
当建立了后验期望(式(9))和后验协方差矩阵(式(10))表达式后,一般通过两种传统方法获得反演结果:①直接代入相应矩阵求解[34];②采用蒙特卡洛方法实现随机采样[35]。在第一种方法中,由于Cm和Cd非常庞大,需要很大的物理存储空间存储。如一个二维剖面包含200个时间采样点、300道数据点,在地震反演中仅存储Cm所需的物理存储空间为(200×300)2×8B≈26.8GB,因此在实际三维地震资料反演中,对所有点进行一次性直接求解几乎不太现实。在第二种方法中,尽管蒙特卡洛方法能较好地对高维数据降维处理,但是此类方法通常需要经过一系列的“拒绝—接受”重复迭代采样过程,计算效率低[36]。
不同于以上两种方法,地质统计学中序贯高斯模拟能够充分利用求解问题的线性和高斯分布特性,是一种非迭代的高效采样方法。此方法并非一次性求解式(9)和式(10)中庞大线性矩阵的所有点,而是在模型空间中随机访问单个点,并且采用“邻域”思想将大型矩阵求解问题转换为许多小型线性矩阵求解问题,适用于任意高维问题。
序贯模拟的基本思想为将已模拟点作为条件数据,同原始已知点一起,在给定邻域内参与下一个点的计算,直至模拟完成随机路径中所有节点。借鉴这种思想,本文采用井震联合的贝叶斯序贯随机反演方法,为了求解方便,在邻域内将观测数据划分为A、B两类数据。A类数据为模型参数的直接测量值,包括测井数据和先前模拟的点,也称为“硬数据”或者“点数据”;B类数据为模型参数的线性平均观测值,即通过线性正演算子获得的测量数据,也称为“软数据”或者“体数据”,这里指地震数据。联合两类观测数据,式(4)可改写为
| $ \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{d}}_{{\rm{obsA}}}}}\\ {{\mathit{\boldsymbol{d}}_{{\rm{obsB}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{G}}_{\rm{A}}}}&{\bf{0}}\\ {\bf{0}}&{{\mathit{\boldsymbol{G}}_{\rm{B}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{m}}_{\rm{A}}}}\\ {{\mathit{\boldsymbol{m}}_{\rm{B}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{e}}_{\rm{A}}}}\\ {{\mathit{\boldsymbol{e}}_{\rm{B}}}} \end{array}} \right] $ | (11) |
或简化为
| $ {\mathit{\boldsymbol{d}}_{{\rm{obs}}\left( {{\rm{A}} + {\rm{B}}} \right)}} = {\mathit{\boldsymbol{G}}_{{\rm{A}} + {\rm{B}}}}{\mathit{\boldsymbol{m}}_{{\rm{A}} + {\rm{B}}}} + {\mathit{\boldsymbol{e}}_{{\rm{A}} + {\rm{B}}}} $ | (12) |
式中:dobsA、GA、mA和eA分别代表A类观测数据、正演算子、模型参数和误差项;dobsB、GB、mB和eB分别代表B类观测数据、正演算子、模型参数和误差项;dobs(A+B)、GA+B、mA+B和eA+B代表A、B两类数据的联合参数。这里需要注意的是,与地震正演算子GB不同,直接观测的A类数据正演算子GA为简单的单位矩阵,不依赖于任何物理规律。
类似单一数据类型的后验解(式(9)、式(10)),对联合数据(式(12))进行贝叶斯反演,分别得到在测井数据(A类)和地震数据(B类)共同约束下的后验期望
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\tilde m}}}_{{\rm{A}} + {\rm{B}}}} = {\mathit{\boldsymbol{m}}_{{\rm{prior}}\left( {{\rm{A}} + {\rm{B}}} \right)}} + {\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{m}}\left( {{\rm{A}} + {\rm{B}}} \right)}}\mathit{\boldsymbol{G}}_{{\rm{A}} + {\rm{B}}}^{\rm{T}}\left[ {{\mathit{\boldsymbol{G}}_{{\rm{A}} + {\rm{B}}}}{\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{m}}\left( {{\rm{A}} + {\rm{B}}} \right)}}\mathit{\boldsymbol{G}}_{{\rm{A}} + {\rm{B}}}^{\rm{T}} + } \right.}\\ {{{\left. {{\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{d}}\left( {{\rm{A}} + {\rm{B}}} \right)}}} \right]}^{ - 1}}\left[ {{\mathit{\boldsymbol{d}}_{{\rm{obs}}\left( {{\rm{A}} + {\rm{B}}} \right)}} - \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{m}}_{{\rm{prior}}\left( {{\rm{A}} + {\rm{B}}} \right)}}} \right]} \end{array} $ | (13) |
| $ \begin{array}{l} {{\mathit{\boldsymbol{\tilde C}}}_{\mathit{\boldsymbol{m}}\left( {{\rm{A}} + {\rm{B}}} \right)}} = {\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{m}}\left( {{\rm{A}} + {\rm{B}}} \right)}} - {\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{m}}\left( {{\rm{A}} + {\rm{B}}} \right)}}\mathit{\boldsymbol{G}}_{{\rm{A}} + {\rm{B}}}^{\rm{T}}\left[ {{\mathit{\boldsymbol{G}}_{{\rm{A}} + {\rm{B}}}}{\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{m}}\left( {{\rm{A}} + {\rm{B}}} \right)}}\mathit{\boldsymbol{G}}_{{\rm{A}} + {\rm{B}}}^{\rm{T}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\left. {{\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{d}}\left( {{\rm{A}} + {\rm{B}}} \right)}}} \right]^{ - 1}}{\mathit{\boldsymbol{G}}_{{\rm{A}} + {\rm{B}}}}{\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{m}}\left( {{\rm{A}} + {\rm{B}}} \right)}} \end{array} $ | (14) |
式中:mprior(A+B)和dobs(A+B)均为(NA+NB)维列向量,NA、NB分别为邻域内A、B类数据的采样点数;Cm(A+B)和Cd(A+B)分别为(NA+NB)2维模型协方差矩阵和数据协方差矩阵,表达式为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{m}}\left( {{\rm{A}} + {\rm{B}}} \right)}} = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{m}}{\rm{AA}}}}}&{{\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{m}}{\rm{AB}}}}}\\ {\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{m}}{\rm{AB}}}^{\rm{T}}}&{{\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{m}}{\rm{BB}}}}} \end{array}} \right]\\ {\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{d}}\left( {{\rm{A}} + {\rm{B}}} \right)}} = \left[ {\begin{array}{*{20}{c}} {\bf{0}}&{\bf{0}}\\ {\bf{0}}&{{\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{d}}{\rm{BB}}}}} \end{array}} \right] \end{array} \right. $ | (15) |
式中:CmAA、CmBB分别为A、B类数据的模型协方差矩阵;CmAB为A、B类数据的互协方差矩阵;CdBB为B类数据的数据协方差矩阵。在Cd(A+B)中,假设A类数据为准确值,并假设A、B两类数据的误差不相关,因此A类数据的协方差矩阵和两类数据的互协方差矩阵都为0。
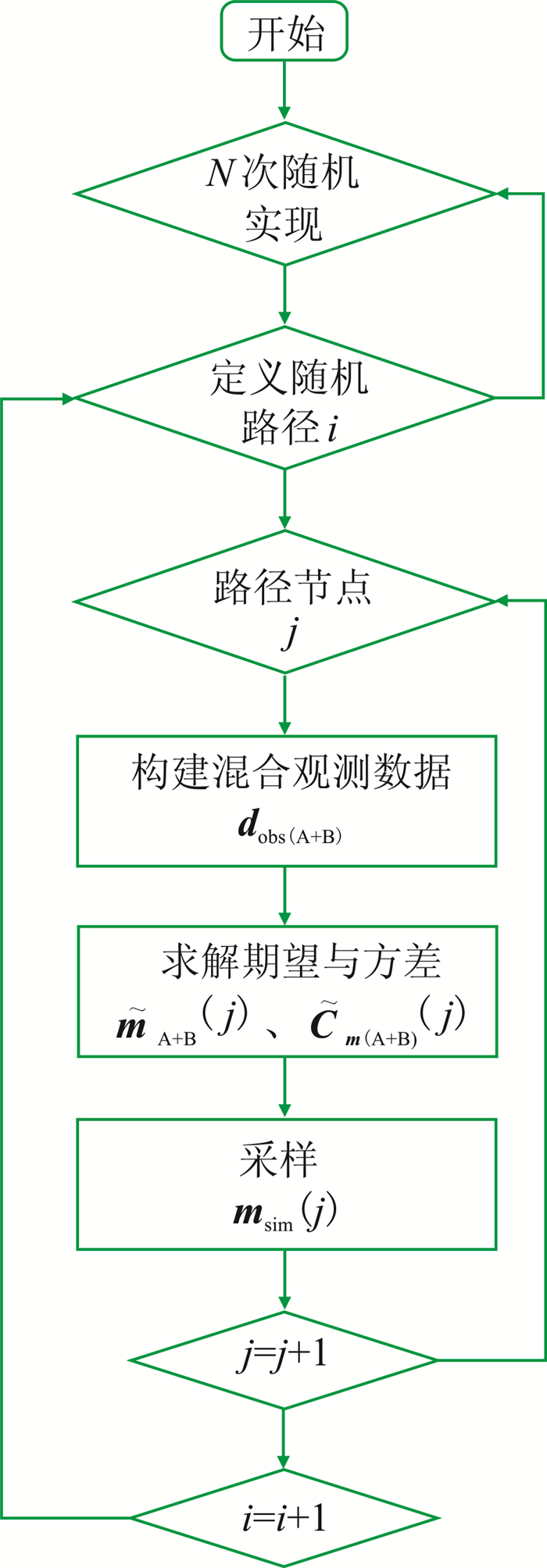
|
图 1 算法流程 图中 |
为了验证贝叶斯序贯随机反演算法的有效性,利用无条件序贯高斯随机模拟算法生成一个二维薄互层波阻抗模型,作为实际地下地层的参考模型,并且从二维模型中抽取一道作为测井数据,即A类数据(图 2)。
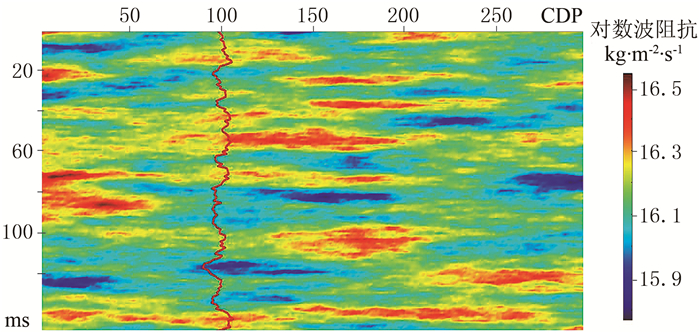
|
图 2 合成波阻抗参考模型 模型共301道, 道间距为10m, 纵向采样点数为150,采样间隔为1ms。对数波阻抗均值为16.15kg·m-2·s-1,方差为0.01(kg·m-2·s-1)2,水平变差函数变程为1000m(或100道),垂直变差函数变程为10ms(或10个采样点),设置变差函数为球状变差函数 |
图 3为根据图 2生成的合成地震记录与常数背景初始模型,其中合成地震记录(图 3a)作为B类数据,常数背景模型(图 3b)在地质统计学模拟中作为全局期望,在地震反演中作为反演初始模型。以合成地震记录(图 3a)中的测井数据(A类)和地震数据(B类)作为观测数据,分别进行B类数据最小二乘法确定性反演、A类数据序贯高斯模拟及A、B两类数据联合贝叶斯序贯反演测试,分析贝叶斯序贯反演方法的优势。图 4为地震数据(B类)最小二乘法反演结果,反演输入数据只有地震数据dobsB和地震数据协方差矩阵Cd,此时的最小二乘解为
| $ {\mathit{\boldsymbol{m}}_{{\rm{LSI}}}} = {\mathit{\boldsymbol{m}}_0} + {\mathit{\boldsymbol{G}}^{\rm{T}}}{\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{G}}^{\rm{T}}} + {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{d}}}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{d}}_{{\rm{obsB}}}} - \mathit{\boldsymbol{G}}{\mathit{\boldsymbol{m}}_0}} \right) $ | (16) |
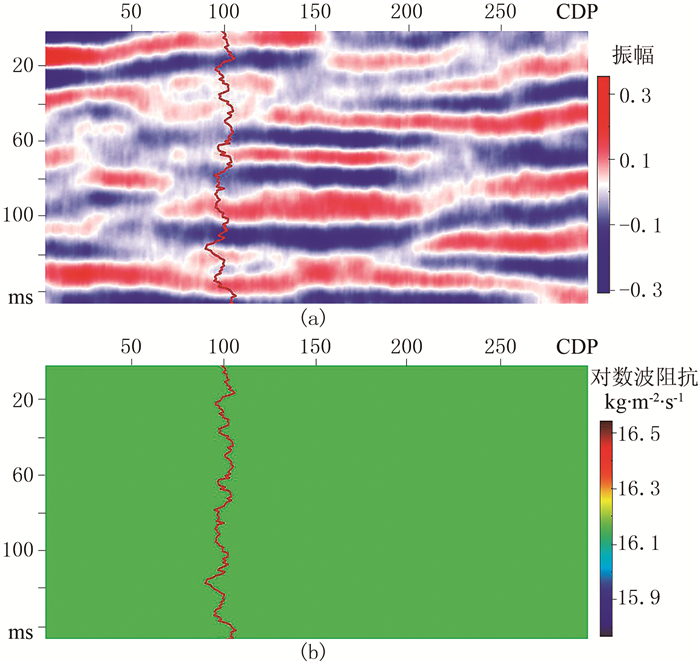
|
图 3 根据图 2生成的合成地震记录(a)与常数背景初始模型(b) 子波选用主频30Hz的雷克子波,并且在合成地震记录中添加了10%的高斯相关噪声 |
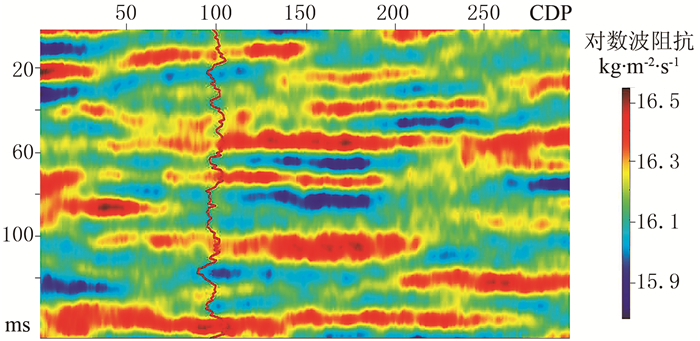
|
图 4 地震数据(B类)最小二乘法反演结果 |
由图 4可见,与实际波阻抗参考模型(图 2)相比,最小二乘反演结果的纵向分辨率与地震资料相当,只能反映参考模型中参数的变化趋势,不能刻画测井曲线的细节。事实上,最小二乘反演为一种过度光滑的估计方法,而且没有添加先验信息约束,反演结果仅依赖地震资料,因此反演结果分辨率低。
图 5为测井数据(A类)序贯高斯模拟2次实现结果,反演输入数据只有测井数据dobsA和模型协方差矩阵Cm。由图 5可见:模拟结果的分辨率与参考模型(图 2)相当,且在井点处的结果与测井资料完全吻合;由于缺乏地震数据约束,模拟结果的不确定性高(图 5箭头处),2次实现结果的差别非常大。因此在缺乏井资料时,传统的地质统计学方法不适用于井间模型参数预测。
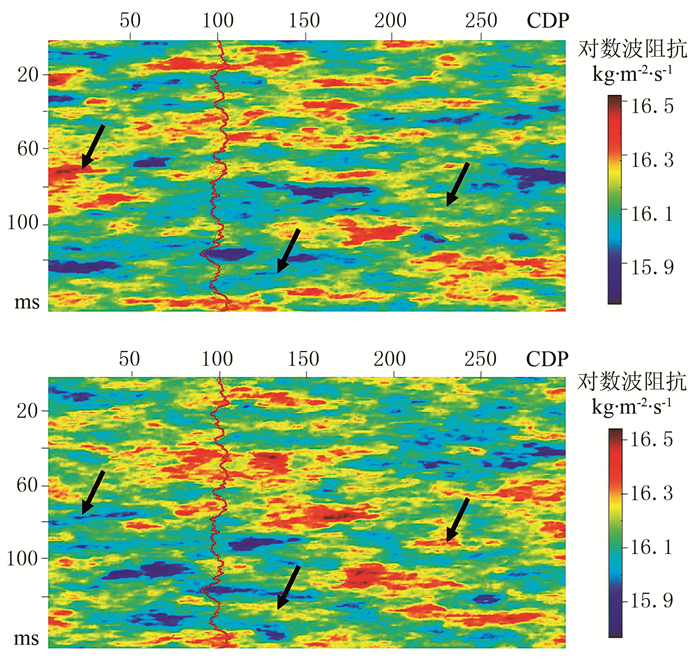
|
图 5 测井数据(A类)序贯高斯模拟2次实现结果 |
图 6为井震联合(A+B类)数据贝叶斯序贯反演3次实现结果,输入数据为模型协方差矩阵Cm和数据协方差矩阵Cd。由图 6可见,3次实现的分辨率与参考模型(图 2)相当,不仅在井点处与测井曲线完全吻合,且降低了实现结果的不确定性(图 6箭头处),3次实现结果整体特征相似,反映了地震数据约束的一致性;在小尺度条件下,3次反演结果间具有微小的差异,这种差异反映了不确定的地下介质非均质性。
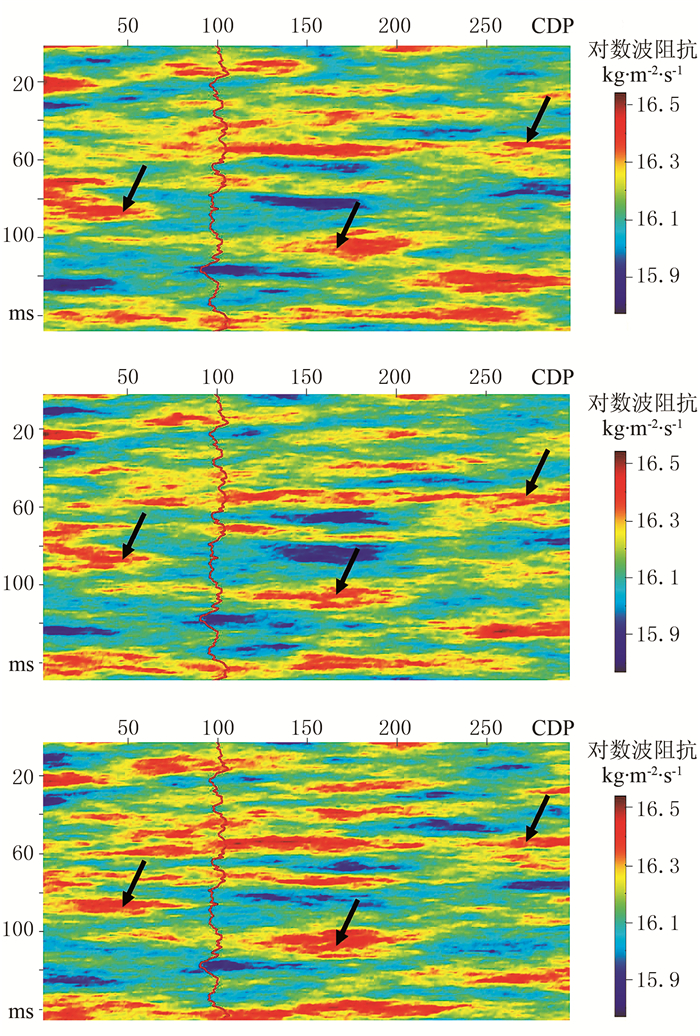
|
图 6 井震联合(A+B类)数据贝叶斯序贯反演3次实现结果 |
图 7为不同结果合成地震记录与实际地震记录残差。由图可见:最小二乘反演结果(图 7b)和序贯高斯模拟(图 7c)的残差均与实际噪声(图 7a)相差较大,其中后者与实际噪声的差异更大,而前者逐道反演的痕迹明显,反映了没有利用模型参数横向相关性的缺点;贝叶斯序贯反演结果的残差(图 7d)与实际地震噪声(图 7a)在幅度和形态上较接近(图 7a和图 7d箭头处)。上述结果表明,井震联合数据贝叶斯序贯反演方法得到的模型参数精度最高。
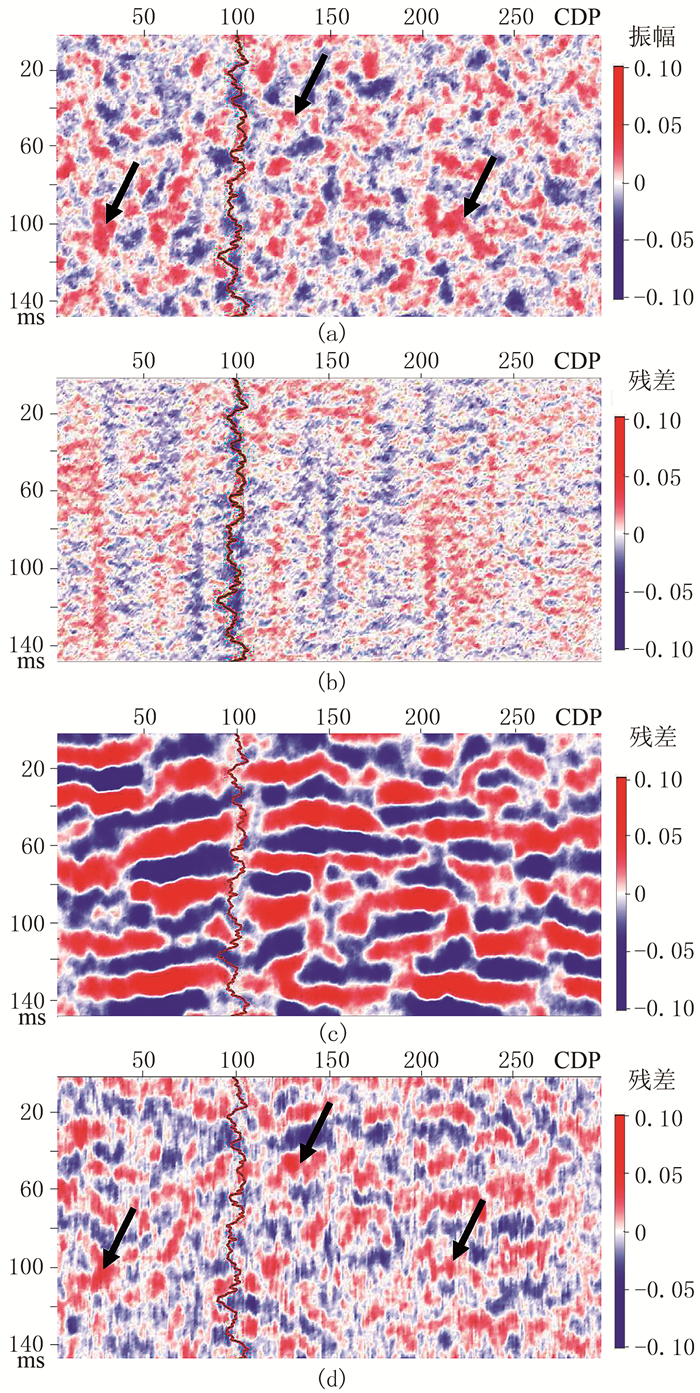
|
图 7 不同结果合成地震记录与实际地震记录残差 (a)实际噪声;(b)最小二乘反演;(c)序贯高斯模拟;(d)贝叶斯序贯反演 |
图 8为水平、垂直方向反演结果变差函数。由图可见:由于A+B类数据贝叶斯序贯反演过程使用了模型的空间结构信息Cm,因此所得水平、垂直变差函数均与参考模型变差函数匹配较好,其中水平方向变程约为1000m(图 8a),垂直方向变程约为10ms(图 8b);最小二乘反演结果(B类)由于没有利用模型参数的空间结构信息,反演结果的水平(图 8a)、垂直(图 8b)变差函数与参考模型变差函数差别较大。
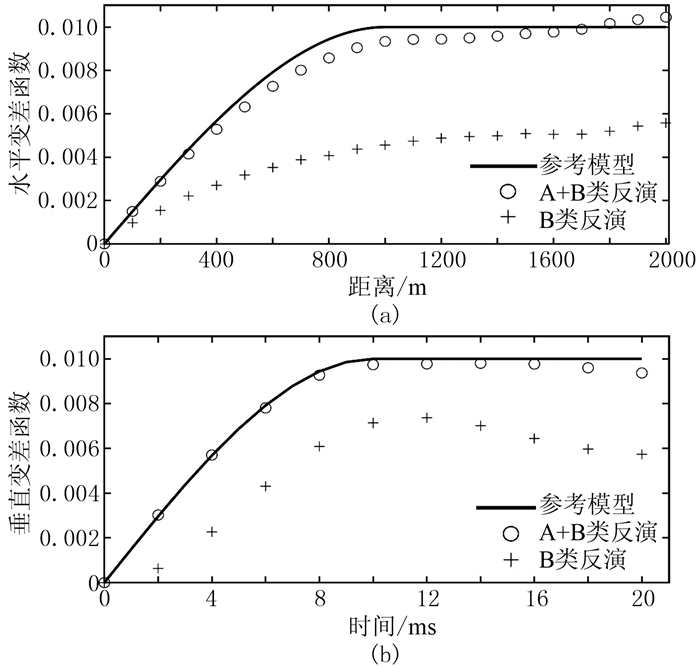
|
图 8 水平(a)、垂直(b)方向反演结果变差函数 |
模型测试分析结果表明,贝叶斯序贯随机反演方法采用邻域思想将高维数据降维处理,适用于任意的高维数据反演,同时能够克服最小二乘法反演的光滑效应以及序贯高斯模拟不确定性大的问题,可获得高分辨率且相对稳定的反演结果。
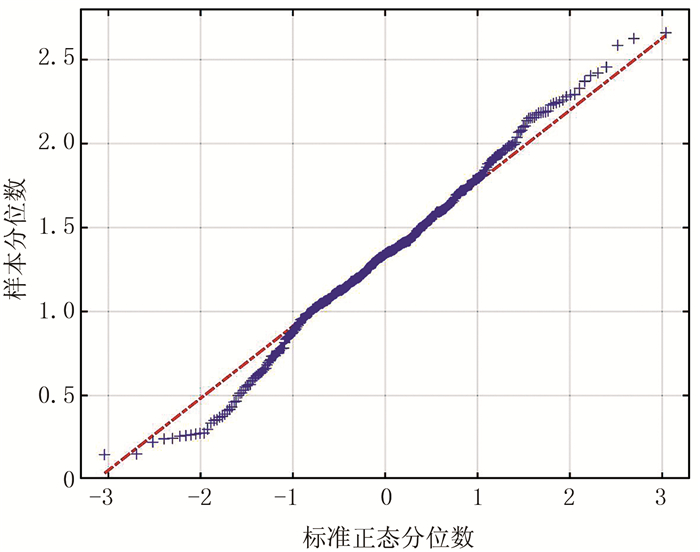
3 实际应用为了进一步检验贝叶斯序贯随机反演方法的实际应用效果,以中国东海盆地西湖凹陷N井区进行试验,试验数据来自一条过井三维地震剖面(图 9),其中测井合成地震记录与实际井旁道对应较好(图 9箭头处)。图 10为W1井对数域弹性参数正态分布检验Q-Q图。由图可见,数据点基本位于正态分布参考线之上,表明贝叶斯序贯随机反演方法对于研究区的适用性。

|
图 9 实际地震剖面与测井合成记录标定 纵向时间采样间隔为1 ms,采样点数为620个,道间距为25 m,共400道,地震资料主频为32 Hz。黑色曲线为井震标定后的测井合成地震记录,测井合成记录选用主频为32 Hz的雷克子波 |
|
图 10 W1井对数域弹性参数正态分布检验Q-Q图 |
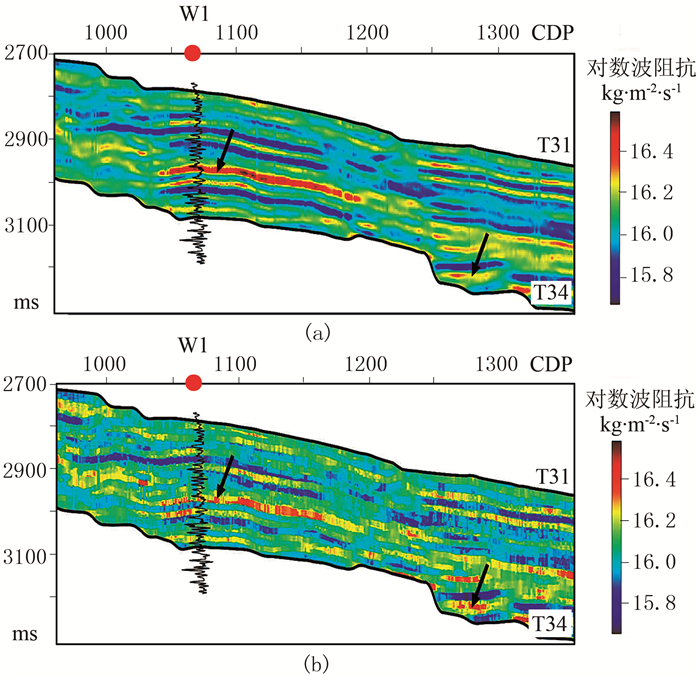
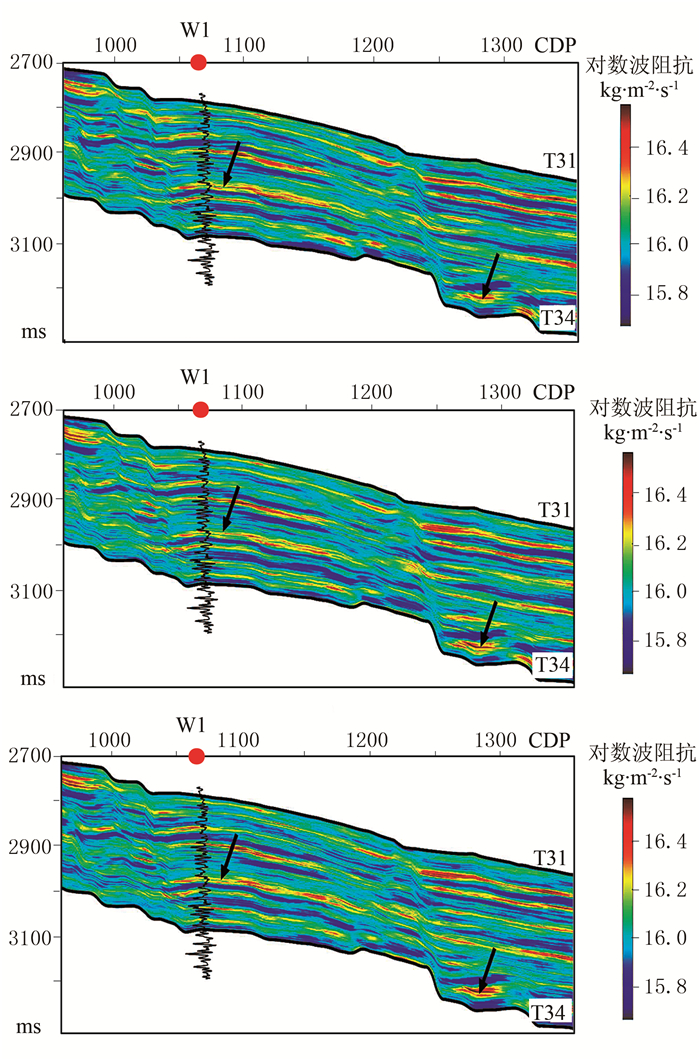
图 11为模型法、稀疏脉冲法对图 9的反演结果,图 12为贝叶斯序贯随机反演3次实现结果。由图可见,3种反演方法得到的波阻抗剖面在整体上具有相似性,但模型法反演结果在纵向上更光滑(图 11a黑色箭头处),稀疏脉冲法反演结果则展示了一个更“块状”化的结果(图 11b黑色箭头处),贝叶斯序贯随机反演方法则提供了多个与井曲线分辨率相当的反演结果(图 12)。
|
图 11 模型法(a)、稀疏脉冲法(b)对图 9的反演结果 |
|
图 12 贝叶斯序贯随机反演3次实现结果 利用贝叶斯序贯随机反演方法对图 9进行了100次随机实现 |
事实上,之所以产生上述反演结果是由采用的反演方法决定的。模型法反演直接对低频初始模型进行迭代扰动,当正演模拟数据与观测数据达到一定的匹配标准时停止迭代;稀疏脉冲反演是在反射系数稀疏准则的约束下,对地震资料反褶积获得宽带反射系数,然后再通过递推等算法获得绝对阻抗;贝叶斯序贯随机反演将测井数据和已模拟点作为硬数据,在地质统计信息和地震数据的共同约束下,参与计算下一个点,因此测井信息在遍历随机路径的过程中得到传播,从而使反演结果具有高分辨率特征,且横向变化特征清晰、自然。
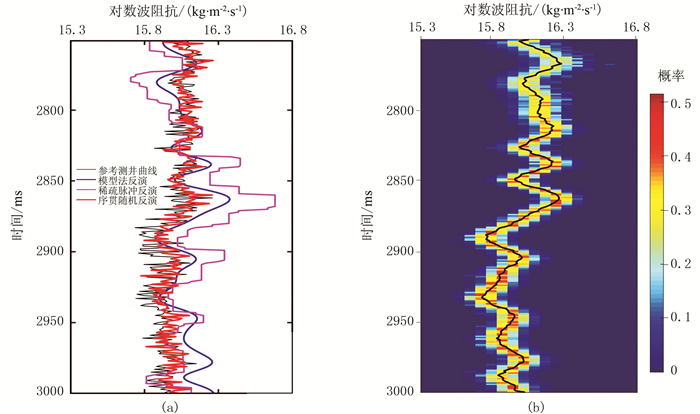
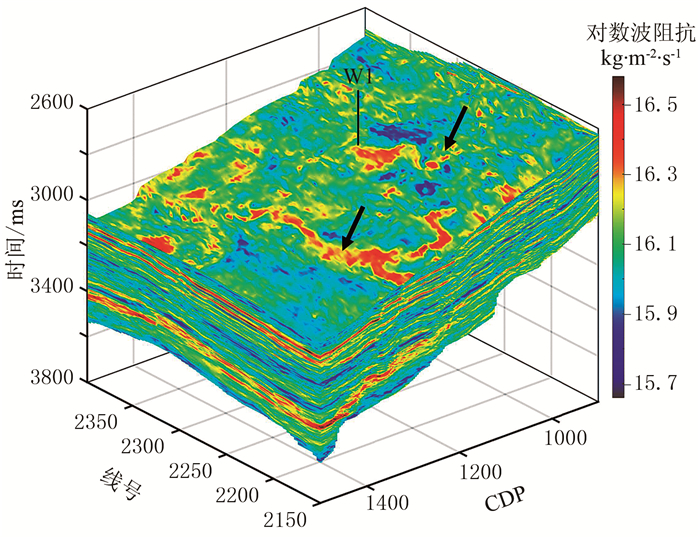
图 13为盲井反演结果、序贯随机反演概率解。由图可见:在恢复井曲线波阻抗的中低频相对变化时,3种方法给出了等价结果,而序贯随机反演方法则展示了更高频的阻抗变化细节(图 13a);对比概率分布与真实井曲线,能够获得在当前数据条件下反演结果的不确定性程度(图 13b)。模型法反演与稀疏脉冲反演这类确定性反演方法,由于只能给出一个唯一解,无法评价反演结果的不确定性与风险,而风险评估在勘探决策中具有重要作用,这是利用贝叶斯序贯随机反演方法进行地质解释的另一优势。图 14为三维贝叶斯序贯随机反演最大后验解。由图可见,沿目的层顶界切片明显展示了两条河道特征(图中箭头处),与研究区三角洲前缘水下分流河道沉积背景相符合。
|
图 13 盲井反演结果(a)、序贯随机反演概率解(b) 图b的黑色实线是100次随机反演实现的平均 |
|
图 14 三维贝叶斯序贯随机反演最大后验解 |
本文采用高分辨率贝叶斯波阻抗序贯随机反演方法,在贝叶斯理论框架下整合地震数据、测井数据和地质空间结构先验信息,并且将线性反演理论与克里金算法相联系,采用序贯模拟方法高效随机实现后验概率分布。数值算例表明:与常规波阻抗最小二乘法反演相比,该方法分辨率高、反演结果受先验统计学参数约束,且输出的多个波阻抗反演实现可用于不确定性评价;与纯粹基于测井数据的序贯高斯随机模拟方法相比,该方法最大的优点就是考虑了地震数据约束,降低了反演结果的不确定性。针对实际数据,对比、分析了模型法反演、稀疏脉冲法反演、贝叶斯序贯随机反演结果,表明贝叶斯序贯随机反演方法在提高反演纵向分辨率与不确定性评价方面具有良好的应用前景。
| [1] |
Lindseth R O. Synthetic sonic logs-a process for stratigraphic interpretation[J]. Geophysics, 1979, 44(1): 3-26. DOI:10.1190/1.1440922 |
| [2] |
Pendrel J. Seismic inversion-still the best tool for re-servoir characterization[J]. CSEG Recorder, 2006, 31(1): 5-12. |
| [3] |
Yuan S Y, Wang S X, Luo C, et al. Simultaneous multitrace impedance inversion with transform-domain sparsity promotion[J]. Geophysics, 2015, 80(2): R71-R80. DOI:10.1190/geo2014-0065.1 |
| [4] |
Luo Y N, Huang H D, Yang Y D, et al. Deepwater reservoir prediction using broadband seismic-driven impedance inversion and seismic sedimentology in the South China Sea[J]. Interpretation, 2018, 6(4): O17-O29. DOI:10.1190/INT-2018-0029.1 |
| [5] |
Yuan S Y, Wang S X, Luo Y N, et al. Impedance inversion by using the low-frequency full-waveform inversion result as an a priori model[J]. Geophysics, 2019, 84(2): R149-R164. DOI:10.1190/geo2017-0643.1 |
| [6] |
Francis A. Limitations of deterministic and advanta-ges of stochastic seismic inversion[J]. CSEG Recorder, 2005, 30(2): 5-11. |
| [7] |
Bosch M, Mukerji T, Gonzalez E F. Seismic inversion for reservoir properties combining statistical rock physics and geostatistics:a review[J]. Geophysics, 2010, 75(5): A165-A176. |
| [8] |
Cooke D, Cant J. Model-based seismic inversion:com-paring deterministic and probabilistic approaches[J]. CSEG Recorder, 2010, 35(4): 28-39. |
| [9] |
Ulrych T J, Sacchi M D, Woodbury A. A Bayes tour of inversion:a tutorial[J]. Geophysics, 2001, 66(1): 55-69. DOI:10.1190/1.1444923 |
| [10] |
Valentine A P, Sambridge M. Optimal regularization for a class of linear inverse problem[J]. Geophysical Journal International, 2018, 215(2): 1003-1021. DOI:10.1093/gji/ggy303 |
| [11] |
Cooke D A, Schneider W A. Generalized linear inversion of reflection seismic data[J]. Geophysics, 1983, 48(6): 665-676. DOI:10.1190/1.1441497 |
| [12] |
刘百红, 李建华, 郑四连. 应用近似L0范数的稀疏脉冲反演[J]. 石油地球物理勘探, 2018, 53(5): 961-968. LIU Baihong, LI Jianhua, ZHENG Silian. Seismic sparse spike inversion based on L0 norm approximation[J]. Oil Geophysical Prospecting, 2018, 53(5): 961-968. |
| [13] |
Tarantola A. Inverse Problem Theory[M]. Philadelphia: The Society for Industrial and Applied Mathematics, 2005.
|
| [14] |
Scales J A, Tenorio L. Prior information and uncer-tainty in inverse problems[J]. Geophysics, 2001, 66(2): 389-397. DOI:10.1190/1.1444930 |
| [15] |
Fournier A, Mosegaard K, Omre H, et al. Assessing uncertainty in geophysical problems-Introduction[J]. Geophysics, 2013, 78(3): B1-B2. |
| [16] |
Zhang R, Sen M K, Phan S, et al. Stochastic and deterministic seismic inversion methods for thin-bed resolution[J]. Journal of Geophysics and Engineering, 2012, 9(5): 611-618. |
| [17] |
Yin X Y, Sun R Y, Wang B L, et al. Simultaneous inversion of petrophysical parameters based on geostatistical a priori information[J]. Applied Geophysics, 2014, 11(3): 311-320. DOI:10.1007/s11770-014-0445-1 |
| [18] |
郭同翠, 姜明军, 纪迎章, 等. 叠前地质统计学反演在页岩甜点和薄夹层预测中的应用——以西加拿大盆地W区块为例[J]. 石油地球物理勘探, 2020, 55(1): 167-175. GUO Tongcui, JIANG Mingjun, JI Yingzhang, et al. The application of prestack geostatistical inversion in the prediction of shale sweet spots and thin interbeds:a case study of Block W in Western Canada Basin[J]. Oil Geophysical Prospecting, 2020, 55(1): 167-175. |
| [19] |
Haas A, Dubrule O. Geostatistical inversion-a sequential method of stochastic reservoir modelling constrained by seismic data[J]. First Break, 1994, 12(11): 561-569. |
| [20] |
Mariethoz G, Caers J. Multiple-Point Geostatistics:Stochastic Modeling with Training Images[M]. United Kingdom: John Wiley & Sons, 2015.
|
| [21] |
Cordua K S, Hansen T M, Gulbrandsen M L, et al. Mixed-point geostatistical simulation:A combination of two and multiple-point geostatistics[J]. Geophysical Research Letters, 2016, 43(17): 9030-9037. DOI:10.1002/2016GL070348 |
| [22] |
González E F, Mukerji T, Mavko G. Seismic inversion combining rock physics and multiple-point geostatistics[J]. Geophysics, 2007, 73(1): R11-R21. |
| [23] |
Journel A, Zhang T. The necessity of a multiple-point prior model[J]. Mathematical Geology, 2007, 38(5): 591-610. DOI:10.1007/s11004-006-9031-2 |
| [24] |
罗红梅, 杨培杰, 王长江, 等. 基于多点地质统计学多数据联合约束的岩相模拟[J]. 石油地球物理勘探, 2015, 50(1): 162-169. LUO Hongmei, YANG Peijie, WANG Changjiang, et al. Lithofacies simulation based on multi-point geostatistics multiple data joint constraints[J]. Oil Geophy-sical Prospecting, 2015, 50(1): 162-169. |
| [25] |
Larsen A L, Ulvmoen M, Omre H, et al. Bayesian lithology/fluid prediction and simulation on the basis of a Markov-chain prior model[J]. Geophysics, 2006, 71(5): R69-R78. DOI:10.1190/1.2245469 |
| [26] |
田玉昆, 周辉, 袁三一. 基于马尔科夫随机场的岩性识别方法[J]. 地球物理学报, 2013, 56(4): 1360-1368. TIAN Yukun, ZHOU Hui, YUAN Sanyi. Lithologic discrimination method based on Markov random-field[J]. Chinese Journal of Geophysics, 2013, 56(4): 1360-1368. |
| [27] |
刘兴业, 李景叶, 陈小宏, 等. 联合多点地质统计学与序贯高斯模拟的随机反演方法[J]. 地球物理学报, 2018, 61(7): 2998-3007. LIU Xingye, LI Jingye, CHEN Xiaohong, et al. A stochastic inversion method integrating multi-point geostatistics and sequential Gaussian simulation[J]. Chinese Journal of Geophysics, 2018, 61(7): 2998-3007. |
| [28] |
Buland A, Omre H. Bayesian linearized AVO inver-sion[J]. Geophysics, 2003, 68(1): 185-198. DOI:10.1190/1.1543206 |
| [29] |
Russell B H. Introduction to Seismic Inversion Me-thods[M]. Tulsa: Society of Exploration Geophysicists, 1988.
|
| [30] |
Luo Y, Huang H, Yang Y, et al. Integrated prediction of deepwater gas reservoirs using Bayesian seismic inversion and fluid mobility attribute in the South China Sea[J]. Journal of Natural Gas Science and Engineering, 2018. DOI:10.1016/j.jngse.2018.08.019 |
| [31] |
杨晓, 祝厚勤, 王彦飞. 弹性阻抗反演的后验正则化方法[J]. 石油地球物理勘探, 2018, 53(4): 791-797. YANG Xiao, ZHU Houqin, WANG Yanfei. A posteriori regularization method for elastic impedance inversion[J]. Oil Geophysical Prospecting, 2018, 53(4): 791-797. |
| [32] |
Mosegaard K, Hansen T M. Inverse Methods:Problem Formulation and Probabilistic Solutions[M]. New Jersey: John Wiley & Sons, 2016.
|
| [33] |
Hansen T M, Journel A G, Tarantola A, et al. Linear inverse Gaussian theory and geostatistics[J]. Geophysics, 2006. DOI:10.1190/1.2345195 |
| [34] |
Bosch M. The optimization approach to lithological tomography:combining seismic data and petrophysics for porosity prediction[J]. Geophysics, 2004, 69(5): 1272-1282. DOI:10.1190/1.1801944 |
| [35] |
Bosch M, Cara L, Rodrigues J, et al. A Monte Carlo approach to the joint estimation of reservoir and elastic parameters from seismic amplitudes[J]. Geophy-sics, 2007, 72(6): O29-O40. |
| [36] |
Sambridge M, Mosegaard K. Monte Carlo methods in geophysical inverse problems[J]. Reviews of Geophysics, 2002, 40(3): 1-3. |



 李祺鑫, 北京市朝阳区太阳宫南街6号中海油研究总院, 100028。Email:
李祺鑫, 北京市朝阳区太阳宫南街6号中海油研究总院, 100028。Email: