2 中国石化胜利油田工程有限公司钻井工艺研究院, 山东东营 257000
2 Drilling Technology Research Institute of Shengli Petroleum Engineering Corporation Limited, SINOPEC, Dongying, Shandong 257000, China
孔隙度是储层评价、油气预测的重要参数[1-2]。孔隙度不仅受控于岩石的孔隙结构,还与岩石的颗粒组分密切相关[3],这为利用岩相作为约束条件准确预测孔隙度提供了可靠依据[4-7]。
许多学者以岩石物理特征为基础,利用地震反演方法预测储层参数[8-10]。随着人工智能和机器学习技术的快速发展,多种分类、回归、聚类算法也被应用于储层参数预测。早期学者多利用统计学方法,如朴素贝叶斯分类器[11]、模糊逻辑[12]、支持向量机[13]等分析测井相。在地震属性数据基础上,张阳等[14]提出模糊C均值地震属性聚类的沉积相分析方法,庞锐等[15]利用K均值聚类进行地震相识别。在储层参数预测中,应用较为广泛的是神经网络[16-17]算法;其他的回归算法,如支持向量回归(SVR)[18]、K近邻法[19]、随机森林[20-21]等也被应用于储层预测。
由Zhang等[22]提出的BIRCH(Balanced Iterative Reducing and Clustering Using Hierarchies)方法是一种基于距离的无监督学习层次聚类算法,计算效率较高。邵峰晶等[23]提出了可变多阈值聚类(Multi-threshold BIRCH Clustering,M-BIRCH)方法实现了对任意形状簇的聚类。本文在考虑计算机系统内存以及聚类质量等因素,通过启发式设定阈值,并基于Agglomerative算法[24]的全局聚类进一步优化该算法,以井点处孔隙度数据和地震声波阻抗属性作为输入,确定岩相类型;然后在同一相带内使用岭回归(Ridge Regression, RR)方法预测储层孔隙度,以提高预测精度。
1 多阈值BIRCH聚类分析 1.1 BIRCH聚类原理BIRCH算法是将数据集中的样本划分为多个不相交的类,并且这些类具有类内对象相似、类间对象相异的特点。每个类可表示一种相,称为“簇”。基于距离度量的算法能够发现具有相近尺度和密度的球状簇。
BIRCH算法可通过聚类特征(CF)对地震属性进行聚类。以波阻抗数据为例,假设在某个簇中存在N个波阻抗样本{xi},i=1,2,…,N,将聚类特征定义为三元组
| $ \mathrm{CF}=(N, \mathrm{LS}, \mathrm{SS}) $ | (1) |
式中:N为簇中波阻抗样本的数量;LS为N个波阻抗样本的线性和,即
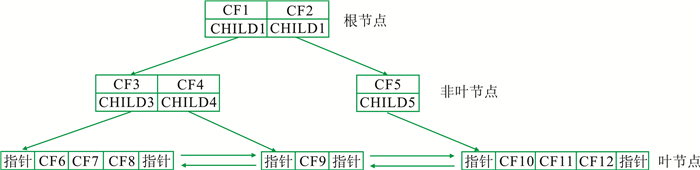
聚类特征树(CF树)用于存储层次聚类的簇的特征,是一棵高度平衡树,即它的子树的高度差的绝对值不超过1,并且所有子树都是一棵平衡树。CF树中的非叶子节点存储了其子节点的聚类特征的总和,其中节点的每个聚类特征和它指向子节点的指针组成条目。CF树具有三个参数:分支因子的非叶节点数B、叶节点数L和簇半径阈值T。其中,B是特征树中每个非叶节点最多包含的子节点的数量,L是每个叶节点最多包含的CF向量的数量,T为同一叶子节点中的数据点满足的阈值。图 1给出B=2、L=3的CF树结构示例。
|
图 1 CF树结构示例B=2,L=3 |
由于BIRCH算法忽视了簇与簇之间的关系,对叶子节点中的簇设定同一阈值,因而聚类效果不稳定且有一定局限性。多阈值BIRCH聚类方法是对每个聚类特征都设定一个阈值T,即将每个簇的CF三元组改为四元组(N,LS,SS,T),每个簇可以具有不同的阈值。在CF树重建过程中,当两个簇需要合并为一个簇时,新簇的阈值由合并定理求取。
合并定理为:假定将n个簇Ci(i=1,2,…,n)合并,聚类特征CFi=(Ni,LSi,SSi,Ti),合并后新簇W的聚类特征为
| $ \left\{\begin{array}{l} N=\sum\limits_{i=1}^{n} N_{i} \\ \mathrm{LS}=\sum\limits_{i=1}^{n} \mathrm{LS}_{i} \\ \mathrm{SS}=\sum\limits_{i=1}^{n} \mathrm{SS}_{i} \\ T=\max \left[\operatorname{dist}\left(W . \operatorname{mean}, C_{i} . \text { mean }\right)+T_{i}\right] \end{array}\right. $ | (2) |
式中:Ci.mean、W.mean分别表示簇Ci、新簇W的质心;dist(W.mean,Ci.mean)为簇间距离,计算公式为
| $ \operatorname{dist}=\sqrt{\frac{\mathrm{SS}_{1}}{N_{1}}+\frac{\mathrm{SS}_{2}}{N_{2}}-\frac{2 \mathrm{LS}_{1} \times \mathrm{LS}_{2}}{N_{1} N_{2}}} $ | (3) |
式中:SS1、LS1、N1表示簇C的三元组;SS2、LS2、N2表示簇W的三元组。
根据式(2),通过簇的聚类特征计算簇间距离,动态调整、增加阈值T。阈值的提升使原始CF树中的条目进一步合并,进而重建一棵较小的CF树。调整后的阈值不仅包括原有簇的所有波阻抗样本,而且大大增加了新的波阻抗样本插入的可能性,最终产生基于不同阈值的聚类结果。
2 岭回归原理回归分析[26]是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。岭回归[27]是一种通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价获得回归系数的更符合实际、更可靠的回归分析方法,它对数据扰动敏感的病态矩阵的拟合要优于最小二乘法。
如果给出标签数据D={{xi, yi}:i=1, 2, …, m},其中:xi为波阻抗数据;yi为已知的孔隙度;m为样本点的个数。考虑线性回归问题f(xi; β)=
| $ \begin{aligned} \min _{\boldsymbol{\beta} \in \boldsymbol{R}^{p}} J(\boldsymbol{\beta})=& \min _{\boldsymbol{\beta} \in \boldsymbol{R}^{p}} \frac{1}{2 m}\left\{\sum\limits_{i=1}^{m}\left[y_{i}-\varepsilon-f\left(\boldsymbol{x}_{i} ; \boldsymbol{\beta}\right)\right]^{2}+\right.\\ &\left.\lambda\|\boldsymbol{\beta}\|^{2}\right\} \end{aligned} $ | (4) |
式中:λ是调节参数;Rp表示p维实数集。
岭回归的代价函数是一个凸函数,同最小二乘法一样,当代价函数梯度(即一阶导数)等于0时可求得全局最优解。由下式最终得到岭回归模型的最优系数向量
| $ \hat{\boldsymbol{\beta}}=\left(\boldsymbol{X}^{\mathrm{T}} \boldsymbol{X}+k \boldsymbol{I}\right)^{-1} \boldsymbol{X}^{\mathrm{T}} \boldsymbol{Y} $ | (5) |
式中k为岭参数。
3 相控孔隙度预测相控孔隙度预测是以沉积相及其特征等作为约束条件而降低储层孔隙度预测的多解性的一种技术。本文应用M-BIRCH方法对波阻抗数据聚类分析、划分岩相带,在此基础上应用岭回归方法对同一相带中的孔隙度与波阻抗建立回归关系,最终进行孔隙度的精确预测。
3.1 关键技术 3.1.1 初始阈值的设定根据M-BIRCH聚类过程,阈值是通过簇间距离进行更新的,即阈值的大小与簇间距离、类内平均距离相关,也就是说阈值的选择与波阻抗数据分布有关。本文采用启发式方法设定初始阈值,首先在整个数据集中随机选取N对波阻抗样本,将每一个样本都作为一个簇,根据簇的CF条目,利用式(3)计算簇之间的距离;然后计算距离(dist)的期望E(dist)和方差D(dist);最后设定初始阈值
| $ T=[E(\text { dist })+0.25 D(\text { dist })] P $ | (6) |
式中P为预先设定的百分比。
预先定义一个较小的P,通过较小的T对波阻抗数据进行分割。分割后的数据集通过提升阈值重新归并到较小的CF树,并将数据装入内存。在生成CF树的过程中,若出现内存不够的情况,可以通过提升P定义较大的初始阈值重建较小的CF树。计算初始阈值T后,就可以建立一棵初始CF树。
3.1.2 动态构建CF树CF树的构建是BIRCH聚类算法的关键。随着波阻抗数据的不断加入,将不断地重建CF树。波阻抗数据按照与各个CF的距离依次插入到各条目中合并为簇,这样距离相近的波阻抗将处于相同的簇中。不同的岩相带波阻抗存在差异,重建CF树能够不断地区分波阻抗数据,从而完成相带划分的目的。把每个波阻抗数据都看作为独立的簇,动态建立CF树的过程也就是将簇的聚类特征CF插入到CF树的过程,具体如下。
(1) 从根节点开始递归向下,通过计算CF与插入节点包含的各条目中CF的距离,寻找距离最短的路径及叶节点。
(2) 如果CF与该叶节点各条目中的CF之间的距离小于阈值T,则选择阈值最小的条目,用合并算法将CF与该条目的CF合并,并自下向上相应地修改各节点的条目。
(3) 如果CF无法与该条目的CF合并,则判断该条目所在叶节点的CF数量是否小于L。若小于L,则将CF新建为一个条目,并将该条目插入到距离最近的条目后面,相应修改CF树的结构。否则分裂该叶节点,原则是以距离最远的两个条目为种子进行分裂,剩余的条目按照距离最近原则合并到这两个条目中,并更新整个CF树。
3.1.3 全局聚类对CF使用聚类算法进行全局聚类,能够得到较好的聚类效果[22]。本文使用层次聚类算法中的凝聚法,即Agglomerative算法[24]。这是一种自底向上的方法,不需要求取目标函数,即不存在局部最小和对初始点敏感的问题。其算法描述如下。
输入:阻抗样本、聚类数目
输出:聚类结果
将每个阻抗样本都作为一个独立的簇;
重复:
计算两两簇之间的距离,找出距离最小的两个簇c1和c2;
将c1和c2合并为一个簇;
直到达到聚类数目或其他设定的条件结束。
3.1.4 优化岭参数当自变量之间存在线性关系时,自变量相关矩阵行列式近似为0,导致最小二乘估计失效。在岭回归训练过程中,通过选取合适的岭参数,可以减少这种多重共线性的影响。当X存在多重共线性时,矩阵XTX的特征值至少有一个接近于0,可用XTX行列式的值表示多重共线性的严重程度。因此,令
| $ D(k)=\operatorname{det}\left(\boldsymbol{X}^{\mathrm{T}} \boldsymbol{X}+k \boldsymbol{I}\right)=\prod\limits_{i=1}^{p}\left(\lambda_{i}+k\right) $ | (7) |
式中I为p×p的单位矩阵。由式(7)可知,D(k)随着k的增加而增大,当0 < D(k) < 0.001时,该模型具有严重共线性;当0.001 < D(k) < 0.01时,具有中等共线性;当0.01 < D(k) < 0.05时,具有轻微共线性;当D(k)>0.05时,几乎不具有共线性。因此,认定在D(k)>0.01的范围内将最小的k值作为最终的岭参数[28]。
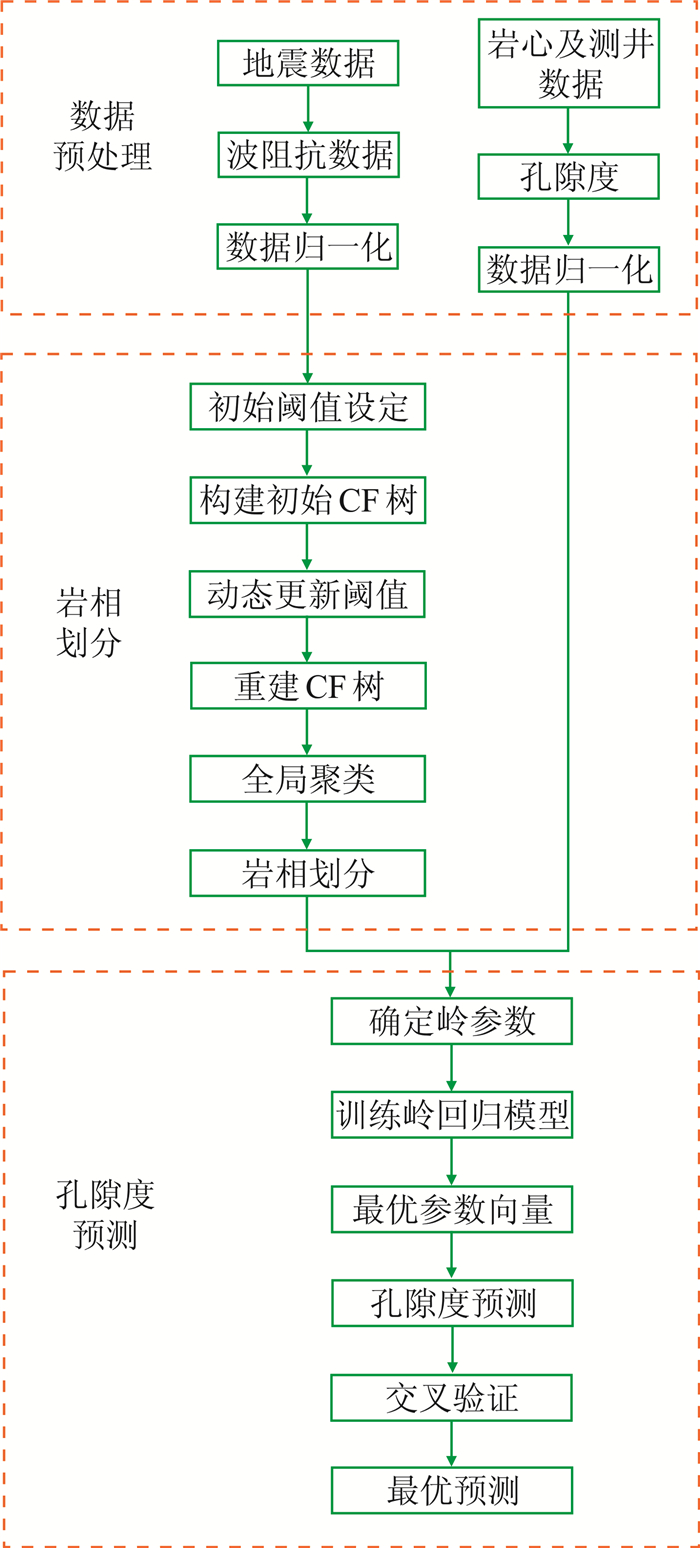
3.2 相控孔隙度预测流程相控孔隙度预测主要分为三个阶段。第一阶段为数据预处理,主要是对波阻抗数据网格化处理,并将波阻抗和孔隙度数据进行归一化;第二阶段为相带的划分,即使用波阻抗训练样本训练M-BIRCH模型,并将该数据划分为设定的类别数目,然后利用训练好的模型预测波阻抗数据的所属岩相类别;第三阶段为岭回归的训练与预测,即分别在每一类岩相内根据波阻抗数据分布初始化岭参数,然后利用井点处的孔隙度和波阻抗数据进行岭回归训练, 得到最优系数向量
|
图 2 相控孔隙度预测流程 |
在以地震、测井资料为基础的储层孔隙度预测中,首先需要对数据进行预处理,即对地震、测井数据反演得到波阻抗数据,通过岩心分析及测井解释得到井点孔隙度数据;然后将波阻抗和孔隙度数据进行归一化处理,使其处于同一数量级中,以便于分析。
M-BIRCH使用聚类特征CF表征一个簇,即划分岩相,并采用平衡树结构,能够满足数据的可伸缩性,处理大规模数据集速度较快。利用M-BIRCH聚类算法划分岩相可以归纳为三个步骤:第一步是扫描波阻抗数据,确定初始阈值,构造初始CF树,在CF树构造过程中,首先要确定两个参数,即非叶子节点数B和叶子节点数L,CF树的大小可以通过调节这两个参数进行调整;第二步是随着波阻抗数据的不断加入,重建CF树,并且动态更新阈值,在重建过程中,只通过叶节点重新构建一棵新树,并不需要重新访问所有数据[23];第三步是用CF代替原有数据集进行聚类。当CF树构建完成之后,选用Agglomerative算法对叶节点中的簇进行全局聚类。
在相带的约束下,利用井点处孔隙度与波阻抗数据进行非井点处的孔隙度预测。在每个相带内都会由岭回归计算得到最优参数估计量,在此基础上,由未标签波阻抗数据可计算得到孔隙度预测值。
利用交叉验证方法将井点处预测的孔隙度值与已知的孔隙度进行误差分析。本文采用交叉验证方法,即选择w-1口井的波阻抗和孔隙度数据作为训练集进行模型训练,一口井作为测试集验证模型及参数。这样循环w次,使每口井都作为测试集进行检验,最后选择损失函数评估最优的模型及参数。
3.3 算法效率分析M-BIRCH的核心在于第一步,即CF树建立,其余都是对聚类结果进行优化。使用M-BIRCH进行沉积相研究时,加入数据样本时的时间复杂度为
综上所述,应用M-BIRCH和RR方法预测孔隙度的时间复杂度为
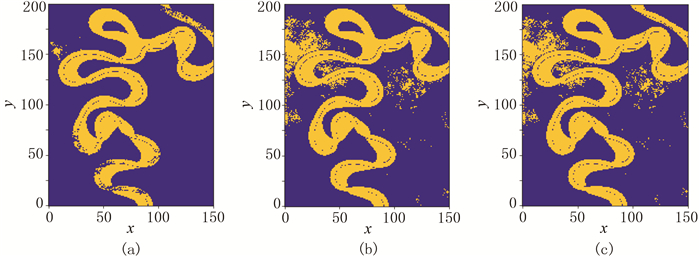
Stanford VI-E模型[29]包含三层前积型河道,三维地震数据具150×200×200个网格,每个网格的尺寸在水平(x和y)方向上均为25m,在垂直(z)方向上均为1m。本文实验采用第二层,即网格数为150×200×40。为了简化实验数据,将该系统中的点坝和河道砂体合并为砂岩相(图 3c中的黄色部分),将洪泛平原和边界合并为页岩相(图 3c中的蓝色部分)。
|
图 4 不同方法的岩相预测 (a)M-BIRCH方法;(b)BIRCH方法;(c)K-means方法 |

|
图 5 不同方法预测的孔隙度 (a)M-BIRCH+RR方法;(b)BIRCH+RR方法;(c)SVR方法;(d)K-means+RR方法 |

|
图 6 不同噪声情况下波阻抗切片(左)和本文方法预测的岩相(中)、孔隙度(右) (a)20%噪声;(b)40%噪声;(c)60%噪声;(d)80%噪声 |
图 3a为水平切片(网格数为150×200),即输入数据。图 3b显示孔隙度与波阻抗之间存在着负相关关系。但是,其相关系数和偏移量很大程度上依赖于不同岩相的不连续性,并且孔隙度在每个岩相带内具有低可变性。因此,一旦岩相结构已知,便可通过回归方法根据波阻抗估计孔隙度。
4.1.1 多阈值BIRCH+RR方法预测实验中,将15%的输入数据作为训练集,85%数据作为测试集。设定用于计算初始阈值的百分比P为0.1、非叶节点数B和叶节点数L均为30。图 4为图 3a作为输入的岩相预测。与图 3c相比,M-BIRCH比BIRCH[22]、K-均值(K-means)[15]方法能更准确识别河道。图 4a左上方实际为页岩相,但BIRCH、K-means方法却将其划分为砂岩相。
本文使用调整兰德系数(ARI)[30]进行量化描述。ARI用来描述数据分布的吻合程度,计算公式为
| $ \mathrm{ARI}=\frac{\mathrm{RI}-E(\mathrm{RI})}{\mathrm{MAX}(\mathrm{RI})-E(\mathrm{RI})} $ | (8) |
| $ \mathrm{RI}=\frac{a+b}{C_{n_{\mathrm{samples}}}^{2}} $ | (9) |
式中:RI是兰德指数;假设给定实际类别信息为U,V为聚类结果,a、b分别为在类别U与V中都是相同和不同类别的元素对个数;C2nsamples是数据集中可以组成的总元素对的个数,nsamples表示样本数量。ARI取值范围为[-1, 1],值越大意味着聚类结果与真实情况越吻合。
如表 1所示,M-BIRCH算法的ARI为0.95,明显优于另外两种算法的聚类效果。
|
|
表 1 不同方法预测相带的性能比较 |
图 5为不同方法预测的孔隙度。图 5c为使用SVR[31]回归方法进行的预测,即考虑只存在一种相带的情况。对比图 3d,可以看出图 5c中的孔隙度低值(蓝色部分)并没有拟合到真实的结果,因此相控法孔隙度预测结果比SVR方法预测结果更符合实际情况。
表 2为三种方法孔隙度预测的性能比较。M-BIRCH+RR(本文方法)预测结果的均方误差(MSE)以及平均绝对误差(MAE)最小,说明本文方法比另外三种方法预测精度高。从确定性相关系数(R2)也可得知,本文方法预测结果与实际结果匹配程度更高。另外,使用SVR方法预测结果的MSE达到0.92288,相对于M-BIRCH+RR、K-means+RR方法,SVR方法可行性不高,误差较大。从方法的运行效率来看,SVR方法虽然运行时间较短,但是最后结果不理想;K-means+RR方法的运行时间最长,但是精度不是最高;与BIRCH+RR相比,M-BIRCH+RR方法虽然牺牲时间效率,但效果更好(R2值高,MSE值低)。
|
|
表 2 不同方法孔隙度预测性能比较 |
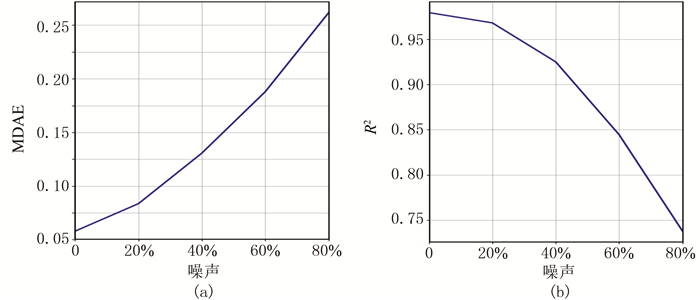
分别向波阻抗数据中输入0~80%的高斯噪声,利用M-BIRCH+RR方法预测岩相,最终得到孔隙度预测结果如图 6所示。当噪声不断增加时,对岩相划分结果影响不大,M-BIRCH方法仍能较准确地区分出砂岩相和页岩相。图 7a是在不同的高斯噪声下中位绝对误差(MDAE)的变化,可以看出MDAE随着高斯噪声线性增加。图 7b是在不同的高斯噪声下确定性相关系数的变化,R2随着高斯噪声的增加不断降低,即使高斯噪声达到80%,M-BIRCH+RR方法预测结果的R2仍能达到75%左右。因此,即使存在一定的噪声,仍然不影响其性能,说明本文方法具有较高稳定性和抗干扰能力。
|
图 7 本文方法灵敏度分析 (a)不同噪声时中位绝对误差;(b)不同噪声时确定性相关系数 |
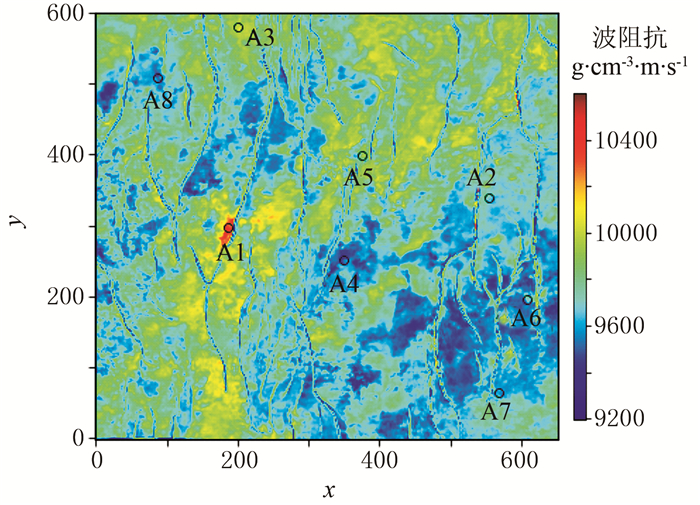
研究区主要为三角洲前缘沉积,分支河道砂体发育。目的层埋深大,压实作用强,岩性致密。研究区内共有8口井,有效储层预测难度大。针对上述难点,采用本文方法进行相控孔隙度预测。采用8口探井的岩心及测井资料作为标记样本,储层数据网格的尺寸在水平(x和y)方向上均为20m。选取其中一个时间切片(网格数为653×600)的波阻抗样本,如图 8所示。预测过程中,首先对波阻抗数据进行网格化处理,将井点处的孔隙度数据应用到离井点位置最近的网格点中,并对井点处孔隙度和阻抗数据进行归一化;然后采用本文方法进行岩相划分和孔隙度预测;最后采用交叉验证方法对预测结果进行误差分析,即利用7口井作为训练数据,剩余1口井作为验证数据。
|
图 8 波阻抗切片 |
预测结果如图 9所示。从图 9a可以看出,M-BIRCH方法根据波阻抗数据将储层划分为两类,黄色部分对应原始数据的高波阻抗值,蓝色对应低波阻抗值,较好地刻画了河道砂体的分布。孔隙度预测结果如图 9b所示。利用稀疏标记训练预测的孔隙度能够反映河道砂体横向展布规律,井点处结果与波阻抗分布、砂岩发育位置均有很好的对应关系,验证了本文方法的合理性。

|
图 9 实际地震数据预测结果 (a)M-BIRCH方法预测的岩相,黄色为页岩相;(b)M-BIRCH+RR方法预测的孔隙度 |
由三种方法在研究区的实验结果性能比较(表 3)可知,K-means+RR的性能最差,均方根误差最高,可靠性较差。相对而言,M-BIRCH+RR方法的MSE较BIRCH+RR方法、K-means+RR方法略小,说明M-BIRCH+RR方法是可靠的。
|
|
表 3 不同方法的性能比较 |
本文考虑不同岩相之间波阻抗数据的差异,提出一种多阈值BIRCH聚类的无监督学习方法,并引入Agglomerative算法进行全局聚类,得到准确的岩相预测结果;然后在岩相约束下以井点处的波阻抗和孔隙度为输入,采用优化的岭回归方法在同一岩相内进行孔隙度预测。模型数据实验表明,与其他划分岩相的传统聚类方法相比,M-BIRCH方法受异常数据的干扰较小、适应性更好、运行效率更高。实际数据应用表明,使用M-BIRCH算法与岭回归结合的方法对孔隙度预测能够得到合理且准确的结果。
| [1] |
Wang J, Cao Y C, Liu K Y, et al. Identification of se-dimentary-diagenetic facies and reservoir porosity and permeability prediction:An example from the Eocene beach-bar sandstone in the Dongying Depression, China[J]. Marine and Petroleum Geology, 2017, 82: 69-84. |
| [2] |
Miller K, Vanorio T, Yang S, et al. A scale-consistent method for imaging porosity and micrite in dual-porosity carbonate rocks[J]. Geophysics, 2019, 84(3): MR115-MR127. |
| [3] |
Álvarez P, Rangel J, Martinez M.Mapping porosity distribution in a vuggy carbonate reservoir integrating seismic attributes with borehole image logs through a supervised facies analysis[C].SEG Technical Program Expanded Abstracts, 2009, 28: 1880-1884.
|
| [4] |
Ashraf U, Zhu P M, Yasin Q, et al. Classification of reservoir facies using well log and 3D seismic attributes for prospect evaluation and field development:A case study of Sawan gas field, Pakistan[J]. Journal of Petroleum Science and Engineering, 2019, 175: 338-351. |
| [5] |
Xu Y, Yang H, Liu Y, et al. Application of seismic facies and attributes analysis on the identification of Permian igneous rock[J]. International Journal of Mining Science and Technology, 2012, 22(4): 471-475. |
| [6] |
朱超, 刘占国, 杨少勇, 等. 利用相控分频反演预测英西湖相碳酸盐岩储层[J]. 石油地球物理勘探, 2018, 53(4): 832-841. ZHU Chao, LIU Zhanguo, YANG Shaoyong, et al. Lacustrine carbonate reservoir prediction in Yingxi, Qaidam Basin with the facies-constrained and segmented-frequency-band inversion[J]. Oil Geophysical Prospecting, 2018, 53(4): 832-841. |
| [7] |
井涌泉, 栾东肖, 张雨晴, 等. 基于地震属性特征的河流相叠置砂岩储层预测方法[J]. 石油地球物理勘探, 2018, 53(5): 1049-1058. JING Yongquan, LUAN Dongxiao, ZHANG Yuqing, et al. Fluvial facies inter-bedded sand reservoir prediction with seismic multi-attributes[J]. Oil Geophysical Prospecting, 2018, 53(5): 1049-1058. |
| [8] |
de Figueiredo L P, Grana D, Santos M, et al. Bayesian seismic inversion based on rock-physics prior mode-ling for the joint estimation of acoustic impedance, porosity and lithofacies[J]. Journal of Computational Physics, 2017, 336: 128-142. |
| [9] |
李金磊, 陈祖庆, 王良军, 等. 相控技术在低勘探区生屑滩相储层预测中的应用[J]. 岩性油气藏, 2017, 29(3): 110-117. LI Jinlei, CHEN Zuqing, WANG Liangjun, et al. Application of facies-controlled technique to bioclastic shoal reservoir prediction in less well zones[J]. Lithologic Reservoirs, 2017, 29(3): 110-117. |
| [10] |
王海龙, 曲永强, 张巧凤, 等. 松辽盆地深层沙河子组致密砂岩储层预测[J]. 石油地球物理勘探, 2017, 52(增刊2): 129-134. WANG Hailong, QU Yongqiang, ZHANG Qiaofeng, et al. Tight-sand reservoir prediction in the deep Shahezi formation, Songliao Basin[J]. Oil Geophysical Prospecting, 2017, 52(S2): 129-134. |
| [11] |
He J H, Ding W L, Jiang Z X, et al. Logging identification and characteristic analysis of the lacustrine organic-rich shale lithofacies:A case study from the Es3l shale in the Jiyang Depression, Bohai Bay Basin, Eastern China[J]. Journal of Petroleum Science and Engineering, 2016, 145: 238-255. |
| [12] |
Saggaf M M, Nebrija E L. A fuzzy logic approach for the estimation of facies from wire-line logs[J]. AAPG Bulletin, 2003, 87(7): 1223-1240. |
| [13] |
Wang G C, Carr T R, Ju Y W, et al. Identifying organic-rich Marcellus Shale lithofacies by support vector machine classifier in the Appalachian basin[J]. Computers & Geosciences, 2014, 64: 52-60. |
| [14] |
张阳, 邱隆伟, 李际, 等. 基于模糊C均值地震属性聚类的沉积相分析[J]. 中国石油大学学报(自然科学版), 2015, 39(4): 53-61. ZHANG Yang, QIU Longwei, LI Ji, et al. Sedimentary facies analysis based on cluster of seismic attri-butes by fuzzy C-means algorithm[J]. Journal of China University of Petroleum (Edition of Natural Science), 2015, 39(4): 53-61. |
| [15] |
庞锐, 魏嘉.利用K均值聚类方法进行地震相识别[C].中国地球物理学会第二十四届年会论文集, 2008. PANG Rui, WEI Jia.Seismic facies identification using K-means clustering[C]. Proceedings of the 24th Annual Meeting of the Chinese Geophysical Society, 2008. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGDW200810001113.htm |
| [16] |
Irani R, Nasimi R. Evolving neural network using real coded genetic algorithm for permeability estimation of the reservoir[J]. Expert Systems with Applications, 2011, 38(8): 9862-9866. |
| [17] |
Tahmasebi P, Javadpour F, Sahimi M. Data mining and machine learning for identifying sweet spots in shale reservoirs[J]. Expert Systems with Applications, 2017, 88: 435-447. |
| [18] |
Saffarzadeh S, Shadizadeh S R. Reservoir rock permeability prediction using support vector regression in an Iranian oil field[J]. Journal of Geophysics and Engineering, 2012, 9(3): 336-344. |
| [19] |
Pratama H.Machine learning: using optimized KNN (K-Nearest Neighbors) to predict the facies classifications[C].The 13th SEGJ International Symposium, 2018, 538-541.
|
| [20] |
Baziar S, Shahripour H B, Tadayoni M, et al. Prediction of water saturation in a tight gas sandstone re-servoir by using four intelligent methods:a comparative study[J]. Neural Computing and Applications, 2018, 30(4): 1171-1185. |
| [21] |
宋建国, 高强山, 李哲. 随机森林回归在地震储层预测中的应用[J]. 石油地球物理勘探, 2016, 51(6): 1202-1211. SONG Jianguo, GAO Qiangshan, LI Zhe. Application of random forests for regression to seismic reservoir prediction[J]. Oil Geophysical Prospecting, 2016, 51(6): 1202-1211. |
| [22] |
Zhang T, Ramakrishnan R, Livny M. BIRCH:a new data clustering algorithm and its applications[J]. Data Mining and Knowledge Discovery, 1997, 1(2): 141-182. |
| [23] |
邵峰晶, 张斌, 于忠清. 多阈值BIRCH聚类算法及其应用[J]. 计算机工程与应用, 2004, 40(12): 174-176. SHAO Fengjing, ZHANG Bin, YU Zhongqing. BIRCH clustering algorithm with muti-threshold[J]. Computer Engineering and Applications, 2004, 40(12): 174-176. |
| [24] |
Olson C F. Parallel algorithms for hierarchical clustering[J]. Parallel Computing, 1995, 21(8): 1313-1325. |
| [25] |
韦相. 基于密度的改进BIRCH聚类算法[J]. 计算机工程与应用, 2013, 49(10): 201-205. WEI Xiang. Improved BIRCH clustering algorithm based on density[J]. Computer Engineering and Applications, 2013, 49(10): 201-205. |
| [26] |
李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012: 21-23. LI Hang. Statistical Learning Method[M]. Tsinghua University Press, Beijing, 2012: 21-23. |
| [27] |
Hoerl A E, Kennard R W. Ridge regression:biased estimation for nonorthogonal problems[J]. Technometrics, 1970, 12(1): 55-67. |
| [28] |
王琪, 冷林峰, 常永莲. 改进岭回归与主成分回归的股指跟踪研究[J]. 重庆理工大学学报(自然科学), 2018(1): 212-221. WANG Qi, LENG Linfeng, CHANG Yonglian. Improvement of ridge regression and principal component regression in stock index tracking[J]. Journal of Chongqing University of Technology(Natural Science), 2018(1): 212-221. |
| [29] |
Lee J, Mukerji T.The Stanford VI-E reservoir: A synthetic data set for joint seismic-EM time-lapse monitoring algorithms[C].25th Annual Report, Stanford Center for Reservoir Forecasting, Stanford University, Stanford, CA, 2012.
|
| [30] |
Steinley D. Properties of the Hubert-Arabie adjusted Rand index[J]. Psychological Methods, 2004, 9(3): 386-396. |
| [31] |
张长开, 姜秀娣, 朱振宇, 等. 基于支持向量机的属性优选和储层预测[J]. 石油地球物理勘探, 2012, 47(2): 282-285. ZHANG Changkai, JIANG Xiudi, ZHU Zhenyu, et al. Attributes selection and reservoir prediction based on support vector machine[J]. Oil Geophysical Prospecting, 2012, 47(2): 282-285. |



 孙歧峰, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)计算机科学与技术学院, 266580。Email:
孙歧峰, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)计算机科学与技术学院, 266580。Email:
