地震岩石物理研究各种地震属性参数与油藏参数之间的关系,是地震解释技术从定性到定量、从叠后到叠前、从岩性到流体转换及发展的重要基础。地震岩石物理实验则在地震资料与储层及流体性质之间架起联系和沟通的桥梁,也是非常重要的基础性研究。目前,岩石物理实验通常以超声测试为主,通过计算波的走时得到岩石的声学参数,其频率范围一般在兆赫兹量级以上,显然将超声测量结果直接应用于测井岩石物理的标定以及地震(30~200Hz)定量解释会存在一定风险。因此,业界一直在探寻一种直接测量地震频段岩石物理参数的技术。
在国外,Spencer[1]首次采用应力—应变测试原理进行了岩石波速与衰减的实验,测试了应变幅值接近10-7数量级、频率范围是4~400Hz条件下不同谐波穿过岩样时波动引起的模量变化,进而计算得到岩样的纵、横波速度。德国柏林大学Paffenholz等[2]采用与Spencer相同的原理建立了一套低频测试系统,该系统由纵波测量系统和横波测量系统构成,纵波测量的频率范围是0.003~300Hz,横波测量的频率范围是0.03~100Hz。
美国科罗拉多矿业学院Batzle研制了一套科研型低频测量设备,实现了5~2000Hz频段纵、横波速度和衰减参数的测量。结果表明:速度频散和衰减受流体流动性(岩石渗透率与孔隙流体黏滞系数的比值)的影响较大;还特别指出,低流体流动性岩石可能在地震频段产生强频散[3-6]。Madonna等[7]曾设计一种低频地震衰减测试设备,但只能在常温常压下进行。Mikhaltsevitch等[8]设计了联合多层压电转换器和三轴岩心夹持器的测试仪,可在地震频段和远震波频率(小于1Hz)测量岩石弹性和非弹性属性。
国内的低频岩石物理研究主要集中于理论方面。李维新等[9]根据不同流体状态下的岩心数据统计分析了岩石弹性参数变化规律,提出低孔低渗岩石更接近斑块饱和模型。通过对不同地区的实例研究,任科英[10]认为:对物性较好的岩样,频散现象较弱,此时基于岩心测试数据所做的岩石物理研究可用于指导地震勘探;而对物性较差的岩样,频散现象较为明显,此时需审慎应用测试结果。勾彬彬等[11]基于Collet喷射流模型,分析了流体替换在裂缝孔隙介质中的影响,发现速度随频率发生频散和衰减,高低频极限时速度趋于平稳,逆品质因子随频率先增后减。张繁昌等[12]用数值模拟法研究了硬币型裂缝介质的频散与衰减,认为随裂缝尺度变大或流体黏度增强,衰减峰值频率向低频移动;相对于平行裂缝方向,垂直方向的速度和衰减变化最大,且当介质饱含气时,反射系数明显大于含水、含油介质。
王大兴等[13]研究了含气地层的物性响应后认为:含气饱和度大于60%时,纵波Q值变化明显;物性越好,含气饱和度越高;纵波Q值越小,吸收越强。王峣钧等[14]通过含气饱和度—反射系数频率梯度—反射系数交会图构建岩石物理量板,用于估计储层含气饱和度。
从2010年开始,低频变频测量技术逐渐引入中国并得到发展。中国石油大学(北京)、中国石油勘探开发研究院、中国矿业大学(北京)等先后引进了低频测量设备,开展了低频测试的实验与研究[15-16],实现了低频弹性参数的测量。中国石化胜利油田物探研究院通过对低频测量设备的改进与完善,包括重新设计超声探头,实现了高、低频岩石物理参数的同时测量。
本文利用实验室高、低频联合测试技术,针对含不同流体的岩样开展跨频段岩石物理实验,进而分析纵波速度随饱和度、流体性质、物性参数及频率的变化规律,并探讨其机理。
1 实验方法 1.1 测量原理跨频段岩石物理参数测量中的高频速度测量原理较简单,同常规超声实验一样,利用超声波透射方法对岩石进行测量,通过观测波的走时推算岩石速度。与常规超声实验不同之处,是测量超声的同时还要兼顾低频岩石物理参数的测量,因此需用特制超声换能器。
低频岩石物理参数测量是跨频段岩石物理参数测量中的核心部分,其测量原理与超声完全不同。在低频测量中,由于地震波频率(几十赫兹)较低,波长较长,若使用脉冲透射法测量则岩心长度需达到数十米,这在实验室几乎不可能。而共振法则需将岩心制成又扁又窄的长条,一方面要求岩心质地坚硬,另一方面流体驱替实验也很难进行。应力—应变法则能实现低频率下准确而连续的岩石物理参数测量,岩心制备相对简易,疏松岩石也可测量,主要难点是待测岩石的应变量(≤10-6)极弱。
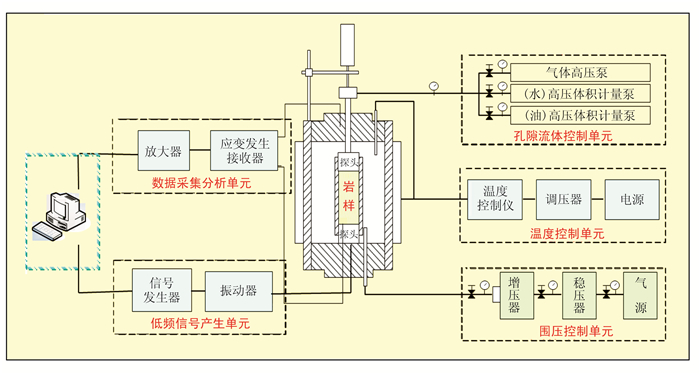
图 1为跨频段岩石物理参数测量系统框架。首先计算机控制信号发生器发出特定频率(1~2000Hz)正弦波信号,该信号经功率放大器放大后传至振动器,振动器随即产生相应频率的振动,致使岩样和参考铝块变形。固定在岩样和参考铝块表面的应变片感应到该应变(≤10-6),其电阻值发生变化,通过一组电路将对应的电阻值变化量(相当于应变)转变为电压信号,电压信号经信号放大器和模数转换,被采集系统接收,经过平均、锁相、存储等处理,最终得到待测岩样和参考铝块的应变量,继而可求得岩样低频情况下的物性参数。温度、压力控制单元可改变岩样的温度、压力测试状态,流体控制单元能改变待测岩样的含流体状态,从而实现岩样在不同温度、压力、饱含不同流体状态情况下的跨频段岩石物理参数测试。
|
图 1 跨频段岩石物理参数测量系统的框架图 |
岩样制备是跨频段岩石物理测量的关键环节,直接决定测试能否成功。
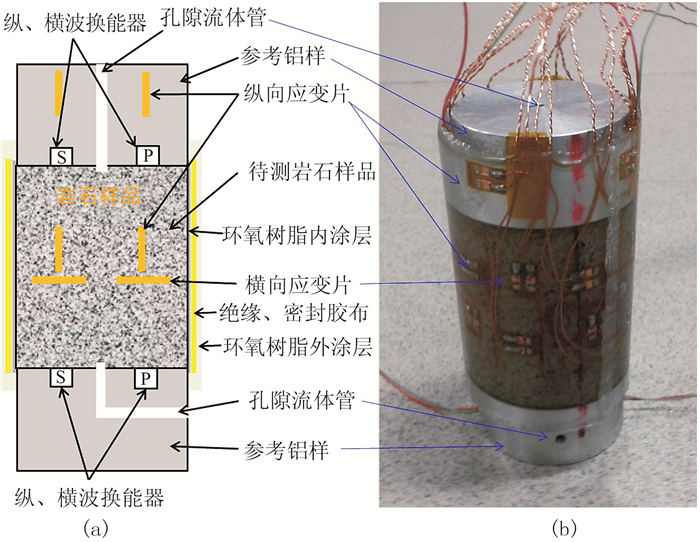
包括以下步骤:①将待测岩样制作成直径约38mm、高度介于50~70mm的圆柱体,两个端面磨平,凸起不得超过0.1mm;②在待测岩样表面涂抹一薄层(内层)环氧树脂胶,并粘贴上绝缘、防渗透胶布,保证胶布平整光滑,目的是防止孔隙流体从岩样表面渗透流出造成应变片失灵;③将两块内嵌有超声P波和S波换能器的参考铝块分别粘贴于待测岩样上下两端;④在岩样表面胶布上粘贴8个应变片,其中4个平行于岩样轴向、4个垂直于岩样轴向,参考铝块表面粘贴4个平行于岩样轴向的应变片,这些不同位置和方位的应变片能同时记录岩样和参考铝块的应变量;⑤用环氧树脂胶做(外层)密封处理,一是防止加压过程中提供围压的气体进入岩样,二是保护传感元件不受围压气体影响。图 2是岩样实物及示意图。
|
图 2 标准岩样示意图(a)和实物图(b) |
总体而言,一位熟练实验员制作一个标准岩样约需3天;制作过程中每一步都须进行质检,确保岩样制作合乎要求。
1.3 岩石物理参数计算在实验中所用参考铝块是一种完全弹性、均质、各向同性的物质,弹性模量不随温度(-20~100℃)、压力(0~40MPa)、频率发生变化,若其杨氏模量(72GPa)已知,则由岩石应变和铝块应变的比值即可算出岩石弹性模量。
采用正弦波激发,即施加于岩石的应力为正弦波变化的应力。根据弹性波传播理论,在岩石中产生的应变表示为位移对空间位置的一阶偏导数,即
| $ \varepsilon_{33}=\frac{\partial u}{\partial x}=F_{0} \cos (\sqrt{\frac{\rho}{E}} \times \omega x) \sin (\omega t) $ | (1) |
式中:u为位移;x为位置;ω为频率;ρ为密度;E为杨氏模量;F0为外加应力的初始幅度。
由纵向应变和横向应变的比值可计算出岩石中的泊松比υ,即
| $ v=\frac{\varepsilon_{11}}{\varepsilon_{33}} $ | (2) |
式中ε11、ε33分别为岩样的纵向和横向应变(图 2中分别由贴在岩样上的纵向应变和横向应变片测得)。
岩石中的杨氏模量E的计算公式为
| $ E=E^{\mathrm{al}} \frac{\varepsilon_{33}^{\mathrm{al}}}{\varepsilon_{33}} $ | (3) |
式中Eal、ε33al分别为铝块的杨氏模量和应变,其中铝块的应变由贴在铝块上的应变片测量。
由杨氏模量E和泊松比υ可计算出剪切模量u和体积模量K
| $ u=\frac{E}{2(1+v)} $ | (4) |
| $ K=\frac{E}{3(1+2 v)} $ | (5) |
纵、横波速度则分别为
| $ V_{\mathrm{P}}=\sqrt{\frac{K+\frac{4}{3}}{\rho}} $ | (6) |
| $ V_{\mathrm{S}}=\sqrt{\frac{u}{\rho}} $ | (7) |
超声频率下纵波速度(VPu)和横波速度(VSu)通过传播时间法测量获得,其表达式分别为
| $ V_{\mathrm{P}}^{\mathrm{u}}=\frac{L}{t_{\mathrm{P}}^{\mathrm{u}}} $ | (8) |
| $ V_{\mathrm{S}}^{\mathrm{u}}=\frac{L}{t_{\mathrm{S}}^{\mathrm{u}}} $ | (9) |
式中:L为岩样长度;tPu和tSu分别为超声纵、横波穿过岩样的时间。
2 岩样测量 2.1 岩样物性参数选取两块岩样:岩样A为高孔、高渗泥质砂岩,岩样B为中孔、中渗泥质砂岩。其泥质含量、孔隙度、渗透率等参数如表 1所示。
|
|
表 1 实验岩样物性参数表 |
先对泥质砂岩样品A、B开展不同含水饱和度(气水两相)时跨频段岩石物理参数测量。分别对A、B两块岩样进行水饱和实验,水从孔隙流体管线注入,注入量由恒速恒压泵精确控制,通过注入水体积计算岩样的含水饱和度。然后,水从另一端孔隙流体管线流出,直到流出的水体积为孔隙体积的3倍,此时认为岩样孔隙中完全注满水,含水饱和度为100%。为了保障实验成功,流体驱替实验中,一般要求围压大于孔压,本实验中围压为5MPa,孔压为2MPa。最后,从孔隙流体管注入高压空气驱替岩样中的水,直至水全部流出。
再对岩样A、B开展不同含甘油饱和度(气、甘油两相)的跨频段岩石物性测量。注入甘油过程类似于注水。常温下甘油黏度约为水的1000倍(水的黏度为1cP),因此甘油注入过程较慢。
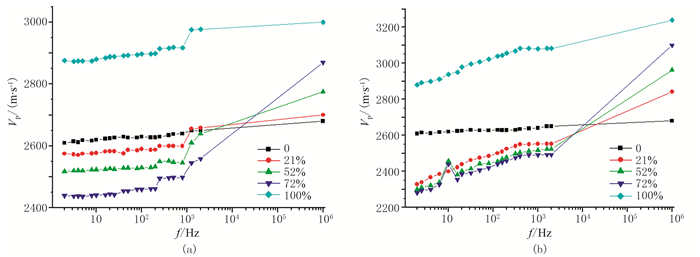
图 3展示岩样A分别充填不同饱和度的水或甘油时,纵波速度随频率的变化规律。当充注较稀薄的流体(水,1cP)时,纵波速度在地震频段无明显频散;但在测井频段有一定的频散趋势。当充填非常黏稠的流体(甘油,1410cP)时,纵波速度在地震频段有显著的频散;而在测井与超声频段无频散。
|
图 3 不同流体饱和度下岩样A纵波速度与频率关系 (a)含水;(b)含甘油 |
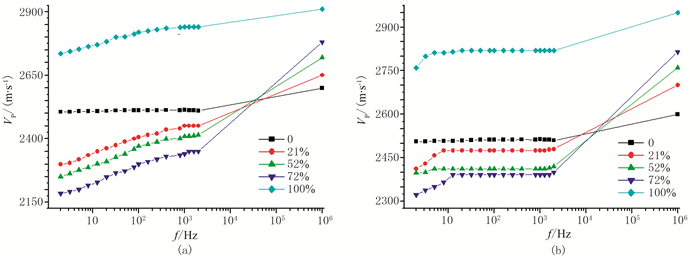
图 4展示岩样B分别充填不同饱和度的水或甘油时,纵波速度随频率的变化情况。当充注稀薄流体(水)时,纵波速度在地震—测井频段有显著频散;而当充填甘油时,该频段频散并不显著,频散曲线显示频散可能发生在地震频段以下。此现象与Batzle的结论[6]相吻合,即纵波速度频散频段随流体流动性的增强而增高。岩体低渗透率或流体高黏滞性都能促成低流动性;反之亦然。
|
图 4 不同流体饱和度下岩样B纵波速度与频率关系 (a)含水;(b)含甘油 |
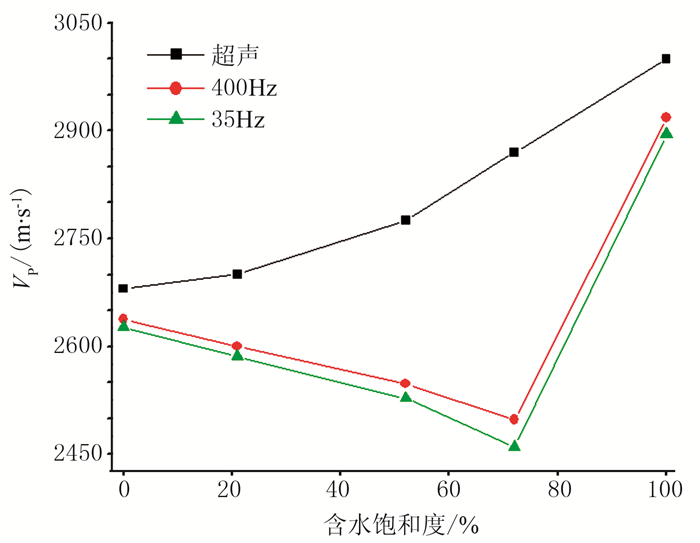
以岩样A为例,从饱和度对速度的影响关系(图 5)看:在地震频段,当高孔渗岩样含水饱和度为0~100%,纵波速度先减后增,测试结果显示速度最低时对应的饱和度为72%,亦即72%(或大于72%)可能为一个临界饱和度,在此之前地震纵波速度随含水饱和度的增加而降低,而超过72%后,地震纵波速度随饱和度的增加而增大;在超声频段,该临界饱和度规律并不存在,超声纵波速度随饱和度的增加而持续增加,说明含水的高孔渗岩样在高、低频段纵波速度受饱和度影响的规律并不一致。
|
图 5 不同频段下岩样A含水饱和度与纵波速度关系 |
这种差异可用BGW-BGH模型理论解释。在低频条件下,低饱和度岩样孔隙压力有足够时间达到均衡,流体(水)能充分流动,流体弹性模量满足Wood方程;随饱和度缓慢增加,此时岩样的整体密度会增加,造成纵波速度降低;而高(大于临界)饱和度时,因封闭的边界条件使流体无法充分流动,从而产生孔隙压力差,造成弹性模量增大,且增加幅度大于密度增加幅度,导致纵波速度增加。在高频条件下,由于波传播时间较快,流体来不及流动,各种饱和度下的孔隙压力都不均衡,流体弹性模量满足Gassmann-Hill方程,即随饱和度增加而变大,且大于岩样整体密度的增加幅度。因此,超声纵波速度随饱和度的增加而增加,接近BGH理论极限。
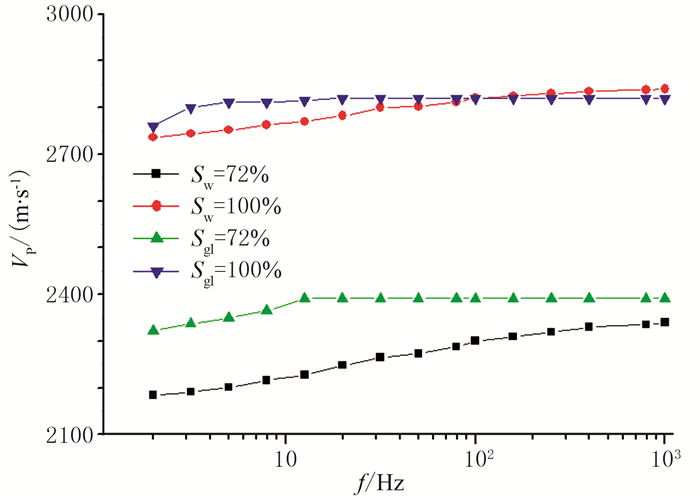
3.2 流体黏度针对同一岩样,因实测数据只有两种流体(水和甘油)驱替,对低频测试而言,二者最大差异是流体黏度,其次才是密度。以岩样B为例,在地震频段,含水饱和度为72%和100%时,纵波速度随频率增加而增加;饱含甘油时,变化并不明显;在小于10Hz情况下,饱含甘油则频散明显(图 6)。其主要原因是甘油黏度较大(约为水的1000倍),流动性较差,孔隙压力平衡时间较长,故特征频率低于地震频段。
|
图 6 岩样B含不同流体时频率与纵波速度的关系 |
渗透率是控制孔隙流体流动的重要因素。对于泥质砂岩,其孔隙度与渗透率通常呈正相关。因此,孔隙度越大,孔隙连通性和孔隙流体流动性越好。从图 3a、图 4a可见,随着渗透率的减小,流动性减弱,频散明显的频段趋低。
4 结论通过对两块孔渗特性不同的泥质砂岩样品开展高、低频联合测试,分析了物性参数、饱和度、流体黏度及频率对岩石物理参数的影响。实验结果表明:孔隙流体流动性越强,频散特征频段频率越高;频散特征频段与孔隙度、渗透率呈正相关,与流体黏度呈负相关。与饱和度的关系较复杂,高频段纵波速度随饱和度的增加持续增加;低频段则存在一个临界饱和度,低于临界饱和度,纵波速度随饱和度增加而减小;高于临界饱和度,纵波速度随饱和度增加而增加。临界饱和度与孔隙流体流动性相关。
| [1] |
Spencer J W. Stress relaxation at low frequencies in fluid saturated rocks:attenuation and modulus dispersion[J]. Journal Geophysics Research, 1981, 86(B3): 1803-1812. |
| [2] |
Paffenholz J, Burkhardt H. Absorption and modulus measurements in the seismic frequency and strain range on partially saturated sedimentary rocks[J]. Journal of Geophysical Research, 1989, 94(B7): 9493-9507. |
| [3] |
Batzle M, Han D H, Castagna J.Fluids and frequency dependent seismic velocity of rocks[C].SEG Technical Program Expanded Abstracts, 1999, 18: 5-8.
|
| [4] |
Batzle M, Hofmann R, Han D H, et al. Fluids and frequency dependent seismic velocity of rocks[J]. The Leading Edge, 2001, 20(2): 168-171. |
| [5] |
Batzle M L, Han D H, Hofmann R. Fluid mobility and frequency-dependent seismic velocity-Direct measurements[J]. Geophysics, 2006, 71(1): N1-N9. |
| [6] |
Adam L, Batzle M. Elastic properties of carbonates from laboratory measurements at seismic and ultrasonic frequencies[J]. The Leading Edge, 2008, 27(8): 1026-1032. |
| [7] |
Madonna C, Tisato N, Boutareaud S, et al.A new la-boratory system for the measurement of low frequency seismic attenuation[C].SEG Technical Program Expanded Abstracts, 2010, 29: 2675.
|
| [8] |
Mikhaltsevitch V, Lebedev M, Gurevich B.A low-frequency laboratory apparatus for measuring elastic and anelastic properties of rocks[C].SEG Technical Program Expanded Abstracts, 2011, 30: 2256-2260.
|
| [9] |
李维新, 史謌, 王红, 等. 岩石物理弹性参数规律研究[J]. 地球物理学进展, 2007, 22(5): 1380-1385. LI Weixin, SHI Ge, WANG Hong, et al. The study on the relationships of elastic properties of rock physics[J]. Progress in Geophysics, 2007, 22(5): 1380-1385. |
| [10] |
任科英. 实验室岩心声学速度测试中的频散现象[J]. 石油地球物理勘探, 2011, 46(5): 779-782. REN Keying. Velocity dispersion of ultrasonic core measurement in laboratory[J]. Oil Geophysical Prospecting, 2011, 46(5): 779-782. |
| [11] |
勾彬彬, 陈学华, 瞿雷, 等. 依赖频率的裂缝孔隙介质弹性属性及参数影响[J]. 石油地球物理勘探, 2018, 53(6): 1235-1240. GOU Binbin, CHEN Xuehua, QU Lei, et al. Frequency-dependent elastic properties in fractured porous media and impact parameters[J]. Oil Geophysical Prospecting, 2018, 53(6): 1235-1240. |
| [12] |
张繁昌, 桑凯恒, 路亚威. 硬币型裂缝介质的频散与衰减[J]. 石油地球物理勘探, 2019, 54(4): 836-843. ZHANG Fanchang, SANG Kaiheng, LU Yawei. Frequency dispersion and attenuation of porous rocks with penny shaped fractures[J]. Oil Geophysical Prospecting, 2019, 54(4): 836-843. |
| [13] |
王大兴, 辛可峰, 李幼铭, 等. 地层条件下砂岩含水饱和度对波速及衰减影响的实验研究[J]. 地球物理学报, 2006, 49(3): 908-914. WANG Daxing, XIN Kefeng, LI Youming, et al. An experimental study of influence of water saturation on velocity and attenuation in sandstone under stratum conditions[J]. Chinese Journal of Geophysics, 2006, 49(3): 908-914. |
| [14] |
王峣钧, 陈双全, 王磊, 等. 基于斑块饱和模型利用地震波频散特征分析含气饱和度[J]. 石油地球物理勘探, 2014, 49(4): 715-722. WANG Yaojun, CHEN Shuangquan, WANG Lei, et al. Gas saturation analysis with seismic dispersion attribute based on patchy-saturation model[J]. Oil Geophysical Prospecting, 2014, 49(4): 715-722. |
| [15] |
未晛, 王尚旭, 赵建国, 等. 含流体砂岩地震波频散实验研究[J]. 地球物理学报, 2015, 58(9): 3380-3388. WEI Xian, WANG Shangxu, ZHAO Jianguo, et al. Laboratory study of velocity dispersion of the seismic wave in fluid-saturated sandstones[J]. Chinese Journal of Geophysics, 2015, 58(9): 3380-3388. |
| [16] |
马霄一, 王尚旭, 赵建国, 等. 岩石跨频段实验研究[J]. 地球物理学进展, 2018, 33(5): 1943-1950. MA Xiaoyi, WANG Shangxu, ZHAO Jianguo, et al. Laboratory study of rocks in multi-frequency band[J]. Progress in Geophysics, 2018, 33(5): 1943-1950. |



 李民龙, 山东省东营市东营区北一路210号胜利油田物探研究院, 257022。Email:
李民龙, 山东省东营市东营区北一路210号胜利油田物探研究院, 257022。Email: