2 青岛海洋科学与技术试点国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266061;
3 中国海洋大学海洋地球科学学院, 山东青岛 266100
2 Functional Laboratory for Marine Mineral Resources Assessment and Prospecting, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266061, China;
3 College of Marine Geosciences, Ocean University of China, Qingdao, Shandong 266100, China
非常规油气(页岩气、页岩油和煤层气等)储层具有低孔、低渗等物性特点,极难形成自然产能[1],而水力压裂是增大储层渗透率、提高油气产能的主要手段[2-3]。在压裂注液过程中,裂隙压力会发生变化,导致裂隙扩张或岩石破裂,并在射孔周围发生一系列微小地震事件。通过监测、记录微震事件信号并对微震事件精确定位,可得到裂缝的方位、长度、高度和缝型等多种属性参数[4-6]。
地面微地震监测凭借操作简便、观测范围大、覆盖次数高且成本较低等优势,得到越来越广泛的应用[7-9],尤其是在压裂井附近缺少监测井的情况下,地面微地震监测往往是现实的选择。但由于地下介质的吸收作用和地面噪声的干扰,与井中监测资料相比,地面微震资料信噪比较低,致使难以识别、拾取初至时间[10-11],从而限制了基于识别、拾取初至的定位方法的应用。因此,无须识别、拾取初至的微震偏移成像定位方法成为地面微震监测震源定位方面的研究热点[12-15]。
2004年Kao等[12]提出震源扫描(Source scanning algorithm,SSA)定位方法。该方法的主要优势是不需要拾取初至,也不用模拟地震记录,通过对地下目标区范围和地震记录时段的系统扫描,完成震源成像,获得整个震源分布[16];其缺点是对低信噪比资料的处理效果欠佳。地震发射层析成像(Seismic emission tomography,SET)[17-18]是与SSA类似的常用的震源定位算法,它对低信噪比地震记录有较强的适应性,但定位精度易受初至极性的影响[19]。
针对上述缺陷,何勇等[20]通过引入震源机制极性校正项消除初至极性的影响;Liang等[21]采用格点扫描叠加方法,对离散震源位置及由震源机制组成的全空间进行离散扫描,并利用震源机制校正记录极性,得到裂隙展布的更丰富信息,但搜索样本数目太大,计算效率较低。徐克彬等[22]提出基于L-M算法的射线反传聚焦定位方法,提高了计算效率,但需拾取监测区坐标点到检波器的时差,不适用于低信噪比微震资料处理。基于波形互相关的震源定位方法利用同震源地震事件通常在波形上具有相似性和随机噪声之间互不相关的特点[23-24],有效地压制了随机噪声的影响。Zhebel[25]通过相邻道的互相关处理消除振幅极性反转的影响,但易受地面台站布设方式和数量的影响。
考虑到基于偏移叠加的微震定位方法不能兼顾消除噪声和初至极性反转对震源成像能量及对定位精度的影响,本文将振幅叠加能量改进为波形互相关系数相乘能量,并作为成像能量值,模型和实际数据测试结果证明本文方法能较好地消除噪声和初至极性反转的影响,提高震源成像分辨率和定位精度。
1 震源成像方法原理与步骤 1.1 微震成像函数基于偏移叠加成像的微震定位方法无须拾取初至数据,通过叠加原理压制噪声,是地面微震资料定位的一种有效技术。常规偏移类振幅叠加方法所用的偏移成像函数主要有
| $ E_{\mathrm{S} 1}\left(\boldsymbol{\eta}_{i}\right)=\frac{\sum\limits_{\mathrm{rec}=1}^{N} u_{\mathrm{rec}}\left(\boldsymbol{\eta}_{i}, \mathrm{rec}\right)}{N} $ | (1) |
| $ E_{\mathrm{S} 2}\left(\boldsymbol{\eta}_{\boldsymbol{i}}\right)=\frac{\sum\limits_{\mathrm{rec}=1}^{N}\left|u_{\mathrm{rec}}\left(\boldsymbol{\eta}_{i}, \mathrm{rec}\right)\right|}{N} $ | (2) |
| $ E_{\mathrm{S} 3}\left(\boldsymbol{\eta}_{\boldsymbol{i}}\right)=\frac{\sum\limits_{\mathrm{ree}=1}^{N} c_{\mathrm{rec}} u_{\mathrm{rec}}\left(\boldsymbol{\eta}_{i}, \mathrm{rec}\right)}{N} $ | (3) |
式中:urec(ηj, rec)为地下网格点ηj到第rec个(微)地震道的振幅值;crec为第rec个地震道的初至极性;N为检波器的数量。
若水力压裂破裂产生的微地震震源机制主要成分为双力偶震源,则地表检波点接收的初至极性振幅呈四象限分布[26]。式(1)是对波形振幅直接线性叠加,正负极性会导致振幅相互抵消而减小,使成像质量变差;式(2)是对波形振幅取绝对值后再线性叠加,虽可消除初至正负极性对叠加能量的削减,但同时也增强了噪声影响;式(3)利用震源机制得到的初至极性对微地震记录做校正后线性叠加,但需估计震源机制,导致计算效率低,且线性叠加方式对低信噪比地面微震资料中的噪声压制能力不足,并降低震源定位精度。
针对上述线性叠加成像函数定位方法的不足,利用同震源波形的相关性与随机噪声不相关的差异,达到对震源成像和压制噪声的目的,提出基于波形互相关的震源定位方法[23]。相应的成像函数[25-27]表达式
| $ E_{\mathrm{SC} 1}\left(\boldsymbol{\eta}_{j}\right)=\sum\limits_{\mathrm{rec}=1}^{N} \frac{\sum\limits_{k=1}^{W} u_{\mathrm{ref}}\left(\boldsymbol{\eta}_{j}, \mathrm{ref}, k\right) u_{\mathrm{rec}}\left(\boldsymbol{\eta}_{j}, \mathrm{rec}, k\right)}{N \sqrt{u_{\mathrm{ref}}^{2}\left(\boldsymbol{\eta}_{j}, \mathrm{ref}, k\right) u_{\mathrm{rec}}^{2}\left(\boldsymbol{\eta}_{j}, \mathrm{rec}, k\right)}} $ | (4) |
| $ E_{\mathrm{SC} 2}\left(\boldsymbol{\eta}_{\boldsymbol{j}}\right)=\sum\limits_{\mathrm{rec}=1}^{N} \frac{\left|\sum\limits_{k=1}^{W} u_{\mathrm{ref}}\left(\boldsymbol{\eta}_{\boldsymbol{j}}, \operatorname{ref}, k\right) u_{\mathrm{rec}}\left(\boldsymbol{\eta}_{\boldsymbol{j}}, \mathrm{rec}, k\right)\right|}{N \sqrt{u_{\mathrm{ref}}^{2}\left(\boldsymbol{\eta}_{\boldsymbol{i}}, \operatorname{ref}, k\right) u_{\mathrm{rec}}^{2}\left(\boldsymbol{\eta}_{\boldsymbol{i}}, \mathrm{rec}, k\right)}} $ | (5) |
| $ \begin{array}{l} E_{\mathrm{SC} 3}\left(\boldsymbol{\eta}_{j}\right) \\ \quad=\sum\limits_{\mathrm{rec}=1}^{N} \frac{\sum\limits_{k=1}^{W} u_{\mathrm{rec}}\left(\boldsymbol{\eta}_{j}, \mathrm{rec}, k\right) u_{\mathrm{rec}+1}\left(\boldsymbol{\eta}_{j}, \mathrm{rec}+1, k\right)}{N \sqrt{u_{\mathrm{rec}}^{2}\left(\boldsymbol{\eta}_{j}, \mathrm{rec}, k\right) u_{\mathrm{rec}+1}^{2}\left(\boldsymbol{\eta}_{j}, \mathrm{rec}+1, k\right)}} \end{array} $ | (6) |
式中:W为所取时间窗口的长度;k为时窗W中第k个采样点;urec(ηj, rec,k)为地下网格点ηj到第rec个地震道、k时刻的振幅值;uref(ηj, ref,k)为地下网格点ηj到参考道ref、k时刻的振幅值。
式(4)表示互相关叠加成像函数,利用波形互相关虽可较好地压制随机噪声,但在处理初至极性反转时,用互相关叠加将正负抵消,会削减震源处成像能量值;式(5)表示绝对值互相关叠加成像函数,若对互相关值取绝对值后叠加,会增强噪声影响。因此,式(4)和式(5)成像函数都不能消除初至极性反转带来的影响。式(6)是相邻道互相关叠加成像函数,利用正负波形互相关系数相消规避了初至极性反转的影响,但易受地面检波器布设方式和数量影响。因此,基于互相关叠加的成像函数都不能同时兼顾消除噪声和初至极性带来的不利影响。
基于偏移叠加类成像函数的定位方法都是通过叠加方式取得震源处成像能量,但对低信噪比地面微震监测资料而言,通过叠加方式难以使真实震源处能量很好地“聚焦”,致使震源处成像分辨率较低,即定位误差较大。虽然互相关叠加成像函数是将各台站作为参考台站并与其他台站记录波形做互相关,以此增加叠加次数,增大震源处能量值,提高震源成像分辨率,但却降低了计算效率。
针对地面微震监测资料信噪比低、台站接收的初至极性反转和计算效率低等问题及其对偏移叠加类定位方法带来的不利影响,本文将互相关叠加成像函数中的“叠加”改为“相乘”,得到下列互相关相乘成像函数
| $ E_{\mathrm{MC}}\left(\boldsymbol{\eta}_{\boldsymbol{i}}\right)=\prod\limits_{\mathrm{rec}=1}^{N-1} \frac{\left|\sum\limits_{k=1}^{W} u_{\mathrm{rec}}\left(\boldsymbol{\eta}_{i}, \mathrm{rec}, k\right) u_{\mathrm{rec}}\left(\boldsymbol{\eta}_{i}, \mathrm{rec}+1, k\right)\right|}{\sqrt{u_{\mathrm{rec}}^{2}\left(\boldsymbol{\eta}_{i}, \mathrm{rec}, k\right) u_{\mathrm{rec}}^{2}\left(\boldsymbol{\eta}_{i}, \mathrm{rec}+1, k\right)}} $ | (7) |
式中EMC(ηj)为网格点ηj的互相关相乘成像函数。该函数首先计算波形互相关函数,提高了对有效信号的检测能力,压制微震记录上的随机噪声。计算的互相关系数虽有正负之分,但通过相乘它们并不会相互抵消,反而会因震源处的波形互相关程度较高,大数值相乘后会比小数值相乘的结果大许多,使得震源处的能量值更加“突出”和聚焦,且能压制噪声在空间成像域中形成的假像,从而提高震源处的成像分辨率和定位精度。
1.2 震源定位步骤(1) 首先选取某一个地震道作为参考道ref;
(2) 据监测范围划定成像目标区,建立该区域速度模型,用矩阵网格按一定尺寸将该模型离散化,形成三维网格,各网格点均成为一个潜在震源位置;
(3) 用射线追踪法计算速度模型中每个网格点到各地震道相对参考道的初至时差Δtcal=[t1-tref,t2-tref,…,tN-tref],tref为参考道初至时间;
(4) 假设地下某网格点坐标为ηj(xj,yi,zi),对网格点ηj到所有地震道微震记录按Δtcal做时差校正后,通过上述成像函数得到网格点ηj的能量总和。
(5) 遍历地下所有网格点后,可获得一个四维数组(x,y,z,E),其中(x,y,z)为对应网格点位置,E为各网格在不同时刻的成像能量值。
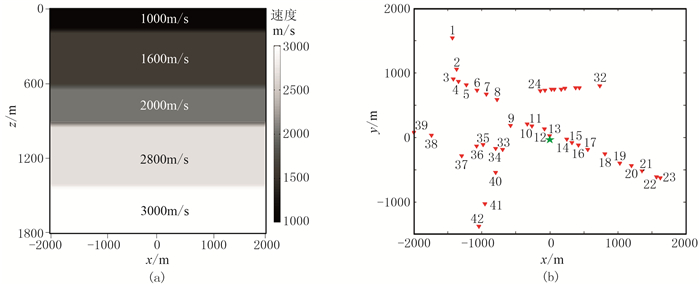
2 理论模拟数据实验 2.1 模型及合成记录首先用理论模型数据对本文方法进行测试,分别从抗噪性、初至极性及多震源分辨率等方面与其他成像函数的定位结果做对比,并讨论速度误差及成像函数中时窗长度对成像结果的影响。模型尺寸为4000m×4000m×1800m,由5个水平地层组成,对应的4个界面的深度分别为200、600、900和1400m,各地层的速度从上到下依次递增(图 1a)。采用某油田实际地面微震监测检波器的不规则布设(图 1b),检波阵列共42个检波器。
|
图 1 速度模型(a)及地面检波器展布(b)示意图 红色三角为检波器,绿色五星为模拟震源的平面位置 |
微震事件记录S(n)由震源子波w(n)与透射系数序列R(n)褶积而成,合成含噪微震记录表示为
| $ S(n)=w(n) * R(n)+N\left(0, \sigma^{2}\right) $ | (8) |
式中:n为微震记录采样点序号;N(0,σ2)是均值为0、方差为σ2的高斯白噪声;震源子波采用雷克子波
| $ w(t)=\left(1-2 \pi f t^{2}\right) \exp \left(-\pi f t^{2}\right) $ | (9) |
式中:f为震源子波主频;t为微震子波持续时间。微震资料信噪比RS/N的计算公式为
| $ R_{\mathrm{S} / \mathrm{N}}=\frac{1}{N} \sum \frac{r_{\mathrm{S}}}{r_{\mathrm{N}}} $ | (10) |
式中:rS表示信号振幅值的均方根值;rN表示噪声幅值的均方根值。
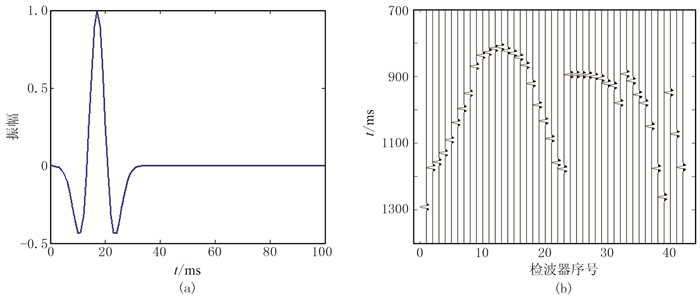
假设微地震事件的发震位置为(0,0,1450m),模型的理论初至由三维射线追踪[28]计算得到,震源子波(图 2a)主频为60Hz,由式(8)和式(9)合成的微震记录如图 2b所示。
|
图 2 震源子波(a)及合成微震记录(b) |
地面微震监测系统的监测台站通常布设于地表,因受地表各种噪声和地层吸收的影响,地面微震监测资料信噪比低,初至识别和拾取困难。
对上述无噪声微震记录(图 2b)添加不同强度高斯白噪声,形成信噪比为0.1~0.9的微震记录;利用不同成像函数测试这些低信噪比微震记录的定位效果。图 3是其中信噪比分别为0.4和0.2的两张微震记录,可见有效微震信号完全淹没于噪声中,无法识别和拾取有效微震信号的初至。

|
图 3 信噪比为0.4(a)和0.2(b)的含随机噪声合成微震记录 |
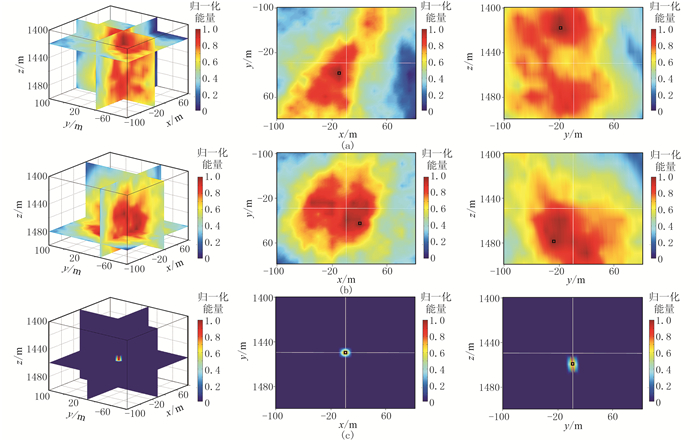
图 4和图 5是对上述两张微震记录分别利用线性叠加、互相关叠加和互相关相乘三种成像函数得到的定位结果。可见随着信噪比的减小,叠加类成像函数的成像结果变差;互相关相乘成像函数(图 4c、图 5c)的成像分辨率和定位精度都更高,表明互相关成像函数对低信噪比资料处理效果更佳。

|
图 4 信噪比为0.4的微震记录用不同成像函数的成像结果 (a)线性叠加成像函数;(b)互相关叠加成像函数;(c)互相关相乘成像函数 |
|
图 5 信噪比为0.2的微震记录用不同成像函数的成像结果 (a)线性叠加成像函数;(b)互相关叠加成像函数;(c)互相关相乘成像函数 |
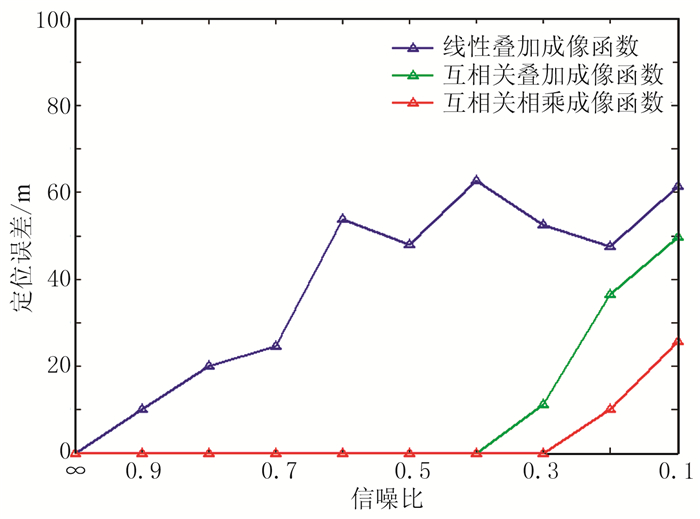
图 6是不同成像函数的定位误差随信噪比变化的对比,显然互相关成像函数具更强抗噪能力。
|
图 6 不同成像函数定位误差随信噪比的变化 |
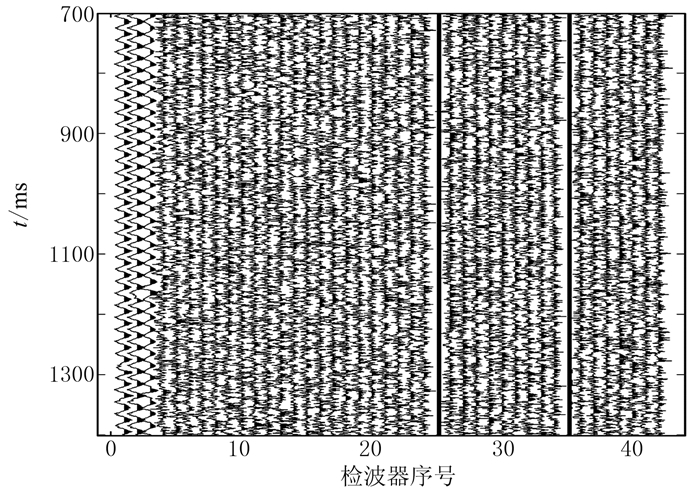
在实际水力压裂施工中,地面检波器不仅会受随机噪声影响,而且会受固定干扰、点脉冲等噪声影响,甚至出现坏道或异常道。对图 3a微震记录中某些地震道添加固定频率干扰噪声(第1、2和3道)和坏道(第25和35道),得到图 7所示微震记录。
|
图 7 信噪比为0.4的含固定频率噪声和坏道微震记录 |
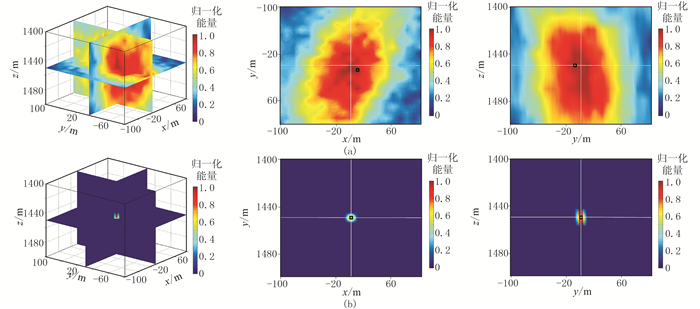
因线性叠加成像函数无法满足低信噪比微震资料的定位,故只利用互相关叠加和互相关相乘两种成像函数做定位成像(图 8)并进行对比。可见互相关叠加成像函数受固定干扰、点脉冲等噪声和坏道影响,成像分辨率和定位精度降低,而互相关相乘成像函数仍具有较高震源分辨率和定位精度。当然,在进行实际定位工作的处理阶段时,可对微震监测资料进行预处理,剔除较明显的坏道。
|
图 8 对图 7所示微震记录采用互相关叠加(a)和互相关相乘(b)成像函数得到的定位成像结果 |
实际资料显示微地震震源机制有很强的双力偶震源成分,其振幅极性在地面呈四象限分布,震源定位时线性叠加成像函数不能同时兼顾噪声压制和振幅反转问题,易影响震源定位的精确;而极性修正叠加成像函数计算效率低,且易将定位误差带入到震源机制反演中,造成震源机制反演误差较大,对后续的微地震资料解释造成困扰。互相关叠加成像函数在压制噪声方面具一定优势,但在处理初至极性反转问题上仍不够理想。
仍采用图 1所示的速度模型和地面微震监测系统(包括震源位置)。为使地面检波器的振幅极性呈四象限分布,设计了压裂裂缝模型:方位角、倾角和滑动角分别为25°、50°、80°,震源机制如图 9右上角所示。根据P波初动极性在震源球上的极射赤面投影可得各检波点振幅极性分布,相应的合成微震记录如图 10所示,可见信噪比为0.4的含噪微震记录(图 10b)中有效信号无法识别,初至难以拾取。由于模拟有效信号的初至极性发生反转,利用绝对值互相关叠加成像、相邻道互相关叠加和互相关相乘成像函数分别进行定位成像测试。

|
图 9 震源机制“沙滩球”及对应的检波器极性分布 实心三角为正极性,空心三角为负极性 |

|
图 10 无噪(a)和信噪比为0.4的含噪(b)初至极性反转合成微震记录 |
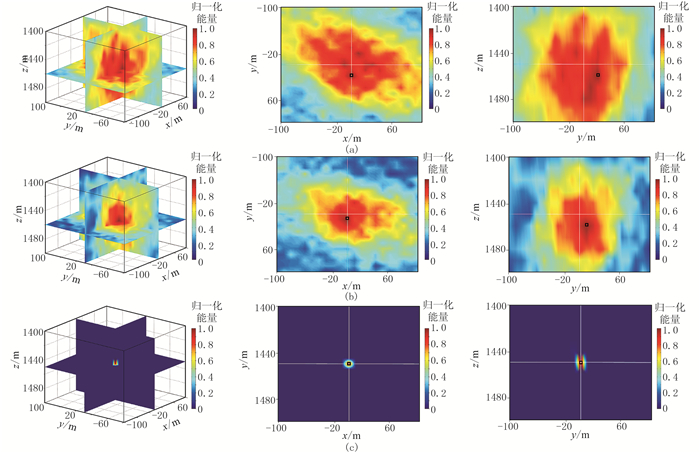
图 11为绝对值互相关叠加、相邻道互相关叠加和互相关相乘成像函数的定位成像结果。可见互相关相乘成像函数不受初至极性反转影响,在震源处仍呈现较高成像分辨率,且定位精度高。这是缘于该成像函数利用波形互相关系数相乘的形式,巧妙地解决了振幅极性反转对叠加能量的影响。
|
图 11 初至极性反转的微震记录用不同成像函数的定位成像结果 (a)绝对值互相关叠加成像函数;(b)相邻互相关叠加成像函数;(c)互相关相乘成像函数 |
水力压裂诱发的微地震沿裂缝延伸方向会有多个震源同时或连续激发,因此对于微震源定位方法来说,应该还具有能准确识别多个震源且同时进行精确定位的能力,当各道有效信号不能区分时,传统定位方法不再适用。
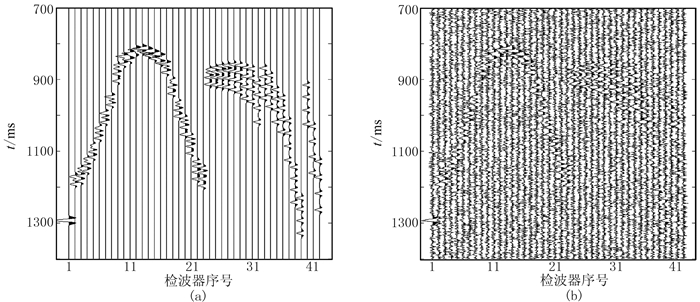
设计了4个震源同时激发,震源位置分别为(-100m,-100m,1450m)、(0,0,1450m)、(100m,100m,1450m)和(200m,200m,1450m)。分别用线性叠加、互相关叠加和互相关相乘成像函数对多震源合成微震记录进行定位成像测试,得到无噪多震源微震记录(图 12a)和信噪比为0.5的微震记录(图 12b)。由于部分微震事件到达同一个检波器的初至相近,导致部分检波器接收微震信号叠加在一起,无法准确分辨发生微震事件的个数。
|
图 12 无噪(a)和信噪比为0.5的含噪(b)多震源合成微震记录 |
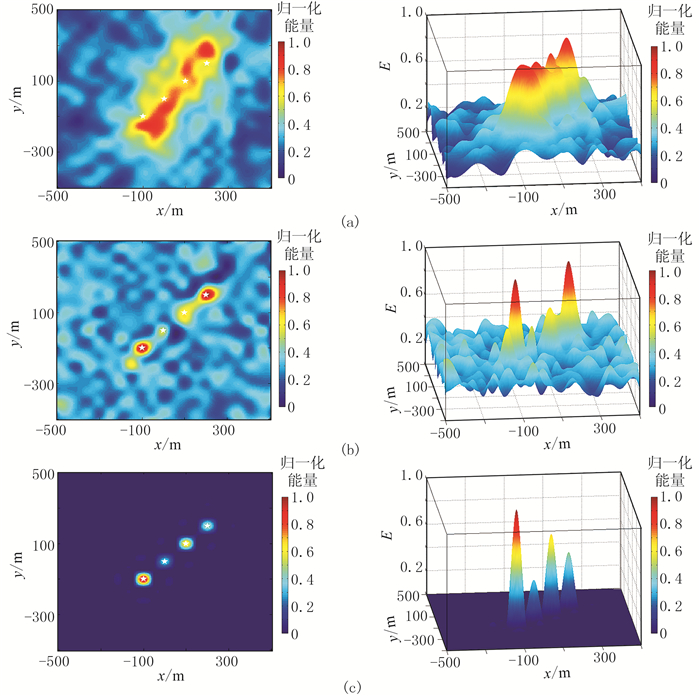
由于4个理论震源深度都为1450m,故只显示z=1450m处x-y平面的成像结果。图 13为线性叠加、互相关叠加和互相关相乘成像函数在z=1450m的成像定位结果。相比于叠加类(线性和互相关叠加)成像函数,互相关相乘成像函数的定位成像分辨率更高,虽然个别震源能量值相对较小,但与真实震源位置吻合度高,易于识别震源位置,表明互相关相乘成像函数对多震源处理效果更佳。
|
图 13 信噪比为0.5的多震源微震记录用不同成像函数的定位成像结果 (a)线性叠加成像函数;(b)互相关叠加成像函数;(c)互相关相乘成像函数 |
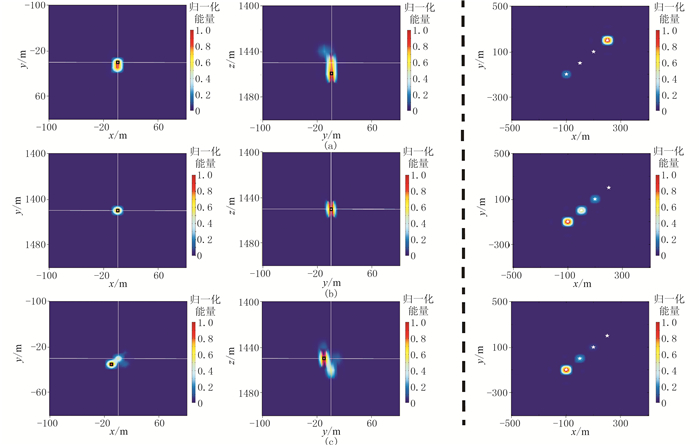
利用互相关成像函数做定位成像处理需选取合适的时窗长度,为了对比不同时窗长度对定位成像结果的影响,分别采用单震源(图 3a)和多震源(图 12b)记录进行定位成像,得到如图 14所示定位成像结果。当选取的时窗长度完全包含有效信号时,无论是定位分辨率还是定位精度都较高(图 14b),而当选取的时窗长度未完全包含有效信号时,定位分辨率和定位精度较差(图 14a)。因此,时窗长度应尽可能完全包含有效信号,以保证不同地震道的有效信号之间具有较高相关度,提高震源分辨率和定位精度。但时窗长度也不宜取太长,避免包含太多噪声记录,降低有效信号之间的相关程度,影响定位精度(图 14c)。
|
图 14 不同时窗长度W的单震源(黑虚线左侧)及多震源(黑虚线右侧)定位成像结果 (a)W=25;(b)W=40;(c)W=50 |
分别将图 1a模型的速度值增大和减少20%、15%、10%和5%,采用与前述相同的处理流程和参数,在速度模型不准确的情况下对合成微震记录(图 10b)进行定位成像结果分析,得到不同速度扰动的定位误差(计算震源位置与理论震源位置(0,0,1450m)之差)对比。从图 15易见,速度模型误差对定位结果影响较大,且当模型出现负的速度扰动时,其定位误差大于正的速度扰动,故利用射孔信号对速度模型进行校正显得尤为重要。

|
图 15 不同速度扰动下的定位误差对比 |
将本文方法应用于M油田相邻两段压裂过程的地面微震监测实际资料。监测台站布设如图 16a所示,大致呈星形共安置了42个检波器。压裂井口坐标为(0,0,0),两段压裂的射孔深度分别为2930m和2865m,第一和第二段射孔坐标(图 16a中红色点)分别位于(112m,672m,2930m)和(105m,670m,2865m)。利用压裂井声波测井曲线建立一维速度模型(图 16c),该模型划分为10个水平层,划分依据为测井曲线速度值突变处即为地层分界面。第二段射孔微震记录做过带通滤波预处理(图 16d)。

|
图 16 实际地面微震监测系统与资料 (a)观测系统立体图;(b)观测系统俯视图;(c)地层速度曲线;(d)第二段射孔微震信号 蓝色三角为检波器,红色五星为射孔点,黑色线为压裂井轨迹 |
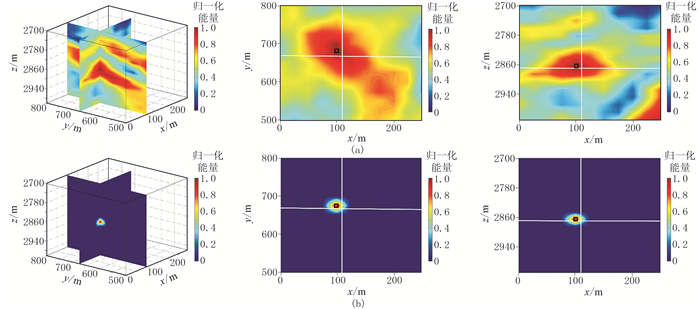
根据射孔坐标将定位成像区域范围划为x∈[-100m,300m],y∈[-500m,900m],z∈[2600m,3200m]。利用互相关叠加和互相关相乘成像函数得到第二段射孔记录的成像结果(图 17)。互相关叠加成像函数的定位射孔位置坐标为(100m,680m,2860m),定位误差(计算射孔位置与实际射孔位置之差)为12.24m;互相关相乘成像函数的定位坐标为(100m,675m,2860m),定位误差为8.66m,精度更高。从定位成像结果可知,互相关叠加成像函数定位成像结果的能量“聚焦”分辨率较低,出现大面积局部能量极值现象,能量“聚焦”不够集中,一定程度上干扰了震源位置的确定。互相关相乘能量“聚焦”的震源分辨率显著高于叠加法能量“聚焦”的分辨率,几乎没有出现大面积的能量极大值现象,说明互相关相乘成像函数对空间成像域中虚假成像“噪声”有明显压制作用,有利于微震事件位置的精确确定。
|
图 17 对射孔记录用互相关叠加(a)和互相关相乘(b)成像函数得到的定位成像结果 |
从实际射孔事件微震定位结果可知:基于偏移成像的微震定位方法对低信噪比微震资料具有良好处理效果;但基于叠加能量成像函数的微震定位方法具有较大局限性;而基于互相关相乘成像函数能较好地改善震源成像分辨率,提高定位精度。
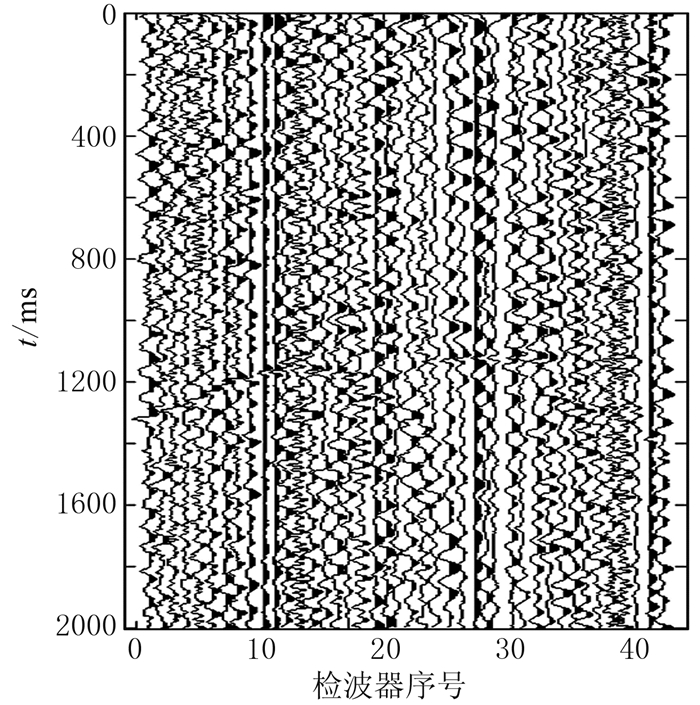
针对低信噪比实际微震监测记录(图 18),进行了微震事件检测和成像对比分析(图 19)。可知互相关相乘成像函数的定位成像结果具有较高的成像分辨率,更易于震源位置的识别。根据偏移类定位方法的基本原理,分别利用两种成像函数所得到的震源位置到各个检波器的初至旅行时,对实际监测微震记录(图 18)做时差校正,得到校正后的微震记录(图 20)。利用互相关叠加成像函数的定位结果做时差校正后,微震事件波形同相轴曲线清晰度不够高,且校正后的微震事件波形同相轴未被“拉平”,导致出现较大定位误差。而利用互相关相乘成像函数的定位结果对微震记录时差校正后,微震事件波形同相轴被“拉平”,定位精度较高。
|
图 18 实际监测中的低信噪比微震事件记录 |
|
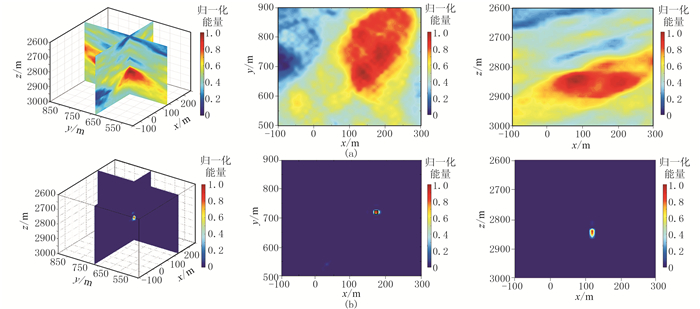
图 19 针对低信噪比实际微震资料用互相关叠加(a)和互相关相乘(b)成像函数所得定位成像结果 |
|
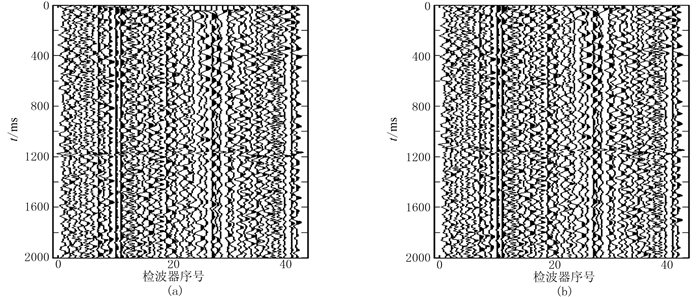
图 20 互相关叠加(a)和互相关相乘(b)成像函数定位结果的微震记录时差校正 |
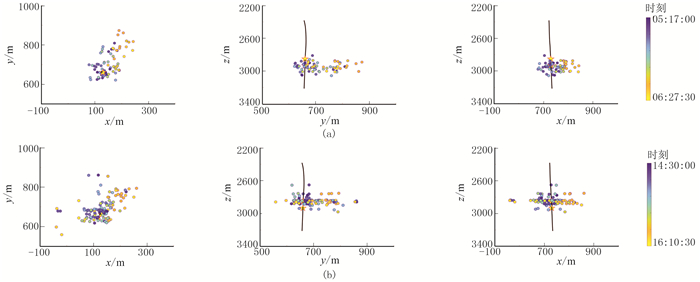
对相邻两段压裂过程中地面微地震连续监测资料进行定位处理,图 21为井旁地震记录。分别利用互相关叠加和互相关相乘成像函数得到两段压裂的微震事件定位结果(图 22)。利用互相关叠加成像函数得到的微震事件(图 22a)较为分散,尤其在射孔点位置周围微震事件较为稀疏,且微震事件定位结果在垂向范围较分散,分层现象不明显,将会影响对油藏改造体积(SRV)的精确估计;利用互相关相乘成像函数得到的微震事件(图 22b)较连续和聚集,更能反映实际裂隙的走向,且在垂直方向微震事件出现较明显的与射孔深度相关的分层现象,表明定位结果的可信度更高。图 23为利用互相关相乘成像函数所得到的微震事件位置随时间的变化。可见发震时间较早的微震事件(深蓝色)主要分布在射孔点位置附近,分布较集中;随着压裂进行,微震事件逐渐远离射孔点位置向北东向发展(深黄色),分布较为分散,表明定位结果较为合理。对这两段压裂裂隙的评估结果:方位角约为45°,西侧裂缝分布长约为70m,东侧裂缝分布长约为200m。
|
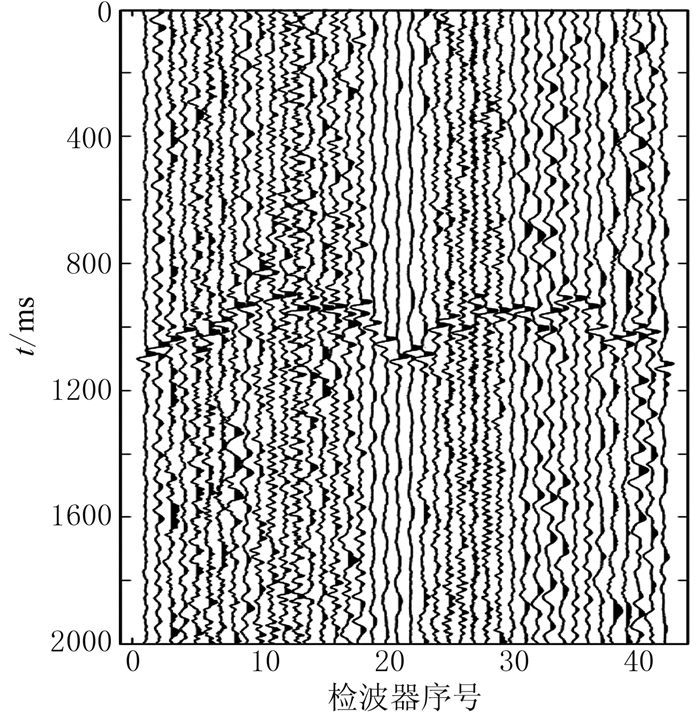
图 21 井旁地震记录 |
|
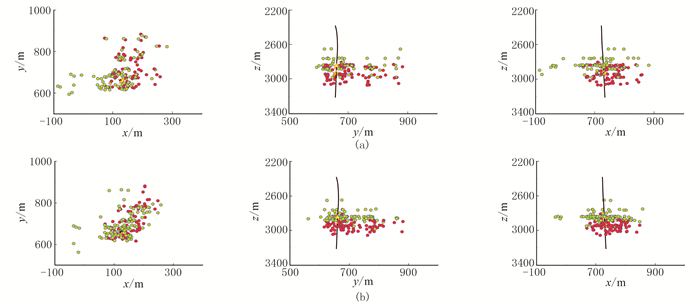
图 22 互相关叠加(a)和互相关相乘(b)成像函数对第二段微地震记录的定位结果 红色圆点和绿色圆点分别表示第一段和第二段压裂的震源分布,黄色五角星为射孔点;从左到右对应x-y、y-z和x-z平面投影 |
|
图 23 微震事件位置随时间变化关系 (a)第一段压裂;(b)第二段压裂 |
基于偏移叠加成像的微震定位方法较适用于低信噪比微震资料的定位。但基于叠加能量的定位方法不能同时兼顾消除噪声和初至极性反转对震源叠加能量的影响,降低定位精度。本文提出的基于微地震记录互相关相乘的成像函数微震定位方法,能显著削弱随机噪声和初至极性反转对震源能量聚焦的影响,压制空间域噪声产生的假像,提高震源成像分辨率及微震事件的定位精度。
计算互相关时要选取合适的时窗长度,在实际应用时,可根据射孔信号给出一个估计值。与偏移成像类方法相似,速度模型对成像和定位有较大影响,因此用这类方法需构建精确的速度模型,或要求在成像的同时校正速度模型。
| [1] |
刘振武, 撒利明, 杨晓, 等. 页岩气勘探开发对地球物理技术的需求[J]. 石油地球物理勘探, 2011, 46(5): 810-818. LIU Zhenwu, SA Liming, YANG Xiao, et al. Needs of geophysical technologies for shale gas exploration[J]. Oil Geophysical Prospecting, 2011, 46(5): 810-818. |
| [2] |
Maxwell S C, Rutledge J, Jones R, et al. Petroleum reservoir characterization using downhole microseismic monitoring[J]. Geophysics, 2010, 75(5): A129-A137. |
| [3] |
杜开元, 段国斌, 徐刚, 等. 深层页岩气井压裂加砂工艺优化的微地震评价[J]. 石油地球物理勘探, 2018, 53(增刊2): 148-155. DU Kaiyuan, DUAN Guobin, XU Gang, et al. Microseismic event evaluation for sand fracture optimization in deep shale-gas wells[J]. Oil Geophysical Prospecting, 2018, 53(S2): 148-155. |
| [4] |
Anikiev D, Valenta J, Staněk F, et al. Joint location and source mechanism inversion of microseismic events:benchmarking on seismicity induced by hydraulic fracturing[J]. Geophysical Journal International, 2014, 198(1): 249-258. DOI:10.1093/gji/ggu126 |
| [5] |
Zhebel O, Eisner L.Simultanous microseismic event localization and source mechanism determination[C].SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [6] |
刘星, 金衍, 林伯韬, 等. 利用微地震事件重构三维缝网[J]. 石油地球物理勘探, 2019, 54(1): 102-111. LIU Xing, JIN Yan, LIN Botao, et al. A 3D network reconstruction method based on microseismc events[J]. Oil Geophysical Prospecting, 2019, 54(1): 102-111. |
| [7] |
Eisner L, Hulsey B J, Duncan P, et al. Comparison of surface and borehole locations of induced seismicity[J]. Geophysical Prospecting, 2010, 58(5): 809-820. DOI:10.1111/j.1365-2478.2010.00867.x |
| [8] |
Chambers K, Kendall J M, Brandsberg-Dahl S, et al. Testing the ability of surface arrays to monitor microseismic activity[J]. Geophysical Prospecting, 2010, 58(5): 821-830. DOI:10.1111/j.1365-2478.2010.00893.x |
| [9] |
余洋洋, 梁春涛, 康亮, 等. 微地震地面监测系统的优化设计[J]. 石油地球物理勘探, 2017, 52(5): 974-983. YU Yangyang, LIANG Chuntao, KANG Liang, et al. Design optimization surface-based microseismic monitoring system for hydraulic fracturing[J]. Oil Geophysical Prospecting, 2017, 52(5): 974-983. |
| [10] |
崔庆辉, 尹成, 刁瑞, 等. 地面微地震监测数据处理难点及对策[J]. 油气藏评价与开发, 2017, 7(1): 7-13. CUI Qinghui, YIN Cheng, DIAO Rui, et al. Difficulties and countermeasure of surface microseismic monitoring data processing[J]. Reservoir Evaluation and Development, 2017, 7(1): 7-13. |
| [11] |
刘晗, 张建中, 黄忠来. 利用同步挤压变换检测微地震信号[J]. 中国科技论文, 2015, 10(21): 2472-2476. LIU Han, ZHANG Jianzhong, HUANG Zhonglai. Microseismic event detection based on synchrosqueezing wavelet transform[J]. China Science Paper, 2015, 10(21): 2472-2476. |
| [12] |
Kao H, Shan S J. The source-scanning algorithm:mapping the distribution of seismic sources in time and space[J]. Geophysical Journal of the Royal Astronomical Society, 2004, 157(2): 589-594. DOI:10.1111/j.1365-246X.2004.02276.x |
| [13] |
Bardainne T, Gaucher E, Cerda F, et al.Comparison of picking-based and waveform-based location methods of microseismic events: Application to a fracturing job[C].SEG Technical Program Expanded Abstracts, 2009, 28: 1547-1551.
|
| [14] |
Gharti H N, Oye V, Kühn D, et al.Simultaneous microearthquake location and moment-tensor estimation using time-reversal imaging[C].SEG Technical Program Expanded Abstracts, 2011, 30: 1632-1637.
|
| [15] |
Trojanowski J, Eisner L. Comparison of migration-based location and detection methods for microseismic events[J]. Geophysical Prospecting, 2016, 65(1): 1-17. |
| [16] |
王云宏. 基于DIRECT算法的微震震源快速网格搜索定位方法研究[J]. 地球物理学进展, 2016, 31(4): 1700-1708. WANG Yunhong. Grid-search method on micro-seismic fast location based on DIRECT algorithm[J]. Progress in Geophysics, 2016, 31(4): 1700-1708. |
| [17] |
王维波, 周瑶琪, 春兰. 地面微地震监测SET震源定位特性研究[J]. 中国石油大学学报(自然科学版), 2012, 36(5): 45-55. WANG Weibo, ZHOU Yaoqi, CHUN Lan. Characte-ristics of source localization by seismic emission tomography for surface based on microseismic monitoring[J]. Journal of China University of Petroleum (Natural Science Edition), 2012, 36(5): 45-55. |
| [18] |
Eaton D W, Akram J, St-Onge A, et al.Determining microseismic event locations by semblance-weighted stacking[C].Proceedings of the CSPG CSEG CWLS Convention, 2011.
|
| [19] |
Staněk F, Anikiev D, Valenta J, et al. Semblance for microseismic event detection[J]. Geophysical Journal International, 2014, 201(3): 1362-1369. |
| [20] |
何勇, 张建中, 李同宇. 改进的震源扫描定位方法[J]. 中国科技论文, 2016, 11(21): 2450-2455. HE Yong, ZHANG Jianzhong, LI Tongyu. Improved source-scanning algorithm for microseismic location[J]. China Science Paper, 2016, 11(21): 2450-2455. |
| [21] |
Liang C, Yu Y, Yang Y, et al. Joint inversion of source location and focal mechanism of microseismicity[J]. Geophysics, 2016, 81(2): KS103-KS111. DOI:10.1190/GEO-2015-0272.1 |
| [22] |
徐克彬, 陈祖斌, 刘玉海, 等. 基于L-M算法的微地震定位方法[J]. 石油地球物理勘探, 2018, 53(4): 765-769, 790. XU Kebin, CHEN Zubin, LIU Yuhai, et al. A microseismic localization method based on L-M inversion algorithm[J]. Oil Geophysical Prospecting, 2018, 53(4): 765-769, 790. |
| [23] |
Grandi S.Microseismic event location by cross-correlation migration of surface array data for permanent reservoir monitoring[C].Extended Abstracts of 71st EAGE Conference & Exhibition, 2009, CP127.
|
| [24] |
Gibbons S J, Ringdal F. The detection of low magnitude seismic events using array-based waveform correlation[J]. Geophysical Journal International, 2006, 165(1): 149-166. DOI:10.1111/j.1365-246X.2006.02865.x |
| [25] |
Zhebel O.Imaging of Seismic Events, the Role of Imaging Conditions, Acquisition Geometry and Source Mechanisms[D].University Hamburg, Hamburg, 2013.
|
| [26] |
姚振岸, 孙成禹, 唐杰, 等. 基于不同震源机制的黏弹各向异性微地震波场模拟[J]. 石油地球物理勘探, 2017, 52(1): 63-70. YAO Zhen'an, SUN Chengyu, TANG Jie, et al. Micro-seismic forward in viscoelastic anisotropic media based on different focal mechanisms[J]. Oil Geophysical Prospecting, 2017, 52(1): 63-70. |
| [27] |
Trojanowski J, Eisner L. Comparison of migration-based location and detection methods for microseismic events[J]. Geophysical Prospecting, 2017, 65(1): 1-17. DOI:10.1111/1365-2478.12456 |
| [28] |
Huang Y, Zhang J, Liu Q H. Three-dimensional GPR ray tracing based on wavefront expansion with irregular cells[J]. IEEE Transactions on Geoscience & Remote Sensing, 2011, 49(2): 679-687. |



 张建中, 山东省青岛市松岭路238号中国海洋大学海洋地球科学学院, 266100。Email:
张建中, 山东省青岛市松岭路238号中国海洋大学海洋地球科学学院, 266100。Email: