2 中国石油大学(北京)油气资源与探测国家重点实验室, 北京 102249
2 State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum(Beijing), Beijing 102249, China
全波形反演是一种精确的地下弹性参数重建方法,它充分利用地震记录中包含的动力学和运动学信息,以波动方程为数学模型建立目标泛函,通过不断迭代优化目标泛函使正演波场与实际波场差值最小,得到目标泛函的最优解,重构地下物性参数,服务油气勘探开发。全波形反演既可以在时间域进行也可以在频率域进行[1-3]。全波形反演主要包括正演和反演两个步骤。正演过程中常用的方法有迭代法和直接求接法;反演过程利用迭代优化方法逐步对初始模型进行修改直到满足误差要求。迭代优化是全波形反演中最重要的部分。全波形反演的优化算法主要包括梯度法和牛顿法。梯度法主要包括最速下降法[4-6]和非线性共轭梯度法[7-8];牛顿法主要包括高斯牛顿法[9]、拟牛顿法[10]、截断牛顿法[11]和全牛顿法[9, 12]。牛顿法收敛快但计算量和内存消耗较大,在实际反演过程中主要采用非线性共轭梯度法和高斯牛顿法。在每次迭代优化中都需要多次正演计算,这会大大增加计算量,因此研究一种高效的反演算法尤为重要。
为解决扰动较大的逆散射问题,同时提高解逆散射问题的效率,van den Berg等[13]从逆散射理论出发,基于源型积分方程[14]提出积分型对比源反演(IE-CSI)方法。该方法是一种解逆散射问题的高效方法,通过不断优化目标函数更新对比源(散射源)和对比度(扰动),在迭代优化的过程中只需进行一次全正演运算,从而提高了反演效率。van Dongen等[15]将该方法应用到三维声波成像,验证了该方法的高效性。Wang等[16]采用WKBJ近似方法求解Green函数的思路研究了对比源反演方法。由于积分型对比源反演是基于积分方程提出的,在实际反演中需要求解Green函数,在均匀或者水平渐变的背景模型条件下可以得到Green函数,但当模型比较复杂时就很难求解Green函数。为了进一步拓展对比源反演方法的适用范围,Abubakar等[17-18]研究了有限差分对比源反演(FDCSI)方法,并且将该方法成功推广到地震全波形反演。FDCSI适用于较复杂的背景模型,其构造的正演算子只与背景模型和频率有关。由于迭代求解过程中频率和背景模型保持不变,因此不需要重新构造正演算子,只需进行一次LU分解,提高了计算效率。基于以上优点,FDCSI具有处理大尺度数据的优势[19]。Han等[20]和He等[21]分别对地震弹性波和声波数据进行FDCSI反演,实现了多参数反演。段晓亮等[22]利用对比源反演研究了地层衰减对地震波速度逆散射反演的影响。
FDCSI计算效率较高,但是对目标函数的优化采用的是常规共轭梯度法,因而收敛较慢。为了解决收敛速度的问题,进一步提高FDCSI效率,本文在反演中采用混合快速共轭梯度(HFCG)法优化目标函数。HFCG法是在快速迭代收缩阈值算法(FISTA)[23-25]和快速共轭梯度法(FCG)[26]的基础上改进得到的一种适用于FDCSI的快速收敛优化方法。FISTA是一种一阶优化近似分裂算法,该方法能够加速目标泛函收敛[25]。HFCG比常规共轭梯度法收敛更快。该方法通过修改迭代公式加速目标泛函收敛,因此不会增加总的计算量,能够很好地平衡计算量与收敛速度。模型测试结果表明,该方法能够明显加速收敛,并提高反演结果精度。
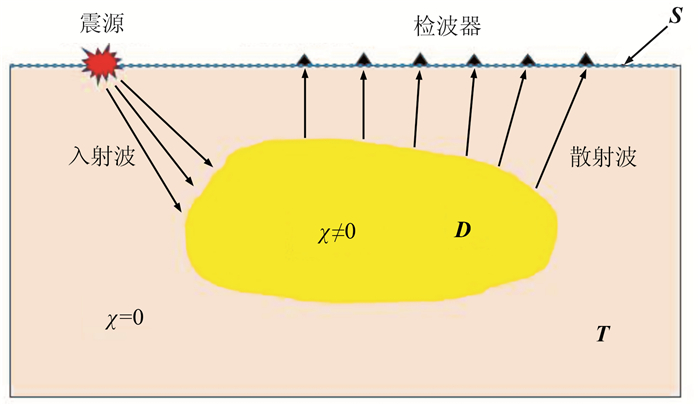
1 FDCSI基本理论 1.1 问题描述对比源反演是为了解决逆散射问题[12](图 1)。当目标域中的物性参数(如速度、密度等)不同于总区域背景模型参数时,对比度χ≠0(存在扰动)。地震波传播到目标域时会产生散射波,并被布置在S域上的检波器接收到,利用接收到的散射波反演对比度χ、重建目标域D的物性参数即是解逆散射问题。
|
图 1 逆散射示意图 图中S表示数据域(检波器所在位置);D表示目标域;T为总空间 |
在频率空间域中,声波在介质中传播满足Helmholtz方程,因此散射问题中,第j炮的总波场Ujtol和背景波场Ujinc(入射波场)可以简化为[27-29]
| $ \boldsymbol{H} \boldsymbol{U}_{j}^{\mathrm{tol}}=\boldsymbol{S}_{j} $ | (1) |
| $ \boldsymbol{H}_{\mathrm{b}} \boldsymbol{U}_{j}^{\mathrm{inc}}=\boldsymbol{S}_{j} $ | (2) |
式中:H和Hb分别为与模型和背景有关的稀疏阻抗矩阵;Sj为震源项。
定义对比度χ(模型扰动)为[18]
| $ \chi^{(\boldsymbol{r})}=\left[\frac{k(\boldsymbol{r})}{k_{\mathrm{b}}(\boldsymbol{r})}\right]^{2}-1=\frac{c^{-2}(\boldsymbol{r})-c_{\mathrm{b}}^{-2}(\boldsymbol{r})}{c_{\mathrm{b}}^{-2}(\boldsymbol{r})} \quad \boldsymbol{r} \in \boldsymbol{D} $ | (3) |
式中:r为空间坐标;k和c分别为模型的波数和速度;kb和cb分别为背景模型的波数和速度。
根据总波场、背景波场和散射波场的关系,可得[16]
| $ \boldsymbol{U}_{j}^{\mathrm{sct}}=\boldsymbol{U}_{j}^{\mathrm{tol}}-\boldsymbol{U}_{j}^{\mathrm{inc}} \quad \boldsymbol{r} \in \boldsymbol{T} $ | (4) |
| $ \boldsymbol{U}_{j}^{\mathrm{sct}}=\boldsymbol{A}_{\mathrm{b}}^{-1} \boldsymbol{\chi} \boldsymbol{U}_{j}^{\mathrm{tol}} \quad \boldsymbol{r} \in \boldsymbol{T} $ | (5) |
式中:Ab=Kb-1Hb, Kb为背景模型的波数对角阵;χ为对比度构成的对角矩阵。
在S域上接收到的散射波为[17]
| $ \boldsymbol{U}_{j}^{\mathrm{set}}=\boldsymbol{M}^{\mathrm{S}}\left(\boldsymbol{A}_{\mathrm{b}}^{-1} \boldsymbol{\chi} \boldsymbol{U}_{j}^{\mathrm{tol}}\right) \quad \boldsymbol{r} \in \boldsymbol{S} $ | (6) |
式中MS为将T域中的散射波映射到S域的算子。式(6)即为数据方程。
根据式(4)可以得到状态方程
| $ \boldsymbol{U}_{j}^{\mathrm{tol}}=\boldsymbol{U}_{j}^{\mathrm{inc}}+\boldsymbol{M}^{\mathrm{D}}\left(\boldsymbol{A}_{\mathrm{b}}^{-1} \chi \boldsymbol{U}_{j}^{\mathrm{tol}}\right) \quad \boldsymbol{r} \in \boldsymbol{D} $ | (7) |
MD为将T域中的散射波映射到D域的算子。
引入对比源(散射源)[18]
| $ \boldsymbol{W}_{j}=\chi \boldsymbol{U}_{j}^{\mathrm{tol}} $ | (8) |
式(6)和式(7)可以改写为[18]
| $ \boldsymbol{U}_{j}^{\mathrm{sct}}=\boldsymbol{M}^{\mathrm{S}}\left(\boldsymbol{A}_{\mathrm{b}}^{-1} \boldsymbol{W}_{j}\right) \quad \boldsymbol{r} \in \boldsymbol{S} $ | (9) |
| $ \boldsymbol{W}_{j}=\chi \boldsymbol{U}_{j}^{\mathrm{inc}}+\chi \boldsymbol{M}^{\mathrm{D}}\left(\boldsymbol{A}_{\mathrm{b}}^{-1} \boldsymbol{W}_{j}\right) \quad \boldsymbol{r} \in \boldsymbol{D} $ | (10) |
在地震勘探中,由于目标空间等同于地下空间,因此实际情况中T域与D域是相等的。
1.2 有限差分对比源反演在频率域FDCSI过程中,需要同时满足数据方程式(9)和状态方程式(10),不断优化求解对比源Wj和对比度χ,目标泛函为[17-18]
| $ \begin{array}{c} C\left(\boldsymbol{\chi}, \boldsymbol{W}_{j}\right)=C^{\mathrm{s}}\left(\boldsymbol{W}_{j}\right)+C^{\mathrm{D}}\left(\boldsymbol{W}_{j}, \boldsymbol{\boldsymbol{\chi}}\right) \\ =\frac{\sum\limits_{j}\left\|\boldsymbol{d}_{\mathrm{obs}, j}^{\mathrm{sct}}-\boldsymbol{M}^{\mathrm{S}}\left(\boldsymbol{A}_{\mathrm{b}}^{-1} \boldsymbol{W}_{j}\right)\right\|_{\mathrm{s}}^{2}}{\sum\limits_{j}\left\|\boldsymbol{d}_{\mathrm{obs}, j}^{\mathrm{sct}}\right\|_{\mathrm{s}}^{2}}+ \\ \frac{\sum\limits_{j}\left\|\boldsymbol{\chi} \boldsymbol{U}_{j}^{\mathrm{inc}}-\boldsymbol{W}_{j}+\boldsymbol{\chi} \boldsymbol{M}^{\mathrm{D}}\left(\boldsymbol{A}_{\mathrm{b}}^{-1} \boldsymbol{W}_{j}\right)\right\|_{\mathrm{D}}^{2}}{\sum\limits_{j}\left\|\boldsymbol{\chi} \boldsymbol{U}_{j}^{\mathrm{inc}}\right\|_{\mathrm{D}}^{2}} \end{array} $ | (11) |
式中:CS(Wj)和CD(Wj, χ)分别为数据方程的残差和状态方程的残差;dobs, jsct为地表观测散射记录。
定义S域和D域的L2范数为[17]
| $ \left\{\begin{array}{l} \|\boldsymbol{a}\|_{\boldsymbol{S}}^{2}=\int_{\boldsymbol{S}} \boldsymbol{\boldsymbol{a}}(\boldsymbol{r}) \bar{\boldsymbol{a}}(r) \mathrm{d} \boldsymbol{r} \\ \|\boldsymbol{a}\|_{\boldsymbol{D}}^{2}=\int_{\boldsymbol{D}} \boldsymbol{\boldsymbol{a}}(\boldsymbol{r}) \bar{\boldsymbol{a}}(r) \mathrm{d} \boldsymbol{r} \end{array}\right. $ | (12) |
式中:a表示向量;a为a的复共轭。
从式(11)可以看出,反演过程中需要不断更新对比源Wj和对比度χ。采取先更新对比源Wj、再更新对比度χ的方式完成每一次迭代。求解目标泛函关于对比源Wj的Fréchet导数,得到第n次迭代目标泛函关于对比源Wj的梯度[17]
| $ \begin{aligned} \boldsymbol{g}_{j, n}^{W}=&\left.\frac{\partial C^{\mathrm{S}}\left(\boldsymbol{W}_{j}\right)}{\partial \boldsymbol{W}_{j}}\right|_{W_{j}=w_{j, n-1}}+\left.\frac{\partial C^{\mathrm{D}}\left(\boldsymbol{W}_{j}, \boldsymbol{\chi}_{n-1}\right)}{\partial \boldsymbol{W}_{j}}\right|_{w_{j}=w_{j, n-1}} \\ =&-2 \eta^{\mathrm{s}}\left(\boldsymbol{A}_{\mathrm{b}}^{*}\right)^{-1} \boldsymbol{M}^{\mathrm{s} *} \boldsymbol{\phi}_{j, n-1}-2 \lambda \eta_{n}^{\mathrm{D}}\left[\boldsymbol{\beta}_{j, n-1}-\right.\\ &\left.\left(\boldsymbol{A}_{\mathrm{b}}^{*}\right)^{-1} \boldsymbol{M}^{\mathrm{D} *}\left(\overline{\boldsymbol{\chi}}_{n-1} \boldsymbol{\beta}_{j, n-1}\right)\right] \end{aligned} $ | (13) |
式中
| $ \left\{\begin{array}{l} \eta^{\mathrm{S}}=\left(\sum\limits_{j}\left\|\boldsymbol{d}_{\mathrm{obs}, j}^{\mathrm{sct}}\right\|_{\mathrm{S}}^{2}\right)^{-1} \\ \eta_{n-1}^{\mathrm{D}}=\left(\sum\limits_{j}\left\|\chi_{n-1} \boldsymbol{U}_{j}^{\mathrm{inc}}\right\|_{\mathrm{D}}^{2}\right)^{-1} \\ \boldsymbol{\phi}_{j, n}=\boldsymbol{d}_{\mathrm{obs}, j}^{\mathrm{sct}}-\boldsymbol{M}^{\mathrm{S}}\left(\boldsymbol{A}_{\mathrm{b}}^{-1} \boldsymbol{W}_{j, n}\right) \\ \boldsymbol{\beta}_{j, n}=\boldsymbol{\chi} \boldsymbol{U}_{j}^{\mathrm{inc}}-\boldsymbol{W}_{j, n}+\boldsymbol{\chi}_{n} \boldsymbol{M}^{\mathrm{D}}\left(\boldsymbol{A}_{\mathrm{b}}^{-1} \boldsymbol{W}_{j, n}\right) \end{array}\right. $ | (14) |
其中:“*”表示共轭转置;χ为χ的复共轭。
采用常规PR(Polak-Ribiere)共轭梯度法[30]更新对比源,其迭代公式为
| $ \boldsymbol{W}_{j, n}=\boldsymbol{W}_{j, n-1}+\alpha_{j, n}^{\boldsymbol{W}} \boldsymbol{v}_{j, n} $ | (15) |
式中:vj, n为PR搜索方向;αWj, n为更新步长。把更新后的对比源Wj, n代入式(11),并极小化C(χn-1, Wj, n),可得到最优更新步长。
利用更新后的对比源Wj, n,根据式(7)和式(8),得到总波场Uj, ntol和对比度χn的迭代公式为
| $ \boldsymbol{U}_{j, n}^{\mathrm{tol}}=\boldsymbol{U}_{j}^{\mathrm{inc}}+\boldsymbol{M}^{\mathrm{D}}\left(\boldsymbol{A}_{\mathrm{b}}^{-1} \boldsymbol{W}_{j, n}\right) $ | (16) |
| $ \boldsymbol{\chi}_{n}=\frac{\sum\limits_{j} \operatorname{Re}\left(\boldsymbol{W}_{j, n} \overline{\boldsymbol{U}}_{j, n}^{\mathrm{tol}}\right)}{\sum\limits_{j}\left|\boldsymbol{U}_{j, n}^{\mathrm{tol}}\right|^{2}} $ | (17) |
式中Re(·)表示求实部。
初始模型会影响反演结果,因此采取波场反传方法得到初始对比源Wj, 0和初始对比度χ0[14]
| $ \begin{aligned} &\boldsymbol{W}_{j, 0}=\frac{\left\|\left(\boldsymbol{A}_{\mathrm{b}}^{*}\right)^{-1}\left(\boldsymbol{M}^{\mathrm{S} *} \boldsymbol{d}_{\mathrm{obs}, j}^{\mathrm{sct}}\right)\right\|_{\mathrm{D}}^{2}}{\left\|\boldsymbol{M}^{\mathrm{S}}\left\{\boldsymbol{A}_{\mathrm{b}}^{-1}\left[\left(\boldsymbol{A}_{\mathrm{b}}^{*}\right)^{-1}\left(\boldsymbol{M}^{\mathrm{S} *} \boldsymbol{d}_{\mathrm{obs}, j}^{\mathrm{sct}}\right)\right]\right\}\right\|_{\mathrm{s}}^{2}} \times\\ &\left(\boldsymbol{A}_{\mathrm{b}}^{*}\right)^{-1}\left(\boldsymbol{M}^{\mathrm{S} *} \boldsymbol{d}_{\mathrm{obs}, j}^{\mathrm{sct}}\right) \end{aligned} $ | (18) |
| $ \boldsymbol{U}_{j, 0}^{\mathrm{tol}}=\boldsymbol{U}_{j}^{\mathrm{inc}}+\boldsymbol{M}^{\mathrm{D}}\left(\boldsymbol{A}_{\mathrm{b}}^{-1} \boldsymbol{W}_{j, 0}\right) $ | (19) |
| $ \chi_{0}=\frac{\sum\limits_{j} \operatorname{Re}\left(\boldsymbol{W}_{j, 0} \overline{\boldsymbol{U}}_{j, 0}^{\mathrm{tol}}\right)}{\sum\limits_{j}\left|\boldsymbol{U}_{j, 0}^{\mathrm{tol}}\right|^{2}} $ | (20) |
反演过程中主要的计算量是计算(Ab)-1和(Ab*)-1, 这两个算子只与背景模型和反演频率有关,单频反演过程中这两个算子是不变的。因此,在单频反演过程中,只需利用一次LU分解以求解这两个算子,并保存分解结果,用于下一次迭代,提高计算效率。
FDCSI算法能够高效求解逆散射问题,但是常规共轭梯度法的优化方法收敛速度慢,降低了反演效率。因此本文将快速迭代收缩阈值算法(FISTA)[23]引入FDCSI,提高反演效率。
2 混合快速共轭梯度法HFCG法与常规共轭梯度法相比,主要是修改了对比源更新迭代公式,这仅增加少量点乘运算,但大大提高了反演的收敛速度。常规共轭梯度法的迭代公式为式(15),式中的vj, n即是通过PR共轭梯度法得到的搜索方向。HFCG法参考快速迭代收缩阈值算法,通过修改式(15)中的Wj, n-1达到快速收敛的效果,用Qj, n-1替代式(15)中的Wj, n-1。Qj, n-1的表达式为[23]
| $ \boldsymbol{Q}_{j, n-1}=\boldsymbol{W}_{j, n-1}+\frac{t_{n}-1}{t_{n+1}}\left(\boldsymbol{W}_{j, n-1}-\boldsymbol{W}_{j, n-2}\right) $ | (21) |
| $ t_{n+1}=\frac{1+\sqrt{1+4 t_{n}^{2}}}{2} $ | (22) |
式中t1=1,修改后的迭代形式如下[22]
| $ \boldsymbol{W}_{j, n}=\boldsymbol{Q}_{j, n-1}+\alpha_{j, n}^{W} \boldsymbol{v}_{j, n} $ | (23) |
当目标泛函残差趋于收敛时,式(23)的迭代收敛曲线存在抖动,因此在趋于收敛时采用常规共轭梯度法进行优化迭代,进一步减小目标泛函残差。则HFCG的迭代公式为
| $ \boldsymbol{W}_{j, n}=\left\{\begin{array}{ll} \boldsymbol{Q}_{j, n-1}+\alpha_{j, n}^{W} \boldsymbol{v}_{j, n} & n<N_{\text {unstable }} \\ \boldsymbol{W}_{j, n-1}+\alpha_{j, n}^{W} \boldsymbol{v}_{j, n} & n \geqslant N_{\text {unstable }} \end{array}\right. $ | (24) |
式中Nunstable为迭代收敛曲线出现不稳定现象时的迭代次数。
3 模型算例为了验证方法的有效性,分别针对水平层状模型和重采样后的Marmousi模型进行数值模拟实验。实验中把上一个频率反演的结果作为下一个频率反演的背景模型。
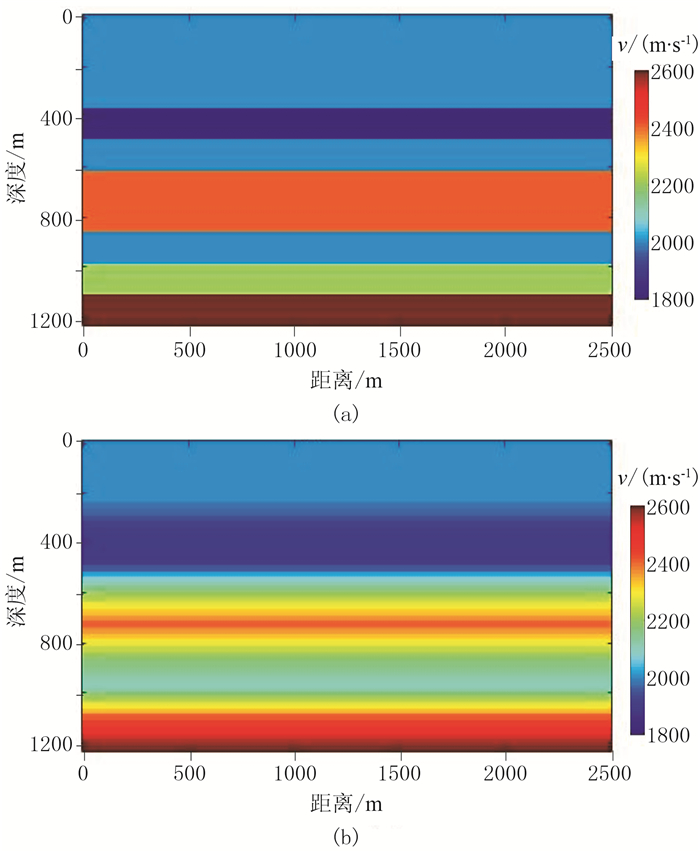
3.1 水平层状模型水平层状模型如图 2a所示,该模型共有七层,速度范围是1800~2600m/s,模型深度为1225m。模型被离散为100(x)×49(z)个网格。采用地表放炮,共13炮,炮间距为200m;101个检波器均匀分布在地表,道间距为25m,每炮激发共101道接收。根据频率选取原则[31]选择6个频率进行反演,分别为3.0、4.2、6.1、8.7、12.5、17.8Hz,每个频率迭代30次,把低频点反演结果作为高频点反演的背景模型。背景模型是真实模型经二维平滑处理得到的,如图 2b所示。
|
图 2 水平层状速度模型 (a)真实速度模型;(b)背景模型 |
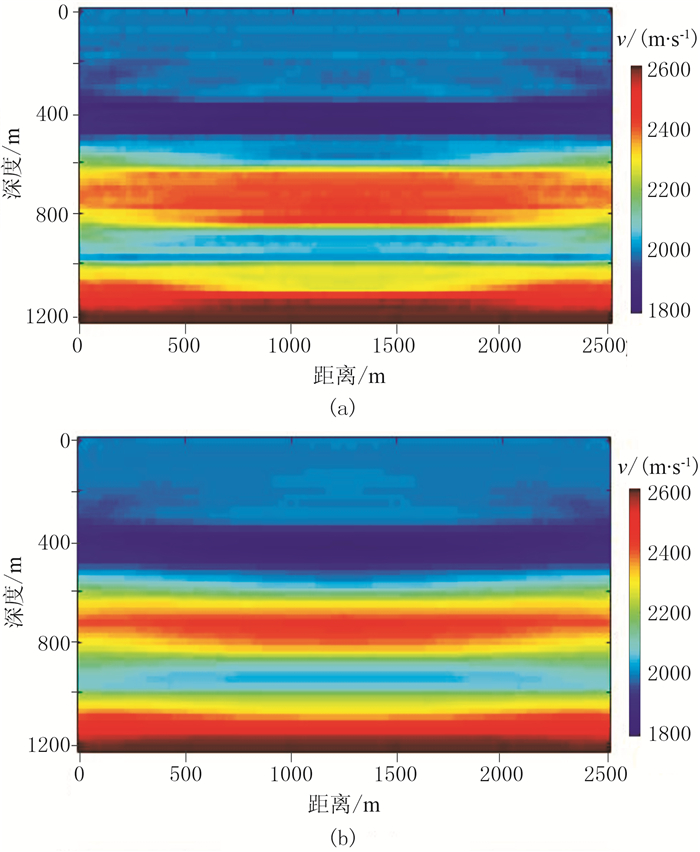
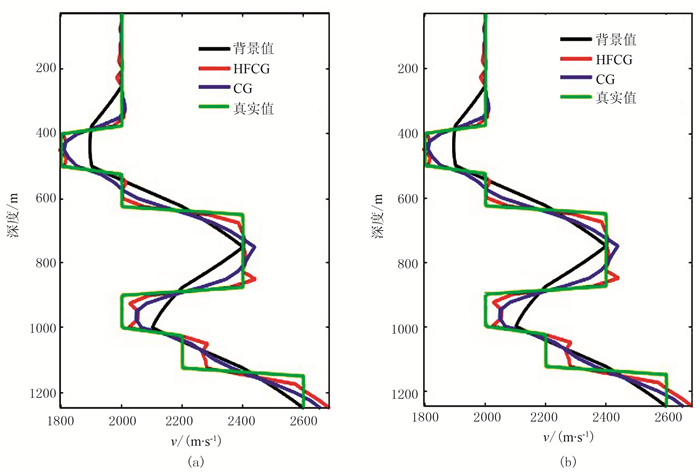
分别采用HFCG法和常规共轭梯度法得到的反演结果见图 3。对比图 3a与图 3b可以看出,采用HFCG法得到的结果分辨率更高、收敛效果更好。两种方法反演结果与真实速度模型的L2范数残差分别为4292.3和5376.5,可见HFCG法反演结果更接近真实速度。图 4为x=1000m和x=1600m处纵向速度对比,可以看出HFCG法对界面具有更好的识别和刻画能力。
|
图 3 采用HFCG(a)和常规共轭梯度法(b)反演的速度剖面 |
|
图 4 x=1000m(a)和x=1500m(b)处不同方法纵向速度曲线对比 |
图 5为两种方法6个频率的目标泛函收敛曲线对比。从图中可以看出,HFCG法具有非常明显的快速收敛优势,该方法在很少的迭代次数时就可实现目标泛函的收敛。

|
图 5 不同频率时HFCG法(红线)与常规共轭梯度法(蓝线)目标泛函收敛曲线对比 (a)3.0Hz; (b)4.2Hz; (c)6.1Hz; (d)8.7Hz; (e)12.5Hz; (f)17.8Hz |
对Marmousi模型进行抽稀,抽稀后的速度模型如图 6a所示。模型被离散为368×160个网格。采用地表激发和地表接收的观测系统,共47炮,炮间距为200m,369道检波器均匀分布在地表,道间距为25m,每炮激发369道接收。选取9个频率进行反演,分别为2、3、4、5、6、8、10、12、16Hz,每个频率均迭代100次,把低频点反演结果作为高频点反演的背景模型。与水平层状模型一样,背景模型也是真实模型经二维平滑处理得到的,如图 6b所示。

|
图 6 抽稀的Marmousi模型 (a)速度模型;(b)背景速度模型 |
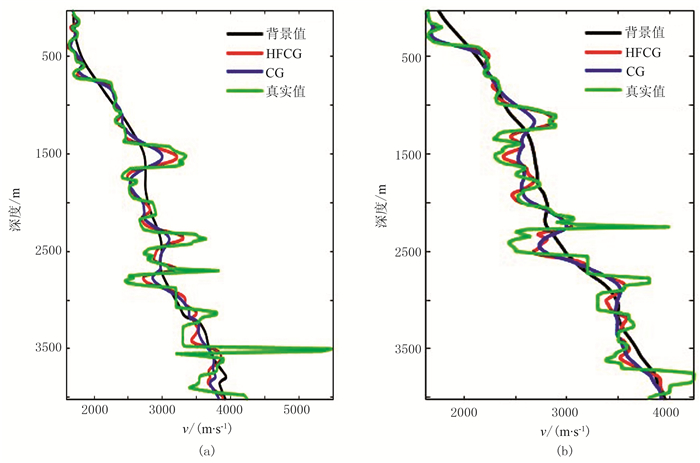
分别采用HFCG法和常规共轭梯度法对图 6所示模型进行反演,结果见图 7。可以看出,采用HFCG法的结果优于常规共轭梯度法反演结果,其反演结果分辨率更高。两种方法反演结果与真实模型的L2范数残差分别为49115和55991。图 8为模型纵向速度曲线对比,可以看出HFCG法反演结果更接近真实模型。

|
图 7 采用HFCG法(a)和常规共轭梯度法(b)的Marmousi模型速度反演剖面 |
|
图 8 x=4000m(a)和x=5200m(b)处HFCG法和常规共轭梯度法反演纵向速度曲线对比 |
图 9为HFCG法和常规共轭梯度法在不同频率的目标泛函收敛曲线对比。可以看出,每个频率迭代100次后,HFCG法的目标泛函已经收敛,而常规共轭梯度法的目标泛函还未收敛,可见前者具有非常明显的快速收敛优势,只需很少的迭代次数就可实现目标泛函的收敛。

|
图 9 HFCG法(红线)与常规共轭梯度法(蓝线)在不同频率的目标泛函收敛曲线对比 (a)2Hz; (b)3Hz; (c)4Hz; (d)5Hz; (e)6Hz; (f)8Hz;(g)10Hz; (h)12Hz; (i)16Hz |
为了验证HFCG法的有效性,分别对水平层状模型(图 2)和Marmousi模型(图 6)运用HFCG法和常规共轭梯度法进行反演效率定量测试,比较、分析在相同的迭代终止条件下两种方法的迭代次数。本文采用的迭代终止条件是数据残差
| $ \mathrm{ERR}=\frac{\sum\limits_{j}\left\|\boldsymbol{d}_{\mathrm{obs}, j}^{\mathrm{sct}}-\boldsymbol{d}_{\mathrm{cal}, j}^{\mathrm{sct}}\right\|_{\boldsymbol{D}}^{2}}{\sum\limits_{j}\left\|\boldsymbol{d}_{\mathrm{obs}, j}^{\mathrm{sct}}\right\|_{\boldsymbol{D}}^{2}} \leqslant 0.005 $ | (25) |
式中dcal, jsct为计算的散射波场。HFCG法需额外计算极少量的点乘运算,与单次迭代时间相比可以忽略,因此可仅通过迭代次数对比两种方法反演的效率。
采用HFCG和常规共轭梯度法分别对图 2所示水平层状模型进行反演,满足式(25)时的反演结果见图 10。从图中可以看出,当迭代误差终止条件相同时,两种方法反演得到水平层状模型基本相同。HFCG法和常规共轭梯度法的反演迭代次数分别为122和271,前者较后者的计算效率提高了近55%。

|
图 10 水平层状模型反演结果 (a)HFCG法反演结果;(b)常规共轭梯度法反演结果 |
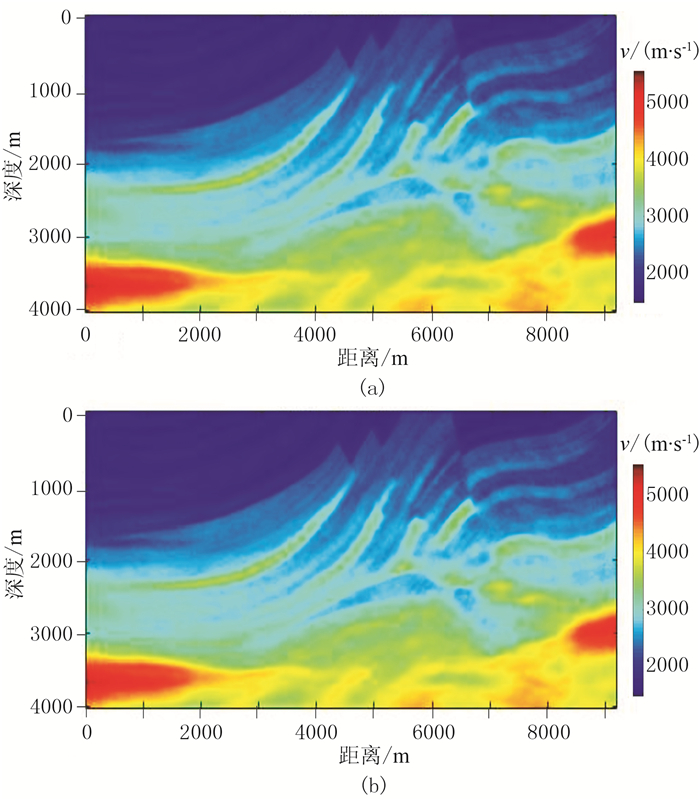
采用HFCG和常规共轭梯度法分别对图 6所示Marmousi模型进行反演,满足式(25)时的反演结果见图 11。从图中可以看出,当迭代误差终止条件相同时,两种方法反演得到Marmousi模型基本相同。经统计,HFCG法和常规共轭梯度法反演的迭代次数分别为617和1183,前者较后者的计算效率提高了近49%。
|
图 11 Marmousi模型反演结果 (a)HFCG法;(b)常规共轭梯度法 |
有限差分对比源反演利用有限差分算子构造反演算子,可求解逆散射问题,适用于复杂介质的对比源反演。运用该方法对单个频率数据进行反演,正、反演算子只与背景模型有关,无需改变背景模型。因此只需构造一次正反演算子,进行一次LU分解,减少了正反演计算量,提高了反演效率。本文在常规共轭梯度法对比源反演的基础上引入适用于对比源反演的混合快速共轭梯度法,在不增加计算量的基础上加速目标泛函收敛,进一步提高了反演效率。基于HFCG法的FDCSI方法具有明显加速目标泛函收敛的优势,适用于大数据量反演。
本文只研究了介质密度为常数的频率域声波方程FDCSI方法。对于复杂地下介质,后续可针对密度参数,开展弹性波方程FDCSI的研究。
| [1] |
Tarantola A. A strategy for nonlinear elastic inversion of seismic reflection data[J]. Geophysics, 1986, 51(5): 1893-1903. |
| [2] |
Pratt R G, Worthington M H. Inverse theory applied to multisource cross-hole tomography:Part 1, Acoustic wave-equation method[J]. Geophysical Prospecting, 1990, 38(3): 287-310. |
| [3] |
李海山, 杨午阳, 雍学善. 三维一阶速度-应力声波方程全波形反演[J]. 石油地球物理勘探, 2018, 53(4): 730-736. LI Haishan, YANG Wuyang, YONG Xueshan. Three-dimensional full waveform inversion based on the first-order velocity-stress acoustic wave equation[J]. Oil Geophysical Prospecting, 2018, 53(4): 730-736. |
| [4] |
Choi Y, Shin C, Min D J, et al. Efficient calculation of the steepest descent direction for source-independent seismic waveform inversion:an amplitude approach[J]. Journal of Computational Physics, 2005, 208: 455-468. |
| [5] |
Jang U, Min D J, Shin C. Comparison of scaling me-thods for waveform inversion[J]. Geophysical Prospecting, 2009, 57(1): 49-59. |
| [6] |
Chi B, Dong L, Liu Y. Full waveform inversion me-thod using envelope objective function without low frequency data[J]. Journal of Applied Geophysics, 2014, 109: 36-46. |
| [7] |
Pratt R G. Seismic waveform inversion in the frequency domain, Part 1:Theory and verification in a physical scale model[J]. Geophysics, 1999, 64(3): 888-901. |
| [8] |
Kamei R, Pratt R G, Tsuji T. Misfit functions in Laplace-Fourier domain waveform inversion, with application to wide-angle ocean bottom seismograph data[J]. Geophysical Prospecting, 2014, 62(5): 1054-1074. |
| [9] |
Pratt R G, Shin C, Hick G J. Gauss-Newton and full Newton methods in frequency space seismic waveform inversion[J]. Geophysical Journal International, 1998, 133(2): 341-362. |
| [10] |
Brossier R, Operto S, Virieux J. Seismic imaging of complex onshore structures by 2D elastic frequency domain full waveform inversion[J]. Geophysics, 2009, 74(6): WCC105-WCC118. |
| [11] |
Métivier L, Bretaudeau F, Brossier R, et al. Full waveform inversion and the truncated Newton method:quantitative imaging of complex subsurface structures[J]. Geophysical Prospecting, 2014, 62(6): 1353-1375. |
| [12] |
Kim W K, Min D J. A new parameterization for frequency-domain elastic full waveform inversion for VTI media[J]. Journal of Applied Geophysics, 2014, 109: 88-110. |
| [13] |
van den Berg P M, Ralph E K. A contrast source inversion method[J]. Inverse Problems, 1997, 13(6): 1607-1620. |
| [14] |
Tarek M H, Michael L O. Simultaneous nonli-near reconstruction of two-dimensional permittivity and conductivity[J]. Radio Science, 1994, 29(4): 1101-1118. |
| [15] |
van Dongen, Koen W A, William M D. A full vectorial contrast source inversion scheme for 3D acoustic imaging of both compressibility and density profiles[J]. Journal of the Acoustical Society of America, 2007, 121: 1538-1549. |
| [16] |
Wang S D, Wu R S, Liu Y F.The contrast source inversion for reflection seismic data[C].Extended Abstracts of 78th EAGE Conference and Exhibition, 2016, 01540.
|
| [17] |
Abubakar, Hu W, van den Berg P M, et al. A finite-difference contrast source inversion method[J]. Inverse Problems, 2008, 24(6): 065004-065020. |
| [18] |
Abubakar, Hu W, Tarek M H, et al. Application of the finite-difference contrast-source inversion algorithm to seismic full-waveform data[J]. Geophysics, 2009, 74(6): WCC47-WCC58. |
| [19] |
Abubakar, Pan G, Li M, et al. Three-dimensional seismic full-waveform inversion using the finite-difference contrast source inversion method[J]. Geophysical Prospecting, 2011, 59(5): 874-888. |
| [20] |
Han B, He Q, Chen Y, et al. Seismic waveform inversion using the finite-difference contrast source inversion method[J]. Journal of Applied Mathematics, 2014, 109: 1-11. |
| [21] |
He Q, Han B, Chen Y, et al. Application of the finite-difference contrast source inversion method to multi-parameter reconstruction using seismic full-waveform data[J]. Journal of Applied Geophysics, 2016, 124: 4-16. |
| [22] |
段晓亮, 翟鸿宇, 王一博, 等. 地层衰减对地震波速度逆散射反演的影响研究[J]. 地球物理学报, 2016, 59(10): 3788-3797. DUAN Xiaoliang, ZHAI Hongyu, WANG Yibo, et al. Effect of stratigraphic attenuation on inverse-scattering seismic velocity inversion[J]. Chinese Journal of Geophysics, 2016, 59(10): 3788-3797. |
| [23] |
Beck A, Teboulle M. A fast iterative shrinkage-thre-sholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(1): 183-202. |
| [24] |
Chambolle A, Dossal C. On the convergence of the iterates of the "fast iterative shrinkage/thresholding algorithm"[J]. Journal of Optimization Theory and Applications, 2015, 166(3): 968-982. |
| [25] |
陈少利, 杨敏. 改进变步长快速迭代收缩阈值算法[J]. 计算机技术与发展, 2017, 27(10): 69-73. CHEN Shaoli, YANG Min. An improved fast iterative shrinkage-thresholding algorithm with variable step size[J]. Computer Technology and Development, 2017, 27(10): 69-73. |
| [26] |
张广智, 孙昌路, 潘新朋, 等. 快速共轭梯度法频率域声波全波形反演[J]. 石油地球物理勘探, 2016, 51(4): 730-737. ZHANG Guangzhi, SUN Changlu, PAN Xinpeng, et al. Fast conjugate gradient method for frequency domain acoustic wave full waveform inversion[J]. Oil Geophysical Prospecting, 2016, 51(4): 730-737. |
| [27] |
Jo C H, Shin C S, Suh J H. An optimal 9-point, finite-difference, frequency-space, 2-D scalar wave extrapolator[J]. Geophysics, 1996, 61(2): 529-537. |
| [28] |
董士骑, 韩立国, 胡勇, 等. 基于MCPML边界条件的频率域声波方程高精度模拟[J]. 石油地球物理勘探, 2018, 53(1): 47-54. DONG Shiqi, HAN Liguo, HU Yong, et al. Acoustic equation high-accuracy modeling in the frequency domain based on MCPML absorbing boundary[J]. Oil Geophysical Prospecting, 2018, 53(1): 47-54. |
| [29] |
成景旺, 吕晓春, 顾汉明, 等. 基于柯西分布的频率域全波形反演[J]. 石油地球物理勘探, 2014, 49(5): 940-945. CHENG Jingwang, LYU Xiaochun, GU Hanming, et al. Full waveform inversion with Cauchy distribution in the frequency domain[J]. Oil Geophysical Prospecting, 2014, 49(5): 940-945. |
| [30] |
Polyak B T. The conjugate gradient method in extremal problems[J]. USSR Computational Mathematics & Mathematical Physics, 1969, 9(4): 94-112. |
| [31] |
Sirgue L, Pratt R G. Efficient waveform inversion and imaging:A strategy for selecting temporal frequencies[J]. Geophysics, 2004, 69(1): 231-248. |



 王守东, 北京市昌平区府学路18号中国石油大学(北京), 102249。Email:
王守东, 北京市昌平区府学路18号中国石油大学(北京), 102249。Email: