2 中国石油化工股份有限公司华东分公司, 江苏南京 210011;
3 中海石油(中国)有限公司天津分公司 天津 300452
2 East China Branch, Sinopec, Nanjing, Jiangsu 210011, China;
3 CNOOC(China) Tianjin Company, Tianjin 300452, China
全波形反演[1-4](FWI)依据地震数据的动力学特征提取速度参数,与旅行时层析等基于地震数据的运动学特征的方法相比,可以获得更精确的地下速度结构参数。
尽管FWI具有恢复地下精细速度信息的能力,但是仍然存在许多限制,如易陷入局部极值、缺失低频信息、对初始模型要求高等,反演实际数据时缺少准确的震源子波信息是主要制约因素之一[5]。早期FWI在模型试算时通常假设震源子波是已知的——已知震源特性反演法(KSS)。在实际资料处理中最直接的方法是从直达波中提取子波特征,但是由于地球介质中传播路径的影响,直达波并不是真实的震源子波。Song等[6]、Pratt[7]先后在频率域提出了包含子波迭代估算的反演方法(IES),假设初始速度模型以及子波都接近真实情况,在反演过程中同时迭代、更新速度模型和震源子波。如果反演的模型严重偏离真实模型,那么在迭代中将会得到不正确的子波,两者相互影响,导致反演无法收敛到真实解。
为了避免对子波的估计,Zhou等[8]提出了频率域归一化振幅反演法(ATN),其基本原理是在每个频率中用单炮记录平均振幅对炮集的每个接收点振幅进行归一化,以消除震源特性信息。Lee等[9]提出了标准道归一化的FWI(STN)。与ATN相比,STN使用单一参考道,并且使用频率域波场数据。Choi等[10]提出了两种与子波无关的频率域振幅型目标函数:一种具反褶积作用,与ATN的目标函数形式基本一致,但是使用单一的参考道振幅数据,利用传统的直接计算雅可比矩阵的方式计算梯度;另一种具褶积作用,将模拟数据和观测数据分别与参考道的观测数据和模拟数据相乘,然后使用新得到的数据构建基于L2范数的目标函数。由于数据同时包含理论子波和实际子波的影响,在相减过程中自然消去了子波的影响,从而达到不依赖于子波的效果。Greenhalgh等[11]基于声波方程仅利用数据的振幅谱对浅层地震模型数据进行KSS、IES和ATN,认为KSS反演效果最好。Xu等[12]利用井间模型的频率域弹性波场数据进行KSS、IES、ATN和STN,认为无论对于多分量还是单分量数据,KSS和IES能得到较好的反演效果,ATN反演效果次之,STN对参考道的依赖性很大,反演效果最差。Choi等[13]利用弹性波对数波场数据测试了子波估计型目标函数和频率域不依赖子波型目标函数对噪声的敏感性,对于含随机噪声数据,子波估计型目标函数效果更好,对于含相干噪声数据则相反。Choi等[14]将频率域基于褶积的不依赖于子波的FWI用于时间域声波方程,认为使用平均参考道的效果好于使用单一参考道,且在已知子波情况下的反演效果最好。敖瑞德等[15]结合时间域不依赖子波的FWI与包络反演,通过对比包络、包络对数和包络平方三种目标函数反演结果,发现包络对数目标函数的深层反演效果最好。Zhang等[16]针对时间域FWI的参考道褶积过程中由褶积和相关运算产生的噪声问题,提出对参考道加时窗的方式加快收敛以改善反演效果。杨涛等[17]在弹性波混合域实现了不依赖子波的FWI。
本文利用频率域单频数据特点,在复数域设计了一种类似于实数域表征数据相似性的目标函数(SOD)。SOD与相干性衡量目标函数的结构相似[18],可在一定程度上降低反演的非线性。基于互相关的新方法可以弱化模拟数据与观测数据间的振幅匹配,更适合于实际应用。在构造目标函数时,自然消除了震源子波的影响,而且不需要使用参考道,从而避免了由于STN参考道选择不当导致收敛缓慢或无法收敛的缺陷。ATN可以使用频率域波场数据或只使用振幅数据。若使用频率域波场数据,由于求和所用的参考道数据为复数型,求和后不能校正数据能量,甚至求和后结果的振幅接近零时会导致反演不稳定;若只使用振幅数据虽然可以避免上述缺陷,但是缺少相应的相位信息,也难以达到频率域波场数据的反演精度[12]。文中的SOD反演法(下文简称SOD)使用频率域波场数据,并且不需要参考道求和,因此避免了ATN的缺陷。通过模型试算,对比了STN、ATN和SOD的反演结果,其中STN和ATN使用振幅型数据,SOD使用频率域波场数据。首先对STN、ATN和SOD三种方法做无噪数据测试,用不同的子波生成模拟记录,以验证方法的有效性;然后用一个梯度模型测试SOD的稳定性[19-20];最后在单炮记录中加入不同信噪比的随机噪声,测试SOD对含噪数据的适应性。
1 方法原理 1.1 频率域波动方程求解在频率域,声波波动方程为
| $ \frac{\omega^{2}}{K(\boldsymbol{x})} u(\boldsymbol{x}, \omega)+\nabla\left[\frac{1}{\rho(\boldsymbol{x})} \nabla u(\boldsymbol{x}, \omega)\right]=f(\boldsymbol{x}, \omega) $ | (1) |
式中:K(x)为体积模量,x为笛卡尔坐标下的介质空间位置;ρ(x)为密度;u(x, ω)和f(x, ω)分别为频率域波场值和震源值,ω为角频率。本文将式(1)用有限差分格式离散[21-22],并加入合适的边界条件,得到矩阵表达形式
| $ \boldsymbol{S}(\omega) \boldsymbol{U}(\omega)=\boldsymbol{F}(\omega) $ | (2) |
式中:S(ω)为与模型参数、频率、离散格式以及边界条件有关的阻抗矩阵,设模型中共有n个节点,则S为n阶的大型稀疏矩阵,其非零元素对称分布在主对角线及两边,但是由于两边的值大小不同,所以它并非是对称矩阵;U(ω)为所有模型节点的频域波场值按照一定顺序排列得到的n维列向量;F(ω)为频率域的点源或组合形式的震源构成的n维列向量。
针对式(2)的大型稀疏方程组的求解,通常可以使用分解法和迭代法。使用分解法直接求解(如LU分解),只需要对S(ω)一次分解,就可以利用分解结果求解多个震源的波场,体现了频率域正演的高效性。
1.2 目标函数频率域中,观测记录和模拟记录的共炮点道集用格林函数可分别表示为
| $ d_{i j}(\omega)=f_{i}^{d}(\omega) G_{i j}^{d}(\omega) $ | (3) |
| $ u_{i j}(\omega)=f_{i}^{u}(\omega) G_{i j}^{u}(\omega) $ | (4) |
式中:dij和uij分别为频率域波场的观测值和模拟值,i=1, 2, …, Ns、j=1, 2, …, Nr分别为炮点和检波点序号,Ns和Nr分别为炮点数和检波点数;fid和Gijd分别为观测记录中第i炮的频率域震源和格林函数;fiu和Giju分别为模拟记录中第i炮的频率域震源和格林函数。
对于第i炮,定义
| $ E_{1}=\frac{\left(\sum\limits_{j} u_{i j} d_{i j}^{*}\right)\left(\sum\limits_{j} u_{i j} d_{i j}^{*}\right)^{*}}{\left(\sum\limits_{j} u_{i j} u_{i j}^{*}\right)\left(\sum\limits_{j} d_{i j} d_{i j}^{*}\right)}=\frac{\left(\boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{d}_{i}^{*}\right)\left(\boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{d}_{i}^{*}\right)^{*}}{\left(\boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{u}_{i}^{*}\right)\left(\boldsymbol{d}_{i}^{\mathrm{T}} \boldsymbol{d}_{i}^{*}\right)} $ | (5) |
式中:ui和di分别为第i炮的检波点处的模拟值和观测值组成的列向量;上角标*表示复数共轭。将波场值的格林函数代入式(5),得到
| $ E_{1}=\frac{\left(\sum\limits_{j} G_{i j}^{u} G_{i j}^{d *}\right)\left(\sum\limits_{j} G_{i j}^{u} G_{i j}^{d *}\right)^{*}}{\left(\sum\limits_{j} G_{i j}^{u} G_{i j}^{u *}\right)\left(\sum\limits_{j} G_{i j}^{d} G_{i j}^{d *}\right)} $ | (6) |
由式(6)可见,E1中并不包含震源特征信息,具有不依赖子波的性能。因此,本文构建了不依赖子波的目标函数
| $ \begin{aligned} E_{\mathrm{SOD}}=& \frac{1}{N_{\mathrm{s}}} \sum\limits_{i}\left(1-E_{1}\right) \\ &=\frac{1}{N_{\mathrm{s}}} \sum\limits_{i}\left[1-\frac{\left(\boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{d}_{i}^{*}\right)\left(\boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{d}_{i}^{*}\right)^{*}}{\left(\boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{u}_{i}^{*}\right)\left(\boldsymbol{d}_{i}^{\mathrm{T}} \boldsymbol{d}_{i}^{*}\right)}\right] \\ & \quad i=1, 2, \cdots, N_{\mathrm{s}} \end{aligned} $ | (7) |
式中E1类似于实数域中夹角余弦的平方,其值域为[0, 1],当反演结果非常接近真实模型值时,E1接近1。为了使最优解时对应的目标函数值最小,所以式中使用
记E1的分子和分母对某一模型参数m1的偏导数分别为ξ和η,则
| $ \xi=\left(\boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{d}_{i}^{*}\right)^{*} \sum\limits_{j} \frac{\partial u_{i j}}{\partial m_{1}} d_{i j}^{*}+\boldsymbol{u}_{i}^{\top} \boldsymbol{d}_{i}^{*}\left(\sum\limits_{j} \frac{\partial u_{i j}}{\partial m_{1}} d_{i j}^{*}\right)^* $ | (8) |
| $ \eta=\boldsymbol{d}_{i}^{\mathrm{T}} \boldsymbol{d}_{i}^{*} \sum\limits_{j}\left[\frac{\partial u_{i j}}{\partial m_{1}} u_{i j}^{*}+u_{i j}\left(\frac{\partial u_{i j}}{\partial m_{1}}\right)^{*}\right] $ | (9) |
若取实部,则有
| $ \operatorname{Re}\left[\frac{\partial u_{i j}}{\partial m_{1}} u_{i j}^{*}+u_{i j}\left(\frac{\partial u_{i j}}{\partial m_{1}}\right)^{*}\right]=2 \operatorname{Re}\left(\frac{\partial u_{i j}}{\partial m_{1}} u_{i j}^{*}\right) $ | (10) |
所以目标函数对某一模型参数m1的导数为
| $ \begin{aligned} &\begin{aligned} \frac{\partial E_{\mathrm{SOD}}}{\partial m_{1}}=& 2 \operatorname{Re}\left[\sum\limits_{i}\left(\boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{d}_{i}^{*}\right)\left(\boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{d}_{i}^{*}\right)^{*} \sum\limits_{j} \frac{\partial u_{i j}}{\partial m_{1}} u_{i j}^{*}-\right.\\ &\left.\left(\boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{u}_{i}^{*}\right)\left(\boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{d}_{i}^{*}\right)^{*} \sum\limits_{j} \frac{\partial u_{i j}}{\partial m_{1}} d_{i j}^{*}\right] / \end{aligned}\\ &\left[\left(\boldsymbol{d}_{i}^{\mathrm{T}} \boldsymbol{d}_{i}^{*}\right)\left(\boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{u}_{i}^{*}\right)^{2}\right] \end{aligned} $ | (11) |
为使公式简约,记
| $ \left\{\begin{array}{l} C_{1}=\frac{2\left(\boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{d}_{i}^{*}\right)\left(\boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{d}_{i}^{*}\right)^{*}}{\left(\boldsymbol{d}_{i}^{\mathrm{T}} \boldsymbol{d}_{i}^{*}\right)\left(\boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{u}_{i}^{*}\right)^{2}} \\ C_{2}=\frac{2\left(\boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{u}_{i}^{*}\right)\left(\boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{d}_{i}^{*}\right)^{*}}{\left(\boldsymbol{d}_{i}^{\mathrm{T}} \boldsymbol{d}_{i}^{*}\right)\left(\boldsymbol{u}_{i}^{\mathrm{T}} \boldsymbol{u}_{i}^{*}\right)^{2}} \end{array}\right. $ | (12) |
则式(11)变为
| $ \frac{\partial E_{\mathrm{SOD}}}{\partial m_{1}}=\sum\limits_{i} \operatorname{Re}\left(C_{1} \sum\limits_{j} \frac{\partial u_{i j}}{\partial m_{1}} u_{i j}^{*}-C_{2} \sum\limits_{j} \frac{\partial u_{i j}}{\partial m_{1}} d_{i j}^{*}\right) $ | (13) |
将上式写成矩阵形式
| $ \frac{\partial E_{\mathrm{SOD}}}{\partial m_{1}}=\sum\limits_{i} \operatorname{Re}\left[\left(\frac{\partial \boldsymbol{u}_{i}}{\partial m_{1}}\right)^{\mathrm{T}}\left(\begin{array}{c} C_{1} u_{i 1}^{*}-C_{2} d_{i 1}^{*} \\ C_{1} u_{i 2}^{*}-C_{2} d_{i 2}^{*} \\ \vdots \\ C_{1} u_{i n}^{*}-C_{2} d_{i n}^{*} \end{array}\right)\right] $ | (14) |
如果计算的是全部模型参数的偏导数,则可以得到目标函数对整个模型参数m的梯度
| $ \frac{\partial E_{\mathrm{SOD}}}{\partial \boldsymbol{m}}=\sum\limits_{i} \operatorname{Re}\left[\left(\frac{\partial \boldsymbol{u}_{i}}{\partial \boldsymbol{m}}\right)^{\mathrm{T}} \boldsymbol{r}_{i}\right] $ | (15) |
其中
| $ r_{i, k}=\left\{\begin{array}{cl} C_{1} u_{i k}^{*}-C_{2} d_{i k}^{*} & k=j \\ 0 & k \neq j \end{array}\right. $ |
为了避免直接计算雅可比矩阵
| $ \frac{\partial E_{\mathrm{SOD}}}{\partial \boldsymbol{m}}=\sum\limits_{i} \operatorname{Re}\left[\left(\boldsymbol{V}_{i}\right)^{\mathrm{T}}\left(\boldsymbol{S}_{i}^{-1}\right)^{\mathrm{T}} \boldsymbol{r}_{i}\right] $ | (16) |
由式(16)可见,SOD对应的梯度与常规L2型目标函数的梯度形式相似,都非常简洁,因此并不会增加额外的计算量。
2 模型试算本文采用CSEG速度模型(图 1)验证基于数据相似性的不依赖子波的频率域FWI的有效性,并与STN、ATN的反演效果对比。本文使用的优化方法为共轭梯度法,并取一个较小值作为固定步长与归一化后的共轭梯度相乘更新模型。
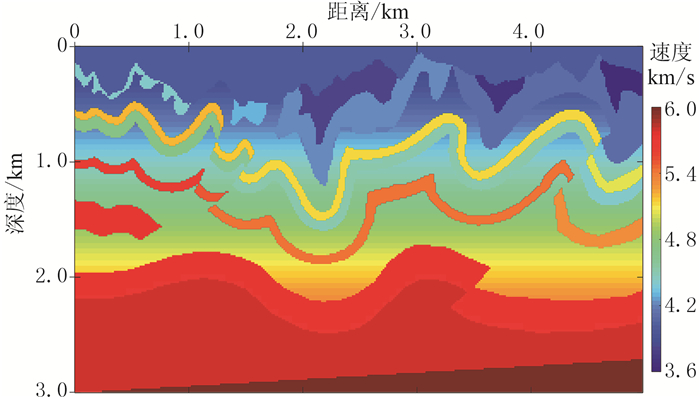
|
图 1 CSEG速度模型 水平网格数为332, 垂直网格数为200,水平与垂直网格尺寸均为15m,模型尺寸为4.98km×3.00km。震源位于z=15m处,起始炮位于x=60m处,炮间距为30m,共110炮。检波器设置在地表进行全接收,时间采样间隔为1ms,采样点数为2000,总记录长度为2s |
为了验证SOD的有效性,本文用常密度声波波动方程测试各反演方法的效果。采用频率域有限差分正演模拟,差分格式采用二阶最优9点格式[25]。初始速度模型为平滑模型(图 2),用于生成观测记录的准确子波为雷克子波(图 3a),主频为15Hz,最大振幅为1.0。为了测试本文方法对不同子波的处理能力,选取主频均为15Hz、不同振幅的子波(图 3b~图 3f,其中图 3b、图 3c、图 3e、图 3f的最大振幅为1.0,图 3d的最大振幅为2.0)作为生成模拟记录的震源子波,反演的频率范围为1~20Hz,频率间隔为1 Hz,共20个频率,每个频率迭代20次,低频的反演结果作为相邻高频的输入。同时,为了提高计算效率,采用振幅编码的方式将110炮编码成40个超级炮[26-27],为避免由于随机编码对反演结果的影响,测试中统一使用同一套编码矩阵。
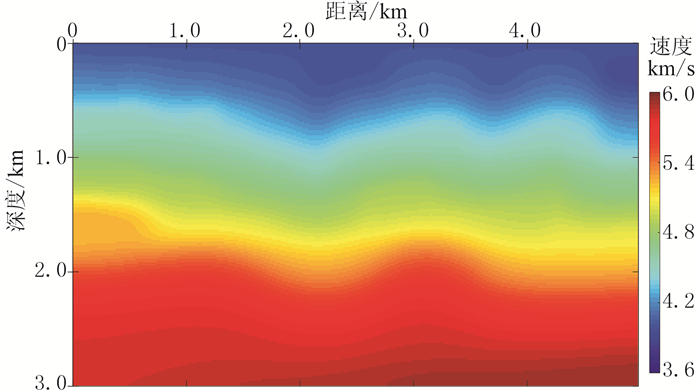
|
图 2 平滑模型 |
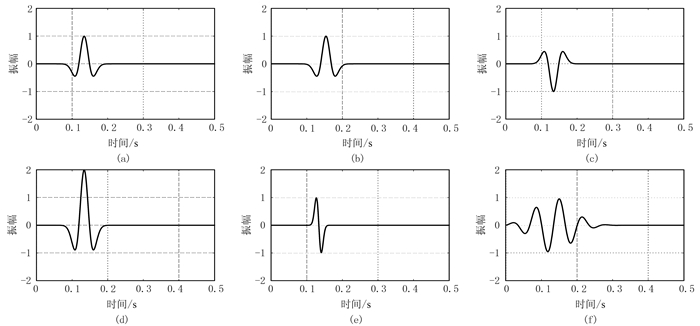
|
图 3 主频为15 Hz、不同振幅的子波 (a)生成观测记录的雷克子波;(b)生成模拟记录的雷克子波(0.02s延迟);(c)极性与图a相反的雷克子波;(d)最大振幅为2的雷克子波;(e)高斯函数的一阶导数;(f)复杂子波 |
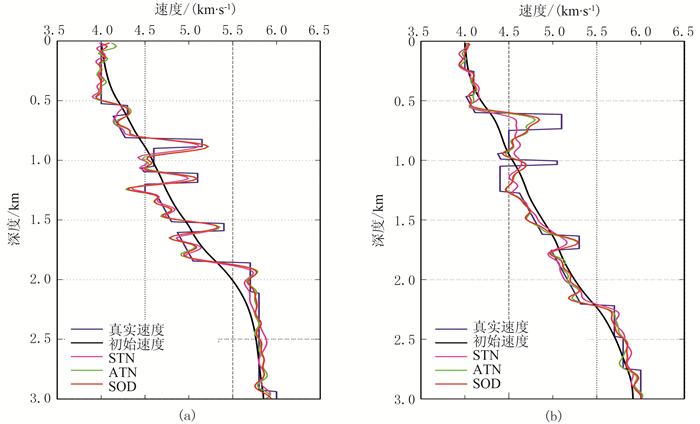
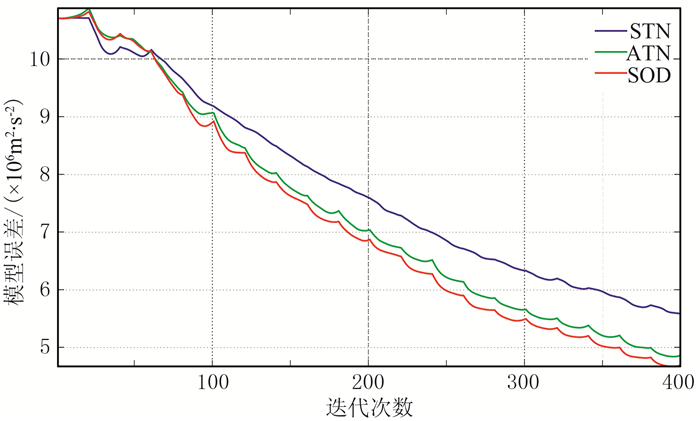
图 4为选取复杂子波(图 3f)的不同方法的反演结果。由图可见,不同方法在复杂子波的情况下仍能较好地反演速度模型,特别是浅层反演效果较好,其中STN的深层更新效果较差(图 4a),ATN有所改进(图 4b),SOD的反演效果最好(图 4c)。上述结果表明,本文方法在子波主频相同的情况下反演结果不依赖子波。图 5为由图 4得到的1.5km、3.0km处单道速度曲线。由图可见,与ATN和SOD相比,STN的拟合较差,3.0km处单道速度曲线(图 5b)在500~1500m深度范围较平滑,因此STN更新不足;ATN则有较大改善;SOD曲线最接近真实速度曲线。图 6为模型误差收敛曲线。由图可见,SOD收敛更好。综上所述,本文提出的SOD的反演结果不依赖子波,而且与另两种不依赖子波的反演方法(ATN、STN)相比,反演精度更高。
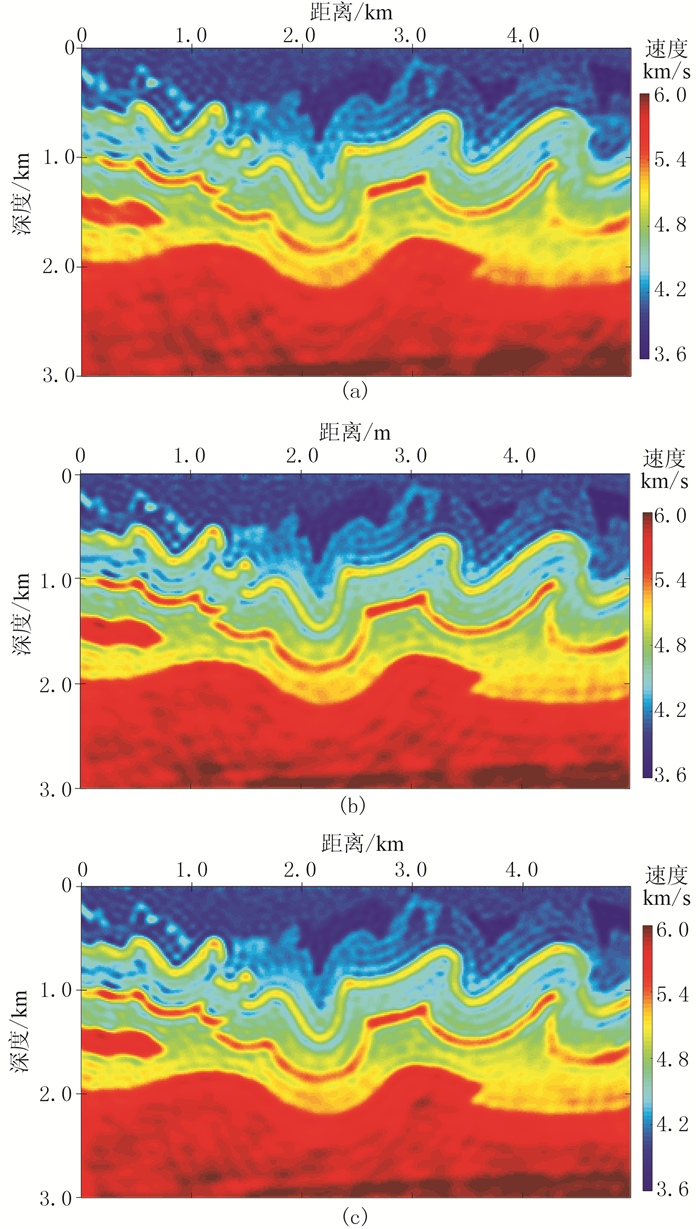
|
图 4 选取复杂子波(图 3f)的不同方法的反演结果 (a)STN;(b)ATN;(c)SOD |
|
图 5 由图 4得到的1.5km(a)、3.0km(b)处单道速度曲线 |
|
图 6 模型误差收敛曲线 |
值得注意的是,选用STN反演时,参考道的选择是一个非常重要的问题。理论上,子波具有时变和空变特征,炮检距越小,能量越大,畸变越小,因此小炮检距参考道优于大炮检距参考道。但是炮记录经过编码后,参考道选取原则要相应改变。因此,为了减小由于参考道的选择而导致各个超级炮产生的梯度间能量差异,本文设计了四种参考道选取方式。
(1) 邻近参考道。以(12×i)m所在道作为参考道,i=1, …, 40,即在计算每一个超级炮的梯度时依次从左向右以120m为间隔选取参考道。
(2) 远炮检距参考道。当i=1, …, 20时,以(120×i+166)m所在道作为参考道,即第1炮选取286m所在道为参考道,依次从左向右以120m为间隔选取参考道;当i=21, …, 40时,以(120×i-166)m所在道作为参考道,即第21炮选取2354m所在道为参考道,依次从左向右以120m为间隔选取参考道。
(3) 最小振幅参考道。编码后观测记录中最小振幅所在道。
(4) 最大振幅参考道。编码后观测记录中最大振幅所在道。
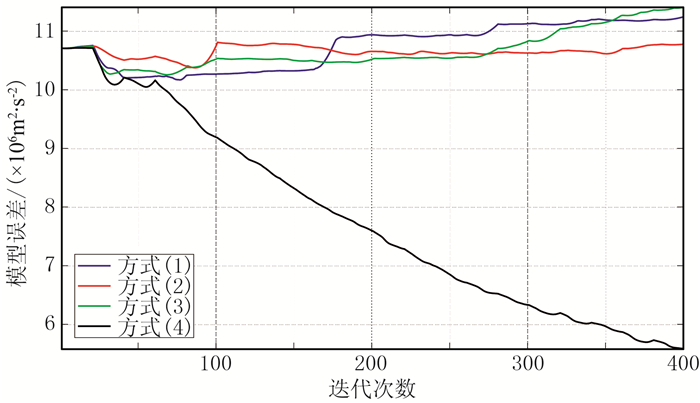
图 7为四种参考道选取方式对应的反演结果。由图可见:方式(1)~方式(3)的反演结果只能得到一个大致的背景模型,无法反演精细构造;方式(4)模型误差值为真实速度与反演速度差的平方和,下同反演结果与真实模型较吻合。图 8为四种参考道选取方式反演结果模型误差收敛曲线。由图可见:①不同的参考道选取方式对反演结果影响很大,体现了STN的不稳定性,虽然本文的参考道选取方式(方式(4))在一定程度上保证了STN的收敛性,但是基于振幅数据的ATN通过对每道求和后取平均的方式,可以自然地将归一化后的数据能量校正到同一个水平,利于反演结果稳定、高效地收敛;②SOD不需要选取参考道,并且同样具备ATN的优点,同时由于使用了包含更多信息的频率域波场数据,收敛性更好;③方式(4)的误差曲线收敛,方式(1)~方式(3)的误差曲线不收敛。因此在后文STN测试中使用方式(4)的参考道选取方式。

|
图 7 四种参考道选取方式的反演结果 (a)方式(1);(b)方式(2);(c)方式(3);(d)方式(4) |
|
图 8 四种参考道选取方式反演结果模型误差收敛曲线 |
为了测试不同反演方法对初始模型的依赖性,选取一个初始速度模型(图 9a),使用的频率与图 3相同。图 9为初始速度模型及不同方法迭代400次后的反演结果。由图可见:STN反演效果很差,两边和中间都出现了虚假的低速构造(图 9b);与STN相比,ATN在浅层速度较准确,但在深部更新不明显(图 9c);SOD反演结果基本正确,而且明显比ATN更新效果更好,在深部尤其如此(图 9d)。图 10为由图 9抽取的1.5km、3.0km处单道速度曲线。由图可见:在深度小于500m时,三种方法的反演曲线基本与真实速度曲线一致;STN和ATN的中部速度变化异常,深部速度更新不足;SOD速度曲线在中、深部均很接近真实速度曲线,因此SOD对初始模型的依赖性较小,可更稳定、高效地反演模型参数。

|
图 9 初始速度模型及不同方法迭代400次后的反演结果 (a)初始速度模型;(b)STN;(c)ATN;(d)SOD 图a为线性梯度模型,顶部速度为3600m/s,底部速度为6000m/s |

|
图 10 由图 9抽取的1.5km(a)、3.0km(b)处单道速度曲线 |
为了使合成数据测试更接近真实情况,在炮记录中加入一定比例的随机噪声。不同目标函数对噪声的抗噪性不同,L2型目标函数对随机噪声具有较强的稳定性。为了消除子波的影响而引入参考道后,新的规则化数据对噪声的敏感性呈现出明显差异。
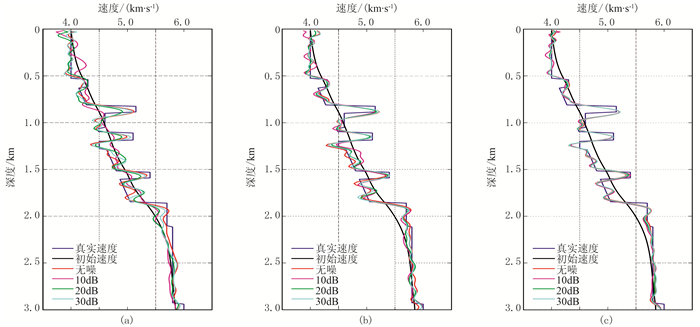
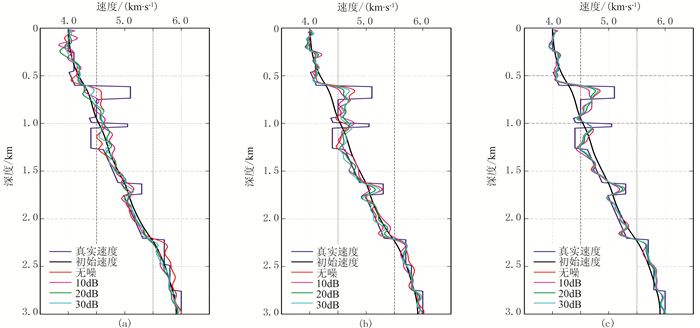
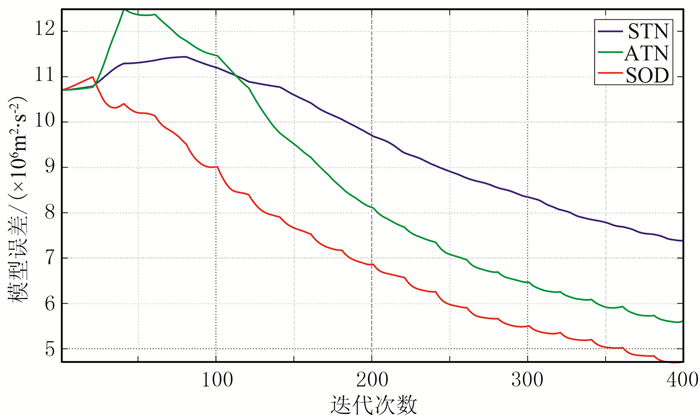
本文在单炮记录中加入了不同信噪比的随机噪声,用以测试噪声对三种目标函数反演结果的影响,反演所使用的频率与图 3相同,初始模型与图 2相同。图 11为在单炮记录中加入信噪比分别为10、20、30dB随机噪声的不同方法反演结果。由图可见:STN受随机噪声影响严重,深部反演效果很差(图 11a);ATN受噪声的影响也较明显(图 11b);SOD受噪声的影响较小(图 11c)。图 12和图 13分别为由图 11抽取的1.5km、3.0km处单道速度曲线。由图可见,由于受噪声影响,不同方法的反演结果在浅层都存在明显波动,表现为:①STN速度曲线非常不稳定(图 12a、图 13a);②ATN速度曲线在深层也存在明显跳动(图 12b、图 13b);③SOD速度曲线对噪声的敏感程度最低,加入不同随机噪声的速度曲线与无噪数据基本一致,表明SOD对噪声具有更好的稳定性(图 12c、图 13c)。图 14为加入信噪比为30dB随机噪声的模型误差收敛曲线。由图可见,STN的收敛性明显变差,ATN次之,SOD收敛性最好,与Choi等[14]的认识一致。

|
图 11 在单炮记录中加入信噪比分别为10dB(上)、20dB(中)、30dB(下)随机噪声的不同方法反演结果 (a)STN;(b)ATN;(c)SOD |
|
图 12 由图 11抽取的1.5km处单道速度曲线 (a)STN;(b)ATN;(c)SOD |
|
图 13 由图 11抽取的3.0km处单道速度曲线 (a)STN;(b)ATN;(c)SOD |
|
图 14 加入信噪比为30dB随机噪声的模型误差收敛曲线 |
Xu等[12]分析了STN和ATN的抗噪性,认为STN目标函数的分子和分母同时包含噪声影响项,ATN目标函数由于对参考道求和从而消除了分母的噪声影响项,因此比STN的抗噪性好。本文提出的SOD目标函数类似于ATN,通过相乘、求和运算使噪声在分子和分母中的比重相当,因此目标函数值较稳定。稳定的目标函数值可以产生稳定的梯度,这在反演过程中至关重要。若局部炮记录产生的梯度能量发生异常,其他炮记录产生的梯度作用相对减弱,反演的收敛速度将变慢,尤其是异常梯度指向局部极小值时,可能导致反演失败。
3 结论准确获取震源子波一直是地震资料处理的难题,本文提出的SOD在构造目标函数的过程中消除了震源子波对反演结果的影响。模型测试发现:①SOD的反演结果不依赖子波,而且与另两种不依赖子波的反演方法(ATN、STN)相比,反演精度更高,对实际资料的处理具有非常重要的意义;②SOD的原理是基于数据间的相似性,对数据间能量差异具有更大的包容性,所以对初始速度模型的依赖性不高;③即使存在随机噪声,通过相乘、求和运算作用在分子和分母中的噪声比重相当,因此SOD目标函数值较稳定;④SOD还可以与炮编码策略结合,有效提高计算效率。
| [1] |
Tarantola A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [2] |
Pratt R G. Frequency-domain elastic wave modeling by finite differences:A tool for cross-hole seismic imaging[J]. Geophysics, 1990, 55(5): 626-632. DOI:10.1190/1.1442874 |
| [3] |
Pratt R G. Inverse theory applied to multi-source cross-hole tomography, Part 2:Elastic wave-equation method[J]. Geophysical Prospecting, 1990, 38(3): 311-329. DOI:10.1111/j.1365-2478.1990.tb01847.x |
| [4] |
Pratt R G, Worthington M H. Inverse theory applied to multi-source cross-hole tomography, Part 1:Acoustic wave-equation method[J]. Geophysical Prospecting, 1990, 38(3): 287-310. DOI:10.1111/j.1365-2478.1990.tb01846.x |
| [5] |
李福元, 韦成龙, 邓桂林, 等. 从海洋地震资料直达波提取震源子波[J]. 石油地球物理勘探, 2019, 54(3): 512-521. LI Fuyuan, WEI Chenglong, DENG Guilin, et al. Source signature extraction from marine seismic direct waves[J]. Oil Geophysical Prospecting, 2019, 54(3): 512-521. |
| [6] |
Song Z M, Williamson P R, Pratt R G. Frequency domain acoustic-wave modeling and inversion of crosshole data:Part Ⅱ-Inversion method, synthetic experiments and real-data results[J]. Geophysics, 1995, 60(3): 796-809. DOI:10.1190/1.1443818 |
| [7] |
Pratt R G. Seismic waveform inversion in the frequency domain, Part 1:Theory and verification in a physical scale model[J]. Geophysics, 1999, 64(3): 888-901. DOI:10.1190/1.1444597 |
| [8] |
Zhou B, Greenhalgh S A. Crosshole seismic inversion with normalized full-waveform amplitude data[J]. Geophysics, 2003, 68(4): 1320-1330. DOI:10.1190/1.1598125 |
| [9] |
Lee K H, Kim H J. Source-independent full-waveform inversion of seismic data[J]. Geophysics, 2003, 68(6): 2010-2015. DOI:10.1190/1.1635054 |
| [10] |
Choi Y, Shin C, Min D J, et al. Efficient calculation of the steepest descent direction for source-independent seismic waveform inversion:An amplitude approach[J]. Journal of Computational Physics, 2005, 208(2): 455-468. |
| [11] |
Greenhalgh S A, Zhou B. Surface seismic imaging by multi-frequency amplitude inversion[J]. Exploration Geophysics, 2003, 34(4): 217-224. DOI:10.1071/EG03217 |
| [12] |
Xu K, Greenhalgh S A, Wang M Y. Comparison of source-independent methods of elastic waveform inversion[J]. Geophysics, 2006, 71(6): R91-R100. DOI:10.1190/1.2356256 |
| [13] |
Choi Y, Min D J. Source-independent elastic waveform inversion using a logarithmic wavefield[J]. Journal of Applied Geophysics, 2012, 76(10): 13-22. |
| [14] |
Choi Y, Alkhalifah T. Source-independent time-domain waveform inversion using convolved wavefields:Application to the encoded multisource waveform inversion[J]. Geophysics, 2011, 76(5): R125-R134. DOI:10.1190/geo2010-0210.1 |
| [15] |
敖瑞德, 董良国, 迟本鑫. 不依赖子波、基于包络的FWI初始模型建立方法研究[J]. 地球物理学报, 2015, 58(6): 1998-2010. AO Ruide, DONG Liangguo, CHi Benxin. Source-independent envelope-based FWI to build an initial model[J]. Chinese Journal of Geophysics, 2015, 58(6): 1998-2010. |
| [16] |
Zhang Q, Zhou H, Li Q, et al. Robust source-inde-pendent elastic full-waveform inversion in the time domain[J]. Geophysics, 2016, 81(2): R29-R44. |
| [17] |
杨涛, 张会星, 史才旺. 不依赖子波的弹性波混合域全波形反演[J]. 石油地球物理勘探, 2019, 54(2): 348-355. YANG Tao, ZHANG Huixing, SHI Caiwang. Wavelet-independent elastic wave full waveform inversion in hybrid domain[J]. Oil Geophysical Prospecting, 2019, 54(2): 348-355. |
| [18] |
Gao F, Williamson P, Pratt R G.A new objective function for full waveform inversion: Differential sem-blance in the data domain[C].SEG Technical Program Expanded Abstracts, 2014, 33: 1178-1183.
|
| [19] |
Liao J P, Guo Z W, Liu H X, et al. Application of frequency-dependent traveltime tomography to 2D crosswell seismic field data[J]. Journal of Environmental & Engineering Geophysics, 2017, 22(4): 421-426. |
| [20] |
Liao J P, Wang H Z, Ma Z T. 2-D elastic wave modeling with frequency-space 25-point finite-difference operators[J]. Applied Geophysics, 2009, 6(3): 259-266. DOI:10.1007/s11770-009-0029-7 |
| [21] |
Pratt R G, Shin C, Hick G J. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion[J]. Geophysical Journal International, 1998, 133(2): 341-362. DOI:10.1046/j.1365-246X.1998.00498.x |
| [22] |
Pratt R G, Symes W.Semblance and differential semblance optimisation for waveform tomography: A frequency domain implementation[C].Sub-basalt Imaging Conference Expanded Abstracts, 2002, 183-184.
|
| [23] |
成景旺, 吕晓春, 顾汉明, 等. 基于柯西分布的频率域全波形反演[J]. 石油地球物理勘探, 2014, 49(5): 940-945. CHENG Jingwang, LYU Xiaochun, GU Hanming, et al. Full waveform inversion with Cauchy diatribution in the frequency domain[J]. Oil Geophysical Prospecting, 2014, 49(5): 940-945. |
| [24] |
周聪, 刘江平, 罗银河, 等. 二维频率域全波场有限差分数值模拟方法[J]. 石油地球物理勘探, 2014, 49(2): 278-287. ZHOU Cong, LIU Jiangping, LUO Yinhe, et al. 2D full-wavefield modeling in frequency domain using finite-difference[J]. Oil Geophysical Prospecting, 2014, 49(2): 278-287. |
| [25] |
Jo C H, Shin C, Suh J H. An optimal 9-point, finite difference, frequency-space, 2-D scalar wave extrapolator[J]. Geophysics, 1996, 61(2): 529-537. |
| [26] |
Godwin J, Sava P.Simultaneous Source Imaging by Amplitude Encoding[R].CWP Report, 2010, 21-42.
|
| [27] |
解飞, 黄建平, 李振春. 一种基于高效迭代解法的频率域全波形反演[J]. 地球物理学报, 2018, 61(8): 1998-2010. XIE Fei, HUANG Jianping, LI Zhenchun. An efficient full waveform inversion in frequency domain based on wavefield iteration method[J]. Chinese Journal of Geophysics, 2018, 61(8): 1998-2010. |



 黄建平, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
黄建平, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: