2 东方地球物理公司研究院处理中心, 河北涿州 072751;
3 东方地球物理公司采集技术中心, 河北涿州 072751;
4 河北工程大学地球科学与工程学院, 河北邯郸 056038
2 BGP Seismic Data Processing Center, Zhuozhou, Hebei 072751, China;
3 BGP Acquisition Technology Center, Zhuozhou, Hebei 072751, China;
4 School of Earth Science and Engineering, Hebei University of Engineering, Handan, Hebei 056038, China
零炮检距叠加成像是地震数据处理过程中的重要环节[1-4],其基本思想是将地震反射信号归位到地下相应的反射点位置,并且在此过程中消除非零炮检距导致的时差,生成零炮检距叠加成像剖面,用于处理过程的质控和叠后偏移成像[5-7]。此外,该方法还可以通过分析数据中所包含的运动学信息求取时间域的叠加速度[8-12],作为地下速度的初始估计。CMP叠加是目前最常用的零炮检距叠加成像方法,该方法假设采集面为水平地表,且地下介质速度横向变化不大,此时地震数据所对应的地下反射点可以视为CMP点,通过对地震数据按照中心点位置生成CMP道集后,便可以进行叠加速度分析和零炮检距叠加成像。
近年来,随着深海油气勘探力度的不断增加,海底节点(OBN)采集得到了越来越广泛的应用[13-17]。同常规的拖缆采集相比,OBN采集具备宽方位、宽频、易于施工等一系列的优势,但是相关的OBN数据处理技术却依然不够完善。OBN数据的震源位于海平面,接收点位于海底,二者之间往往有几百米乃至上千米的高程差,对应的反射点形态是一条时变的曲线,此时常规的CMP叠加已经不再适用。这是因为:一方面,将接收点垂直时移到海平面会严重破坏数据中包含的运动学信息,从而导致错误的叠加速度分析结果;另一方面,使用CMP近似地下的反射点会导致反射信号的弥散,严重影响反射信号的聚焦和最终的叠加成像效果。山地数据的叠加成像处理同样存在上述问题,特别是中国西部探区,不但地表起伏剧烈,地震记录的信噪比也很低,确保低信噪比信号的聚焦性对于零炮检距叠加成像尤为重要。
针对上述问题,本文借鉴共转换点(CCP)叠加的相关思路[18-22],提出了一种适用于OBN和山地数据的时变共反射点(CRP)叠加成像方法。对于每个输入地震道,该方法以叠加速度为基础求取输出剖面中时变的CRP采样点,然后利用双平方根公式计算经由该点的双程地震波走时,并以此为基础将反射地震信号映射累加到该CRP采样点,以完成数据的动校正处理。CRP叠加无需对地震数据进行静校正处理,不但可以有效提高反射信号的聚焦性以改善叠加成像效果,还可以结合常规的叠加速度获取准确的叠加速度。以OBN数据为例,介绍了CRP叠加的基本原理和实现过程,并且给出了针对山地数据的相应实现方案。此外,还探讨了基于CRP道集的叠加速度分析的可行性,并且通过模型和实际资料试算对CRP叠加的应用效果进行了验证。
1 方法原理CRP叠加可以被定义为一个由输入地震数据到输出CRP剖面的时变数据映射过程
| $ D(\boldsymbol{s}, \boldsymbol{r}, t) \rightarrow G(\boldsymbol{m}, \boldsymbol{h}, \tau) $ | (1) |
式中:D(s, r, t)为输入的OBN地震上行波或下行波数据,其中s和r分别代表震源和接收点空间位置,t为地震数据的记录时间;G(m, h, τ)为经过动校正后的输出CRP道,其中m为输出道空间位置,h=r-s为水平炮检距矢量,也代表了输入数据所映射到的CRP剖面的炮检距,τ是以海平面为基准面的双程垂向旅行时,相应的叠加速度vrms(τ)假设为已知量。需要指出的是,CRP叠加的输出基准面同样为海平面,这样即使输入上行与下行波数据中相同层位的反射信号存在很大的时差(海水层导致),但在CRP叠加剖面上仍会归位到相同的位置。
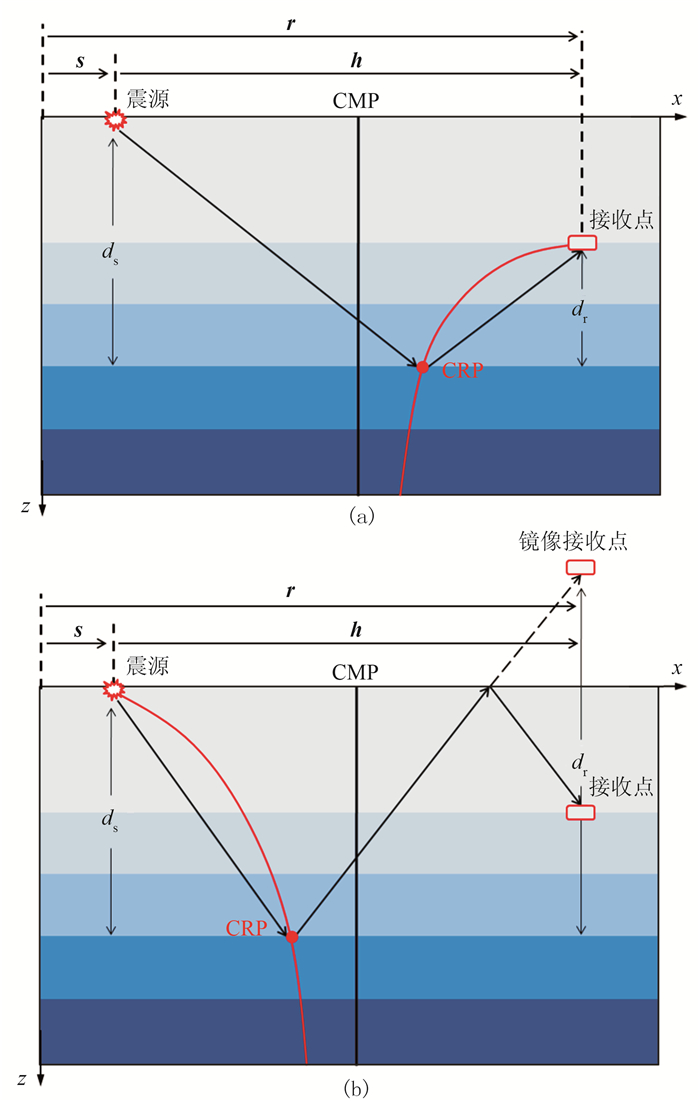
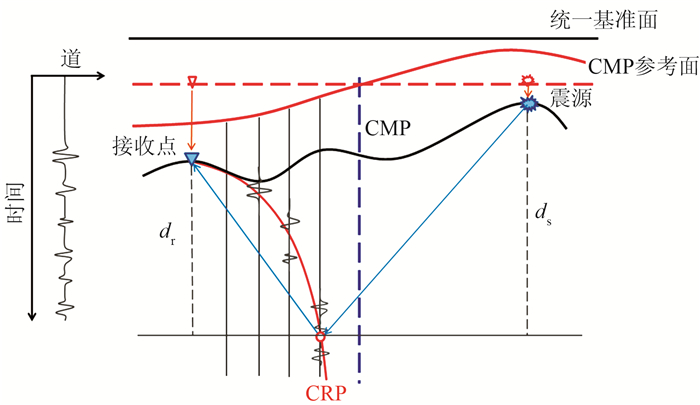
1.1 反射点计算由图 1所示OBN地震波传播路径可知,对于地下的双程垂向走时为τ的任意一层,如果可以求取该层到海平面的垂直距离ds和到接收点(对于下行波是沿海平面的镜像接收点)的垂直距离dr,便可以根据斯奈尔定律求取该层反射点的水平空间位置p(xp,yp)
|
图 1 OBN观测系统示意图 (a)上行波;(b)下行波 |
| $ \boldsymbol{p} \approx \boldsymbol{s}+\frac{d_{{\rm s}}}{d_{{\rm s}}+d_{{\rm r}}} \boldsymbol{h} $ | (2) |
计算ds和dr时需要求取上覆层的层速度。利用Dix公式[1]将叠加速度vs(τ)转化为层速度
| $ v_{i}^{2}=\frac{\tau_{i} v_{\mathrm{s}}^{2}\left(\tau_{i}\right)-\tau_{i-1} v_{\mathrm{s}}^{2}\left(\tau_{i-1}\right)}{\Delta \tau_{i}} $ | (3) |
式中:vi为第i层的层速度;Δτi为该层的双程垂向旅行时;
| $ \left\{\begin{array}{l} d_{\mathrm{s}}=\sum\limits_{i=1}^{N} v\left(\tau_{i}\right) \Delta \tau_{i} \\ d_{\mathrm{r}}=d_{\mathrm{s}}-d_{0} \end{array}\right. $ | (4) |
同样,对于下行波可得
| $ \left\{\begin{array}{l} d_{\mathrm{s}}=\sum\limits_{i=1}^{N} v\left(\tau_{i}\right) \Delta \tau_{i} \\ d_{\mathrm{r}}=d_{\mathrm{s}}+d_{0} \end{array}\right. $ | (5) |
对于每一道输入数据,利用式(2)可以求取该道在输出剖面中每个时间层位的反射点位置。由于所定义的CRP输出道是空间离散的,因此需要将所计算的反射点划分到离散的输出道中,求取离反射点最近的输出道采样点作为该时间层位的CRP采样点
| $ \begin{aligned} \boldsymbol{m}=\left(x_{\mathrm{m}}, y_{\mathrm{m}}\right)=&\left[\operatorname{INT}\left(\frac{x_{p}}{\Delta x}+0.5\right) \Delta x\right., \\ &\left.\operatorname{INT}\left(\frac{y_{p}}{\Delta y}+0.5\right) \Delta y\right] \end{aligned} $ | (6) |
式中:INT(·)为取整函数;Δx和Δy分别为Inline和Crossline方向的输出网格间距。
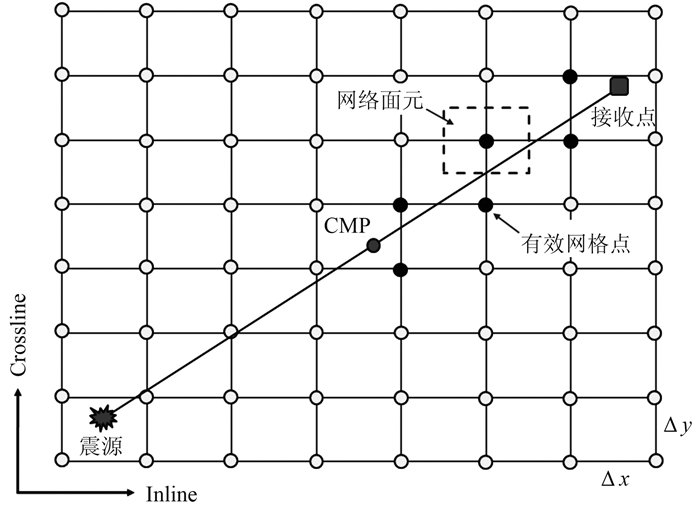
对于每道输入数据,按式(2)所计算的地下反射点只可能出现在炮点和接收点所在的垂直平面内。因此,根据式(6)所求取的CRP采样点也被限定在炮点和接收点连线邻近的输出道中。以图 2所示的OBN上行波CRP叠加输出道地表网格图为例,可以仅选择同炮点和接收点连线相交的网格所对应的CRP输出道作为有效的输出道进行后续计算,从而避免大量的无效计算。
|
图 2 OBN上行波CRP叠加输出道地表网格 只有同CMP和接收点连线相交的网格所对应的CRP输出道(黑色实心点)才是有效输出道 |
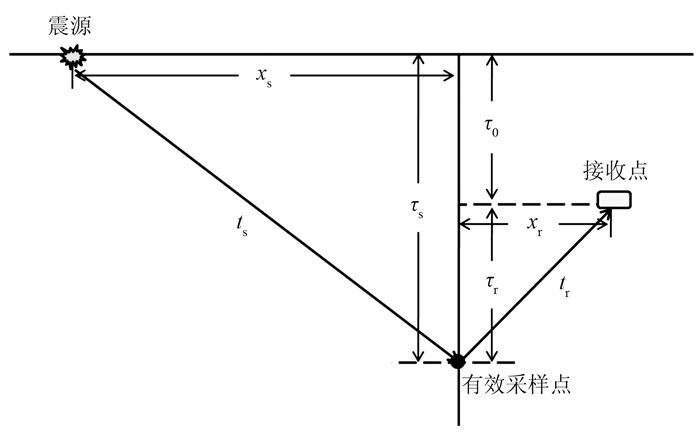
在确定地下的CRP采样点后,需要将输入数据中对应该CRP采样点的反射信号重新归位到该点上,以完成动校正处理(图 3)。假设CRP采样点的双程垂向旅行时为τ,那么可以通过双平方根公式[23-25]
|
图 3 OBN上行波双程旅行时计算示意图 |
| $ t=t_{\mathrm{s}}+t_{\mathrm{r}}=\sqrt{\tau_{\mathrm{s}}^{2}+\frac{x_{\mathrm{s}}^{2}}{v_{\mathrm{s}}^{2}}}+\sqrt{\tau_{\mathrm{r}}^{2}+\frac{x_{\mathrm{r}}^{2}}{v_{\mathrm{r}}^{2}}} $ | (7) |
计算由震源经由该点再到接收点双程旅行时,从而将输入数据中t时刻的振幅映射到该CRP采样点。式中:ts是震源射线路径走时;tr是接收点射线路径走时;xs=|s-m|和xr=|m-r|分别为震源和接收点到输出CRP采样点的水平空间距离;τs和vs分别为震源射线路径的单程垂向走时和叠加速度。以海平面为基准面,因此有
| $ \left\{\begin{array}{l} \tau_{\mathrm{s}}=\frac{\tau}{2} \\ v_{\mathrm{s}}=v_{\mathrm{rms}}(\tau) \end{array}\right. $ | (8) |
其中vrms(τ)为以海平面为基准面的叠加速度;τr和vr分别为以接收点平面为基准面的单程垂向走时和叠加速度。由于OBN数据的接收点和海平面存在巨大的高程差,因此需要通过基准面转换[1]将以海平面为基准面的走时和叠加速度校正为以接收点平面为基准面。对于上行波相应的转换关系为
| $ \left\{\begin{array}{l} \tau_{\mathrm{r}}=\frac{\tau-\tau_{0}}{2} \\ v_{\mathrm{r}}=\sqrt{\frac{v_{\mathrm{rms}}^{2}(\tau) \tau-v_{0}^{2} \tau_{0}}{\tau-\tau_{0}}} \end{array}\right. $ | (9) |
对于下行波转换关系为
| $ \left\{\begin{array}{l} \tau_{\mathrm{r}}=\frac{\tau+\tau_{0}}{2} \\ v_{\mathrm{r}}=\sqrt{\frac{v_{\mathrm{rms}}^{2}(\tau) \tau+v_{0}^{2} \tau_{0}}{\tau+\tau_{0}}} \end{array}\right. $ | (10) |
式中τ0=2d0/v0为接收点处海水层对应的双程垂向旅行时,其中v0为海水速度。
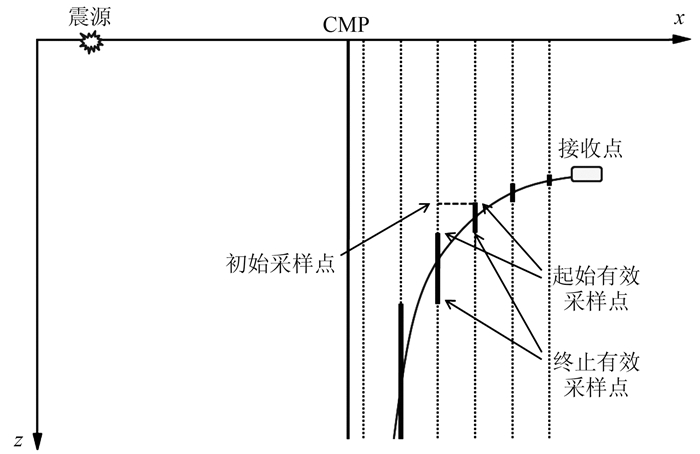
1.4 计算过程如图 4所示,CRP叠加将一道输入数据映射到多个输出道的局部采样点,因此需要设计合理的实现算法以避免针对无效输出道和无效输出样点的冗余运算。以OBN上行波数据为例,CRP叠加的优化计算过程简述如下。
|
图 4 沿震源和接收点连线的CRP叠加垂直剖面 在输出剖面中,只有部分采样点(黑色实线)是有效采样点 |
(1) 对地震数据进行预处理,并且确定CRP输出道集的空间采样间隔、炮检距增量等参数信息。
(2) 对于任意一道输入地震数据,首先计算该道的炮检距,确定该道能够贡献的炮检距域CRP输出剖面;再在CRP输出剖面中,选择同CMP和接收点连线(图 2)相交的网格所对应的输出道,并且按照到接收点水平距离由小到大对输出道进行排序。
(3) 对排序后的输出道进行循环,且将上一道的起始有效CRP采样点作为本道采样点循环的初始样点(图 4),根据式(2)计算输入数据在每个采样点所在时间层位中对应的反射点位置。如果所计算的反射点位置位于该输出道所在的网格内,则认为该采样点为有效CRP采样点;当所计算的反射点不在该道所在的网格内时,结束采样点的循环。
(4) 对于每一个有效CRP采样点,利用式(7)计算震源经该点到接收点的双程旅行时t,并提取该道t时刻的振幅值,将其累加到该采样点。
(5) 对所有的输入地震道,重复步骤(2)~步骤(4)的循环过程,直到所有输出处理完成,最终得到动校正后的CRP道集。
1.5 叠加速度更新除了可以输出信号归位准确的叠加成像剖面外,CRP叠加还可以用于叠加速度更新,该过程可以借鉴常规的叠加速度更新流程实现。首先,利用当前的叠加速度对输出的CRP道集进行反动校正;然后,对反动校后的CRP道集计算速度谱,并且拾取新的叠加速度。
严格来说常规的叠加速度更新流程仅适用于水平地表地震数据,但是实际上对于CRP叠加依然适用。这是因为,如果初始叠加速度是准确的,那么所产生的CRP道集中的同相轴应当是拉平的(至少是近中炮检距),此时对反动校后的CRP道集所求取的更新速度依然是准确的初始叠加速度。反之,如果初始叠加速度偏高(或偏低),那么所产生的CRP道集中的同相轴应当是下拉(或上翘)的,此时对反动校后的CRP道集所求取的更新速度将会低于(或高于)初始速度且更接近于准确值。以此为基础,在几次速度更新迭代后,便可以得到最终的准确叠加速度。
CRP叠加的初始速度一般通过对静校正后OBN数据(校正到海平面)应用常规的CMP速度分析进行求取。虽然垂直时移破坏了数据中所包含的运动学信息,使所求取的初始叠加速度存在误差,但是在应用2~3次上述的CRP速度迭代更新后,便可以获得较为准确的叠加速度。
1.6 山地数据处理地表起伏剧烈的山地地震数据,同样存在震源和接收点巨大高差所导致的时变反射点问题,因此也可以应用CRP叠加改善叠加成像效果。基于山地地震资料处理流程的特点,设计了如下CRP叠加实现方案。
首先进行静校正处理,通过应用高频静校正量将地震数据校正到CMP参考面,相应的叠加速度也以CMP参考面为基准面。此时对静校正后的数据进行CRP叠加,需要将震源和接收点重新校正到真实的地表位置(图 5),并且根据静校正填充速度将CRP输出道对应的叠加速度分别校正到震源和接收点所在的水平基准面。此后,利用上述算法进行反射点和动校正走时的计算,进而提取山地数据CRP道集或进行CRP叠加。
|
图 5 山地数据CRP叠加示意图 |
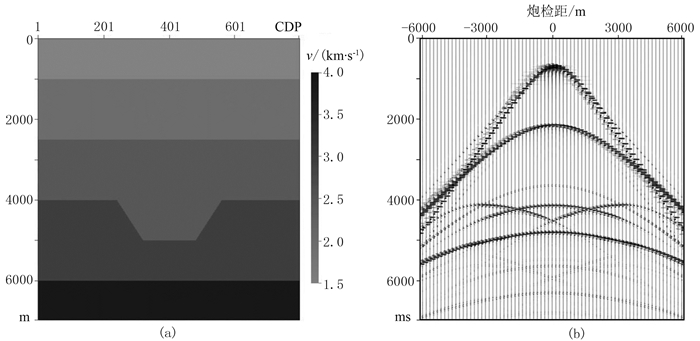
利用一个二维OBN层状模型验证CRP叠加及速度分析的正确性。图 6a为该模型的层速度场,模型网格数为801×701,横向和纵向采样间隔分别为25和10m,其中第一层为海水层,深度为1000m。利用有限差分法模拟了201炮的OBN单炮记录(图 6b),炮点间隔为50m,接收点间隔为200m。
|
图 6 二维层状速度模型(a)及模拟OBN上行波单炮记录(b) |
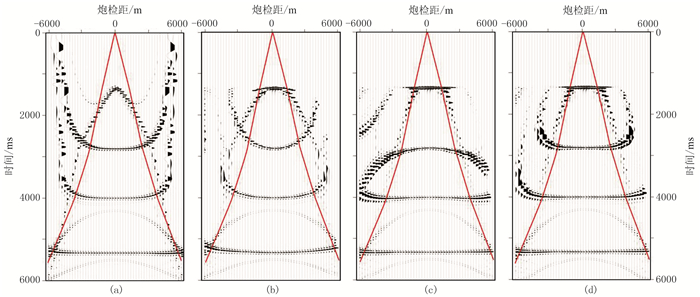
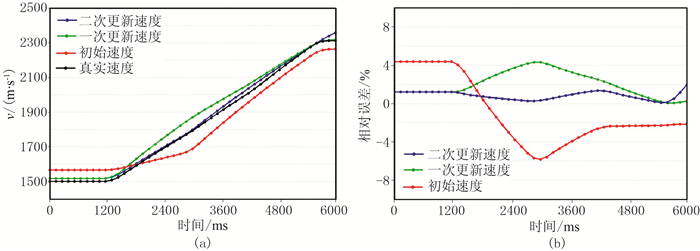
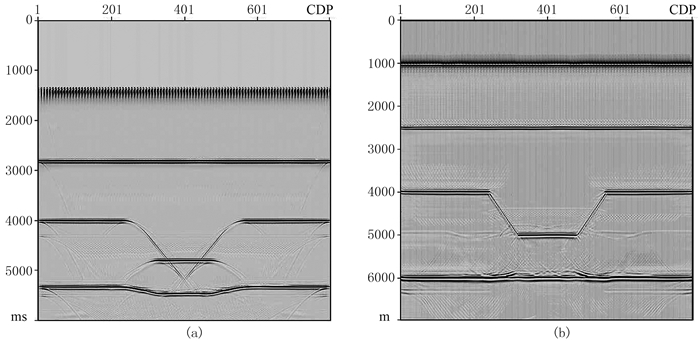
为了验证CRP叠加速度更新的正确性,首先将层速度通过Dix公式转换为均方根速度(图 7a),并将其作为真实速度(至少对于模型的平层部分来说,这种转换是准确的)。再利用垂直时移将数据校正到海平面,并且利用常规的CMP叠加速度分析进行处理,得到叠加速度场(图 7b)和动校正后的CMP道集(图 8a)。可以看出,虽然有效拉平了CMP道集中的近、中炮检距同相轴,但是得到的叠加速度场同真实速度存在很大的差异。然后以CMP叠加速度场为初始速度,以原始的OBN炮记录为输入得到CRP道集(图 8b),道集中同相轴上翘说明初始速度偏低。以产生的CRP道集为基础进行动校速度分析,图 7c和图 7d分别为经过一次和两次更新后的速度场,图 8c和图 8d分别为对应的CRP道集。可以看出,经过两次更新后,CRP道集同相轴有效拉平,更新后速度场也非常接近于真实速度场。为了验证速度更新的准确性,抽取了图 7所示速度场在CDP=180处的速度曲线,并且计算了不同速度的相对误差(图 9)。经过两次迭代后,最大的速度相对误差由6%降至约1%,证明了CRP叠加速度分析的正确性。对最终的CRP道集进行拉伸切除并且叠加,并将生成的CRP叠加剖面(图 10a)进行叠后深度偏移,准确地恢复了地下的真实构造信息(图 10b)。

|
图 7 层状模型叠加速度剖面 (a)真实;(b)常规CMP速度分析;(c)一次CRP速度分析;(d)二次CRP速度更新 |
|
图 8 层状模型CDP=180处的成像道集 (a)初始叠加速度动校正后CMP道集;(b)初始叠加速度抽取的CRP道集;(c)速度一次更新后的CRP道集;(d)速度二次更新后的CRP道集 红色曲线是为了避免远炮检距数据对叠加速度分析的影响而设置的切除线 |
|
图 9 层状模型CDP=180处不同叠加速度(a)及其相对误差曲线(b) |
|
图 10 层状模型最终CRP叠加成像剖面(a)及其叠后深度偏移成像结果(b) |
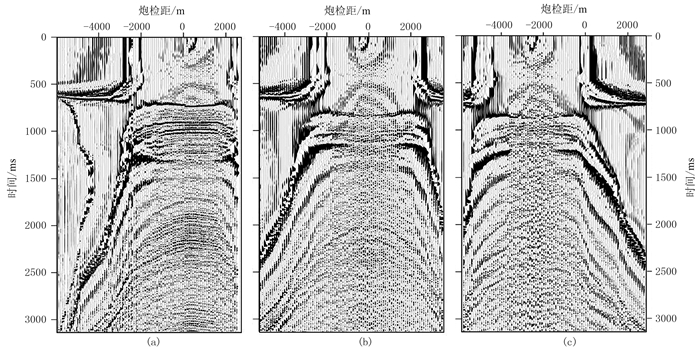
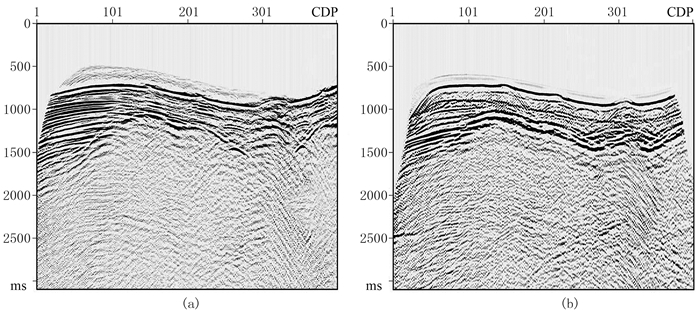
利用一个三维实际OBN数据(海水深度600~800m)测试CRP叠加的应用效果。在CRP叠加之前,应用了气泡噪声压制、水速校正、Z分量去噪等常规OBN处理技术,并将P分量数据和Z分量数据校准后进行上、下行波场分离。将分离后的上行和下行波数据应用常规的CMP叠加进行处理,其中第200线结果如图 11和图 12所示。可见,由于CMP叠加对反射信号的弥散,不论是CMP道集还是叠加剖面,都无法获得有效聚焦的反射能量,成像效果很差。
|
图 11 实际OBN数据第200线不同位置处的CMP道集 (a)CDP=101;(b)CDP=201;(c)CDP=301 |
|
图 12 实际OBN数据第200线CMP叠加成像结果 (a)下行波;(b)上行波 |
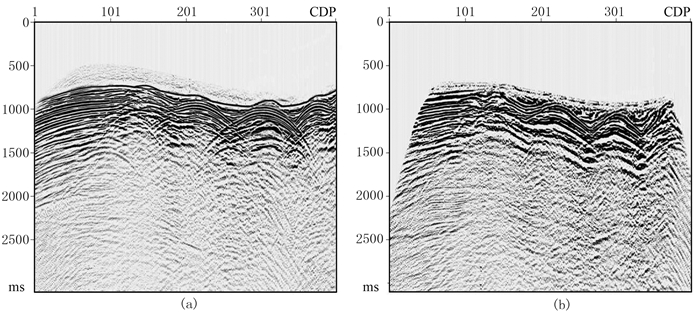
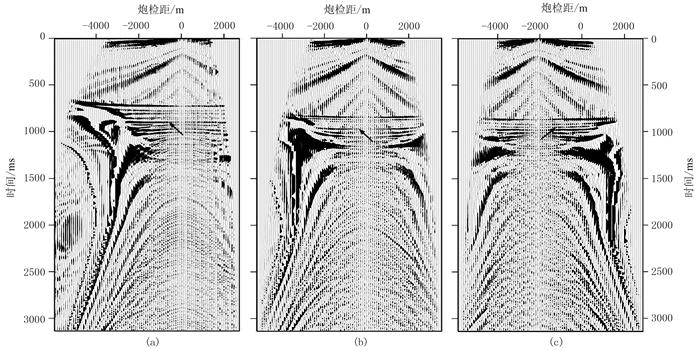
同样使用CMP叠加速度作为初始速度,应用本文所提出的CRP叠加对该数据进行处理。在两次速度更新后便可得到最终的叠加速度。图 13为第200线的上行波和下行波CRP叠加剖面,图 14为抽取的CRP道集。可以看出,CRP道集反射同相轴(如黑色箭头所示)聚焦和拉平较好,CRP叠加剖面也较好地恢复了地下的构造信息。需要注意的是,由于海底接收点的稀疏性和地震波照明范围的差异,上行波CRP叠加剖面的成像范围要窄于下行波,尤其是在海底附近。
|
图 13 实际OBN数据第200线的CRP叠加成像结果 (a)下行波;(b)上行波 |
|
图 14 实际OBN数据第200线不同位置处的CRP道集 (a)CDP=101;(b)CDP=201;(c)CDP=301 |
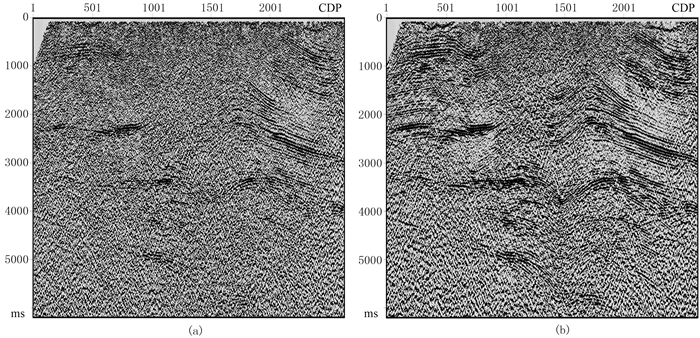
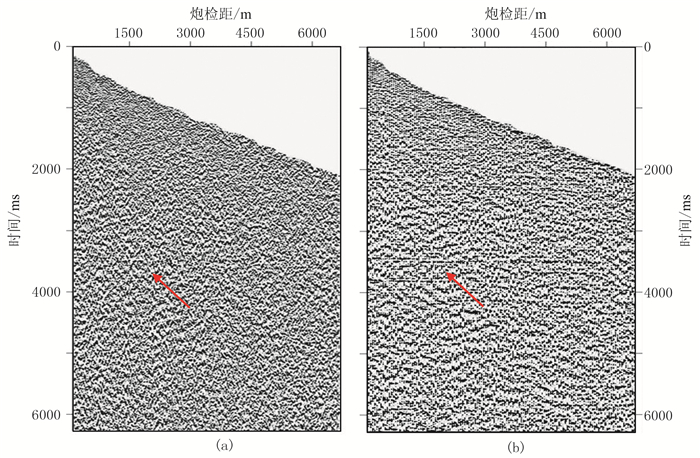
利用一块地表起伏较大的三维低信噪比数据测试CRP叠加对于山地数据的应用效果。在CRP叠加之前,该数据经过了常规去噪和静校正处理,并且应用高频静校正量将数据校正到了CMP参考面。首先应用常规的CMP叠加进行处理,得到第500线的CMP叠加剖面(图 15a),再应用CRP叠加进行速度分析和叠加成像处理,获得CRP叠加剖面(图 15b)。由图 15可以看出,CRP叠加剖面对于地下构造的成像效果明显优于CMP叠加剖面,不但具有更高的信噪比,浅层乃至中深层的地下构造也得到了较好的恢复。对比CDP=1250处的CMP道集和CRP道集可见,CMP道集(图 16a)几乎看不到有效的反射同相轴,而CRP道集(图 16b)可有效辨别中强背景噪声下的反射同相轴。
|
图 15 实际山地数据第500线叠加结果对比 (a)CMP叠加;(b)CRP叠加 |
|
图 16 实际山地数据第500线CDP=1250处动校正后道集 (a)CMP道集;(b)CRP道集 |
为解决震源和检波点高程差对零炮检距叠加成像构成的难题,本文提出了一种适用于OBN和山地数据的CRP叠加成像方法。该方法在地下介质速度横向变化不大的前提下,利用时变的数据映射算法,在将地震信号归位到地下反射点的同时,校正非零炮检距所导致的动校时差。同常规的CMP叠加相比,CRP叠加不但可以改善OBN和山地数据的零炮检距叠加成像效果,还可以提高叠加速度分析的精度。虽然CRP叠加的理论推导同样基于水平层状介质假设,但是当地下横向速度变化不大时,该方法依然适用。模型和实际数据算例验证了CRP叠加的应用效果。
| [1] |
Dix C H. Seismic velocities from surface measure-ments[J]. Geophysics, 1955, 20(1): 68-86. DOI:10.1190/1.1438126 |
| [2] |
Deregowski S M. Common-offset migrations and velocity analysis[J]. First Break, 1990, 8(6): 224-234. |
| [3] |
Causse E, Haugen G U, Rommel B E. Large-offset approximation to seismic reflection traveltimes[J]. Geophysical Prospecting, 2000, 48(4): 763-778. DOI:10.1046/j.1365-2478.2000.00207.x |
| [4] |
Vermeer G J O.3D symmetric sampling of sparse acquisition geometries[C].SEG Technical Program Expanded Abstracts, 2010, 29: 3796-3801.
|
| [5] |
Taner M T, Koehler F. Velocity spectra-digital com-puter derivation and application of velocity functions[J]. Geophysics, 1969, 34(6): 859-881. DOI:10.1190/1.1440058 |
| [6] |
刘军迎, 雍学善, 杨午阳, 等. 转换波叠加速度分析及动校正[J]. 石油地球物理勘探, 2012, 47(2): 231-235. LIU Junying, YONG Xueshang, YANG Wuyang, et al. Converted-wave stacking velocity analysis & moveout correction[J]. Oil Geophysical Prospecting, 2012, 47(2): 231-235. |
| [7] |
孙小东, 贾延睿, 李振春, 等. 粒子群算法参数搜索的共反射面元叠加[J]. 石油地球物理勘探, 2019, 54(4): 782-786. SUN Xiaodong, JIA Yanrui, LI Zhenchun, et al. Common reflection surface stack based on parameter searching by PSO[J]. Oil Geophysical Prospecting, 2019, 54(4): 782-786. |
| [8] |
Beasley C, Lynn W. Thezero-velocitylayer:Migration from irregular surfaces[J]. Geophysics, 1992, 57(11): 1435-1443. DOI:10.1190/1.1443211 |
| [9] |
Thore P D, de Bazelaire E, Ray M P. The three-parameter equation:An efficient tool to enhance the stack[J]. Geophysics, 1994, 59(2): 297-308. DOI:10.1190/1.1443592 |
| [10] |
Specht J.Differential OBC processing techniques[C].SEG Technical Program Expanded Abstracts, 2007, 26: 383-387.
|
| [11] |
Alerini M, Traub B, Ravaut C, et al. Prestack depth imaging of ocean-bottom node data[J]. Geophysics, 2009, 74(6): WCA57-WCA63. DOI:10.1190/1.3204767 |
| [12] |
Boelle J L, Brechet E, Ceragioli E, et al. A large-scale validation of OBN technology for time-lapse studies through a pilot test, deep offshore Angola[J]. The Leading Edge, 2012, 31(4): 397-403. DOI:10.1190/tle31040397.1 |
| [13] |
Grion S, Exley R, Manin M, et al. Mirror imaging of OBS data[J]. First Break, 2007, 25(11): 37-42. |
| [14] |
Dash R, Spence G, Hyndman R, et al. Wide-area imaging from OBS multiples[J]. Geophysics, 2009, 74(6): Q41-Q47. DOI:10.1190/1.3223623 |
| [15] |
Ronen R. Introduction to this special section:Marine and seabed technology[J]. The Leading Edge, 2012, 31(4): 385-386. DOI:10.1190/tle31040385.1 |
| [16] |
Cantillo J, Boelle J L, Lafram A, et al.Ocean-bottom nodes (OBN) repeatability and 4D[C].SEG Technical Program Expanded Abstracts, 2010, 29: 61-65.
|
| [17] |
Smit F.Experiences with OBS node technology in the Greater Mars Basin[C].SEG Technical Program Expanded Abstracts, 2010, 29: 3746-3750.
|
| [18] |
Tessmer G, Behle A. Common reflection point data stacking technique for converted waves[J]. Geophysical Prospecting, 1988, 36(7): 671-688. DOI:10.1111/j.1365-2478.1988.tb02186.x |
| [19] |
Wang S W, Lane M C, Lawton D C.Fast 3-D converted-wave depth-variant common conversion point stacking[R].CREWES Research Report, 1994, 6(25): 1-14.
|
| [20] |
Thomsen L. Converted-wave reflection seismology over inhomogeneous, anisotropic media[J]. Geophysics, 1999, 64(3): 678-690. DOI:10.1190/1.1444577 |
| [21] |
Chen G M, Peron J, Canales L. Rapid VSP-CDP mapping of 3-D VSP data[J]. Geophysics, 2000, 65(5): 1631-1640. DOI:10.1190/1.1444851 |
| [22] |
杨震, 芦俊, 王成祥, 等. 利用非双曲时距校正快速抽取CCP道集[J]. 石油地球物理勘探, 2018, 53(4): 659-665. YANG Zhen, LU Jun, WANG Chengxiang, et al. CCP gather fast extraction based on non-hyperbolic time correction[J]. Oil Geophysical Prospecting, 2018, 53(4): 659-665. |
| [23] |
孙祥娥, 罗国安, 金文昱. 长排列条件下三种时距曲线方程精度分析[J]. 石油地球物理勘探, 2010, 45(2): 244-247. SUN Xiang'e, LUO Guoan, JIN Wenyu. Accuracy analysis for 3 time-distance curve equations under long spread condition[J]. Oil Geophysical Prospecting, 2010, 45(2): 244-247. |
| [24] |
岳玉波, 李振春, 钱忠平, 等. 转换波Kirchhoff叠前时间偏移的成像优化方案[J]. 地球物理学报, 2018, 61(3): 1188-1195. YUE Yubo, LI Zhenchun, QIAN Zhongping, et al. Optimized imaging schemes of PS-wave Kirchhoff prestack time migration[J]. Chinese Journal of Geophysics, 2018, 61(3): 1188-1195. |
| [25] |
王狮虎, 钱忠平, 王成祥, 等. 海底地震数据积分法叠前时间域成像方法[J]. 石油地球物理勘探, 2019, 54(3): 551-557. WANG Shihu, QIAN Zhongping, WANG Chengxiang, et al. Kirchhoff prestack time migration for ocean bottom seismic data[J]. Oil Geophysical Prospecting, 2019, 54(3): 551-557. |



 岳玉波, 河北省涿州市华阳东路物探科技园东方地球物理公司物探技术研究中心, 072751。Email:
岳玉波, 河北省涿州市华阳东路物探科技园东方地球物理公司物探技术研究中心, 072751。Email: