2 中国石化中原油田分公司物探研究院, 河南濮阳 457001
2 Geophysical Exploration Research Institute, Si-nopec Zhongyuan Oilfield Company, Puyang, Henan 457001, China
随着地震勘探技术和计算机性能的发展,弹性波数值模拟与成像技术在勘探领域得到了越来越多的关注[1-3]。利用弹性波偏移算法对多分量数据进行建模和成像,可以提供更多的地下地质构造信息[4-5],如验证亮点反射、评估介质参数和检测裂缝等[6-7]。
地震波场外推通常采用有限差分法[8-12],利用恒定间距的笛卡尔坐标网格近似波动方程的时间和空间偏导数,该方法具有编程简单、运算速度快、能够分析处理各种复杂地质构造中的波动问题等优点[13]。但传统有限差分法忽略了波场的变化,在实际应用中会出现几个方面的问题:第一,地下介质速度随深度变化,地震子波波长也随深度变化,如果网格间距不变,导致波场空间采样不均匀,在低速层会出现欠采样,在高速层会出现过采样,在横向变速剧烈的区域则更严重;第二,地震勘探所面对的区域通常涉及到起伏地表[14]、低速异常体、孔隙裂缝等特殊地质构造,采用固定网格间距的常规深度域采样可能会导致算法的不稳定和精度的降低;第三,当存在地层倒转时,在传统笛卡尔坐标系下,波场延拓方向与波场能量传播的方向不一致[15]。
物理上,地震波波长随介质速度的扰动而变化,因此,网格的设计应该基于真实地下介质的速度扰动[16]。与传统规则的笛卡尔网格相比,根据地下介质速度设计的不规则网格能更精确地描绘复杂地质构造[17-19]。为此,黄超等[20]提出了变网格间距的方法,根据地下介质的速度扰动设计不同的空间网格步长,提高了计算效率;张慧等[21]和曲英铭[22]提出了时空双变的方法,对速度场进行局部加密,同时对时间层也进行了局部变换,提高了对低降速带等复杂地区的计算效率和适用性。这些方法虽然能有效改善过采样现象,提高计算效率,但在过渡区插值时会引入相应的误差,且实施过程较为复杂。
Alkhalifah等[23]首先提出将深度坐标转换成垂向旅行时坐标的思想,并应用于VIT介质声波方程正演模拟,验证了方法的有效性,之后研究了伪深度域坐标下的速度分析,证明在伪深度域进行速度分析要比在深度域更稳定[16];Li等[24]和Sun等[25]完成了伪深度域下的声波最小二乘逆时偏移,该方法能有效降低最小二乘逆时偏移算法对速度的依赖性;Plessix[26]研究了在伪深度域中的声波全波形反演,认为用垂向时间代替深度进行速度分析,能克服反演的零空间问题,从而提供了一个更稳健的算法。“伪深度域”策略是一种能有效改善局部过采样现象、节约内存占用、提高计算效率的方法。
从偏移算法中所采用的速度函数看,地震偏移可分为时间偏移和深度偏移[27]。时间偏移算法具有较高的计算效率,对偏移速度的依赖性小,然而该方法基于速度横向均匀性的假设,当遇到严重的速度横向变化或复杂的速度界面时,成像效果差;深度偏移算法能较好地适应强横向变速的复杂介质,然而该算法对速度的依赖性很强,且计算量大于时间偏移。伪深度域偏移算法对速度做了加权处理,因此能降低对速度的依赖性;而且伪深度域算法本质上也是基于双程波动方程理论,因此其成像精度接近叠前逆时深度偏移。
基于前人的研究成果,本文首先利用坐标变换的链式法则,推导了波场的一阶和二阶导数从深度域到伪深度域的转换形式,然后推导了伪深度域二阶弹性波方程(PDD-EWE);为了提高算法的计算效率,引入了变长度差分算子[28]的等效交错网格[29-31]有限差分法,实现了伪深度域弹性波数值模拟和逆时偏移。结果表明,与深度域方法相比,伪深度域变算子长度差分算法既能保证计算精度,又能显著提高计算效率、降低内存占用。
1 方法原理 1.1 不同坐标系间的映射关系假设坐标系A(x, z)到坐标系B(ξ, η)的映射关系为
| $ \left\{\begin{array}{l} x=x(\xi, \eta) \\ z=z(\xi, \eta) \end{array}\right. $ | (1) |
定义Fa、Fab为任意变量F的一阶导数和二阶导数,有
| $ \left\{\begin{array}{l} F_{a}=\frac{\partial F}{\partial a} \\ F_{a b}=F_{b a}=\frac{\partial^{2} F}{\partial a \partial b} \end{array}\right. $ | (2) |
式中a、b为坐标变量。根据坐标变换的链式法则有
| $ \left\{\begin{array}{l} x_{x}=x_{\varepsilon} \xi_{x}+x_{\eta} \eta_{x}=1 \\ x_{z}=x_{\xi} \xi_{z}+x_{\eta} \eta_{z}=0 \\ z_{x}=z_{\xi} \xi_{x}+z_{\eta} \eta_{x}=0 \\ z_{z}=z_{\xi} \xi_{z}+z_{\eta} \eta_{z}=1 \end{array}\right. $ | (3) |
求解式(3),可以得到两种坐标系下一阶导数的转换关系为
| $ \left\{\begin{array}{l} \xi_{x}=\frac{z_{\eta}}{x_{\xi} z_{\eta}-x_{\eta} z_{\xi}} \\ \xi_{z}=-\frac{x_{\eta}}{x_{\xi} z_{\eta}-x_{\eta} z_{\xi}} \\ \eta_{x}=-\frac{z_{\xi}}{x_{\xi} z_{\eta}-x_{\eta} z_{\xi}} \\ \eta_{z}=\frac{x_{\xi}}{x_{\xi} z_{\eta}-x_{\eta} z_{\xi}} \end{array}\right. $ | (4) |
定义g=xξzη-xηzξ,则任意变量F在两个坐标系下的一阶导数映射关系为
| $ \left\{\begin{array}{l} F_{x}=F_{\xi} \xi_{x}+F_{\eta} \eta_{x}=\frac{1}{g}\left(F_{\xi} \boldsymbol{z}_{\eta}-F_{\eta} \boldsymbol{z}_{\xi}\right) \\ F_{z}=F_{\xi} \xi_{z}+F_{\eta} \eta_{z}=\frac{1}{g}\left(F_{\eta} x_{\xi}-F_{\xi} x_{\eta}\right) \end{array}\right. $ | (5) |
二阶导数映射关系为
| $ \left\{\begin{array}{l} \begin{aligned} F_{x x}=& \frac{1}{g}\left[\frac{1}{g}\left(F_{\varepsilon} z_{\eta}-F_{\eta} z_{\xi}\right)\right]_{\xi} z_{\eta}-\\ & \frac{1}{g}\left[\frac{1}{g}\left(F_{\xi} z_{\eta}-F_{\eta} z_{\xi}\right)\right]_{\eta} z_{\xi} \\ F_{x z}=& \frac{1}{g}\left[\frac{1}{g}\left(F_{\xi} z_{\eta}-F_{\eta} z_{\xi}\right)\right]_{\eta} x_{\xi}-\\ & \frac{1}{g}\left[\frac{1}{g}\left(F_{\xi} z_{\eta}-F_{\eta} z_{\xi}\right)\right]_{\xi} x_{\eta} \\ F_{z z}=& \frac{1}{g}\left[\frac{1}{g}\left(F_{\eta} x_{\xi}-F_{\xi} x_{\eta}\right)\right]_{\eta} x_{\xi}-\\ & \frac{1}{g}\left[\frac{1}{g}\left(F_{\eta} x_{\xi}-F_{\xi} x_{\eta}\right)\right]_{\xi} x_{\eta} \end{aligned} \end{array}\right. $ | (6) |
将Fxx展开,可化为
| $ \begin{aligned} F_{x x}=& \frac{1}{g^{3}}\left(F_{\xi} z_{\eta}-F_{\eta} z_{\xi}\right)\left(g_{\eta} z_{\xi}-g_{\xi} z_{\eta}\right)+\\ & \frac{1}{g^{2}}\left[\left(F_{\xi} z_{\eta}-F_{\eta} z_{\xi}\right)_{\xi} z_{\eta}-\right.\\ &\left.\left(F_{\xi} z_{\eta}-F_{\eta} z_{\hat{\xi}}\right)_{\eta} z_{\xi}\right] \end{aligned} $ | (7) |
定义Fxx=F1, xx+F2, xx,则
| $ \begin{aligned} F_{1, x x}=& \frac{1}{g^{3}}\left(F_{\eta} z_{\xi}-F_{\xi} z_{\eta}\right)\left(x_{\xi \xi} z_{\eta}^{2}-2 x_{\xi \eta} z_{\eta} z_{\xi}+x_{\eta \eta} z_{\xi}^{2}\right)+\\ & \frac{1}{g^{3}}\left(F_{\eta} z_{\xi}-F_{\xi} z_{\eta}\right)\left(x_{\eta} z_{\xi \eta} z_{\xi}-x_{\xi} z_{\eta \eta} z_{\xi}+\right.\\ &\left.x_{\xi} z_{\xi \eta} z_{\eta}-x_{\eta} z_{\xi \xi} z_{\eta}\right) \end{aligned} $ | (8) |
| $ \begin{aligned} F_{2, x x}=& \frac{1}{g^{2}}\left(F_{\xi \xi} z_{\eta}^{2}-2 F_{\eta \xi} \mathcal{z}_{\xi} \mathcal{z}_{\eta}+F_{\eta \eta} z_{\eta}^{2}\right)+\\ & \frac{1}{g^{3}}\left(F_{\xi} x_{\eta}-F_{\eta} x_{\xi}\right)\left(z_{\eta}^{2} z_{\xi \xi}-2 z_{\eta} z_{\xi} \tau_{\xi \eta}+z_{\xi}^{2} z_{\eta \eta}\right)-\\ & \frac{1}{g^{3}}\left(F_{\eta} z_{\xi}-F_{\xi} z_{\eta}\right)\left(x_{\eta} z_{\xi \eta} z_{\xi}-x_{\xi} z_{\eta \eta} z_{\xi}+\right.\\ &\left.x_{\xi} z_{\xi \eta} z_{\eta}-x_{\eta} z_{\xi \xi} z_{\eta}\right) \end{aligned} $ | (9) |
可以看出,式(8)的右端第二项和式(9)的右端第三项相等且符号相反,则式(7)可化简为
| $ \begin{aligned} F_{x x}=& \frac{1}{g^{2}}\left(F_{\xi \xi} \tilde{\varepsilon}_{\eta}^{2}-2 F_{\eta \xi} \mathcal{z}_{\xi} \mathcal{z}_{\eta}+F_{\eta \eta} z_{\xi}^{2}\right)+\\ & \frac{1}{g^{3}}\left(F_{\xi} x_{\eta}-F_{\eta} x_{{\xi}}\right)\left(z_{\eta}^{2} z_{\xi \xi}-2 z_{\eta} z_{\xi} z_{\xi \eta}+z_{\xi}^{2} z_{\eta \eta}\right)+\\ & \frac{1}{\sigma^{3}}\left(F_{\eta} z_{\xi}-F_{\xi} z_{\eta}\right)\left(x_{\xi \xi} z_{\eta}^{2}-2 x_{\eta \xi} \mathcal{z}_{\eta} z_{\xi}+x_{\eta \eta} z_{\xi}^{2}\right) \end{aligned} $ | (10) |
同理,可得Fxz、Fzz的展开形式为
| $ \begin{aligned} F_{x z}=& \frac{1}{g^{2}}\left[\left(x_{\xi} z_{\eta}+x_{\eta} z_{\xi}\right) F_{\eta \xi}-\left(x_{\xi} z_{\xi} F_{\eta \eta}+x_{\eta} z_{\eta} F_{\xi \xi}\right)\right]+\\ & F_{\xi}\left[\frac{x_{\xi} \mathcal{z}_{\eta\eta}-x_{\eta} z_{\xi \eta}}{g^{2}}+\frac{x_{\eta} z_{\eta} g_{\xi}-x_{\xi} \mathcal{Z}_{\eta} g_{\eta}}{g^{3}}\right]+\\ & F_{\eta}\left[\frac{x_{\eta} z_{\xi \xi}-x_{\xi} \mathcal{z}_{\xi \eta}}{g^{2}}+\frac{x_{\xi} z_{\xi} g_{\eta}-x_{\eta} z_{\xi} g_{\xi}}{g^{3}}\right] \end{aligned} $ | (11) |
| $ \begin{aligned} F_{z z}=& \frac{1}{g^{2}}\left(F_{\xi \xi} x_{\eta}^{2}-2 F_{\eta \xi} x_{\xi} x_{\eta}+F_{\eta \eta} x_{\xi}^{2}\right)+\\ & \frac{1}{g^{3}}\left(x_{\eta} F_{\xi}-x_{\xi} F_{\eta}\right)\left(x_{\eta}^{2} z_{\xi \xi}-2 x_{\eta} x_{\xi} z_{\xi \eta}+x_{\xi}^{2} z_{\eta \eta}\right)+\\ & \frac{1}{g^{3}}\left(z_{\xi} F_{\eta}-z_{\eta} F_{\xi}\right)\left(x_{\xi \xi} x_{\eta}^{2}-2 x_{\xi \eta} x_{\eta} x_{\xi}+x_{\eta \eta} x_{\xi}^{2}\right) \end{aligned} $ | (12) |
式(10)~式(12)即为从坐标系A到坐标系B的二阶导数映射关系。
1.2 PDD-EWE公式推导在笛卡尔坐标系外推地震波场时,每个子波波长的网格数可表示为
| $ N=\frac{\lambda}{h}=\frac{v T}{h} $ | (13) |
式中:λ为波长;v为波的传播速度;h为网格间距;T为子波周期。h和T通常是固定的,因此,当速度增大时,每个子波波长的网格点数会增加,导致过采样,加重内存负担。伪深度域的思想是将垂向深度转换成垂直旅行时坐标,然后进行均匀重采样,从而避免过采样。值得注意的是,对垂直旅行时进行均匀重采样时,为避免空间假频,垂向采样间隔应满足
| $ \Delta \eta \leqslant \frac{v_{\min }}{10 f_{\max }} $ | (14) |
伪深度域垂向网格点数为
| $ N_{\mathrm{ppd}}=\frac{t_{\mathrm{max}}}{\Delta \eta}+1 $ | (15) |
式中:vmin为最小速度;fmax为地震波最大频率;tmax为最大单程旅行时。定义从笛卡尔坐标到伪深度域坐标的映射关系为
| $ \left\{\begin{array}{l} \xi=x \\ \eta=\int_{0}^{z} \frac{\mathrm{d} z}{v_{\mathrm{sm}}(x, z)} \end{array}\right. $ | (16) |
式中vsm为平滑速度场。通常,伪深度域垂向网格点数要少于深度域,能节约计算内存占用。同理从伪深度域坐标到笛卡尔坐标的映射关系为
| $ \left\{\begin{array}{l} x=\xi \\ z=\int_{0}^{\eta} v_{\operatorname{sm}}(\xi, \eta) \mathrm{d} \eta \end{array}\right. $ | (17) |
则深度域到伪深度域的一阶、二阶导数映射关系为
| $ \left\{\begin{array}{l} x_{\xi}=1 \\ x_{\eta}=0 \\ z_{\xi}=-m v_{\mathrm{sm}} \\ z_{\eta}=v_{\mathrm{sm}} \\ x_{\xi \xi}=0 \\ x_{\xi \eta}=0 \\ x_{\eta_{\eta}}=0 \\ z_{\xi \xi}=-\left(m_{\xi} v_{\mathrm{sm}}+m v_{\mathrm{sm}_{\xi}}\right) \\ z_{\eta \eta}=v_{\mathrm{sm}_{\eta}} \\ z_{\xi \eta}=-\left(m_{\eta} v_{\mathrm{sm}}+m v_{\mathrm{sm}}\right)=v_{\mathrm{sm}_{\xi}} \end{array}\right. $ | (18) |
式中:m=ηξ为伪深度随水平距离的变化率;vsmξ=
将式(18)代入式(10)~式(12),可以得到变量F在伪深度域中的二阶空间导数
| $ \left\{\begin{aligned} F_{x x}=&\left(F_{\xi \xi}+2 m F_{\xi \eta}+m^{2} F_{\eta \eta}\right)+\\ &\left(m_{\xi}+m m_{\eta}\right) F_{\eta} \\ F_{x z}=& \frac{F_{\xi \eta}+m F_{\eta \eta}+m_{\eta} F_{\eta}}{v_{\rm sm}} \\ F_{z z}=& \frac{1}{v_{{\rm sm}}^{2}} F_{\eta \eta}-\frac{v_{\rm sm}}{v_{\rm sm}^{3}} F_{\eta} \end{aligned}\right. $ | (19) |
在均匀各向同性介质中,以位移表示的二阶常速度弹性波方程在深度域的表达式为
| $ \left\{\begin{array}{l} \frac{\partial^{2} u}{\partial t^{2}}=v_{\mathrm{P}}^{2} \frac{\partial^{2} u}{\partial x^{2}}+v_{\mathrm{S}}^{2} \frac{\partial^{2} u}{\partial z^{2}}+\left(v_{\mathrm{P}}^{2}-v_{\mathrm{S}}^{2}\right) \frac{\partial^{2} w}{\partial x \partial z} \\ \frac{\partial^{2} w}{\partial t^{2}}=v_{\mathrm{S}}^{2} \frac{\partial^{2} w}{\partial x^{2}}+v_{\mathrm{S}}^{2} \frac{\partial^{2} w}{\partial z^{2}}+\left(v_{\mathrm{P}}^{2}-v_{\mathrm{S}}^{2}\right) \frac{\partial^{2} u}{\partial x \partial z} \end{array}\right. $ | (20) |
式中:u、w分别为x、z方向的位移分量;vP、vS分别为纵波速度和横波速度。
将式(19)代入式(20),可得PDD-EWE方程
| $ \left\{\begin{array}{l} \frac{\partial^{2} u}{\partial t^{2}}= v_{\mathrm{P}}^{2}\left[\frac{\partial^{2} u}{\partial \xi^{2}}+2 m \frac{\partial^{2} u}{\partial \xi \partial \eta}+m^{2} \frac{\partial^{2} u}{\partial \eta}+\right.\\ \left.\left(m_{\xi}+m m_{\eta}\right) \frac{\partial u}{\partial \eta}\right]+v_{\mathrm{S}}^{2}\left(\frac{1}{v_{\mathrm{sm}}^{2}} \frac{\partial^{2} u}{\partial \eta^{2}}-\frac{v_{\mathrm{sm}}}{v_{\mathrm{sm}}^{3}} \frac{\partial u}{\partial \eta}\right)+\\ \frac{v_{\mathrm{P}}^{2}-v_{\mathrm{S}}^{2}}{v_{\mathrm{sm}}}\left(\frac{\partial^{2} w}{\partial \xi \partial \eta}+m \frac{\partial^{2} w}{\partial \eta^{2}}+m_{\eta} \frac{\partial w}{\partial \eta}\right) \\ \frac{\partial^{2} w}{\partial t^{2}}=v_{\mathrm{S}}^{2}\left[\frac{\partial^{2} w}{\partial \xi^{2}}+2 m \frac{\partial^{2} w}{\partial \xi \partial \eta}+m^{2} \frac{\partial^{2} w}{\partial \eta^{2}}+\right.\\ \left.\left(m_{\xi}+m m_{\eta}\right) \frac{\partial w}{\partial \eta}\right]+v_{\mathrm{P}}^{2}\left(\frac{1}{v_{\mathrm{sm}}^{2}} \frac{\partial^{2} w}{\partial \eta^{2}}-\frac{v_{\mathrm{sm}}}{v_{\mathrm{sm}}^{3}} \frac{\partial w}{\partial \eta}\right)+\\ \frac{v_{\mathrm{P}}^{2}-v_{\mathrm{S}}^{2}}{v_{\mathrm{sm}}}\left(\frac{\partial^{2} u}{\partial \xi \partial \eta}+m \frac{\partial^{2} u}{\partial \eta^{2}}+m_{\eta} \frac{\partial u}{\partial \eta}\right) \end{array}\right. $ | (21) |
值得注意的是,本文是利用纵波速度实现从深度域到伪深度域的转换。测试结果表明,利用伪深度域的方法转换得到的横波速度场与利用纵横波比得到的横波速度场基本一致。以分量u为例说明式(21)中的空间偏导数等效交错网格有限差分法格式。其一阶导数的离散格式为
| $ \left\{\begin{array}{l} \frac{\partial u_{0, 0}^{0}}{\partial \xi}=\frac{1}{\Delta \xi} \sum\limits_{l=1}^{M} a_{l}\left(u_{l-\frac{1}{2}, 0}^{0}-u_{-l+\frac{1}{2}, 0}^{0}\right) \\ \frac{\partial u_{0, 0}^{0}}{\partial \eta}=\frac{1}{\Delta \eta} \sum\limits_{l=1}^{M} a_{l}\left(u_{0, l-\frac{1}{2}}^{0}-u_{0, -l+\frac{1}{2}}^{0}\right) \end{array}\right. $ | (22) |
二阶导数的离散格式为
| $ \left\{\begin{aligned} \frac{\partial^{2} u_{0, 0}^{0}}{\partial \xi^{2}}=& \frac{1}{\Delta \xi^{2}} \sum\limits_{l=1}^{M} \sum\limits_{m=1}^{M} a_{l} a_{m}\left[\left(u_{m+l-1, 0}^{0}-u_{-m+l, 0}^{0}\right)-\right.\\ &\left.\left(u_{m-l, 0}^{0}-u_{-m-l+1, 0}^{0}\right)\right] \\ \frac{\partial^{2} u_{0, 0}^{0}}{\partial \eta^{2}}=& \frac{1}{\Delta \eta^{2}} \sum\limits_{l=1}^{M} \sum\limits_{m=1}^{M} a_{l} a_{m}\left[\left(u_{0, m+l-1}^{0}-u_{0, -m+l}^{0}\right)-\right.\\ &\left.\left(u_{0, m-l}^{0}-u_{0, -m-l+1}^{0}\right)\right] \\ \frac{\partial^{2} u_{0, 0}^{0}}{\partial \xi \partial \eta}=& \frac{1}{\Delta \xi \Delta \eta} \sum\limits_{l=1}^{M} \sum\limits_{m=1}^{M} a_{l} a_{m}\left[\left(u_{m-\frac{1}{2}, l-\frac{1}{2}}^{0}-\right.\right.\\ &\left.\left.u_{-m+\frac{1}{2}, l-\frac{1}{2}}^{0}\right)-\left(u_{m-\frac{1}{2}, -l+\frac{1}{2}}^{0}-u_{-m+\frac{1}{2}, -l+\frac{1}{2}}^{0}\right)\right] \end{aligned}\right. $ | (23) |
式中:ul, m0为0时刻在网格点(ξ=lΔξ, η=mΔη)的位移,其中Δξ、Δη分别为横、纵向采样间隔;al、am为一阶交错网格差分系数;M为差分算子半长度。等效交错网格实际对二阶导数使用了两次一阶交错网格差分,因此与一阶交错网格具有相同的精度。本文在时间方向采用二阶差分格式。值得注意的是,u和w在实际计算时需要错开半个网格点。
对于PDD-EWE方程,虽然偏导数项的增加提高了计算的复杂度,但由于该方程没有中间变量,与一阶方程相比能节约计算内存。
1.3 变长度差分算子基本原理为了进一步提升算法的计算效率,引入变长度差分算子[23]的思想。在一定的精度要求下,根据速度的不同设计不同长度的差分算子,可有效改善速度的非均匀性导致的计算消耗。
本文的波场延拓方法是基于等效交错网格有限差分法,与传统一阶的交错网格具有相同的精度,因此u分量的一阶空间偏导数的交错网格离散形式为
| $ \begin{aligned} \frac{\partial u}{\partial x}=& \frac{1}{h} \sum\limits_{m=1}^{M} a_{m}\left\{u\left[x+\left(m-\frac{1}{2}\right) h\right]-\right.\\ &\left.u\left[x-\left(m-\frac{1}{2}\right) h\right]\right\} \end{aligned} $ | (24) |
式中h为网格横向间距。
对式(24)进行傅里叶变换,并代入平面波解u=u0exp(ikx),有
| $ \frac{k h}{2}=\sum\limits_{m=1}^{M} a_{m} \sin \left[k h\left(m-\frac{1}{2}\right)\right] $ | (25) |
式中k为波数。基于关系式
| $ \varepsilon(v, M)=\frac{\pi f h}{v}-\sum\limits_{m=1}^{M} a_{m} \sin \left[\frac{2 \pi f h}{v}\left(m-\frac{1}{2}\right)\right] $ | (26) |
当给定f、h后,误差函数只与速度v和差分算子半长度M有关。当给定误差函数ε,则不同的速度会对应不同的差分算子长度,速度越大,需要的差分算子长度越短。根据速度和限定误差,调整差分算子长度,能有效提高计算效率。
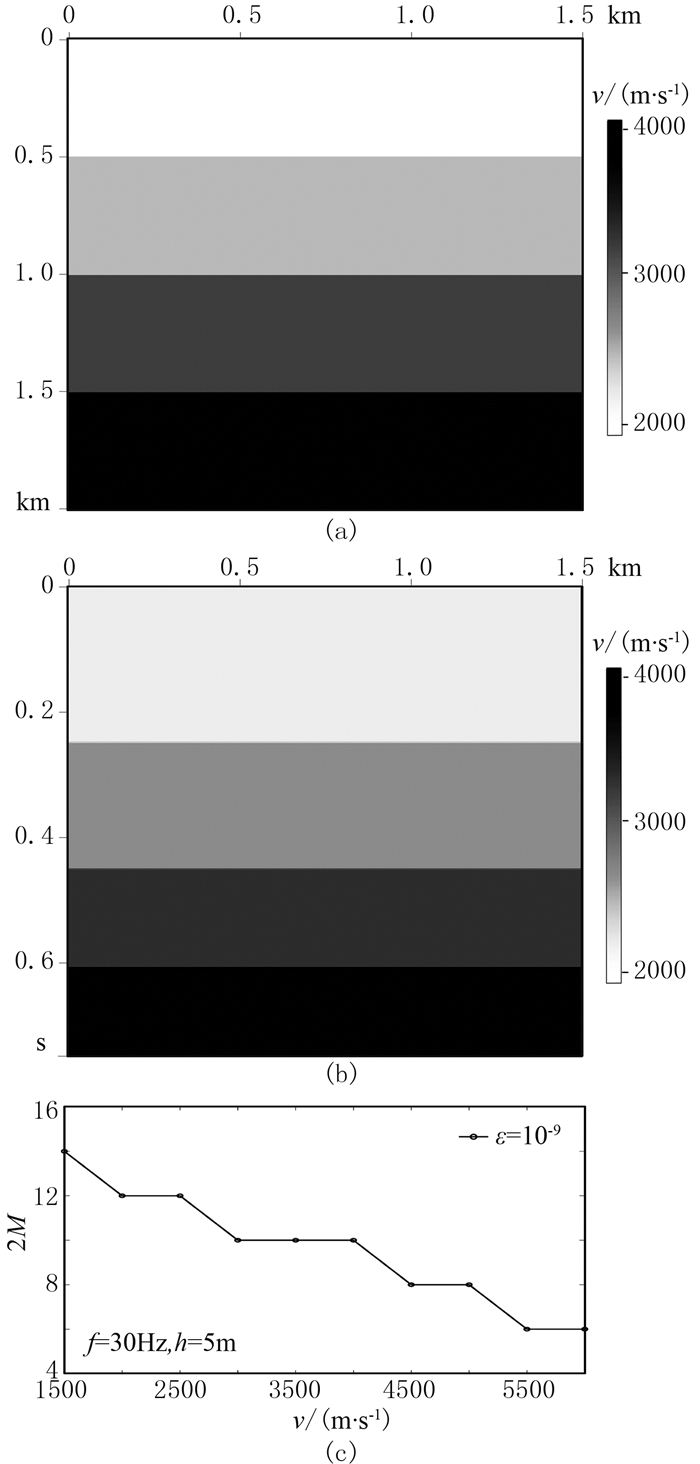
2 数值模拟 2.1 层状介质为了说明本文变长度差分算子伪深度域弹性波数值模拟的有效性和优势,设计一个简单的层状模型,其主要模拟参数为:网格点数为301×401,横、纵向网格间距均为5m,时间采样间隔为0.3ms,总接收时间为2.4s,震源采用主频为30Hz的雷克子波,加载在模型表面中间,振幅增益为104倍,纵横波速比为1.73,深度域纵波速度模型如图 1a所示。首先将模型从深度域转换到伪深度域,在满足采样定理的前提下,取Δη=2.5ms,伪深度域速度模型如图 1b所示,网格点数为301×300。对比图 1b和图 1a可以看出,伪深度域的速度场实际上在浅层低速时被拉伸,深层高速时被压缩,使得垂向波场采样变得均匀,从而避免了过采样。针对模拟参数,根据上文的变长度差分算子计算方法,当f=30Hz、h=5m、将误差控制在10-9时,计算的不同速度对应的不同差分算子长度如图 1c所示。根据图 1c,可以得到层状模型对应的差分算子长度,传统深度域差分算子长度2M=12。另外,在数值模拟的过程中,为防止边界反射带来的干扰,采用海绵吸收边界条件[31],其衰减因子为
|
图 1 层状模型 (a)深度域纵波速度;(b)伪深度域纵波速度;(c)不同速度对应的有限差分算子长度 |
| $ \left\{\begin{array}{l} G(i)=\exp \left\{-\left[a\left(i-n_{\mathrm{p}}\right)\right]^{2}\right\} \\ a=\sqrt{-\frac{\lg 0.9}{n_{\mathrm{p}}^{2}}} \end{array}\right. $ | (27) |
式中:np为吸收边界层厚度,吸收层加在模型外层;i为计算点到外边界的距离;a为衰减系数。在本文的数值模拟和逆时偏移中,吸收层厚度均设为50个网格。
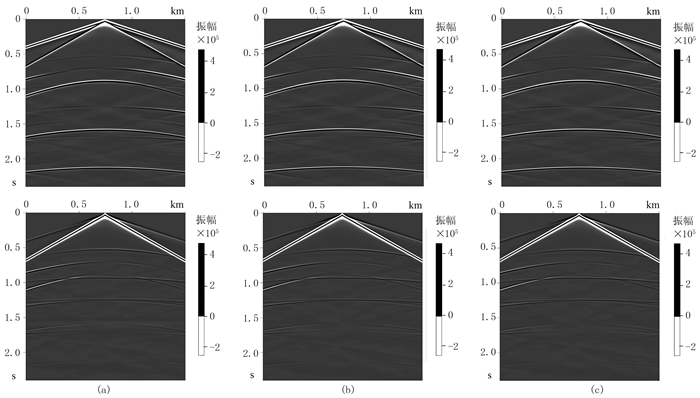
图 2是利用深度域方法、伪深度域方法及引入变长度差分算子后的伪深度域方法得到的层状模型单炮地震记录,从图中可以看出,三种方法模拟的单炮地震记录基本一致。进一步对三种方法模拟的单炮地震记录做残差分析。图 3a为伪深度域与深度域模拟结果的残差,水平和垂直分量的相对误差分别约为0.25%和0.12%。产生这种误差的原因是:将图 1a转换成图 1b时,需要对速度重采样,本文选择了三次样条插值方法。图 3b为伪深度域变长度差分算子与深度域模拟结果的残差,与图 3a基本相同;图 3c为伪深度域变差分算子长度与固定差分算子长度模拟结果的残差,水平和垂直分量的相对误差分别约为1.5×10-6和7.0×10-7,几乎可以忽略不计。原始深度域速度模型网格数为301×401,转换到伪深度域中的速度模型网格数为301×300,相当于节约了25.2%的内存。应用CPU型号为Intel(R) Xeon(R) CPU E5-2630 v4、主频为2.20GHz的计算机,三种方法运行时间分别为3705、3466和2946s,伪深度域变长度差分算子模拟方法与深度域方法相比,效率提高了20.5%,与伪深度域固定长度差分算子模拟方法相比,提高了13.8%。
|
图 2 层状模型不同方法模拟的水平分量(上)和垂直分量(下)单炮记录 (a)深度域方法;(b)伪深度域固定长度差分算子方法;(c)伪深度域变长度差分算子方法 |
2.2 Marmousi模型
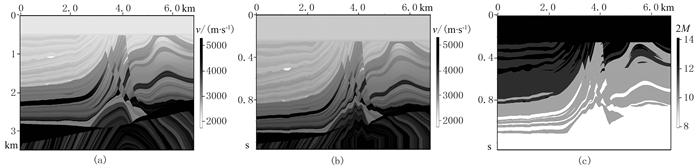
选取Marmousi模型验证本文方法对复杂介质的适用性。将原始Marmousi模型横向按10:1、纵向按3:1抽稀,得到的深度域纵波速度模型,网格数为1360×700,如图 4a所示。将深度域速度场转换到伪深度域,纵向采样间隔Δη=2.5ms,网格数为1360×507,如图 4b所示。可以看出,伪深度域模型浅层被拉伸,深层被压缩,对应的有限差分算子长度如图 4c所示,而传统深度域方法差分算子长度2M=12。模拟参数为:时间采样间隔为0.3ms,空间采样间隔为5m,总接收时间为2.1s,震源采用中心频率为30Hz的雷克子波,振幅增益104倍,纵横波速度比设为1.73。
|
图 4 Marmousi模型 (a)深度域纵波速度;(b)伪深度域纵波速度;(c)有限差分算子长度 |
图 5为传统深度域方法和本文伪深度域变长度差分算子方法弹性波数值模拟单炮记录对比,图 6为两种方法模拟记录在x=2.0km处的单道记录,可以看出本文方法和深度域方法的单道地震记录基本保持一致,没有走时误差,只存在振幅差异,水平和垂直分量最大相对误差分别为0.3%、0.23%。由此可见,伪深度域变长度差分算子弹性波模拟方法适用于复杂介质模型,且能节省约28%内存占用。

|
图 6 Marmousi模型两种方法模拟结果在x=2.0km处单道(左)及局部放大(右) (a)水平分量;(b)垂直分量 |
将本文伪深度域变长度差分算子弹性波模拟方法应用于Marmousi模型的弹性波逆时偏移,验证本文方法的实用价值。模拟参数为:网格数为1360×700,纵横向网格间距为5m,时间采样间隔为0.3ms,总接收时间为3.0s,震源采用主频为30Hz的雷克子波,地面布置61炮,炮点距为100m,采用全接收方式,道间距为5m,速度模型和差分算子长度如图 4所示,吸收边界厚度为50个网格间距。
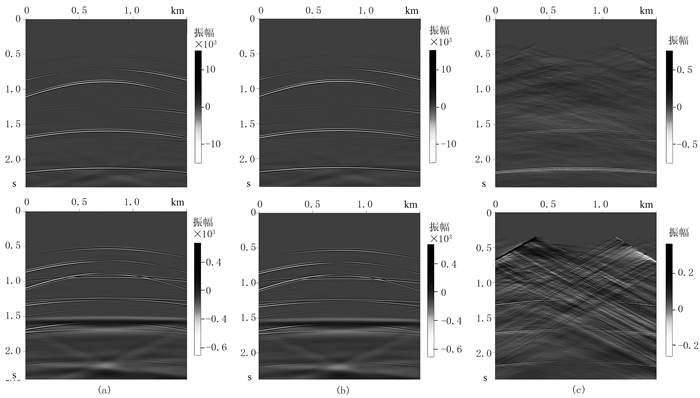
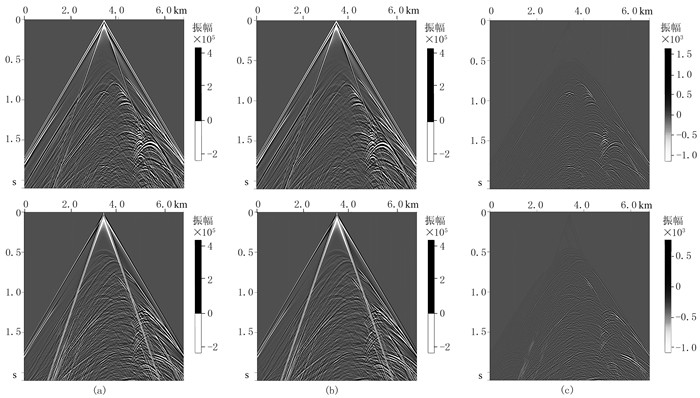
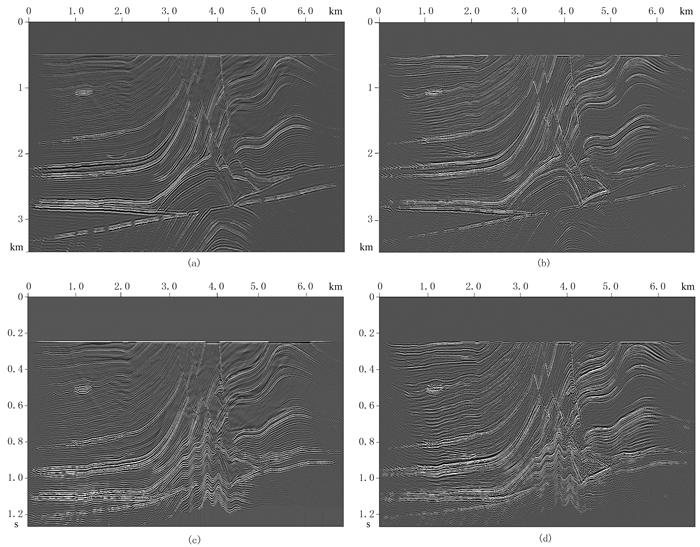
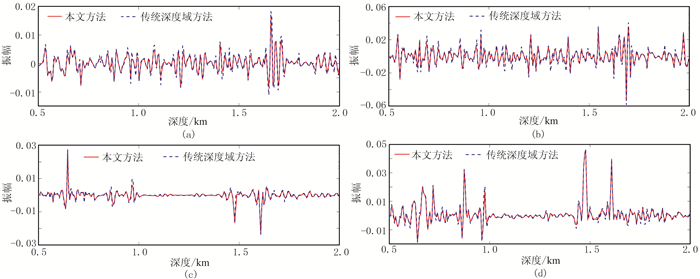
本文逆时偏移采用互相关的成像条件。图 7为常规深度域方法和本文方法Marmousi模型弹性波逆时偏移的PP波和PS波成像结果,可以看出,与传统深度域方法一样,本文方法偏移结果能较好地刻画Marmousi模型的构造层位,可见本文方法能适用于复杂介质的弹性波逆时偏移成像。将图 7c和图 7d转换到深度域,抽取x=2.0和6.0km处单道偏移结果与图 7a和图 7b对比,如图 8所示。可以看出,两种方法的单道曲线之间基本没有深度误差,只存在较小的振幅误差。基于相同的计算机资源(CPU型号为Intel(R) Xeon(R) CPU E5-2630 v4、主频为2.20GHz,18个节点),传统深度域方法Marmousi模型弹性波逆时偏移用时24.5h,本文的伪深度域变长度差分算子方法用时18.5h,效率提升了24.4%。
|
图 7 Marmousi模型两种方法弹性波逆时偏移结果 (a)传统深度域方法PP波成像;(b)传统深度域方法PS波成像;(c)本文方法PP波成像;(d)本文方法PS波成像 |
|
图 8 Marmousi模型两种方法弹性波逆时偏移结果不同位置处单道对比 (a)x=2.0km,PP波成像;(b)x=2.0km,PS波成像;(c)x=6.0km,PP波成像;(d)x=6.0km,PS波成像 |
本文发展了一种基于伪深度域的变长度差分算子有限差分弹性波数值模拟方法,与传统深度域方法相比,有效改善了由于速度差异过大导致的波场采样不均匀现象。理论分析和模型测试结果表明:
(1) 伪深度域弹性波数值模拟方法主要优势在于能节约内存占用,变长度差分算子方法能有效提升计算效率。在保证精度的前提下,与常规深度域方法相比,伪深度域变长度差分算子方法能节省约25%~30%内存,效率提升约20%~25%;
(2) 对速度场在伪深度域重采样处理会导致模拟结果的振幅误差,与传统深度域方法相比,本文方法的简单模型和Marmousi模型模拟结果的振幅相对误差不超过1%;
(3) 将本文方法应用于Marmousi模型弹性波逆时偏移,与常规深度域方法偏移结果的单道波形一致性较好,只存在较小的振幅误差,验证了本文方法对复杂介质模型的适用性。
| [1] |
Xia F, Dong L G, Ma Z T. The numerical modeling of 3-D elastic wave equation using a high-order, staggered-grid finite difference scheme[J]. Applied Geophysics, 2004, 1(1): 38-41. DOI:10.1007/s11770-004-0028-7 |
| [2] |
Li Y Y, Du Y, Yang J D, et al. Elastic reverse time migration using acoustic propagators[J]. Geophysics, 2018, 83(5): S399-S408. |
| [3] |
吴潇, 刘洋, 蔡晓慧. 弹性波波场分离方法对比及其在逆时偏移成像中的应用[J]. 石油地球物理勘探, 2018, 53(4): 710-721. WU Xiao, LIU Yang, CAI Xiaohui. Elastic wavefield separation methods and their applications in reverse time migration[J]. Oil Geophysical Prospecting, 2018, 53(4): 710-721. |
| [4] |
李振春, 雍鹏, 黄建平, 等. 基于矢量波场分离弹性波逆时偏移成像[J]. 中国石油大学学报(自然科学版), 2016, 40(1): 42-48. LI Zhenchun, YONG Peng, HUANG Jianping, et al. Elastic wave reverse time migration based on vector wavefield seperation[J]. Journal of China University of Petroleum(Natural Science Edition), 2016, 40(1): 42-48. DOI:10.3969/j.issn.1673-5005.2016.01.006 |
| [5] |
Chang W F, Mcmechan G A. Elastic reverse-time migration[J]. Geophysics, 1987, 52(3): 243-256. |
| [6] |
Yong P, Huang JP, Li ZC, et al. Elastic-wavereverse-time migration based on decoupled elastic-wave equations and inner-product imaging condition[J]. Journal of Geophysics and Engineering, 2016, 13(6): 953-963. DOI:10.1088/1742-2132/13/6/953 |
| [7] |
Du Q Z, Gong X F, ZHANG M Q, et al. 3D PS-wave imaging with elastic reverse-time migration[J]. Geophysics, 2014, 79(5): S173-S184. DOI:10.1190/geo2013-0253.1 |
| [8] |
Moczo P, Kristek J, Vavrycuk V, et al. 3D heteroge-neous staggered-grid finite-difference modeling of seismic motion with volume harmonic and arithmetic averaging of elastic moduli and densities[J]. Bulletin of the Seismological Society of America, 2002, 92(8): 3042-3066. DOI:10.1785/0120010167 |
| [9] |
Alford R M, Kelly K R, Boore D M. Accuracy of finite-difference modeling of the acoustic wave equation[J]. Geophysics, 1974, 39(6): 834-842. DOI:10.1190/1.1440470 |
| [10] |
Dablain M A. The application of high-order differencing to the scalar wave equation[J]. Geophysics, 1986, 51(1): 54-66. |
| [11] |
Kristek J, Moczo P. Seismic-wave propagation in viscoelastic media with material discontinuities:A 3D fourth-order staggered-grid finite-difference modeling[J]. Bulletin of the Seismological Society of America, 2003, 93(5): 2273-2280. |
| [12] |
刘东洋, 彭苏萍, 师素珍, 等. 基于Lebedev网格的TTI介质二维三分量正演模拟[J]. 石油地球物理勘探, 2018, 53(2): 288-296. LIU Dongyang, PENG Suping, SHI Suzhen, et al. 2D three-component seismic forward modeling in TTI media based on the Lebedev grid[J]. Oil Geophysical Prospecting, 2018, 53(2): 288-296. |
| [13] |
Finkelstein B, Kastner R. Finite difference time do-main dispersion reduction schemes[J]. Journal of Computational Physics, 2007, 221(1): 422-438. DOI:10.1016/j.jcp.2006.06.016 |
| [14] |
李庆洋, 黄建平, 李振春, 等. 起伏地表贴体全交错网格仿真型有限差分正演模拟[J]. 石油地球物理勘探, 2015, 50(4): 633-642. LI Qingyang, HUANG Jianping, LI Zhenchun, et al. Undulating surface body-fitted grid seismic modeling based on fully staggered-grid mimetic finite-difference[J]. Oil Geophysical Prospecting, 2015, 50(4): 633-642. |
| [15] |
Ma X X, Alkhalifah T. Wavefield extrapolation in pseudo depth domain[J]. Geophysics, 2013, 78(2): S81-S91. DOI:10.1190/geo2012-0237.1 |
| [16] |
Alkhalifah T. Tau migration and velocity analysis:Theory and synthetic examples[J]. Geophysics, 2003, 68(4): 1331-1339. DOI:10.1190/1.1598126 |
| [17] |
Tang Y X. Target-oriented wave-equation least-squares migration/inversion with phase-encoded Hessian[J]. Geophysics, 2009, 74(6): WCA95-WCA107. DOI:10.1190/1.3204768 |
| [18] |
Chen Y Q, Dutta G, Dai W, et al. Q-least-squares reverse time migration with viscoacoustic deblurring filters[J]. Geophysics, 2017, 82(6): 425-438. |
| [19] |
梁文全, 王彦飞, 杨长春. 声波方程数值模拟矩形网格有限差分系数确定法[J]. 石油地球物理勘探, 2017, 52(1): 56-62. LIANG Wenquan, WANG Yanfei, YANG Changchun. Acoustic wave equation modeling with rectangle grid finite difference operator and its linear time space domain solution[J]. Oil Geophysical Prospecting, 2017, 52(1): 56-62. |
| [20] |
黄超, 董良国. 可变网格与局部时间步长的交错网格高阶差分弹性波模拟[J]. 地球物理学报, 2009, 52(11): 176-186. HUANG Chao, DONG Liangguo. High-order finite difference method in seismic wave simulation with variable grids and local time-steps[J]. Chinese Journal of Geophysics, 2009, 52(1): 176-186. |
| [21] |
张慧, 李振春. 基于双变网格算法的地震正演模拟[J]. 地球物理学报, 2011, 54(1): 77-86. ZHANG Hui, LI Zhenchun. Seismic wave simulationmethod based on dual-variable grid[J]. Chinese Journal of Geophysics, 2011, 54(1): 77-86. DOI:10.3969/j.issn.0001-5733.2011.01.009 |
| [22] |
曲英铭. 起伏地表直接成像技术研究进展[J]. 石油物探, 2019, 58(5): 625-644. QU Yingming. Research progress of topographic imaging methods[J]. Geophysical Prospecting for Petro-leum, 2019, 58(5): 625-644. DOI:10.3969/j.issn.1000-1441.2019.05.001 |
| [23] |
Alkhalifah T, Fomel S, Biondi A B. The space-time domain:theory and modelling for anisotropic media[J]. Geophysical Journal of the Royal Astronomical Society, 2001, 144(1): 105-113. DOI:10.1046/j.1365-246x.2001.00300.x |
| [24] |
Li Q Y, Huang J P, Li Z C. Cross-correlation least-squares reverse time migration in the pseudo-time domain[J]. Journal of Geophysics and Engineering, 2017, 14(4): 841-851. DOI:10.1088/1742-2140/aa6b33 |
| [25] |
Sun X D, Rui J Y, Min Z, et al. Least squares reverse-time migration in the pseudo depth domain and reservoir exploration[J]. Applied Geophysics, 2018, 15(2): 234-239. DOI:10.1007/s11770-018-0681-x |
| [26] |
Plessix R E. A pseudo-time formulation for acoustic full waveform inversion[J]. Geophysical Journal International, 2013, 192(2): 613-630. DOI:10.1093/gji/ggs056 |
| [27] |
徐基祥, 崔化娟. 关于深度偏移的几个相关概念[J]. 石油地球物理勘探, 2004, 39(3): 259-264. XU Jixiang, CUI Huajuan. Several associated conceptions of depth migration[J]. Oil Geophysical Prospecting, 2004, 39(3): 259-264. DOI:10.3321/j.issn:1000-7210.2004.03.004 |
| [28] |
Liu Y, Sen M K. Finite-difference modeling with a-daptive variable-length spatial operators[J]. Geophy-sics, 2011, 76(4): T79-T89. |
| [29] |
Di Bartolo L, Dors C, Mansur W J. A new family of finite-difference schemes to solve the heterogeneous acoustic wave equation[J]. Geophysics, 2012, 77(5): T187-T199. DOI:10.1190/geo2011-0345.1 |
| [30] |
Yong P, Huang J P, Li Z C, et al. Optimized equivalent staggered-grid FD method for elastic wave mo-deling based on plane wave solutions[J]. Geophysical Journal International, 2017, 208(2): 1157-1172. |
| [31] |
Cerjan C, Kosloff D, Kosloff R, et al. A nonreflecting boundary condition for discrete acoustic and elasticwave equations[J]. Geophysics, 1985, 50(4): 705-708. DOI:10.1190/1.1441945 |



 黄建平, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院地球物理系, 266580。Email:
黄建平, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院地球物理系, 266580。Email: