2 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071;
3 中国石油大学(华东)理学院, 山东青岛 266580
2 Functional Laboratory for Marine Mineral Resources Assessment and Prospecting, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266071, China;
3 College of Science, China University of Petroleum(East China), Qingdao, Shandong 266580, China
分布式声传感(Distributed Acoustic Sensing,DAS)是一种地震信号采集新技术,尤其适用于井中地震资料采集。DAS系统依靠光纤将地震信号获取与传输一体化,光纤作为地震波传感器,同时也作为信号传输介质,利用光纤中的瑞利散射效应实时感知外界波动引起的光纤局部变化,进而获取光纤周围的地震波场信号,几乎可以永久安装在井中采集地震数据或监测地下流体。相比传统检波器,DAS系统具有以下优点。①低成本。光纤本身的成本低廉,且具有耐腐蚀、耐高温、耐高压等特点,经过铠甲封装等处理后可以永久安装在井中,随时获取地震资料,无需再重新布置检波器,节约了大量人力、物力成本。②适用范围更广,更简便、高效。光纤一经安装,不需要人工干预,完全由地面仪器系统控制,由于光纤具备耐高温、耐高压等优点,因此可以大规模长期布设并不易损坏,对于不能布置检波器的注水井或者生产井也同样适用,而且无需占井施工。③可实现井的全部覆盖且具有较高分辨率。井中地震采集时由于传统检波器阵列级数有限,因此需要不断沿井移动以获取整井的地震信息,耗费了大量时间和人力,且空间采样间隔相对较大容易产生空间假频;使用光纤可以完全覆盖整井或需要的深度,空间采样间隔小,避免了空间假频,由光纤获得的数据分辨率取决于DAS系统发射的脉冲宽度,理论上通过改变脉冲宽度可达到很高的分辨率[1-2]。
近十年来,在业界关于DAS系统研制和实际测试成为热点。在DAS系统中,地面仪器系统以特定频率向光纤发射脉冲信号并接收背向瑞利散射信号,具关键控制作用。通常地面仪器主要是窄线宽激光器、掺饵光纤放大器、拉曼放大器、声光调制器、光电探测器以及解调设备的集成体。虽然目前市场上仪器系统的设计原理都是基于瑞利散射效应,但具体设计细节并不完全相同,如,Optasense公司的ODH、OLA系统,测量光纤各点的应变[1, 3],Silixa公司的iDAS(Intelligent Distributed Acoustic Sensor)系统测量光纤各点的应变率[4-6]。随着仪器的发展,众多的实地测试也相继开展。在井中地震勘探领域,早在2009年壳牌公司在加拿大F气藏利用DAS系统开展地球物理监测,论证了DAS系统采集VSP资料的可行性[3];随后挪威国家石油公司在北海油田实地测试井中地震DAS系统[7];Mateeva等[8]在墨西哥湾采集了海上深水VSP DAS数据,部分数据质量较高。在水力压裂监测领域,Cox等[9]阐述了DAS系统微地震监测理论,Molenaar等[10]、Bakku等[11]利用DAS系统开展致密砂岩和页岩水力压裂监测。在二氧化碳封存监测领域,Barberan等[12]、Harris等[13]和Correa等[14]分别在法国Rousse、加拿大Aquistore和澳大利亚Otway利用DAS系统监测二氧化碳封存流体扩散运移,获得了较好的效果。在常规地面地震勘探领域,由于光纤对接近径向入射的地震波敏感性较低,限制了DAS系统的使用,因此人们研究了螺旋缠绕式光纤地震波传感理论,实地测试了经过不同处理的(铠甲处理、螺旋缠绕等)光纤的数据采集效果[2, 15-18],取得了丰硕成果,拓宽了DAS系统的适用范围,为DAS系统的发展奠定了重要基础。
近几年来,中国DAS系统的发展也非常迅速。东方地球物理公司和电子科技大学合作开发了超高应变灵敏度DAS系统(uDAS),空间分辨率较高,在冀东、华北等油田完成了实地试验,取得的数据质量达到了工业化要求[19]。Yu等[20]提出的基于微结构光纤的DAS系统,提高了瑞利散射光的幅值,能有效避免由干涉衰落引起散射光中某些点幅值接近于零的问题。山东省科学院激光研究所发展了多种光纤检波器系统,如光纤激光检波器系统、光纤光栅检波器系统、光纤分布式检波器系统等,分别适用不同应用场景[21-23]。Xu等[24]提出了基于相位载波技术(PGC)解调的DAS系统,在黑龙江、天津等地开展了井中VSP和地面地震测试,取得了较好效果。Wang等[25]、Liang等[26]研究了DAS系统相关算法,包括外差相干差分相位解调算法、机器学习模式识别算法等。总之,中国DAS系统的研究起步虽晚,但发展较迅速,在硬件设备及解调技术方面丰富多样,呈现广阔的应用前景。
在DAS系统的应用中,关键步骤是利用光纤信号恢复地震信号振幅、相位等有效信息,但振动信号到光纤信号间的传递机制较复杂,影响信号转换的因素较多,且目前DAS光纤信号信噪比相对较低,数据采集、处理面临强噪声等问题,因此亟待开展数值模拟研究。本文基于离散光纤瑞利散射干涉模型,在一定假设条件下通过数值模拟深入讨论振动信号到光纤信号间的转换关系;以雷克子波信号为例,分析脉冲宽度、振动强度对DAS光纤信号的波形和信噪比的影响,对比不同光纤空间采样间隔的井中DAS地震记录频谱差异及信噪比。
1 方法原理 1.1 DAS系统原理DAS也被称为DVS(Distributed Vibration Sensing),其系统结构与相位敏感光时域反射计(Phase Optical Time Domain Reflectometer, φ-OTDR)系统结构相同,基本理论为光纤中瑞利散射效应。
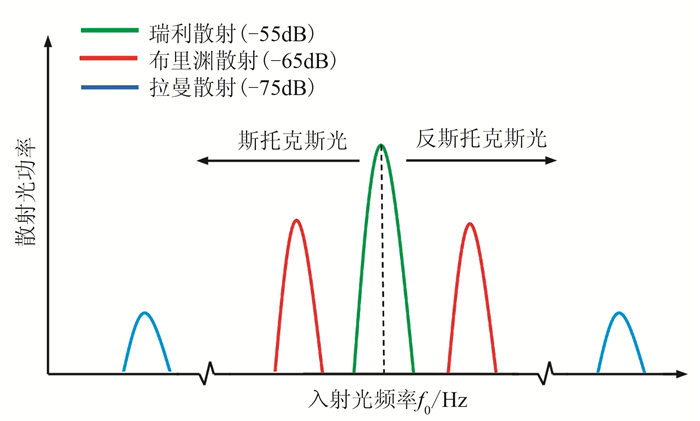
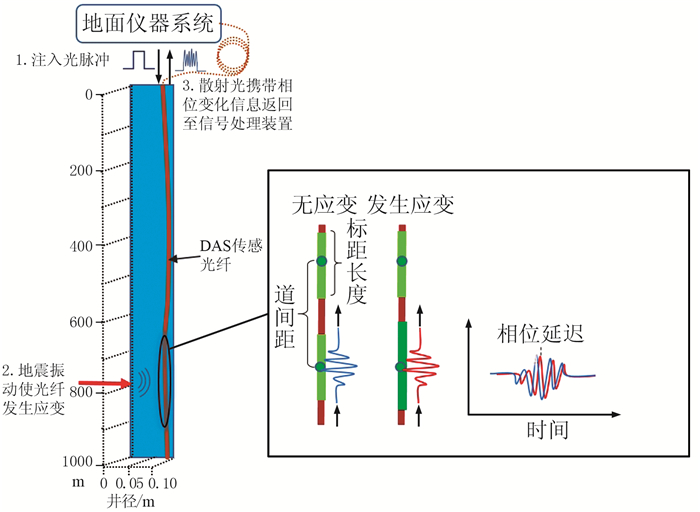
光在光纤传播时会产生弹性光散射和非弹性光散射两类。弹性光散射是入射光与光纤中直径远小于光波波长的粒子发生弹性碰撞的过程,特点是碰撞前、后能量保持不变,散射光的频率和波长保持不变,如瑞利散射;非弹性光散射是光纤分子运动或热运动导致的散射,特点是散射光的能量发生改变,具有一定的频移量,频率增加的称为反斯托克斯光,频率减小的称为斯托克斯光,如布里渊散射、拉曼散射(图 1)。DAS系统利用光纤中的瑞利散射效应测量地震信号,基本结构包括光纤(作为传感器和传输介质)和地面仪器系统(发射脉冲与探测背向瑞利散射信号)。光纤以特定的方法布置在井中或埋于浅地表接收地震信号,地面仪器系统连接光纤并根据瑞利散射原理将振动信号转换为用于解释的地震信号。首先,地面仪器系统以一定的重复频率不断地向光纤中发射特定时间长度的光脉冲,重复频率值和光纤长度有关。由于光纤的光学不均匀性或折射率的不均匀性,导致光在光纤中传播时与光纤中的不均匀点发生弹性碰撞而向各个方向散射(瑞利散射效应),其中一小部分光(幅值约为-65~-55dB)沿光纤反向散射而被地面仪器系统接收。当地震振动信号传输至光纤某一位置时,会导致光纤发生局部应变,引起光学路径的改变,进而导致背向瑞利散射光的相位发生变化。背向瑞利散射光携带相位变化信息返回至地面仪器系统,经过解调恢复处理,得到沿光纤分布的地震波信号(图 2)[27-28]。
|
图 1 光纤中散射光频谱分布 |
|
图 2 井中DAS接收原理示意图 |
地震振动压力使光纤产生局部应变和光学性质(折射率)改变,从而引起光纤中背向瑞利散射光的相位变化,即地震波对光纤中背向瑞利散射光产生相位调制,具体原理如下。
当入射光在光纤中传播时相位φ与传播距离L的关系为
| $ φ=βL $ | (1) |
式中β为光传播常数。由外界振动导致的光相位变化Δφ为φ与L的全微分形式[29-30]
| $ \begin{aligned} \Delta \varphi &=\beta \Delta L+L \Delta \beta \\ &=\beta L \frac{\Delta L}{L}+L \frac{\partial \beta}{\partial n} \Delta n+L \frac{\partial \beta}{\partial a} \Delta a \end{aligned} $ | (2) |
式中:n为光纤纤芯折射率;a为光纤芯径。由式(2)可以看出,外界振动对光相位的影响分为光纤长度变化ΔL(应变效应)、光纤纤芯折射率变化Δn(弹光效应)以及光纤芯径变化Δa(泊松效应)等,通常由于泊松效应很小,可忽略[31-32]。根据光传播的基本原理,有
| $ k_{0}=\frac{2 \pi}{\lambda_{0}} $ | (3) |
| $ \beta=\frac{2 \pi n}{\lambda_{0}}=n k_{0} $ | (4) |
式中:λ0为光在真空的波长;k0为光在真空的波数。由此Δφ可近似为
| $ \Delta \varphi=\beta L \frac{\Delta L}{L}+L k_{0} \Delta n $ | (5) |
式中
| $ \Delta L=e_{z} L $ | (6) |
其中ez为光纤轴向应变。
根据弹光效应基本原理,介质的逆介电张量Bij的变化ΔBij与弹性应变张量Skl之间的关系为[33]
| $ \Delta B_{i j}=P_{i j k l} S_{k l} \quad i, j, k, l=1, 2, 3 $ | (7) |
| $ B_{i j}=\frac{1}{n_{i j}^{2}} \quad i, j=1, 2, 3 $ | (8) |
式中:Pijkl为弹光系数张量;nij为光纤纤芯在不同应力状态下的折射率。因此,可以得到
| $ \Delta B_{i j}=\Delta\left(\frac{1}{n_{i j}^{2}}\right)=-\frac{2}{n_{i j}^{3}} \cdot \Delta n_{i j} $ | (9) |
由应变引起的光纤纤芯折射率变化为
| $ \Delta n_{i j}=-\frac{n_{i j}^{3}}{2} \Delta\left(\frac{1}{n_{i j}^{2}}\right) $ | (10) |
根据胡克定律的各向同性介质应力—应变关系得到
| $ \left(\begin{array}{l} e_{x} \\ e_{y} \\ e_{z} \end{array}\right)=\frac{1}{E}\left(\begin{array}{ccc} 1 & -\nu & -\nu \\ -\nu & 1 & -\nu \\ -\nu & -\nu & 1 \end{array}\right)\left(\begin{array}{l} \sigma_{x} \\ \sigma_{y} \\ \sigma_{z} \end{array}\right) $ | (11) |
式中:σx、σy和σz分别为光纤在x、y、z方向受到的应力;ex、ey和ez分别为光纤在x、y、z方向的应变;E为光纤杨氏模量;ν为泊松比。当光纤在z方向受到外部应力时,其应变为
| $ \left(\begin{array}{l} e_{x} \\ e_{y} \\ e_{z} \end{array}\right)=\frac{1}{E}\left(\begin{array}{ccc} 1 & -\nu & -\nu \\ -\nu & 1 & -\nu \\ -\nu & -\nu & 1 \end{array}\right)\left(\begin{array}{l} 0 \\ 0 \\ \frac{p}{s} \end{array}\right)=\frac{p}{s E}\left(\begin{array}{c} -\nu \\ -\nu \\ 1 \end{array}\right) $ | (12) |
式中:p为光纤受到的轴向压力;s为光纤横截面积。p>0,表示光纤受到轴向拉力,发生拉伸应变;反之,p < 0,表示光纤受到轴向压力,发生压缩应变。根据弹光效应,光纤发生应变时Δnij发生变化,Δnij与应变的关系为[29]
| $ \Delta\left(\frac{1}{n^{2}}\right)=\frac{-2}{n^{3}}\left(\begin{array}{c} \Delta n_{x} \\ \Delta n_{y} \\ \Delta n_{z} \end{array}\right)=\left(\begin{array}{ccc} P_{11} & P_{12} & P_{12} \\ P_{12} & P_{11} & P_{12} \\ P_{12} & P_{12} & P_{11} \end{array}\right)\left(\begin{array}{l} e_{x} \\ e_{y} \\ e_{z} \end{array}\right) $ | (13) |
式中:P11=0.121、P12≈0.270为光纤弹光系数,是衡量应力对介质光学性质(介质折射率)影响的系数;Δnx、Δny、Δnz分别为n在x、y、z方向的变化。将式(12)代入式(13),得到有关Δnx、Δny、Δnz的表达式
| $ \left(\begin{array}{c} \Delta n_{x} \\ \Delta n_{y} \\ \Delta n_{z} \end{array}\right)=\frac{-n^{3} p}{2 s E}\left[\begin{array}{c} P_{12}(1-\nu)-P_{11} \nu \\ P_{12}(1-\nu)-P_{11} \nu \\ P_{11}-2 \nu P_{12} \end{array}\right] $ | (14) |
根据光在单模光纤传播的基本理论,其有效折射率的变化Δneff主要与径向(x、y方向)折射率变化有关,于是得到
| $ \Delta n_{\mathrm{eff}}=-\frac{n^{3} p}{2 s E}\left[P_{12}(1-\nu)-P_{11} \nu\right] $ | (15) |
将式(4)、式(6)、式(15)代入式(5),得
| $ \begin{aligned} \Delta \varphi=& n k_{0} \cdot \Delta L+L k_{0} \cdot \Delta n_{\mathrm{eff}}=n k_{0} L e_{z}-\\ & \frac{1}{2} n^{3} k_{0} L e_{z}\left[P_{12}(1-\nu)-P_{11} \nu\right] \end{aligned} $ | (16) |
利用式(16)可以求取单模光纤受到轴向应力时光纤中背向瑞利散射光的相位变化。
1.2 地震振动信号与DAS信号转换模拟DAS系统使用高相干激光光源,发射的光具有很好的相干性。瑞利散射光是由于光在光纤中传输时与介质中不均匀粒子发生弹性碰撞所引起,其频率、波长等并未发生变化,且同样具有高相干性,因此在脉冲宽度内光纤各点的背向瑞利散射光发生相互干涉、叠加。根据离散光纤瑞利散射干涉模型,将光纤离散成一系列长度为Δd的等效反射镜,则接收到的距发射端L处的瑞利散射光的强度是光脉冲传播到该处时脉冲宽度内N个等效反射镜的背向瑞利散射光相互干涉的结果;由于每个等效反射镜的偏振具有微小的变化,所以这里不考虑散射光偏振的影响。距光纤发射端为mΔd处的散射光幅值为[34-37]
| $ E(m \Delta d)=E_{0} \sum\limits_{k=m}^{m+N-1} r_{k} \mathrm{e}^{\mathrm{i}\left(\varphi_{k}+\Delta \varphi\right)} \mathrm{e}^{-\alpha k \Delta d} $ | (17) |
式中:E0为初始入射光幅值;N为脉冲宽度内的等效反射镜的个数;rk为第k个等效反射镜瑞利散射系数统计值;φk为第k个等效反射镜的相位统计值;Δφ为由外界振动引起的第k个等效反射镜的相位改变量;α为光纤衰减常数[38-39]。由式(17)可见,背向瑞利散射光随传播距离呈指数衰减,其幅值取决于rk。通常,rk介于10-6~10-5。DAS系统根据散射光返回时刻确定散射光位置,其对应关系为
| $ D(t)=\frac{c t}{2 n} $ | (18) |
式中:D为散射光位置距光纤发射端距离;c为光在真空中的速度。接收到的光信号功率P(t)为
| $ P(t)=P_{1}(t)+P_{2}(t) $ | (19) |
其中
| $ P_{1}(t)=E_{0}^{2} \sum\limits_{k=m}^{m+N-1} r_{k}^{2} \exp \left(-2 \alpha \frac{k n \Delta d}{c}\right) $ | (20) |
| $ \begin{aligned} P_{2}(t)=& 2 E_{0}^{2} \sum\limits_{k=m}^{m+N-2} \sum\limits_{j=k+1}^{m+N-1}\left\{r_{k} r_{j} \cos \left(\varphi_{k}-\varphi_{j}\right) \times\right.\\ &\left.\exp \left[-\alpha \frac{(k+j) n \Delta d}{c}\right]\right\} \end{aligned} $ | (21) |
式中:P1(t)为脉冲宽度内N个等效反射镜非相干散射光功率,基本不随光纤应变和折射率变化;P2(t)表示脉冲宽度内不同等效反射镜的背向瑞利散射光相干效应,对光纤轴向应变和折射率的变化较敏感,波形呈锯齿状。
为了探讨DAS系统中关键参数对信号的影响,进行脉冲振动模拟(图 3)。假设某一时刻在光纤500m处存在脉冲振动(图 3a),利用离散光纤瑞利散射干涉模型分别求取振动前、后的散射信号(图 3b),在不考虑系统噪声的情况下对振动前、后的散射信号差分处理,得到振动引起的异常信号(图 3c)。

|
图 3 脉冲振动模拟 (a)振动信号;(b)振动前、后散射信号;(c)差分信号 光纤长度为1000m,n=1.45,E=35GPa,ν=0.17。令等效反射镜间隔为10cm,因此光纤离散时每个等效反射镜的长度远小于脉冲宽度[30] |
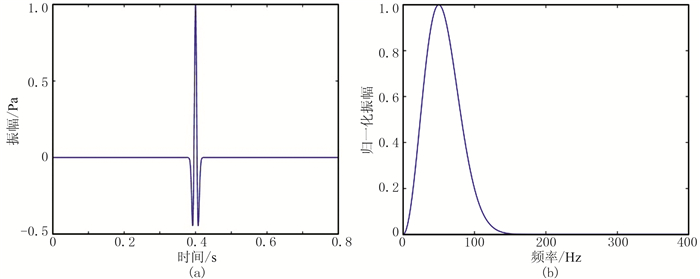
按照上述方法,以主频为50Hz的雷克子波信号为例(图 4),其波长约为19.5m,假设某一时刻在475~525m的范围内存在振动,且光纤的应变全部为轴向,在式(17)的相位项中加入相位噪声模拟系统本身的噪声,不考虑背景压力、温度等因素,分别模拟、分析振动强度、脉冲宽度以及光纤空间采样间隔等3个参数。另外,在实际工作中还需要考虑初始注入功率值。如果初始注入光功率太小会导致瑞利散射信号非常微弱,不利于信号探测;如果初始注入光功率太大超过受激布里渊散射(SBS)阈值,会产生SBS,并与瑞利散射相互干涉造成强烈干扰,压制有效瑞利散射信号。本文并未考虑布里渊散射和拉曼散射,因此不进行初始注入功率测试,但在实际中其影响不可忽略。
|
图 4 雷克子波(a)及其振幅谱(b) |
在地震勘探中,振动强度代表地震震源强度,在振动监测或者安全防护中只需要对振动空间定位,震源强度是未知的,因此该参数通常不予考虑。由于DAS主要用于资源勘探领域,通常使用人工震源(爆炸震源、可控震源等),震源强度是可控的。对于常规地震检波器,前人的很多震源强度方面的经验可供参考,但对于DAS系统作为传感器接收地震信号,目前还缺乏震源强度的认识,因此有必要模拟、分析震源强度可能产生的影响。
以应变代表光纤轴向应力测试振动强度,图 5为不同光纤应变振动强度测试结果。由图可见:当光纤应变为1nε(1nε=1nm/m)时,得到的散射信号波形与振动波形较一致(图 5a),从频谱中仍可看到50Hz主频成分,但高频噪声非常严重(图 5d);当光纤应变提高至10nε时,很好地压制了高频噪声,信噪比得到一定提高,但信号波形出现畸变(图 5b);当光纤应变继续增加至1000nε时,信号波形畸变严重,很难看出原始振动信号,频率成分复杂,主频完全偏离50Hz(图 5c)。从机理上分析其原因,由于得到的光纤每点散射信号来自脉冲宽度内众多散射点信号的叠加,对散射信号的影响始于脉冲前端刚刚到达振动区域,终于脉冲后端刚好离开振动区域。理论上地震波波长不变,其振动影响的散射信号范围不会改变,但总会存在一段变化范围,即脉冲前端开始进入振动区域和脉冲后端开始离开振动区域时。当振动强度太小时,由脉冲宽度内各散射点信号叠加得到的散射信号强度变化太小,不足以超过噪声强度而无法显现,因此振动对散射信号的影响范围很小;当振动强度较大时,在脉冲前端刚开始进入或脉冲后端将要离开振动区域时,即使脉冲宽度内只存在很少的相位变化点,但这些点的相位变化较大,由脉冲宽度内各散射点信号叠加得到的散射信号强度足以超过噪声强度而显现,因此散射信号范围更大甚至超过振动区域。上述结果可能导致信号波形畸变或旁瓣增加,影响信号保真度(图 5e,为显示清晰,进行了上、下平移)[30]。

|
图 5 不同光纤应变振动强度测试结果 (a)1nε;(b)10nε;(c)1000nε;(d)频谱;(e)振动影响范围 |
脉冲宽度为发射光脉冲持续的时间。理论上DAS系统探测到的散射信号是脉冲宽度内所有散射点信号的叠加,脉冲宽度越大表示脉冲在光纤中占的空间长度也越长,测量长度也越大。因此脉冲宽度直接影响DAS系统分辨率,即DAS系统测量的光纤应变的最小距离,即
| $ \Delta z=\frac{c W}{2 n} $ | (22) |
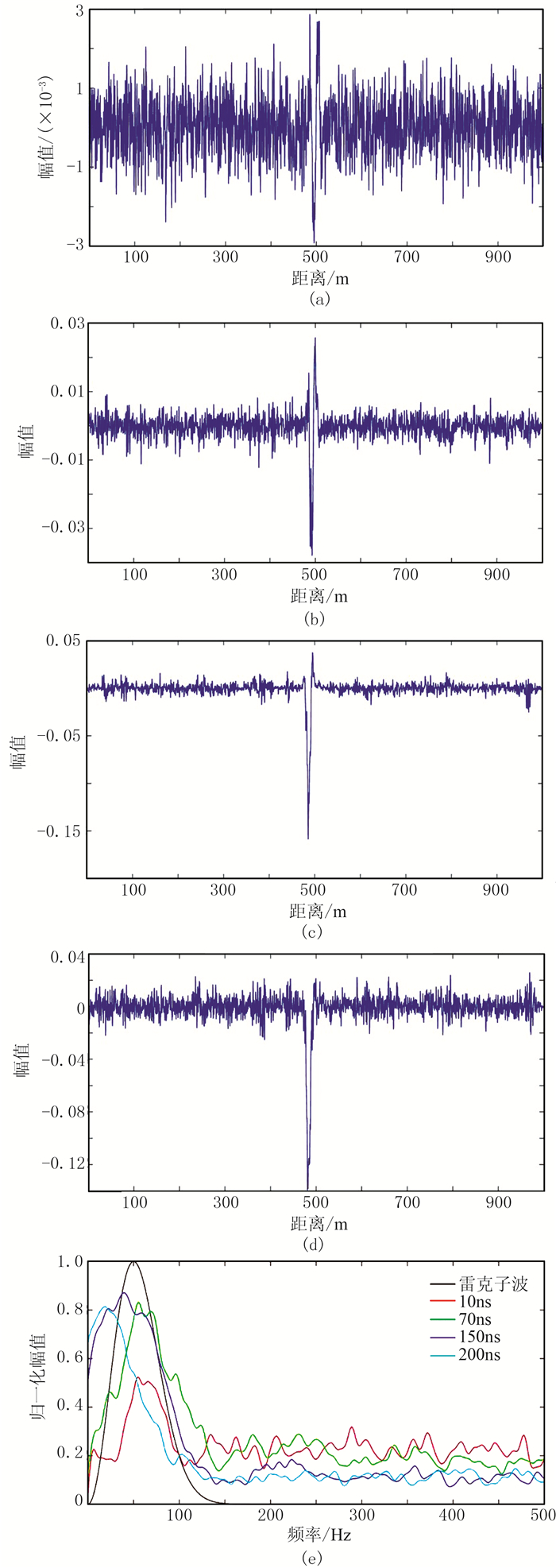
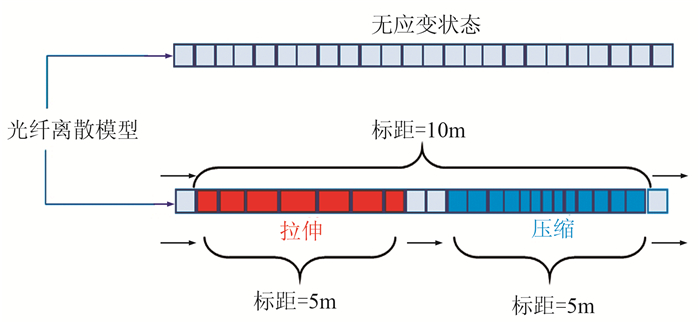
式中W为脉冲宽度。图 6为不同脉冲宽度的信噪比模拟。由图可见:①当脉冲宽度为70ns时,光强信号与原始雷克子波信号波峰、波谷正好相反(图 6b),同样的结果出现在脉冲宽度为10ns(图 6a)、150ns(图 6c)、200ns(图 6d)时,形成原因可能为原始相位的随机性所致。②当脉冲宽度为10ns和70ns时,由频谱可以观察到原始振动波形,主频基本为50Hz,且后者的信噪比较高,信号质量变好,说明当脉冲宽度适当增大时,可在一定程度上提高DAS信号的信噪比(图 6e)。造成上述现象的原因是,理论上光纤内存在大量的瑞利散射点,这些散射点的瑞利散射系数服从一定的概率分布(瑞利分布),脉冲宽度越大,散射点的数量越多,叠加后的散射信号越强,散射信号整体变得相对平滑,也会压制部分噪声而提高信噪比。③当脉冲宽度增至150ns时,信号波形开始畸变,主频开始偏离50Hz(图 6c、图 6e),当脉冲宽度增至200ns时,看不出原始振动信号波形,只能在振动分布范围内看到异常凸起的信号,主频完全偏离50Hz(图 6d、图 6e),不能分辨雷克子波信号的波峰、波谷。上述结果表明,当脉冲宽度过大时,分辨率降低。图 7阐述了光纤应变测量原理,解释了分辨率变化的原因。由图可见:当光纤局部发生应变时,假设以5m的标距长度沿光纤从左向右测量,均可以测量光纤压缩和拉伸引起的背向散射光相位变化;当标距长度等于10m时,标距长度内同时存在拉伸与压缩应变,两者会相互抵消,导致该段光纤不存在应变或应变量与实际不符的假象,即无法准确测量该段光纤的背向散射光相位变化,导致分辨率降低[40]。
|
图 6 不同脉冲宽度的散射信号波形及信噪比测试 (a)10ns;(b)70ns;(c)150ns;(d)200ns;(e)频谱 |
|
图 7 光纤应变测量原理 |
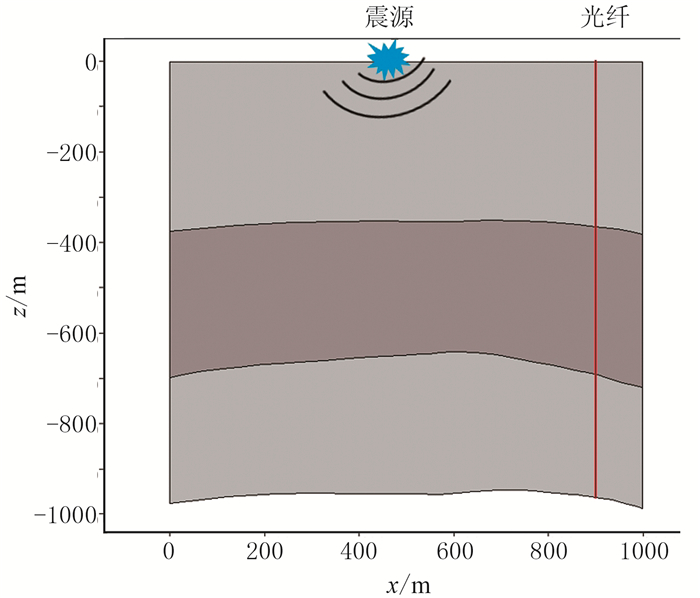
基于DAS系统振动监测测试,建立了井中地震模型模拟井中地震DAS信号,并根据地震记录对比、分析不同光纤空间采样间隔的DAS信号差异。对于井中地震正演模型(图 8),基于有限元方法,采用二维弹性波波动方程模拟弹性波在介质中的传播,以50Hz雷克子波集中力源作为震源,将物理模型分为3层各向同性均匀弹性介质。模拟得到垂直位移分量地震记录作为常规井中地震数据(图 9a)。
|
图 8 井中地震模型 从上往下3层的纵波速度分别为2.6、3.0、3.8km/s,横波速度分别为2.0、2.4、3.0km/s,密度分别为2.0、2.3、2.8g/cm3。为了保证数值模拟精度,每层介质所剖分的最大网格尺度均小于1/6地震波波长。将光纤与z轴平行布置在模型x=900m处,光纤的等效反射镜间隔为10cm,脉冲宽度为70ns,并假设DAS光纤与井壁完全耦合,地震波振动直接传递到光纤没有能量损失,且不考虑背景压力以及背景噪声 |
|
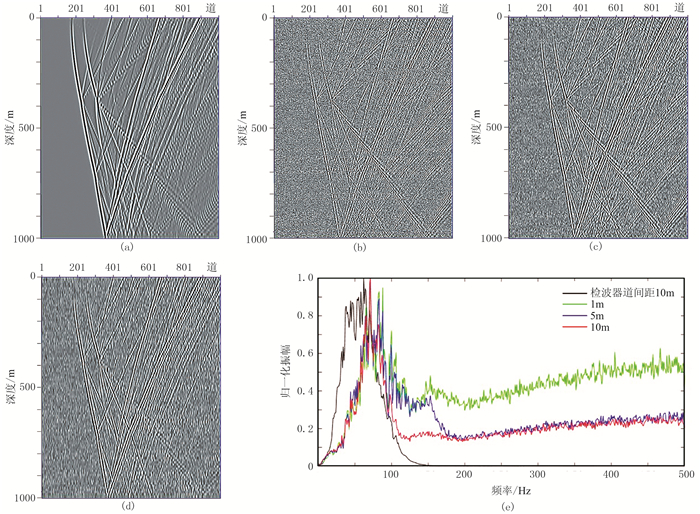
图 9 固定式地震检波器及不同光纤空间采样间隔井中DAS地震记录数值模拟结果 (a)固定式地震检波器(道间距为10m);(b)1m;(c)5m;(d)10m;(e)频谱 |
在实际勘探工作中,DAS系统需要对光纤划分空间道(空间采样间隔),划分的道数与向光纤中发射脉冲的重复频率有关,每一道相当于一个“检波器”,每次记录每道的散射信号,最终组成初始地震数据[41]。模拟DAS系统在井中工作,以特定频率不断地向光纤发射脉冲,每次发射的脉冲都会得到一条瑞利散射曲线,将相邻时间的散射曲线进行移动差分处理,得到模拟初始DAS地震记录。值得注意的是,DAS光纤探测的物理量与常规地震检波器探测的物理量不同,前者测量光纤中散射信号的相位变化,相位变化与地震波对光纤造成的应变呈线性关系,反映外界地震波场的响应;后者测量介质某点的速度或应变。两者虽然测量的物理量不同,但反映的外界的波场信息一致,因此通过对比两者所测信号的频率变化信息,表征DAS光纤与常规地震检波器的差异。
由于光纤尺度与地质模型尺度相差很大,因此可将光纤视为虚拟的。通过叠加DAS相邻道改变信号空间采样间隔,模拟得到不同光纤空间采样间隔的井中DAS地震记录(图 9b~图 9d)。由于常规固定式井中地震检波器级距相对较大(通常为10~20m),为了分析DAS地震记录的特征,将固定式地震检波器地震记录(图 9a)与不同光纤空间采样间隔的DAS地震记录(图 9b~图 9d)进行对比。结果表明:①模拟的井中DAS地震记录基本特征是合理的,说明模拟方法可行;②DAS地震记录的信噪比整体低于固定式地震检波器地震记录,前者主频略微高于50Hz(图 9e),噪声主要来自系统本身的固有高频噪声;③当光纤空间采样间隔分别为1、5、10m时,DAS地震记录中的噪声逐渐降低(图 9e),因此选择合适的光纤空间采样间隔可以有效地提高信噪比、提升信号质量。
3 结论本文基于离散光纤瑞利散射干涉模型,在不考虑背景压力、温度和井壁耦合的理想条件下开展了井中地震DAS信号数值模拟,详细讨论了震源强度、脉冲宽度和光纤空间采样间隔对DAS光纤信号波形特征及信噪比的影响,得到如下认识。
(1) 由于不同设备使用的参数和应变分辨能力不同,因此不同震源强度对DAS光纤信号的影响不同,而且震源强度过大可能导致DAS光纤信号波形畸变或旁瓣增多而影响信号保真度。
(2) 脉冲宽度不但影响DAS系统空间分辨率,而且影响信号质量。对于主频为50Hz、空间波长约为19.5m的雷克子波信号,模拟结果表明,脉冲宽度小于70ns时DAS系统能较好地分辨雷克子波信号的波形,脉冲宽度大于70ns时很难分辨雷克子波信号的波形,脉冲宽度大于150ns时不能分辨雷克子波信号。此外,较小的脉冲宽度常伴有较强的噪声,较大的脉冲宽度在一定程度上可以压制高频噪声、提高信噪比,但不可避免地降低分辨率。
(3) 不同光纤空间采样间隔影响DAS光纤的信号质量。通过相邻道叠加增大光纤空间采样间隔,有利于提高信噪比,模拟结果中当光纤空间采样间隔分别为1、5、10m时,DAS地震记录中的噪声逐渐降低,因此选择合适的光纤空间采样间隔可以有效地提高信噪比、提升信号质量。此外,DAS信号频率通常略高于原始地震信号频率,同时附带系统本身的高频噪声。
尚需指出,实际资料中的观测噪声多来自背景压力、温度和噪声以及井壁耦合等,本文的数值模拟未考虑这些因素,但模拟结果证明模拟方法是可行的。在今后的工作中,将会考虑更多因素的影响,以进一步提高模拟精度。
感谢孙琪真教授、Masoudi A以及审稿专家提供的指导与帮助。
| [1] |
Mateeva A, Lopez J, Potters H, et al. Distributed acoustic sensing for reservoir monitoring with vertical seismic profiling[J]. Geophysical Prospecting, 2014, 62(4): 679-692. |
| [2] |
Spikes K T, Tisato N, Hess T E, et al. Comparison of geophone and surface-deployed distributed acoustic sensing seismic data[J]. Geophysics, 2019, 84(2): A25-A29. |
| [3] |
Mestayer J, Cox B, Wills P, et al.Field trials of distributed acoustic sensing for geophysical monitoring[C].SEG Technical Program Expanded Abstracts, 2011, 30, doi: 10.1190/1.3628095.
|
| [4] |
Parker T R, Shatalin S V, Farhadiroushan M, et al.Distributed acoustic sensing: recent field data and performance validation[C].Second EAGE Workshop on Permanent Reservoir Monitoring 2013-Current and Future Trends, Stavanger, Norway, 2013, doi: 10.3997/2214-4609.20131303.
|
| [5] |
Parker T, Shatalin S, Farhadiroushan M. Distributed acoustic sensing-a new tool for seismic applications[J]. First Break, 2014. DOI:10.3997/1365-2397.2013034 |
| [6] |
Miller D, Parker T, Kashikar S, et al.Vertical seismic profiling using a fibre-optic cable as a distributed acoustic sensor[C].Extended Abstracts of 74th EAGE Conference & Exhibition, 2012, doi: 10.3997/2214-4609.20148799.
|
| [7] |
Madsen K N, Thompson M, Parker T, et al. A VSP field trial using distributed acoustic sensing in a producing well in the North Sea[J]. First Break, 2013. DOI:10.3997/1365-2397.2013027 |
| [8] |
Mateeva A, Mestayer J, Yang Z, et al.Dual-well 3D VSP in deepwater made possible by DAS[C].SEG Technical Program Expanded Abstracts, 2013, 32, doi: 10.1190/segam2013-0667.1.
|
| [9] |
Cox B E, Lehner R, Webster P, et al.Keynote presentation: microseismic data integration: how connecting the dots can help solve the unconventionals puzzle[C].Fifth EAGE Passive Seismic Workshop, 2014, doi: 10.3997/2214-4609.20142154.
|
| [10] |
Molenaar M M, Hill D, Webster P, et al. First downhole application of distributed acoustic sensing for hydraulic-fracturing monitoring and diagnostics[J]. SPE Drilling & Completion, 2012, 27(1): 32-38. |
| [11] |
Bakku S K, Fehler M, Wills P, et al.Vertical seismic profiling using distributed acoustic sensing in a hydrofrac treatment well[C].SEG Technical Program Expanded Abstracts, 2014, 33, doi: 10.1190/segam2014-1559.1.
|
| [12] |
Barberan C, Allanic C, Avila D, et al.Multi-offset seismic acquisition using optical fiber behind tubing[C].Extended Abstracts of 76th EAGE Conference & Exhibition, 2014, doi: 10.3997/2214-4609.20148798.
|
| [13] |
Harris K, White D, Melanson D, et al. Feasibility of time-lapse VSP monitoring at the Aquistore CO2 storage site using a distributed acoustic sensing system[J]. International Journal of Greenhouse Gas Control, 2016, 50(4): 248-260. |
| [14] |
Correa J, Pevzner R, Popik S, et al.Application of 3D VSP acquired with DAS and 3C geophones for site characterization and monitoring program design: preliminary results from stage 3 of the CO2CRC Otway project[C].SEG Technical Program Expanded Abstracts, 2018, 37, doi: 10.1190/segam2018-2996035.1.
|
| [15] |
Hornman K, Kuvshinov B, Zwartjes P, et al.Field trial of a broadside-sensitive distributed acoustic sensing cable for surface seismic[C].Extended Abstracts of 75th EAGE Conference & Exhibition, 2013, doi: 10.3997/2214-4609.20130383.
|
| [16] |
Kuvshinov B N. Interaction of helically wound fibre-optic cables with plane seismic waves[J]. Geophysical Prospecting, 2016, 64(3): 671-688. |
| [17] |
Hornman J C. Field trial of seismic recording using distributed acoustic sensing with broadside sensitive fibre-optic cables[J]. Geophysical Prospecting, 2017, 65(1): 35-46. |
| [18] |
Wang H, Fratta D, Lord N, et al.Distributed acoustic sensing (DAS) field trials for near-surface geotechnical properties, earthquake seismology and mine monitoring[C].SEG Technical Program Expanded Abstracts, 2018, 37: 4953-4957.
|
| [19] |
Yu G, Chen Y Z, Wu J, et al.3D-VSP survey using a DAS system and downhole geophone array in southwest China[C].Extended Abstracts of 81st EAGE Conference & Exhibition, 2019.
|
| [20] |
Yu G, Sun Q, Ai F, et al.Microstructured fiber distributed acoustic sensing system for borehole seismic survey[C].SEG Technical Program Expanded Abstracts, 2018, 37: 4669-4673.
|
| [21] |
Sun Z, Liu X, Zhang F, et al. High sensitivity fiber laser geophone array and field test analysis[J]. Mea-surement, 2015. DOI:10.1016/j.measurement.2015.09.043 |
| [22] |
Shang Y, Yang Y, Wang C, et al. Optical fiber distributed acoustic sensing based on the self-interference of Rayleigh backscattering[J]. Measurement, 2016. DOI:10.1016/j.measurement.2015.09.042 |
| [23] |
Wang J, Hu B, Li W, et al. Design and application of fiber Bragg grating (FBG) geophone for higher sensitivity and wider frequency range[J]. Measurement, 2016. DOI:10.1016/j.measurement.2015.09.041 |
| [24] |
Xu T W, Fang G S, Yue J, et al.Distributed acoustic sensing: system and experiments[C].2017 Opto-electronics & Communications Conference, 2017, doi: 10.1109/OECC.2017.8114770.
|
| [25] |
Wang Z Y, Li L C, Zheng H R, et al.Smart distributed acoustics/vibration sensing with dual path network[C].26th International Conference on Optical Fiber Sensors, Lausanne, 2018, doi: 10.1364/OFS.2018.WF105.
|
| [26] |
Liang J J, Wang Z Y, Lyu Bin, et al. Distributed acoustic sensing for 2D and 3D acoustic source localization[J]. Optics Letters, 2019, 44(7): 1690-1693. |
| [27] |
Mateeva A, Mestayer J, Cox B, et al.Advances in distributed acoustic sensing (DAS) for VSP[C].SEG Technical Program Expanded Abstracts, 2012, 31, doi: 10.1190/segam2012-0739.1.
|
| [28] |
Li M, Wang H, Tao G. Current and future applica-tions of distributed acoustic sensing as a new reservoir geophysics tool[J]. The Open Petroleum Engineering Journal, 2015, 8(1): 272-281. |
| [29] |
Butter C D, Hocker G B. Fiber optics strain gauge[J]. Applied Optics, 1978, 17(18): 2867-2869. |
| [30] |
Masoudi A, Newson T P. Analysis of distributed optical fibre acoustic sensors through numerical modelling[J]. Optics Express, 2017, 25(25): 32021-32040. |
| [31] |
彭飞.相位敏感型光时域反射仪及其应用研究[D].四川成都: 电子科技大学, 2015. PENG Fei.Phase-Sensitive Optical Time Domain Reflectometry & Applications[D].University of Electronic Science and Technology of China, Chengdu, Sichuan, 2015. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D665615 |
| [32] |
于淼.基于双重同源外差相干检测的Φ-OTDR系统的研究及应用[D].吉林长春: 吉林大学, 2017. YU Miao.Research and Application of Phase-Sensitive Optical Time-Domain Reflectometric System Based on Single-source Dual Heterodyne Detection Scheme[D].Jilin University, Changchun, Jilin, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10183-1018000235.htm |
| [33] |
王友钊, 黄静. 光纤传感技术[M]. 陕西西安: 西安电子科技大学出版社, 2015.
|
| [34] |
Park J, Lee W, Taylor H F. Fiber optic intrusion sensor with the configuration of an optical time-domain reflectometer using coherent interference of Rayleigh backscattering[J]. Proceedings of SPIE, 1998, 3555(1): 49-56. |
| [35] |
Park J, Taylor H F. Fiber optic intrusion sensor using coherent optical time domain reflectometer[J]. Japanese Journal of Applied Physics, 2003, 42(6): 3481-3482. |
| [36] |
Chen L, Zhu T, Bao X Y, et al. Distributed vibration sensor based on coherent detection of phase-OTDR[J]. Journal of Lightwave Technology, 2010, 28(22): 3243-3249. |
| [37] |
Liokumovich L B, Ushakov N A, Kotov O I, et al. Fundamentals of optical fiber sensing schemes based on coherent optical time domain reflectometry:signal model under static fiber conditions[J]. Journal of Lightwave Technology, 2015, 33(17): 3660-3671. |
| [38] |
Howard R M. Statistics of coherently detected backscatter and range performance of coherent OTDRs[J]. Optical and Quantum Electronics, 1987, 19(3): 145-168. |
| [39] |
Bao X Y, Zhou D P, Baker C, et al. Recent development in the distributed fiber optic acoustic and ultrasonic detection[J]. Journal of Lightwave Technology, 2017, 35(16): 3256-3267. |
| [40] |
Martin E R.Passive Imaging and Characterization of the Subsurface with Distributed Acoustic Sensing[D].Department of Computinal and Mathematical Engineering, Standford University, California, 2018.
|
| [41] |
Daley T M, Miller D E, Dodds K, et al. Field testing of modular borehole monitoring with simultaneous distributed acoustic sensing and geophone vertical seismic profiles at Citronelle, Alabama[J]. Geophysical Prospecting, 2015, 64(5): 1318-1334. |



 曹丹平, 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
曹丹平, 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: