2 油气资源与探测国家重点实验室, 北京 102249;
3 CNPC物探重点实验室, 北京 102249;
4 同济大学海洋与地球科学学院, 上海 200092
2 State Key Laboratory of Petroleum Resources and Prospecting, Beijing 102249, China;
3 CNPC Key Lab of Geophysical Exploration, Beijing 102249, China;
4 School of Ocean and Earth Science, Tongji University, Shanghai 200092, China
地震波在地下传播会表现出依赖频率的衰减,同时其相位也会因介质的黏滞性而发生变化。基于衰减介质假设建立相应的波动方程并研发相应的波动方程偏移和反演算法,是目前众多学者的研究内容[1-3]。通常使用常Q模型描述地震波的衰减[4],在频率域常Q模型可利用复速度表达,但数值求解频率域的波动方程涉及大量的矩阵和向量运算,效率低。
相对而言,时间域的模拟方法更高效,但需要近似应力—应变之间的卷积关系,且难以准确匹配常Q模型。孙成禹等[5]实现了利用广义线性体构建常Q模型的优化方法,并证实至少需要三个线性体元在给定的频率范围内拟合常Q曲线,才能保证大炮检距地震波衰减和频散的模拟精度。由此所发展的广义线性体黏滞波动方程所包含的表征参数较多(每个线性体元包含两个弛豫时间参数),方程个数也较多,将其作为正演模拟的工具,会增加后续地震偏移和反演的难度。杜启振[6]将广义线性体模型进一步推广至各向异性介质,推导了更加复杂的黏弹性各向异性介质波动方程,并采用伪谱法进行数值模拟。蔡瑞乾等[7]提出了变线性体元数量的数值模拟方法,该方法在不同的区域采用不同个数的线性体元拟合常Q曲线,提高了广义线性体黏滞波动方程数值模拟的计算效率。苑春方等[8]、李晓波等[9]基于Kelvin-Voigt模型和孙成禹等[10]基于Maxwell模型建立了非常Q黏滞波动方程并在时间域进行地震波场模拟。
与传统整数阶导数的局部性质不同,有学者利用分数阶导数的记忆性质描述固体介质的蠕变过程,由此发展了分数阶黏弹性波动方程,用于描述地震波随频率呈指数衰减的物理现象[11]。Carcione等[12]首先引入时间分数阶导数建立符合常Q模型的黏滞声波方程,能准确描述常Q模型,但时间分数阶导数的全局性使数值模拟需要消耗大量的内存存储所有历史时刻波场。孙成禹等[13]利用加权窗函数提高了时间分数阶导数的计算精度,同时利用自适应的窗函数宽度提高了黏滞声波和黏弹性波场数值模拟的计算效率。刘财等[14]基于VIT—双相介质的本构关系和常Q模型推导了时间域分数阶黏弹性波动方程,用于模拟复杂介质中的波场传播。
Carcione[15]从常Q模型的频散关系出发,引入分数阶拉普拉斯算子描述地震波的衰减和频散。与时间分数阶黏滞声波方程相比,分数阶拉普拉斯算子黏滞声波的时间导数为二阶,可利用传统的有限差分法近似,同时分数阶拉普拉斯算子可使用快速傅里叶变换(FFT)计算,因此具有较高的计算效率。Zhang等[16]基于正则化方法推导了解耦的分数阶拉普拉斯算子黏滞声波方程,由于推导过程不是基于波动方程的频散关系,其物理意义不明确。Zhu等[17]及吴玉等[18]受Treeby等[19]在医学成像领域研究的启发,基于常Q模型和平面波的频散关系推导了新的解耦分数阶拉普拉斯算子黏滞声波方程,该方程形式简单,模拟常Q模型的精度高,同时在形式上显式地分离了控制振幅衰减和相位畸变的算子。这种解耦的特点有利于发展稳定的Q补偿逆时偏移技术[20]。
数值求解分数阶拉普拉斯算子黏滞声波方程的难点在于处理空间可变阶数的拉普拉斯算子。由于阶数随空间变化,分数阶拉普拉斯算子的谱响应也随空间变化,对于空间每个不同的阶数,需要单独使用FFT计算分数阶拉普拉斯算子的谱响应,计算效率低。Zhu等[17]直接取空间平均的阶数代替空间可变阶数,其模拟的结果存在较大的误差。Chen等[21]提出两种方法近似空间可变阶数的拉普拉斯算子:其一为利用泰勒近似将空间可变阶数的拉普拉斯算子转化为若干个常分数阶拉普拉斯算子,由此发展了常分数阶拉普拉斯算子黏滞声波方程,简化了数值计算;另一种方法将空间可变分数阶拉普拉斯算子的谱响应视为波数—空间的混合域矩阵,采用矩阵低秩分解方法近似。Chen等[22]证实,基于矩阵低秩分解的时间外推方法比传统伪谱法有更高的时间近似精度和稳定性。Li等[23]提出最小二乘法近似空间可变阶数的拉普拉斯算子,并发展了相应的衰减补偿逆时偏移算法。最小二乘法与泰勒近似法类似,都将变阶数转化为固定阶数,但由最小二乘法导出的黏滞波动方程的表征参数与速度和Q没有显式的表达关系,不利于相应的全波形反演。Wang等[24]将常分数阶拉普拉斯算子黏滞声波方程推广到了黏弹介质;Wang等[25]基于常分数阶拉普拉斯算子黏滞声波方程发展了自适应的衰减补偿逆时偏移方法;Chen等[26]基于常分数阶拉普拉斯算子黏滞声波方程发展了全波形反演方法;Chen等[27]发展了一种矩阵转换法用于求解分数阶拉普拉斯算子黏滞声波方程,该方法是传统有限差分法的推广,与伪谱法相比,矩阵转换法处理各种复杂边界条件更灵活,但计算量更大。
本文基于位移形式的常分数阶拉普拉斯算子黏滞声波方程,推导了一阶速度—压力形式常分数阶拉普拉斯算子黏滞声波方程,并考虑了密度的空间变化;推导了相应的完全匹配层(PML)边界条件以压制虚假反射;采用交错网格伪谱法进行数值模拟。借助数值实验,分析Q对交错网格伪谱法稳定性条件的影响,并验证新的一阶速度—压力黏滞波动方程模拟常Q模型具有较高的精度。
1 常分数阶拉普拉斯算子黏滞声波方程 1.1 一阶速度—压力形式常分数阶拉普拉斯算子黏滞声波方程的建立Chen等[21]推导的位移形式的常分数阶黏滞声波方程为
| $\left(\frac{1}{\mu c_{0}^{2}} \frac{\partial^{2}}{\partial t^{2}}-D+\frac{1}{Q c_{0}} \frac{\partial}{\partial t} L\right) u=s(t)$ | (1) |
式中:u为位移;c0为定义在参考角频率ω0处的地震波速度;Q为地震品质因子;算子D和L为
| $\left\{\begin{array}{l}D=\left(1-\frac{32}{\pi Q}\right) \nabla^{2}-\frac{32}{\pi Q}\left(\frac{c_{0}}{\omega_{\mathrm{d}}}\right)^{\frac{1}{16}}\left(-\nabla^{2}\right)^{\frac{33}{32}} \\ L=\left(1-\frac{32}{\pi Q}\right)\left(-\nabla^{2}\right)^{\frac{1}{2}}+\frac{32}{\pi Q}\left(\frac{c_{0}}{\omega_{\mathrm{d}}}\right)^{\frac{1}{16}}\left(-\nabla^{2}\right)^{\frac{17}{32}}\end{array}\right.$ | (2) |
且有
| $ \mu=\left(\frac{\omega_{\mathrm{d}}}{\omega_{0}}\right)^{\frac{2}{\pi Q}} \cos \frac{1}{Q} \cos ^{2} \frac{1}{2 Q} $ | (3) |
式(2)中:
式(1)是由Zhu等[17]提出的解耦常Q黏滞声波方程的进一步近似,具体的推导过程见附录A。式(1)中算子D主要控制地震波传播过程中的相位变化,算子
为了考虑密度的空间可变以及方便加载PML吸收边界条件,将式(1)等价变换为一阶速度—压力形式,为此引入中间变量
| $ \left\{\begin{array}{l} v_{x}=\frac{\partial u}{\partial x} \\ v_{z}=\frac{\partial u}{\partial z} \\ p=\frac{\partial u}{\partial t} \end{array}\right. $ | (4) |
将中间变量代入式(1),可得
| $ \left\{\begin{array}{l} \frac{1}{\mu c_{0}^{2}} \frac{\partial p}{\partial t}-D_{\mathrm{v}}\left(\frac{\partial v_{x}}{\partial x}+\frac{\partial v_{z}}{\partial x}\right)+\frac{1}{Q c_{0}} L p=\int_{0}^{t} s(l) \mathrm{d} l \\ \frac{\partial v_{x}}{\partial t}=\frac{\partial p}{\partial x} \\ \frac{\partial v_{z}}{\partial t}=\frac{\partial p}{\partial z} \end{array}\right. $ | (5) |
式中
| $ D_{\mathrm{v}}=\left(1-\frac{32}{\pi Q}\right)+\frac{32}{\pi Q}\left(\frac{c_{0}}{\omega_{\mathrm{d}}}\right)^{\frac{1}{16}}\left(-\nabla^{2}\right)^{\frac{1}{32}} $ | (6) |
进一步将密度项ρ加入到一阶波动方程(式(5))中,由此得到变密度的常分数阶拉普拉斯算子黏滞声波方程
| $ \left\{\begin{array}{l} \frac{\partial p}{\partial t}-\mu \rho c_{0}^{2} D_{\mathrm{v}}\left(\frac{\partial v_{x}}{\partial x}+\frac{\partial v_{z}}{\partial x}\right)+\frac{\mu c_{0}}{Q} L p = \mu c_{0}^{2} \int_{0}^{t} s(l) \mathrm{d} l \\ \rho \frac{\partial v_{x}}{\partial t}=\frac{\partial p}{\partial x} \\ \rho \frac{\partial v_{z}}{\partial t}=\frac{\partial p}{\partial z} \end{array}\right. $ | (7) |
在数值求解波动方程式(7)时,采用交错网格配置应力和速度分量,离散的波场变量分别记为
| $ \frac{\partial v_{x}}{\partial x}=\mathrm{F}^{-1}\left[\mathrm{i} k_{x} \exp \left(\frac{\mathrm{i} k_{x} h_{x}}{2}\right) \mathrm{F} v_{x}\right] $ | (8) |
式中:F和F-1分别表示傅里叶正、反变换;kx为x方向的波数;hx为x方向的网格间距。同样,分数阶拉普拉斯算子也采用FFT计算,如
| $ \left(-\nabla^{2}\right)^{\frac{1}{32}} u=\mathrm{F}^{-1}\left[k^{\frac{1}{16}} \mathrm{F}(u)\right] $ | (9) |
式中
卷积型完全匹配层(CPML)吸收边界已被证实对大角度和低频入射的地震波以及倏逝波的吸收效果优于传统的分裂式PML吸收边界条件[28],因此选用CPML吸收边界条件来压制因FFT的周期性而引入的虚假反射。CPML的实质是将实数坐标轴扩展到复数域,以x方向为例,将波动方程中的实数x替换为复数
| $ \frac{\partial \widetilde{x}}{\partial x}=s_{x}=\kappa_{x}+\frac{1}{\alpha_{x}+\mathrm{i} \omega} \int_{0}^{x} d_{x}(s) \mathrm{d} s $ | (10) |
式中:dx为PML区域的衰减函数;κx为改善以掠射形式入射到PML层的地震波吸收效果的系数;αx为改善对低频成分吸收的系数。根据链式求导法则,有
| $ \frac{\partial}{\partial \widetilde{x}}=\frac{\partial}{\partial x} \frac{\partial x}{\partial \widetilde{x}}=\frac{1}{s_{x}} \frac{\partial}{\partial x} $ | (11) |
上式为频率域的相乘关系,返回到时间域对应的卷积关系为
| $ \beta(t)=\mathrm{F}^{-1}\left(\frac{1}{s_{x}}\right) * \frac{\partial}{\partial x} $ | (12) |
根据式(10)中sx的表达式可知
| $ \mathrm{F}^{-1}\left(\frac{1}{s_{x}}\right)=\frac{\delta(t)}{\kappa_{x}}-\frac{d_{x}}{\kappa_{x}^{2}} H(t) \exp \left[-\left(\frac{d_{x}}{\kappa_{x}}+\alpha_{x}\right) t\right] $ | (13) |
式中:δ(t)是狄拉克函数;H(t)是单位阶跃函数。将式(13)代入式(12),可得
| $ \beta(t)=\mathrm{F}^{-1}\left(\frac{1}{s_{x}}\right) * \frac{\partial}{\partial x}=\frac{1}{\kappa_{x}}\left(\frac{\partial}{\partial x}\right)^{t}+\varphi_{x}(t) $ | (14) |
式中φx(t)为辅助变量
| $ \varphi_{x}(t)=-\frac{d_{x}}{\kappa_{x}^{2}} H(t) \mathrm{e}^{-\left(\frac{d_{x}}{\kappa_{x}}+\alpha_{x}\right)t} $ | (15) |
其中αx、κx、dx为
| $ \left\{\begin{array}{l} \alpha_{x}=\alpha_{\max }\left(1-\frac{x}{w}\right) \\ \kappa_{x}=1+\kappa_{\max }\left(\frac{x}{w}\right)^{2} \\ d_{x}=-\frac{3 c_{\max }}{2 w}\left(\frac{x}{w}\right)^{3} \ln R \end{array}\right. $ | (16) |
式中:w为PML厚度;x为PML区域计算点到PML内边界的距离;cmax为最大速度;R是理论反射系数,一般取R=10-5;κmax可取不同值,为简单起见本文取为0;αmax=πfd,其中fd为震源的主频。
式(15)中φx(t)的计算可采用迭代更新
| $ \varphi_{x}(t)=b_{x} \varphi_{x}(t-\Delta t)+a_{x}\left(\frac{\partial}{\partial x}\right)^{t-\Delta t} $ | (17) |
式中Δt为波场外推的时间步长,其他参数定义为[29]
| $ \left\{\begin{array}{l} a_{x}=\frac{d_{x}}{\kappa_{x}\left(d_{x}+\kappa_{x} \alpha_{x}\right)}\left(b_{x}-1\right) \\ b_{x}=\exp \left[-\left(\frac{d_{x}}{\kappa_{x}}+\alpha_{x}\right) \Delta t\right] \end{array}\right. $ | (18) |
式(14)和式(17)表明CPML中的卷积项可以利用递推公式计算,且只需要存储前一个时刻的辅助变量值。
以上推导
| $ \left\{\begin{array}{l} \frac{\partial p}{\partial t}-\mu \rho c_{0}^{2} D_{v}\left(\frac{\partial v_{x}}{\partial x}+\frac{\partial v_{z}}{\partial x}+\varphi_{v_{x} , x}+\varphi_{v_{z}, z}\right)+\frac{\mu c_{0}}{Q} L p \\ =\mu c_{0}^{2} \int_{0}^{t} s(l) \mathrm{d} l \\ \rho \frac{\partial v_{x}}{\partial t}=\frac{\partial p}{\partial x}+\varphi_{p, x} \\ \rho \frac{\partial v_{z}}{\partial t}=\frac{\partial p}{\partial z}+\varphi_{p, z} \end{array}\right. $ | (19) |
由交错网格的配置方式可知辅助变量φvx, x和φvz, z配置在整数时间网格节点上,φp, x和φp, z配置在半时间网格节点上,因此其迭代更新的公式为
| $ \left\{\begin{array}{l} \varphi_{v_{x}, x}^{n}=b_{x} \varphi_{v_{x}, x}^{n-1}+a_{x} \frac{\partial v_{x}^{n-1}}{\partial x} \\ \varphi_{v_{z}, z}^{n}=b_{z} \varphi_{v_{z}, z}^{n-1}+a_{z} \frac{\partial v_{z}^{n-1}}{\partial z} \end{array}\right. $ | (20a) |
| $ \left\{\begin{array}{l} \varphi_{p, x}^{n+\frac{1}{2}}=b_{x} \varphi_{p, x}^{n-\frac{1}{2}}+a_{x} \frac{\partial p^{n-\frac{1}{2}}}{\partial x} \\ \varphi_{p, z}^{n+\frac{1}{2}}=b_{z} \varphi_{p, z}^{n-\frac{1}{2}}+a_{z} \frac{\partial p^{n-\frac{1}{2}}}{\partial z} \end{array}\right. $ | (20b) |
值得注意的是,用于更新φp, x的变量bx和ax落在x方向的半网格节点上,用于更新φp, z的bz和az落在z方向的半网格节点上。
需要指出的是,式(19)中加载CPML吸收边界的方法并不完全严格,因为控制频散的算子Dv和控制衰减的算子L中仍然包含空间导数项,理论上这些导数项也需要作相应的复坐标扩展,但此项工作相当复杂,本文不作深入的研究。数值实验将证实,本文所采用的近似CPML方法仍然能取得较好的吸收效果。
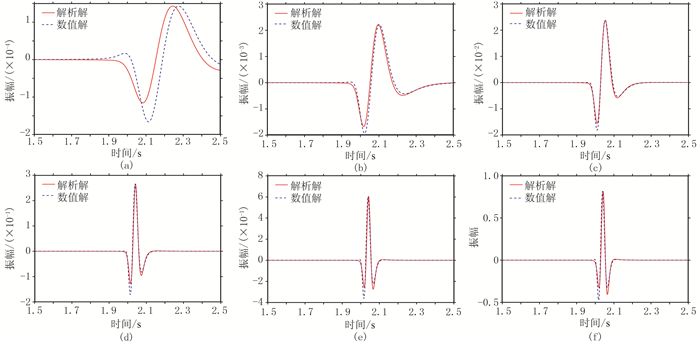
2 数值算例 2.1 均匀模型首先模拟网格数为1100×1100、网格间距为10m的均匀介质中的波场,并与格林函数计算的解析解[30]进行对比。模拟的时间长度为2.5s,时间步长为1ms,采用主频为20Hz的雷克子波作为震源并置于模型的中心,距离震源4km设置一个检波点。定义参考频率20Hz的地震波的速度为2000m/s,密度为2000kg/m3。图 1为接收点处数值模拟的地震道与解析解的对比,其中Q分别为5、10、20、50、80、100。由图 1可知,当Q=5时,数值解的相位明显滞后于解析解,说明本文所推导的常分数阶黏滞声波方程在Q较小时存在较明显的误差;随着Q逐渐增大,数值解的相位与解析解更吻合,但在波峰和波谷处仍存在微小的振幅差异,这可能是由于传播过程中数值频散误差累积造成的(伪谱法采用二阶差分近似时间微分算子,时间近似精度只有二阶)。图 1中数值解与解析解的对比证实了本文所推导的黏滞声波方程能较好地匹配常Q模型,模拟精度高。
网格间距恒定,逐渐增大Δt直至数值模拟
|
图 1 炮检距为4km处数值解与解析解的对比 图a~图f分别对应Q=5、10、20、50、80、100 |
根据稳定性条件,完全弹性声波方程伪谱法数值模拟要求网格比满足

|
图 2 Q值不同时黏滞声波方程交错网格伪谱法模拟所允许的最大网格比 |
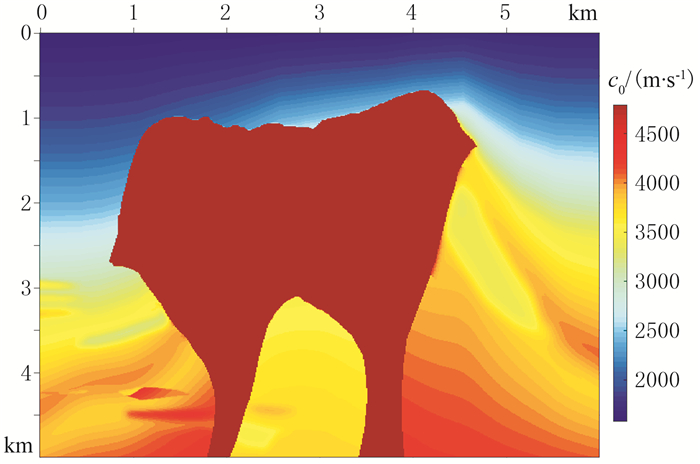
使用BP盐丘模型(图 3)验证本文模拟方法对复杂介质模型的适用性。模型网格数为500×500,参考频率对应的最大速度为4790m/s、最小速度为1579m/s,横、纵向的网格间距分别为12m和10m。使用经验公式Q=8(c0/1000)2和ρ=250c00.25生成相应的Q模型和密度模型,其中c0的单位为m/s、ρ的单位为kg/m3。由此得到的Q模型的最小值约为20,最大值约为183。假设模型的速度定义在参考频率200Hz处,使用主频为20Hz的雷克子波作为震源,并置于(2988m,10m)处。模拟时长为5s,时间采样步长为1ms。为了压制边界反射,在模型四周都设置厚度为10个网格间距的CPML吸收边界。
|
图 3 BP盐丘速度模型 |
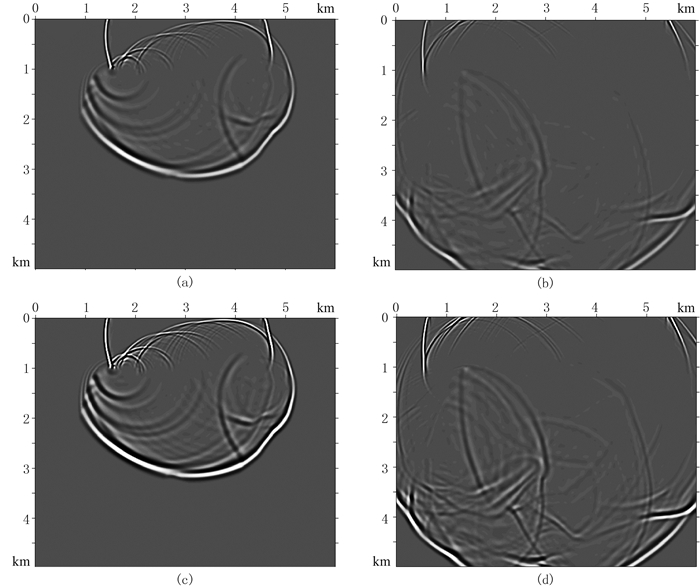
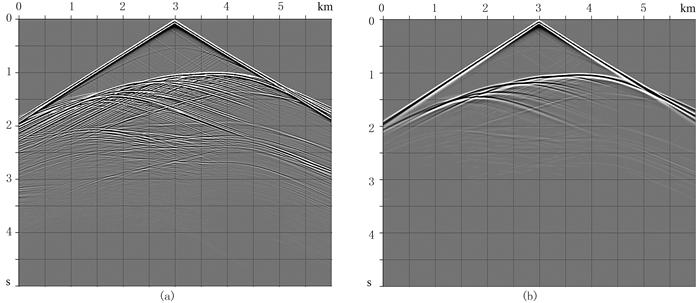
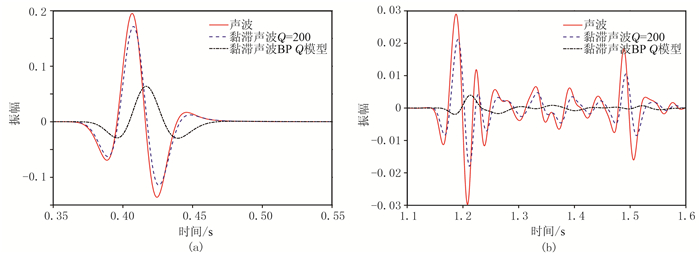
图 4a和4b为模拟的黏滞声波质点振动速度波场切片,时刻分别为1.0和1.5s,图 4c和4d分别为相同时刻的完全弹性声波波场切片。由图可知,介质的黏滞性引起地震波振幅显著衰减。此外,由于使用了CPML吸收边界条件,所模拟的波场中未见明显的边界反射,证实了本文加载CPML方法的可行性。图 5a为地表接收的完全弹性声波共炮点记录,图 5b为对应的黏滞声波记录,可以看出,黏滞性导致1.5s以下反射波振幅明显衰减。为了更清楚地展示介质黏滞性对地震波振幅和相位的影响,抽取(2400m,0)处的地震道进行对比,其中所使用的Q模型包括上述由经验公式生成的非均匀Q模型(近地表最小Q值约为20)以及Q=200的均匀Q模型。图 6a为直达波波形对比,可见介质的黏滞性造成地震波相位的明显滞后,Q越小,相位滞后越明显,振幅衰减也越强;图 6b为主要的反射波形对比,可观察到相同的现象。
|
图 4 BP模型模拟的波场切片 (a)1.0s时刻的黏滞声波;(b)1.5s时刻的黏滞声波;(c)1.0s时刻的完全弹性声波;(d)1.5s时刻的完全弹性声波 |
|
图 5 单炮模拟记录 (a)完全弹性声波;(b)黏滞声波 |
|
图 6 BP模型(2400m,0)处不同Q值模拟结果单道波形对比 (a)直达波;(b)反射波 |
本文将位移形式的常分数阶拉普拉斯算子黏滞声波方程整理推导至一阶速度—压力形式,考虑了空间可变的密度,并仿照声波方程讨论了其卷积型完全匹配层吸收边界条件的加载方法。虽然该完全匹配层吸收边界方法并未完全遵循完全匹配层的理论推导,但数值实验仍证实了其较好的吸收效果。
均匀介质模拟的数值解与解析解的对比证实,本文所推导的常分数阶拉普拉斯算子黏滞声波方程匹配常Q模型的精度较高。数值模拟实验表明,当Q值越小时,其稳定性条件越苛刻,当Q值大于40时,其稳定性条件与模拟传统声波方程相同。BP盐丘模型波场数值模拟结果证实了本文的黏滞声波方程数值模拟方法对复杂介质的适用性。
附录A由Zhu等[17]推导的分数阶拉普拉斯算子黏滞声波方程为
| $ \frac{1}{c^{2}} \frac{\partial^{2} u}{\partial t^{2}}=\eta\left(-\nabla^{2}\right)^{\gamma+1} u+\tau \frac{\partial}{\partial t}\left(-\nabla^{2}\right)^{\gamma+\frac{1}{2}} u $ | (A-1) |
式中
| $ \left\{\begin{array}{l} \eta=-c_{0}^{2 \gamma} \omega_{0}^{2 \gamma} \cos (\pi \gamma) \\ \tau=-c_{0}^{2 \gamma-1} \omega_{0}^{-2 \gamma} \sin (\pi \gamma) \\ c=c_{0} \cos \frac{\pi \gamma}{2} \\ \gamma=\frac{1}{\pi Q} \end{array}\right. $ | (A-2) |
当介质均匀时,分数阶拉普拉斯算子可采用快速傅里叶变换(FFT)进行计算,即
| $ \left\{\begin{array}{l} \left(-\nabla^{2}\right)^{\gamma+1} u=\mathrm{F}^{-1}\left(k^{2 \gamma+2} \mathrm{F} u\right) \\ \left(-\nabla^{2}\right)^{\gamma+\frac{1}{2}} u=\mathrm{F}^{-1}\left(k^{2 \gamma+1} \mathrm{F} u\right) \end{array}\right. $ | (A-3) |
将式(A-1)变换到波数域并经过整理,可得
| $ \begin{array}{c} \frac{1}{c^{2} \cos (\pi \gamma)} \frac{\partial^{2} \tilde{u}}{\partial t^{2}}=-c_{0}^{2 \gamma} \omega_{0}^{-2 \gamma} k^{2 \gamma+2} \tilde{u}- \\ \frac{1}{Q} c_{0}^{2 \gamma-1} \omega_{0}^{-2 \gamma} k^{2 \gamma+1} \frac{\partial^{2} \tilde{u}}{\partial t} \end{array} $ | (A-4) |
式中
| $ \begin{aligned} c_{0}^{2 \gamma} \omega_{0}^{-2 \gamma} k^{2 \gamma+2} &=\lambda c_{0}^{2 \gamma} \omega_{\mathrm{d}}^{-2 \gamma} k^{2 \gamma+2} \\ &=\lambda k^{2}\left(\frac{k}{k_{\mathrm{d}}}\right)^{2 \gamma} \approx \lambda k^{2}\left(1+2 \gamma \ln \frac{k}{k_{\mathrm{d}}}\right) \\ &=\lambda k^{2}\left[1+\frac{2 \gamma}{\varepsilon} \ln \left(\frac{k}{k_{\mathrm{d}}}\right)^{\varepsilon}\right] \end{aligned} $ | (A-5) |
式中:λ=(ωd/ω0)2γ,其中ωd表示震源的主角频率;kd=(ωd/c0)表示主波数。通过选取较小的ε可使(k/kd)ε足够接近1。在此条件下进一步利用泰勒近似,可得
| $ \begin{aligned} c_{0}^{2 \gamma} \omega_{0}^{-2 \gamma} k^{2 \gamma+2} & \approx \lambda k^{2}\left[1+\frac{2 \gamma}{\varepsilon} \ln \left(\frac{k}{k_{\mathrm{d}}}\right)^{\varepsilon}\right] \\ & \approx \lambda k^{2}\left[1-\frac{2 \gamma}{\varepsilon}+\frac{2 \gamma}{\varepsilon}\left(\frac{k}{k_{\mathrm{d}}}\right)^{\varepsilon}\right] \end{aligned} $ | (A-6) |
同样的近似方法可用于式(A-1)右端的第二项,Chen等[21]通过数值分析证实当ε=1/16时,式(A-6)具有很高的精度。经过上述近似之后,空间可变阶数的黏滞声波方程(式(A-1))简化为空间常分数阶拉普拉斯算子黏滞声波方程(式(1))。
| [1] |
Chai X, Wang S, Yuan S, et al. Sparse reflectivity inversion for nonstationary seismic data[J]. Geophy-sics, 2014, 79(3): V93-V105. |
| [2] |
Yuan S, Wang S, Tian N, et al. Stable inversion-based multitrace deabsorption method for spatial continuity preservation and weak signal compensation[J]. Geophysics, 2016, 81(3): V199-V212. DOI:10.1190/geo2015-0247.1 |
| [3] |
李海山, 杨午阳, 雍学善. 二维时间域黏声波全波形反演[J]. 石油地球物理勘探, 2018, 53(1): 87-94. LI Haishan, YANG Wuyang, YONG Xueshan. Visco-acoustic wave full waveform inversion in the 2D time domain[J]. Oil Geophysical Prospecting, 2018, 53(1): 87-94. |
| [4] |
Kjartansson E. Constant Q-wave propagation and attenuation[J]. Journal of Geophysical Research, 1979, 84(B9): 4737-4748. DOI:10.1029/JB084iB09p04737 |
| [5] |
孙成禹, 印兴耀. 三参数常Q黏弹性模型构造方法研究[J]. 地震学报, 2007, 29(4): 348-357. SUN Chengyu, YIN Xinyao. Construction of constant-Q viscoelastic model with three parameters[J]. Acta Seismologica Sinica, 2007, 29(4): 348-357. DOI:10.3321/j.issn:0253-3782.2007.04.002 |
| [6] |
杜启振. 各向异性黏弹性介质伪谱法波场模拟[J]. 物理学报, 2004, 53(12): 4428-4434. DU Qizhen. Wavefield forward modeling with the pseudo-spectral method in viscoelastic and azimuthally anisotropic media[J]. Acta Physica Sinica, 2004, 53(12): 4428-4434. |
| [7] |
蔡瑞乾, 孙成禹, 伍敦仕, 等. 黏声波动方程变机制数有限差分正演[J]. 石油地球物理勘探, 2019, 54(3): 529-538. CAI Ruiqian, SUN Chengyu, WU Dunshi, et al. Finite-difference numerical modeling with variable mechanisms for viscoacoustic wave equation[J]. Oil Geophysical Prospecting, 2019, 54(3): 529-538. |
| [8] |
苑春方, 彭苏萍, 张中杰, 等. Kelvin-Voigt均匀黏弹性介质中传播的地震波[J]. 中国科学(D辑), 2006, 35(10): 957-962. YUAN Chunfang, PENG Suping, ZHANG Zhongjie, et al. Seismic wave propagation in Kelvin-Voigt viscoelastic media[J]. Science in China (Series D), 2006, 35(10): 957-962. |
| [9] |
李晓波, 董良国. 黏弹介质中可变网格地震波传播数值模拟[J]. 石油物探, 2012, 51(1): 1-10. LI Xiaobo, DONG Liangguo. Variable-grid numerical simulation of seismic wave propagation in visco-elastic media[J]. Geophysical Prospecting for Petroleum, 2012, 51(1): 1-10. |
| [10] |
孙成禹, 肖云飞, 印兴耀, 等. 黏弹介质波动方程有限差分解的稳定性研[J]. 地震学报, 2010, 32(2): 147-156. SUN Chengyu, XIAO Yunfei, YIN Xingyao, et al. Study on the stability of finite difference solution of visco-elastic wave equations[J]. Acta Seismologica Sinica, 2010, 32(2): 147-156. |
| [11] |
Chen W, Holm S. Fractional Laplacian time-space mo-dels for linear and nonlinear lossy media exhibiting arbitrary frequency power-law dependency[J]. The Journal of the Acoustical Society of America, 2004, 115(4): 1424-1430. DOI:10.1121/1.1646399 |
| [12] |
Carcione J M, Cavalint F, Mainardi F, et al. Time-domain modeling of constant-Q seismic waves using fractional derivative[J]. Pure and Applied Geophy-sics, 2002, 159(7): 1719-1736. |
| [13] |
孙成禹, 乔志浩, 伍敦仕, 等. 常Q衰减介质分数阶波动方程优化有限差分模拟[J]. 地震学报, 2017, 39(3): 343-355. SUN Chengyu, QIAO Zhihao, WU Dunshi, et al. Modeling of wave equation with fractional derivative using optimal finite-difference method in constant-Q attenuation media[J]. Acta Seismologica Sinica, 2017, 39(3): 343-355. |
| [14] |
刘财, 胡宁, 郭智奇, 等. 基于分数阶时间导数常Q黏弹本构关系的含黏滞流体双相VTI介质中波场数值模拟[J]. 地球物理学报, 2018, 61(6): 2446-2458. LIU Cai, HU Ning, GUO Zhiqi, et al. Numerical simulation of the wavefield in a viscous fluid-saturated two-phase VTI medium based on the constant-Q viscoelastic constitutive relation with a fractional temporal derivative[J]. Chinese Journal of Geophysics, 2018, 61(6): 2446-2458. |
| [15] |
Carcione J M. A generalization of the Fourier pseudospectral method[J]. Geophysics, 2010, 75(6): A53-A56. DOI:10.1190/1.3509472 |
| [16] |
Zhang Y, Zhang P, Zhang H.Compensating for visco-acoustic effects in reverse-time migration[C].SEG Technical Program Expanded Abstracts, 2010, 29: 3160-3164.
|
| [17] |
Zhu T, Harris J M. Modeling acoustic wave propagation in heterogeneous attenuating media using decoupled fractional Laplacians[J]. Geophysics, 2014, 79(3): T105-T116. DOI:10.1190/geo2013-0245.1 |
| [18] |
吴玉, 符力耘, 陈高祥. 基于分数阶拉普拉斯算子解耦的黏声介质地震正演模拟与逆时偏移[J]. 地球物理学报, 2017, 60(4): 1527-1537. WU Yu, FU Liyun, CHEN Gaoxiang. Forward mode-ling and reverse time migration of viscoacoustic media using decoupled fractional Laplacians[J]. Chinese Journal of Geophysics, 2017, 60(4): 1527-1537. |
| [19] |
Treeby B E, Cox B T. Modeling power law absorption and dispersion for acoustic propagation using the fractional Laplacian[J]. Journal of the Acoustical Society of America, 2010, 127(5): 2741-2748. DOI:10.1121/1.3377056 |
| [20] |
Zhu T, Harris J M, Biondi B. Q-compensated reverse-time migration[J]. Geophysics, 2014, 79(3): S77-S87. DOI:10.1190/geo2013-0344.1 |
| [21] |
Chen H, Zhou H, Li Q, et al. Two efficient modeling schemes for fractional Laplacian viscoacoustic wave equation[J]. Geophysics, 2016, 81(5): T233-T249. DOI:10.1190/geo2015-0660.1 |
| [22] |
Chen H, Zhou H, Jiang S, et al. Fractional Laplacian viscoacoustic wave equation low-rank temporal extrapolation[J]. IEEE Access, 2019, 7(1): 93187-93197. |
| [23] |
Li Q, Zhou H, Zhang Q, et al. Efficient reverse time migration based on fractional Laplacian viscoacoustic wave equation[J]. Geophysical Journal International, 2016, 204(1): 488-504. DOI:10.1093/gji/ggv456 |
| [24] |
Wang N, Zhou H, Chen H, et al. A constant fractional-order viscoelastic wave equation and its numerical simulation scheme[J]. Geophysics, 2018, 83(1): T39-T48. |
| [25] |
Wang Y, Zhou H, Chen H, et al. Adaptive stabilization for Q-compensated reverse time migration[J]. Geophysics, 2018, 83(1): S15-S32. DOI:10.1190/geo2017-0244.1 |
| [26] |
Chen H, Zhou H, Zu S.Simultaneous inversion of velocity and Q using a fractional Laplacian constant-Q wave equation[C].Extended Abstracts of 79th EAGE Conference and Exhibition, 2017, ThP409.
|
| [27] |
Chen H, Zhou H, Rao Y, et al. A matrix-transform numerical solver for fractional Laplacian viscoacoustic wave equation[J]. Geophysics, 2019, 84(4): T283-T297. DOI:10.1190/geo2018-0271.1 |
| [28] |
Chen H, Zhou H, Li Y. Application of unsplit convo-lutional perfectly matched layer for scalar arbitrarily wide-angle wave equation[J]. Geophysics, 2014, 79(6): T313-T321. DOI:10.1190/geo2014-0103.1 |
| [29] |
Komatitsch D, Martin R. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation[J]. Geophysics, 2007, 72(5): SM155-SM167. DOI:10.1190/1.2757586 |
| [30] |
Carcione J M, Kosloff D, Kosloff R. Wave propagation simulation in a linear viscoelastic medium[J]. Geophysical Journal International, 1988, 95(3): 597-611. DOI:10.1111/j.1365-246X.1988.tb06706.x |



 周辉, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院地球物理系, 102249。Email:
周辉, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院地球物理系, 102249。Email: