② 东北大学资源与土木工程学院, 辽宁沈阳 110004
② School of Resources and Civil Engineering, Northeastern University, Shenyang, Liaoning 110004, China
地震勘探在地质调查和资源探测方面具有重要作用[1]。实际地震数据往往混杂随机噪声,严重影响数据的分析和处理效果。所以有效去除噪声、获得高信噪比的地震数据是地震勘探首先要解决的问题[2-4]。
随机噪声压制主要是基于有效信号与随机噪声在频率或视速度方面的差异性,常用的方法有中值滤波[5-7]、奇异值分解[8-10]、f-x域预测滤波[11-13]等。小波变换[14-16]作为一种多尺度时频分析手段,能够多尺度分析地震数据,但在处理多维地震数据时效果不明显。而Curvelet变换[17-19]和Contourlet变换[20-22]能够更好地描述地震信号的局部特征,具有突出的稀疏表示能力,可以实现很好的去噪效果。
Guo等[23-24]进一步研究了小波理论,结合多尺度几何分析和膨胀仿射系统,提出了Shearlet变换理论。Shearlet变换继承了小波变换的局部性和多尺度特性。由于Shearlet变换具有很强的方向性,而且其频域支撑是各向异性的,因此Shearlet变换可以用最少的稀疏系数逼近奇异曲线,实现信号的最优稀疏表示。同时Shearlet变换可多尺度描述高维信号的几何特性,且方向的数目随着尺度的增加而增加,因而可以克服小波变换对多维地震数据处理效果不佳的缺陷。
由于Shearlet变换独特的优势,其在多个领域得到了广泛的使用。郑晶等[25]首先对地震数据进行奇异值分解(SVD)去除直达波,然后通过Shearlet变换改进阈值压制随机噪声;李娟等[26]对地震数据进行Shearlet分解,通过增大信号分布集中的方向系数来增强信号与噪声的差异,然后利用峰度特性拾取地震初至波;郑升等[27]对大量含随机噪声的沙漠地震数据进行Shearlet变换,将得到的系数作为输入标签用于训练深度残差卷积神经网络模型,得到预测噪声和有效信号的变换系数;王宪楠等[28]利用探地雷达数据在Shearlet域的差异,采用硬阈值压制探地雷达数据中的随机噪声;刘昕等[29]将非下采样与Shearlet变换结合以压制随机噪声,消除传统Shearlet变换去噪中存在的吉布斯现象;吴一全等[30]基于非下采样Shearlet变换对图像的低频和高频分量分别进行奇异值分解和各向异性扩散,以达到去噪目的,很好地保留了图像的细节信息。
传统的Shearlet变换阈值噪声压制方法,主要考虑信号在Shearlet域尺度层面的特性,针对不同的尺度层设置自适应阈值,却忽略了地震数据在方向上的变化特性。本文通过分析信号在Shearlet域方向上的分布特点,提出阈值随尺度和方向同时自适应变化的噪声压制方法。分别对一组理论模型和两组实际数据进行噪声压制试验,并与传统阈值去噪结果对比,验证本文的尺度和方向自适应阈值法能有效压制噪声,最大程度上保留有效信号,提高地震数据的信噪比。
1 Shearlet变换基本理论 1.1 连续Shearlet变换Guo等[31]基于合成小波理论,结合仿射系统和多尺度几何分析,提出了带有合成膨胀系统的几何变换方法。合成连续膨胀系统在二维空间表达式为
| $ \begin{array}{*{20}{c}} {{\psi _{\mathit{\boldsymbol{AB}}}}\left( \phi \right) = {\phi _{j,l,k}}\left( x \right) = {{\left| {det\mathit{\boldsymbol{A}}} \right|}^{j/2}} \times }\\ {\phi \left( {{\mathit{\boldsymbol{B}}^l}{\mathit{\boldsymbol{A}}^j}x - k:j,l \in \mathit{\boldsymbol{Z}},k \in {\mathit{\boldsymbol{Z}}^2}} \right)} \end{array} $ | (1) |
式中:ψAB(ϕ)为仿射系统函数;ϕ为紧支撑函数,ϕ∈L2(R2),L2为可积分二维空间,R为实数域;x为函数自变量(普通变量);各向异性膨胀矩阵
若ψAB(ϕ)满足Parseval框架[32-33],则称为合成小波。Aj控制尺度变换,Bl控制几何变换。
定义伸缩矩阵H由各向异性膨胀矩阵A和剪切矩阵B构成
| $ \begin{array}{l} \mathit{\boldsymbol{H}} = \mathit{\boldsymbol{BA}} = \left[ {\begin{array}{*{20}{l}} 1&b\\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} a&0\\ 0&{\sqrt a } \end{array}} \right]\\ \;\;\;\; = \left[ {\begin{array}{*{20}{l}} a&{b\sqrt a }\\ 0&{\sqrt a } \end{array}} \right]:\left( {a,b} \right) \in {\mathit{\boldsymbol{R}}^ + } \times \mathit{\boldsymbol{R}} \end{array} $ | (2) |
则可以得到如下连续仿射系统
| $ \begin{array}{l} {\mathit{\boldsymbol{\psi }}_\mathit{\boldsymbol{H}}}\left( \phi \right) = {\mathit{\boldsymbol{\psi }}_{a,b,k}}\left( \phi \right)\\ \;\;\;\;\; = \left\{ {{\mathit{\boldsymbol{\psi }}_{a,b,k}}\left( x \right) = {a^{ - \frac{3}{4}}}\phi \left[ {{\mathit{\boldsymbol{H}}^{ - 1}}\left( {x - t} \right)} \right]:} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;a\left. { \in {\mathit{\boldsymbol{R}}^ + },b \in \mathit{\boldsymbol{R}},k \in {\mathit{\boldsymbol{R}}^2}} \right\} \end{array} $ | (3) |
式中:t为平移参数;ψa, b, k(ϕ)为连续剪切波;ψa, b, k(x)为剪切母函数。剪切波ψa, b, k(ϕ)在各个尺度层对应的频域划分如图 1所示。

|
图 1 Shearlet频域剖分示意图 |
基于剪切波函数,可以定义连续Shearlet变换为
| $ \mathit{\boldsymbol{C}} = {\rm{SH}}\left\{ f \right\} = \left\langle {f,{\phi _{i,l,k}}} \right\rangle $ | (4) |
式中:C为Shearlet系数矩阵;SH{·}为Shearlet变换;〈·,·〉表示内积;f为含噪信号。
同样可以对Shearlet系数矩阵C进行反变换重构原始函数
| $ f = {\rm{S}}{{\rm{H}}^{ - 1}}\left\{ \mathit{\boldsymbol{C}} \right\} $ | (5) |
式中SH-1表示Shearlet逆变换。
1.2 离散Shearlet变换假设尺度参数a=2-j, 剪切参数b=-l(j, l∈Z),用点k∈Z2代替连续Shearlet变换中的平移参数t∈R2,得到Shearlet变换基元素的表达式为
| $ {\psi _{\mathit{\boldsymbol{AB}}}}\left( \phi \right) = {\phi _{j,l,k}}\left( x \right) = {\left| {{\rm{det}}{\mathit{\boldsymbol{A}}_0}} \right|^{j/2}}\phi \left( {\mathit{\boldsymbol{B}}_0^l\mathit{\boldsymbol{A}}_0^jx - k} \right) $ | (6) |
式中:
对于任意f∈L2(R2),离散Shearlet变换需满足
| $ \sum\limits_{j \in \mathit{\boldsymbol{Z}},l \in \mathit{\boldsymbol{Z}},k \in {\mathit{\boldsymbol{Z}}^2}} {{{\left| {\left\langle {f,{\phi _{j,l,k}}} \right\rangle } \right|}^2}} = {\left\| f \right\|^2} $ | (7) |
基于Shearlet变换最优稀疏表示的特点,地震数据经Shearlet变换后得到各分解尺度和方向的Shearlet系数。若Shearlet基函数的方向与地震信号的方向大致相同,则对应较大的Shearlet系数;当两方向相差较大时,Shearlet系数偏小。在实际地震数据中,有效信号分布具有方向性,而随机噪声是随机分布的,所以地震数据经Shearlet变换后,有效信号相比随机噪声会对应较大的Shearlet系数。这样就可以设置一个阈值,利用阈值函数去除随机噪声对应的较小的系数,达到去除随机噪声的目的。然后对处理后的Shearlet系数进行逆变换,得到去噪后的地震信号。
假设待处理的含噪地震数据模型为
| $ f\left( t \right) = u\left( t \right) + n\left( t \right) $ | (8) |
式中:u(t)为有效信号;n(t)为随机噪声。Shearlet变换阈值去噪算法的实质就是从f(t)中得到u(t)。该过程可以分以下三个步骤。
(1) 对含噪地震数据f(t)进行Shearlet变换,获取Shearlet系数
| $ C\left( {j,l,k} \right) = {\rm{SH}}\left\{ {f\left( t \right)} \right\} = \left\langle {f\left( t \right),{\phi _{j,l,k}}} \right\rangle $ | (9) |
(2) 对得到的Shearlet系数进行阈值化
| $ {C_{{\rm{new}}}}\left( {j,l,k} \right) = \left\{ {\begin{array}{*{20}{c}} {C\left( {j,l,k} \right)}&{\left| {C\left( {j,l,k} \right)} \right| \ge {\rm{T}}{{\rm{h}}_j}}\\ 0&{\left| {C\left( {j,l,k} \right)} \right| < {\rm{T}}{{\rm{h}}_j}} \end{array}} \right. $ | (10) |
| $ {\rm{T}}{{\rm{h}}_j} = \sigma \sqrt {2\ln N} \lg \left( {j + 1} \right) $ | (11) |
| $ \sigma = \frac{{{\rm{median}}\left( {\left| \mathit{\boldsymbol{C}} \right|} \right)}}{{0.6745}} $ | (12) |
式中:Cnew(j, l, k)表示阈值化处理后的系数;N表示地震数据的总采样点数;median(·)表示对矩阵所有元素取中值。
(3) 对阈值化处理后的系数Cnew进行逆变换,得到去噪后的有效信号
| $ \hat s\left( t \right) = {\rm{S}}{{\rm{H}}^{ - 1}}\left\{ {{\mathit{\boldsymbol{C}}_{{\rm{new}}}}} \right\} = \sum\limits_{j,l,k} {{C_{{\rm{new}}}}\left( {j,l,k} \right){\phi _{j,l,k}}} $ | (13) |
传统阈值函数在压制随机噪声时,仅对不同分解尺度设置不同的阈值,实现了阈值随分解尺度的自适应。但因为Shealret变换具有多尺度、多方向的特点,所以仅随尺度自适应阈值不能充分发挥Shearlet变换的优势,不能达到满意的去噪效果。虽然地震数据的分布与Shearlet变换的尺度和方向相关性很强,但是在确定的尺度内,却有相似的分布规律,即在一些方向上分布大量的地震数据,而总存在一个方向,该方向地震数据分布最少。而在含有随机噪声的地震数据中,因为随机噪声的分布具有随机性,所以在有效信号分布最少的方向上就会存在有大量的随机噪声,用此噪声来预估实际噪声,并从地震数据中去除噪声,分离出有效地震信号。为此,本文分析了地震数据在Shearlet域不同尺度和不同方向上分布的差异,提出一种衡量地震数据噪声的方法,即将有效信号分布最少的尺度和方向上分布的噪声作为该尺度的噪声,并将其剔除,得到分布在各尺度和方向上的有效地震数据。
类比式(11)阈值随尺度变化的规律设置方向自适应项,结合尺度自适应性,提出一种新的随尺度和方向自适应变化的阈值函数
| $ {\rm{T}}{{\rm{h}}_{j,l}} = \eta \frac{{\sigma \sqrt {2\ln N} \lg \left( {j + 1} \right)}}{{\lg \left( {{e_{j,l}} - \sigma \mathop {\min }\limits_j {e_{j,l}} + 10} \right)}} $ | (14) |
式中:ej, l为尺度j、方向l上的Shearlet变换系数矩阵的L2范数,j=1, 2, …, J,J为分解总尺度;σ为噪声标准差;η为1~10的整数,微调去噪效果;min(·)为最小值函数。
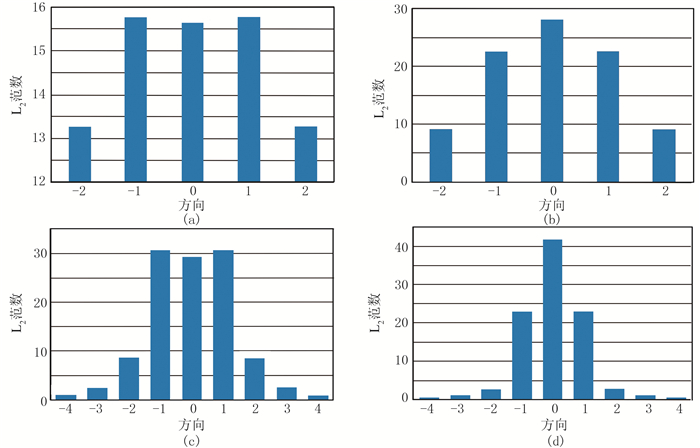
以一合成理论单炮地震记录(图 2)为例说明本文方法的实现过程。该地震记录共包含250道,每道有1000个采样点,采样频率为1ms。对该数据进行Shearlet变换,用于分析地震数据在Shearlet域不同分解尺度和方向上的分布特征。图 3为求取各分解尺度和各方向的Shearlet系数矩阵的L2范数,发现在不同尺度上地震数据的分布存在差异,并且在确定尺度内不同方向上的地震数据也存在着更明显差异。对图 3进行排序得到地震数据经Shearlet变换后在不同尺度、不同方向上的分布规律(图 4)。

|
图 2 合成理论地震数据 |
|
图 3 不同尺度和方向Shearlet变换系数矩阵L2范数柱状图 (a)第1尺度; (b)第2尺度; (c)第3尺度; (d)第4尺度 |

|
图 4 不同尺度和方向Shearlet变换系数矩阵L2范数折线图 (a)第1尺度; (b)第2尺度; (c)第3尺度; (d)第4尺度 |
为了验证本文自适应阈值去噪方法的优越性,分别对一组理论地震数据和叠前、叠后实际地震数据应用本文方法和传统阈值法进行噪声压制试验,比较二者的去噪效果,并统计两种方法去噪后的信噪比、峰值信噪比和均方差。
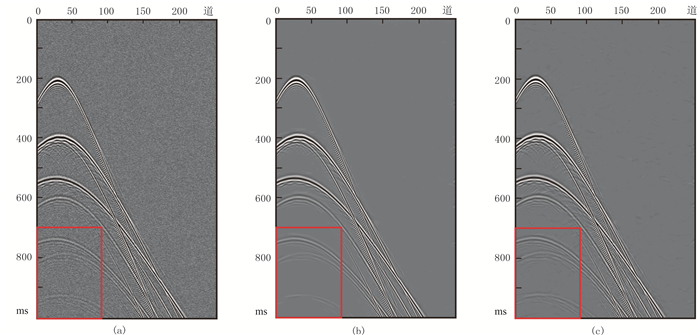
3 理论数据测试利用理论单炮地震记录进行噪声压制试验。试验选择正交小波作为分解母函数,设置4个分解层,角度参数为[1,1,2,2]。理论单炮记录如图 2所示。在理论地震数据中加入白噪声后,地震数据信噪比为5.1539dB(图 5a)。在单炮记录中分布着大量的随机噪声,能量较弱的同向轴被随机噪声淹没,无法有效识别。分别利用基于Shearlet变换的传统硬阈值和自适应阈值两种去噪方法对合成的单炮记录进行随机噪声处理,结果如图 5b和图 5c所示。
|
图 5 两种阈值去噪结果对比 (a)加噪数据道集;(b)硬阈值去噪道集;(c)自适应阈值去噪道集 |
分析图 5可知,自适应阈值方法能有效压制随机噪声,处理后的整个地震记录很干净,能够清楚识别出有效信号,同向轴的连续性也很好。图 6为图 2和图 5红框区域局部放大图,可以发现,模拟理论地震数据在700~1000ms存在能量较弱的有效信号,添加噪声后能量较弱的同向轴被噪声淹没。硬阈值去噪剖面(图 6c)上,箭头所指同向轴几乎不可分辨;而利用本文的自适应阈值进行噪声压制(图 6d),同向轴连续性较好,有效信号得到了很好的重构,说明该方法比硬阈值能更好地保护有效信号、尤其是弱信号的能力。
分析去噪差剖面(图 7), 硬阈值法虽然去除了随机噪声,但不能识别能量较弱的有效信号,造成有效信号损失严重,而且差剖面上也有较多的同向轴出现(图 7a),表明硬阈值不能准确区分信号与噪声,去噪的同时对有效信号造成损伤;用本文方法得到的去噪差剖面(图 7b),几乎没有同向轴出现,说明该方法能够有效区分信号与噪声,在去除随机噪声的同时保留更多的有效地震信息,获得高信噪比的地震数据。

|
图 7 两种阈值方法所去除的噪声道集 (a)硬阈值法;(b)自适应阈值法 |
表 1给出了两种阈值去噪方法去除的理论含噪数据的峰值信噪比(PSNR)、信噪比(SNR)和均方误差(MSE)。可见,自适应阈值法相比硬阈值法,去噪后的剖面具有较大的SNR和PSNR,但MSE却更小,说明自适应阈值去噪效果优于硬阈值法。综上所述,本文提出的自适应阈值法相比于硬阈值法能够更有效去除理论地震数据中的噪声。
|
|
表 1 两种阈值去噪效果指标 |
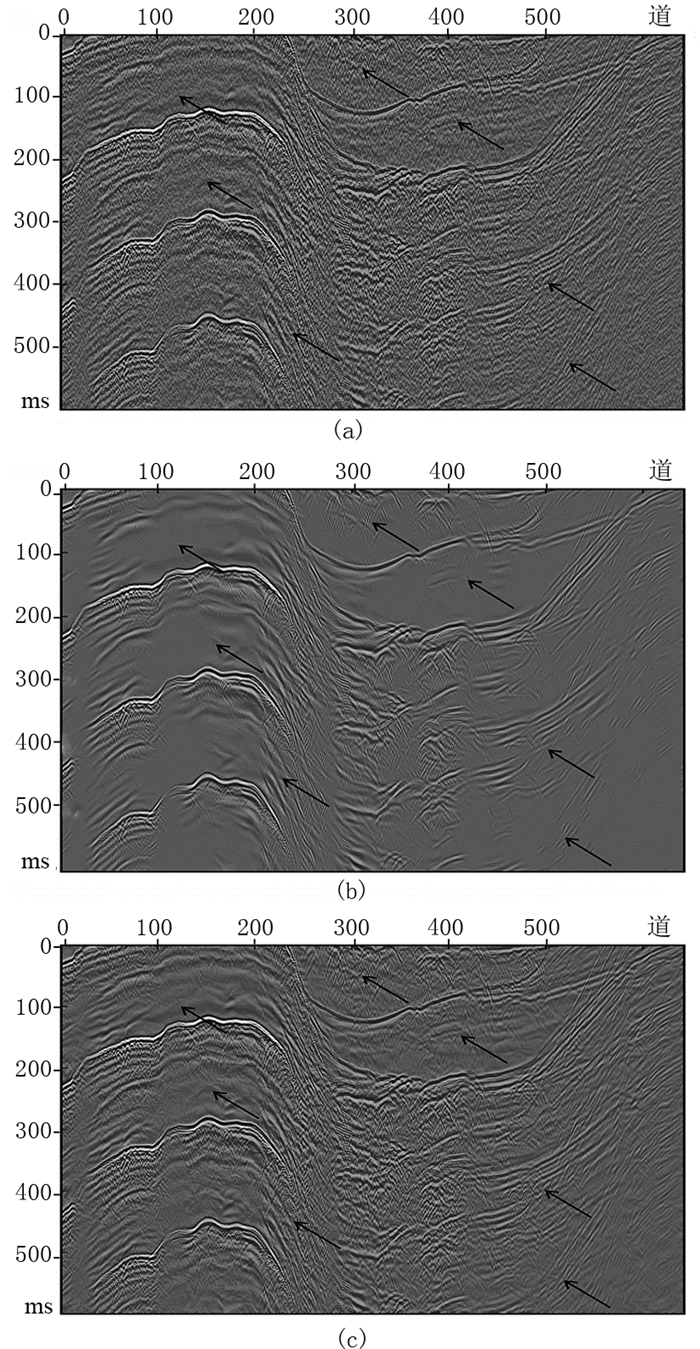
图 8a为一褶皱构造的实际地震叠后剖面,数据含有大量的噪声,同向轴的连续性较差,部分能量较弱的有效信号被噪声淹没。
|
图 8 实际叠后地震数据去噪效果分析 (a)叠后地震剖面;(b)硬阈值去噪剖面;(c)自适应阈值去噪剖面 |
分别利用基于Shearlet变换传统硬阈值和自适应阈值对上述实际地震数据进行随机噪声压制,结果分别如图 8b和图 8c所示。与图 8a对比可以发现,图 8b中地震剖面干净平整,说明随机噪声基本被剔除,但是同向轴的连续性很差;图 8c中,同向轴的连续性更好,且边界信息更加清晰,凸显了被随机噪声淹没的能量较弱的同向轴(图中箭头所指位置)。
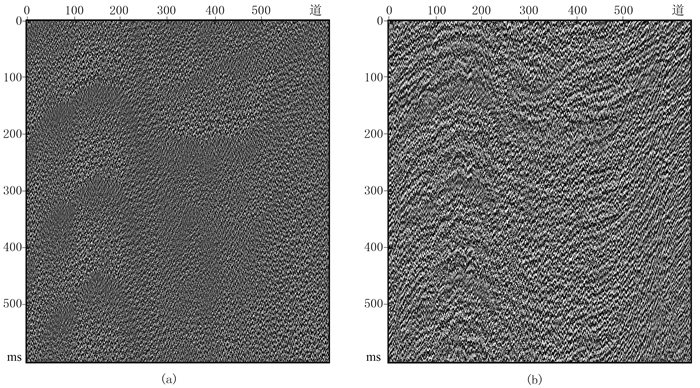
图 9为两种方法去噪的差值剖面,相比于硬阈值去噪差剖面(图 9a),自适应阈值剖面(图 9b)中几乎无有效地震信号分布,说明自适应阈值方法具有更好的保留地震信号的能力,能够有效提高去噪后地震数据的信噪比。
|
图 9 实际叠后地震数据不同方法去除的噪声剖面 (a)硬阈值法;(b)自适应阈值法 |
实际采集的叠前地震记录如图 10a所示,分别应用硬阈值法和自适应阈值法对其进行去噪处理,结果见图 10b和图 10c。图 11是对图 10中红色线框区域的放大图。图 12是不同方法所剔除的噪声。对比可以发现,经自适应阈值法去噪后,随机噪声得到很好的压制,地震道集更平整,同相轴也更清晰,且能够更好地分辨出深部能量较弱的有效地震信号,丰富了地震数据的细节信息。经自适应阈值法处理后得到的差值相比传统硬阈值法明显地具有更少的同相轴。表明本文方法去除了随机噪声的同时能在较大程度上保护地震数据的完整性,实现比硬阈值更好的去噪效果。

|
图 10 实际叠前地震数据去噪效果分析 (a)叠前地震记录;(b)硬阈值去噪道集;(c)自适应阈值去噪道集 |

|
图 12a 实际叠前地震数据硬阈值法去除的噪声 |

|
图 12b 实际叠前地震数据自适应阈值法去除的噪声 |
传统阈值法压制随机噪声只考虑地震信号的分布在尺度上存在差异,因而只能去除部分噪声,阈值设置不合理。为了提高去噪效果,本文统计并分析了理论地震数据在Shearlet域尺度和方向的分布规律,提出一种估计随机去噪方法,并且设置尺度和方向自适应阈值压制随机噪声。基于理论数据和实际地震数据的计算结果,得到以下结论。
(1) Shearlet变换具有多尺度、多方向特性,地震数据在Shearlet域不同尺度和不同方向存在差异。对不同方向上地震数据的统计分析表明,在每一尺度内,总存在某一方向上的地震数据分布最少,而噪声在该方向的分布相对较多。
(2) 因为随机噪声的分布具有随机性,所以将噪声分布相对较多的方向(即该方向上有效地震信号最少)的噪声强度作为该尺度内随机噪声的强度。这样可最大程度上分离噪声,得到较为纯净的有效信号。
(3) 基于地震数据在Shearlet域各尺度和方向的分布差异,设置尺度和方向自适应阈值,去除随机噪声。参考尺度对阈值影响的处理方式,构造方向自适应项,提出一种新的随尺度和方向自适应变化的阈值,解决了传统阈值去噪过程中损失部分有效信号的问题。
(4) 利用两种不同的阈值法对理论地震数据和实际地震数据进行随机噪声压制试验,结果表明本文提出的基于Shearlet变换的自适应阈值估算法相比于传统的硬阈值法能更有效去除地震数据中的随机噪声,保留更多的有效信号。
| [1] |
曹令敏. 地球物理方法在金属矿深部找矿中的应用及展望[J]. 地球物理学进展, 2011, 26(2): 701-708. CAO Lingmin. The application and expectation of the geophysical methods to deep metal mine exploration[J]. Progress in Geophysics, 2011, 26(2): 701-708. |
| [2] |
梁顺军, 梁霄, 陈江力, 等. 山地复杂构造倒转背斜地震剖面反射特征及油气成藏分析[J]. 中国石油勘探, 2019, 24(3): 377-390. LIANG Shunjun, LIANG Xiao, CHEN Jiangli, et al. Seismic reflection features and analysis of hydrocarbon accumulation of reversed anticlines in complicated mountainous areas[J]. China Petroleum Exploration, 2019, 24(3): 377-390. |
| [3] |
侯景瑞. 试论地质勘查和深部地质钻探找矿技术[J]. 世界有色金属, 2019, 35(1): 83-85. HOU Jingrui. Discussion on geological exploration and deep geological drilling prospecting technology[J]. World Nonferrous Metals, 2019, 35(1): 83-85. |
| [4] |
张军华, 吕宁, 田连玉, 等. 地震资料去噪方法综合评述[J]. 石油地球物理勘探, 2005, 40(增刊1): 121-127. ZHANG Junhua, LV Ning, TIAN Lianyu, et al. An overview of the methods for seismic data noise attenuation[J]. Oil Geophysical Prospecting, 2005, 40(S1): 121-127. |
| [5] |
董烈乾, 汪长辉, 李长芬, 等. 利用自适应中值滤波方法压制混叠噪声[J]. 地球物理学进展, 2018, 33(4): 1475-1479. DONG Lieqian, WANG Changhui, LI Changfen, et al. Blending noise removal utilizing an adaptive median filter[J]. Progress in Geophysics, 2018, 33(4): 1475-1479. |
| [6] |
郝波, 卢小平. 基于中值滤波的图像边缘去噪算法研究[J]. 现代计算机, 2019, 20: 38-41. HAO Bo, LU Xiaoping. Research on image edge denoising algorithms on median filtering[J]. Modern Computer, 2019, 20: 38-41. |
| [7] |
孙哲, 王建锋, 王静, 等. 基于时空变中值滤波的随机噪声压制方法[J]. 石油地球物理勘探, 2016, 51(6): 1094-1102. SUN Zhe, WANG Jianfeng, WANG Jing, et al. Random noise elimination based on the time-space variant median filtering[J]. Oil Geophysical Prospecting, 2016, 51(6): 1094-1102. |
| [8] |
鲍伟, 马继涛. 频率域奇异值分解压制随机噪声方法[J]. 科技导报, 2013, 31(21): 58-63. BAO Wei, MA Jitao. Seismic random noise suppression by using frequency-domain singular value decomposition[J]. Science & Technology Review, 2013, 31(21): 58-63. |
| [9] |
徐彦凯, 曹思远, 潘晓, 等. 随机噪声的局部正交压制方法[J]. 石油地球物理勘探, 2019, 54(2): 280-287. XU Yankai, CAO Siyuan, PAN Xiao, et al. A local orthogonalization for seismic random noise suppression[J]. Oil Geophysical Prospecting, 2019, 54(2): 280-287. |
| [10] |
张岩, 任伟建, 唐国维. 应用结构聚类字典学习压制地震数据随机噪声[J]. 石油地球物理勘探, 2018, 53(6): 1119-1127. ZHANG Yan, REN Jianwei, TANG Guowei. Random noise suppression on seismic data based on structured clustering dictionary learning[J]. Oil Geophysical Prospecting, 2018, 53(6): 1119-1127. |
| [11] |
刘婷婷, 陈阳康. F-X域经验模式分解与多道奇异谱分析相结合去除随机噪声[J]. 石油物探, 2016, 55(1): 67-75. LIU Tingting, CHEN Yangkang. Random noise atte-nuation based on EMD and MSSA in F-X domain[J]. Geophysical Prospecting for Petroleum, 2016, 55(1): 67-75. |
| [12] |
赵德斌, 黄真萍, 王春梅. F-X域奇异值分解预测滤波法随机噪声衰减[J]. 石油物探, 1998, 37(3): 29-33. ZHAO Debin, HUANG Zhenping, WANG Chunmei. Random noise attenuation using filtering in F-X domain by singular value decomposition[J]. Geophysical Prospecting for Petroleum, 1998, 37(3): 29-33. |
| [13] |
康冶, 于承业, 贾卧, 等. f-x域去噪方法研究[J]. 石油地球物理勘探, 2003, 38(2): 136-138. KANG Ye, YU Chengye, JIA Wo, et al. A study on noise-suppression method in f-x domain[J]. Oil Geophysical Prospecting, 2003, 38(2): 136-138. |
| [14] |
覃发兵, 徐振旺, 啜晓宇, 等. 基于经验小波变换的地震资料噪声压制方法[J]. 中国石油勘探, 2018, 23(5): 100-110. QIN Fabing, XU Zhenwang, CHUAI Xiaoyu, et al. Seismic noise suppression based on empirical wavelet transformation[J]. China Petroleum Exploration, 2018, 23(5): 100-110. |
| [15] |
高静怀, 毛剑, 满蔚仕, 等. 叠前地震资料噪声衰减的小波域方法研究[J]. 地球物理学报, 2006, 49(4): 1155-1163. GAO Jinghuai, MAO Jian, MAN Weishi, et al. On the denoising method of prestack seismic data wavelet domain[J]. Chinese Journal of Geophysics, 2006, 49(4): 1155-1163. |
| [16] |
Sid-Ali O, Leila A. Random seismic noise attenuation data using the discrete and the continuous wavelet transforms[J]. Arabian Journal of Geosciences, 2014, 7(7): 2531-2537. |
| [17] |
徐伟.基于Curvelet变换的地震资料去噪方法研究与应用[D].四川成都: 成都理工大学, 2017. XU Wei.Research and Application of Seismic Data Denoising Method Based on Curvelet Transform[D].Chengdu University of Technology, Chengdu, Sichuan, 2017. http://d.wanfangdata.com.cn/Periodical/hgbzjlzl201710064 |
| [18] |
金丹, 程建远, 王保利, 等. 基于Curvelet变换的地震资料弱信号识别及去噪方法[J]. 煤炭学报, 2016, 41(2): 332-337. JIN Dan, CHENG Jianyuan, WANG Baoli, et al. Seismic weak signal identification and noise elimination based on Curvelet domain[J]. Journal of China Coal Society, 2016, 41(2): 332-337. |
| [19] |
张恒磊, 张云翠, 宋双, 等. 基于Curvelet域的叠前地震资料去噪方法[J]. 石油地球物理勘探, 2008, 42(5): 508-513. ZHANG Henglei, ZHANG Yuncui, SONG Shuang, et al. Curvelet domain-based prestack seismic data denoise method[J]. Oil Geophysical Prospecting, 2008, 42(5): 508-513. |
| [20] |
王建花, 王守东, 刘燕峰. 基于Contourlet系数相关性的地震噪声压制方法[J]. 中国海上油气, 2016, 28(1): 35-40. WANG Jianhua, WANG Shoudong, LIU Yanfeng. Seismic noise suppression method based on correlation of Contourlet coefficients[J]. China Offshore Oil and Gas, 2016, 28(1): 35-40. |
| [21] |
刘磊, 刘振, 张军华. 曲波阈值法地震弱信号识别及去噪方法研究[J]. 地球物理学进展, 2011, 26(4): 1415-1422. LIU Lei, LIU Zhen, ZHANG Junhua. Denoising and detecting seismic weak signal based on Curvelet thresholding method[J]. Progress in Geophysics, 2011, 26(4): 1415-1422. |
| [22] |
刘燕峰, 邹少峰, 居兴国. 基于Contourlet变换的K-L变换地震随机噪声自适应衰减方法[J]. 石油物探, 2017, 56(5): 676-683. LIU Yanfeng, ZOU Shaofeng, JU Xingguo. Seismic random noise self-adaptive attenuation method based on K-L transform in the Contourlet-domain[J]. Geophysical Prospecting for Petroleum, 2017, 56(5): 676-683. |
| [23] |
Guo K, Labate D, Lim W Q, et al. Wavelets with composite dilations[J]. Electronic Research Society, 2004, 10(9): 78-87. |
| [24] |
Guo K, Labate D, Lim W Q, et al. Wavelets with composite dilations and their MRA properties[J]. Applied and Computational Harmonic Analysis, 2006, 20(2): 202-236. |
| [25] |
郑晶, 余可, 王鹏越, 等. 基于Shearlet变换的探地雷达数据噪声压制研究[J]. 矿业科学学报, 2017, 2(3): 228-234. ZHENG Jing, YU Ke, WANG Pengyue, et al. GPR data noise attenuation bases on the Shearlet transform[J]. Journal of Mining Science and Technology, 2017, 2(3): 228-234. |
| [26] |
李娟, 计硕, 李月, 等. 基于Shearlet变换和峰度特性的井中微地震初至波拾取[J]. 吉林大学学报(工学版), 2019, 49(1): 290-295. LI Juan, JI Shuo, LI Yue, et al. First arrival pickup of downhole microseismic signal based on Shearlet transform and kurtosis characteristic[J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(1): 290-295. |
| [27] |
郑升, 李月, 董新桐. Shearlet域深度残差CNN用于沙漠地震信号去噪[J]. 吉林大学学报(信息科学版), 2019, 37(1): 1-7. ZHENG Sheng, LI Yue, DONG Xintong. Shearlet domain deep residual CNN for removing noise from de-sert seismic signals[J]. Journal of Jilin University(Information Science Edition), 2019, 37(1): 1-7. |
| [28] |
王宪楠, 刘四新, 程浩. Shearlet变换在GPR数据随机噪声压制中的应用[J]. 吉林大学学报(地球科学版), 2017, 47(6): 1855-1864. WANG Xiannan, LIU Sixin, CHENG Hao. Application of Shearlet transform for supressing random noise in GPR data[J]. Journal of Jilin University(Earth Science Edition), 2017, 47(6): 1855-1864. |
| [29] |
刘昕, 陈祖斌, 王东鹤, 等. 基于非下采样shearlet变换的微地震随机噪声压制[J]. 煤炭技术, 2016, 35(1): 128-129. LIU Xin, CHEN Zubin, WANG Donghe, et al. Microseismic random noise attenuation based on non-subsampled Shearlet transformation[J]. Coal Technology, 2016, 35(1): 128-129. |
| [30] |
吴一全, 李立, 陶飞翔. 基于Shearlet域各向异性扩散和稀疏表示的图像去噪[J]. 应用科学学报, 2014, 32(3): 221-228. WU Yiquan, LI Li, TAO Feixiang. Image denoising based on anisotropic diffusion and sparse representation in Shearlet domain[J]. Journal of Applied Science, 2014, 32(3): 221-228. |
| [31] |
Guo K, Labate D. Optimally sparse multidimensional representation using shearlets[J]. SIAM Journal on Mathematical Analysis, 2007, 39(1): 298-318. |
| [32] |
童思友, 高航, 刘锐, 等. 基于Shearlet变换的自适应地震资料随机噪声压制[J]. 石油地球物理勘探, 2019, 54(4): 744-750. TONG Siyou, GAO Hang, LIU Rui, et al. Seismic random noise adaptive suppression based on the Shearlet transform[J]. Oil Geophysical Prospecting, 2019, 54(4): 744-750. |
| [33] |
陈欢, 陈清江. 二维Parseval小波框架包的性质[J]. 兰州理工大学学报, 2017, 43(3): 157-162. CHEN Huan, CHEN Qingjiang. Properties of two-dimensional Parseval wavelet-framed packets[J]. Journal of Lanzhou University of Technology, 2017, 43(3): 157-162. |



 程浩, 辽宁省沈阳市和平区文化路3号巷11号东北大学资源与土木工程学院, 110004。Email:
程浩, 辽宁省沈阳市和平区文化路3号巷11号东北大学资源与土木工程学院, 110004。Email:

