② 中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 湖南长沙 410083;
③ 有色资源与地质灾害探查湖南省重点实验室, 湖南长沙 410083;
④ 承德石油高等专科学校, 河北承德 067000
② Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring(Central South University), Ministry of Education, Changsha, Hunan 410083, China;
③ Hunan Key Laboratory of Nonferrous Resources and Geological Hazard Detection, Changsha, Hunan 410083, China;
④ Chengde Petroleum College, Chengde, Hebei 067000, China
由于地震勘探现场采集环境的复杂化,所得地震数据很容易混杂各种噪声干扰,甚至会严重掩盖有效信号,导致其难以分辨。因此,去噪成为地震数据处理的最重要步骤[1-3]。地震数据中噪声主要分为随机噪声和相干噪声,常用的去噪方法有奇异值分解[4-5]、小波去噪[6-7]、曲波去噪[8-10]和多项式拟合[11-12]等,其中基于稀疏变换的去噪方法因易于实施且普适性强,成为主流去噪方法。但在处理较复杂地震数据时,这类方法的去噪效果也难如人意,因此亟待探寻一种更有效的去噪方法。
近年来,随着硬件、算法和大数据等方面的快速发展,人工智能在诸多领域得到了广泛的应用,尤其在图像去噪[13-14]、分类[15]和目标检测[16]等领域已成功地解决了许多其他方法难以处理的问题。Jain等[17]用卷积神经网路对自然图像去噪,得到了与马尔可夫随机模型相近或更优的结果;并指明神经网络模型可避免马尔可夫模型在概率学习和推断过程中计算复杂度较高的问题。Xie等[18]综合稀疏编码与深度神经网络,提出了栈式稀疏去噪自编码器。Burger等[19]将多层感知机用于图像去噪,指出若训练集足够多,则利用MLP模型可达成当前最优的图像去噪效果。在地震勘探领域,深度学习类方法也得到快速发展和广泛应用,如地震数据时深转换[20]、层析成像[21]和有效信号识别[22]等。
本文提出一种基于MLP的地震数据去噪方法:通过对已有地震数据训练得到一个五层神经网络模型;用反向传播算法调节各层神经元的权重;然后将含噪数据作为输入进行去噪处理并输出结果。为了进一步验证该方法压制噪声和保护有效信号的能力,选择曲波去噪方法做对比分析。分别针对合成数据和实测地震数据进行去噪处理,结果表明本文MLP去噪方法拥有更强去噪能力,尤其在保护构造细节方面显著优于曲波去噪方法。
1 基于MLP的地震去噪模型构建 1.1 MLP去噪机理地震数据构成可用下式表示
| $ \mathit{\boldsymbol{x}}{\rm{ = }}\mathit{\boldsymbol{y}}{\rm{ + }}\mathit{\boldsymbol{n}} $ | (1) |
式中:y为不含噪地震数据;n为噪声;x为含噪地震数据。据MLP建立输入x与输出y之间的关系
| $ \mathit{\boldsymbol{y}} = H(\mathit{\boldsymbol{x}};\mathit{\boldsymbol{\theta }}) $ | (2) |
式中:H表示MLP网络结构;θ表示网络参数的集合。地震去噪可定义为将一个含噪数据映射到一个噪声较少的数据,为此需构建一个MLP网络结构模型表示映射关系。
1.2 MLP网络结构MLP也被称为人工神经网络[23]或多层神经网络,主要由输入层(Input layer)、输出层(Output layer)和隐层(Hidden layer)三部分构成,其中输入层和输出层分别只有一个,隐层可以是一层或多层拓扑结构。输入层用于接收数据,它不进行任何计算,仅将数据按不同权重传递到相邻的隐层,隐层通过非线性激活函数对数据进行处理,随后传递到输出层,最后从输出层输出最终结果。
一个简单的三层感知机可表示为
| $ f(\mathit{\boldsymbol{x}}) = {\mathit{\boldsymbol{b}}_2} + {\mathit{\boldsymbol{W}}_2}s\left( {{\mathit{\boldsymbol{b}}_1} + {\mathit{\boldsymbol{W}}_1}\mathit{\boldsymbol{x}}} \right) $ | (3) |
式中:W1、b1分别是输入层与隐层之间的权重矩阵和偏置矩阵;W2、b2分别是隐层与输出层之间的权重矩阵和偏置矩阵;s是Sigmoid激活函数,能将输入的连续实值变换为0和1之间的输出,若是很大负数,输出为0;若是很大正数,则输出为1。
图 1显示一个拥有n个输入神经元、m个输出神经元、q个隐层神经元的三层神经网络。为了方便表示,将每个神经元的偏置b看作输入为1时对应的权重的第0个分量。从该图可见MLP中每层含有多个节点,各层的节点与下一层的节点完全连接。输入层的节点个数表示输入数据的维数,隐层上的节点个数与训练数据有关,输出层节点个数表示输出数据的维数。
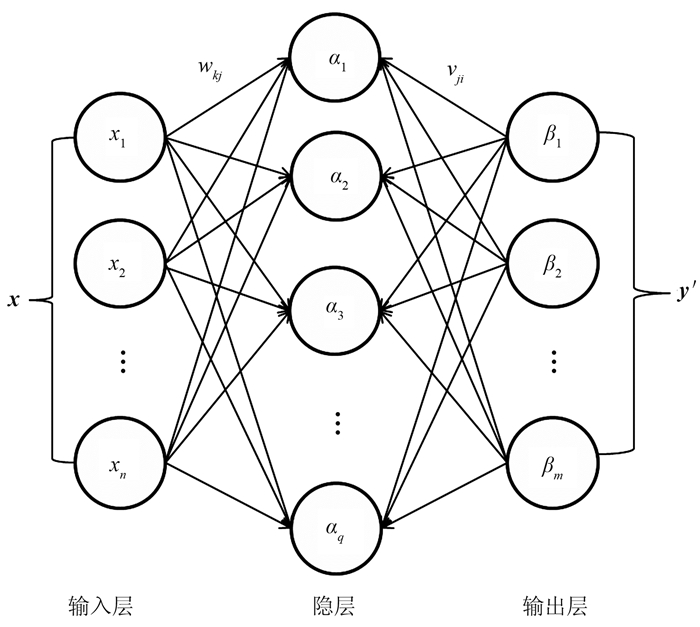
|
图 1 三层感知机示意图 y′为网络输出;wkj为输入层第k个神经元与隐层第j个神经元间的权重;vji为隐层第j个神经元与输出层第i个神经元间的权重;α和β分别是隐层和输出层接收到的数据 |
训练MLP就是利用地震数据调节其网络参数。当MLP的输出与地震数据的标记值(未受噪声干扰的数据)之差达到足够小时,可认为该MLP训练完成。网络的训练一般需要循环多次,每次包含前向传播和反向传播两个过程,并且采用梯度下降方式调节网络参数。
1.3.1 前向传播以图 1所示的三层感知机为例,计算输入为x时的网络输出,具体过程如下。
隐层第j个神经元接收到的输入为
| $ {\alpha _j} = \sum\limits_{k = 1}^n {{w_{kj}}} {x_k} $ | (4) |
式中xk为输入数据x在输入层第k个神经元上的分量。通过Sigmoid激活函数,隐层对接收到的数据αj进行处理并传递给输出层,则输出层第i个神经元接收到的输入为
| $ {\beta _i} = \sum\limits_{j = 0}^q {{v_{ji}}} {\rm{Sigmoid}}\left( {{\alpha _j}} \right) $ | (5) |
网络输出y′由输出层m个神经元输出βi构成
| $ \mathit{\boldsymbol{y'}} = {\left[ {{\beta _1}, {\beta _2}, \cdots , {\beta _m}} \right]^{\rm{T}}} $ | (6) |
MLP中输出层权重可直接用误差更新,但隐层中不存在误差,故对隐层不能直接用梯度下降方式调整参数,而是先将误差通过链式法则反向传播至隐层,再采用梯度下降方法处理。
由式(6)可得网络输出和实际输出的均方误差
| $ E = \frac{1}{2}\sum\limits_{i = 0}^m {{{\left( {{{y'}_i} - {y_i}} \right)}^2}} $ | (7) |
式中yi表示实际输出数据y在输出层第i个神经元上的分量。误差逆传播算法基于梯度下降策略,以网络的负梯度方向对权重进行调整
| $ \begin{array}{l} \Delta {v_{ji}} = - \eta \frac{{\partial E}}{{\partial {v_{ji}}}} = - \eta \frac{{\partial E}}{{\partial {{y'}_i}}}\frac{{\partial {{y'}_i}}}{{\partial \beta }}\frac{{\partial {\beta _{ji}}}}{{\partial {v_{ji}}}}\\ \;\;\;\;\;\; = \eta {{y'}_i}\left( {1 - {{y'}_i}} \right)\left( {{y_i} - {{y'}_i}} \right)s\left( {{\alpha _j}} \right) \end{array} $ | (8) |
| $ {v_{ji}} \leftarrow {v_{ji}} + \Delta {y_{ji}} $ | (9) |
式中η是神经网络学习率在(0,1)间的取值。同理,其他权重系数都可通过上述反向传播过程得到。
1.4 MLP去噪方法特点及优势MLP可逼近任何非线性函数,通过在大量地震数据上进行训练更新式(2)中的θ,从而学习得到一个能表征复杂映射关系的多层网络结构。
作为传统的地震去噪方法,曲波变换虽然能对地震信号有较强的稀疏表示能力,但用单一的固定基难以对不同的地震信号进行最优表征。与其相比,MLP是一种数据驱动的地震去噪方法,它可根据训练样本提取地震信号的本质特征,从而自适应地对地震信号进行表征。
2 实验设置 2.1 数据集划分和标记选择SEG(勘探地球物理学家协会)官网提供的地震数据集,其中包含二维数据和三维数据。
针对三维地震数据,将其沿剖面展开为多个二维数据。因相邻三道地震信号有很强的相似性,每隔三道选取一组二维数据[24]。为了降低地震数据类型对网络泛化能力的影响,本文使用同一方式生成训练集、测试集和验证集数据,且陆地和海洋地震数据的占比相同。考虑到神经网络对噪声类型不敏感,向不含噪的三种数据集掺入随机噪声和脉冲噪声作为样本标签,含此两种噪声的样本各占50%。
2.2 数据预处理不同地震数据的取值范围不同,应在输入网络前对其进行归一化以消除相关影响。网络的输入神经元个数是确定的,需对不同道集和不同采样时间的地震数据进行分割或零值填充。
2.3 超参数超参数是网络训练前设置的参数,包括隐层层数、神经元个数和学习率等。超参数对训练结果有很大影响,如学习率的不同会改变网络收敛速度。本文构建模型的隐层个数按照Burger等[19]的方法设置,其他参数据验证集误差手动调节(表 1)。
|
|
表 1 模型参数 |
在网络训练过程中,验证集用于调整超参数。根据不同模型在验证集上的表现决定所要选择的超参数;同时,验证集也用于监控模型是否发生“过拟合”。据图 2所示误差曲线可评估所构建模型是否处于“过拟合”或“欠拟合”。
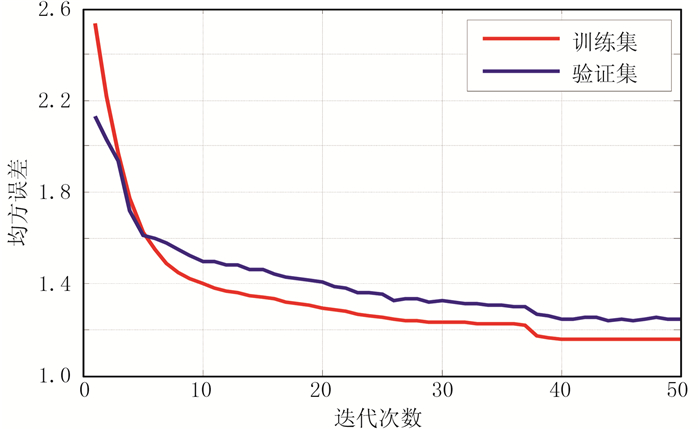
|
图 2 验证集和训练集的均方误差随迭代次数的变化 |
从图 2可见:训练集和验证集的误差曲线总体上随迭代次数增加呈下降趋势;前6次迭代误差曲线的下降速度很快,之后下降速度逐渐减小;在第37次迭代又出现了一次较明显下降,此后随迭代次数的继续增加误差趋于不变,此时训练集和验证集上各自的相对误差都很低,且这二者十分接近,表明模型具有较好的泛化能力。
3 模型数据测试选取已训练好的MLP模型对合成数据进行去噪,所含噪声为高斯白噪声。作为对比,同时采用曲波变换法做去噪处理。以通用的信噪比表征法评判MLP方法的去噪效果
| $ {R_{{\rm{s}}/{\rm{N}}}} = 10 \times \lg \frac{{\left\| \mathit{\boldsymbol{y}} \right\|_{\rm{F}}^2}}{{\left\| {\mathit{\boldsymbol{y - y'}}} \right\|_{\rm{F}}^2}} $ | (10) |
式中RS/N为信号与噪声强度的比值(dB),此处y和y′分别指原始的和去噪后地震数据。
3.1 MLP对高斯白噪声的压制图 3a为均匀背景中嵌入一个正方形的简单模型:背景区域尺寸为256×256,其数据值为10;正方形尺寸为100×100,其数据值为100。在相应的频率—波数域图像(图 3d)上,发现其能量主要集中为“十字型”。但在加入随机噪声后(图 3b,信噪比为6.3dB)的频率—波数域分布上,部分频率—波数域信息被随机噪声混杂而难以识别(图 3e),特别是能量相对较弱的“十字型”末端,几乎无法分辨。在采用MLP去噪后的时间域(图 3c)和频率域(图 3f)图像上,随机噪声得到较好压制,在噪声与有效信号难以分辨处也取得很好效果。
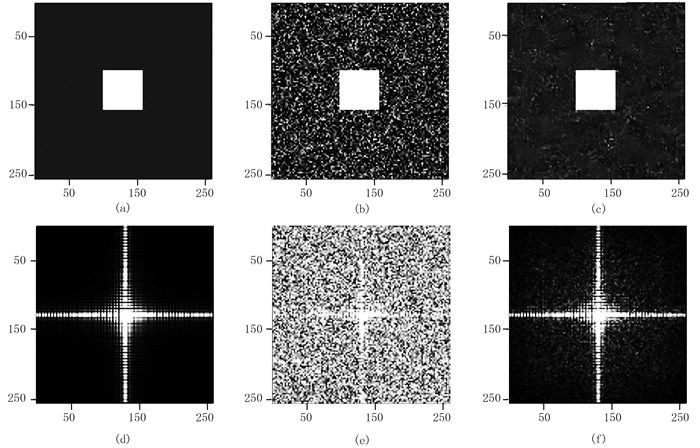
|
图 3 MLP去噪效果 (a)原始数据时间—空间域显示;(b)含噪数据时间—空间域显示(RS/N=6.3dB);(c)MLP去噪后时间—空间域显示(RS/N=21.43dB) (d)原始数据频率—波数域显示;(e)含噪数据频率—波数域显示(RS/N=6.3dB);(f)MLP去噪后频率—波数域显示(RS/N=21.43dB) |
图 4a所示原始地震数据共有100道,采样点数为512,采样率为1ms,图中构造复杂区(能量集中)位置用红框做了标示。向该数据加入高斯白噪声(图 4b),其信噪比变为4.25dB。对该含噪数据做曲波去噪处理(图 4c),所得结果与含噪数据差值(图 4d)的信噪比为8.22dB,比原含噪数据提高了3.97dB。但可见部分复杂构造区依旧存在噪声,尤其在图 4d红框标示处明显残存一些有效信号(将部分信号当作噪声滤除),因此曲波方法去噪效果欠佳。采用MLP去噪后(图 4e)的信噪比增至12.62dB,显然MLP方法对噪声去除得更彻底,对构造细节的保护也更强,整体上与原始信号更接近。

|
图 4 合成数据去噪结果 (a)合成数据;(b)含噪数据(RS/N=4.25dB);(c)曲波去噪结果(RS/N=8.22dB);(d)曲波去噪结果与含噪数据差值;(e)MLP去噪结果(RS/N=12.62dB);(f)MLP去噪结果与含噪数据差值 |
针对原始合成数据加入强度分别为1,2,…,7dB的噪声,计算不同强度噪声下去噪结果的信噪比(图 5)。可见两种方法去噪结果的信噪比都随含噪数据信噪比的增大而增大,其中MLP去噪效果明显好于曲波法,在3~5dB范围信噪比差值达到最大,且在强噪声下MLP方法仍能取得很好效果,表明该方法在不同噪声强度下去噪效果稳定。
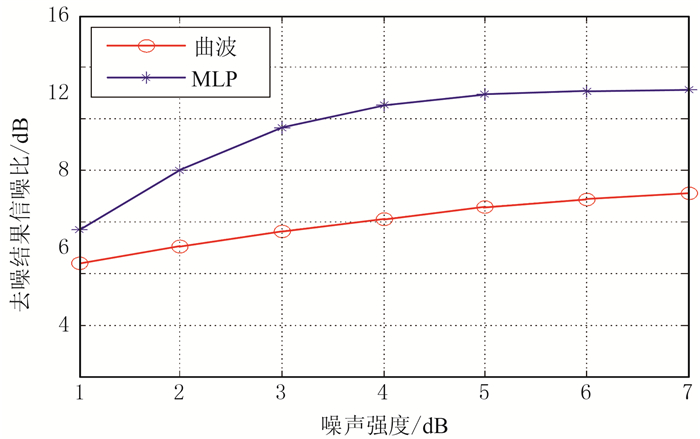
|
图 5 合成数据去噪结果信噪比随噪声强度的变化 |
图 6a所示的陆地地震数据共有128道,每道采样点为256个。相比于合成数据,其构造更复杂,存在较多断点;对其加入高斯白噪声后(图 6b),信噪比为4.05dB。采用曲波去噪后(图 6c)虽较好地重构了有效信号,但在红框标示的同相轴顶部仍存在较多噪声(图 6d),难以有效识别周围数据。而采用MLP方法在压制噪声(图 6e)的同时,同相轴的轮廓更清晰,断点附近的构造细节也得到了很好保护,如在红框标示区更易识别同相轴边界(图 6f)。

|
图 6 陆地地震数据去噪结果 (a)陆地地震数据;(b)含噪数据(RS/N=4.05dB);(c)曲波去噪结果(RS/N=7.18 dB);(d)曲波去噪结果与含噪数据差值;(e)MLP去噪结果(RS/N=10.50dB);(f)MLP去噪结果与含噪数据差值 |
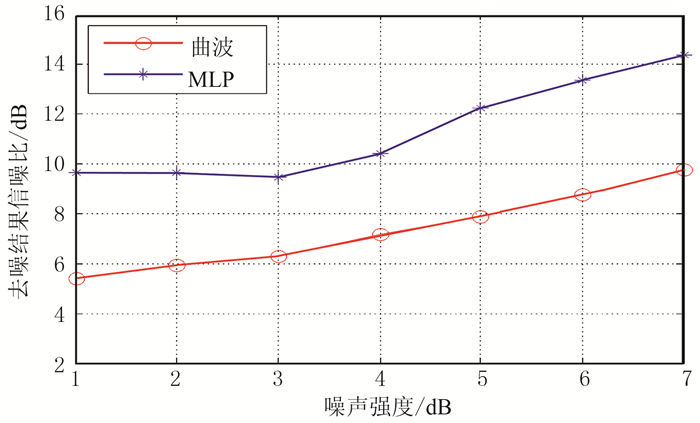
图 7是不同噪声强度下陆地地震数据去噪后的信噪比折线图。可见当处理存在较多复杂构造的数据时,MLP方法去噪结果的信噪比明显高于曲波法,虽然在1~3dB范围MLP方法去噪效果未明显改善,但仍比曲波好。
|
图 7 陆地数据去噪结果信噪比随噪声强度的变化 |
图 8a为原始海洋数据的灰度显示,共有128道,采样点数为256,采样率为1ms。相比于陆地数据,其纹理结构简单且多为直线。加入噪声后(图 8b),其信噪比为3.19dB,噪声使得部分纹理不清晰,对一些能量弱的同相轴已无法分辨。

|
图 8 海洋地震数据去噪结果 (a)原始海洋地震数据;(b)含噪数据(RS/N=3.19dB);(c)曲波去噪结果(RS/N=9.51dB);(d)曲波去噪结果与含噪数据差值;(e)MLP去噪结果(RS/N=13.63dB);(f)MLP去噪结果与含噪数据差值 |
从曲波法(图 8c)和MLP(图 8e)去噪结果看,对于能量较强的同相轴,两种方法都取得了较好去噪效果。但对红框标示的能量较弱的同相轴而言,曲波法未能很好地重构这些数据,从差值(图 8d)也可见曲波法去噪后仍存有较多噪声,甚至一些有效信号也被压制;MLP去噪结果(图 8e)展示了更清晰的地层结构,同相轴连续性更好,其差值(图 8f)显示去噪彻底、干净。
图 9展示了不同噪声强度下海洋数据的信噪比折线图。显然MLP方法去噪结果的信噪比高于曲波法,且与前面合成数据(图 5)和陆地地震数据(图 7)的去噪结果显示类似,两种方法的去噪结果的信噪比与含噪数据的信噪比呈正相关。

|
图 9 海洋数据去噪结果信噪比随噪声强度的变化 |
前面主要介绍了MLP方法对高斯白噪声的去噪效果,但考虑到实际地震数据中存在多种类型噪声,这里以脉冲噪声为例进一步验证MLP方法对非高斯类噪声的压制能力。
图 10所示的地震数据共有100道,采样点为256个,主要由三个较强能量的同相轴组成。加入脉冲噪声后地震数据(图 10b)的信噪比为10.65dB。从其曲波法去噪结果(图 10c)上可见仍存在很多脉冲噪声,去噪效果显然不理想;采用MLP方法去噪后(图 10d),很好地压制了脉冲噪声,三个同相轴的边界很清晰,且其能量几乎未被减弱,信噪比增至21.01dB。

|
图 10 脉冲噪声去噪结果 (a)原始模拟数据;(b)加噪数据(RS/N=10.65dB);(c)曲波去噪结果(RS/N=12.38dB);(d)MLP去噪结果(RS/N=21.01dB) |
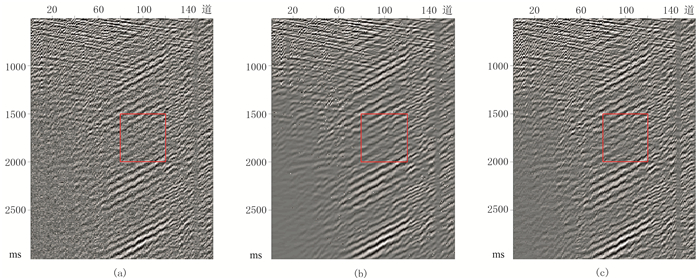
针对M地区实际陆地地震数据进行测试。截取的部分实测地震数据(图 11a)共有160道,采样点为2500个,可见其中含有较强随机噪声,能量较弱的有效信号被压制。
|
图 11 实际地震数据去噪结果 (a)原始数据;(b)曲波去噪结果;(c)MLP去噪结果 |
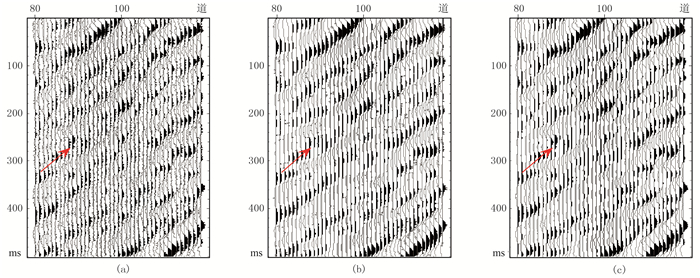
为了更好地对比曲波(图 11b)和MLP(图 11c)的去噪效果,对图中红框标示区域进行放大,并绘制了如图 12所示的波形变面积图。发现曲波和MLP去噪方法都削弱了噪声影响,但曲波法去噪结果中仍残留较多随机噪声,影响了对部分弱地震信号的识别(图 12b),去噪效果欠佳;而MLP方法对随机噪声的压制更彻底,且更充分地保护了能量弱的地震信号(图 12c红色箭头所示)。
|
图 12 实测数据波形变面积图 (a)原始数据;(b)曲波去噪波形变面积图;(c)MLP去噪波形变面积图 |
本文主要介绍了基于MLP的去噪方法,针对不同类型(含噪)地震数据对比分析了MLP方法的去噪能力,得到了如下结论:相比于曲波变换法,MLP方法在压制噪声的同时能有效保护原始数据,对一些构造复杂区域能实现很好地重构;对不同信噪比数据,MLP方法处理效果更稳定,且对脉冲噪声等非高斯类噪声也有较好压制效果。
尽管MLP方法已取得较好去噪效果,但本文仅对高斯噪声和非高斯脉冲噪声进行了处理,而对地震信号中其他噪声,如有色噪声和时空变随机噪声等,未做相关研究和去噪处理,不能预判MLP方法的效果。因此,今后将致力于对实际地震数据中存在的其他各类噪声的压制。
| [1] |
张军华, 吕宁, 田连玉, 等. 地震资料去噪方法技术综合评述[J]. 地球物理学进展, 2006, 21(2): 546-553. ZHANG Junhua, LYU Ning, TIAN Lianyu, et al. An overview of the methods and techniques for seismic data noise attenuation[J]. Progress in Geophysics, 2006, 21(2): 546-553. DOI:10.3969/j.issn.1004-2903.2006.02.033 |
| [2] |
张良, 韩立国, 许德鑫, 等. 基于压缩感知技术的Shearlet变换重建地震数据[J]. 石油地球物理勘探, 2017, 52(2): 220-225. ZHANG Liang, HAN Liguo, XU Dexin, et al. Seismic data reconstruction with Shearlet transform based on compressed sensing technology[J]. Oil Geophysical Prospecting, 2017, 52(2): 220-225. |
| [3] |
Tang G, Ma J, Yang H. Seismic data denoising based on learning-type over complete dictionaries[J]. App-lied Geophysics, 2012, 9(1): 27-32. DOI:10.1007/s11770-012-0310-z |
| [4] |
徐彦凯, 曹思远, 潘晓, 等. 随机噪声的局部正交压制方法[J]. 石油地球物理勘探, 2019, 54(2): 280-287. XU Yankai, CAO Siyuan, PAN Xiao, et al. A local orthogonalization for seismic random noise suppression[J]. Oil Geophysical Prospecting, 2019, 54(2): 280-287. |
| [5] |
乐友喜, 杨涛, 曾贤德. CEEMD与KSVD字典训练相结合的去噪方法[J]. 石油地球物理勘探, 2019, 54(4): 729-736. YUE Youxi, YANG Tao, ZENG Xiande. Seismic denoising with CEEMD and KSVD dictionary combined training[J]. Oil Geophysical Prospecting, 2019, 54(4): 729-736. |
| [6] |
章珂, 刘贵忠, 邹大文, 等. 二进小波变换方法的地震信号分时分频去噪处理[J]. 地球物理学报, 1996, 39(2): 265-271. ZHANG Ke, LIU Guizhong, ZOU Dawen, et al. Seismic data time-frequency domain denoising based on dyadic wavelet transform[J]. Chinese Journal of Geophysics, 1996, 39(2): 265-271. DOI:10.3321/j.issn:0001-5733.1996.02.013 |
| [7] |
张旭东, 詹毅, 马永琴. 不同信号的小波变换去噪方法[J]. 石油地球物理勘探, 2007, 42(增刊): 118-123. ZHANG Xudong, ZHAN Yi, MA Yongqin. Approaches of denoise by wavelet ferent signals[J]. Oil Geophysical Prospecting, 2007, 42(S): 118-123. |
| [8] |
张华, 陈小宏, 李红星, 等. 曲波变换三维地震数据去噪技术[J]. 石油地球物理勘探, 2017, 52(2): 226-232. ZHANG Hua, CHEN Xiaohong, LI Hongxing, et al. 3D seismic data de-noising approach based on Curvelet transform[J]. Oil Geophysical Prospecting, 2017, 52(2): 226-232. |
| [9] |
Hennenfent G, Herrmann F J. Seismic denoising with nonuniformly sampled curvelets[J]. Computing in Science and Engineering, 2006, 8(3): 16-25. DOI:10.1109/MCSE.2006.49 |
| [10] |
Neelamani R, Baumstein A, Gillard D G, et al. Cohe-rent and random noise attenuation using the curvelet transform[J]. The Leading Edge, 2008, 27(2): 240-248. DOI:10.1190/1.2840373 |
| [11] |
邹梦, 冯民富, 张华, 等. 三维叠前相干干扰的正交多项式拟合压制方法[J]. 石油地球物理勘探, 2014, 49(3): 475-479. ZOU Meng, FENG Minfu, ZHANG Hua, et al. 3D pre-stack coherent noise suppression with orthogonal polynomial fitting[J]. Oil Geophysical Prospecting, 2014, 49(3): 475-479. |
| [12] |
杨云飞, 王华忠, 曹景忠. 正交多项式逼近去白噪[J]. 石油地球物理勘探, 2001, 36(6): 704-706. YANG Yunfei, WANG Huazhong, CAO Jingzhong. Using orthogonal polynomials for eliminating white noise[J]. Oil Geophysical Prospecting, 2001, 36(6): 704-706. DOI:10.3321/j.issn:1000-7210.2001.06.007 |
| [13] |
Lore K G, Akintayo A, Sarkar S, et al. LLNet:A deep auto encoder approach to natural low-light image enhancement[J]. Pattern Recognition, 2017, 61(1): 650-662. |
| [14] |
Xu L, Ren J S, Liu C, et al.Deep convolutional neural network for image deconvolution[C].Neural Information Processing Systems, 2014: 1790-1798.
|
| [15] |
Lee H, Kwon H. Going deeper with contextual CNN for hyperspectral image classification[J]. IEEE Transactions on Image Processing, 2017, 26(10): 4843-4855. DOI:10.1109/TIP.2017.2725580 |
| [16] |
Russakovsky O, Deng J, Su H, et al. Image net large scale visual recognition challenge[J]. International Journal of Computer Vision, 2015, 115(3): 211-252. DOI:10.1007/s11263-015-0816-y |
| [17] |
Jain V, Seung H S.Natural image denoising with convolutional networks[C].Neural Information Proce-ssing Systems, 2008, 769-776.
|
| [18] |
Xie J, Xu L, Chen E, et al.Image denoising and inpainting with deep neural networks[C].Neural Information Processing Systems, 2012, 341-349.
|
| [19] |
Burger H C, Schuler C J, Harmeling S, et al.Image denoising: Can plain neural networks compete with BM3D?[C].Computer Vision and Pattern Recognition, 2012, 2392-2399.
|
| [20] |
Roth G, Tarantola A. Neural networks and inversion of seismic data[J]. Journal of Geophysical Research, 1994, 99(B4): 6753-6768. DOI:10.1029/93JB01563 |
| [21] |
Nath S K, Chakraborty S, Singh S K, et al. Velocity inversion in cross-hole seismic tomography bycounter-propagation neural network, genetic algorithm and evolutionary programming techniques[J]. Geophysical Journal International, 1999, 138(1): 108-124. DOI:10.1046/j.1365-246x.1999.00835.x |
| [22] |
赵明, 陈石, Dave Yuen. 基于深度学习卷积神经网络的地震波形自动分类与识别[J]. 地球物理学报, 2019, 62(1): 374-382. ZHAO Ming, CHEN Shi, Dave Yuen. Waveform classification and seismic recognition by convolution neural network[J]. Chinese Journal of Geophysics, 2019, 62(1): 374-382. |
| [23] |
Basheer I A, Hajmeer M N. Artificial neural networks:fundamentals, computing, design, and application[J]. Journal of Microbiological Methods, 2000, 43(1): 3-31. DOI:10.1016/S0167-7012(00)00201-3 |
| [24] |
张银雪, 田学民. 基于改进PSO-ICA的地震信号去噪方法[J]. 石油地球物理勘探, 2012, 47(1): 56-62. ZHANG Yinxue, TIAN Xuemin. Seismic denoising based on the modified particle swarm optimization-independent component analysis[J]. Oil Geophysical Prospecting, 2012, 47(1): 56-62. |



 汤井田, 湖南省长沙市岳麓区麓山南路932号中南大学地球科学与信息物理学院应用地球物理系, 410083。Email:
汤井田, 湖南省长沙市岳麓区麓山南路932号中南大学地球科学与信息物理学院应用地球物理系, 410083。Email: