在常规地震数据处理中,要求震源和检波器的位置固定,只有这样才能进行共中心点叠加、速度分析、偏移等处理步骤[1-2]。但是在海洋拖缆地震数据采集中,为了保持拖缆平直,采集船必须以一定的航速持续航行,因此拖缆上的检波器(水听器)在数据采集过程中一直是运动的,不满足常规地震数据处理要求。检波器位置的移动会造成地震反射旅行时误差,影响后续地震数据处理的可靠性,同时降低时移地震资料匹配精度[3]。
针对检波器移动对地震数据的影响[4],人们进行了大量研究。William[5]指出,海上可控震源的移动会引起地震数据的相位扭曲(多普勒效应),提出利用F-K滤波消除相位差异;Schultz等[6]通过坐标变换校正震源和检波器移动引起的地震数据相位变化;Gary等[7]论述了震源和检波器移动对海上可控震源采集数据的影响,并提出利用时差校正消除检波器移动的影响,利用反褶积消除震源移动影响的方法。Jan[8]提出了一种校正检波器移动效应的时变方法。薛东川等[9]采用地震数据空间插值消除检波器移动引起的位置变化,并在四维地震勘探数据中进行了验证。
本文研究了拖缆采集中检波器位置变化对反射旅行时的影响,提出利用炮检距、船速和叠加速度计算检波器移动造成的旅行时误差及其校正方法,并进行了误差分析及实际数据验证。
1 检波器移动校正原理 1.1 原理海上利用拖缆采集地震数据时,当震源激发后检波器不是固定的,而是随着拖缆一直在运动,会引起反射旅行时误差,在地震数据处理中需要校正这种误差。
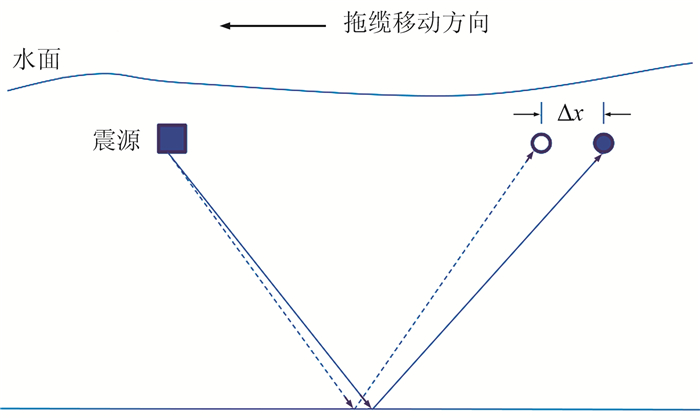
当缆前放炮时,检波器发生移动,检波器移动水平距离为(图 1)
| $ \Delta x = {v_{\rm{B}}}t $ | (1) |
|
图 1 缆前放炮检波器移动时差校正示意图 检波器从实心圆圈处移动到空心圆圈处,虚线为波场传播的实际路径, 实线为波场传播的理论路径 |
式中:vB为拖缆船航行速度;t为地震反射旅行时。
由于
| $ \sin \theta = \frac{{\Delta r}}{{\Delta x}} = \frac{{{v_{\rm{W}}}\Delta t}}{{{v_{\rm{B}}}t}} $ | (2) |
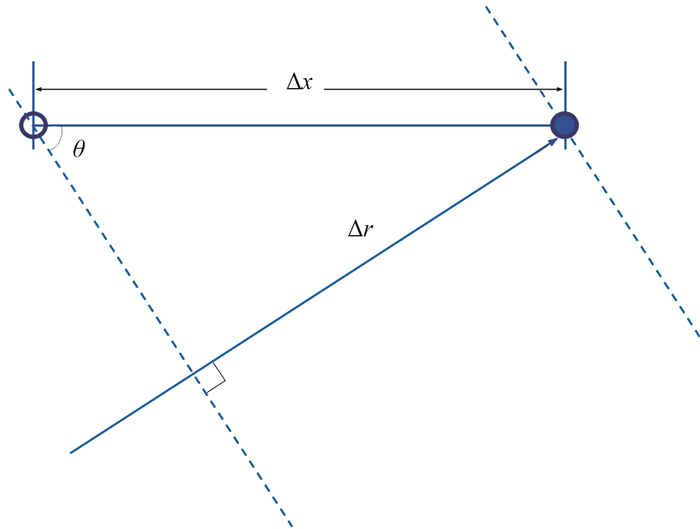
则检波器移动造成的旅行时误差为(图 2)
| $ \Delta t = \frac{{{v_{\rm{B}}}}}{{{v_{\rm{W}}}}}t\sin \theta $ | (3) |
|
图 2 缆前放炮检波器移动时差计算示意图 虚线为不同时刻的波前面。地震波传播距离误差为Δr=vWΔt,Δt为检波器移动造成的旅行时误差 |
式中vW为地震波在水中的传播速度。在实际勘探中,由于船速vB远小于地下介质的叠加速度v,则Δx远小于地震波传播距离、Δt远小于地震波旅行时t,因此式(2)的微分形式为
| $ \sin \theta = {v_{\rm{W}}}\frac{{{\rm{d}}t}}{{{\rm{d}}x}} $ | (4) |
地震反射波旅行时公式[10]为
| $ t = {\left[ {t_0^2 + {{\left( {\frac{x}{v}} \right)}^2}} \right]^{\frac{1}{2}}} $ | (5) |
式中:x为炮检距;t0为零炮检距处自激自收时间。
式(5)对x求导,得
| $ \frac{{{\rm{d}}t}}{{{\rm{d}}x}} = \frac{1}{2}{\left[ {t_0^2 + {{\left( {\frac{x}{v}} \right)}^2}} \right]^{ - \frac{1}{2}}}2\frac{x}{{{v^2}}} = \frac{x}{{t{v^2}}} $ | (6) |
把式(6)和式(4)代入式(3),得
| $ \Delta t = \frac{{{v_{\rm{B}}}x}}{{{v^2}}} $ | (7) |
设原始记录时间为t1,校正后时间为t2,则检波器移动校正旅行时为
| $ {t_2} = {t_1} + \Delta t $ | (8) |
同理,可得到缆后放炮检波器移动校正旅行时为
| $ {t_2} = {t_1} - \Delta t $ | (9) |
从式(7)可以看出,检波器移动引起的旅行时误差Δt是时变的,与vB和x成正比,与v2成反比。在拖缆地震数据采集中,vB和x为已知,只有v与地下介质有关。对于水平层状介质,v等于均方根速度;对于单一倾斜地层,v等于地层介质速度除以地层倾角的余弦[11];对于复杂的实际地下介质,通过速度分析获得v。
一般情况下,vB恒定,v随着t增大而增大(不考虑速度反转)。由式(7)可知,随着t增大,Δt减小,因此在相同x的情况下,海底反射波的校正时差最大。
1.2 误差分析由于上述公式采用特定假设条件,导致旅行时计算结果与精确值存在误差。随着检波器移动,地震波传播距离变小(图 1),则
| $ t_2^2 = t_0^2 + \frac{{{x^2}}}{{{v^2}}} $ | (10) |
| $ t_1^2 = t_0^2 + \frac{{{{\left( {x - \Delta x} \right)}^2}}}{{{v^2}}} $ | (11) |
在Δx小于一个CMP间距的情况下,可以认为式(10)与式(11)的叠加速度相同,则
| $ t_2^2 - t_1^2 = \frac{{{x^2}}}{{{v^2}}} - \frac{{{{\left( {x - \Delta x} \right)}^2}}}{{{v^2}}} $ | (12) |
即
| $ \left( {{t_2} + {t_1}} \right)\Delta t = \frac{1}{{{v^2}}}\left[ {{x^2} - {{\left( {x - \Delta x} \right)}^2}} \right] $ | (13) |
整理后得到
| $ \Delta t = \frac{1}{{{v^2}\left( {2{t_1} + \Delta t} \right)}}\left[ {2x\Delta x - {{\left( {\Delta x} \right)}^2}} \right] $ | (14) |
即
| $ {v^2}{\left( {\Delta t} \right)^2} + 2{t_1}{v^2}\Delta t + \left[ {{{\left( {\Delta x} \right)}^2} - 2x\Delta x} \right] = 0 $ | (15) |
解式(15),得
| $ \Delta t = \frac{{\sqrt {t_1^2{v^2} + 2x{v_{\rm{B}}}{t_1} - v_{\rm{B}}^2t_1^2} }}{v} - {t_1} $ | (16) |
理论上,存在Δt≤0的情况,即当
| $ \Delta t = \sqrt {t_1^2 + \frac{{2x{v_{\rm{B}}}{t_1}}}{{{v^2}}} - {{\left( {\frac{{{v_{\rm{B}}}}}{v}} \right)}^2}t_1^2} - {t_1} $ | (17) |
在实际地震勘探中,由于vB≪v,则
| $ \Delta t = {t_1}\sqrt {1 + \frac{{2x{v_{\rm{B}}}}}{{{v^2}{t_1}}}} - {t_1} $ | (18) |
将式(18)利用泰勒级数展开,并略去高阶项得到
| $ \Delta t = {t_1}\left( {1 + \frac{{x{v_{\rm{B}}}}}{{{v^2}{t_1}}}} \right) - {t_1} $ | (19) |
整理后得到
| $ \Delta t = \frac{{{v_{\rm{B}}}x}}{{{v^2}}} $ | (20) |
式(7)与式(20)相同,说明式(7)是式(16)的近似。下面分析式(7)(相对于式(16))计算结果的相对误差。
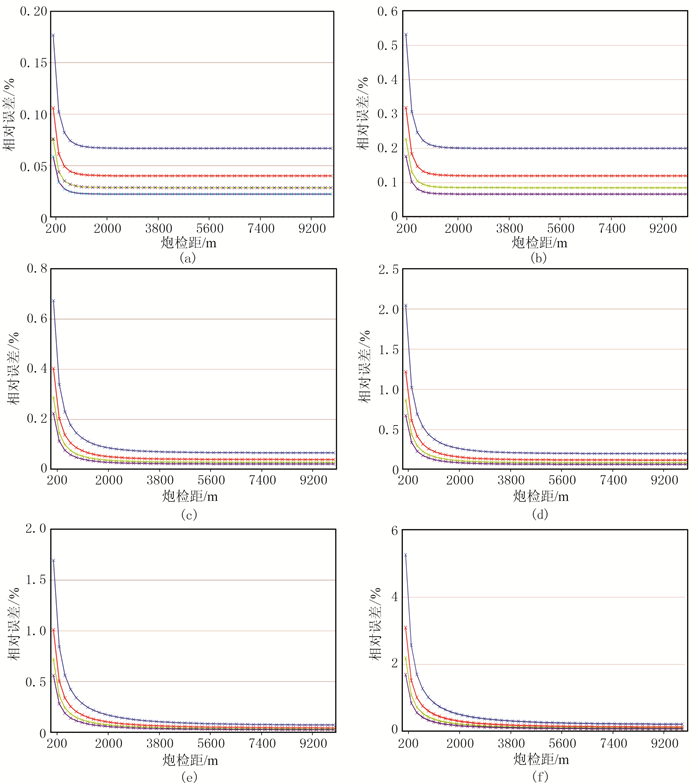
图 3为不同深度、船速、叠加速度的校正时差相对误差随炮检距变化曲线。由图可见:①在相同深度和船速情况下,校正时差相对误差随介质叠加速度增大、炮检距增大而减小,并且在近炮检距处,随着炮检距增大校正时差相对误差急剧变小,随后变化非常微小;在相同深度、相同介质叠加速度、相同炮检距情况下,校正时差相对误差随船速增大而增大;在相同船速、相同介质叠加速度、相同炮检距情况下,校正时差相对误差随深度增大而增大。②在海底深度达到5000m时,只要适当控制船速(图 3e),校正时差相对误差也很小(小于2%),满足常规地震数据处理要求,而式(7)的计算量和计算复杂度远低于式(16),因此采用式(7)可以大大提高检波器移动时差计算效率。
|
图 3 不同深度、船速、叠加速度的校正时差相对误差随炮检距变化曲线 (a)深度500m、船速1m/s;(b)深度500m、船速3m/s;(c)深度2000m、船速1m/s;(d)深度2000m、船速3m/s;(e)深度5000m、船速1m/s;(f)深度5000m、船速3m/s。蓝色、红色、绿色和紫色曲线分别对应叠加速度为1500、2500、3500和4500m/s |
对MD地区海洋拖缆资料进行试验,采用缆前放炮,拖缆船移动速度为2m/s,最大炮检距为10000m,地震波在海水中的传播速度为1500m/s。
图 4为检波器移动校正前、后炮集及其远炮检距数据放大显示。由图可见,经检波器移动校正后,随着旅行时增加,检波器移动造成的影响被消除(图 4b),尤其是在远炮检距处校正时差接近9ms(图 4d红色箭头处)。

|
图 4 检波器移动校正前(a)、后(b)炮集及其远炮检距数据放大显示(c、d) |
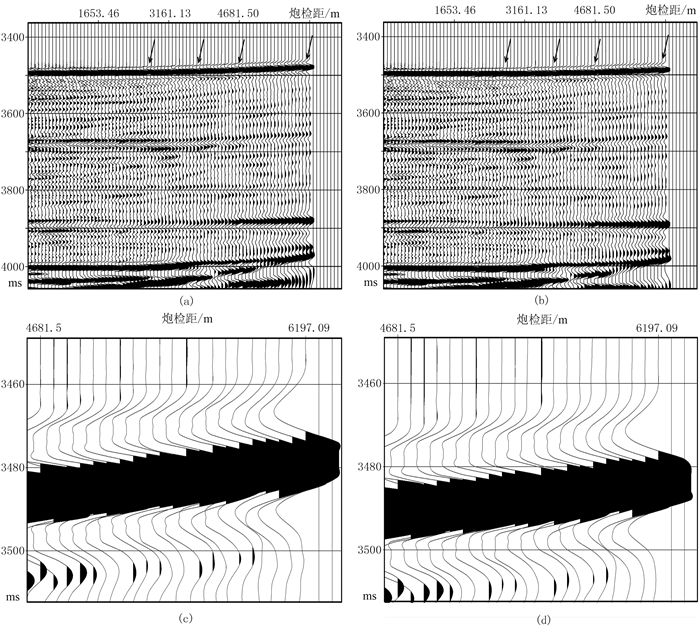
图 5为检波器移动校正前、后的动校正CMP道集及其远炮检距数据放大显示。由图可见,经检波器移动校正后,随旅行时增加,在相同叠加速度的情况下明显减弱了过校正现象(图 5b箭头处),在远炮检距数据处非常明显(图 5d),这也有利于速度分析。
|
图 5 检波器移动校正前(a)、后(b)的动校正CMP道集及其远炮检距数据放大显示(c、d) |
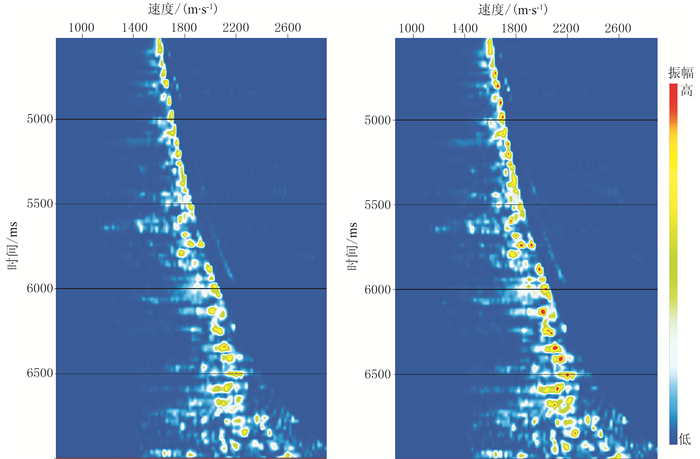
图 6为检波器移动校正前、后速度谱。由图可见,检波器移动校正后速度谱能量更聚焦(图 6右),利于速度拾取。
|
图 6 检波器移动校正前(左)、后(右)速度谱 |
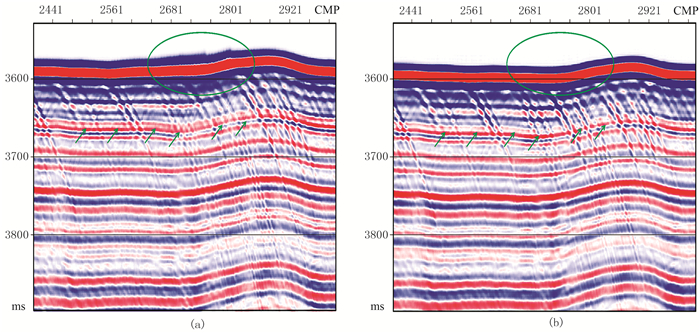
图 7为检波器移动校正前、后叠加剖面。由图可见,检波器移动校正后,海底成像的连续性明显变好(图 7b圆圈处),海底附近的同相轴更清晰(图 7b箭头处)。
|
图 7 检波器移动校正前(a)、后(b)叠加剖面 |
本文提出了一种校正海洋拖缆移动引起的地震反射旅行时误差的方法。由该方法计算的海洋拖缆移动引起的旅行时误差是时变的,与炮检距和船速成正比,与叠加速度的平方成反比。
检波器移动校正能有效消除海洋拖缆移动对地震反射旅行时的影响,明显改善动校正后CMP道集的拉平程度,提高速度谱的聚焦度,为地震数据速度分析、成像提供高质量数据。
| [1] |
渥·伊尔马滋著; 黄绪德, 袁明德译.地震数据处理[M].北京: 石油工业出版社出版, 1994.
|
| [2] |
Zhou Z Z and Ma G K.Phase-driven deghosting of slanted and horizontal streamer data[C].SEG Technical Program Expanded Abstracts, 2016, 35: 4756-4759.
|
| [3] |
Gary H and Helmut J.Effects of source and receiver motion on seismic data[C].SEG Technical Program Expanded Abstracts, 1990, 9: 859-862.
|
| [4] |
Eiken O, Haugen G U, Schonewille M, et al. A proven method for acquiring highly repeatable towed streamer seismic data[J]. Geophysics, 2003, 68(4): 1303-1309. DOI:10.1190/1.1598123 |
| [5] |
William H D. Marine vibrators and the Doppler effect[J]. Geophysics, 1988, 53(11): 1388-1398. DOI:10.1190/1.1442418 |
| [6] |
Schultz P S, Pieprzak A W, Johnson G R, et al.Simple theory for correction of marine vibroseis phase dispersion[C].SEG Technical Program Expanded Abstracts, 1989, 8: 660-662.
|
| [7] |
Gary H , Helmut J. The effects of source and receiver motion on seismic data[J]. Geophysical Prospecting, 1995, 43(2): 221-244. DOI:10.1111/j.1365-2478.1995.tb00133.x |
| [8] |
Jan D.The effects of receiver motion on seismic data and velocity analysis[C].SEG Technical Program Expanded Abstracts, 2001, 20: 1890-1893.
|
| [9] |
薛东川, 朱振宇, 王小六, 等. 海上拖缆采集地震数据接收点位移校正[J]. 石油地球物理勘探, 2017, 52(1): 1-7. XUE Dongchuan, ZHU Zhenyu, WANG Xiaoliu, et al. A receiver motion correction method for streamer data[J]. Oil Geophysical Prospecting, 2017, 52(1): 1-7. |
| [10] |
李振春, 张军华. 地震数据处理方法[M]. 山东东营: 中国石油大学出版社, 2004.
|
| [11] |
陆基孟. 地震勘探原理[M]. 山东东营: 中国石油大学出版社, 2006.
|



 马光凯, 河北省涿州市华阳东路物探科技园物探技术研究中心, 072751。Email:
马光凯, 河北省涿州市华阳东路物探科技园物探技术研究中心, 072751。Email: