“两宽一高”(宽频、宽方位、高密度)地震勘探具有较宽方位角、更强照明度、更高覆盖次数等优势,是现阶段复杂储层、油气藏勘探的有效手段[1],也成为油气地震勘探技术发展的一个重要方向,但因成本高于常规地震采集而限制其广泛应用。压缩感知地震采集是一种高效、经济的地震采集方式,有望较大幅度降低地震采集成本,从而为“两宽一高”地震技术的常规化奠定基础。
压缩感知技术是图像和信号采集、处理领域的一项新技术,它使得信号采集不再受限于经典的奈奎斯特采样定律。通过随机观测,采集一个远小于奈奎斯特的样本就能较好地表征和重构信号[2-3],从而为高效地震采集提供可能。马坚伟[4-6]提出了利用压缩感知技术降低现场采集数据量的思想。陈生昌等[7]、王汉闯等[8]也在理论上进行了压缩感知采集设计相关研究,给出了压缩感知高效地震采集的基本框架。基于陆上工区及配套采集装备,周松等[9]进行了压缩感知采集观测系统设计与数据重构方面卓有成效的研究。吕公河等[10]也将压缩感知采集方法成功地应用于陆上勘探。Charles等[11]、Mosher等[12]和李成博等[13]将压缩感知地震应用于多个实际工区,从不同角度进一步证明了该方法的有效性和经济性。以上研究成果均表明:对于同样的地震采集任务,压缩感知地震在确保采集质量的情况下,耗费更少的采集资源,或在耗费同样采集资源情况下,能获取更多采集信息、更优采集品质。
压缩感知要求随机采样,而随机采样的方式也有若干种,如高斯、伯努利等。这些随机采样方式容易造成采样局部过密或过稀,不利于信号重构。Jitter随机是一种优化的随机方式,它在突出局部随机的同时,又确保了总体上的均匀性[14-15]。本文将Jitter随机采样模式应用于海上压缩感知地震采集观测系统设计,并给出了一套基于压缩感知的地震数据重构方法;利用这套方法开展模型正演和实际数据的海上压缩感知仿真采集设计与处理试验。结果表明:受限于采集硬件而不能完全随机的情况下,基于Jitter模式的海上压缩感知地震采集在节省约三分之一采集资源的前提下亦能取得与常规采集相当的效果。
1 方法原理 1.1 海上压缩感知采集设计由于海上地震采集设备的限制,并不是每个维度上都能进行压缩感知的随机优化设计。例如,在进行海底电缆(OBC)地震采集时,道间距已经被硬件固定,无法实施道间距随机优化。所以,进行海上压缩感知地震采集设计时,要充分考虑现有采集设备的可实现性[16]。
对拖缆而言,道间距固定,无法进行压缩感知设计,而缆间距可以进行随机优化设计,从而以较少的缆达到更多缆的采集效果,但施工时较难控制;对于海底电缆而言,道间距固定,但接收线间距可考虑压缩感知的随机优化设计,以较少的缆达到更多缆的采集效果;对于海底节点(OBN),其道间距和接收线间距都能进行随机优化设计,甚至能实现整个平面上的位置随机优化设计,从而减少投放的OBN数目。
对于震源来说,既可通过压缩感知随机优化设计提高炮间距,提高炮船航速,又能通过压缩感知设计,提高炮线间距,减少炮船航次。
如前所述,任意随机容易出现大范围的空缺或是局部的太密,不利于信号重构。Jitter随机是一种优化的随机方式[14-15],它先将采样点等间隔地分布于待采样空间,然后让样点在一定范围内随机出现,避免了局部太稀或太密现象的出现,因而在随机优化设计时,选用Jitter模式。
Jitter采样的总体思想是将待采样空间按不同维度均匀分成若干段,在每一段内进行采样点位置的随机抖动,保证采样整体的均匀性和局部的随机性。假设信号原本密集采样的样点数为N,Jitter采样点数为n,则Jitter采样因子为γ=N/n。当γ为奇数时,Jitter采样可表达为
| $ y(i) = f(j)\;\;\;\;i = 1, \cdots , n $ | (1) |
式中:y(i)是Jitter第i个采样结果;f是待采集的信号;j=(1-γ)/2+iγ+εi是第i个Jitter样点对应的原始规则密集采样点序号,其中ε是在[-(ξ-1)/2, (ξ-1)/2]区间呈均匀概率分布的整数,且ξ是控制抖动幅度的变量, 满足0≤ξ≤γ, γ控制样点的宏观分布,即控制Jitter采样的宏观平均间隔。当γ为偶数时,表达式略作修改即可。
压缩感知采集设计的基本流程可表述为:①根据先验信息(如已知的构造信息等)建立地下速度模型;②基于该模型和地质信息进行常规采集正演,得到模拟的常规采集数据;③设计Jitter模式随机采样参数,使观测矩阵的不相干性达到最大,正演得到模拟的Jitter随机压缩感知数据;④通过数据重构等评价方式,将压缩感知数据重构结果与常规采集数据对比,对基于Jitter随机的压缩感知观测系统进行评价和迭代更新。
1.2 海上压缩感知地震处理压缩感知数据处理的关键环节在于压缩感知地震数据的重构,即将不规则的压缩感知地震数据重构成为规则的常规地震数据。它不仅能建起压缩感知数据与后续常规处理方法之间的桥梁,而且可将信息反馈给压缩感知采集设计,进而指导压缩感知采集设计。
压缩感知地震数据重构的基本原理是稀疏反演,即L0范数约束下的目标函数求解[17]
| $ {\mathit{\boldsymbol{J}}_{{\rm{min}}}}(\mathit{\boldsymbol{d}}) = \left\| {{\mathit{\boldsymbol{d}}^{{\rm{obs}}}} - \mathit{\boldsymbol{Sd}}} \right\|_2^2 + \mu {\left\| {\mathit{\boldsymbol{Cd}}} \right\|_0} $ | (2) |
式中:d是完整的地震数据,亦即待重构得到的地震数据;S是采样矩阵;dobs是得到的含有缺失道的地震数据,此处为不规则的压缩感知数据,地震数据重构即是由dobs恢复d;‖·‖0表示L0范数;C是某一稀疏变换算子;μ是调节前、后两项权重的参数。
由于该目标函数的求解是非凸优化问题,可通过非凸Lp范数的Hankel矩阵降秩求解[18],也可采用L1范数代替L0范数,采用阈值迭代求解。
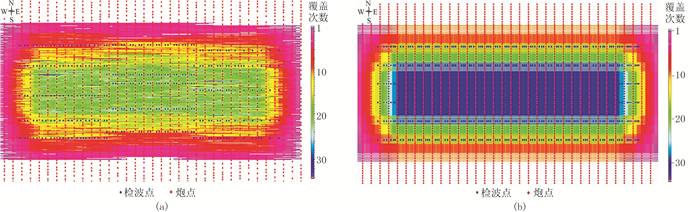
2 模型压缩感知仿真采集设计与处理 2.1 模型的压缩感知采集设计经典的三维逆掩推覆体模型(图 1a)具有复杂的逆掩推覆体、古河道等构造,用于地震勘探方法研究具有较好代表性。其长和宽均为8000m;设计了12个OBC的Patch,其分布如图 1b所示。对12个Patch均采用三维有限差分正演模拟。受限于正演计算量,正演模拟的主频只有20Hz,且炮线间距固定为200m。以Patch 4为例,图 1b中检波点分布于ABCD所在绿色区域,炮点分布于E′F′G′H′所在红色区域(图 1b)。

|
图 1 地震正演模拟及压缩感知观测系统 (a)推覆体速度模型;(b)OBC采集12个Patch分布图;(c)Patch 4压缩感知数据的炮、检点及覆盖次数分布图 |
基于上述地质模型,进行了常规采集观测系统设计,具体参数如表 1所示。利用常规采集观测系统进行正演,得到了常规采集地震数据。然后采用Jitter随机优化模式,设计了压缩感知采集观测系统(表 1),正演模拟基于Jitter随机的压缩感知数据。
|
|
表 1 主要采集参数对比表 |
理论上,炮点间距、道间距、炮线间距、接收线间距都能进行Jitter随机优化设计。但考虑到OBC硬件限制,且受限于正演模拟时炮线间距固定为200m,道间距和炮线间距都未采用随机优化设计。本文仅对炮点间距、接收线间距进行了Jitter随机优化设计。即便如此,压缩感知采集资源仍比常规采集约节省33%。本文“采集资源量”是指采集施工现场必须的炮点、检波点、炮线、检波线总量,即意味着炮船航速、OBN投点、炮船航次或OBC布缆条数等。从Patch 4的压缩感知数据炮点、检波点和覆盖次数分布图(图 1c)可看出,该观测系统局部是不规则、不均匀的,但整体上是较均匀的。
2.2 模型数据的压缩感知处理对压缩感知地震数据进行处理,关键环节是对其进行重构,恢复出常规规则采集的地震数据。
数据重构方法有多种,彭佳明等[19]对这些方法的特点进行了总结。采用傅里叶变换作为稀疏变换,是压缩感知地震数据重构的一种常用办法[20-21]。这种方法效率虽高,但处理数据时有一难点,即针对弯曲同相轴需要开窗口[22],以使窗内数据同相轴近似为直线。当窗口太大时,同相轴线性性质欠佳,重构精度不足;而窗口太小时,参与变换的样点数少,同样带来误差。对此,采用先道集拉平,重构后再反拉平的办法。这既能显著增强同相轴的线性性质,又能减小轴的倾角,有利于压制假频。
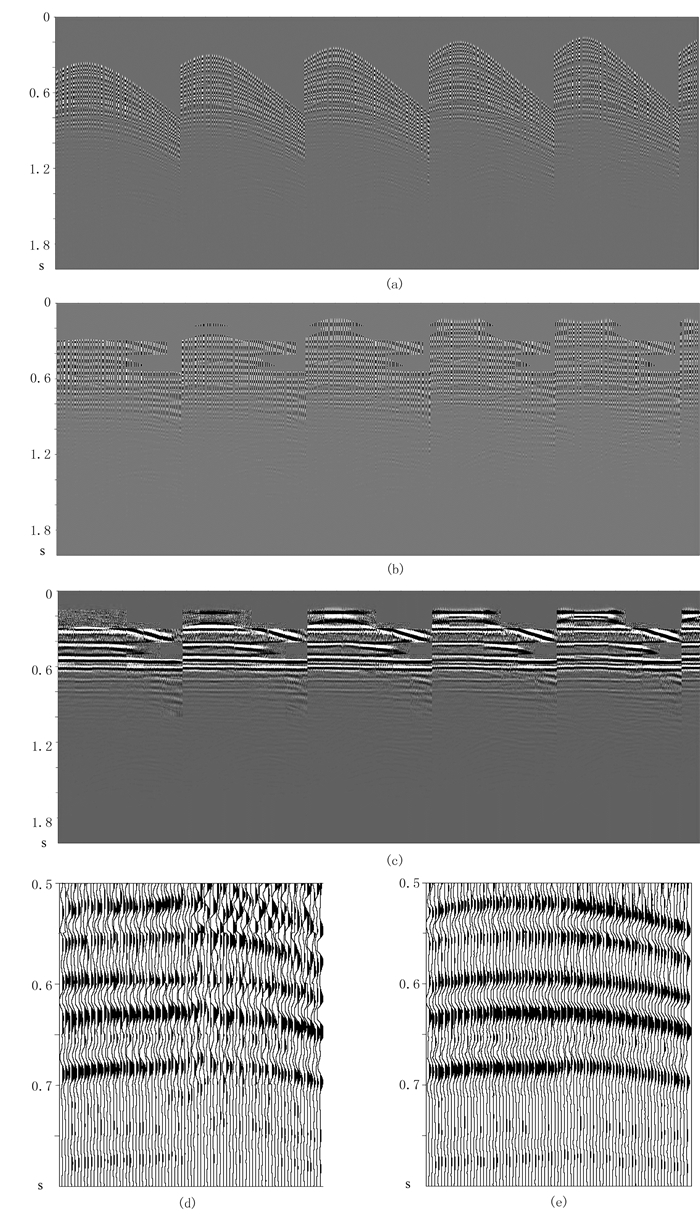
对以Jitter采样模式置入空道的压缩感知地震道集(图 2a)做拉平处理,得到图 2b所示的拉平后道集,随后对其做重构处理(图 2c);图 2d是未做拉平处理就做重构所得道集的局部放大,再对拉平后重构道集(图 2c)做反拉平,得到其局部放大道集(图 2e)。可见拉平后地震数据重构效果更好。
|
图 2 道集及其放大显示的对比 (a)置入空道后的压缩感知道集;(b)拉平处理后的压缩感知道集;(c)拉平后再进行重构的道集;(d)未做拉平就进行重构所得道集的局部放大;(e)拉平后进行重构所得道集反拉平后的局部放大 |
图 3a是Patch 3~Patch5的Jitter随机压缩感知地震数据炮点、检波点和覆盖次数分布图,可见炮点、检波点和覆盖次数在整体均匀的前提下都存在一定的局部不均匀性。对比经压缩感知地震数据重构后的炮点、检波点和覆盖次数分布图(图 3b),可见压缩感知重构后,其整体和局部都变得很均匀。
|
图 3 Patch3~Patch5地震数据的炮点、检波点和覆盖次数分布图 (a)压缩感知数据;(b)压缩感知数据重构后 |
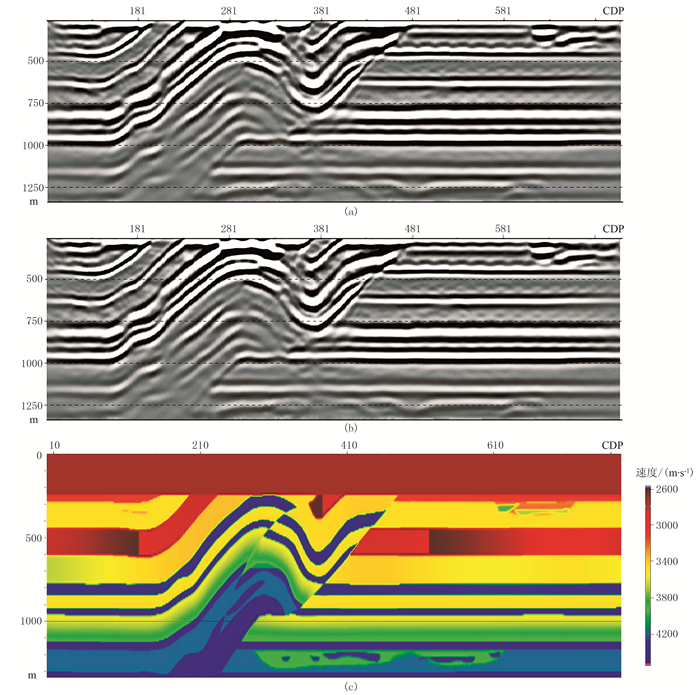
对比常规采集数据(图 4a)、Jitter随机压缩感知采集数据重构后(图 4b)的克希霍夫叠前深度偏移成像结果及对应的速度剖面(图 4c),可见在节省约1/3采集资源情况下,Jitter随机压缩感知采集数据经处理后能达到与常规采集相当的效果。
|
图 4 常规采集与压缩感知采集数据的成像效果对比 (a)Inline 300常规采集数据成像剖面;(b)压缩感知采集数据处理后成像剖面;(c)速度模型剖面 |
宽方位地震采集比窄方位采集具有许多优势,但其成本较高。为了研究宽方位对中深层潜山内幕成像的改善作用,中国海油在M区海域做了OBC宽方位地震采集试验,采集了满覆盖面积约100km2的三维试验数据。主要采集参数如表 2所示。
|
|
表 2 主要采集参数对比表 |
由于工区水深较浅,OBC是较理想的采集方式,处理结果也证明了该采集方式对于改善潜山内幕成像的良好效果。若采用OBN采集,成本将显著增加。基于上述已采集OBC数据,尝试进行基于Jitter随机的压缩感知OBN采集观测系统设计,仅从理论上探索基于Jitter随机的OBN压缩感知采集的可行性和经济性。受限于该数据的实际观测系统,许多维度难以实现随机优化设计,如炮线间距、接收线间距都已固定为200m,若进行压缩感知随机优化,则重采样时必然有许多目标线处难以获得数据。因此,仅对炮点间距、检波点间距做了基于Jitter随机的压缩感知优化设计。
基于常规OBC宽方位采集参数,采用Jitter随机优化模式,设计了OBN压缩感知宽方位采集观测系统及其主要参数(表 2)。对比可知,该压缩感知宽方位采集的耗费资源仅为常规宽方位OBN采集的2/3。
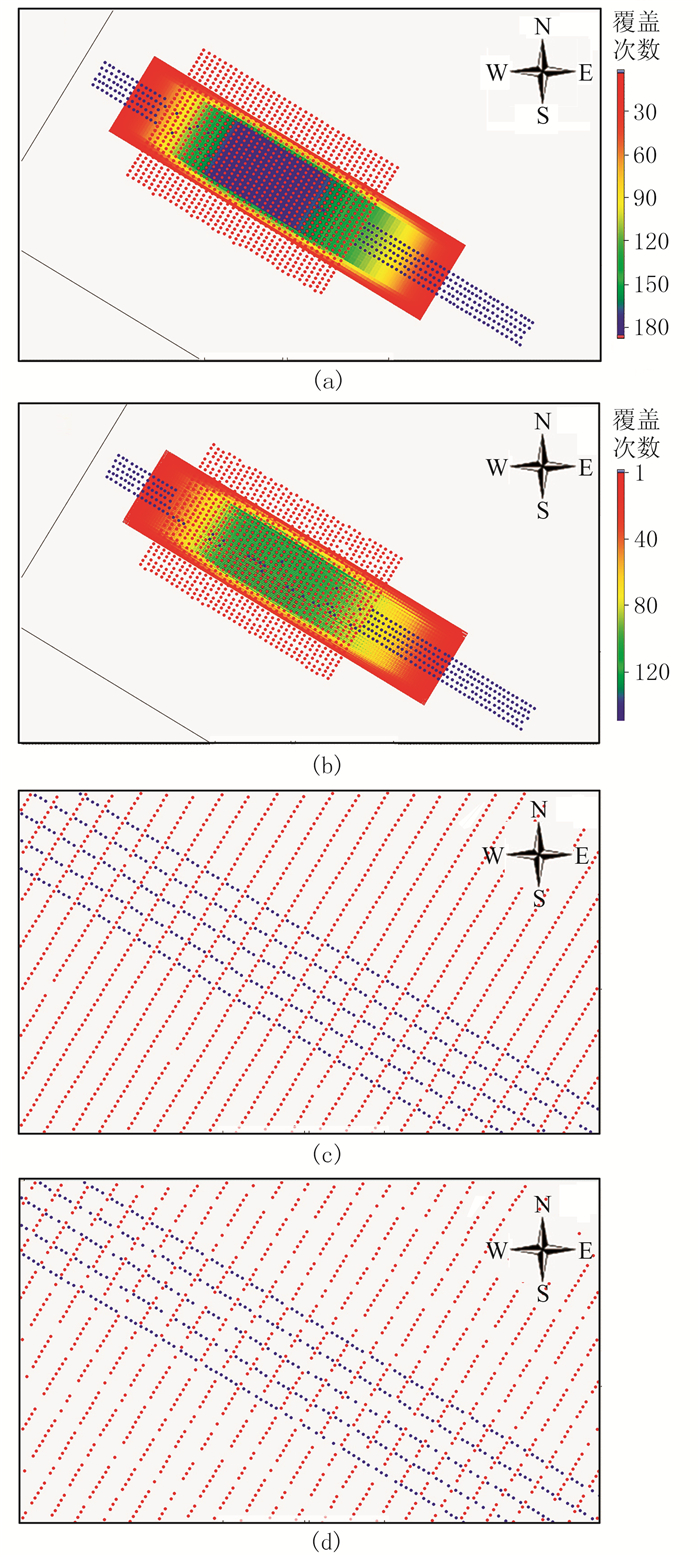
图 5为常规宽方位数据(图 5a)、基于Jitter随机的压缩感知宽方位数据(图 5b)Patch5的炮点、检波点和覆盖次数分布及其对应的炮、检点分布的放大显示(图 5c、图 5d)。可见常规宽方位数据的炮点、检波点分布规则、均匀;而基于Jitter随机的压缩感知宽方位数据的炮点、检波点分布表现为整体上是均匀的,局部是随机、不均匀的。
|
图 5 常规宽方位与基于Jitter随机的压缩感知宽方位地震数据的炮点、检波点和覆盖次数分布图 (a)常规宽方位;(b)压缩感知宽方位;(c)和(d)对应为图a和图b中炮、检点分布的放大显示 |
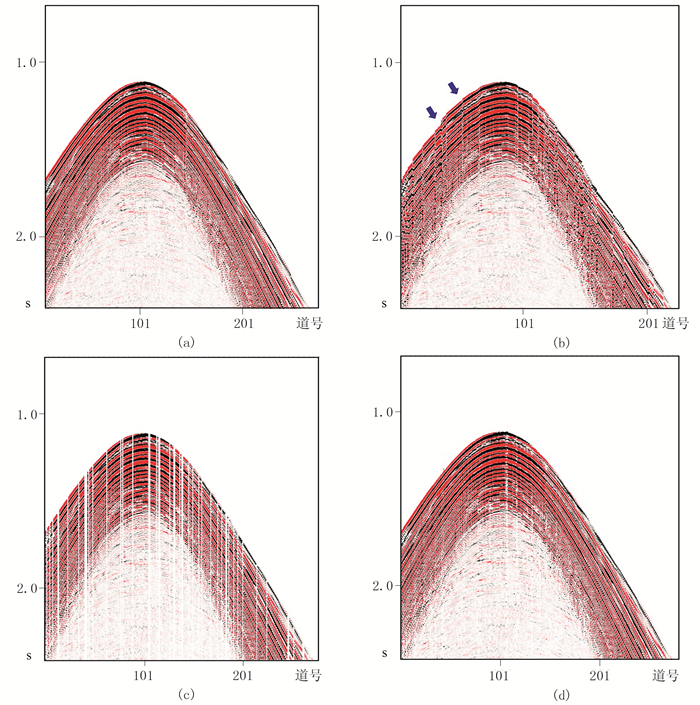
选取常规宽方位OBC实际地震数据(图 6a)和仿真压缩感知OBN宽方位数据一个炮集的一条接收缆(图 6b),可见常规地震数据的初至时间是光滑的,而压缩感知数据在初至时间上出现跳跃。分别对该压缩感知数据进行网格化(bin)处理(图 6c)和压缩感知重构(图 6d),经此处理后压缩感知数据已逼近常规宽方位OBC数据。
|
图 6 实际数据及不同处理方式的道集对比 (a)原始OBC炮集;(b)Jitter随机压缩感知重采样炮集;(c)压缩感知炮集网格化(bin)后炮集;(d)压缩感知数据重构后炮集 |
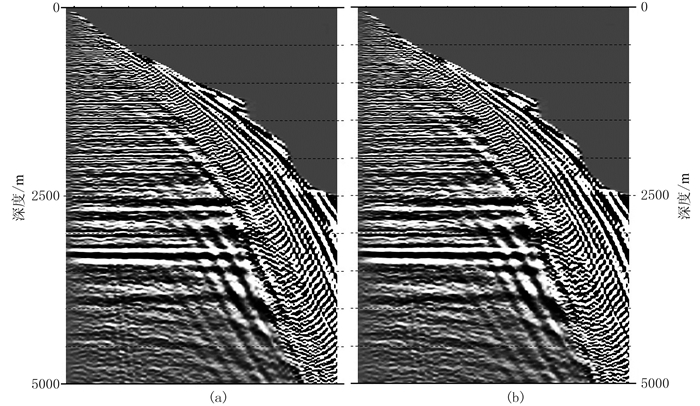
对比常规数据(图 7a)与压缩感知重构后数据(图 7b)的克希霍夫叠前深度偏移成像道集,以及常规数据(图 8a)、压缩感知数据重构后数据(图 8b)的克希霍夫叠前深度偏移成像剖面及二者的差剖面(图 8c),发现二者仅在潜山顶部振幅略有差异,对潜山内幕成像则无影响。因此,无论是成像道集还是成像剖面,压缩感知数据经过处理后都达到了与常规采集数据相当的效果。
|
图 7 克希霍夫叠前深度偏移道集对比 (a)OBC常规数据偏移;(b)压缩感知数据经过重构后的偏移 |

|
图 8 克希霍夫叠前深度偏移成像剖面对比 (a)OBC常规数据偏移;(b)压缩感知数据重构后偏移;(c)差剖面 |
因受限于实际数据采集已设定的观测系统及参数,在仅对炮点间距和检波点间距进行随机优化设计的条件下,采集资源比常规采集节省了约1/3。
4 结束语本文利用基于Jitter随机采样的压缩感知采集观测系统设计模块对模型正演数据和实际资料进行了仿真压缩感知采集观测系统设计,并充分考虑了现有采集设备的可实现性。将常规采集数据与仿真压缩感知采集数据重构后的道集(炮集)、偏移成像结果对比可见,在节省较多采集资源前提下,基于Jitter模式的压缩感知采集数据经处理后能达到常规采集数据的效果,表明基于Jitter模式的压缩感知采集对海上OBC、OBN具有良好的适应性。因此,在确保数据采集质量的前提下,Jitter模式的压缩感知地震采集对降低海上地震数据采集成本具有现实意义和广阔应用前景。
| [1] |
张建军, 刘红星, 孙强, 等. "两宽一高"地震采集技术在鄂东缘致密砂岩气藏勘探中的应用[J]. 石油地球物理勘探, 2018, 53(增刊2): 1-6. ZHANG Jianjun, LIU Hongxing, SUN Qiang, et al. Broadband, wide-azimuth and high-density seismic acquisition for the tight sand gas exploration in the east margin of Ordos Basin[J]. Oil Geophysical Prospecting, 2018, 53(S2): 1-6. |
| [2] |
Candès E, Romberg J, Tao T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207-1223. DOI:10.1002/cpa.20124 |
| [3] |
Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. |
| [4] |
马坚伟.稀疏促进地震勘探[C].中国地球物理学会第二十七届年会论文集, 湖南长沙, 2011. MA Jianwei.Sparsity-promoting seismic exploration[C].Proceedings of the 27th Annual Meeting of China Geophysical Society, Changsha, Hunan, 2011. |
| [5] |
马坚伟. 压缩感知走进地球物理勘探[J]. 石油物探, 2018, 57(1): 24-27. MA Jianwei. Compressive sensing in geophysical exploration[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 24-27. DOI:10.3969/j.issn.1000-1441.2018.01.002 |
| [6] |
Ma J W, Yu S W. Sparsity in compressive sensing[J]. The Leading Edge, 2017, 36(8): 646-652. DOI:10.1190/tle36080646.1 |
| [7] |
陈生昌, 陈国新, 王汉闯. 稀疏性约束的地球物理数据高效采集方法初步研究[J]. 石油物探, 2015, 54(1): 24-35. CHEN Shengchang, CHEN Guoxin, WANG Hanchuang. The preliminary study on high efficient acquisition of geophysical data with sparsity constrains[J]. Geophysical Prospecting for Petroleum, 2015, 54(1): 24-35. DOI:10.3969/j.issn.1000-1441.2015.01.004 |
| [8] |
王汉闯, 陶春辉, 陈生昌, 等. 基于稀疏约束的地震数据高效采集方法理论研究[J]. 地球物理学报, 2016, 59(11): 4246-4265. WANG Hanchuang, TAO Chunhui, CHEN Sheng-chang, et al. Study on highly efficient seismic data acquisition method and theory based on sparsity constraint[J]. Chinese Journal of Geophysics, 2016, 59(11): 4246-4265. DOI:10.6038/cjg20161126 |
| [9] |
周松, 吕尧, 吕公河, 等. 基于压缩感知的非规则地震勘探观测系统设计与数据重建[J]. 石油物探, 2017, 56(5): 617-625. ZHOU Song, LYU Yao, LYU Gonghe, et al. Irregular seismic geometry design and data reconstruction based on compressive sensing[J]. Geophysical Prospecting for Petroleum, 2017, 56(5): 617-625. DOI:10.3969/j.issn.1000-1441.2017.05.001 |
| [10] |
吕公河, 邸志欣, 霍守东, 等. 基于压缩感知的地震数据采集实践[J]. 石油物探, 2018, 57(6): 831-841. LYU Gonghe, DI Zhixin, HUO Shoudong, et al. Seismic data acquisition based on compressive sensing[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 831-841. DOI:10.3969/j.issn.1000-1441.2018.06.005 |
| [11] |
Charles C M, Erik K, Sam T K.Compressive seismic imaging[C].SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [12] |
Mosher C C, Kaplan S T.Non-uniform optimal sampling for seismic survey design[C].Extended Abstracts of 74th EAGE Conference & Exhibition, 2012, 333-336.
|
| [13] |
李成博, 张宇. CSI:基于压缩感知的高精度高效率地震资料采集技术[J]. 石油物探, 2018, 57(4): 537-542. LI Chengbo, ZHANG Yu. CSI:An efficient high-resolution seismic acquisition technology based on compressive sensing[J]. Geophysical Prospecting for Petroleum, 2018, 57(4): 537-542. DOI:10.3969/j.issn.1000-1441.2018.04.006 |
| [14] |
Hennenfent G, Herrmann F J. Simply denoise:wavefield reconstruction via jittered under sampling[J]. Geophysics, 2008, 73(3): V19-V28. DOI:10.1190/1.2841038 |
| [15] |
Wason H, Herrmann F J.Time-jittered ocean bottom seismic acquisition[C].SEG Technical Program Expanded Abstracts, 2013, 32: 1-6.
|
| [16] |
黄小刚. 浅谈海上压缩感知地震勘探[J]. 石油物探, 2019, 58(2): 162-175. HUANG Xiaogang. Offshore seismic exploration based on compressive sensing[J]. Geophysical Prospecting for Petroleum, 2019, 58(2): 162-175. DOI:10.3969/j.issn.1000-1441.2019.02.002 |
| [17] |
黄小刚, 王一博, 刘伊克, 等. 半径-斜率域加权反假频地震数据重建[J]. 地球物理学报, 2014, 57(7): 2278-2290. HUANG Xiaogang, WANG Yibo, LIU Yike, et al. Weighted anti-alias seismic data reconstruction in R-P domain[J]. Chinese Journal of Geophysics, 2014, 57(7): 2278-2290. |
| [18] |
刘群, 付丽华, 张婉娟. 非凸Lp范数三维地震数据重建[J]. 石油地球物理勘探, 2019, 54(5): 979-987, 996. LIU Qun, FU Lihua, ZHANG Wanjuan. 3D seismic data reconstruction based on non-convex Lp norm[J]. Oil Geophysical Prospecting, 2019, 54(5): 979-987, 996. |
| [19] |
彭佳明, 付丽华, 张雪敏. 应用快速不动点延续算法的地震数据重建[J]. 石油地球物理勘探, 2019, 54(6): 1195-1205. PENG Jiaming, FU Lihua, ZHANG Xuemin. Seismic data reconstruction based on fast fixed point continuation algorithm[J]. Oil Geophysical Prospecting, 2019, 54(6): 1195-1205. |
| [20] |
Abma R, Kabir N. 3D interpolation of irregular data with a POCS algorithm[J]. Geophysics, 2006, 71(6): E91-E97. DOI:10.1190/1.2356088 |
| [21] |
Galloway E and Sacchi M D.POCS method for seismicdata reconstruction of irregularly sampled data[C].Abstract of CSPG-CSEG-CWLS Joint Convention, Calgary, Canada, 2007, 555.
|
| [22] |
温睿, 刘国昌, 冉扬. 压缩感知地震数据重建中的三个关键因素分析[J]. 石油地球物理勘探, 2018, 53(4): 682-693. WEN Rui, LIU Guochang, RAN Yang. Three key factors in seismic data reconstruction based on compressive sensing[J]. Oil Geophysical Prospecting, 2018, 53(4): 682-693. |



 黄小刚, 北京市朝阳区太阳宫南街6号院中海油研究总院有限责任公司, 100028。Email:
黄小刚, 北京市朝阳区太阳宫南街6号院中海油研究总院有限责任公司, 100028。Email: