20世纪30年代,在地震勘探中,地球物理学家们将几个检波器接收的数据叠加起来作为一道数据输出,大幅度地提高了地震资料信噪比,于是有关“组合”的理论研究和实践便在地球物理领域逐渐展开。组合内检波器数目、组内距、各检波点接收到信号的能量加权和延时量是组合响应函数的四种重要自变量,也是组合参数设计的主要内容。
早期的地震数据现场采集一般只考虑检波器数目、组内距对信噪比的影响。Klipsch[1]从统计学角度给出了信噪比与组合个数间的关系;Johnson[2]基于天线理论推导了组合响应函数的表达式,奠定了地震勘探组合理论基础;Dean等[3]分析了地震记录中相干噪声强度与模拟检波器个数和间距的关系,通过获取检波器间相关系数寻求最佳间距,进而压制相干噪声和背景噪声。
针对加权系数设计:Holzman[4]提出了切比雪夫多项式加权组合方式,因其具有可调节的压制比、最窄的通放带宽度及压制带极值均匀相等的特点而受到广泛关注;Rietsch[5]改进了切比雪夫多项式权系数计算公式,在确保计算精度前提下,提高了计算效率;Simaan[6]提出了一种最佳组合滤波器设计方法,在频率域以约束计算量和检波器数量最小化来确定权系数,对于相干噪声压制和频率选择效果明显且成本较低;Hanna[7]将多重衰减条件应用于组合权系数与延时量计算,从多重相干干扰和随机噪声中提取反射信号。
对于延时组合:Johnson[8]根据近地表噪声与有效波到达检波器的时差,由检波器位置确定延时量,通过延时叠加提升信噪比;King等[9]采用选取参考道与各独立地震道做互相关的方法确定延时量,用于地震数据组合叠加;Mao等[10]通过线性化波形反演技术同时估计组合的延时量和权系数;Bagaini[11]基于系数矩阵构建各检波器延时量、接收时差的方程,通过最小二乘法求解延时量,证明在低信噪比条件下也能较准确地估计延时量。
调研以往相关研究成果,发现组合问题涉及的四种参数虽都已被较详细地探讨过,但仍存在几方面的不足:首先,因组合设计的目的不同,四种参数鲜有被综合考虑,如Dean等[3]是以相关系数大小设计组合个数和间距,Holzman[4]是以控制通放带形态设计组内距和加权系数,Simaan[6]以检波器数量最小化确定权系数,Hanna[7]设计组合权系数与延时量是为了压制随机噪声等;其次,参数设计时未考虑频率,如Mao等[10]以波形反演技术估计组合的延时量与权系数,或未考虑复频地震波的频率差异,如在切比雪夫多项式权系数设计中被压制的频率成分都是等权重的;再次,参数设计并没有遵循特定的目标函数,如韦成龙等[12]是以限定子波主峰同相叠加时差小于某约定值来设定海洋立体枪阵延时量,张鹏等[13]在设计海上空气枪点震源时忽略了子波和能量的方向性差异,何宝庆等[14]在研究宽线采集数据的组合时讨论了线距、线数、孔径、信号频率等参数,虽给出了宽线采集系统的响应函数,但未给出这些组合参数设计的依据函数。
“组合”本身不可避免地会引起低通滤波效应,同时伴随AVO响应的畸变。若未综合考虑参与组合的各类因素,可能还会加剧这一问题。本文从具有复频性质的地震波组合响应入手,建立包含四种组合参数的目标函数,通过全局寻优实现设计,期望对地震数据进行室内组合时,能在提高信噪比的同时减弱低通滤波效应和AVO畸变现象。
1 组合参数设计相控理论源于雷达设计,意指通过控制不同组合单元发射/接收简谐波的相位,达到控制组合整体输出响应形态的目的。在初相位一致、频率稳定前提下,相位控制就转化为各子单元的时差控制。
1.1 组合响应姜弢等[15]给出了单频简谐波的组合响应函数。设组合内有N个检波器,相邻检波器间距为d,当波长为λ的平面简谐波以与竖直方向呈θ角入射到组合内时,叠加后的能量响应可表示为
| $ F(\theta ) = \sum\limits_{i = 0}^{N - 1} {{\alpha _i}} \exp \left[ {{\rm{j}}i\left( {\frac{{2{\rm{ \mathsf{ π} }}f}}{v}d\sin \theta - \Delta \varphi } \right)} \right] $ | (1) |
式中:i为检波器编号;j为虚数单位;f为简谐波频率;v为地震波速度;Δφ为相邻检波器接收相位差;αi为加权系数,在采集现场组合中因不能改变各检波器输出能量比例,故通常设定αi=1。
根据欧拉公式,将式(1)分解为
| $ F(\theta ) = \frac{{\sin \left[ {N\frac{{{\rm{ \mathsf{ π} }}fd}}{v}(\sin \theta - \Delta \varphi )} \right]}}{{N\sin \left[ {\frac{{{\rm{ \mathsf{ π} }}fd}}{v}(\sin \theta - \Delta \varphi )} \right]}} $ | (2) |
显然,当θ=0°时,该组合响应F(θ)=1。
如图 1所示,检波器组合实际上是方向滤波器,响应因子取值区间是0~1。F(θ)=1表示来自θ方向的地震波是全通放的,F(θ)=0代表该角度方向能量全压制。当地震波的频率和传播速度确定后,视波数(k*=f/v·sinθ)是入射角θ的函数,故组合接收也是视波数滤波。

|
图 1 简谐波组合能量响应 |
对于具有一定频宽的地震子波,其组合响应为多个频率成分各自组合响应的线性加权叠加,则地震子波的组合响应为
| $ F(\theta ) = \sum\limits_{{f_l} = {f_{\min }}}^{{f_{\max }}} S \left( {{f_l}} \right)\frac{{\sin \left[ {N\frac{{{\rm{ \mathsf{ π} }}{f_l}d}}{v}(\sin \theta - \Delta \varphi )} \right]}}{{N\sin \left[ {\frac{{{\rm{ \mathsf{ π} }}{f_l}d}}{v}(\sin \theta - \Delta \varphi )} \right]}} $ | (3) |
式中:fmin、fmax分别为频带宽度内的最小和最大频率;fl为该频带内某单一频率;S(fl)为子波各频率成分的权系数。若接收子波为Ricker子波,则S(fl)可用其振幅谱表达为
| $ S\left( {{f_l}} \right) = \frac{{4f_l^2\sqrt {\rm{ \mathsf{ π} }} }}{{f_{\rm{m}}^3}}{{\rm{e}}^{ - \frac{{f_l^2}}{{f_{\rm{m}}^2}}}} $ | (4) |
式中fm为Ricker子波主频。
在进行室内组合时,可灵活设置组内各道的能量比例,即不再限定αi=1。若假设各检波器接地耦合性一致,则同一子波到达组内各检波器的相位差Δφ可由接收时间差Δt替代,即Δφ=2πflΔt。
综合式(1)和式(3),可推导出不等权组合响应
| $ F(\theta ) = \frac{{\sum\limits_{{f_l} = {f_{{\rm{min }}}}}^{{f_{{\rm{max }}}}} S \left( {{f_l}} \right)\sqrt {{{\left\{ {\sum\limits_{i = 0}^{N - 1} {{\alpha _i}} \cos \left[ {2{\rm{ \mathsf{ π} }}{f_l}\left( {\frac{d}{v}\sin \theta - \Delta t} \right)} \right]} \right\}}^2} + {{\left\{ {\sum\limits_{i = 0}^{N - 1} {{\alpha _i}} \sin \left[ {2{\rm{ \mathsf{ π} }}{f_l}\left( {\frac{d}{v}\sin \theta - \Delta t} \right)} \right]} \right\}}^2}} }}{{\sum\limits_{{f_l} = {f_{\min }}}^{{f_{{\rm{max }}}}} {\sum\limits_{i = 0}^{N - 1} {{a_i}} } S\left( {{f_l}} \right)}} $ | (5) |
反射地震勘探中,噪声和有效信号到达地表时入射角具有差异:噪声主要来源于近地表,入射角较大;反射信号来自一个锥角区间,入射角随炮检距增大而增大,随目的层加深而减小(图 2)。当目的层倾斜时,上倾方向入射角会大于下倾方向;当浅地表存在低降速带,入射角又会进一步减小,即实际入射角会因地层构造形态和检波器在排列中位置的不同而有差异,是时、空变的。为简化计算,应用中可估算一个最大反射角,将尽可能多地囊括反射信号,该入射角通常由中、深目的层深度H和排列长度L求得
| $ {\theta _{{\rm{max}}}} = {\rm{arc}} \ {\rm{tan}}\left( {\frac{l}{{2H}}} \right) $ | (6) |

|
图 2 检波点入射信号分布示意图 |
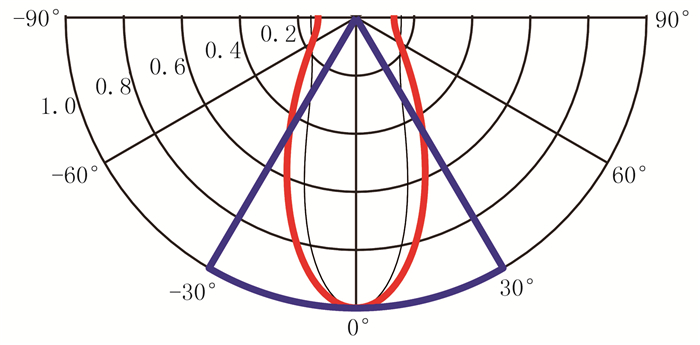
当有效信号最大入射角度确定后,即可据此设计组合参数。理想的组合效果是将噪声成分完全压制掉,有效信号部分充分保护起来,即一个“门”式滤波响应(图 3中蓝线)。这在实践中难以实现,尤其是考虑到应用中有限的组合个数和较大组内距的实情。参考图 3中的复频能量响应(红线),在“门”内除0°外其他角度也会被不同程度地压制(此即组合会损伤有效波的缘由),而在“门”外,噪声也会被通放。因此,更现实的方案是摒弃绝对压制思路,寻求信噪比相对改善——采用有效信号区与噪声干扰区的能量比值最大来设计组合参数,该比值被称为理论信噪比。
|
图 3 复频子波组合能量响应 |
统计反射波入射角度范围内能量总和
| $ {E_{\rm{s}}} = \int_{ - {\theta _{{\rm{max}}}}}^{ + {\theta _{{\rm{max}}}}} F (\theta ){\rm{d}}\theta $ | (7) |
将Es与干扰波入射范围内能量总和En之比值,定义理论信噪比
| $ P = \frac{{{E_{\rm{s}}}}}{{{E_{\rm{n}}}}} = \frac{{{E_{\rm{s}}}}}{{E - {E_{\rm{s}}}}} $ | (8) |
式中E为检波器接收全空间范围内能量总和。
将式(7)代入式(8),可得
| $ P = \frac{{\int_{ - {\theta _{{\rm{max}}}}}^{ + {\theta _{{\rm{max}}}}} F (\theta ){\rm{d}}\theta }}{{\int_{ - \frac{{\rm{ \mathsf{ π} }}}{2}}^{\frac{{\rm{ \mathsf{ π} }}}{2}} F (\theta ){\rm{d}}\theta - \int_{ - {\theta _{{\rm{max}}}}}^{ + {\theta _{{\rm{max}}}}} F (\theta ){\rm{d}}\theta }} $ | (9) |
在该式中:当传播速度v、频率权系数S、L和H确定以后,参照式(5),影响P取值的就是组合个数N、组合加权系数α、组内距d、延时量Δt,因此求解目标函数max{P(N, d, α, Δt)}即变为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial P}}{{\partial N}} = 0}\\ {\frac{{\partial P}}{{\partial d}} = 0}\\ {\frac{{\partial P}}{{\partial \Delta t}} = 0}\\ {\frac{{\partial P}}{{\partial \alpha }} = 0} \end{array}} \right. $ | (10) |
直接给出式(10)的解析解是困难的,实际求解采用数值逼近法。同时,根据徐峰等[16]相控组合理论,为了不出现非设计方向的能量泄漏(噪声区能量响应因子值极大),组内距、组合个数、地震波主波长三者之间应满足
| $ dN < \lambda $ | (11) |
联合式(10)与式(11),即可确定最优组合参数。
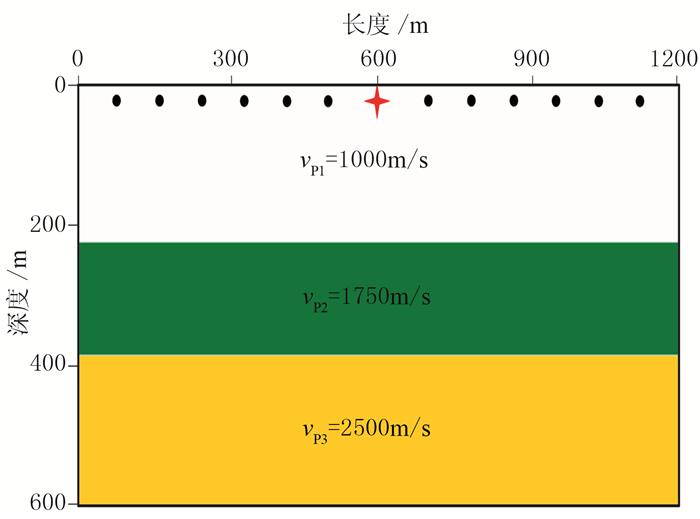
2 数值模拟设计的二维地震地质模型(图 4)的尺寸为1200m×600m,包含三套水平地层,采用主频为30Hz的雷克子波,震源置于(600m,10m)处,检波器排列铺设于地表。
|
图 4 三层二维地震地质模型 |
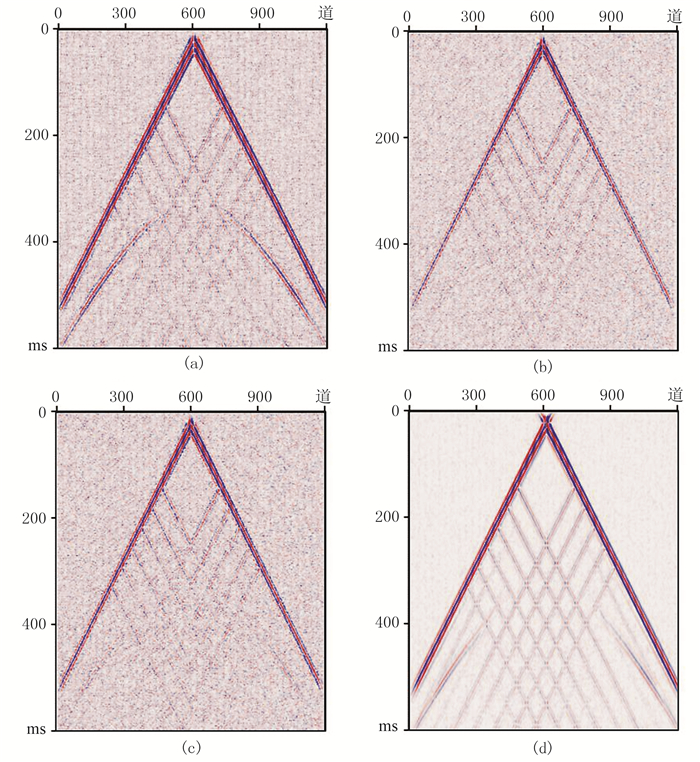
通过波动方程正演,得到单炮记录(图 5a);然后在上述模型地表向下15m处均匀布设高速散射点(图 4中黑点,v=1600m/s),模拟绕射源,加入60%随机噪声后再次正演得到图 5b;基于图 5b分别得到常规组合(图 5c)、延时等权组合(图 5d)、延时加权组合(图 5e)、F-K滤波后(图 5f)的模拟单炮记录及对应的组合中被压制的噪声成分(图 6)。

|
图 5 原始及组合处理后的模拟单炮记录 (a)原始不含噪单炮记录;(b)含背景噪声和散射干扰单炮记录;(c)常规组合;(d)延时等权组合;(e)延时加权组合;(f)F-K滤波 |
|
图 6 模拟记录中压制的噪声 (a)常规组合;(b)延时等权组合;(c)延时加权组合;(d)F-K滤波 |
在地震数据现场采集中,常规组合仅考虑检波器个数N和组内距d两个参数。根据模型参数,用式(6)算得接收有效波最大角度为26.6°,以理论信噪比P值最大为目标函数,兼用式(11)作为约束条件,计算得到最优组合参数为N=7、d=5。
从常规组合的模拟单炮记录(图 5c)并结合图 6a可见:常规组合对于散射干扰和随机干扰均有相当不错的压制效果,但对有效信号的损伤也较大。
再从各套组合数据第350道归一化频谱分析(图 7)及第二反射层AVO曲线统计(图 8)中,可看到常规组合的低通特征明显、AVO畸变严重。

|
图 7 第350m检波道记录频谱分析 |

|
图 8 模拟记录第二层反射AVO曲线 |
与现场组合相比,室内组合更灵活。例如:可对检波器个数N、延时量Δt、组内距d及加权系数αi四种参数同时进行设置;下面分别进行不考虑权系数变化的延时等权组合和考虑权系数变化的延时加权组合参数设计(表 1)。
|
|
表 1 组合参数优化计算结果 |
从延时等权组合后的模拟单炮记录(图 5d)并结合图 6b可知,延时组合能同时压制背景噪声和散射噪声,对有效波的损伤小于常规组合。
延时加权组合通过同时控制延时量和加权系数,可提高理论信噪比。从延时加权组合后模拟单炮记录(图 5e)并结合图 6c可知,与常规组合和延时等权组合相比,延时加权组合后散射干扰与背景噪声进一步被压制,有效信号损伤更小;另外,从图 7、图 8中可见该组合的频带特征基本保持与原始资料一致,且AVO畸变较小。
2.3 F-K滤波F-K滤波作为一种常用的室内资料处理手段,是根据噪声干扰与有效波在视速度和频率上的差异进行滤波。
从F-K滤波结果(图 5f)并结合图 6d可见:与延时加权组合相比,F-K滤波较好地压制了散射干扰,但因散射干扰倾角与直达波倾角、远炮检距有效波倾角近似一致,难以避免地对直达波和有效波也进行了一定程度压制;相对散射干扰,随机干扰的压制效果则较差,部分有效信号仍淹没于干扰中。对比延时加权组合与F-K滤波的频谱(图 7),可见二者频带特征与原始资料基本一致,都能较好地保持频率信息;同时,二者的AVO畸变(图 8)也都较小。
综合考虑噪声压制能力、频带保持能力、AVO曲线畸变影响程度等,认为延时加权组合是一种较好的室内组合接收方案。
3 实际数据分析采用四川某地实际采集地震记录进一步做室内组合试验分析。原始记录虽已做过现场一次静校正、初至切除、去除异常强振幅噪声等处理(图 9a),但仍存在随机干扰、线性干扰、面波等成分,有效反射在中远道欠连续,其能量与噪声背景相近,给后期识别造成一定困扰。

|
图 9 实际地震记录组合处理结果 (a)原始记录;(b)常规组合;(c)延时加权组合;(d)F-K滤波 |
选取相邻7道(N=7)分别进行常规组合(图 9b)和延时加权组合(图 9c)处理,可见组合处理后随机噪声都得到较彻底压制,反射轴从背景噪声中凸显出来。但另一方面,常规组合在中远道对有效波损伤较大;而延时加权组合则考虑到了传播时差,对有效反射能做到同相叠加,因此增强了连续性,保护效果更好。从其F-K滤波结果(图 9d)可见,线性干扰及面波得到较好压制,但随机噪声的压制效果不甚理想,有效反射未能得到相对充分的凸显。
4 讨论与结论组内距、组合个数、加权系数、延时量、输入子波频率成分等,都会影响组合输出的空间能量响应形态。根据有效信号和噪声在入射角度上的差异,可将空间划分为指向目的层的有效反射部分和近地表的潜在噪声部分,这两部分的能量比值构成了理论信噪比。
使理论信噪比达到最大,就是组合参数优化设计的目标和结果。常规组合一般只考虑检波器组合个数和组内距两参数,试验表明这种组合方式对噪声干扰压制较好,但对反射振幅也有一定程度损害,且造成主频降低。延时等权组合将延时量加入目标函数,控制接收相位差使反射波能量同相叠加,从而保证了主频与原始资料接近,减轻了对反射振幅的损害,但也增强了与有效波方向近似的干扰波能量。延时加权组合综合考虑了检波器组合数目、组内距、延时量和加权系数等因素,在保证反射波振幅同相叠加的同时,通过加权系数能进一步调整组合方向因子形态,进而压制干扰,整体上提高了地震记录信噪比。
对比延时加权组合与F-K滤波的效果得知,二者在压制规则干扰和频带保持方面都有较好表现,但F-K滤波对随机噪声压制能力不足,而这恰好是组合类方法的优势。因此,应用延时加权组合手段压制噪声具有良好应用前景。
| [1] |
Klipsch P W. Some aspects of multiple recording in seismic prospecting[J]. Geophysics, 1936, 1(3): 365-377. DOI:10.1190/1.1437129 |
| [2] |
Johnson C H. Steady state polar sensitivity curves[J]. Geophysics, 1939, 4(1): 33-52. |
| [3] |
Dean T, Dupuis J C, Hassan R. The coherency of ambient seismic noise recorded during land surveys and the resulting implications for the effectiveness of geophone arrays[J]. Geophysics, 2015, 80(3): P1-P10. DOI:10.1190/geo2014-0280.1 |
| [4] |
Holzman M. Chebyshev optimized geophone array[J]. Geophysics, 1963, 28(2): 145-155. DOI:10.1190/1.1439160 |
| [5] |
Rietsch E. Geophone sensitivities for Chebyshev optimized arrays[J]. Geophysics, 1979, 44(6): 1142-1143. DOI:10.1190/1.1441000 |
| [6] |
Simaan M. Optimum array filters for array data signal processing[J]. IEEE Transactions on Acoustics Speech & Signal Processing, 1983, 31(4): 1006-1015. |
| [7] |
Hanna M T. Multiple signal extraction by multiple interference attenuation in the presence of random noise in seismic array data[J]. IEEE Transactions on Signal Processing, 2003, 51(7): 1683-1694. DOI:10.1109/TSP.2003.812729 |
| [8] |
Johnson K R. Correlation function of teleseismic noise[J]. Bulletin of the Seismological Society of America, 1968, 58(2): 521-538. |
| [9] |
King D W, Mereu R F, Muirhead K J. The mea-surement of apparent velocity and azimuth using adaptive processing techniques on data from the warramunga seismic array[J]. Geophysical Journal of the Royal Astronomical Society, 1973, 35(1-3): 137-167. |
| [10] |
Mao W J, Gubbins D. Simultaneous determination of time delays and stacking weights in seismic array beamforming[J]. Geophysics, 1995, 60(2): 491-502. DOI:10.1190/1.1443786 |
| [11] |
Bagaini C. Performance of time-delay estimators[J]. Geophysics, 2005, 70(4): V109-V120. DOI:10.1190/1.1996909 |
| [12] |
韦成龙, 杨蜀冀, 关晓春, 等. 立体延迟气枪震源分析[J]. 石油地球物理勘探, 2014, 49(6): 1027-1033. WEI Chenglong, YANG Shuji, GUAN Xiaochun, et al. A delayed up-down sub-array airgun source[J]. Oil Geophysical Prospecting, 2014, 49(6): 1027-1033. |
| [13] |
张鹏, 杨凯, 李欣, 等. 海上空气枪点震源阵列的优化设计及应用[J]. 石油地球物理勘探, 2015, 50(4): 588-599. ZHANG Peng, YANG Kai, LI Xin, et al. The optimal design of point source air-gun array in marine and its application[J]. Oil Geophysical Prospecting, 2015, 50(4): 588-599. |
| [14] |
何宝庆, 谢小碧. 宽线地震数据采集和处理的数值模拟[J]. 石油地球物理勘探, 2019, 54(3): 500-511. HE Baoqing, XIE Xiaobi. A numerical investigation on wide-line seismic data acquisition and processing[J]. Oil Geophysical Prospecting, 2019, 54(3): 500-511. |
| [15] |
姜弢, 林君, 杨冬, 等. 相控震源定向地震波信号分析[J]. 地球物理学报, 2008, 51(5): 1551-1556. JIANG Tao, LIN Jun, YANG Dong, et al. Analysis of directional seismic signal based on phased-array vibrator system[J]. Chinese Journal of Geophysics, 2008, 51(5): 1551-1556. DOI:10.3321/j.issn:0001-5733.2008.05.030 |
| [16] |
徐峰, 刘福烈, 梁向豪. 基于相控理论的炮点组合设计技术[J]. 石油地球物理勘探, 2011, 46(2): 170-175. XU Feng, LIU Fulie, LIANG Xianghao. A method for source array design based on the phased-array theory[J]. Oil Geophysical Prospecting, 2011, 46(2): 170-175. |



 刘福烈, 四川省成都市新都区新都大道8号西南石油大学地球科学与技术学院, 610500。Email:
刘福烈, 四川省成都市新都区新都大道8号西南石油大学地球科学与技术学院, 610500。Email: