2 中国石油大学(华东)地球科学与技术学院, 山东青岛 266580;
3 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071
2 School of Geosciences, China University of Petroleum(East China), Qingdao, Shandong 266580, China;
3 Laboratory for Marine Resources, Qingdao National Laboratory for Marine Science and Techno-logy, Qingdao, Shandong 266071, China
实际地震数据在空间方向往往存在不规则的缺失道,要想得到完整的地震数据,通常需做插值处理[1-2]。完整的地震数据适合多道处理技术,如多次波分离[3-6]、地震偏移和反演[7-8]等。近年来,压缩感知方法[9-13]广泛用于地震数据插值,通过重建非等间距随机采样的少量地震数据以得到完整的地震数据。
压缩感知方法可以归结为一个L2-L0最优化问题,其中包含重建误差的L2范数最小化约束和变换域系数的L0范数最小化约束[14]。在压缩感知方法中可以使用不同的数学变换方法,如傅里叶变换[2]、小波变换[15]、曲波变换[12, 16]、Dreamlet变换[14, 17]、Shearlet变换[18]、Seislet变换[13, 19]等。为了求解压缩感知方法中的L2-L0最优化问题,Wang等[14]提出了一种改进的迭代算法,可以有效地同时衰减随机噪声和进行数据插值,并可降低随机噪声对插值精度的影响。但是,在地震数据中存在异常强噪声[20-21],包括极性反转噪声、膨胀噪声和突发噪声等[20, 22],基于重建误差L2范数最小化约束的压缩感知方法假设重建误差(包含消除的噪声)满足高斯分布。因此,上述压缩感知方法不能去除满足超高斯分布的异常噪声。此外,剩余的异常噪声还会降低插值精度。
本文提出采用Huber范数[23-24]代替L2范数对重建误差施加最小化约束。其中,Huber范数的最小化约束实际上等价于对大重构误差(异常噪声)的L1范数最小化约束和对小重构误差(高斯随机噪声)的L2范数最小化约束。在地震数据处理中,鲁棒性意味着处理结果对地震数据中的异常振幅不敏感,即该异常振幅不会对处理结果产生负面影响。因为对大重建误差施加了L1范数最小化约束,所以提出的基于重建误差Huber范数最小化约束的压缩感知方法对异常噪声具有很好的鲁棒性。同时,这种方法还可以减少异常噪声对插值精度的影响。拟合误差的L1范数最小化约束已用于地震数据处理,如在同时激发震源和层析成像的分离中消除异常噪声的影响。此外,通过引入理论上构建的伪地震数据将Huber范数最小化问题转化为L2范数最小化问题[22, 25]。通过这种转化,可以有效地求解基于重建误差Huber范数最小化约束的压缩感知方法的Huber-L0最优化问题。此外,引入的迭代优化算法已经成功用于矩阵填充问题和图像恢复领域[25]。Zhao等[22]成功利用该迭代优化算法消除强噪声,但没有用于插值处理。与传统的基于重建误差L2范数最小化约束的压缩感知方法相比,本文提出的基于重建误差Huber范数最小化约束的压缩感知方法在提高插值精度的同时,能有效地衰减地震数据中的强异常噪声。
凸集投影(Projection onto Convex Sets)算法[2, 14]、迭代阈值算法[26]等是利用压缩感知实现数据插值的常用最优化算法,本文以凸集投影算法为例介绍压缩感知方法,首先求解得到稀疏变换域中的插值数据,然后再将插值数据从变换域转换到时间—空间域[2, 12, 27]。本文的主要贡献是引入重建误差的Huber范数最小化约束,并推导出一种有效的最优化算法求解压缩感知方法中的Huber-L0最优化问题,并从数学模型、最优化问题和求解算法等方面描述了所提方法。模拟数据和实际数据的处理结果验证了方法的有效性。
1 数学模型和最优化问题不规则采样的地震数据s是由完整的无噪声地震数据dtr得到的,即
| $ \boldsymbol{s}=\boldsymbol{R} \boldsymbol{d}_{\mathrm{tr}}+\boldsymbol{n} $ | (1) |
式中:R为对角采样矩阵;n为高斯随机噪声和异常噪声。
为了恢复dtr,构建L2-L0最优化问题[14, 16, 28]
| $ \arg \min\limits_{\boldsymbol{x}}f(x | s) =\arg\min\limits_{\boldsymbol{x}}\left(\left\|s-\boldsymbol{R} \boldsymbol{C}^{\mathrm{T}} \boldsymbol{x}\right\|_{2}^{2}+\alpha\|\boldsymbol{x}\|_{0}\right) $ | (2) |
式中:dtr=CTx,x为稀疏变换系数,CT为逆稀疏变换;α为正则化参数。
式(2)的L2-L0最优化问题包含重建误差的L2范数最小化约束。为了消除超高斯分布的异常噪声,给出如下Huber-L0最优化问题
| $ \arg \min\limits_{\boldsymbol{x}}g(x | s) =\arg \min\limits_{\boldsymbol{x}}\left[\sum\limits_{i=1}^{N} \rho\left(\boldsymbol{s}-\boldsymbol{R} \boldsymbol{C}^{\mathrm{T}} \boldsymbol{x}\right)_{i}+\alpha\|\boldsymbol{x}\|_{0}\right] $ | (3) |
式中N为dtr的总采样点个数。Huber范数[23-24]ρ(ai)作用在标量上,定义为
| $ \rho\left(a_{i}\right)=\left\{\begin{array}{cc} a_{i}^{2} & \left|a_{i}\right| \leqslant c \\ c\left(2\left|a_{i}\right|-c\right) & \left|a_{i}\right|>c \end{array}\right. $ | (4) |
式中变量ai=(s-RCTx)i表示重建误差的采样点。阈值c为区分L1和L2范数的阈值[29-30],即
| $ c=1.345 \sigma $ | (5) |
其中
| $ \sigma \approx \frac{\operatorname{median}|\boldsymbol{a}-\operatorname{median}(\boldsymbol{a})|}{0.6745} $ |
式中median(a)表示计算向量a={ai}的中值, 其中i=1, 2, …, N。式(5)可以改写为
| $ c=c_{0}[\operatorname{median}|\boldsymbol{a}-\operatorname{median}(\boldsymbol{a})|] $ | (6) |
其中c0≈1.994。
本文在实际数据处理中研究了式(6)中系数c0的其他取值对插值精度的影响。基于重建误差Huber范数最小化约束的压缩感知方法实际上是对异常噪声施加L1范数最小化约束,对高斯随机噪声施加L2范数最小化约束。
2 最优化问题的求解算法对于基于重建误差L2范数最小化约束的压缩感知方法,求解L2-L0最优化问题(式(2))的迭代步骤(附录A)为[14]
| $ \hat{\boldsymbol{d}}^{(k)}=\lambda \boldsymbol{s}+(\boldsymbol{I}-\lambda \boldsymbol{R}) \boldsymbol{d}^{(k-1)} $ | (7) |
| $ \boldsymbol{x}^{(k)}=T_{\phi}\left[\hat{\boldsymbol{C}} \hat{\boldsymbol{d}}^{(k)}\right] $ | (8) |
| $ \boldsymbol{d}^{(k)}=\boldsymbol{C}^{\mathrm{T}} \boldsymbol{x}^{(k)} $ | (9) |
式中:λ∈(0, 1]为加权系数;I为单位矩阵;k为迭代次数;C为正稀疏变换;d(k)为第k次迭代的插值结果;
| $ T_{\phi}(a)=\left\{\begin{array}{ll} a & |a| \geqslant \phi \\ 0 & |a|<\phi \end{array}\right. $ | (10) |
式中ϕ为作用于标量a上的阈值。本文选择的数据驱动阈值为[31]
| $ \left\{\begin{array}{l} \phi^{(1)}=v^{(1)} \\ \phi^{(k)}=v^{(j)} \\ \phi^{(K)}=v^{\left(N_{v}\right)} \\ j=\left\lceil(k-1) N_{v} /(K-1)\right\rceil \\ k=1, 2, \cdots, K \end{array}\right. $ | (11) |
| $ \left\{\begin{array}{l} \lambda_{\min }=\phi_{\min } \max\limits_{i}\left\{\left|\left(\boldsymbol{Cs}\right)_{i}\right|\right\} \\ \lambda_{\max }=\phi_{\max } \max\limits_{i}\left\{\left|\left(\boldsymbol{Cs}\right)_{i}\right|\right\} \end{array}\right. $ | (12) |
式中:K为最大迭代次数;ϕmin、ϕmax分别为最小、最大阈值;序列{|Cs|∈[λmin, λmax]}按其中元素振幅的下降顺序排列可以得到向量v,v(j)为v中的第j个元素,Nv为v的长度。式(11)中的算子
通过式(8)的硬阈值操作,基于重建误差L2范数最小化约束的压缩感知方法可以有效衰减随机噪声,随机噪声包含在稀疏变换后的小绝对值系数中。经过随机噪声衰减,基于重建误差L2范数最小化约束的压缩感知方法可将高信噪比的插值数据从变换域变换到时间—空间域。因此,利用式(7)~式(9),基于重建误差L2范数最小化约束的压缩感知方法可同时衰减随机噪声和进行插值计算[14]。
本文提出的基于重建误差Huber范数最小化约束的压缩感知方法,在数据插值的同时衰减地震异常噪声。为了求解Huber-L0最优化问题(式(3)),基于重建误差Huber范数最小化约束的压缩感知方法构建以下伪地震数据[22, 25]
| $ \boldsymbol{p}=\boldsymbol{R} \boldsymbol{d}+\frac{1}{2} \psi(\boldsymbol{e}) $ | (13) |
| $ \boldsymbol{e=s-Rd} $ | (14) |
式中:e为重构误差;ψ(·)为Huber范数ρ(·)的导数,定义为
| $ \psi(a)=\left\{\begin{array}{cl} 2 a & |a| \leqslant c \\ 2 \operatorname{sgn}(a) c & |a|>c \end{array}\right. $ | (15) |
其中
| $ \operatorname{sgn}(a)=\left\{\begin{array}{cl} 1 & a>0 \\ 0 & a=0 \\ -1 & a<0 \end{array}\right. $ |
为符号函数。
将式(14)代入式(15),得
| $ \psi(e)=\left\{\begin{array}{cc} 2(\boldsymbol{s-R d}) & |\boldsymbol{e}| \leqslant c \\ 2 \operatorname{sgn}(\boldsymbol{s-R d}) c & |\boldsymbol{e}|>c \end{array}\right. $ | (16) |
其中绝对值操作|·|应用于向量时,表示对其中的每一个元素取绝对值。将式(16)代入式(13),得到伪地震数据
| $ \boldsymbol{p}=\left\{\begin{array}{cl} \boldsymbol{s} & |\boldsymbol{e}| \leqslant c \\ \boldsymbol{R} \boldsymbol{d}+\operatorname{sgn}(\boldsymbol{e}) c & |\boldsymbol{e}|>c \end{array}\right. $ | (17) |
伪地震数据中绝对值小于阈值c的随机噪声被保留,绝对值大于c的异常噪声被衰减到c。
根据式(2),可以得到x的梯度表达式f(x|s)
| $ \partial_{x} f(\boldsymbol{x} | \boldsymbol{s})=-2 \boldsymbol{C} \boldsymbol{R}^{\mathrm{T}}\left(\boldsymbol{s}-\boldsymbol{R} \boldsymbol{d}^{\mathrm{T}} \boldsymbol{x}\right)+\alpha \partial_{x}\|\boldsymbol{x}\|_{0} $ | (18) |
以p替换式(18)的s,得
| $ \begin{array}{c} \partial_{x} f(\boldsymbol{x} | \boldsymbol{p})=-2 \boldsymbol{C} \boldsymbol{R}^{\mathrm{T}}\left[\boldsymbol{R} \boldsymbol{d}+\frac{1}{2} \psi(\boldsymbol{e})-\boldsymbol{R} \boldsymbol{C}^{\mathrm{T}} \boldsymbol{x}\right]+\\ \alpha \partial_{x}\|\boldsymbol{x}\|_{0} \end{array} $ | (19) |
由式(9)可知d=CTx,并代入式(19),得
| $ \partial_{x} f(\boldsymbol{x} | \boldsymbol{p})=-\boldsymbol{C} \boldsymbol{R}^{\mathrm{T}} \psi(\boldsymbol{e})+\alpha \partial_{x}\|\boldsymbol{x}\|_{0} $ | (20) |
将式(14)代入式(20),得
| $ \partial_{x} f(\boldsymbol{x} | \boldsymbol{p})=-\boldsymbol{C} \boldsymbol{R}^{\mathrm{T}} \psi(\boldsymbol{s}-\boldsymbol{R} \boldsymbol{d})+\alpha \partial_{x}\|\boldsymbol{x}\|_{0} $ | (21) |
并将d=CTx代入式(21),得
| $ \partial_{x} f(\boldsymbol{x} | \boldsymbol{p})=-\boldsymbol{C} \boldsymbol{R}^{\mathrm{T}} \psi\left(\boldsymbol{s}-\boldsymbol{R} \boldsymbol{C}^{\mathrm{T}} \boldsymbol{x}\right)+\alpha \partial_{x}\|\boldsymbol{x}\|_{0} $ | (22) |
同样地,根据式(3)可以得到x的梯度表达式g(x|s)
| $ \partial_{x} g(\boldsymbol{x} | \boldsymbol{s})=-\boldsymbol{C} \boldsymbol{R}^{\mathrm{T}} \psi\left(\boldsymbol{s}-\boldsymbol{R} \boldsymbol{C}^{\mathrm{T}} \boldsymbol{x}\right)+\alpha \partial_{x}\|\boldsymbol{x}\|_{0} $ | (23) |
由式(22)、式(23)可知
| $ \partial_{x} f(\boldsymbol{x} | \boldsymbol{p})=\partial_{x} g(\boldsymbol{x} | \boldsymbol{s}) $ |
即代价函数f(x|p)的梯度与代价函数g(x|s)的梯度相等。L2-L0最优化问题的代价函数(伪地震数据作为输入)与Huber-L0最优化问题的代价函数相同[22, 25]。利用式(13)构建伪地震数据p(k),令s=p(k),并采用式(7)~式(9),可以求解Huber-L0最优化问题(式(3))。因此,通过引入伪地震数据,可以将Huber范数最小化问题转化为L2范数最小化问题,并可以将求解L2-L0最优化问题转化为求解Huber-L0最优化问题。求解式(3)的优化算法在最大迭代次数为K时收敛或得到最精确的求解结果,相应的迭代算法为:
输入:s、R、CT、C、λ∈(0, 1]、K、ϕmin、ϕmax;
初始化:x(0)=Tϕ[C(λs)];
令迭代次数k=0;
(1) d(k)=CTx(k);
(2) k=k+1;
(3) 若k达到了最大迭代次数K,则停止迭代;
(4) e(k)=s-Rd(k-1);
(5)
(6)
(7)
输出:插值结果d(k),同时衰减了随机噪声和异常噪声。
利用上述算法求解Huber-L0最优化问题的可行性已得到验证[25]。在算法的每一步迭代中使用伪地震数据,可以有效地求解式(3)。
3 数值算例将基于重建误差Huber范数最小化约束的压缩感知方法用于模拟数据和实际数据,并与基于重建误差L2范数最小化约束的压缩感知方法[14]的处理结果对比。此外,选择曲波变换作为稀疏变换。
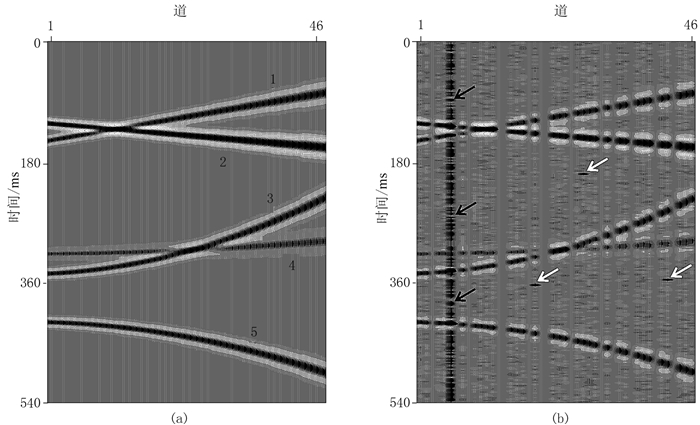
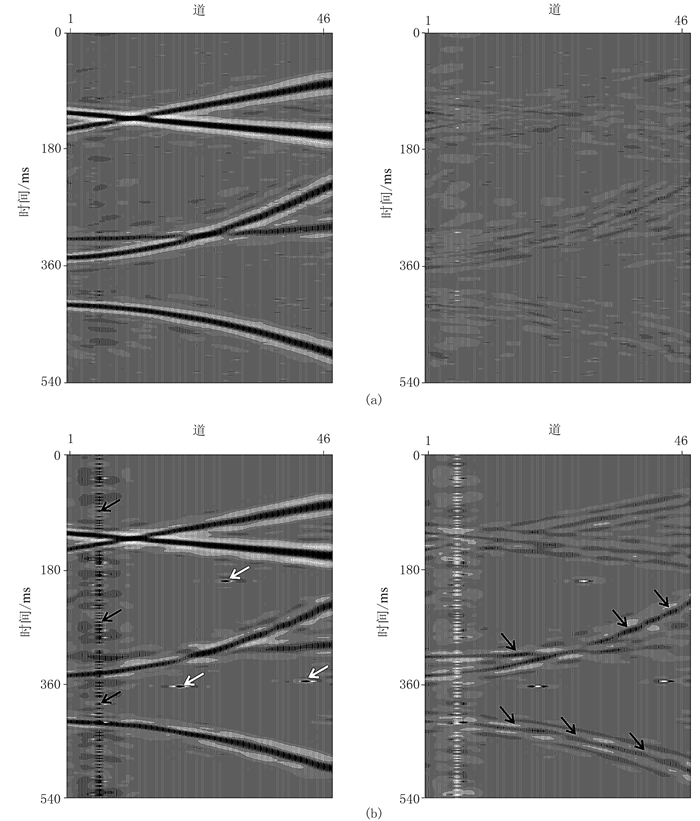
3.1 模拟数据图 1为合成数据。由图可见,包含随机噪声和异常噪声的不完整地震数据(图 1b)相对真实数据(图 1a)缺失14道数据,异常噪声包括尖锐脉冲噪声(白色箭头处)以及强振幅噪声(黑色箭头处)。
|
图 1 合成数据 (a)真实数据;(b)包含随机噪声和异常噪声的不完整地震数据 共46道数据,每道271个采样点,采样间隔为2ms。图a中存在5个同相轴,其中1和2为线性同相轴,3、4和5为弯曲同相轴,这些同相轴中子波的频率随炮检距的增加而逐渐变低,反映了波形和振幅的横向变化。对图a数据添加25dB的高斯随机噪声,并利用Jitter采样理论[32]得到不规则采样数据,然后再添加异常噪声,得到图b |
对于基于重建误差Huber范数最小化约束和基于重建误差L2范数最小化约束的压缩感知方法,选取λ=1、K=80、ϕmin和ϕmax分别为0.02和0.80,采用反复试错的方法得到满意的数据重建结果。此外,采用式(5)计算基于重建误差Huber范数最小化约束的压缩感知方法的阈值c。为了定量评价两种方法的插值效果,定义信噪比
| $ \mathrm{S} / \mathrm{N}=10 \lg \frac{\left\|\boldsymbol{d}_{\mathrm{tr}}\right\|_{2}^{2}}{\left\|\boldsymbol{d}-\boldsymbol{d}_{\mathrm{tr}}\right\|_{2}^{2}} $ |
式中dtr为真实数据。
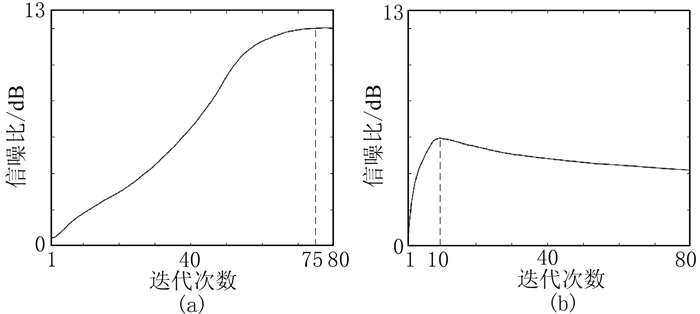
图 2为不同压缩感知方法的信噪比随迭代次数的变化曲线。由图可见:基于重建误差L2范数最小化约束的压缩感知方法在第80次迭代时没有收敛,在第10次迭代时信噪比最高(图 2b);基于重建误差Huber范数最小化约束的压缩感知方法在第75次迭代时收敛(图 2a)。
|
图 2 不同压缩感知方法的信噪比随迭代次数的变化曲线 (a)基于重建误差Huber范数最小化约束;(b)基于重建误差L2范数最小化约束 |
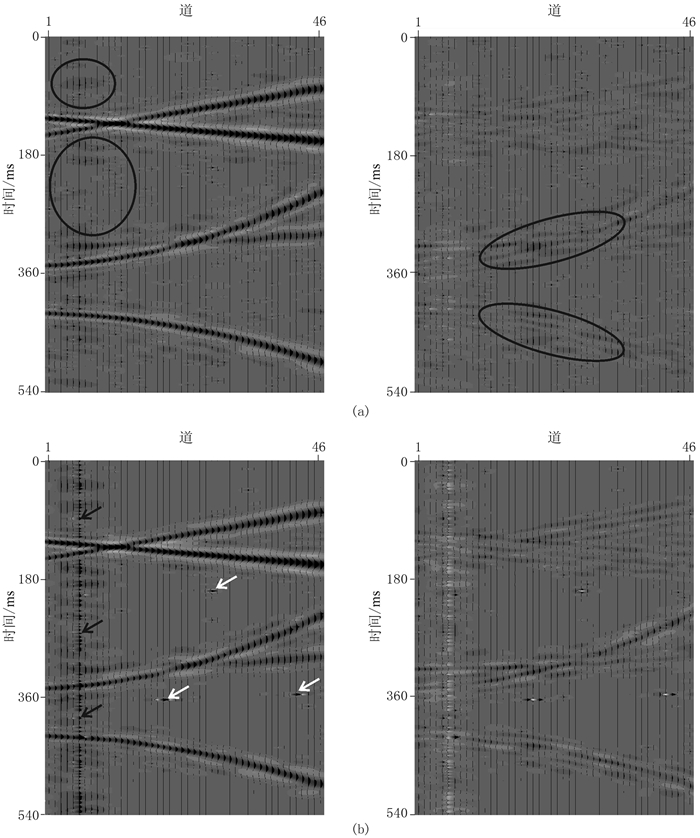
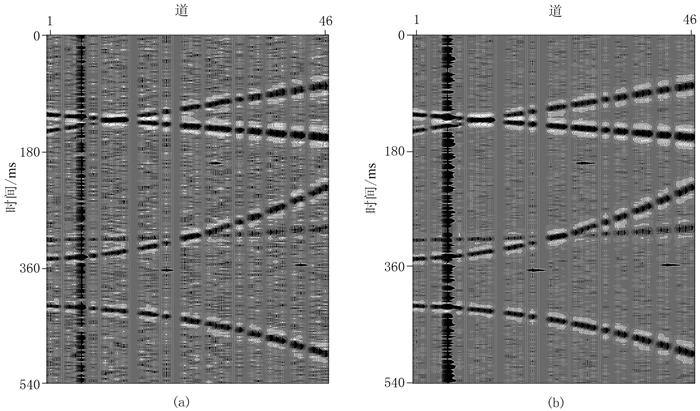
图 3为不同压缩感知方法的插值结果及其与图 1a数据的差值。由图可见:①基于重建误差Huber范数最小化约束(图 3a左)与基于重建误差L2范数最小化约束(图 3b左)的压缩感知方法的插值结果的信噪比分别为12.00和6.00,即前者的信噪比更高;②基于重建误差L2范数最小化约束的压缩感知方法不能有效地去除异常噪声(图 3b左的黑、白色箭头处),且导致明显的信号损伤(图 3b右的黑色箭头处);③基于重建误差Huber范数最小化约束的压缩感知方法对大的重建误差施加了L1范数最小化约束,可以更好地消除强振幅异常噪声,并减弱异常噪声对插值结果的影响,能更好地保护有效信号(图 3a)。
|
图 3 不同压缩感知方法的插值结果(左)及其与图 1a数据的差值(右) (a)基于重建误差Huber范数最小化约束(迭代75次);(b)基于重建误差L2范数最小化约束(迭代10次) |
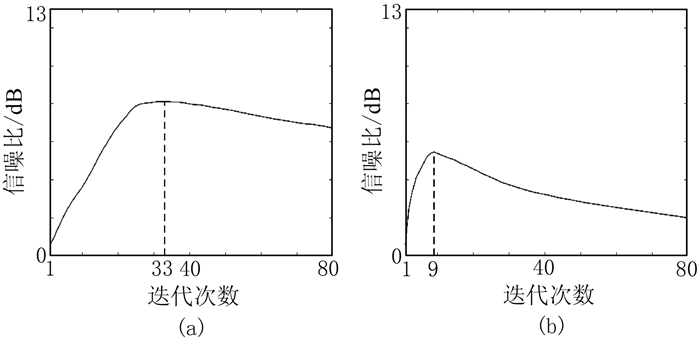
图 4为图 1a数据添加随机噪声和异常噪声的不完整地震数据。对于基于重建误差Huber范数最小化约束和基于重建误差L2范数最小化约束的压缩感知方法,选取λ=1、K=80、ϕmin和ϕmax分别为0.03和0.70,采用反复试错的方法尽可能得到满意的数据重建结果。图 5为不同压缩感知方法得到的图 4a数据重建结果信噪比随迭代次数的变化曲线。由图可见,基于重建误差Huber范数最小化约束和基于重建误差L2范数最小化约束的压缩感知方法在第80次迭代时都没有收敛,前者在第33次迭代时信噪比最高(图 5a),后者在第9次迭代时信噪比最高(图 5b)。
|
图 4 图 1a数据添加随机噪声和异常噪声的不完整地震数据 (a)高斯随机噪声强于图 1b;(b)异常噪声强度是图 1b的2倍 对图 1a分别添加15、25dB的高斯随机噪声,并利用Jitter采样理论得到不规则采样数据,然后在其中添加异常噪声,分别得到图a、图b。采样后有效信号的振幅、位置和异常噪声的振幅、位置同图 1 |
|
图 5 不同压缩感知方法得到的图 4a数据重建结果信噪比随迭代次数的变化曲线 (a)基于重建误差Huber范数最小化约束;(b)基于重建误差L2范数最小化约束 |
图 6为不同压缩感知方法的图 4a数据插值结果及其与图 1a数据的差值。由图可见:①基于重建误差Huber范数最小化约束(图 6a左)与基于重建误差L2范数最小化约束(图 6b左)的压缩感知方法的插值结果的信噪比分别为8.12和5.46,即前者的信噪比更高,但低于图 3a左(12.00),并存在残余噪声(图 6a左黑色椭圆处)及信号损伤(图 6a右黑色椭圆处)。因此,当不完整地震数据中包含幅度更大的高斯随机噪声时,基于重建误差Huber范数最小化约束的压缩感知方法在重建结果中会产生更多的残余噪声,并造成信号损伤。②基于重建误差L2范数最小化约束的压缩感知方法不能有效地去除异常噪声(图 6b左的黑、白色箭头处),插值结果的信噪比(5.46)小于图 3b左(6.00)。因此,当不完整地震数据中包含幅度更大的高斯随机噪声时,基于重建误差L2范数最小化约束的压缩感知方法会降低插值精度,仍然不能有效去除异常噪声。
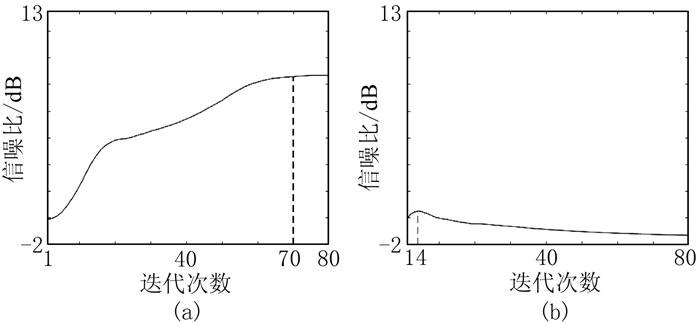
对于基于重建误差Huber范数最小化约束和基于重建误差L2范数最小化约束的压缩感知方法,选取λ=1、K=80、ϕmin和ϕmax分别为0.03和0.85,并采用反复试错的方法尽可能得到满意的数据重建结果。图 7为不同压缩感知方法得到的图 4b数据重建结果信噪比随迭代次数的变化曲线。由图可见,基于重建误差Huber范数最小化约束的压缩感知方法在第70次迭代时收敛(图 7a),基于重建误差L2范数最小化约束的压缩感知方法在第80次迭代时没有收敛,在第4次迭代时信噪比最高(图 7b)。
|
图 7 不同压缩感知方法得到的图 4b数据重建结果信噪比随迭代次数的变化曲线 (a)基于重建误差Huber范数最小化约束;(b)基于重建误差L2范数最小化约束 |
图 8为不同压缩感知方法的图 4b数据插值结果及其与图 1a数据的差值。由图可见:①基于重建误差Huber范数最小化约束(图 8a左)和基于重建误差L2范数最小化约束(图 8b左)的压缩感知方法的插值结果的信噪比分别为10.59和0.52,即前者的信噪比更高,但略低于图 3a左(12.00),并存在残余的强振幅噪声(图 8a左白色箭头处)。因此,当不完整地震数据中包含更强的异常噪声时,基于重建误差Huber范数最小化约束的压缩感知方法在重建结果中会产生残余的异常噪声,降低插值精度。②基于重建误差L2范数最小化约束的压缩感知方法不能有效去除异常噪声(图 8b左的黑、白色箭头处),插值结果的信噪比(0.52)小于图 3b左(6.00)。因此,当不完整地震数据中包含幅度更大的异常噪声时,基于重建误差L2范数最小化约束的压缩感知方法会降低插值精度,仍然不能有效去除异常噪声。
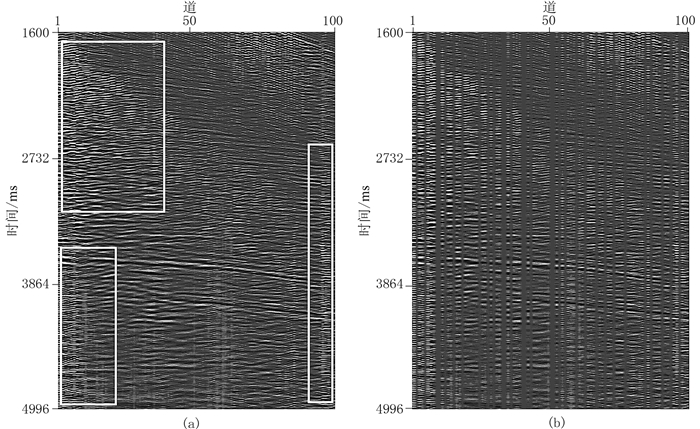
3.2 实际数据图 9为实际共炮点道集。由图可见,原始数据中存在明显的异常噪声(图 9a的白色框内),包含异常噪声的不完整地震数据缺失35%的数据(图 9b)。对于基于重建误差Huber范数最小化约束和基于重建误差L2范数最小化约束的压缩感知方法,选取λ=1、K=130、ϕmin与ϕmax分别为0.006和0.95,采用反复试错的方法尽可能得到满意的数据重建结果。此外,采用式(5)计算基于重建误差Huber范数最小化约束的压缩感知方法中的阈值c。
|
图 9 实际共炮点道集 (a)原始数据;(b)包含异常噪声的不完整地震数据 为了更好地显示处理结果,只显示了1600~4996ms的100道数据,采样间隔为4ms。对图a数据利用Jitter采样理论得到不规则采样数据,然后在其中添加异常噪声,得到图b |
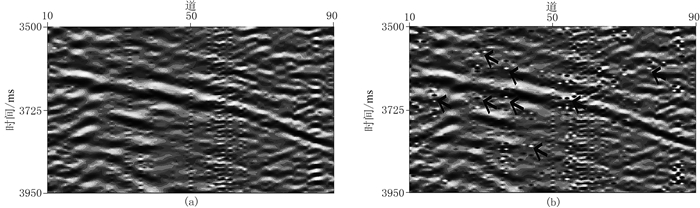
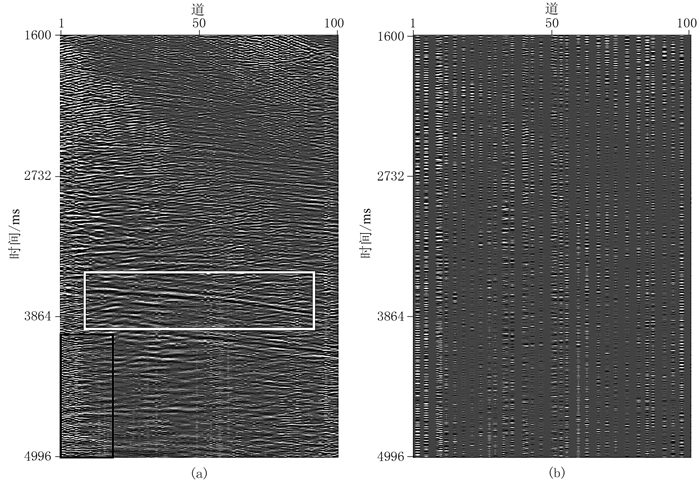
图 10为基于重建误差Huber范数最小化约束的压缩感知方法的插值结果及其与图 9a数据的差值,图 11为基于重建误差L2范数最小化约束的压缩感知方法的插值结果及其与图 9a数据的差值,图 12为图 10a、图 11a白色方框区域的局部放大。由图可见:①基于重建误差L2范数最小化约束的压缩感知方法在插值结果中残留了明显的异常脉冲噪声(图 12b的黑色箭头处),该异常脉冲噪声是由原始数据的异常噪声(图 9a的白色框内)引起的。②基于重建误差Huber范数最小化约束的压缩感知方法的插值结果(图 10a、图 12a)对大的重建误差施加了L1范数最小化约束,与基于重建误差L2范数最小化约束的压缩感知方法的插值结果(图 11a、图 12b)相比,前者的异常脉冲噪声更少,且对异常噪声的敏感性更低,插值精度更高。

|
图 10 基于重建误差Huber范数最小化约束的压缩感知方法的插值结果(c0=1.994)(a)及其与图 9a数据的差值(b) |
|
图 11 基于重建误差L2范数最小化约束的压缩感知方法的插值结果(a)及其与图 9a数据的差值(b) |
式(5)和式(6)中的参数c为区分Huber范数中L1范数和L2范数的阈值。由式(17)可知,伪地震数据中绝对值小于c的随机噪声被保留,绝对值大于c的异常噪声被衰减到c。c变大,异常噪声衰减效果减弱;c变小,异常噪声衰减效果增强,即c0值决定了c值,调整c0值可以改变c值,进而影响异常噪声衰减效果和插值精度。
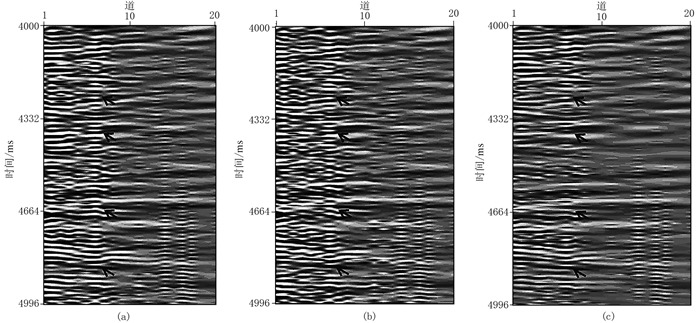
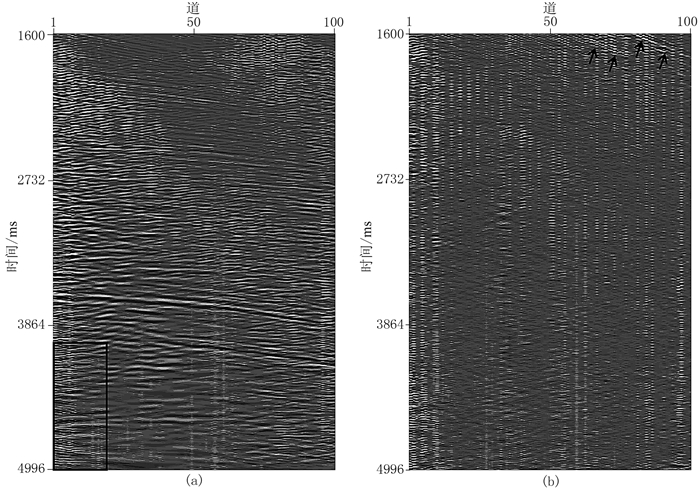
图 13为图 10a、图 11a、图 14a黑色方框区域的局部放大。由图可见:基于重建误差L2范数最小化约束的压缩感知方法不能有效消除异常噪声(图 13b的黑色箭头处);当c0=1.994时,基于重建误差Huber范数最小化约束的压缩感知方法的插值结果中仍然存在异常噪声(图 13a的黑色箭头处);保持其他参数不变,选取c0=0.7,基于重建误差Huber范数最小化约束的压缩感知方法更好地衰减了异常噪声(图 13c的黑色箭头处),然而有效信号受到损伤(图 14b的黑色箭头处)。因此,减小c0值虽然可更好衰减异常噪声,但容易损伤强有效信号。
|
图 14 基于重建误差Huber范数最小化约束的压缩感知方法的插值结果(c0=0.7)(a)及其与图 9a数据的差值(b) |
本文提出了基于重建误差Huber范数最小化约束的压缩感知方法,可以在插值处理的同时衰减地震随机噪声和异常噪声。该方法采用Huber范数对大的重构误差施加L1范数最小化约束。此外,采用L0范数对插值结果的曲波域系数施加稀疏约束。通过在每次迭代中构造伪地震数据,可以有效地求解Huber-L0最优化问题。模拟数据和实际数据处理结果表明,与基于重建误差L2范数最小化约束的压缩感知方法相比,基于重建误差Huber范数最小化约束的压缩感知方法可以更好地去除异常噪声。另外,还讨论了高斯随机噪声的强度、异常噪声强度和参数选取对插值精度的影响。在信噪比的定量计算和插值结果的图像显示方面,基于重建误差Huber范数最小化约束比基于重建误差L2范数最小化约束的压缩感知方法的插值效果更好。
附录A 求解L2-L0最优化问题的迭代步骤文献[2, 13-14, 31]采用如下迭代步骤求解L2-L0最优化问题(式(2))
| $ \boldsymbol{x}^{(k)}=T_{\phi}\left[\boldsymbol{C} \boldsymbol{d}^{(k)}\right] $ | (A-1) |
| $ \hat{\boldsymbol{d}}^{(k)}=\boldsymbol{C}^{\mathrm{T}} \boldsymbol{x}^{(k)} $ | (A-2) |
| $ \boldsymbol{d}^{(k)}=\boldsymbol{s}+(\boldsymbol{I}-\boldsymbol{R}) \hat{\boldsymbol{d}}^{(k-1)} $ | (A-3) |
式中:k为迭代次数;C为正稀疏变换;CT为逆稀疏变换;d(k)为第k次迭代的插值结果;
式(A-1)~式(A-3)假设采集的地震数据不含噪声。为了更好地消除地震数据中的高斯随机噪声,文献[33-34]采用加权迭代步骤
| $ \boldsymbol{x}^{(k)}=T_{\phi}\left[\boldsymbol{C} \boldsymbol{d}^{(k)}\right] $ | (A-4) |
| $ \hat{\boldsymbol{d}}^{(k)}=\boldsymbol{C}^{\mathrm{T}} \boldsymbol{x}^{(k)} $ | (A-5) |
| $ \boldsymbol{d}^{(k)}=\lambda s+(\boldsymbol{I}-\lambda \boldsymbol{R}) \hat{\boldsymbol{d}}^{(k-1)} $ | (A-6) |
与式(A-3)相比,式(A-6)增加了加权系数λ∈(0, 1]。λ可以弱化随机噪声对插值精度的影响,然而地震数据s中仍然有部分随机噪声被引入迭代过程,降低了插值精度。
随机噪声包含在稀疏变换后的小绝对值系数中。硬阈值算子Tϕ可以去除变换域中的小绝对值系数,进而有效地衰减随机噪声。文献[14]交换了式(A-4)中的硬阈值操作和式(A-6)中的加权映射操作,得到如下迭代步骤
| $ \hat{\boldsymbol{d}}^{(k)}=\lambda s+(\boldsymbol{I}-\lambda \boldsymbol{R}) \boldsymbol{d}^{(k-1)} $ | (A-7) |
| $ \boldsymbol{x}^{(k)}=T_{\phi}\left[\boldsymbol{C} \hat{\boldsymbol{d}}^{(k)}\right] $ | (A-8) |
| $ \boldsymbol{d}^{(k)}=\boldsymbol{C}^{\mathrm{T}} \boldsymbol{x}^{(k)} $ | (A-9) |
变换域系数x(k)不包含与高斯随机噪声有关的小绝对值系数,因此反变换后的插值结果d(k)具有较高的信噪比和插值精度。
| [1] |
李振春, 张军华. 地震数据处理方法[M]. 山东东营: 中国石油大学出版社, 2004.
|
| [2] |
Abma R, Kabir N. 3D interpolation of irregular data with a POCS algorithm[J]. Geophysics, 2006, 71(6): E91-E97. DOI:10.1190/1.2356088 |
| [3] |
Berkhout A J, Verschuur D J. Estimation of multiple scattering by iterative inversion, Part I:Theoretical consideration[J]. Geophysics, 1997, 62(5): 1586-1595. DOI:10.1190/1.1444261 |
| [4] |
Li Z X, Lu W K. Adaptive multiple subtraction based on 3D blind separation of convolved mixtures[J]. Geophysics, 2013, 78(6): V251-V266. DOI:10.1190/geo2012-0455.1 |
| [5] |
Li Z X, Li Z C, Lu W K. Multichannel predictive deconvolution based on the fast iterative shrinkage thresholding algorithm[J]. Geophysics, 2016, 81(1): V17-V30. |
| [6] |
Li Z X, Li Z C. Accelerated 3D blind separation of convolved mixtures based on the fast iterative shrin-kage thresholding algorithm for adaptive multiple subtraction[J]. Geophysics, 2018, 83(2): V99-V113. DOI:10.1190/geo2016-0384.1 |
| [7] |
Plessix R E, Muler W A. Frequency-domain finite-difference amplitude-preserving migration[J]. Geophysical Journal International, 2004, 157(3): 975-987. DOI:10.1111/j.1365-246X.2004.02282.x |
| [8] |
Hamid H, Pidlisecky A. Multitrace impedance inversion with lateral constraints[J]. Geophysics, 2015, 80(6): M101-M111. DOI:10.1190/geo2014-0546.1 |
| [9] |
Candès E J, Romberg J K, Tao T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207-1223. DOI:10.1002/cpa.20124 |
| [10] |
Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [11] |
Ma J W. Compressed sensing by iterative thresholding of geometric wavelets:a comparing study[J]. International Journal of Wavelets, Multiresolution and Information Processing, 2011, 9(1): 63-77. DOI:10.1142/S0219691311003992 |
| [12] |
白兰淑, 刘伊克, 卢回忆, 等. 基于压缩感知的Curvelet域联合迭代地震数据重建[J]. 地球物理学报, 2014, 57(9): 2937-2945. BAI Lanshu, LIU Yike, LU Huiyi, et al. Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing[J]. Chinese Journal of Geophysics, 2014, 57(9): 2937-2945. |
| [13] |
Gan S W, Wang S D, Chen Y K, et al. Compressive sensing for seismic data reconstruction via fast projection onto convex sets based on seislet transform[J]. Journal of Applied Geophysics, 2016, 130(5): 194-208. |
| [14] |
Wang B F, Wu R S, Chen X H, et al. Simultaneous seismic data interpolation and denoising with a new adaptive method based on dreamlet transform[J]. Geophysical Journal International, 2015, 201(2): 1180-1192. |
| [15] |
陈祖斌, 王丽芝, 宋杨, 等. 基于压缩感知的小波域地震数据实时压缩与高精度重构[J]. 石油地球物理勘探, 2018, 53(4): 674-681. CHEN Zubin, WANG Lizhi, SONG Yang, et al. Seismic data real-time compression and high-precision reconstruction in the wavelet domain based on the compressed sensing[J]. Oil Geophysical Prospecting, 2018, 53(4): 674-681. |
| [16] |
Wang B F. An efficient POCS interpolation method in the frequency-space domain[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(9): 1384-1387. DOI:10.1109/LGRS.2016.2589260 |
| [17] |
王新全, 耿瑜, WU Rushan, 等. 基于压缩感知的Dream-let域数据重构方法及应用[J]. 石油地球物理勘探, 2015, 50(3): 399-404. WANG Xinquan, GENG Yu, WU Rushan, et al. Seismic data reconstruction in Dreamlet domain based on compressive sensing[J]. Oil Geophysical Prospecting, 2015, 50(3): 399-404. |
| [18] |
张良, 韩立国, 许德鑫, 等. 基于压缩感知技术的Shearlet变换重建地震数据[J]. 石油地球物理勘探, 2017, 52(2): 220-225. ZHANG Liang, HAN Liguo, XU Dexin, et al. Seismic data reconstruction with Shearlet transform based on compressed sensing technology[J]. Oil Geophysical Prospecting, 2017, 52(2): 220-225. |
| [19] |
刘财, 李鹏, 刘洋, 等. 基于Seislet变换的反假频迭代数据插值方法[J]. 地球物理学报, 2013, 56(5): 1619-1627. LIU Cai, LI Peng, LIU Yang, et al. Iterative data interpolation beyond aliasing using Seislet transform[J]. Chinese Journal of Geophysics, 2013, 56(5): 1619-1627. |
| [20] |
Chen K, Sacchi M D. Robust reduced-rand filtering for erratic seismic noise attenuation[J]. Geophysics, 2015, 80(1): V1-V11. |
| [21] |
Raphael S, Viguier G, Gondoin R, et al. Multidimensional simultaneous random plus erratic noise attenuation and interpolation for seismic data by joint low-rank and sparse inversion[J]. Geophysics, 2015, 80(6): WD129-WD141. DOI:10.1190/geo2015-0066.1 |
| [22] |
Zhao Q, Du Q Z, Gong X F, et al. Signal-preserving erratic noise attenuation via iterative robust sparsity-promoting filter[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(6): 3547-3560. DOI:10.1109/TGRS.2018.2802462 |
| [23] |
Guitton A, Symes W W. Robust inversion of seismic data using the Huber norm[J]. Geophysics, 2003, 68(4): 1310-1319. DOI:10.1190/1.1598124 |
| [24] |
Huber P J, Ronchetti E M.Robust Statistics(Second Edition)[M].John Wiley & Sons, New Jersey, 2011, 693.
|
| [25] |
Wong R K W, Lee T C M. Matrix completion with noisy entries and outliers[J]. Journal of Machine Learning Research, 2017, 18(1): 1-25. |
| [26] |
Daubechies I, Defrise M, De M C. An iterative thre-sholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on Pure and Applied Mathematics, 2004, 57(11): 1413-1457. DOI:10.1002/cpa.20042 |
| [27] |
温睿, 刘国昌, 冉扬. 压缩感知地震数据重建中的三个关键因素分析[J]. 石油地球物理勘探, 2018, 53(4): 682-693. WEN Rui, LIU Guochang, RAN Yang. Three key factors in seismic data reconstruction based on compressive sensing[J]. Oil Geophysical Prospecting, 2018, 53(4): 682-693. |
| [28] |
Wang F J, Hua Q S, Liu C S. Boundary function me-thod for inverse geometry problem in two-dimensional anisotropic heat conduction equation[J]. Applied Mathematics Letters, 2018. DOI:10.1016/j.aml.2018.05.004 |
| [29] |
Holland P W, Welsh R E. Robust regression using iteratively reweighted least-squares[J]. Communications in Statistics-Theory and Methods, 1977, 6(9): 813-827. DOI:10.1080/03610927708827533 |
| [30] |
Huber P J. Robust estimation of a location parameter[J]. The Annals of Mathematical Statistics, 1964, 35(1): 73-101. |
| [31] |
Gao J J, Stanton A, Naghizadeh M, et al. Convergence improvement and noise attenuation considerations for beyond alias projection non convex sets reconstruction[J]. Geophysical Prospecting, 2013, 61(S1): 138-151. |
| [32] |
Hennenfent G, Herrmann F J. Simply denoise:Wavefield reconstruction via jittered undersampling[J]. Geo-physics, 2008, 73(3): V19-V28. |
| [33] |
Gao J J, Chen X H, Li J Y, et al. Irregular seismic data reconstruction based on exponential threshold model of POCS method[J]. Applied Geophysics, 2010, 7(3): 229-238. DOI:10.1007/s11770-010-0246-5 |
| [34] |
Yang P L, Gao J H, Chen W C. On analysis-based two-step interpolation methods for randomly sampled seismic data[J]. Computers & Geosciences, 2013, 51(2): 449-461. |



 李钟晓, 山东省青岛市市南区宁夏路308号青岛大学电子信息学院, 266071。Email:
李钟晓, 山东省青岛市市南区宁夏路308号青岛大学电子信息学院, 266071。Email: