② 中国石油东方地球物理公司研究院华北分院, 河北任丘 062552
② Huabei Branch, GRI, BGP, CNPC, Renqiu, Hebei 062552, China
地震初至拾取技术应用非常广泛,特别是在折射波和面波勘探[1]、地表静校正[2-3]、海上检波器二次定位[4]以及层析成像[5]等领域具有重要作用。初至拾取精度在一定程度影响后续地震数据处理效果,因此准确拾取初至非常重要。
为了提高初至拾取精度,业界已经提出了众多初至拾取方法,如能量比值法[6]、图像处理技术[7]、神经网络技术[8]、时频分析[9]、分形方法[10]、小波分解[11]等。由于不同初至拾取方法的适用性不同,导致不同条件下的初至拾取精度和计算效率存在较大差异,因此要根据工区地震资料的特点选取合适的初至拾取方法。随着油气勘探与开发程度的深入,复杂地形中的地震初至拾取尤为重要,因此急需寻找一种快速、有效的初至拾取方法。
BP神经网络是一种结构简单、适应性和自组织性很强的多层前向性神经网络,可操作性强,能模拟任意的非线性输入、输出关系,可较好地拾取初至[12-13]。但是BP神经网络属于静态网络,样本集的额外学习存在较大困难,在复杂地形下难以较好地拾取初至。针对上述问题,目前有多种改进方案,如附加动量法[14]、弹性BP算法[15]、学习速度自适应法[16]、牛顿法[17]、模拟退火法[18]等。然而,附加动量法和弹性BP算法建模方法的网络结构复杂、样本数目过多、网络收敛速度慢,牛顿法和模拟退火法建模过程中输入、输出节点过多,网络结构臃肿,不利于优化。学习速度法虽然输入、输出节点数减少,收敛速度快,但是依然存在参数过多的问题。
本文充分考虑上述方法的特点,结合动量法和可变学习速度法,构建的网络结构简单,参数少,收敛速度快。通过分析、对比不同地震属性对初至的识别和判断差异,选取均方根振幅比、曲线长度比、振幅、频率等4种特征属性作为输入。所提方法的关键在于改善神经网络的构建,以避免训练过程中出现噪声干扰,加强网络的性能和稳定性,具有较高的初至拾取精度和效率。
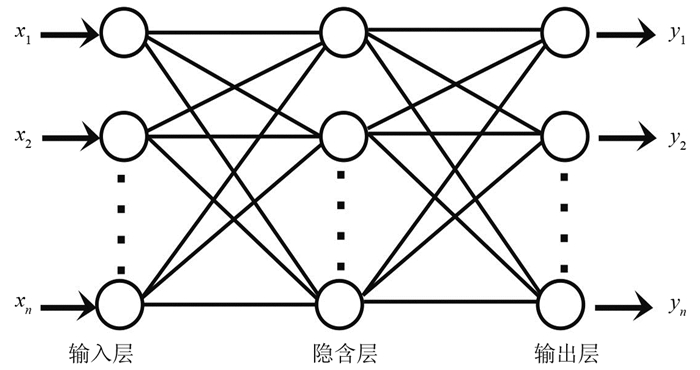
1 方法原理BP神经网络由输入层、若干隐含层和输出层相互连接构成[13],每层由若干个结点组成,每一个结点表示一个神经元,上、下层结点间通过权联接,同一层结点间没有联系[19],通过重复修正层与层间的权值完成神经网络学习。经典的3层BP网络结构如图 1所示。
|
图 1 3层BP神经网络示意图 x1,x2,…,xn为输入,y1,y2,…,yn为输出 |
BP神经网络的运行主要为信息正向传播过程和误差反向传播过程两个阶段[20]。信息正向传播过程将训练样本从输入层传播到输出层,计算网络输出值。通过对比网络输出与期望输出,计算每个输出节点的误差值。若误差超过预设的最小误差,则转入反向传播过程,将实际网络输出与期望输出之间的误差沿原来联结的通路反馈给输入层,并调整各层神经元的连接权值。对于连接权值的调整,一般采用梯度下降法,以使输出误差达到最小[21]。
由于BP神经网络具有逼近任意连续函数和非线性映射的能力,因此得到广泛应用。利用BP神经网络拾取初至,就是通过建立的神经网络学习初至样本,以此建立一个识别并提取初至的分类规则。初至样本由一系列稳定的地震属性组成,通过神经网络输出初至拾取结果。人工神经网络拾取初至的具体步骤为:①人工拾取地震初至,提取其地震属性作为学习样本;②利用建立的学习样本训练神经网络;③利用训练好的网络自动拾取初至。传统的能量比法和可变学习速度法等由于方法原理的限制,易受信噪比的影响,网络输出的拾取结果不甚理想。本文通过改进的网络构建算法,从校正量和学习速度综合入手,提升了学习算法的稳定性,提高网络的收敛速度和效率,初至拾取结果较好。
1.1 改进的神经网络预测方法标准BP算法在网络学习时需要修正权值w(t+1)和阈值θ(t+1),通常根据t时刻负梯度方向修正,而没有考虑以前时刻的梯度方向,使训练过程产生振荡,训练误差大,收敛缓慢[22]。另外一个重要原因是学习速度选择不当,即:学习速度太小,收敛太慢;学习速度太大,则可能修正过头,导致振荡甚至发散。
在初至拾取过程中,通过神经网络前一次迭代学习时的校正量影响本次校正量,从而加速网络学习收敛过程[22],权值和阈值更新公式分别为
| $ \Delta w\left( k \right) = \alpha \Delta w\left( {k - 1} \right) - \eta \frac{{\partial {E_{\rm{A}}}}}{{\partial w}} $ | (1) |
| $ \Delta \theta \left( k \right) = \alpha \Delta \theta \left( {k - 1} \right) - \eta \frac{{\partial {E_{\rm{A}}}}}{{\partial \theta }} $ | (2) |
式中:α为动量因子;η为学习速度;k为迭代次数;EA为所有样本输入一次后的总均方根误差。
由式(1)可见:当前次迭代的校正量Δw(k-1)、Δθ(k-1)过调时,惯性项与本次误差校正项Δw(k)、Δθ(k)符号相反,使本次实际校正量减小,减小了振荡;当前次校正量欠调时,惯性项与本次误差校正项符号相同,校正加速[23]。
为解决学习速度与收敛速度间的问题,通常令学习速度η为变值且具自适应性,即
| $ \eta \left( {t + 1} \right) = \left\{ {\begin{array}{*{20}{l}} {\left( {1 + \beta } \right)\eta }&{{E_{\rm{A}}}\left( t \right) > {E_{\rm{A}}}\left( {t - 1} \right)}\\ {\left( {1 - \beta } \right)\eta }&{{E_{\rm{A}}}\left( t \right) \le {E_{\rm{A}}}\left( {t - 1} \right)} \end{array}} \right. $ | (3) |
式中β为一小正数,一般取0.01~0.03。
式(3)说明,当误差减小时应增大学习速度,误差增大时应减小学习速度,从而有效缩短学习时间[24]、提高训练精度。
式(1)和式(2)中的动量因子项表示神经网络在预测初至的学习中积累的学习经验,对网络的权值和阈值调整具缓冲作用,根据学习误差使网络训练找到取最优的权值和阈值。但是由于算法原因,不能根据实际情况调整学习速度。可变学习速度法通常根据当前网络的训练情况适当地调整学习速度,在初至拾取的不同阶段使用不同的学习速度提高训练效率,但没有具体考虑误差变化情况。本文结合动量法和可变学习法改进BP算法,在学习过程中根据误差曲面的平滑程度和误差函数的变换情况自适应地设置学习速度。若误差曲面平滑,且误差数值逐渐减少,说明网络的学习结果与预期结果接近,表明当前的学习速度增量是正向的,可以继续增大学习速度;当误差曲面陡峭,且误差数值逐渐增大,表明当前的学习速度增量是负向的,需要适当减小学习速度,减少权值和阈值的增量,并取消该次权值的调整。新方法的权值和阈值更新公式分别为
| $ \Delta w\left( k \right) = \alpha \Delta w\left( {k - 1} \right) - \left( {1 - \alpha } \right)\eta \frac{{\partial {E_{\rm{A}}}}}{{\partial w}} $ | (4) |
| $ \Delta \theta \left( k \right) = \alpha \Delta \theta \left( {k - 1} \right) - \left( {1 - \alpha } \right)\eta \frac{{\partial {E_{\rm{A}}}}}{{\partial \theta }} $ | (5) |
算法中BP神经网络训练采用批处理方式,使权值在整个训练集出现后才更新一次。算法规则为:
(1) 若均方根误差在权值更新后增加,且超过某个设置的百分数(取值为1%~5%),则权值更新被取消,将学习速度乘以(1-β)(β值为0.01~0.03),并将动量因子α置0;
(2) 若均方根误差在权值更新后减少,则权值更新被接受,且将学习速度乘以(1+β),如果α为0,则恢复到以前的值(设为0.65);
(3) 若均方根误差的增长小于ε,则权值更新被接受,但学习速度保持不变。如果α为0,则恢复到以前的值。
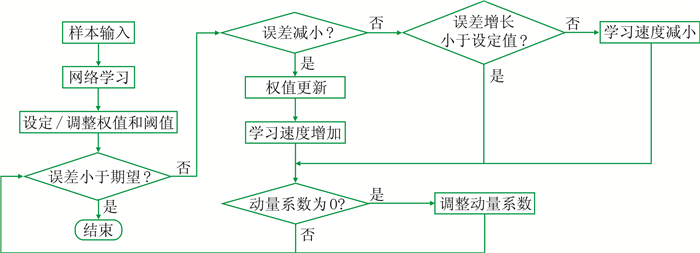
改进算法流程如图 2所示。
|
图 2 改进的神经网络方法流程示意图 |
为测试新方法的收敛性能,以一个1×10×1的3层BP网络构成一个三角函数生成器对新算法进行仿真实验。三角函数生成器表达式、弧度输入周期分别为
| $ {y_i} = 0.4\sin \left( {{\rm{ \mathsf{ π} }}{x_i}} \right)\cos \left( {8{\rm{ \mathsf{ π} }}{x_i}} \right) + 0.5 $ | (6) |
| $ {x_i} = \frac{i}{{50}}\;\;\;\;\;i = 0, \cdots ,49 $ | (7) |
从输入端输入弧度值,模拟得到函数值。将输入周期分为50等分,并作为训练模式。式中:xi为输入的弧度值;yi为输出的振幅值。
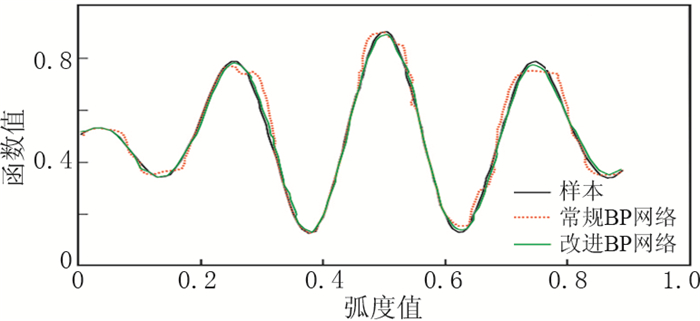
将训练集分别由经典BP神经网络和改进后的BP神经网络训练,然后对比测试结果(图 3)的收敛性能,并进行误差分析(表 1)。
|
图 3 训练样本集对比 |
|
|
表 1 试验数据误差分析 |
图 4为改进算法与常规BP算法的收敛速度。由图可见:常规BP网络在整个收敛过程中,均方根误差下降较平缓,迭代5000次后样本的均方根误差为7.82×10-4;改进算法收敛速度明显快于常规BP算法,在迭代1000次之前样本均方根误差已收敛到0.001,迭代5000次后样本均方根误差为4.15×10-4。

|
图 4 改进算法与常规BP算法的收敛速度 常规BP网络的η为0.18;改进算法的初始η为0.18,α为0.75,β为0.03,均方根误差增长上限为1% |
神经网络初至拾取方法从本质上说就是统计、分类初至与非初至,通过神经网络训练样本建立一个分类规则,分类规则的正确与否取决于神经网络训练的好坏、特征属性选取是否恰当[7]。改进的神经网络预测方法已经解决网络构建问题,还需要选取网络输入参数中的地震特征属性。稳定以及能正确区分初至波的特征属性是神经网络识别初至波的前提。文中将均方根振幅比、曲线长度比、瞬时强度比、振幅、频率等特征属性作为神经网络输入[25],特征属性选取的好坏对后续初至拾取精度影响很大。
2.1 均方根振幅比属性在实际应用中,为增加均方根振幅比的稳定性,在均方根振幅比公式中添加稳定因子,即
| $ {A_i} = {\left\{ {\frac{{{{\left[ {\sum\limits_{t = {T_0}}^{{T_2}} {{x^2}} \left( t \right)} \right]}^{\frac{1}{2}}} + \gamma E}}{{{{\left[ {\sum\limits_{t = {T_1}}^{{T_0}} {{x^2}} \left( t \right)} \right]}^{\frac{1}{2}}} + \gamma E}}} \right\}^{\frac{1}{2}}} $ | (8) |
式中:x(t)为地震道数据;γ为稳定因子,取值范围为0.1~0.5;E为地震道的相对能量;T1、T2、T0分别为不同时窗的端点(图 5)。

|
图 5 地震数据时窗示意图 |
应用模拟地震记录分析均方根振幅特征(图 6),可明显区分初至波与非初至波。

|
图 6 均方根振幅比统计柱状图 中间的“柱子”表示初至波的均方根振幅比,左、右两边的“柱子”分别表示初至波前、后的非初至波的均方根振幅比 |
在一个时窗内,曲线长度的计算公式为
| $ S = \sum\limits_{i = {T_0}}^{{T_1}} {\sqrt {{{\left( {{A_{i + 1}} - {A_i}} \right)}^2} + \Delta {T^2}} } $ | (9) |
式中:ΔТ为地震数据采样率;Ai为当前时间位置处的振幅值。
图 7为曲线长度比统计柱状图。由图可见:在初至前的2个时窗内主要是随机噪声,振幅值不大,曲线长度比接近1;初至之后的2个时窗内波形相似,曲线长度比也接近1。因此,利用曲线长度比属性能很好地识别初至波与非初至波。

|
图 7 曲线长度比统计柱状图 中间的“柱子”表示初至波的曲线长度比,左、右两边的“柱子”分别表示初至波前、后的非初至波的曲线长度比 |
瞬时强度是指地震波形的瞬时包络,通过希尔伯特变换得到原始记录数据的复地震道,能够分离地震波形的瞬时包络、瞬时频率、瞬时相位等属性。设原始地震道为x(t),则复地震道为
| $ u\left( t \right) = x\left( t \right) + i\bar x\left( t \right) $ | (10) |
式中
| $ {V_i} = \frac{{\sum\limits_{t = {T_0}}^{{T_2}} {{{\left| {u\left( t \right)} \right|}^2}} + mC}}{{\sum\limits_{t = {T_1}}^{{T_0}} {{{\left| {u\left( t \right)} \right|}^2}} + mC}} $ | (11) |
式中:

|
图 8 瞬时强度比属性分布图 |
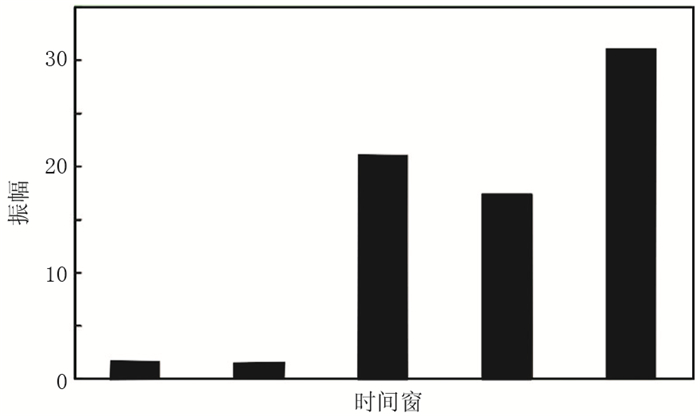
初至前、后的波形振幅差异较大,单独的振幅属性只能识别初至与初至前的波形,不能区分初至与初至后的波形(图 9)。
|
图 9 振幅统计柱状图 |
振幅属性属于半稳定属性,必须结合其他地震属性才能有效识别初至波。将均方根振幅比与振幅属性结合,可判断初至波与非初至波的边界(图 10)。

|
图 10 均方根振幅比—振幅属性交会图 |
为更好地识别初至波,通常采用短时窗傅里叶变换求取地震波主频作为频率属性。在一个高斯窗内对地震信号做傅里叶变换
| $ D\left( {\omega ,\tau } \right) = \int_L x \left( t \right){g_{\rm{a}}}\left( {t - \tau } \right){{\rm{e}}^{ - {\rm{i}}\omega t}}{\rm{d}}t $ | (12) |
式中:L为积分变换的实轴部分;ga(t-τ)为高斯窗函数;ω为角频率。
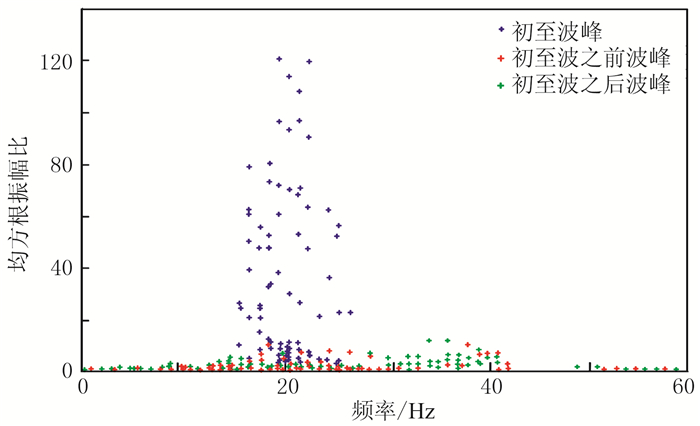
经过分析可知,同振幅属性一样,频率属性也属于半稳定性属性,因此必须结合其他属性才能有效识别初至波。将均方根属性比与频率属性结合,可以清晰识别初至波与非初至波的边界(图 11)。
|
图 11 均方根振幅比—主频属性交会图 |
从以上分析可知,均方根振幅比、曲线长度比以及瞬时强度比等属性可以有效地识别初至波与非初至波,这些属性较为稳定。但是振幅、频率等属性只能分辨初至与初至前的波形,不能区分初至与初至后的波形。因此,需要结合其他特征属性才能有效识别初至波。
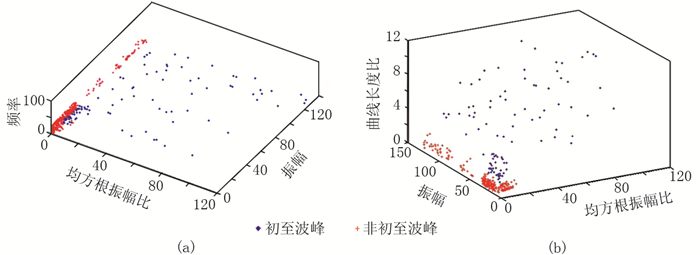
为更加准确地识别和判断初至波,通常结合3种特征属性识别和判断初至波。通过多属性交会图,可以判断初至波与非初至波的边界(图 12)。
|
图 12 属性交会图 (a)频率—均方根振幅比—振幅;(b)曲线长度比—振幅—均方根振幅比 |
从属性交会图可以看出,与单一特征属性相比,多种特征属性的组合稳定性更高,初至拾取精度较高,但是振幅、频率等半稳定性属性组合并不能有效识别初至波。为进一步提高初至拾取的精度和效率,从2个稳定性属性、2个半稳定性属性中任意选取3个属性组合作为输入,可更好地识别初至波,能够满足不同条件下的初至拾取要求。选定特征属性后,对建立的神经网络进行学习并训练初至拾取过程。
3 模型测试采用神经网络拾取初至之前,首先对神经网络进行训练,因此要建立初至的拾取样本作为网络输入。本次测试模拟多个单炮无噪记录,手动拾取1炮的初至波峰作为训练集,训练集的输出格式如表 2所示。根据训练集中的炮记录号、道号和初至波峰时间提取初至波特征属性,同时搜索初至前、后的非初至波,将初至波、非初至波的特征属性作为训练样本并进行保存,该样本集涵盖所有炮检距的初至波与非初至波的4个特征属性。实际地震记录由于地层的吸收衰减,不同炮检距数据的振幅差异较大,在提取地震属性前需要对地震数据归一化以消除振幅差异,提高初至拾取精度。
|
|
表 2 训练集输出信息 |
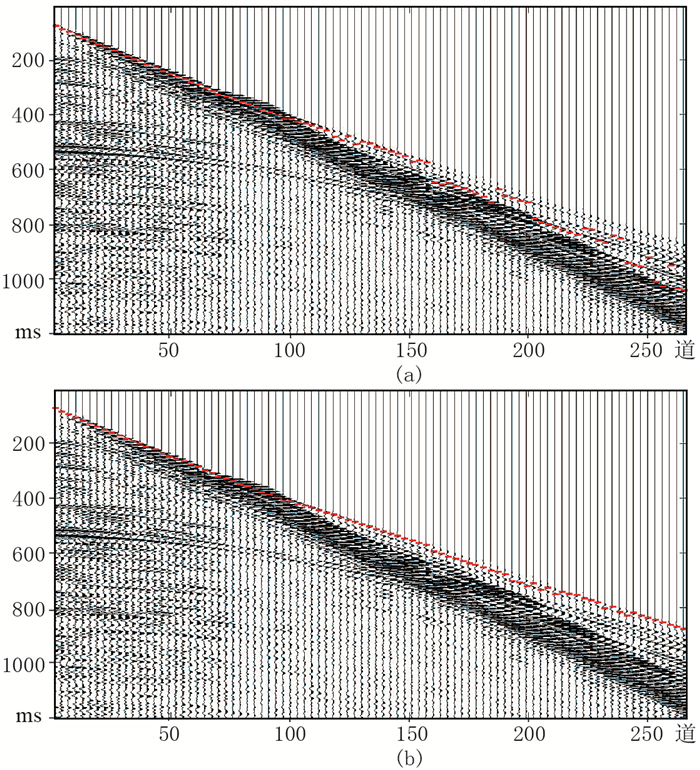
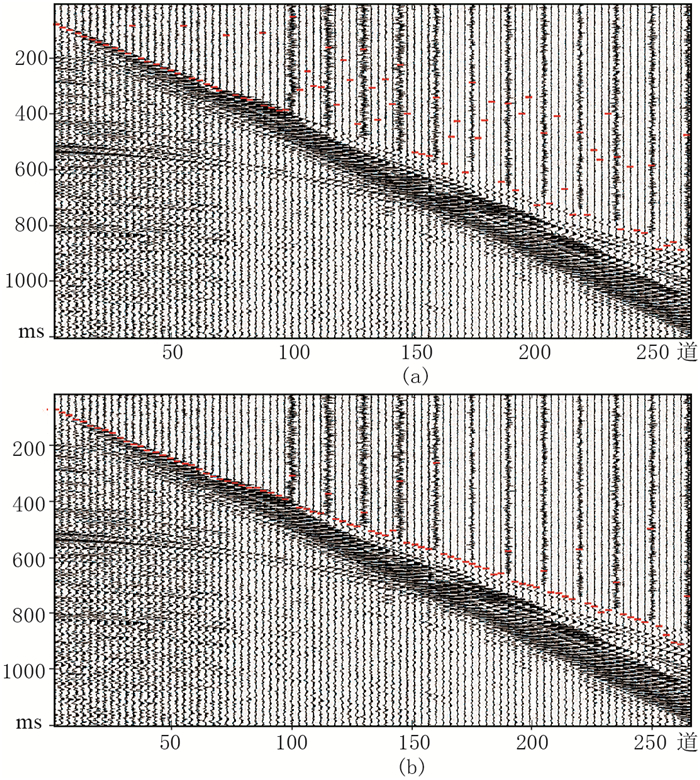
运用训练样本,分别采用改进方法与常规BP网络方法对无噪单炮记录(图 13)、含噪单炮记录(图 14)拾取初至。由图可见:①随着炮检距变大,折射波能量衰减较快,直达波仍然保持较强能量。常规BP网络初至拾取结果中部分地震道的初至为直达波(图 13a);改进方法的稳定性更好,可更准确地识别能量相对较弱的初至波(图 13b)。②当信噪比较低时,改进方法抗噪性较高,由于受噪声影响,依然存在部分初至波拾取错误(图 14b)。
|
图 13 无噪单炮记录初至拾取结果 (a)常规BP网络;(b)改进方法 |
|
图 14 含噪单炮记录(部分道数据添加相干噪声)初至拾取结果 (a)常规BP网络;(b)改进方法 |
为进一步提高初至拾取精度,通常情况下需要核对检查初至拾取结果,矫正错误较大的初至拾取时间点。为减少人工耗时,在初至拾取过程中采用奇异值检测技术控制初至拾取的质量,提高初至拾取精度和效率。在模拟记录内,神经网络在各道数据内拾取的初至时间为Ti(i=1, 2, …, R),则相邻道数据的初至拾取时间差为
| $ \Delta {T_i} = {T_{i + 1}} - {T_i}\;\;\;\;i = 1,2, \cdots ,R $ | (13) |
式中Ti为第i地震道的初至时间。
所有相邻道初至拾取误差的标准方差为
| $ \sigma = {\left[ {\frac{1}{2}\sum\limits_{i = 1}^{R - 1} {{{\left( {\Delta {T_i} - \bar T} \right)}^2}} } \right]^{\frac{1}{2}}} $ | (14) |
式中T为所有相邻道初至拾取误差的均值。
依据式(13)、式(14)建立初至拾取精度判断标准
| $ \Delta {T_i} - \bar T > \xi \sigma \;\;\;\;i = 1,2, \cdots ,R - 1 $ | (15) |
式中ξ为误差评判参数,通常取值范围为1~2。
保留满足式(15)的初至拾取时间点,否则予以剔除,并按照相邻道的初至拾取时间插值设立初至拾取参考点,即
| $ {T_i} = \frac{{{T_{i - 1}} + {T_{i + 1}}}}{2}\;\;\;\;i = 2,3, \cdots ,R - 1 $ | (16) |
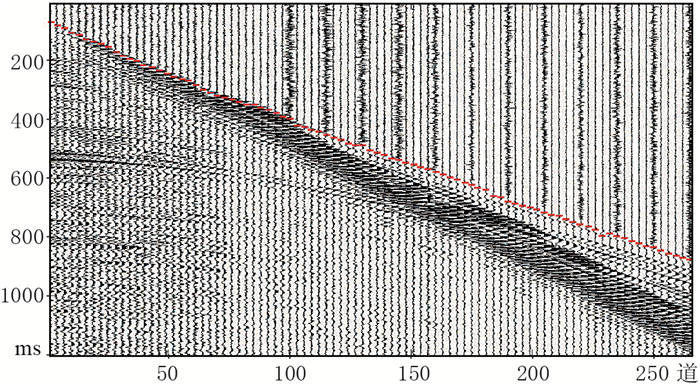
由式(16)重新拾取初至时间,再由式(15)进行判断,若符合要求则接受,否则继续计算参考点重新拾取初至。图 15为对图 14b数据自动质控的初至拾取结果。由图可见,在原出现拾取错误的位置得到了正确的拾取结果。
|
图 15 对图 14b数据自动质控的初至拾取结果 |
A区属典型的山地地貌,地表为丘陵和山地,山前带推覆体发育。地表及地下地质条件复杂,断裂发育,构造变形强烈,地层倾角大。干扰波主要以面波、地表散射为主,地震数据整体信噪比较低。从单炮分频记录上看,各频段干扰波严重,有效信号弱,单炮记录品质较差。通过相关软件拾取前1炮300道数据作为训练集训练新建立的BP神经网络。每道提取5组训练样本(1个初至波峰和4个非初至波峰)作为初始训练,考虑到地层对地震波的吸收衰减作用,地震记录中的近远炮检距数据振幅差异较大,因此在提取特征属性前对地震数据归一化以消除振幅差异[11]。根据训练集中的初至拾取时间,提取初至波和非初至波的特征属性作为训练样本,本次测试中定义初至波的输出为1,非初至波的输出为0。训练样本信息如表 3所示。
|
|
表 3 训练样本信息 |
通过人工拾取的训练样本训练神经网络后,采用定义搜索时窗的方法提高拾取效率。拟合训练集中初至波峰时间—炮检距关系曲线估算初至波峰时间,根据估算时间定义一个搜索时窗,只需在该时窗范围内搜索初至波峰即可获得后续初至。由于激发采用炸药震源,初至时间为起跳时间[26],而初至波峰和起跳时间存在3/4周期的差异,因此利用提取的频率信息f求取时移量
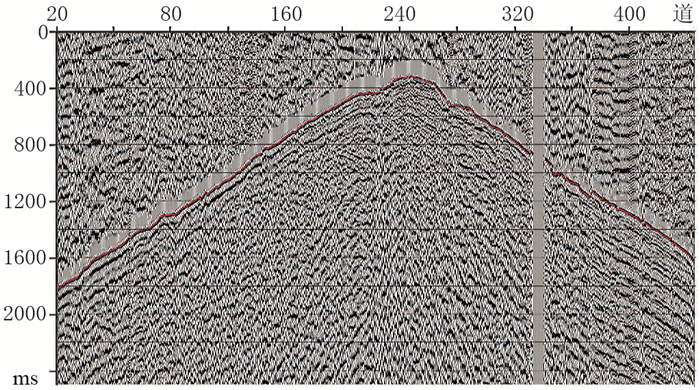
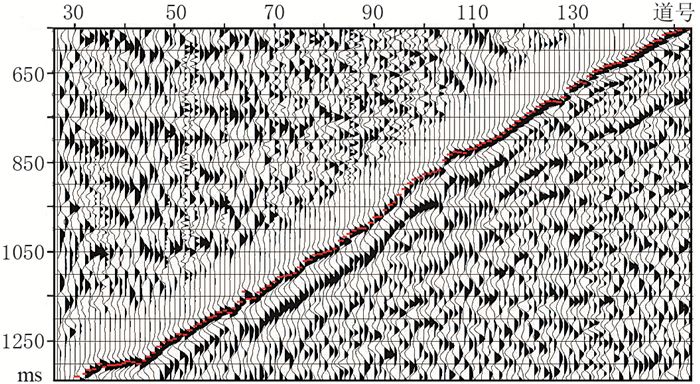
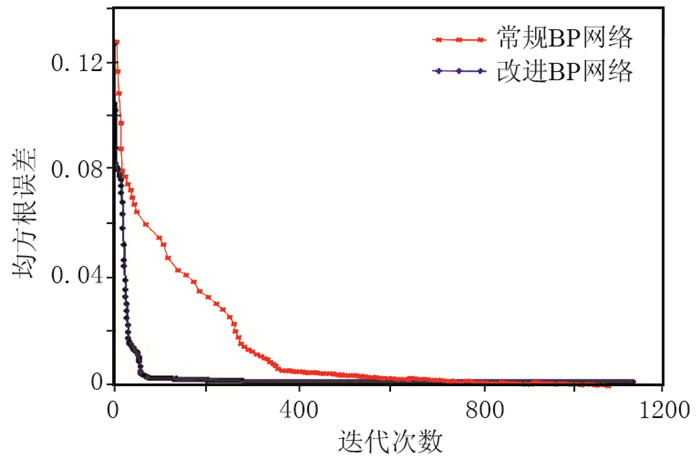
图 16为改进算法初至波自动拾取结果,图 17为图 16的局部放大,图 18为均方根误差随迭代次数的变化曲线。由图可见:拾取的初至波非常连贯,拾取结果完全正确(图 16、图 17);改进方法具有较高的拾取效率和精度(图 18)。
|
图 16 改进算法初至波自动拾取结果 初始学习速度η=0.18,α=0.75。经过1783次迭代,均方根误差最终收敛到0.000695。红色线条表示拾取的初至波 |
|
图 17 图 16的局部放大 |
|
图 18 均方根误差随迭代次数的变化曲线 |
B区构造变形强烈,以逆掩推覆为主,致使浅、深层构造不协调,目的层反射波组在浅层信噪比略高,基本连续,中、深层信噪比低,连续性不好。在横向上,随着地层变形增大,反射波组连续性变差。随着炮检距增大,直达波的振幅大于初至波,且在噪声干扰下,常规初至拾取方法很难取得较好效果。图 19为B区实际资料初至波拾取结果。由图可见,改进方法的初至拾取精度较高。

|
图 19 B区实际资料初至波拾取结果 红色线条表示拾取的初至波 |
常规BP神经网络地震初至拾取方法的精度和计算效率存在较大差异,本文提出了综合动量法和可变学习速度的BP神经网络地震初至拾取改进方法。改进方法在综合考虑初至波的多个特征属性基础上,提高了初至拾取精度,算法更稳定且收敛性更好,极大地提高了网络训练速度。
| [1] |
曾庆才, 曾同生, 欧阳永林, 等. 复杂山地层析反演静校正新方法及应用[J]. 石油地球物理勘探, 2017, 52(3): 418-425, 441. ZENG Qingcai, ZENG Tongsheng, OUYANG Yonglin, et al. A new tomographic inversion for static corrections in complex mountain areas[J]. Oil Geophysical Prospecting, 2017, 52(3): 418-425, 441. |
| [2] |
潘龙, 刘宜文, 郑鸿明, 等. 初至波剩余静校正技术在南安集海地区的应用[J]. 石油地球物理勘探, 2019, 54(2): 274-279. PAN Long, LIU Yiwen, ZHENG Hongming, et al. First-break residual static corrections applied in the southern part of Anjihai area[J]. Oil Geophysical Prospecting, 2019, 54(2): 274-279. |
| [3] |
谢春, 刘玉柱, 董良国, 等. 基于声波方程的有限频伴随状态法初至波旅行时层析[J]. 石油地球物理勘探, 2015, 50(2): 274-282. XIE Chun, LIU Yuzhu, DONG Liangguo, et al. First arrival tomography with finite frequency adjoint state method based on acoustic wave equation[J]. Oil Geophysical Prospecting, 2015, 50(2): 274-282. |
| [4] |
程远方, 李素闪, 张文栋, 等. 海底电缆资料处理关键技术及其应用[J]. 石油地球物理勘探, 2017, 52(增刊2): 26-31. CHENG Yuanfang, LI Sushan, ZHANG Wendong, et al. Key techniques for OBC data processing[J]. Oil Geophysical Prospecting, 2017, 52(S2): 26-31. |
| [5] |
杨国权, 丁鹏程, 李振春, 等. 应用线性方程程函方程和整形正则化的三维初至波旅行时层析[J]. 石油地球物理勘探, 2017, 52(2): 264-272. YANG Guoquan, DING Pengcheng, LI Zhenchun, et al. 3D first arrival traveltime tomography with lineari-zed eikonal equation and shaping regularization[J]. Oil Geophysical Prospecting, 2017, 52(2): 264-272. |
| [6] |
左国平, 王彦春, 隋荣亮. 利用能量比法拾取地震初至的一种改进方法[J]. 石油物探, 2004, 43(4): 345-347. ZUO Guoping, WANG Yanchun, SUI Rongliang. An improved method for first arrival pickup using energy ratio[J]. Geophysical Prospecting for Petroleum, 2004, 43(4): 345-347. DOI:10.3969/j.issn.1000-1441.2004.04.008 |
| [7] |
岳龙, 刘怀山, 刘凯, 等. 基于时频分析的初至拾取方法研究[J]. 石油物探, 2015, 54(5): 508-520. YUE Long, LIU Huaishan, LIU Kai, et al. First-break picking based on time-frequency analysis[J]. Geophysical Prospecting for Petroleum, 2015, 54(5): 508-520. DOI:10.3969/j.issn.1000-1441.2015.05.004 |
| [8] |
牛沛琛, 张建中. 基于数字图像处理的地震波初至时间检测[J]. 计算机与现代化, 2007(4): 27-30. NIU Peichen, ZHANG Jianzhong. First arrival picking based on image processing methods[J]. Computer and Modernization, 2007(4): 27-30. DOI:10.3969/j.issn.1006-2475.2007.04.009 |
| [9] |
盛冠群, 李振春, 王维波, 等. 基于小波分解与高阶统计量的微地震初至拾取方法研究[J]. 石油物探, 2015, 54(5): 388-395. SHENG Guanqun, LI Zhenchun, WANG Weibo, et al. A new automatic detection method of microseismic events based on wavelet decomposition and high-order statics[J]. Geophysical Prospecting for Petroleum, 2015, 54(5): 388-395. |
| [10] |
曹茂森, 任青文, 万林梅, 等. Length分形维算法拾去地震波初至[J]. 石油地球物理勘探, 2004, 39(5): 509-514. CAO Maosen, REN Qingwen, WAN Linmei, et al. Length fractal dimension method for picking seismic first break[J]. Oil Geophysical Prospecting, 2004, 39(5): 509-514. DOI:10.3321/j.issn:1000-7210.2004.05.004 |
| [11] |
宋建国, 李赋真, 徐维秀, 等. 改进的神经网络级联相关算法及其在初至拾取中的应用[J]. 石油地球物理勘探, 2018, 53(1): 8-16. SONG Jianguo, LI Fuzhen, XU Weixiu, et al. An improved neural-network cascade-correlation algorithm and its application in seismic first break picking[J]. Oil Geophysical Prospecting, 2018, 53(1): 8-16. |
| [12] |
Murat M E, Rudman A J. Automated first arrival picking:A neural network approach[J]. Geophysical Prospecting, 1992, 40(6): 587-604. DOI:10.1111/j.1365-2478.1992.tb00543.x |
| [13] |
王金峰, 罗省贤. BP神经网络的改进及其在初至拾取中的应用[J]. 物探化探技术, 2006, 28(1): 14-17. WANG Jinfeng, LUO Shengxian. The improved BP neural network and its application in seismic first breaks picking[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2006, 28(1): 14-17. |
| [14] |
Steven F. Multiple classifier architectures and their application to credit risk assessment[J]. European Journal of Operational Research, 2011. DOI:10.1016/j.ejor.2010.09.029 |
| [15] |
Thomas L, Crook J, Edelman D. Credit Scoring and Its Applications[M]. Society for Industrial and Applied Mathematics, 2017.
|
| [16] |
高明亮, 于生宝, 郑建波, 等. 基于IGA算法的电阻率神经网络反演成像研究[J]. 地球物理学报, 2016, 59(11): 4372-4382. GAO Mingliang, YU Shengbao, ZHENG Jianbo, et al. Research of resistivity imaging using neural network based on immune genetic algorithm[J]. Chinese Journal of Geophysics, 2016, 59(11): 4372-4382. DOI:10.6038/cjg20161136 |
| [17] |
Domingos P O, Silva F M, Neto H C.An efficient and scalable architecture for neural networks with backpropagation learning[C].International Conference on Field Programmable Logic and Applications, 2005, 89-94.
|
| [18] |
张繁昌, 印兴耀. 用模拟退火神经网络技术进行波阻抗反演[J]. 石油大学学报(自然科学版), 1997, 21(6): 16-18. ZHANG Fanchang, YIN Xingyao. Impedance inversion by using annealing neural network[J]. Journal of China University of Petroleum(Edition of Natural Science), 1997, 21(6): 16-18. |
| [19] |
宋江涛, 邓小宝, 魏海涛. 航空发动机试车台推力仿真技术研究[J]. 计算机仿真, 2012, 29(1): 67-70. SONG Jiangtao, DENG Xiaobao, WEI Haitao. Research on simulating test-bed thrusts of aero-engine[J]. Computer Simulation, 2012, 29(1): 67-70. DOI:10.3969/j.issn.1006-9348.2012.01.017 |
| [20] |
蒋宗礼. 人工神经网络导论[M]. 北京: 高等教育出版社, 2001: 39-44.
|
| [21] |
陈钢花, 董维武. 遗传神经网络在煤质测井评价中的应用[J]. 测井技术, 2011, 35(2): 171-175. CHEN Ganghua, DONG Weiwu. Application of genetic neural network to coal quality evalution based on log data[J]. Well Logging Technology, 2011, 35(2): 171-175. DOI:10.3969/j.issn.1004-1338.2011.02.015 |
| [22] |
刘军伟, 余小清, 万旺根, 等. 基于改进型BP神经网络的音频多分类[J]. 上海大学学报(自然科学版), 2012, 18(2): 127-131. LIU Junwei, YU Xiaoqing, WAN Wanggen, et al. Multiple classification of audio based on improved BP neural network[J]. Journal of Shanghai University(Natural Science Edition), 2012, 18(2): 127-131. |
| [23] |
高伟华. 基于混合智能技术的抽油机电力故障诊断方法的研究[J]. 计算机与数字工程, 2018, 46(9): 1905-1910. GAO Weihua. Research on power fault diagnosis method of pumping unit based on HIS[J]. Computer & Digital Engineering, 2018, 46(9): 1905-1910. DOI:10.3969/j.issn.1672-9722.2018.09.041 |
| [24] |
李义宝, 张学勇, 马建国, 等. 基于BP神经网络的改进算法研究[J]. 合肥工业大学学报(自然科学版), 2005, 28(6): 668-671. LI Yibao, ZHANG Xueyong, MA Jianguo, et al. Study of improving algorithms based on the BP neural network[J]. Journal of Hefei University of Technology(Natural Science), 2005, 28(6): 668-671. DOI:10.3969/j.issn.1003-5060.2005.06.024 |
| [25] |
Hart D I.Improving the reliability of first break picking with neural networks[C].SEG Technical Program Expanded Abstracts, 1996, 15: 1662-1665.
|
| [26] |
刘志成. 初至智能拾取技术[J]. 石油物探, 2007, 46(5): 521-530. LIU Zhicheng. First break intelligent picking technique[J]. Geophysical Prospecting for Petroleum, 2007, 46(5): 521-530. DOI:10.3969/j.issn.1000-1441.2007.05.015 |



 曹晓莉, 山东省东营市东营区牛庄镇镇前街173号中石化地球物理公司胜利分公司, 257086。Email:
曹晓莉, 山东省东营市东营区牛庄镇镇前街173号中石化地球物理公司胜利分公司, 257086。Email: