② 中国地质大学(武汉)地球物理与空间信息学院, 湖北武汉 430074
② Institute of Geophysics and Geomatics, China University of Geosciences(Wuhan), Wuhan, Hubei 430074, China
海洋地震资料多次波压制技术主要分为两大类:①基于多次波与一次波差异的滤波技术[1-4];②多次波预测结合自适应相减技术[5-9]。第一类针对多次波压制技术不仅仅适用于海洋地震资料多次波压制,对陆上多次波也可以进行有效压制[10-12]。第二类对复杂多次波、长短周期多次波具有更好压制效果及更广适用范围,因而也得到了推广应用。
第二类中的基于波动方程的多次波预测可分为波场延拓法与反馈迭代法[8]。前者是在已知海底情况下,利用单程波或双程波方程进行波场外推;后者则是一种完全的数据驱动方法,不需任何先验信息,但对于复杂、低信噪比情况,其预测模型往往与实际模型存在较大偏差。Morley[13]对基于波动方程预测多次波的延拓算子进行了推导,并给出了近似的简化形式;随后,也有很多业界人士[14-16]采用不同近似方式对Morley方法进行了研究和完善,如Wiggins[17]基于该方法,在炮域利用Kirchhoff求和方式进行波场外推。耿伟峰等[18]研究了基于单程波的复杂海底多次波预测方法,较准确地预测了起伏海底产生的多次波。但对于特别复杂的海底情况,单程波法需历经非常繁杂的正演运算才能预测出多次波,时效上无法企及简便快捷的相移法;同时,对于高阶多次波,还需反复进行延拓才能预测。
复杂海底下地层反射往往不是规则的双曲线同相轴,同时绕射波很发育,使下伏地层反射同相轴表现出低信噪比特征,一次有效反射波难以分辨。通常,自由表面多次波压制(Surface Related Multiple Elimination,SRME)包含两个隐含前提条件:①震源子波已知;②褶积过程中格林函数可近似估计。由于子波及精确格林函数均为未知,实际处理中常用地震数据代替地震子波,而格林函数采用近似解,导致SRME预测模型仅符合多次波运动学特征,而振幅和相位等动力学特征与实际多次波难以完全匹配,因此后续需通过最小二乘自适应相减从原始数据中去除多次波[8]。由于格林函数无法较好地近似复杂海底多次波,SRME预测模型与实际多次波偏差较大,该偏差主要体现在数据信噪比、同相轴连续性、多次波模型的运动学与动力学准确性等方面,致使后续难以真正做到“自适应相减”而压制多次波。针对陆架坡折区,张连群等[19]采用组合法压制多次波,但对于波传播路径复杂的陆坡区,仍存在多次波预测信噪比低、多次波残留等问题。
针对崎岖海底多次波路径复杂、绕射波及绕射多次波发育等问题,文中重点研究了基于单、双程波动方程多次波预测法,即首先将海面地震记录延拓到海底,再次延拓到海面就可得到多次波模型。通过与SRME预测多次波模型对比,理论模型及实际数据试验表明该方法预测的多次波模型具有更高的信噪比、与实际多次波在很多情况下的动力学和运动学特征的吻合度更高,更有利于后续自适应相减消除多次波。
由于该方法需已知岩石物理模型,会限制该技术对多次波预测的完整性,因此文中对比了仅有海底模型、完整真实速度模型及SRME预测多次波模型结果。数据试算表明:若仅已知海底模型,在地下存在多个强阻抗界面的情况下该方法预测多次波是不完整的。通过与真实完整速度模型预测结果对比,由于海洋地震资料多次波主要是自由表面多次波(Surface Related Multiple,SRM),该方法也能预测大部分多次波。因此,建议将该方法与SRME技术联合预测多次波模型,多次采用自适应匹配相减可提高复杂海底多次波压制效果。
1 波动方程延拓多次波预测海洋地震资料多次波压制的最主要任务是去除与自由表面相关的多次波,它是指由地下反射界面反射的地震波到达自由界面检波器后,在自由界面再进行至少一次下行反射,然后在地下经过一定传播路径重新返回自由界面检波器,并被接收到的地震波。由于海底及海面通常是两个强反射界面,尤其是海面,其反射系数近似为-1,海洋地震资料多次波以此界面反射多次波为主,相对于其他界面反射形成的SRM及层间多次波,这些多次波具有能量强、多次波反射阶数较高等特点。
海洋地震勘探主要是用拖缆采集并接收纵波数据,故文中采用一阶速度—应力声波方程
| $ \left\{\begin{array}{l} \frac{\partial p}{\partial t}=\rho v^{2}\left(\frac{\partial v_{x}}{\partial x}+\frac{\partial v_{z}}{\partial z}\right) \\ \frac{\partial v_{x}}{\partial t}=\frac{1}{\rho} \frac{\partial p}{\partial x} \\ \frac{\partial v_{z}}{\partial t}=\frac{1}{\rho} \frac{\partial p}{\partial z} \end{array}\right. $ | (1) |
进行波场延拓。式中:p为地下介质的应力;v为地下介质纵波速度;vx、vz分别为地下介质水平和垂直方向振动速度;ρ为地下介质密度。
基于式(1)的多次波预测需已知地下介质的纵波速度和密度模型,若只是预测与海底海面相关的多次波,则仅需知道海底深度、海底(地层)纵波速度及密度、海水的纵波速度和密度。海水及海底(地层)纵波速度和密度采用工区经验参数,其中海水纵波速度为1500m/s、密度为1.0g/cm3,海底(地层)纵波速度为1650m/s、密度为1.8g/cm3。海底(地层)速度和密度可通过估计方式得到,也可设定为一个经验值,其准确度对多次波模型预测结果的影响不很显著;海底深度则可从地震数据中提取。
基于式(1)的多次波预测过程包含两大步骤:
(1) 首先将海面地震记录prec向海底延拓,此过程把地震记录当成边界条件,即p(t, x, z=0)=prec,采用顺时外推记录海底每一时刻的地震记录即可得延拓到海底的地震记录p1=p(t, x, z=wb),其中wb为海底深度;
(2) 将步骤(1)中延拓到海底的地震记录p1再延拓到海面,此时把步骤(1)中延拓到海底的记录作为边界条件,即p(t, x, z=wb)=p1,顺时外推到海面即可得到多次波模型M=p(t, x, z=0);可通过设置自由边界条件得到水体多阶多次波模型。
如果应用单程波进行延拓,整个计算过程与一阶速度—应力声波方程延拓一致,本文首先将地震数据从t-x域变换到f-kx域
| $ p(t,x)\mathop \Rightarrow \limits^{{\rm{FFT}}} P\left( {f,{k_x}} \right) $ | (2) |
式中FFT为正傅里叶变换。
采用相移法对接收数据进行延拓
| $ P\left(f, k_{x}\right)_{z+\Delta z}=P\left(f, k_{x}\right)_{z} \exp \left[\pm \frac{2 {\rm \pi} f}{v} \sqrt{1-\left(\frac{v k_{x}}{2 \pi f}\right)^{2}}\right] $ | (3) |
式中:v为介质纵波速度;±分别对应上、下行波;Δz为延拓步长。
再将延拓后的数据变换回t-x域得到延拓后的地震记录
| $ {P_z}\left( {f,{k_x}} \right)\mathop \Rightarrow \limits^{{\rm{IFFT}}} {P_z}(t,x) $ | (4) |
式中IFFT为反傅里叶变换。
2 SRME多次波预测SRME技术也是基于波动方程理论,通常采用迭代褶积计算方式。SRME模型预测迭代式为
| $ P_{0}^{\mathit{n}+1}=P-P_{0}^{\mathit{n}} A^{n+1} P $ | (5) |
式中:P为输入数据,包含一次有效反射波和多次波数据;P0为不包含多次波的一次有效反射波数据;A为与自由表面相关的算子;n为迭代次数。
由式(5)可知,只要给出一个不包含多次波的数据P0及输入数据P,即可得到一个新的不包含多次波的数据。由于实际数据P0是未知的,因此通常假设P0=P。
假设实际数据已经消除了子波、震源及检波器影响,同时不包含直达波和折射波。在频率域预测SRM包含以下步骤:
(1) 将时间域输入数据p(t, x)变换到频率域P(ω, x),其中x为炮点、检波点坐标;
(2) 迭代预测SRM:Mn+1(ω, x)=P0n(ω, x)×An-1P(ω, x);
(3) 将频率域多次波模型Mn+1(ω, x)变换到时间域mn+1(t, x)。
SRME也可在时间域进行计算,步骤(2)中的频率域乘积变为时间域褶积即可。
上述过程实际上将任意一个多次波看作是两个一次波或一次波与多次波二次反射形成的结果,对原始数据沿时间做褶积、沿空间叠加求和得到。将所有满足多次波路径的地震道两两褶积并求和,即可预测某一炮检对地震道的所有自由表面多次波。
3 数据测试为了测评文中方法对复杂海底多次波模型预测的有效性及局限性,设计了如图 1所示的速度模型,该模型中包含一个陆架坡折区、崎岖海底,海底以下还包含一个高速砂体。分别针对仅有水层海底纵波速度—密度模型、真实纵波速度—密度模型利用本文方法预测多次波,并对比纵波速度—密度模型对多次波预测结果的差异。模型计算最大炮检距为6000m,最小炮检距为0,炮点距为25m。图 1显示了第1炮的炮点、检波点位置。图 2a和图 2b为陆架坡折下伏包含SRM与不包含SRM数据,由于受到绕射波和绕射多次波影响,陆架坡折下炮集数据信噪比明显降低,有效信号同相轴被绕射波及绕射多次掩盖而难以识别。

|
图 1 陆架坡折、崎岖海底速度(a)和密度(b)模型 |
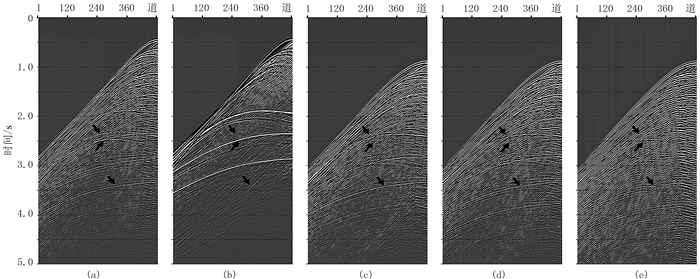
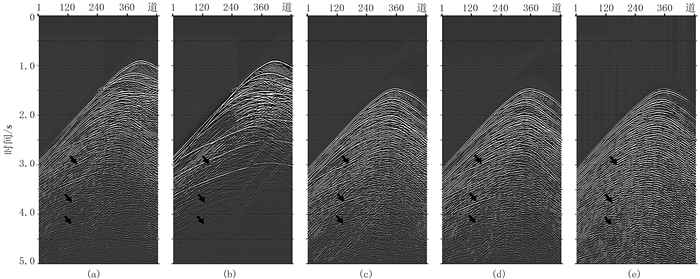
图 2和图 3为陆架坡折区不同方法预测多次波模型对比图,其中图 2为第88炮、图 3为第168炮。从图中可见箭头标注处存在一个明显的连续多次波同相轴,SRME方法预测的多次波模型信噪比明显偏低,同相轴连续性较差;而波动方程预测的多次波模型,无论是海底模型还是真实速度模型,其结果数据信噪比均较高,与实际数据多次波动力学及运动学特征更加吻合。同时,从图 2d中可见向上箭头所指同相轴在仅已知海底模型的情况下,无法预测该多次波,而完整模型和SRME均可预测出该同相轴,说明基于模型的多次波预测方法存在一定局限性,但从图 2c与图 2d的对比可知其多次波预测结果差异性较小。
|
图 2 陆架坡折区多次波预测模型对比(第88炮) (a)包含SRM;(b)不含SRM;(c)真实速度模型预测多次波模型;(d)仅海底模型预测多次波模型;(e)SRME方法预测多次波模型 |
|
图 3 陆架坡折区多次波预测模型对比(第168炮) (a)包含SRM;(b)不含SRM;(c)真实速度模型预测多次波模型;(d)仅海底模型预测多次波模型;(e)SRME方法预测多次波模型 |
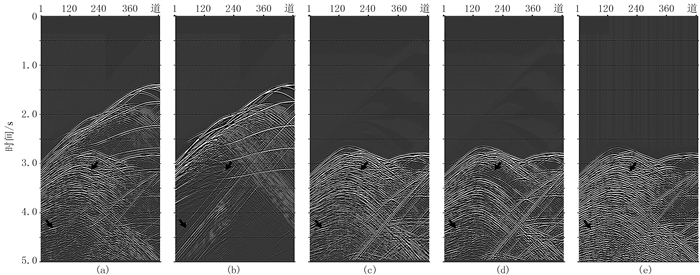
图 4为包含陆坡及崎岖海底反射的炮点处不同方法预测多次波模型对比图。对于陆坡及崎岖海底地区,受海底起伏地形影响,格林函数无法较好地近似复杂海底多次波(图 4a),SRME预测多次波模型(图 4e)与实际多次波振幅偏差较为明显,更具体地说这种偏差主要体现在前述的数据信噪比、同相轴连续性、多次波模型的运动学与动力学准确性,致使后续自适应相减无法较好地压制多次波。
|
图 4 崎岖海底多次波预测模型对比(第268炮) (a)包含SRM;(b)不含SRM;(c)真实速度模型预测多次波模型;(d)仅海底模型预测多次波模型;(e)SRME方法预测多次波模型 |
对比仅海底模型多次波预测模型(图 4d)与真实速度模型多次波预测模型(图 4c,上方箭头指示处),仅海底模型无法预测所有多次波,这种差异性体现较为明显。而相比于其他位置处,两种模型预测的多次波模型差异则不明显。从上面陆架坡折区(图 2、图 3)预测结果对比看,也说明了相同的问题。
针对崎岖海底及陆架坡折等复杂海底构造,文中所提波动方程多次波预测方法具有较大优势。同时,在仅已知海底模型的情况下也存在一定的不足。若采用波动方程与SRME加权联合预测复杂海底多次波模型,则可大大提高多次波预测准确度,进而提高复杂海底多次波压制效果。
图 5为第418炮处自由表面接收数据(图 5a)及双程波(图 5b)、单程波(图 5c)预测多次波模型。此处仅采用海底模型,单程波计算采用相移叠加法。由于该处海底相对复杂,主要是炮点处反射点存在剧烈横向变化,相移法无法较好地近似其格林函数。可见双程波可较好地预测该处的多次波模型,但单程波却无法准确预测该处的多次波模型。这就说明了采用简单相移法基于单程波预测多次波时,在复杂海底可能存在多次波模型预测不准确的情况,若想准确利用单程波预测多次波模型,则需选择更适应于速度横向变化的单程波求解方法,或采用双程波动方程做波场延拓。

|
图 5 崎岖海底自由表面接收数据(a)及与双程波(b)、单程波(c)预测多次波预测模型的对比(第418炮) |
为了验证基于模型的波动方程预测方法对实际地震资料的应用效果,选择南海西部崎岖海底坡折区原始地震测线(图 6)做测试。其最小炮检距为182m,最大炮检距为5000m,道距为12.5m。在进行波动方程多次波预测前,先要利用叠前深度偏移对海底进行准确的成像。拾取海底数据建立海底模型,海水及海底岩石物理参数选取前文所述模型参数,再做多次波预测。

|
图 6 实际崎岖海底坡折区偏移叠加剖面 |
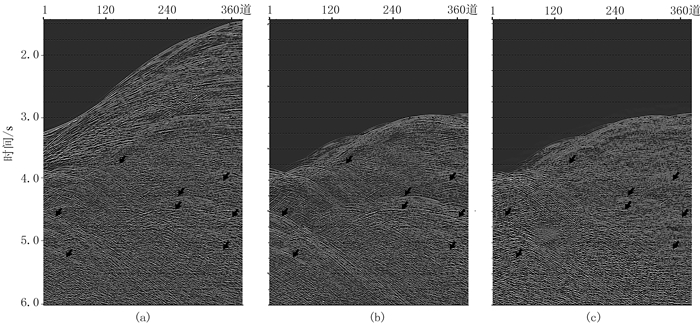
图 7为图 6白色虚线位置处波动方程与SRME方法预测结果的对比。相对于SRME预测多次波,与模型数据预测结果相一致,波动方程预测多次波(图 7b)的信噪比、波形运动学及动力学特征都要更准确。SRME可预测出大部分多次波,但多次波模型的信噪比、同相轴连续性(图 7c)要明显偏低。
|
图 7 实际崎岖海底坡折区地震数据(a)波动方程(b)及SRME(c)多次波预测结果对比 |
针对崎岖海底多次波路径复杂、绕射波及绕射多次波发育等情形,文中提出了基于单程波与双程波波动方程延拓的多次波预测方法,重点研究、对比了基于模型的波动方程预测法及SRME预测法对复杂海底多次波预测效果。基于模型的波动方程预测方法,首先将海面地震记录延拓到海底,再延拓到海面得到多次波模型。理论模型及实际数据试验结果表明:与SRME预测法相比,所提方法预测的多次波模型具有更高信噪比、与实际多次波在大多情况下动力学和运动学特征吻合度更高,更有利于后续自适应相减消除多次波。
本文方法的应用需已知完整的岩石物理模型,若仅已知海底情况则其预测效果会受到影响;但由于海洋地震多次波主要是SRM,通过与完整真实速度模型预测结果对比,即使仅已知海底岩石物理参数,应用本文方法仍能预测到大部分多次波。
建议兼顾基于模型的波动方程预测法及基于数据驱动的SRME技术各自的优点,并采用自适应匹配相减,以更彻底地消除复杂海底多次波。
| [1] |
Ryu J V. Decomposition (DECOM) approach applied to wave field analysis with seismic reflection records[J]. Geophysics, 1982, 47(6): 869-883. |
| [2] |
Hampson D. Inverse velocity stacking for multiple elimination[J]. Journal of Canadian Society Exploration Geophysicist, 1986, 22(1): 44-55. |
| [3] |
Foster D, Mosher C. Suppression of multiple reflec-tions using the Radon transform[J]. Geophysics, 1992, 57(3): 386-395. |
| [4] |
谢俊法, 孙成禹, 韩文功. 迭代抛物Radon变换法分离一次波与多次波[J]. 石油地球物理勘探, 2014, 49(1): 76-81. XIE Junfa, SUN Chengyu, HAN Wengong. Iterative parabolic Radon transform for primary and multiple separations[J]. Oil Geophysical Prospecting, 2014, 49(1): 76-81. |
| [5] |
Verschuur D J. Seismic Multiple Removal Techniques Past, Present and Future[M]. EAGE Publication, 2006.
|
| [6] |
丁在宇, 杨勇, 王一鸣, 等. 浅海拖缆地震数据处理中关键技术的应用与效果[J]. 石油地球物理勘探, 2017, 52(增刊2): 56-63. DING Zaiyu, YANG Yong, WANG Yiming, et al. Key processing techniques for shallow water tow-streamer seismic data[J]. Oil Geophysical Prospecting, 2017, 52(S2): 56-63. |
| [7] |
叶月明, 赵昌垒, 姚根顺, 等. 数据驱动型层间多次波预测方法研究[J]. 石油地球物理勘探, 2014, 49(2): 244-251. YE Yueming, ZHAO Changlei, YAO Genshun, et al. Study of data-driven interbed multiple prediction[J]. Oil Geophysical Prospecting, 2014, 49(2): 244-251. |
| [8] |
Verschuur D J and Berkhout A J. Estimation of multi-ple scattering by iterative inversion, Part Ⅱ:Practical aspects and examples[J]. Geophysics, 1997, 62(5): 1596-1611. |
| [9] |
赵保宗, 孙永清, 李学聪. 基于波动方程的多次波压制方法应用研究[J]. 地球物理学进展, 2010, 25(1): 272-281. ZHAO Baozong, SUN Yongqing, LI Xuecong. The progress of the multiple attenuation method based on the wave-equation[J]. Progress in Geophysics, 2010, 25(1): 272-281. |
| [10] |
曾华会, 王孝, 杨维, 等. 分级组合多次波压制技术——以玛湖地区为例[J]. 石油地球物理勘探, 2018, 53(增刊2): 13-19. ZENG Huahui, WANG Xiao, YANG Wei, et al. Stepped-combination multiples suppression:an example in Mahu Area[J]. Oil Geophysical Prospecting, 2018, 53(S2): 13-19. |
| [11] |
刘语, 刘建红, 刘国峰, 等. 陆上地震资料多次波识别与压制技术[J]. 石油地球物理勘探, 2018, 53(增刊1): 24-28. LIU Yu, LIU Jianhong, LIU Guofeng, et al. Multiple identification and suppression on land seismic data[J]. Oil Geophysical Prospecting, 2018, 53(S1): 24-28. |
| [12] |
戴晓峰, 徐右平, 甘利灯, 等. 川中深层——超深层多次波识别和压制技术-以高石梯-磨溪连片三维区为例[J]. 石油地球物理勘探, 2019, 54(1): 54-64. DAI Xiaofeng, XU Youping, GAN Lideng, et al. Deep & ultra-deep multiple suppression in Central Sichuan:an example of Gaoshiti-Moxi[J]. Oil Geophysical Prospecting, 2019, 54(1): 54-64. |
| [13] |
Morley L.Predictive Techniques for Marine Multiple Suppression[D].Stanford University, 1982.
|
| [14] |
Bernth H and Sonneland L.Wavefield extrapolation techniques for prestack attenuation of water reverberations[C].SEG Technical Program Expanded Abstracts, 1983, 2: 264-265.
|
| [15] |
Berryhill J R and Kim Y C. Deep-water peg legs and multiples:Emulation and suppression[J]. Geophy-sics, 1986, 51(12): 2177-2184. |
| [16] |
Taner M T. Long period sea-floor multiples and their suppression[J]. Geophy-sical Prospecting, 1980, 28(1): 30-48. |
| [17] |
Wiggins J W. Attenuation of complex water-bottom multiples by wave-equation-based prediction and subtraction[J]. Geophysics, 1988, 53(12): 1527-1539. |
| [18] |
耿伟峰, 柯本喜, 吴艳辉. 波场延拓法压制海底多次波研[J]. 天然气工业, 2007, 27(增刊1): 222-224. GENG Weifeng, KE Benxi, WU Yanhui. Study on water bottom multiple attenuation based on wavefield continuation[J]. Natural Gas Industry, 2007, 27(S1): 222-224. |
| [19] |
张连群, 陈宝书, 李松康, 等. 白云凹陷陆架-陆坡区多次波压制技术[J]. 石油地球物理勘探, 2018, 53(2): 236-242. ZHANG Lianqun, CHEN Baoshu, LI Songkang, et al. Multiple suppression in continental shelf and slope areas of Baiyun Depression[J]. Oil Geophysical Prospecting, 2018, 53(2): 236-242. |



 黎孝璋, 广东省湛江市坡头区22号信箱中海石油(中国)有限公司湛江分公司, 524057。Email:
黎孝璋, 广东省湛江市坡头区22号信箱中海石油(中国)有限公司湛江分公司, 524057。Email: