海洋地震勘探中,受海水面虚反射影响,采集的原始地震数据包括地下反射波和鬼波。由于鬼波的陷频特性,限制了地震勘探的频带宽度,降低了地震资料的分辨率[1]。因此,要获得宽频带地震资料,必须消除鬼波的影响。
在此背景下,业界陆续推出并应用了上下缆[2-4]、上下源[3]、双检[4]等海洋地震勘探技术。近年来,变深度缆采集技术及相关的去鬼波算法受到学者关注。即摒弃常规拖缆采集的将拖缆固定在某一深度的方式,而采用CGG公司首创的检波器沉放深度随炮检距增大而增大的变深度缆采集方式[5]。变深度缆中不同检波器沉放深度具有陷频多样性,叠加不同道集,能同时在低频端和高频端两个方向拓宽频带[6]。针对鬼波压制,Soubaras[7]提出联合反褶积方法;张振波等[8]将斜缆宽频地震勘探技术应用于珠江口盆地;许自强等[9]采用最优化联合反褶积算法压制鬼波,在实际数据处理中取得良好效果;Wang等[10-11]基于Bootstrap方法做加窗处理和镜像偏移,估计鬼波延迟时间,在f-x-y域和τ-p域压制鬼波;王冲等[12]采用最小二乘反演迭代算法,获得准确的鬼波延迟时间;叶林等[13]提出利用峰值因子搜寻最优延迟时间压制鬼波。为了提高计算的稳定性,张威等[14]基于LSMR算法反演求解海面观测的上行波场,再延拓到拖缆以压制斜缆鬼波;吴娟等[15]在高斯束偏移中加入稳定求解的鬼波补偿算子,更利于消除鬼波影响;王建花等[16]基于波场延拓和反演,增加约束条件压制变深度缆鬼波;马继涛等[17]基于波场外推和阈值截断压制鬼波。
大多数鬼波压制方法假设海面反射系数为-1,但实际上海面反射系数并不等于-1,同时,不同时间海面各处反射系数并不完全相同。Masoomzadeh等[18]在估计鬼波延迟时间时,假设海面反射系数是频率和慢度的函数。王冲等[19]基于理论下行波与实际下行波之间的平方误差最小理论,在频率慢度域计算了鬼波与一次反射波振幅系数和延迟时间。
在重点调研了变深度缆镜像记录及联合反褶积算法相关文献的基础上,本文提出一种基于非高斯性最大化的变深度缆鬼波压制方法,以负熵为非高斯性度量,采用滑动时空数据窗口克服海面反射系数随时间变化和延迟时间随地层深度变化问题,获取最优海面反射系数和延迟时间,用联合反褶积算法较彻底地压制了鬼波。
1 变深度缆联合反褶积算法变深度缆某一深度zi所接收到的实际波场p(x, zi, t)是由深部地层反射的上行波场u(x, zi, t)与该上行波场因海面反射产生的下行波场d(x, zi, t)之和构成,即
| $ p\left( {x,{z_i},t} \right) = u\left( {x,{z_i},t} \right) + d\left( {x,{z_i},t} \right) $ | (1) |
对式(1)沿时间t做一维傅里叶变换,得到
| $ P\left( {x,{z_i},\omega } \right) = U\left( {x,{z_i},\omega } \right) + D\left( {x,{z_i},\omega } \right) $ | (2) |
在图 1中:沉放深度z1=zr处拖缆接收到的总波场为p(x, z1, t),上、下行波场分别为u(x, z1, t)和d(x, z1, t);拖缆位置往下zr处设定为“假想海面”,以此为对称面,往下zr处即是相对于变深度缆接收点的镜像接收点,其沉放深度z2=3zr,则该假想拖缆接收到的总波场为p(x, z2, t),对应的上、下行波场分别为u(x, z2, t)和d(x, z2, t)。各波场对时间t的一维傅里叶变换分别记为P(x, z1, ω)、P(x, z2, ω)、U(x, z1, ω)、U(x, z2, ω)、D(x, z1, ω)和D(x, z2, ω)。
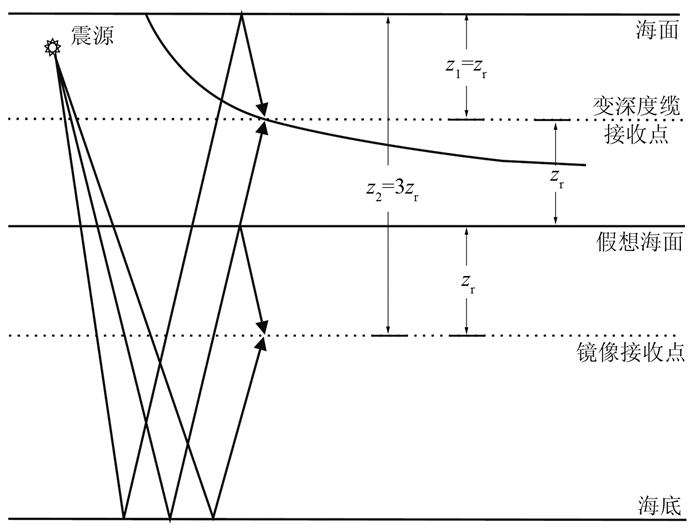
|
图 1 波场传播示意图 |
要求镜像拖缆接收的下行波等于实际拖缆接收的上行波,即
| $ D\left( {x,{z_2},\omega } \right) = U\left( {x,{z_1},\omega } \right) $ | (3) |
假设海面反射系数为-r,下行波场是上行波场在海面的反射而产生,因此下行波场可以由单程波场延拓算子得到
| $ \left\{ {\begin{array}{*{20}{l}} {D\left( {x,{z_1},\omega } \right) = - rU\left( {x,{z_1},\omega } \right){{\rm{e}}^{ - {\rm{j}}k{z_1}}}}\\ {D\left( {x,{z_2},\omega } \right) = - rU\left( {x,{z_2},\omega } \right){{\rm{e}}^{ - {\rm{j}}k\left( {{z_2} - {z_1}} \right)}}} \end{array}} \right. $ | (4) |
式中:波数
将式(3)代入式(4)得
| $ U\left( {x,{z_2},\omega } \right) = - \frac{1}{r}U\left( {x,{z_1},\omega } \right){{\rm{e}}^{{\rm{j}}k\left( {{z_2} - {z_1}} \right)}} $ | (5) |
再将式(3)~式(5)代入式(2),得到
| $ P\left( {x,{z_1},\omega } \right) = U\left( {x,{z_1},\omega } \right)\left[ {1 - r{{\rm{e}}^{ - {\rm{j}}k\left( {{z_2} - {z_1}} \right)}}} \right] $ | (6) |
| $ P\left( {x,{z_2},\omega } \right) = U\left( {x,{z_2},\omega } \right)\left[ {1 - \frac{1}{r}{{\rm{e}}^{ - {\rm{j}}k\left( {{z_2} - {z_1}} \right)}}} \right] $ | (7) |
联立式(6)与式(7),可得
| $ P\left( {x,{z_2},\omega } \right) = - r{{\rm{e}}^{{\rm{j}}k\left( {{z_2} - {z_1}} \right)}}P\left( {x,{z_1},\omega } \right) $ | (8) |
通过式(8)可得到镜像记录,镜像记录等于原始记录施加一个算子,镜像算子可以表示为
| $ J\left( {x,\omega } \right) = - r{{\rm{e}}^{{\rm{j}}k\left( {{z_2} - {z_1}} \right)}} = - r{{\rm{e}}^{{\rm{j}}\omega \tau }} $ | (9) |
式中τ为上行波与下行波之间的延迟时间。
式(6)、式(7)可改写成
| $ P\left( {x,{z_1},\omega } \right) = U\left( {x,{z_1},\omega } \right){G_1}\left( {x,\omega } \right) $ | (10) |
| $ P\left( {x,{z_2},\omega } \right) = U\left( {x,{z_2},\omega } \right){G_2}\left( {x,\omega } \right) $ | (11) |
式中
| $ {G_1}\left( {x,\omega } \right) = 1 - r{{\rm{e}}^{ - {\rm{j}}k\left( {{z_2} - {z_1}} \right)}} = 1 - r{{\rm{e}}^{ - {\rm{j}}\omega \tau }} $ | (12) |
| $ {G_2}\left( {x,\omega } \right) = 1 - \frac{1}{r}{{\rm{e}}^{ - {\rm{j}}k\left( {{z_2} - {z_1}} \right)}} = 1 - r{{\rm{e}}^{ - {\rm{j}}\omega \tau }} $ | (13) |
镜像记录也可表示为
| $ P\left( {x,{z_2},\omega } \right) = - r{{\rm{e}}^{ - {\rm{j}}\omega \tau }}P\left( {x,{z_1},\omega } \right) $ | (14) |
上述问题的最小平方解是
| $ \begin{array}{l} U\left( {x,{z_1},\omega } \right)\\ \; = \frac{{{{\left[ {{G_1}\left( {x,\omega } \right)} \right]}^ * }P\left( {x,{z_1},\omega } \right) + {{\left[ {{G_2}\left( {x,\omega } \right)} \right]}^ * }P\left( {x,{z_2},\omega } \right)}}{{{{\left[ {{G_1}\left( {x,\omega } \right)} \right]}^2} + {{\left[ {{G_2}\left( {x,\omega } \right)} \right]}^2}}} \end{array} $ | (15) |
上标“*”表示共轭运算。在实际地震记录与其镜像记录已知的情况下,式(15)可求得变深度缆的上行波场U(x, z1, ω),即鬼波压制后的频率域波场。
2 非高斯性最大化的参数搜索实际地震信号具有非高斯分布的特性[20]。由中心极限定理可知:多个相互独立的随机信号的和比单个信号更趋于高斯分布。实际地震记录包括一次波和鬼波,即一次波的非高斯性大于实际地震记录的非高斯性。因此,鬼波压制效果最好的地震记录的非高斯性最大。
在所有方差相等的随机变量中,高斯变量具有最大熵,非高斯性越强熵越小。负熵J可作为一种非高斯性度量。为便于计算,选用负熵近似式
| $ J\left( y \right) = {\left[ {E\left( {G\left( y \right)} \right) - E\left( {G\left( v \right)} \right)} \right]^2} $ | (16) |
式中:v是具有零均值、单位方差的高斯信号;y是具有零均值、单位方差的随机信号;E(·)表示求期望值;G(·)是可选非线性函数,这里选择G(x)=-e0.5x2。负熵近似式对噪声不敏感,具有良好的鲁棒性,计算快速。
在上述联合反褶积算法中,海面反射系数和鬼波延迟时间是影响上行波准确性的两个最重要参数,但实际上并不能得到准确的海面反射系数和鬼波延迟时间。建立基于非高斯性最大化的目标函数
| $ \mathop {\max }\limits_{{r^i},{\tau ^j}} \left\{ {{{\left[ {E\left( {G\left( {{u_0}\left( n \right)} \right)} \right) - E\left( {G\left( {v\left( n \right)} \right)} \right)} \right]}^2}} \right\} $ | (17) |
其中
| $ {u_0}\left( n \right) = \frac{1}{{\sqrt {\frac{1}{N}\sum\limits_{n = 1}^N {{u^2}\left( n \right)} } }}u\left( n \right) $ |
式中:u0(n)是对u(n)零均值化和方差归一化的结果;v(n)是均值为0、方差为1的高斯信号。当u0(n)或u(n)为高斯信号时,目标函数等于0;而当u0(n)或u(n)越趋向于非高斯信号,目标函数越大于0;反之亦然。因此,当目标函数最大时,代表此时的参数为最优的反射系数和延迟时间。
本文通过网格搜索方法寻找鬼波参数。首先,设置参数空间{(r(i), τ(j))|i=1, …, m; j=1, …, n},其中,
同一检波点接收到的鬼波与反射波之间的延迟时间随地层深度变化(图 2),同一道的鬼波延迟时间不完全相同。海面反射系数并不是恒定值,而是随时间发生变化。单道地震记录只选定固定的延迟时间和反射系数进行去鬼波处理,很难取得理想的压制效果。因此,必须沿时间和空间进行窗口划分,离散化地震记录,使同一窗口内的地震记录的延迟时间近似相等,同时确定海面反射系数。
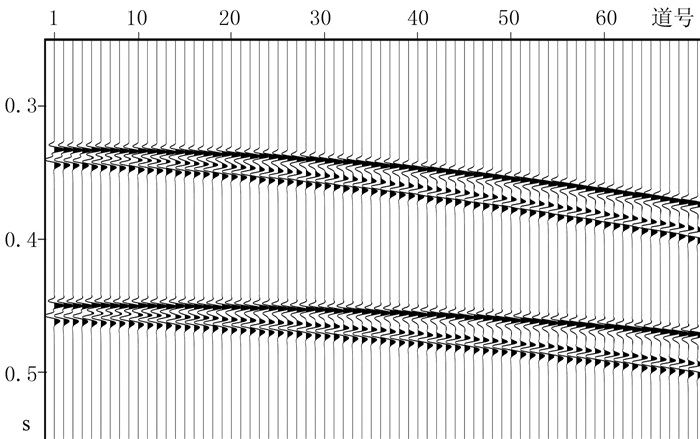
|
图 2 鬼波与一次反射波间延迟时随炮检距和旅行时变化示意图 |
变深度缆各接收点的鬼波延迟时间与拖缆沉放深度有关,随着沉放深度增大,鬼波延迟时间也逐渐增大。因此,窗口在空间方向上不能太大,否则很难找到一个较准确的延迟时间。实际海面是粗糙起伏的,反射系数也不是一成不变的;同样,在时间域也需选取适当窗口。在本文中,选择滑动窗口为3~5道、300~400ms(图 3)。在此基础上,需扩大搜索鬼波延迟时间范围的上、下限,选择适当步长,以便能覆盖窗口内的各道的准确的延迟时间。滑动数据窗口在地震记录上有规律地移动,后续窗口与前一窗口有重叠部分,保证地震记录被各窗口完全覆盖。对地震记录做滑动窗口处理,使窗口内去鬼波记录非高斯性最大化,从而获得窗口内的最优延迟时间和反射系数,克服鬼波参数变化问题。滑动窗口完全覆盖整条记录后,将各窗口鬼波延迟时间和海面反射系数代入式(12)和式(13),继而通过式(15)得到去鬼波后的频率—空间域地震记录。
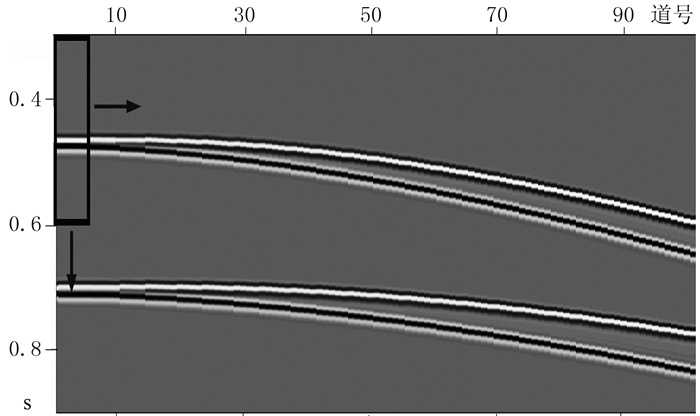
|
图 3 地震记录滑动窗口示意图 |
为了验证基于非高斯性最大化方法的有效性,首先模拟一次波和鬼波,选择鬼波参数:反射系数r为-0.960,鬼波延迟时间τ为45.00ms,设置反射系数范围[-1.0:0.001:-0.6]、延迟时间(ms)范围[40:0.01:50],利用联合反褶积计算上行波场;再计算得到二维负熵图谱(图 4),利用上述方法搜索负熵最大值,搜寻最优参数。估算参数re=-0.961和τe=45.00ms很接近初始设定参数。
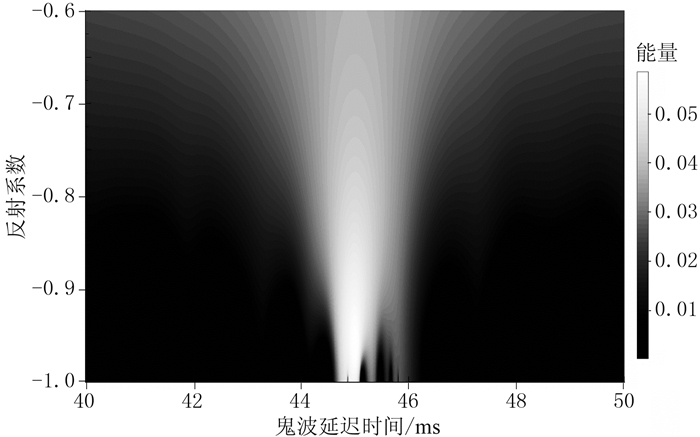
|
图 4 二维负熵示意图 |
图 5显示部分参数对的去鬼波结果,第一道为原始鬼波信号,第二道为获得的最优参数去鬼波结果,其余道是参数空间中随机选取的部分参数去鬼波结果。通过对比,可见不同的鬼波参数对鬼波压制效果产生了很大影响,利用负熵估计出来的参数能很好地压制鬼波。因此,基于非高斯性最大化能够选择最优的鬼波参数。
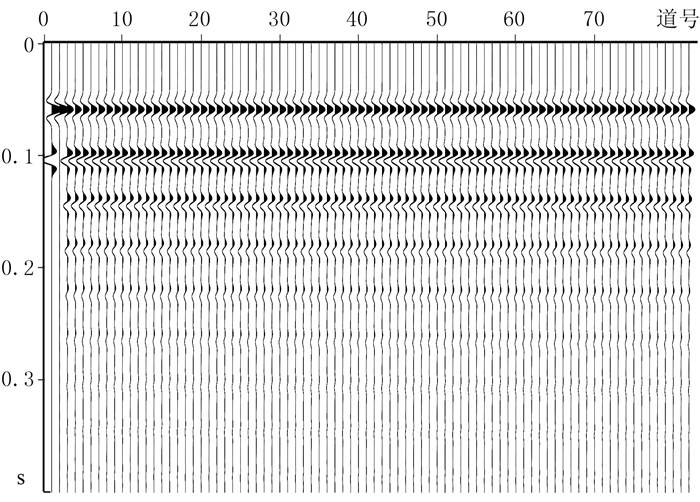
|
图 5 鬼波参数对于鬼波压制效果的影响 |
为了检测基于非高斯性最大化的变深度缆联合反褶积算法压制鬼波的效果,对水平层状模型的合成变深度缆单炮记录做鬼波压制试处理。模拟时采用主频为50Hz的雷克子波,记录道数为101,道间距为6m,采样间隔为0.5ms,记录时间为0.9s,炮检距为0,单边放炮,拖缆沉放深度为6~50m。
图 6a为正演模拟的变深度缆单炮记录,对其加入随机噪声以测试本文方法的抗噪性。随着炮检距增大,拖缆沉放深度逐渐增大,鬼波与一次波之间的延迟时间相应增大,在地震记录上表现为同相轴由开始时的相互重叠到慢慢分离,且两者距离越来越大。在压制鬼波过程中,首先设定反射系数搜索下限为-1.0,搜索上限为-0.6,步长为0.01;延迟时间τ(=2d/c)的搜索上限为1.5τ,下限为0.5τ,步长为0.1ms。滑动窗口在时空域地震记录上有规律地移动,获得各窗口的二维负熵图谱,搜寻其中的最大值,分别得到各窗口内最优海面反射系数和鬼波延迟时间;基于式(15),对模拟的原始地震记录和镜像记录(图 6b)应用联合反褶积法求得去鬼波波场(图 6c)。
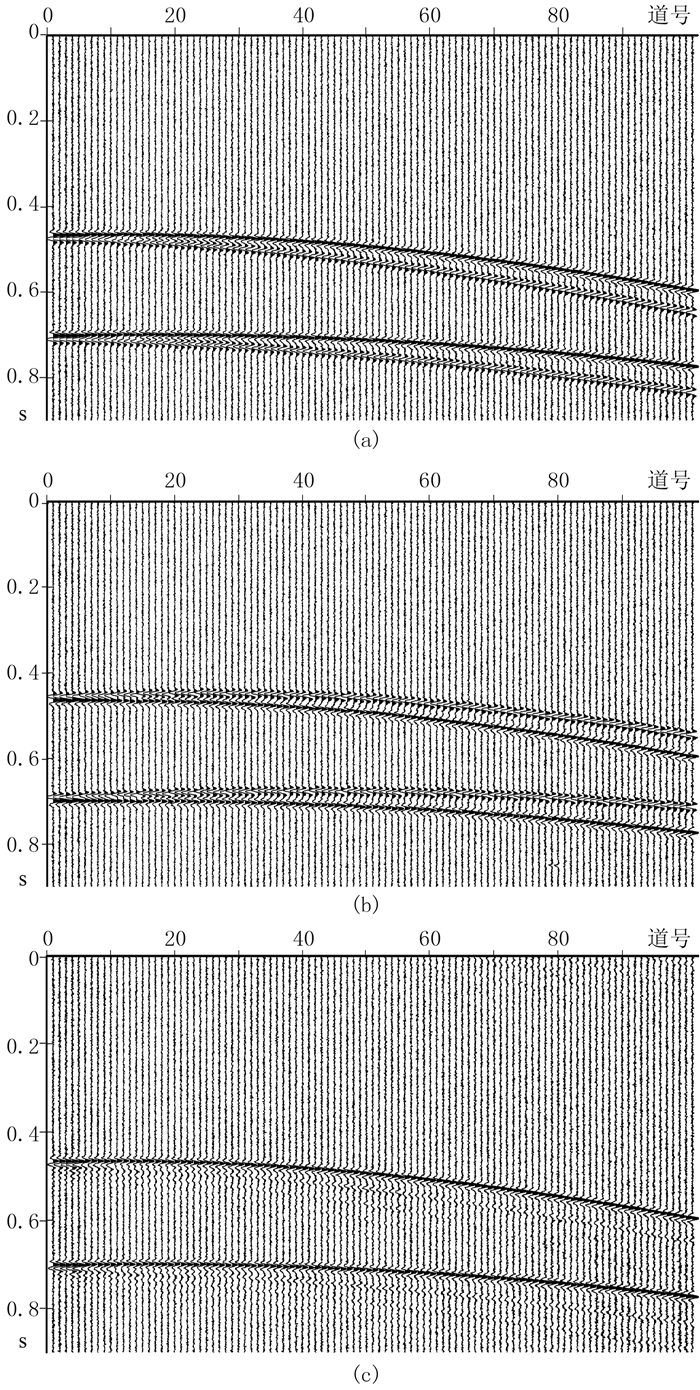
|
图 6 模拟的原始(a)、镜像(b)及去鬼波后(c)的地震记录 |
镜像记录与原始地震记录存在明显的同相轴相位差异:镜像记录首先接收到的是鬼波,因此其同相轴相位最初是负的;而原始地震记录首先接收到的是一次反射波,其同相轴相位最初是正的。
对比图 6a与图 6c,可见运用本文方法对原始地震记录进行处理后,在含噪情况下鬼波已被较彻底地去除,只剩下一次反射波;同时表明噪声的存在对本文方法去鬼波效果的影响极小。
总之,模型测试结果表明:本文方法在含噪情况下能有效压制鬼波,且抗噪性强、精度高。
4.3 实际数据处理用实际采集的变深度缆数据进行非高斯性最优化去鬼波算法测试。施工参数为:拖缆沉放深度5~50m,道间距12.5m,采样间隔2ms,记录长度7.2s。先对该变深度缆单炮记录做预处理(图 7a,选取2.0~4.0s,1~110道)并得到对应镜像记录(图 7b);再应用本文方法做滤波处理,得到去鬼波后地震记录(图 7c)。
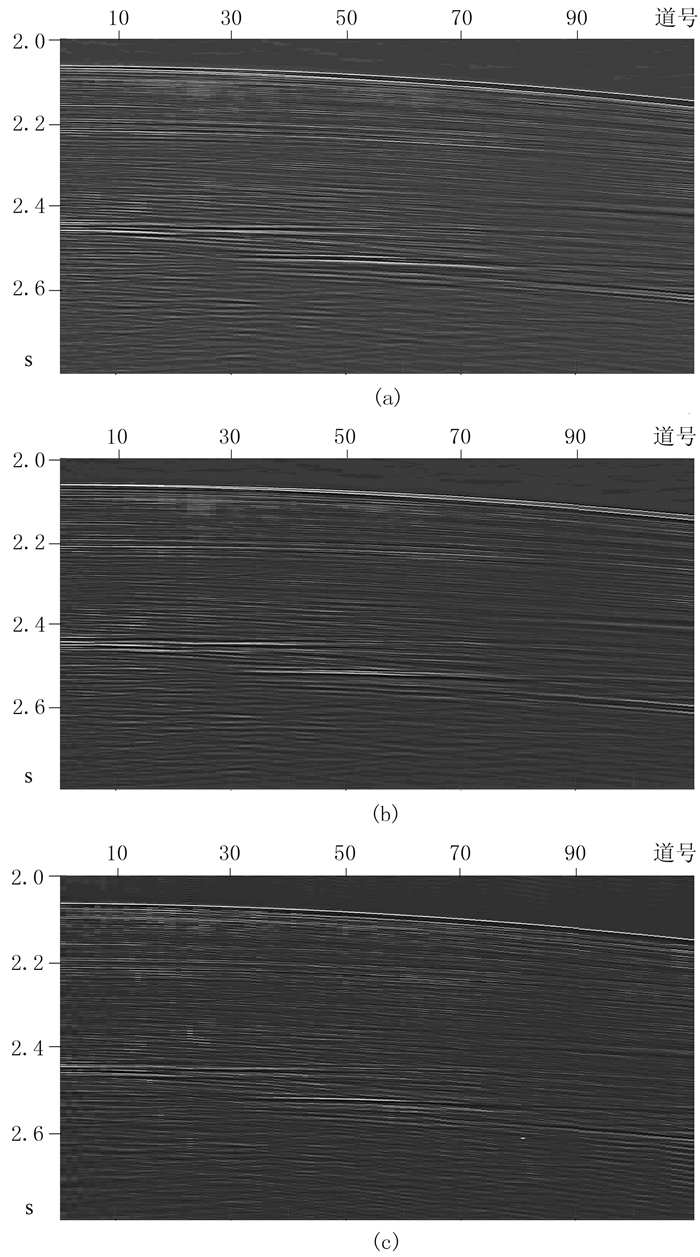
|
图 7 实际(a)、镜像(b)及压制鬼波后(c)的地震记录 |
由于鬼波的存在,在反射波同相轴之后会出现与其相位相反的虚假同相轴(图 7a),降低了地震剖面的分辨率。因鬼波延迟时间和反射系数都能较准确地获取,故在利用本文方法获得的镜像记录(图 7b)中对应位置处都会呈现明显的相位相反。
从实际地震记录及其鬼波压制后记录的局部放大(图 8)可见:经去鬼波处理后地震记录(图 8b)中鬼波被彻底压制,只剩下一次波同相轴,且与原始记录中的反射波基本重合。充分说明本文提出的基于非高斯性最大化的最优化联合反褶积算法对实际海上变深度缆数据中的鬼波具有较强压制作用。
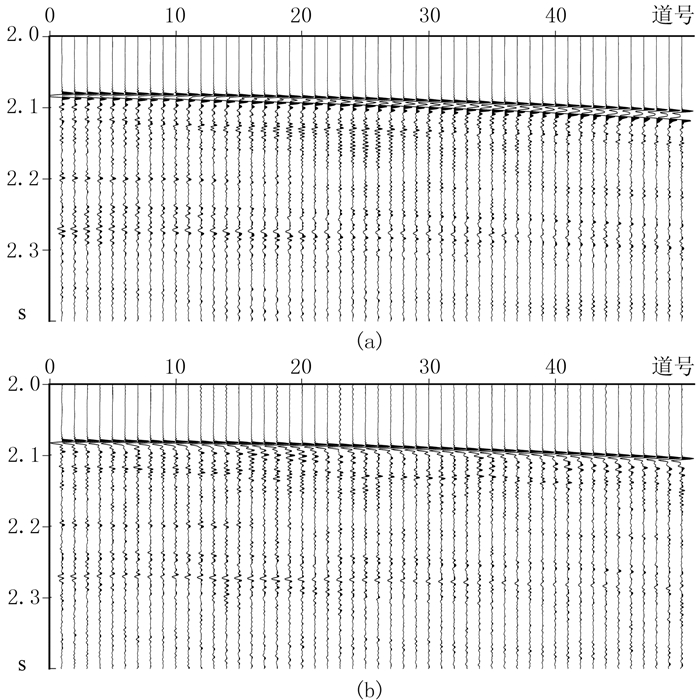
|
图 8 实际地震记录鬼波压制前(a)、后(b)的局部放大 |
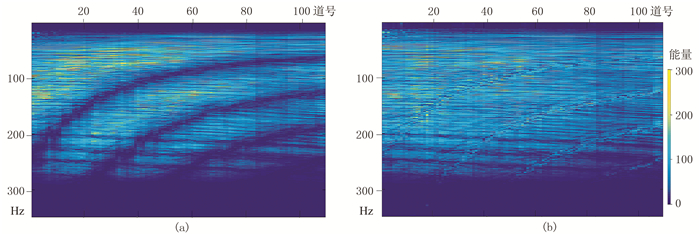
图 9为实际地震数据鬼波压制前、后的频谱。对比发现用本文方法压制鬼波后(图 9b)频谱中的陷波点已基本消除,陷波频率的能量得到了补偿,低频和高频能量都有显著提高。
|
图 9 实际地震数据鬼波压制前(a)、后(b)的频谱 |
文中分析、对比了模拟的和实际的变深度缆单炮记录鬼波压制方法及效果,并得到如下结论:
(1) 以负熵度量去鬼波结果的非高斯性,可得到精确的海面反射系数和鬼波延迟时间,从而获得理想的鬼波压制效果。
(2) 采用滑动时空数据窗口可克服海面反射系数和鬼波延迟时间的变化问题,获得精确镜像记录和去鬼波记录,提高了变深度缆资料处理精度。
(3) 在同相轴干涉严重的复杂构造区及大炮检距情况下,时空域压制鬼波存在局限性,鬼波压制效果欠佳。这是后续研究的课题。
| [1] |
吴志强. 海洋宽频地震勘探技术新进展[J]. 石油地球物理勘探, 2014, 49(3): 421-430. WU Zhiqiang. New advances in marine broadband seismic exploration[J]. Oil Geophysical Prospecting, 2014, 49(3): 421-430. |
| [2] |
赫建伟, 侯志平, 万欢, 等. 海上上下缆地震采集资料特点分析[J]. 工程地球物理学报, 2013, 10(4): 431-436. HE Jianwei, HOU Zhiping, WAN Huan, et al. The analysis of seismic data characteristics by over/under towed-streamer acquisition[J]. Chinese Journal of Engineering Geophysics, 2013, 10(4): 432-436. |
| [3] |
赵仁永, 张振波, 轩义华. 上下源、上下缆地震采集技术在珠江口的应用[J]. 石油地球物理勘探, 2011, 46(4): 517-521. ZHAO Renyong, ZHANG Zhenbo, XUAN Yihua. Application of over/under streamer and over/under source seismic acquisition in Peral River Mouth Basin[J]. Oil Geophysical Prospecting, 2011, 46(4): 517-521. |
| [4] |
张振波, 轩义华, 刘宾, 等. 双检与上下缆地震数据联合成像[J]. 石油地球物理勘探, 2014, 49(5): 884-891. ZHANG Zhenbo, XUAN Yihua, LIU Bin, et al. Joint imaging of dual-sensor and over-under streamer data[J]. Oil Geophysical Prospecting, 2014, 49(5): 884-891. |
| [5] |
Soubaras R, Dowles R. Variable-depth stream:a broadband marine solution[J]. First Break, 2012, 28(12): 89-96. |
| [6] |
唐进, 杨凯, 顾汉明, 等. 海上变深度缆地震采集宽频机理分析[J]. 地球物理学进展, 2015, 30(5): 2386-2392. TANG Jin, YANG Kai, GU Hanming, et al. The broadband mechanism analysis for marine variable-depth streamer acquisition[J]. Progress in Geophy-sics, 2015, 30(5): 2386-2392. |
| [7] |
Soubaras R.Deghosting by joint deconvolution of a migration and a mirror migration[C].SEG Technical Program Expanded Abstracts, 2010, 29: 3406-3410.
|
| [8] |
张振波, 李东方. 斜缆宽频地震勘探技术在珠江口盆地的应用[J]. 石油地球物理勘探, 2014, 49(3): 451-456. ZHANG Zhenbo, LI Dongfang. Variable-depth streamer seismic acquisition and processing in Pearel River Mouth Basin[J]. Oil Geophysical Prospecting, 2014, 49(3): 451-456. |
| [9] |
许自强, 方中于, 顾汉明, 等. 海上变深度缆数据最优化压制鬼波方法及其应用[J]. 石油物探, 2015, 54(4): 404-413. XU Ziqiang, FANG Zhongyu, GU Hanming, et al. The application of optimal deghosting algorithm on marine variable-depth streamer data[J]. Geophysical Prospecting for Petroleum, 2015, 54(4): 404-413. DOI:10.3969/j.issn.1000-1441.2015.04.006 |
| [10] |
Wang P, Peng C.Premigration deghosting for marine towed streamer data using a bootstrap approach[C].SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [11] |
Wang P, Ray S, Peng C, et al.Premigration deghos-ting for marine towed streamer data using a bootstrap approach in tau-p domain[C].SEG Technical Program Expanded Abstracts, 2013, 32: 4221-4225.
|
| [12] |
王冲, 顾汉明, 许自强, 等. 最小二乘反演迭代算法在压制海上变深度缆采集数据虚反射中的应用[J]. 地球物理学报, 2016, 59(5): 1790-1803. WANG Chong, GU Hanming, XU Ziqiang, et al. The application of least-squares inversion iteration algorithm to deghost for marine variable-depth streamer data[J]. Chinese Journal of Geophysics, 2016, 59(5): 1790-1803. |
| [13] |
叶林, 韩立国, 李洪建, 等. 基于峰值因子最大化的鬼波压制方法[J]. 世界地质, 2016, 35(4): 1101-1108. YE Lin, HAN Liguo, LI Hongjian, et al. Deghosting method based on maximization of peak factor[J]. Global Geology, 2016, 35(4): 1101-1108. DOI:10.3969/j.issn.1004-5589.2016.04.021 |
| [14] |
张威, 韩立国, 李洪建, 等. 基于LSMR算法的斜缆数据鬼波压制方法[J]. 石油地球物理勘探, 2017, 52(3): 434-441. ZHANG Wei, HAN Liguo, LI Hongjian, et al. De-ghosting of variable-depth streamer data based on LSMR[J]. Oil Geophysical Prospecting, 2017, 52(3): 434-441. |
| [15] |
吴娟, 白敏, 张华. 基于高斯束偏移的鬼波压制[J]. 石油地球物理勘探, 2018, 53(3): 443-448. WU Juan, BAI Min, ZHANG Hua. Deghosting with Gauss beam migration[J]. Oil Geophysical Prospecting, 2018, 53(3): 443-448. |
| [16] |
王建花, 王艳冬, 刘国昌. 基于波场延拓和反演的变深度缆地震数据鬼波压制方法[J]. 石油地球物理勘探, 2017, 52(5): 885-893. WANG Jianhua, WANG Yandong, LIU Guochang. A deghosting method on variable-depth streamer data based on wavefield extrapolation and inversion[J]. OilGeophysical Prospecting, 2017, 52(5): 885-893. |
| [17] |
马继涛, 王艳冬, 陈小宏, 等. 基于波场外推和阈值截断的鬼波压制方法[J]. 石油地球物理勘探, 2018, 53(2): 227-235. MA Jitao, WANG Yandong, CHEN Xiaohong, et al. A ghost suppression method based on wavefield extra-polation and threshold truncation[J]. Oil Geophysical Prospecting, 2018, 53(2): 227-235. |
| [18] |
Masoomzadeh H, Hardwick A, Baldock S, et al.Re-datuming and deghosting of variable-depth streamer data[C].SEG Technical Program Expanded Abstracts, 2015, 34: 4610-4614.
|
| [19] |
王冲, 顾汉明, 许自强, 等. 频率慢度域自适应迭代反演算法压制海上倾斜缆鬼波方法及其应用[J]. 地球物理学报, 2016, 59(12): 4677-4689. WANG Chong, GU Hanming, XU Ziqiang, et al. The application of adaptive iteration inversion algorithm to deghost for marine variable-depth streamer data in frequency-slowness domain[J]. Chinese Journal of Geophysics, 2016, 59(12): 4677-4689. DOI:10.6038/cjg20161227 |
| [20] |
Walden A T. Non-Gaussian reflectivity, entropy, and deconvolution[J]. Geophysics, 1985, 50(12): 2862-2888. DOI:10.1190/1.1441905 |



 韩立国, 吉林省长春市西民主大街938号吉林大学地球探测科学与技术学院, 130026。Email:
韩立国, 吉林省长春市西民主大街938号吉林大学地球探测科学与技术学院, 130026。Email: