② 中国地质大学(北京)地球物理与信息技术学院, 北京 100083
② School of Geophysics and Information Technology, China University of Geosciences(Beijing), Beijing 100083, China
在多波多分量地震勘探中,通常采用纵波震源激发、三分量(X-Y-Z)或四分量(X-Y-Z-P, P为水检分量)检波器接收,各分量上采集的数据为混合波场(这里暂不考虑Y和P分量),其Z分量和X分量上既含有纵(P)波(ZP、XP),也含有横(S)波(ZS、XS)。当近地表速度很低时,反射波在近地表可视作近垂直出射,此时基本可不做波场分离;但遇到基岩出露或在海底时,波的出射角较大,波场耦合和能量泄漏极为严重。为了得到全纵波和全横波地震记录,须对不同分量上的混合波场进行分离[1-4]
常用的波场分离方法有两大类。一类是基于运动学特征,即在τ-p域下,利用视速度差异进行波场分离[5-7]。该类方法仅考虑单一波场特征,是对全波场的一种近似研究,对于受低速带、起伏地表影响的复杂地质构造的资料,分离效果欠理想。如李远钦等[8]利用Radon变换对VSP数据进行波场分离,但对大井源距的VSP资料会造成强烈的能量弥散效应,分离滤波因子的设计尚待完善。随后,李彦鹏等[9]又提出了一种基于坐标拉伸的线性τ-p变换法,拉伸后的数据更容易在τ-p域中分离,但坐标拉伸和非等间距道内插大大增加了计算难度,使其难以推广于实际应用。Radon变换对近炮检距的能量贡献和远炮检距的数据截断效应,使得波场分离后的数据在水平方向上产生空间假频,波场间的相互干涉并不能完全消除。巩向博等[10]有针对性地提出了压制截断效应的Radon变换法对VSP资料做波场分离,该方法具有快速、保幅性强等优势,大幅度提高了资料的分辨率,但对大炮检距数据的灵敏度依旧很低。
另一类分离方法是基于波场的动力学特征,即利用地震波的偏振特性进行极化滤波。在相位、振幅和极化特性保持原始关系不变的情况下,对模型数据有很好的分离效果。但对于低信噪比实际数据,因其振幅和相位常会发生畸变,故影响分离效果和保真度[11-13]。Benhama等[14]提出过利用偏振性设计滤波器的空间滤波方法;朱衍镛等[15]在其基础上优化了滤波因子,提高了分离效果,但因损失掉部分有效波,从而降低了保幅性。随后,波动方程方法[16-18]受到青睐。胡天跃等[19]根据极化矢量和慢度的差异,利用最小方差约束条件,从数据中获取偏振方向和振幅并对纵、横波进行重构,从而进行波场分离。该方法不依赖近地表地层信息,但对振幅和相位的要求很高。
通过调研众多相关文献,本文将重点聚焦于Al-anboori等[20]提出的基于τ-p变换的三分量地震数据中纵波与转换(SV)波的近似分离方法。当入射角不变时,入射波可被视为平面波的一个分量。在τ-p域内,提取近地表纵波速度作为入射波速度,对球面波做平面波分解,即对Z分量和X分量通过坐标系的矢量旋转,可使其沿纵波和横波各自偏振方向分离,分离后Z分量为全纵波,X分量为全横波,但能量不能完全恢复。
对此,本文提出一种基于τ-p域空间矢量旋转波场分离方法,达到纵、横波波场分离的目的。模型试算表明该方法既满足了波场分离的保真度,又在一定程度上解决了波场泄漏问题,对波场分离技术的研究和应用提供了有益参考。
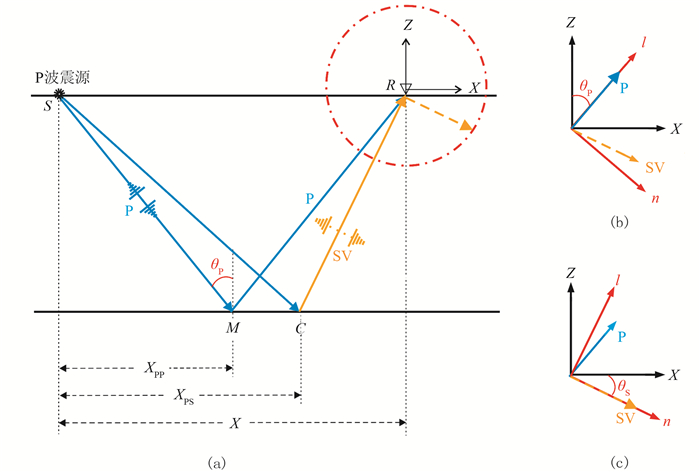
1 方法原理根据弹性波理论,在各向同性介质中P波的质点振动方向在炮—检连线所在的垂向平面内,且与地震波的传播方向一致,SV波的质点振动方向与地震波的传播方向垂直。
提取近地表速度作为入射波速度场,将原始地震数据由笛卡尔坐标系(Z-X)经矢量旋转(图 1)到射线坐标系(n-l)。理想情况下,假设P波以倾角θP倾斜入射均匀各向同性单层水平介质,P-P波与P-SV波在Z-X平面内完全极化,P-P波偏振方向与反射路径平行,P-SV波偏振方向与反射路径垂直。
|
图 1 纵横波运动学及动力学特征与极化平面矢量旋转 (a)P-P、P-SV波传播及偏振;(b)Z分量P-P、P-SV波由Z-X平面旋转至n-l平面;(c)X分量P-P、P-SV波由Z-X平面旋转至n-l平面 n为射线法向方向(与纵波传播方向垂直),l为射线径向方向(与纵波传播方向平行),S为激发点,R为检波点,M为共中心点在界面的投影,C为转换点,X为炮检距,XPP为共中心点在地面投影与激发点的距离,XPS为转换点在地面投影与激发点的距离,纵波入射角和P-P波反射角为θP,P-SV波反射角为θS |
根据多分量检波器的接收特性,uxP、uxS、uzP、uzS分别是X分量和Z分量的能量投影,全纵波记录简记为uP=uxP+uzP,全横波记录简记为uS=uxS+uzS。对不同分量上的能量进行正交分解,可得
| $ \left\{ \begin{array}{l} {u_z} = {u_{\rm{P}}}\cos {\theta _{\rm{P}}} - {u_{\rm{S}}}\sin {\theta _{\rm{S}}}\\ {u_x} = {u_{\rm{P}}}\sin {\theta _{\rm{P}}} + {u_{\rm{S}}}\cos {\theta _{\rm{S}}} \end{array} \right. $ | (1) |
式中:uz为地表沿Z方向接收的垂直偏振分量记录;ux为地表沿X方向接收的径向水平偏振分量记录;uxP=uPsinθP为接收的X分量纵波记录;uxS=uScosθS为X分量横波记录;uzP=uPcosθP为Z分量纵波记录;uzS=uScosθS为Z分量横波记录。解得
| $ \left\{ \begin{array}{l} {u_{\rm{S}}} = \frac{{{u_x}\cos {\theta _{\rm{P}}} - {u_z}\sin {\theta _{\rm{P}}}}}{{\cos {\theta _{\rm{P}}}\cos {\theta _{\rm{S}}} + \sin {\theta _{\rm{P}}}\sin {\theta _{\rm{S}}}}}\\ {u_{\rm{P}}} = \frac{{{u_z}\cos {\theta _{\rm{S}}} + {u_x}\sin {\theta _{\rm{S}}}}}{{\cos {\theta _{\rm{P}}}\cos {\theta _{\rm{S}}} + \sin {\theta _{\rm{P}}}\sin {\theta _{\rm{S}}}}} \end{array} \right. $ | (2) |
将该式写成矩阵形式
| $ \left( {\begin{array}{*{20}{l}} {{u_{\rm{S}}}}\\ {{u_{\rm{P}}}} \end{array}} \right) = \frac{1}{K}\left( {\begin{array}{*{20}{c}} {\cos {\theta _{\rm{P}}}}&{ - \sin {\theta _{\rm{P}}}}\\ {\sin {\theta _{\rm{S}}}}&{\cos {\theta _{\rm{S}}}} \end{array}} \right)\left( {\begin{array}{*{20}{l}} {{u_x}}\\ {{u_z}} \end{array}} \right) = \mathit{\boldsymbol{R}}\left( {\begin{array}{*{20}{l}} {{u_x}}\\ {{u_z}} \end{array}} \right) $ | (3) |
显然有
| $ \mathit{\boldsymbol{R}} = \frac{1}{K}\left( {\begin{array}{*{20}{c}} {\cos {\theta _{\rm{P}}}}&{ - \sin {\theta _{\rm{P}}}}\\ {\sin {\theta _{\rm{S}}}}&{\cos {\theta _{\rm{S}}}} \end{array}} \right) $ | (4) |
式中:R为使波场分离的空间矢量旋转矩阵,可视作一个偏振滤波器,能分离纵、横波波场;K=cosθP×cosθS+sinθPsinθS为滤波系数。
当地下介质含有N个反射层时,检波器会接收到来自地下不同反射层的信息,它们对应不同的反射角(θPi, θSi, i=1, 2, …, n),实际上检波器记录了这些反射信息的总和。因此,在Z-X域内该方法很难实现,通常将其转换至τ-p域内进行分离。于是有
| $ {u_{\rm{r}}}\left( {x,t} \right) = \sum\limits_{i = 1}^n {{u_i}} \left[ {{x_i},{t_0} + \left( {i - 1} \right)\Delta t} \right] $ | (5) |
式中:ur(x, t)为检波点接收到总的波场值;ui(xi, t0)为地下反射波自激自收时对应的波场值;t0为自激自收时;Δt为采样间隔。
根据Snell定律和近地表视速度特征,可得
| $ \left\{ {\begin{array}{*{20}{l}} {\sin {\theta _{\rm{P}}} = {V_{\rm{P}}}{p_{\rm{P}}}}\\ {\sin {\theta _{\rm{S}}} = {V_{\rm{S}}}{p_{\rm{S}}}}\\ {\cos {\theta _{\rm{P}}} = {V_{\rm{P}}}{q_{\rm{P}}}}\\ {\cos {\theta _{\rm{S}}} = {V_{\rm{S}}}{q_{\rm{S}}}} \end{array}} \right. $ | (6) |
式中:V为近地表纵、横波速度;p、q为对应的水平慢度、垂直慢度。
对式(5)做τ-p变换,得
| $ {S_{\rm{r}}}\left( {\tau ,p} \right) = \sum {{u_{\rm{r}}}} \left( {{x_i},\tau + p{x_i}} \right)\Delta {x_i} $ | (7) |
式中:Sr(τ, p)为(τ, p)域地震波响应;Ur(t, x)为(T, X)域地震波响应,且t=τ+px。
在τ-p域做正交分解,得到垂直分量Sz(τ, p)和水平分量Sx(τ, p)。将二者代入式(3)、式(4),可得
| $ \left[ {\begin{array}{*{20}{l}} {{u_n}\left( {\tau ,p} \right)}\\ {{u_l}\left( {\tau ,p} \right)} \end{array}} \right] = \mathit{\boldsymbol{R}}\left[ {\begin{array}{*{20}{l}} {{u_x}\left( {\tau ,p} \right)}\\ {{u_z}\left( {\tau ,p} \right)} \end{array}} \right] $ | (8) |
从式(6)得到
| $ \left\{ {\begin{array}{*{20}{l}} {{q_{\rm{P}}} = \sqrt {V_{\rm{P}}^{ - 2} - p_{\rm{P}}^2} }\\ {{q_{\rm{S}}} = \sqrt {V_{\rm{S}}^{ - 2} - p_{\rm{S}}^2} } \end{array}} \right. $ | (9) |
将式(9)代入式(8),就有
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{S_l}\left( {\tau ,p} \right)}\\ {{S_n}\left( {\tau ,p} \right)} \end{array}} \right] = \frac{1}{K}\left( {\begin{array}{*{20}{c}} {{p_{\rm{S}}}{V_{\rm{S}}}}&{ - \sqrt {V_{\rm{S}}^{ - 2} - p_{\rm{S}}^2} {V_{\rm{S}}}}\\ {\sqrt {V_{\rm{P}}^{ - 2} - p_{\rm{P}}^2} {V_{\rm{P}}}}&{{p_{\rm{P}}}{V_{\rm{P}}}} \end{array}} \right) \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {{S_x}\left( {\tau ,p} \right)}\\ {{S_z}\left( {\tau ,p} \right)} \end{array}} \right] \end{array} $ | (10) |
对Sl(τ, p)、Sn(τ, p)分别进行τ-p逆变换,得到
| $ \left\{ \begin{array}{l} {{\tilde u}_{x{\rm{S}}}}\left( {t,{x_j}} \right) = \sum {{S_n}} \left( {{p_k},\tau = t - {p_k}{x_j}} \right)\\ {{\tilde u}_{x{\rm{P}}}}\left( {t,{x_j}} \right) = \sum {{S_l}} \left( {{p_k},\tau = t - {p_k}{x_j}} \right) \end{array} \right. $ | (11) |
式中
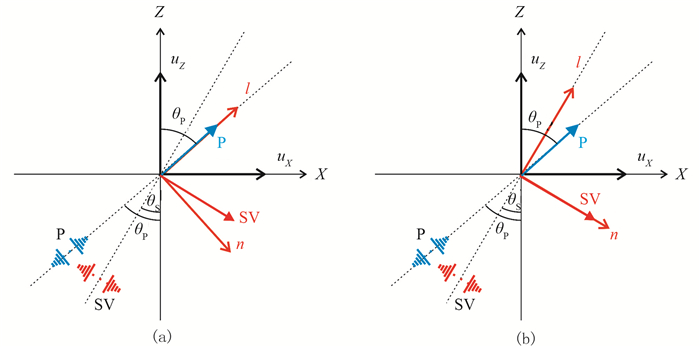
从图 2可知,数据以近地表纵波视速度进行矢量旋转,由Z-X域旋转至n-l域,P-P波能量全部旋转至l轴;同理,以近地表横波视速度做矢量旋转,P-SV波能量全部旋转至n轴。此时全纵波能量uP全部在l轴上,全横波能量uS全部在n轴上。
|
图 2 笛卡尔坐标系到射线坐标系的极化旋转示意图 (a)P-P、P-SV波据近地表纵波视速度将能量由Z-X域旋转至n-l域,P-P波无能损,P-SV波被压制;(b)P-P、P-SV波据近地表横波视速度将能量由Z-X域旋转至n-l域,P-SV波无能损,P-P波被压制 |
选用由简单水平层状模型和复杂Marmousi Ⅱ模型生成的模型道作为试算数据。基于简单模型对比不同方法之间的分离效果;利用复杂模型进一步验证分离方法的包容性和适用性。
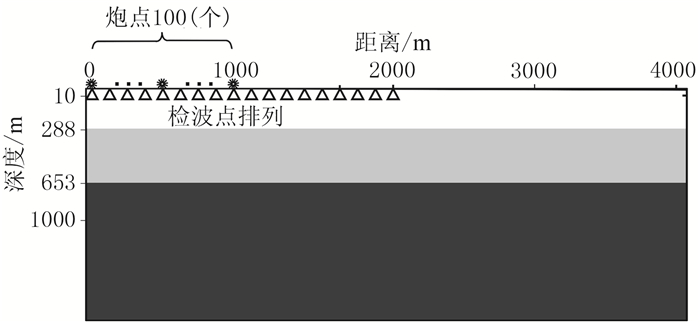
2.1 水平层状模型建立一个半空间各向同性水平均匀层状介质模型(图 3),采用射线追踪法进行模型正演生成三分量人工合成地震记录[21]。
|
图 3 理论模型示意图 |
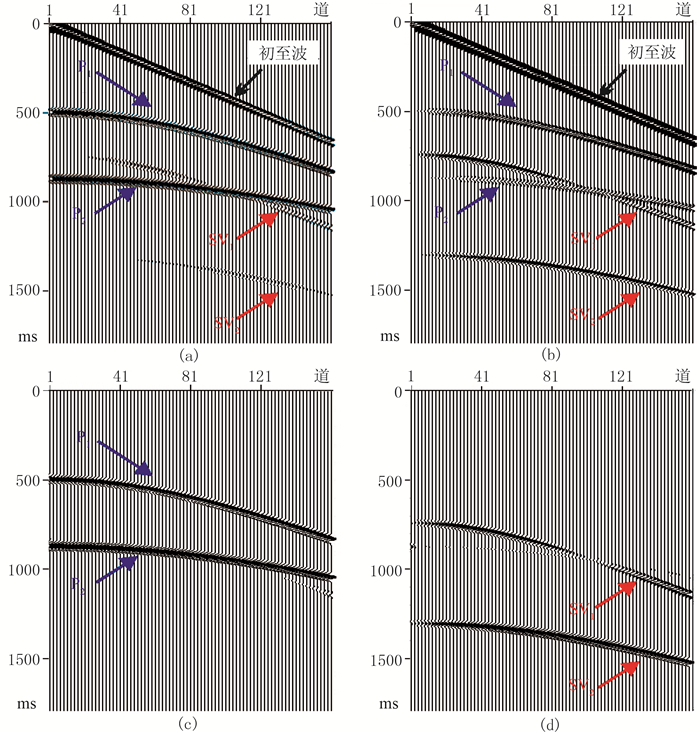
用图 3理论模型合成了Z分量(图 4a)和X分量(图 4b)地震记录。利用近地表视速度信息,基于τ-p域矢量旋转法(新方法)压制Z分量的干扰波P-P,提高Z分量的P-SV有效波。波场分离处理前先切除初至波。对比分离前(图 4a)、后(图 4c)的Z分量,P-SV波被剥离,滤波后P-P波振幅能量较滤波前有明显提升。同理,对比分离前(图 4b)、后(图 4d)的X分量,P-P波作为干扰波被压制,P-SV波的振幅能量有很大提升。图 4b中SV1与P2轴相交处(977ms),P-P波、P-SV波二者同时到达对应检波器,纵、横波产生耦合现象。对比图 4d的对应位置,X分量依然显示出很好的分离效果。由于受到模型层厚限制,且入射倾角角度近似,即便在τ-p域纵、横波速度差异明显,依然会对波场分离质量产生影响。因此,在图 4d中波场耦合现象对应位置处,虽然P-P波被压制,但对P-SV波的能量仅造成轻微损伤;对比图 4b与图 4d,第二层P-SV波的能量明显增强。
|
图 4 图 3模型数据波场分离前、后对比 (a)分离前Z分量;(b)分离前X分量;(c)分离后Z分量;(d)分离后X分量 Pi为第i(=1, 2)层P-P波,SVi为第i(=1, 2)层P-SV波;蓝色箭头指示P-P波同向轴;红色箭头指示P-SV波同向轴 |
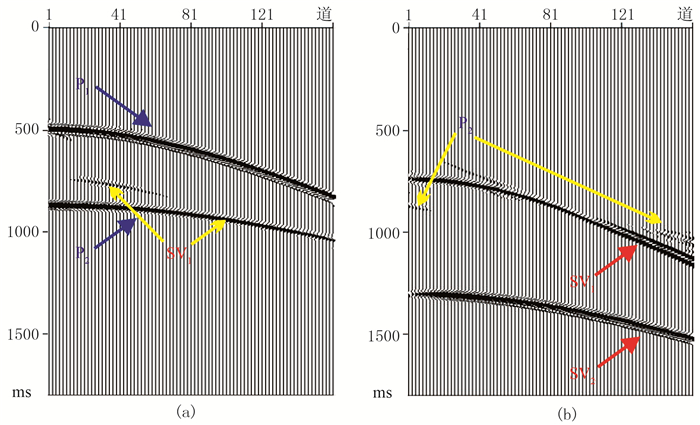
对同一模型数据采用常规τ-p域切分法[22]进行试算,所得波场分离结果(图 5)与上述基于τ-p域矢量旋转(新)方法结果(图 4c、图 4d)对比表明,新方法更好地保留了原始波场特征,同相轴能量更强,保幅性更好。在图 4c中Z分量P-SV波较清晰地分离,而常规方法(图 5a)仍有混波现象(部分SV1未被滤掉),P-P波(P2)能量也未完全恢复;在X分量上,常规方法(图 5b)的混波影响更严重,因τ-p域内切分,造成混波位置出现空间假频(SV1轴上方产生因切分形成的噪声痕迹),且近炮检距处还残留部分P-P波(P2),而新方法(图 4d)无论是近炮检距还是远炮检距均达到理想分离效果,且未出现空间假频现象。
|
图 5 τ-p域切分法分离的纵、横波场 (a)Z分量;(b)X分量 黄色虚线箭头在图a中指向被压制的P-SV波,在图b中指向被压制的P-P波;其他同图 4 |
图 6从叠加剖面角度展示了分离效果,可见经滤波处理后整体上P-P波同相轴更平整清晰,锯齿状毛边被弱化,连续性得到改善。在图 6a中,P-SV波速度分析不准确,导致叠加时同向轴未能聚焦,成层欠清晰。将P-SV波分离至X分量(图 6d)时,P-SV波的同向轴就呈现出很强连续性。此外,由于本方法在分离时能解决能量泄漏、信号损伤等问题,因此其成像效果及分辨率均有显著提高。

|
图 6 对图 4的道集记录生成叠加剖面对比分离效果 (a)合成记录Z分量叠加剖面uz;(b)分离后Z分量叠加剖面 |
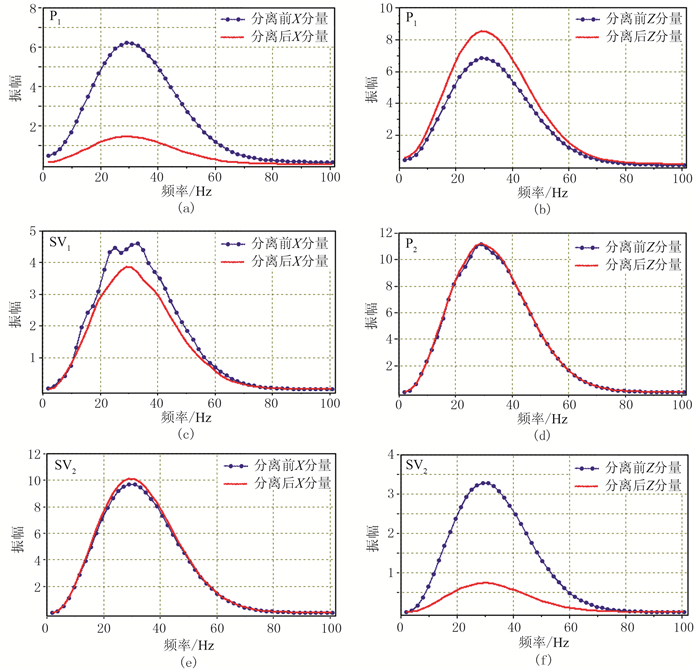
对模型分离前后数据(图 4)做频谱分析(图 7)。对比X分量(图 7a),可见分离后P1轴振幅的最大值降至分离前的78.28%;在Z分量(图 7b)上P1轴的振幅最大值有明显抬升,表明P-P波能量在X分量被压制,在Z分量得以恢复。同理,对比图 7e与图 7f可知,P-SV波在X分量得到恢复,在Z分量被压制。图 7c和图 7d为波场耦合处,由于P2轴与SV1轴两者交叉,导致振幅曲线发生畸变,这种畸变明显影响X分量的P-SV波(SV1),振幅曲线由两个极大值变为一个最大值,且呈现明显衰减,但对Z分量的P-P波(P2)能量几乎未造成影响。这与道集上的表征相吻合。
|
图 7 对图 4的第100~161道的频谱分析 (a)X分量第一层P-P波(P1)频谱;(b)Z分量第一层P-P波(P1)频谱;(c)X分量第一层P-SV波(SV1)频谱;(d)Z分量第二层P-P波(P2)频谱;(e)X分量第二层P-SV波(SV2)频谱;(f)Z分量第二层P-SV波(SV2)频谱 |
图 8为对该模型理论记录进行波场分离前、后F-K域的二维振幅谱。在F-K域中,能够清晰地分辨出不同分量记录中有效反射的能量和干扰反射能量的分布特征。经过波场分离后P-P波、P-SV波的振幅谱能量得到清晰的分离并各自归位。

|
图 8 对图 4模型道做F-K域振幅谱处理对比分离前后效果 (a)合成记录分离前Z分量F-K谱;(b)合成记录分离后Z分量F-K谱;(c)合成记录分离前X分量F-K谱;(d)合成记录分离后X分量F-K谱 |
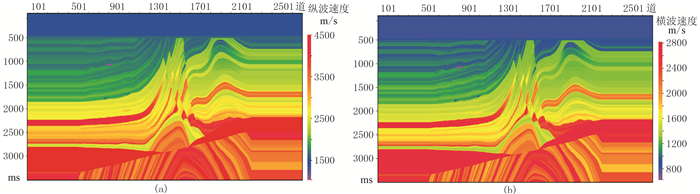
对Marmousi Ⅱ模型(图 9)采用弹性波动方程做正演模拟,模拟记录上可见一次波、多次波、折射波、转换波、首波、面波、界面波及复杂散射等[23]。
|
图 9 Marmousi Ⅱ模型(Marmousi模型的延拓)纵波(a)、横波(b)速度场[23] |
图 10为Marmousi Ⅱ模型第85炮单炮记录及其不同分量的分离效果。炮集的X分量发生极性反转,Z、X分量均出现了P-P波和P-SV波。利用基于τ-p域矢量旋转法对该数据进行波场分离。在Z分量上,水底反射波变得更清晰,P-SV波得到有效压制,初至波杂乱的偏振现象变得较规则,数据的信噪比有明显提升(图 10a、图 10b);在X分量上,P-P波强反射轴被压制,P-SV波变得更突显,深层有效波能量得到补充(图 10c、图 10d)。

|
图 10 Marmousi Ⅱ模型(第85炮记录,炮检距7100m)基于τ-p域矢量旋转波场分离前后对比 (a)单炮记录Z分量;(b)分离后Z分量;(c)单炮记录X分量;(d)分离后X分量。框内红色箭头指示分离效果明显的位置 |
另一方面,Z分量的小炮检距浅中层段(图 10a、图 10b顶部矩形)分离效果较理想,中深层段也有一定滤波作用;但对于大炮检距(图 10a、图 10b底部矩形)的波场分离效果相对较弱。在实际应用中,大炮检距数据会造成拉伸畸变而影响后续叠加效果,一般需做切除处理,因此可忽略该部分的分离效果。X分量上,浅中层段(图 10c、图 10d顶部、中部矩形)分离效果突出,深层因偏振极性耦合严重,使得整个数据分离效果较差。对此,尚需做进一步研究。
综上分析,本文方法对类似Marmousi Ⅱ的复杂地震模型数据也有显著的应用效果。
3 实际数据试算针对海上三维OBN原始三分量单炮记录的Z分量(图 11a)和X分量(图 11b),因该数据有较严重的检波器定向问题,故在分离前须首先对X分量进行水平分量坐标旋转;然后利用本文所提方法分离纵横波场。可见两分量各自对应的绿框区域(图 11c、图 11d)内的良好分离效果。

|
图 11 海上三维OBN原始单炮记录及其分离效果 (a)分离前Z分量;(b)分离前X分量;(c)分离后Z分量;(d)分离后X分量。绿色框标示分离前、后的对比区域 |
对于陆上某二维地震资料的单炮记录的Z分量(图 12a)和X分量(图 12b),也用本文方法进行了波场分离。

|
图 12 陆上二维原始单炮记录及其分离效果 |
由于该数据的信噪比较高,波场分离的效果(图 12c、图 12d)更佳。
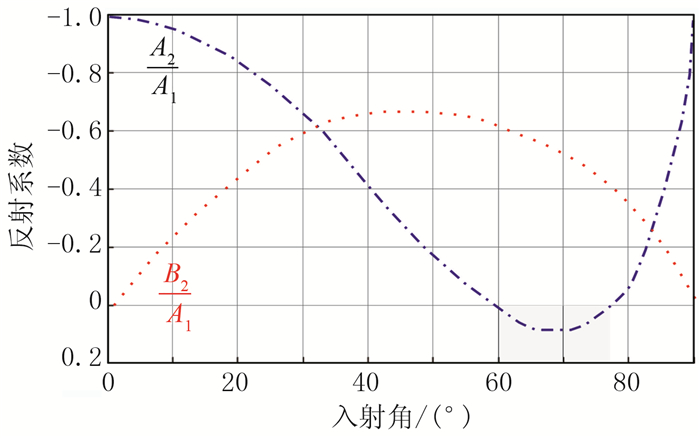
4 讨论 4.1 反射系数与极性反转自由界面上地震波反射特点如图 13所示。理论上,通常假设泊松比为0.25,纵横波速度比为1.732。当P波入射角θP∈[0°, 90°],且RPP=0时,对应横坐标有两个角度值,分别是60°和77°13′,即介质中仅存在P-SV转换波;当RPS=0时,对应横坐标角度值分别为0°和90°,即介质中仅存在P-P波[24],此时式(1)可变为
|
图 13 自由界面反射系数[24] A1为入射P波振幅,A2为反射P-P波振幅,B2为反射P-SV波振幅,P-P波反射系数为A2/A1,P-SV波反射系数为αB2/βA1,其中α/β为纵横波速度比 |
| $ \begin{array}{l} {u_x} = {u_{\rm{P}}}{p_{\rm{P}}}{V_{\rm{P}}}\\ {u_z} = - {u_{\rm{P}}}{q_{\rm{P}}}{V_{\rm{P}}} \end{array} $ | (12) |
同理,当以横波入射(RSP=0),即反射波仅有S-SV波,不存在S-P波时,式(1)可变为
| $ \begin{array}{l} {u_x} = {u_{\rm{S}}}{q_{\rm{S}}}{V_{\rm{S}}}\\ {u_z} = {u_{\rm{S}}}{P_{\rm{S}}}{V_{\rm{S}}} \end{array} $ | (13) |
在θP∉[60°, 77°13′]时,RPP<0,表面反射的P-P波在界面(z=0)处的振动方向也会与RPP>0时相反,即产生极性反转。从图 13不难看出:θP∈[0°, 90°]时,RPS为非负,即X分量产生的有效波P-SV的极性不反转。
4.2 影响大炮检距分离效果的因素无论是Marmousi Ⅱ理论模型验证还是实际数据的试算,利用本文方法对大炮检距波场进行分离,其效果均欠佳。射线坐标系下纵、横波能量比可表示为
| $ \frac{{{u_{l{\rm{P}}}}}}{{{u_{{\rm{tot}},{\rm{P}}}}}} = \frac{{{u_{n{\rm{S}}}}}}{{{u_{{\rm{tot,S}}}}}} = \cos \left( {{\theta _{\rm{P}}} - {\theta _{\rm{S}}}} \right) $ | (14) |
式中:ulP为l分量上的P-P波;utot, P为全纵波;unS为n分量上的P-SV波;utot, S为全横波。
将式(6)代入式(14)得
| $ \frac{{{u_{l{\rm{P}}}}}}{{{u_{{\rm{tot}},{\rm{P}}}}}} = \frac{{{u_{n{\rm{S}}}}}}{{{u_{{\rm{tot,S}}}}}} = {V_{\rm{P}}}{V_{\rm{S}}}\left( {{q_{\rm{P}}}{p_{\rm{S}}} + {p^2}} \right) $ | (15) |
该式表明波场分离的质量随慢度增加而降低,由此可知大炮检距资料分离效果差的根本原因。
4.3 速度选取对分离效果的影响式(15)还表明影响波场分离的两个关键参数是近地表速度VP和VS,即速度选取不准确会影响最终分离效果。误差轴上P-P波能量占比为
| $ \frac{{{{u'}_{n{\rm{P}}}}}}{{{u_{{\rm{tot}},{\rm{P}}}}}} = \sin \left( {{{\theta '}_{\rm{P}}} - {\theta _{\rm{P}}}} \right) = {V_{\rm{P}}}{{V'}_{\rm{P}}}p\left( {{q_{\rm{P}}} - {{q'}_{\rm{P}}}} \right) $ | (16) |
式中:θ′P为P波入射角误差;V′P为速度误差;u′nP为旋转至轴n′(误差轴)上的P-P波;q′P=
| $ \frac{{{{u'}_{n{\rm{S}}}}}}{{{u_{{\rm{tot}},{\rm{S}}}}}} = \cos \left( {{{\theta '}_{\rm{P}}} - {\theta _{\rm{S}}}} \right) = {V_{\rm{S}}}{{V'}_{\rm{P}}}\left( {{{q'}_{\rm{P}}}{q_{\rm{S}}} - {p^2}} \right) $ | (17) |
式中u′nS为旋转至轴n′上的P-SV波。
由式(16)、式(17)可得
| $ \frac{{{{u'}_{n{\rm{P}}}}}}{{{{u'}_{n{\rm{S}}}}}} = \frac{{{u_{{\rm{tot}},{\rm{P}}}}}}{{{u_{{\rm{tot}},{\rm{S}}}}}}\frac{{{V_{\rm{P}}}}}{{{V_{\rm{S}}}}}\frac{{p\left( {{q_{\rm{P}}} - {{q'}_{\rm{P}}}} \right)}}{{\left( {{{q'}_{\rm{P}}}{q_{\rm{S}}} + {p^2}} \right)}} $ | (18) |
该式(18)表明,VP对于能量恢复的影响很大。VP值过大比过小会引发更多的能量泄漏问题。
5 结论与认识本文提出一种有效分离P-P波和P-SV波波场的方法,达到Z分量上为近似全纵波、X分量为近似全横波的效果。该方法的优势在于可根据分量类型,自由选择待分离的干扰波。此外,分离效果的决定性因素是近地表视速度,精度依赖于视速度的估计误差。通过对层状模型、Marmousi Ⅱ复杂模型及海上、陆上实际资料的试算,验证了所提波场分离方法的有效性,特别是在复杂地表情况下依旧有出色表现。该方法还很好地解决了波场分离的能量泄漏、空间假频等问题。
但在近地表低速带或纵横波极度耦合的情况下,混波干扰使此方法分离效果较差;对于大炮检距处的数据分离,其效果也有待提高。这将是下一步研究的重点。
| [1] |
吴潇, 刘洋, 蔡晓慧. 弹性波波场分离方法对比及其在逆时偏移成像中的应用[J]. 石油地球物理勘探, 2018, 53(4): 710-721. WU Xiao, LIU Yang, CAI Xiaohui. Elastic wavefield separation methods and their applications in reverse time migration[J]. Oil Geophysical Prospecting, 2018, 53(4): 710-721. |
| [2] |
张建磊, 田振平, 王成祥. 二维交错网格纵横波分离的弹性波模拟及应用[J]. 石油地球物理勘探, 2008, 43(6): 717-722. ZHANG Jianlei, TIAN Zhenping, WANG Cheng-xiang. Elastic wave simulation of P-and S-waves se-paration by 2-D staggered grid and application[J]. Oil Geophysical Prospecting, 2008, 43(6): 717-722. DOI:10.3321/j.issn:1000-7210.2008.06.018 |
| [3] |
赫建伟, 邓勇, 邓盾, 等. 基于非高斯性最大化的起伏海面环境下双检信号波场分离[J]. 石油地球物理勘探, 2018, 53(4): 694-702. HE Jianwei, DENG Yong, DENG Dun, et al. Dual-sensor signal wavefield separation based on non-Gaussianity maximum under undulating sea surface[J]. Oil Geophysical Prospecting, 2018, 53(4): 694-702. |
| [4] |
赵彦青, 萧蕴诗. 基于稀疏表示的非零井源距VSP波场分离方法[J]. 石油地球物理勘探, 2017, 52(1): 27-33. ZHAO Yanqing, XIAO Yunshi. Offset VSP wave field separation based on sparse representation[J]. Oil Geophysical Prospecting, 2017, 52(1): 27-33. |
| [5] |
Greenalgh S A, Mason I M, Lucas E, et al. Controlled direction reception filtering of P- and S-waves in τ-p space[J]. Geophysical Journal International, 1990, 100: 221-234. DOI:10.1111/j.1365-246X.1990.tb02482.x |
| [6] |
吴律, 武克奋, 孙力. τ-p变换方法及其在地震资料处理中的应用[J]. 石油物探, 1986, 25(1): 37-53. WU Lv, WU Kefen, SUN Li. τ-p transforms and application in seismic data processing[J]. Geophysical Prospecting for Petroleum, 1986, 25(1): 37-53. |
| [7] |
Zhou B, Greenalgh S A. Linear and parabolic τ-p transforms revisited[J]. Geophysics, 1994, 59(7): 1133-1149. DOI:10.1190/1.1443669 |
| [8] |
李远钦, 牟永光, 吴律. Radon变换在VSP波场分离中的应用[J]. 石油地球物理勘探, 1990, 25(6): 653-661. LI Yuanqin, MOU Yongguang, WU Lv. Application of the Radon transform to VSP wave field separation[J]. Oil Geophysical Prospecting, 1990, 25(6): 653-661. |
| [9] |
李彦鹏, 马在田. 坐标拉伸后的线性拉冬变换法波场分离[J]. 石油地球物理勘探, 1998, 33(5): 611-615, 624. LI Yanpeng, MA Zaitian. Wave field separation by linear Radon transform after coordinate stretch[J]. Oil Geophysical Prospecting, 1998, 33(5): 611-615, 624. |
| [10] |
巩向博, 单刚义, 刘冰. 压制截断效应的Radon变换在波场分离中的应用[J]. 吉林大学学报:地球科学版, 2007, 37(增刊1): 74-77. GONG Xiangbo, SHAN Gangyi, LIU Bing, et al. Wave field decomposition via eliminating truncation artifacts of Randon transform[J]. Journal of Jilin University(Earth Science Edition), 2007, 37(S1): 74-77. |
| [11] |
李铜基. 极化滤波[J]. 海洋技术, 1996, 15(4): 130-137. LI Tongji. Polarization filtering[J]. Journal of Ocean Technology, 1996, 15(4): 130-137. |
| [12] |
Cho W H, Spencer T W. Estimation of polarization and slowness in mixed wavefields[J]. Geophysics, 1992, 57(6): 805-814. DOI:10.1190/1.1443294 |
| [13] |
Esmersoy C. Inversion of P and SV waves from multicomponent offset vertical seismic profiles[J]. Geophysics, 1990, 55(1): 39-50. DOI:10.1190/1.1442770 |
| [14] |
Benhama A, Cliet C, Dubesset M. Study and applications of spatial directional filtering in three-component recordings[J]. Geophysical Prospecting, 1988, 36(6): 591-613. DOI:10.1111/j.1365-2478.1988.tb02182.x |
| [15] |
朱衍镛. 二分量记录的空间方向滤波[J]. 石油地球物理勘探, 1995, 30(增刊2): 116-125. ZHU Yanyong. Spatial directional filtering in two-component recordings[J]. Oil Geophysical Prospecting, 1995, 30(S2): 116-125. |
| [16] |
马德堂, 朱光明. 弹性波波场P波和S波分解的数值模拟[J]. 石油地球物理勘探, 2003, 38(5): 482-486. MA Detang, ZHU Guangming. Numerical modeling of P-wave and S-wave separation in elastic wavefield[J]. Oil Geophysical Prospecting, 2003, 38(5): 482-486. DOI:10.3321/j.issn:1000-7210.2003.05.005 |
| [17] |
李振春, 张华, 刘庆敏, 等. 弹性波交错网格高阶有限差分法波场分离数值模拟[J]. 石油地球物理勘探, 2007, 42(5): 510-515. LI Zhenchun, ZHANG Hua, LIU Qingmin, et al. Numeric simulation of elastic wavefield separation by staggering grid high-order finite-difference algorithm[J]. Chinese Journal of Geophysics, 2007, 42(5): 510-515. DOI:10.3321/j.issn:1000-7210.2007.05.006 |
| [18] |
井涌泉, 高红伟, 王维红. 二维各向同性介质P波S波分离方法研究[J]. 地球物理学进展, 2008, 23(5): 1412-1416. JING Yongquan, GAO Hongwei, WANG Weihong. The study of P-waves and S-waves separation in two-dimensional isotropic media[J]. Progress in Geophy-sics, 2008, 23(5): 1412-1416. |
| [19] |
胡天跃, 张广娟, 赵伟. 多分量地震波波场分解研究[J]. 地球物理学报, 2004, 47(3): 504-508. HU Tianyue, ZHANG Guangjuan, ZHAO Wei. Decom-position of multicomponent seismic wavefields[J]. Chinese Journal of Geophysics, 2004, 47(3): 504-508. DOI:10.3321/j.issn:0001-5733.2004.03.021 |
| [20] |
Al-anboori A, Van der Baan M, Kendall J M. Appro-ximate separation of pure-mode and converted waves in 3-C reflection seismics by τ-p transform[J]. Geophysics, 2005, 70(3): V81-V86. DOI:10.1190/1.1926578 |
| [21] |
Guest S, Kendall J M. Modeling seismic waveforms in anisotropic media using Maslov asymptotic theory[J]. European Journal of Heart Failure, 1993, 12(4): 860-862. |
| [22] |
Tatham R H, Keeney J W, Noponen I. Application of the tau-p transform (slant-stack) in processing seismic reflection data[J]. Exploration Geophysics, 1983, 14(4): 163-172. |
| [23] |
Martin G S, Wiley R, Marfurt K J. Marmousi 2:An elastic upgrade for Marmousi[J]. The Leading Edge, 2006, 25(2): 156-166. DOI:10.1190/1.2172306 |
| [24] |
Muller G, Weber M, Rumper G, et al. Theory of Elastic Waves[M]. Geo Forschungs Zentrum German Research Centre, 2007.
|



 张婧, 河北省涿州市华阳东路东方地球物理公司科技园物探技术研究中心, 072751。Email:
张婧, 河北省涿州市华阳东路东方地球物理公司科技园物探技术研究中心, 072751。Email: