0 引言

在地震数据采集过程中，因受多种条件或因素限制，如障碍物、禁区、风化带或经济成本等的影响，所采集数据往往出现不完整的现象。缺失的地震数据无疑对后期地震数据处理和成像造成不良影响，如多次波的去除、AVO分析及波动方程偏移成像等。因此，探寻恢复性能良好的地震数据重建方法对地震数据处理及解释具有重要的意义。

对于缺失地震数据的重建问题，业界已对其进行了较全面、深入的研究。一类是基于预测滤波的重建方法^[1-2]，该类方法假设原始地震数据具有有限个线性同相轴，基于线性同相轴在频率—空间域的可预测性，利用数据低频成分得到的预测滤波器对数据的高频成分进行插值重建。但该类方法通常需利用窗函数进行插值，窗函数参数的设定不当易引起重建误差。另一类是基于稀疏变换的压缩感知重建方法，该类方法先将非稀疏地震数据通过某种稀疏变换进行稀疏表示，再采用压缩感知理论对稀疏系数进行估计，最后对稀疏系数进行稀疏反变换得到数据的重建。根据其稀疏变换方法的不同，可将此类方法分成两个亚类：①基于固定字典的稀疏变换，如Fourier变换^[3-5]、Radon变换^[6-8]、Curvelet变换^[9-13]、Seislet变换^[14-15]和Dreamlet变换^[16-17]等；②基于字典学习的稀疏变换构造地震数据的稀疏字典^[18-21]。因字典的构造基于数据的结构特征，故与基于固定字典的稀疏变换相比，基于字典学习的稀疏变换对地震数据具有更稀疏的表示。

近年来，基于降秩的方法已成功应用于缺失地震数据的重建。该类方法假设完整地震数据经某种变换后成为一个低秩矩阵，如Hankel矩阵变换^[22-25]、纹理块变换^[26]和坐标变换^[27]等。由于数据的缺失会使矩阵的秩增加，从而可通过低秩矩阵补全算法对缺失数据进行重建。另外，也可将地震数据构造为一个张量，从而将地震数据重建问题转化为低秩张量补全问题^[28-30]。

Jia等^[31]和Wang等^[32]推出了基于机器学习的方法用于地震数据的重建，该方法通过大量的训练数据学习输入的缺失数据与输出的完整数据间的潜在关系，找到最优的回归平面或网络结构，然后用训练好的平面或网络对缺失地震数据进行重建。该类方法能对规则缺失地震数据进行有效重建且具有抗假频能力，但当训练数据与测试数据存在特征差异时将产生重建误差。

SLIM方法基于迭代最小化稀疏学习，由Tan等^[33]于2010年提出，并被成功地应用于MIMO雷达目标估计。随后，它也被应用于点源定位^[34]和SAR图像超分辨率重建^[35]等领域。SLIM方法是一种数据自适应的非参数方法，它具有高分辨率谱估计性能，可从随机缺失的数据中获得数据的高精度谱估计。

本文充分利用三维地震数据频率切片的二维谐波结构特性和SLIM方法特点，对缺失地震数据进行重建。该方法核心是从缺失地震数据中重建数据频率切片的谐波谱。即先采用循环最小化方法对谐波谱进行迭代估计，再对所得谱估计做反傅里叶变换得到重建数据；同时，为缩短数据重建时间，采用共轭梯度最小二乘法实现重建过程中的矩阵求逆。合成和实际三维地震数据实验结果均表明，SLIM方法能较好地重建随机缺失地震道数据。

1 理论基础 1.1 三维地震数据的重建模型

假设三维地震数据体在空间方向含有有限个平面波，则此数据体二维频率切片可表示为^[36]

$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{D}}_\omega } = {\left[ {{d_\omega }\left( {m,n} \right)} \right]_{M \times N}}\;\;\;m = 1, \cdots ,M,n = 1, \cdots ,N\\ {d_\omega }\left( {m,n} \right) = \sum\limits_{k = 1}^K {{u_k}} \left( \omega \right){{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathit{ π} }}\omega \left( {m\Delta x{p_{k,x}} + n\Delta y{p_{k,y}}} \right)}} \end{array} \right. $

(1)

式中：K表示平面波个数；ω表示频率分量；u_k(ω)表示第k个平面波对应的振幅；p_{k, x}和p_{k, y}分别表示第k个平面波x和y方向的射线参数；Δx和Δy分别表示x和y方向的采样间隔；m和n分别表示x和y方向的采样序号(对应最大值为M、N)。令

$ {\mathit{\Theta }_k}\left( {\omega ,m,n} \right) = \omega \left( {m\Delta x{p_{k,x}} + n\Delta y{p_{k,y}}} \right) $

则式(1)可写成

$ {d_\omega }\left( {m,n} \right) = \sum\limits_{k = 1}^K {{u_k}} \left( \omega \right){{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathit{ π} }}{\mathit{\Theta }_k}\left( {\omega ,m,n} \right)}} $

(2)

令d_ω(m, n)=d(m, n), u_k(ω)=u_k, Θ_k(ω, m, n)=Θ_k(m, n), D=D_ω, d=vec(D)∈C^MN, 则由式(1)得

$ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{Fu}} $

(3)

式中：u=[u₁, u₂, …, u_K]^T; F=[f₁f₂, …, f_K]且$\boldsymbol{f}_{k}=\left[\mathrm{e}^{-\mathrm{j} 2 \pi \theta_{k}(1, 1)}, \quad \mathrm{e}^{-\mathrm{j} 2 \pi \theta_{k}(2, 1)}, \quad \cdots, \quad \mathrm{e}^{-\mathrm{j} 2 \pi \theta_{k}(M, 1)}, \quad \cdots\right.$，$\left.\mathrm{e}^{-\mathrm{j} 2 \pi \theta_{k}(1, N)}, \cdots, \mathrm{e}^{-\mathrm{j} 2 \pi \theta_{k}(M, N)}\right]^{\mathrm{T}}$; (·)^T表示转置运算；vec(·)表示矩阵向量化。

考虑缺失地震数据的重建问题，存在

$ {\mathit{\boldsymbol{d}}_\Omega } = \mathit{\boldsymbol{Rd}} $

(4)

式中：d_Ω∈C^L(L＜MN)表示观测到的不完整地震数据；d表示完整的地震数据；R表示随机采样矩阵。

在对实际缺失地震数据进行重建时，由于某些频率分量往往会超出所定义的频率范围，从而给数据带来一定的噪声或误差^[37]，因此式(4)改写为

$ {\mathit{\boldsymbol{d}}_\Omega } = \mathit{\boldsymbol{Rd}} + \mathit{\boldsymbol{e}} $

(5)

式中e表示噪声项。此处目的是据不完整地震数据d_Ω恢复完整地震数据d。结合式(3)和式(5)，缺失地震数据的重建问题可进一步表示为

$ {\mathit{\boldsymbol{d}}_\Omega } = \mathit{\boldsymbol{Au}} + \mathit{\boldsymbol{e}} $

(6)

式中A=RF。

1.2 基于SLIM方法的三维地震数据重建

基于SLIM方法的缺失地震数据重建问题(式(6))可表示为如下优化问题^[33-35]

$ \left( {\mathit{\boldsymbol{\hat u}},\hat \eta } \right) = \mathop {\min }\limits_{\mathit{\boldsymbol{u}},\eta } g\left( {\mathit{\boldsymbol{u}},\eta } \right) $

(7)

式中

$ \begin{array}{*{20}{c}} {g\left( {\mathit{\boldsymbol{u}},\eta } \right) = L\lg \eta + \frac{1}{\eta }\left\| {{\mathit{\boldsymbol{d}}_\Omega } - \mathit{\boldsymbol{Au}}} \right\|_2^2 + }\\ {\sum\limits_{k = 1}^{\tilde K} {\frac{2}{q}\left( {{{\left| {{u_k}} \right|}^q} - 1} \right)} } \end{array} $

(8)

式中：‖·‖₂表示L₂范数；u表示待估计稀疏系数；η表示噪声能量；设定参数$0<q \leqslant 1, \widetilde{K}>K$。进一步定义：$\sum\limits_{k=1}^{\bar{K}}\left(\frac{2}{q}\right)\left(\left|u_{k}\right|^{q}-1\right)$为稀疏促进项；Llgη+ $\frac{1}{\eta }\left\| {{\mathit{\boldsymbol{d}}_\Omega } - \mathit{\boldsymbol{Au}}} \right\|_2^2$为数据拟合项，此项是使数据的重构误差达到最小。下面利用CM方法^[38]对参数u和η交替迭代更新，得到最优${\boldsymbol{\hat u}}$和$\hat{\eta}$。

设第i次迭代的稀疏系数和噪声能量分别为uⁱ和ηⁱ，求g(u, ηⁱ)关于u^H的偏导数，并令$\frac{\partial}{\partial \boldsymbol{u}^{\mathrm{H}}}$g(u，ηⁱ)=0，可得

$ \frac{1}{{{\eta ^i}}}{\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{Au}} - \frac{1}{{{\eta ^i}}}{\mathit{\boldsymbol{A}}^{\rm{H}}}{\mathit{\boldsymbol{d}}_\Omega } + {\mathit{\boldsymbol{P}}^{ - 1}}\mathit{\boldsymbol{u}} = {\bf{0}} $

(9)

式中：P=diag{p}, 其中diag{·}表示对角化；$\boldsymbol{p}=\left[\left|u_{1}\right|^{2-q}, \left|u_{2}\right|^{2-q}, \cdots, \left|u_{\tilde{K}}\right|^{2-q}\right]^{\mathrm{T}} ; \partial(\cdot)$表示求偏导数；（·）^H表示共轭转置运算。

为得到稀疏系数u的第i+1次迭代表达式，令P=Pⁱ, 且有Pⁱ=diag{pⁱ}, $\boldsymbol{p}^{i}=\left[\left|u_{1}^{i}\right|^{2-q}, \left|u_{2}^{i}\right|^{2-q}, \cdots\right.$$\left.\left|u_{\tilde{K}}^{i}\right|^{2-q}\right]^{\top}$，则由式(9)可得

$ \mathit{\boldsymbol{u}} = {\left[ {{\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{A}} + {\eta ^i}{{\left( {{\mathit{\boldsymbol{P}}^i}} \right)}^{ - 1}}} \right]^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{H}}}{\mathit{\boldsymbol{d}}_\Omega } $

(10)

于是，稀疏系数u的第i+1次迭代更新表达式为

$ \begin{array}{l} {\mathit{\boldsymbol{u}}^{i + 1}} = {\left[ {{\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{A}} + {\eta ^i}{{\left( {{\mathit{\boldsymbol{P}}^i}} \right)}^{ - 1}}} \right]^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{H}}}{\mathit{\boldsymbol{d}}_\Omega }\\ \;\;\;\;\;\; = {\mathit{\boldsymbol{P}}^i}{\mathit{\boldsymbol{A}}^{\rm{H}}}{\left[ {{\mathit{\boldsymbol{A}}^{\rm{H}}}{\mathit{\boldsymbol{P}}^i}\mathit{\boldsymbol{A}} + {\eta ^i}\mathit{\boldsymbol{I}}} \right]^{ - 1}}{\mathit{\boldsymbol{d}}_\Omega } \end{array} $

(11)

式中I表示单位矩阵。为得到参数η的估计，类似地，求g(uⁱ, η)关于η的偏导数，并令$\frac{\partial}{\partial \eta} g\left(\boldsymbol{u}^{i}, \eta\right)=\bf{0}$，可得

$ \eta = \frac{1}{L}\left\| {{\mathit{\boldsymbol{d}}_\Omega } - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{u}}^i}} \right\|_2^2 $

(12)

则参数η的第i+1次迭代更新表达式为

$ {\eta ^{i + 1}} = \frac{1}{L}\left\| {{\mathit{\boldsymbol{d}}_\Omega } - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{u}}^{i + 1}}} \right\|_2^2 $

(13)

据上述分析，基于SLIM方法的三维地震数据重建可用交替迭代方式，包括如下具体步骤。

(1) 将缺失地震道数据变换到频率域，得到频率切片d_Ω；

(2) 输入采样矩阵R，构造矩阵A=RF，这里$\boldsymbol{F} \in \boldsymbol{C}^{\mathrm{M} \mathrm{N} \times \tilde{K}}$为二维傅里叶变换矩阵，设置q=1，迭代精度控制参数ε₁=10^-3；

(3) 初始化：$u_{k}^{0}=\frac{A(:, k) d_{\Omega}}{\|A(\because, k)\|_{2}^{2}}, k=1, 2, \cdots, \widetilde{K}$, $\eta^{0}=\frac{\left\|\boldsymbol{d}_{\Omega}-\boldsymbol{A} \boldsymbol{u}^{0}\right\|_{2}^{2}}{L}$;

(4) 利用式(11)更新稀疏系数uⁱ；

(5) 利用式(13)更新参数ηⁱ；

(6) 重复步骤(4)~步骤(5)，对稀疏系数u和噪声能量η做交替更新，若满足$\frac{\left\|\boldsymbol{u}^{i}-\boldsymbol{u}^{i-1}\right\|_{2}}{\left\|\boldsymbol{u}^{i}\right\|_{2}} \leqslant \varepsilon_{1}$，则停止迭代更新，输出稀疏系数的估计$\hat{\boldsymbol{u}}=\boldsymbol{u}^{\prime}$；否则，继续重复步骤(4)~步骤(5)；

(7) 对稀疏系数$\boldsymbol{\hat u}$做二维逆傅里叶变换，得到重建的频率切片$\boldsymbol{\hat{d}}$；

(8) 将重建的频域数据做逆傅里叶变换，完成三维地震数据的重建。

1.3 共轭梯度最小二乘法

在应用SLIM方法重建三维地震数据的过程中，稀疏系数u的更新涉及矩阵的逆的计算，即式(11)中的$\left(\boldsymbol{A}^{\mathrm{H}} \boldsymbol{P} \boldsymbol{A}+\eta \boldsymbol{I}\right)^{-1}$部分，此部分的计算复杂度较高。因此，为减小计算复杂度，本文采用共轭梯度最小二乘方法(Conjugate Gradient Least Squares，CGLS)^[39]对$\left(\boldsymbol{A}^{\mathrm{H}} \boldsymbol{P} \boldsymbol{A}+\eta \boldsymbol{I}\right)^{-1} \boldsymbol{d}_{\Omega}$求解。令

$ \mathit{\boldsymbol{v}} = {\left( {{\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{PA}} + \eta \mathit{\boldsymbol{I}}} \right)^{ - 1}}{\mathit{\boldsymbol{d}}_\Omega } $

(14)

进一步，将式(14)改写为

$ \mathit{\boldsymbol{v}} = {\left( {{\mathit{\boldsymbol{B}}^{\rm{H}}}\mathit{\boldsymbol{B}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{H}}}\mathit{\boldsymbol{z}} $

(15)

式中$\boldsymbol{B}=\left[\begin{array}{c} \boldsymbol{P}^{\frac{1}{2}} \boldsymbol{A}^{\mathrm{H}} \\ \eta^{\frac{1}{2}} \boldsymbol{I} \end{array}\right], \boldsymbol{z}=\left[\begin{array}{c} \boldsymbol{0} \\ \eta^{-\frac{1}{2}} \boldsymbol{d}_{\Omega} \end{array}\right]$。由式(15)可知，式(14)可转化为如下最小二乘问题的最优解

$ \mathop {\min }\limits_\mathit{\boldsymbol{v}} \left\| {\mathit{\boldsymbol{Bv}} - \mathit{\boldsymbol{z}}} \right\|_2^2 $

(16)

因此，$\left(\boldsymbol{A}^{\mathrm{H}} \boldsymbol{P} \boldsymbol{A}+\eta \boldsymbol{I}\right)^{-1} \boldsymbol{d}_{\Omega}$的求解就等价于求解最小二乘问题(式(16))的最优解。下面采用CGLS方法对式(16)求解，包括如下具体步骤。

(1) 初始化：$\boldsymbol{v}_{0}=\bf{0}, \boldsymbol{r}_{0}=-\boldsymbol{B}^{\mathrm{H}} \boldsymbol{z}, \boldsymbol{c}_{0}=-\boldsymbol{r}_{0}, \varepsilon_{2}=10^{-6}$;

(2) 计算h_j=B^HBc;

(3) 计算$\alpha=\frac{\left\|\boldsymbol{r}_{j}\right\|_{2}^{2}}{\boldsymbol{c}_{j}^{\mathrm{H}} \boldsymbol{h}_{j}}$;

(4) 更新v_j+1=v_j+αc_j;

(5) 更新r_j+1=r_j+αh_j;

(6) 更新$c_{j+1}=-r_{j+1}+\frac{c_{j}\left\|r_{j+1}\right\|_{2}^{2}}{\left\|r_{j}\right\|_{2}^{2}}$;

(7) 若满足$\frac{\left\|\boldsymbol{r}_{j+1}\right\|_{2}^{2}}{\left\|\boldsymbol{d}_{\Omega}\right\|_{2}^{2}} \leqslant \varepsilon_{2}$, 则停止迭代，输出参数v的估计$\mathit{\boldsymbol{\hat v = }}{\mathit{\boldsymbol{v}}_{j + 1}}$，否则再重复步骤(2)~步骤(6)。

综合以上分析，基于SLIM方法的三维缺失地震数据重建的具体流程如图 1所示。

2 数值实验

采用一个合成三维地震数据和两个真实三维地震数据验证本文基于SLIM的重建方法的效能，并选用了基于频率切片的MSSA方法进行对比。

以信噪比作为重建效果的度量指标，定义为

$ {R_{{\rm{S}}/{\rm{N}}}} = 10 \times \lg \frac{{\left\| \mathit{\boldsymbol{s}} \right\|_{\rm{F}}^2}}{{\left\| {\mathit{\boldsymbol{s}} - \mathit{\boldsymbol{\hat s}}} \right\|_{\rm{F}}^2}} $

(17)

式中：‖·‖_F表示Frobenius范数；s表示原始的完整三维地震数据体，$\boldsymbol{\hat s}$表示重建的三维地震数据体。从式(17)可知，R_S/N值越大数据重建效果越好。

2.1 合成数据

合成的地震记录由主频为40Hz的Ricker子波产生，尺寸为64×64×256，即沿主测线(Inline)方向和联络线(Crossline)方向的数据采样点个数均为64，沿时间轴的数据采样个数为256。

图 2b为相对于完整采样数据(图 2a)随机缺失50%的地震道数据。分别利用MSSA(图 2c)和SLIM(图 2d)方法对缺失地震道数据进行重建并给出了对应的重建误差(图 2e、图 2f)。在SLIM方法中，选取参数q=1；在MSSA方法中，选取秩为5。为近似满足线性平面波的假设，本次实验中对数据沿空间方向做分窗处理，窗口尺寸为32×32。从图 2可见：两种方法均能对缺失地震道数据进行较好的重建，本文SLIM方法的重建信噪比为55.1dB，而MSSA方法的重建信噪比为39.2dB，显然前者重建误差较小、信噪比更高，表明SLIM方法重建结果优于MSSA方法。

图 3为该合成的完整地震数据(图 3a)和缺失数据(图 3b)沿联络线方向切片的F-K谱对比图，可见数据缺失后出现明显的假频现象。对比MSSA(图 3c)和SLIM(图 3d)两种重建方法的F-K谱，看到此两种方法都能有效地去除假频现象，但MSSA方法在重建过程中出现部分能量丢失，进一步证明本文方法的重建结果优于MSSA方法。

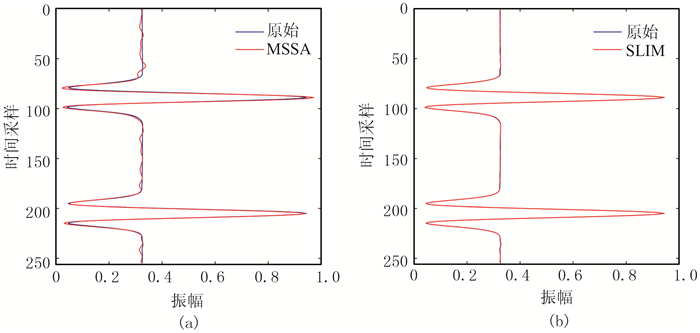
从上述分别用MSSA和SLIM方法重建的地震数据中随机抽取一道与原始地震道数据做对比(图 4)。可见SLIM方法重建的波形(图 4b)比MSSA方法(图 4a)更逼近于原始波形，表明本文基于SLIM方法比MSSA方法能更精确地重建缺失地震道数据。

2.2 实际数据

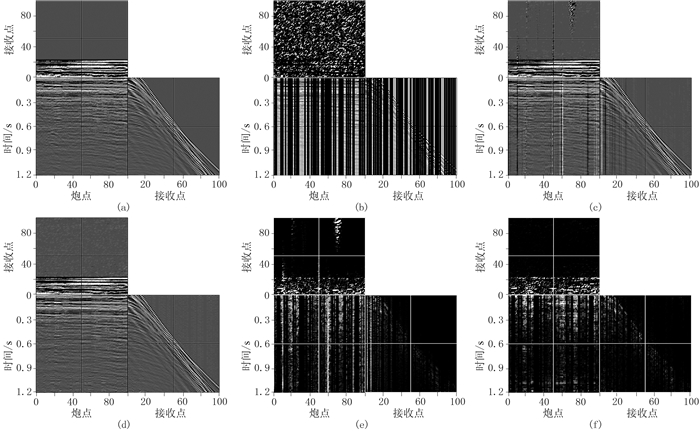
采用实际地震数据进一步验证SLIM方法的重建性能。第一个数据实例选自Petroleum Geo-Systems的叠前三维海洋数据集。实验中采样地震数据的尺寸为100×100×300，即沿炮点和接收点方向的采样数据点个数均为100，时间采样率为4ms，沿时间轴的采样点个数为300。在重建过程中，SLIM方法的参数q设置为1，MSSA方法的秩选为18，窗口尺寸设置为25×25。针对该叠前完整地震数据(图 5a)和随机缺失50%地震道数据(图 5b)，分别利用MSSA和SLIM方法对缺失地震道数据进行重建处理，得到两种方法的重建结果(图 5c、图 5d)及其重建误差(图 5e、图 5f)。可见两种方法都能较好地对数据进行重建，但MSSA方法(图 5c)对于部分细节信息没有完全重建出来，而SLIM方法(图 5d)较好地对细节信息进行了重建；实验中，SLIM方法的重建信噪比为35.8dB，而MSSA方法的重建信噪比为29.2dB。因此，该处理结果表明SLIM方法的重建效果优于MSSA方法。

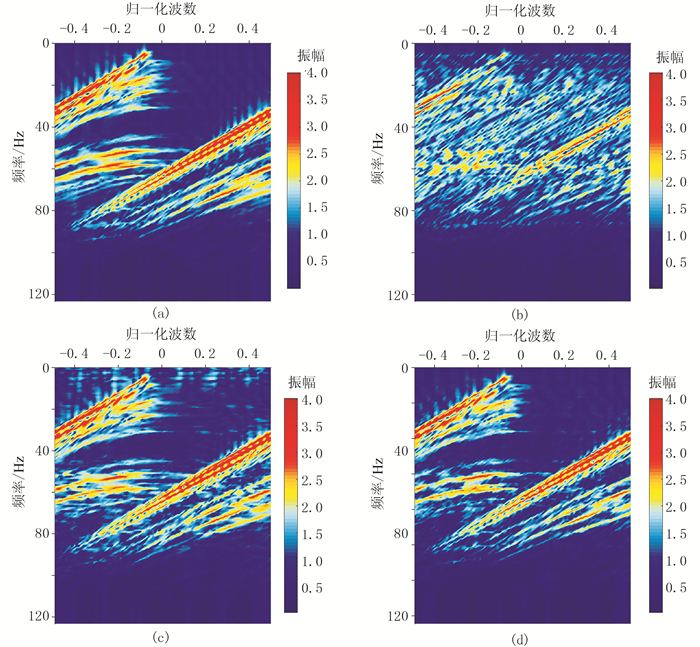
图 6为叠前完整地震数据(图 6a)和缺失地震数据(图 6b)沿联络线方向切片的F-K谱对比图，可见数据缺失引起了明显的假频，SLIM(图 6d)和MSSA(图 6c)方法都能有效地恢复真实的F-K谱，且能一定程度上抑制假频。但MSSA在重建过程中出现了部分能量丢失，而SLIM方法则有效的保留了原始数据的能量。

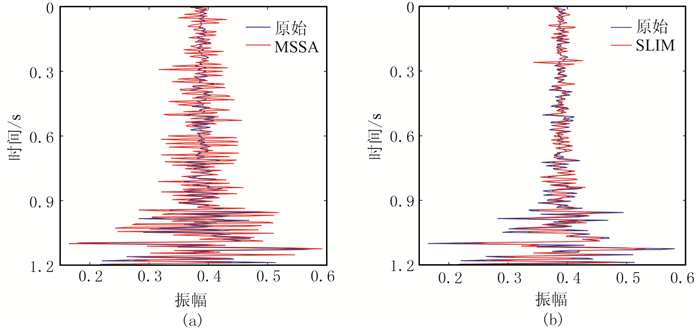
图 7为随机抽取的单道缺失地震道数据的重建结果比较图，可见SLIM方法重建的地震道(图 7b)比MSSA方法(图 7a)更接近于真实的地震道数据。

第二个数据实例来自新西兰Crown Minerals的叠后地震数据集Parihaka-3D。实验地震数据尺寸为100×100×300，即沿主测线和联络线方向的采样数据点个数均为100，时间采样率为3ms，沿时间轴的采样点个数为300。在重建过程中，SLIM方法的参数q=1，MSSA方法的秩选取为25，窗口尺寸设置为25×25。

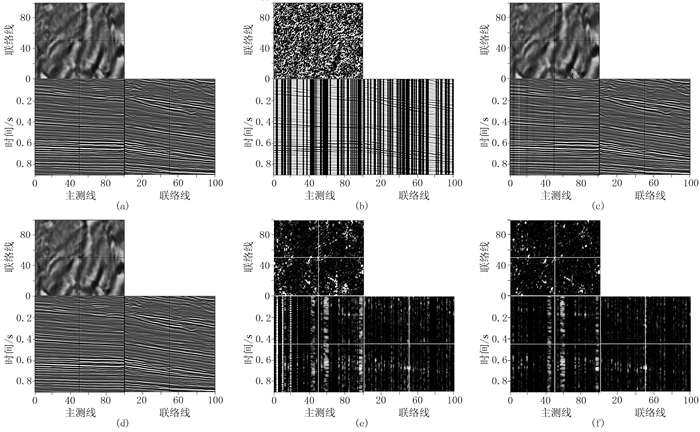
针对叠后完整地震数据(图 8a)和随机缺失50 %地震数据(图 8b)，分别利用MSSA和SLIM方法对缺失地震道数据进行重建处理，得到两种方法的重建结果(图 8c、图 8d)及其重建误差(图 8e、图 8f)。可见MSSA方法的重建信噪比为31.5dB，SLIM方法的重建信噪比为37.4dB，因此SLIM方法重构效果更好。

图 9为叠后完整地震数据(图 9a)和缺失地震数据(图 9b)沿联络线方向切片的F-K谱对比图，可见SLIM方法(图 9d)有效地压制了假频，且重建的F-K谱比MSSA方法(图 9c)更接近于真实数据的F-K谱。图 10为随机抽取的单道地震数据的重建结果比较，可见SLIM方法(图 10b)的重建结果更接近于原始海洋地震数据波形。

3 结论

本文研究了三维随机缺失地震道数据的重建。将三维地震数据频率切片具有的二维谐波结构与基于迭代最小化稀疏学习的SLIM方法相结合，实现了三维随机缺失地震数据的重建。通过人工合成与实际三维数据的实验处理，得出以下认识和结论：

(1) SLIM方法对人工合成和实际三维地震数据均具有较好的重建效果；

(2) 与经典的基于频率切片的矩阵降秩MSSA方法相比，SLIM方法具有更高的重建性能；

(3) 本文采用CGLS算法实现SLIM方法在迭代过程中的矩阵求逆运算，在保证重建效果的同时提高了重建数据的计算效率。

本文只针对三维缺失地震数据重建策略进行了研究，如何对三维地震数据同时进行去噪和重建将是后期进一步研究的课题。