一直以来,高质量的原始地震数据是现场数据采集的主要目标。但受限于现场采集的条件、环境及施工成本,往往无法达到对采集区域的全覆盖;现场采集的原始地震数据也会因检波器或人为因素而导致部分道集缺失甚至无法使用。因此,研究人员尝试利用压缩感知方法解决这一问题。其理论思路是通过设计合适的观测系统对工区进行部分观测,再利用压缩感知方法重建恢复观测的低维地震数据,以得到完整地震资料。即通过重建方式解决此地震数据采集难题[1]。
2006年Donoho[2]提出压缩感知理论,该理论在采样方面突破传统Nyquist采样定理的限制,为地震数据采样提供新途径——尽可能地既压缩采集成本又能实现对工区地震资料的完整采集[3]。随着压缩感知理论的逐渐成熟,在图像、医学、雷达等领域广泛采用傅里叶变换作为稀疏变换基并得到成功应用[4-5]。
但地震信号具有非规则、突变性的特点,由于傅里叶变换作为一种全局变换仅是对时间维积分,在某时刻不能很好地刻画地震信号的局部频谱特征,地震信号的稀疏性不能被完全地表达,导致重建效果欠佳。人们试图通过选取稀疏表达能力更强的变换方式改善这一问题[6-11]。根据地震数据的曲线特征,Herrman等[12]提出基于Curvelet变换的地震数据插值重建方法(Curvelet Recovery by Sparsity-Promoting Inversion,CRSI);在此基础上还解决了傅里叶变换和小波变换对地震数据不能良好稀疏表示的问题[13-14]。冯飞等[15]将Shearlet变换应用于压缩感知领域,其更优良的方向性、稀疏性被研究人员所青睐。张良等[16]对比多种压缩感知稀疏基,指出Shearlet变换作为压缩感知稀疏变换基具有更高重建精度,但它对计算机性能的要求过高,实际处理中的计算效率是亟待解决的主要问题。
针对稀疏变换的稀疏表达能力和计算效率以及对数据重建效果的影响等,本文也尝试通过探寻一种适用稀疏变换方法来解决此类问题。
S变换作为一种良好的时频域信号分析方法,于1996年由Stockwell等[17]首次提出。结合短时傅里叶变换和小波变换的局部化思想,将基本小波函数设置为简谐波与Gaussian函数乘积的形式。其窗函数具有随频率增加而减小的可变性,当信号处于低频段时将视窗变宽;反之,处于高频段时将视窗变窄,可获得较高的时间分辨率,克服其他滤波方法的窗函数宽度固定不变的缺陷。根据压缩感知对稀疏变换基的要求,需对S变换进行正交变换以得到新的变换形式。Stockwell[18]提出一种基于S变换的正交时频表示方法——离散正交S变换(Discrete orthonormal S-transform,DOST),使用一组正交基函数对频谱进行局部化,保留了S变换的固有特性,且降低了冗余度,提高了运算速度。杨晋吉等[19]将DOST应用于人脸识别,即将其引入图像处理领域,且阐明了该变换方法具备良好的稀疏性[20-21]。
为了有效解决原始高维数据体的恢复重建效率问题,本文首次引入DOST作为压缩感知稀疏变换基,提出利用DOST和压缩感知的地震数据重建方法。即在简述DOST原理及压缩感知理论框架的基础上,用DOST方法将原始地震数据稀疏变换至时频域,结合压缩感知算法重构地震数据。通过模型试算验证了DOST稀疏变换法应用于压缩感知的可行性,并与基于FFT和Shearlet变换的压缩感知地震数据重建结果做对比分析,证明利用DOST稀疏变换法的有效性;以实例进一步论证该方法对实际现场采集地震数据的适用性。
1 基本理论 1.1 压缩感知理论通过采集得到的不完整地震记录,在压缩感知理论框架下根据其稀疏性将不完整地震数据的重建问题转化为数学方程的形式
| $ \boldsymbol{Y}=\boldsymbol{\Phi} \boldsymbol{X} $ | (1) |
式中:X∈RN表示理想状态下的完整地震数据;Y∈RM表示实际采集到的部分(压缩观测)地震数据;Φ∈RM×N(M < < N)表示采样矩阵。
引入DOST将地震数据稀疏表示为
| $ \boldsymbol{X}=\boldsymbol{\psi}_{\mathrm{DOST}} \boldsymbol{\theta} $ | (2) |
式中:
合并式(1)和式(2),得到
| $ \boldsymbol{Y}=\boldsymbol{\Phi} \boldsymbol{\psi}_{\mathrm{DOST}} \boldsymbol{\theta}=\boldsymbol{A}_{\mathrm{DOST}} \boldsymbol{\theta} $ | (3) |
式中ADOST为M×N阶感知矩阵,其过程是非自适应性感知测量,压缩感知理论强调使用的采样矩阵Φ必须具备有限性、等距的条件,即RIP(Restricted Isometry Property)准则,定义为存在一个常数εq使P的每个向量y满足(1-εq)‖y‖22≤‖Py‖22≤(1+εq)‖y‖22,其中P是一个a×b阶矩阵,q∈[1,b]是一个整数。
由于向量θ是由稀疏变换求得的稀疏矩阵,具备稀疏性,求解最小L0范数的问题等价于式(3),即
| $ \hat{\boldsymbol{\theta}}=\arg \min \limits_{\boldsymbol{\theta}}\|\boldsymbol{\theta}\|_{0} \quad \text { s.t. } \quad \boldsymbol{Y}=\boldsymbol{\Phi} \boldsymbol{\Psi}_{\mathrm{DOST}} \boldsymbol{\theta} $ | (4) |
在压缩感知理论中,通常将求解θ的最小L0范数问题等价转化为求解θ的最小L1范数问题,结合实际处理中的误差干扰并对L1范数和L2范数进行平衡误差约束,引入λ作为平衡算子,构建新的近似方程
| $ \hat{\boldsymbol{\theta}}=\arg \min \limits_{\boldsymbol{\theta}} \lambda\|\boldsymbol{\theta}\|_{1}+\left\|\boldsymbol{Y}-\boldsymbol{\Phi} \boldsymbol{\Psi}_{\mathrm{DOST}} \boldsymbol{\theta}\right\|_{2}^{2} $ | (5) |
S变换能克服短时傅里叶变换不能调节分析窗口频率的问题,而且引入了小波变换的多分辨率分析。DOST是在S变换的基础上进行改进,可用一个时间序列h[kT]与Ψ[kT][υ,β,τ]的基函数之间的内积表示
| $ S\{\boldsymbol{h}[k T]\}=S\left(\tau T, \frac{v}{N T}\right)=\sum\limits_{k=0}^{N-1} \boldsymbol{h}[k T] \boldsymbol{\Psi}[k T]_{[v, \beta, \tau]} $ | (6) |
式中:υ表示频率变量对应的频带中心位置;β为频带宽度;τ为时间变量;T为输入信号的采样周期。
在此基础上,通过引入υ、β、τ三个参数划分原始时频谱,得到所需正交基向量,每个基向量代表不同的时频区块。在一般情况下,第k个基函数Ψ[kT][υ,β,τ]被定义为
| $ \begin{aligned} \boldsymbol{\Psi}[k T]_{[v, \beta, \tau]}=& \frac{1}{\sqrt{\beta}} \sum\limits_{f=v-\frac{\beta}{2}}^{v+\frac{\beta}{2}-1} \exp \left(\mathrm{i} 2 \pi \frac{k}{N} f\right) \times \\ & \exp \left(-\mathrm{i} 2 \pi \frac{\tau}{\beta} f\right) \exp (-\mathrm{i} \pi \tau) \end{aligned} $ | (7) |
式中:f为输入信号的采样频率;
DOST是通过用N个线性无关的点表示时频信号代替S变换中N×N的时频空间,对于任意长度为N的输入信号,进行离散S变换后,得到的系数为N个,对每个系数计算需要进行O(N)次,总体系数复杂度为O(N3);而DOST通过一个系数来代替由DOST时频谱划分N个区域中的一个,将整体算法复杂度降为O(N2),在保留信号中有效信息点的同时,大幅降低算法复杂度,保证时频分辨率情况下改进整体算法计算效率。时频分辨的提高有助于原始信号能量的集中,使时频矩阵内的非零项减少,进而改善稀疏变换的稀疏性,提高整体算法计算速度并兼顾保留有效信号,最终得到高质量的重建结果。
1.3 重建算法在构建基于DOST的地震数据重建算法的基础上对地震数据重建,本文采用快速凸集投影算法(FPOCS)[22-23]求解式(5)。FPOCS算法是通过在常规POCS(凸集投影)算法基础上引入步长tk,实现在单次循环内对变换量的可控性,从而提高单次迭代计算效率、减少迭代次数、更快得到接近目标函数的解,重建算法收敛速度更快,重建结果的精度也更高。算法具体流程如下。
输入:采样矩阵Φ,缺失地震数据Y,最大迭代次数K,单位矩阵I,阈值函数Tλ;
(1)
(2)
(3)
(4) 应用阈值模型减小λ;
(5) i=i+1;
(6) 如果i<K或不满足收敛条件,跳转到(1);否则,
输出:重建地震数据
从总体上看,以压缩感知理论重构地震数据主要包括三大步骤:
第一步,测量矩阵的设计,使用Jitter采样确保采样随机性且保证重建精度[24];
第二步,使用DOST将测量所得地震数据从高维域内投影到时频域中进行稀疏表示;
第三步,信号重建算法的设计,利用FPOCS算法高效地重建原始信号。
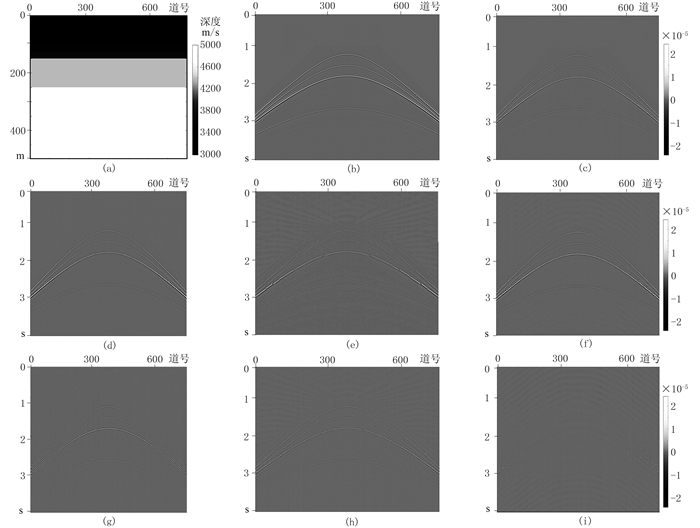
2 模型试算构建的速度模型(图 1a)的激发点位于中间第400道地表处,共760道接收,道间距为10m,每道2000个时间采样点,采样间隔为2ms,采用主频为20Hz的雷克子波。对正演所得原始地震记录(图 1b)使用Jitter采样法得到抽稀采样50%的地震数据(图 1c);分别采用以DOST、FFT、Shearlet变换为稀疏基的方法获得重建地震数据(图 1d~图 1f);再分别与原始地震记录相减可得对应差值剖面(图 1g~图 1i)。
|
图 1 三种方法模型数据重建结果对比 (a)速度模型;(b)原始模型数据;(c)压缩50%采样后不完整数据;(d)、(e)、(f)对应以FFT、Shearlet、DOST为稀疏基的重建结果;(g)、(h)、(i)对应以FFT、Shearlet、DOST为稀疏基重建结果与图b的差值 |
根据上述基于DOST方法得到的重建剖面,首先可确认该方法对压缩感知地震数据重建的可行性;进一步对比基于DOST、FFT和Shearlet三种变换方法的重建结果及其差值,可见DOST方法(图 1f)对应的同相轴比后两者(图 1d、图 1e)更光滑、连续,能量更强,整体恢复效果更佳。
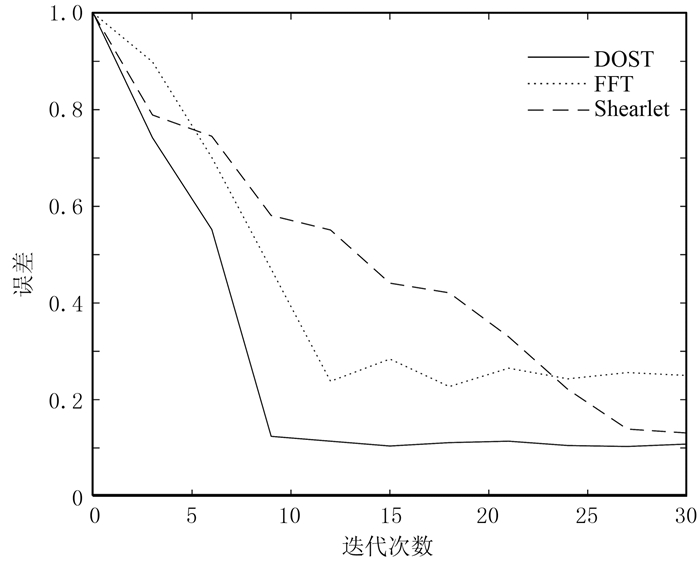
图 2中绘制三条误差曲线对比三种方法的计算效率,其中误差值、信噪比分别为
|
图 2 模型数据三种方法重建误差随迭代次数的变化曲线 |
| $ E_{\mathrm{r}}=\left\|\mathit\Phi_{n}\left(\boldsymbol{Y}-\boldsymbol{A} \theta_{n}\right)\right\|_{2} $ | (8) |
| $ R_{\mathrm{s} / \mathrm{N}}=10 \times \lg \frac{\|\boldsymbol{X}\|_{2}^{2}}{\|\hat{\boldsymbol{X}}-\boldsymbol{X}\|_{2}^{2}} $ | (9) |
此处n表示迭代序号。
针对50%压缩采样情况下的数据,使用三种稀疏变换方法能较好地重建大部分真实数据。在收敛速度方面,运用相同阈值时,本文方法收敛速度最快,对比重建时间、误差值及信噪比(表 1),可知Shearlet方法的重建时间远多于其他两种方法。综合考虑收敛速度、重建时间、最终误差、信噪比等因素,本文方法得到数据重建效果最好。因此,从正演模型数据验证了本文方法对恢复重建缺失地震数据的有效性。
|
|
表 1 三种方法地震数据重建结果对比 |
在模型试算基础上,针对实际数据使用基于压缩感知的DOST方法进行处理,并与基于FFT和Shearlet的方法的处理结果进行对比。
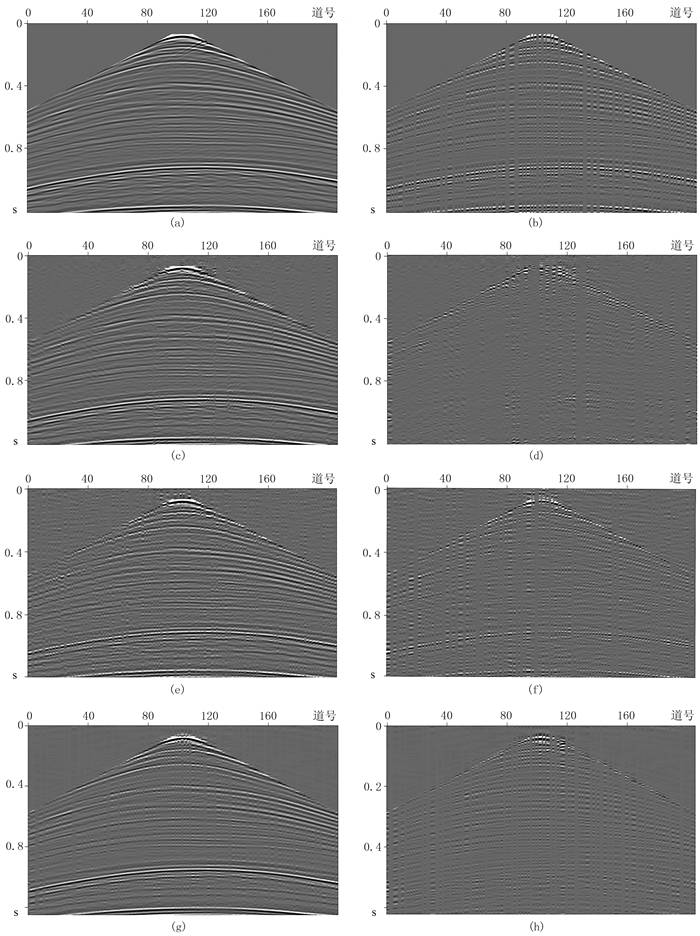
选取M工区201道单炮记录,每道600个时间采样点,采样间隔为2ms。从原始单炮记录(图 3a)可见同相轴光滑、连续,噪声较弱;对其进行Jitter压缩采样,得到缺失50%的单炮记录(图 3b);使用本文方法处理得到的重构单炮记录(图 3c)上整体同相轴恢复较好,引入噪声较少;而使用基于FFT方法所得重建单炮记录(图 3e)上部分同相轴连续性较差;使用基于Shearlet方法所得重建单炮记录(图 3g)上对缺失道的恢复能量较弱。整体对比本文、FFT和Shearlet三种方法重建结果与原始单炮记录的差值(图 3d、图 3f、图 3h),可见本文方法所得能量丢失较少、地震记录整体恢复重建效果最好,表明本文方法重建效果优于基于FFT、Shearlet变换的方法。
|
图 3 实际单炮地震数据三种方法重建结果对比 (a)原始单炮记录;(b)缺失50%的单炮记录;(c)、(e)、(g)对应使用本文、FFT、Shearlet方法重建的单炮记录;(d)、(f)、(h)对应使用本文、FFT、Shearlet方法所得重建结果与原始数据的差值剖面 |
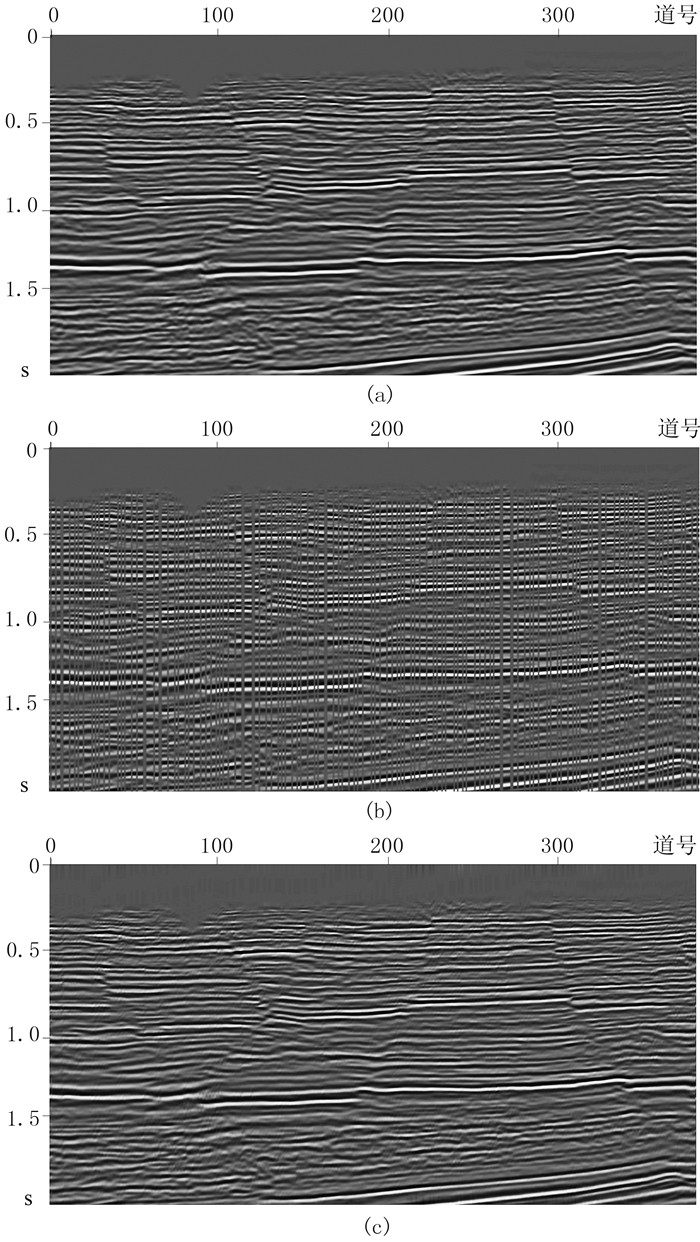
再选取N工区380道叠后地震资料[25],每道1000个时间采样点,采样间隔为2ms。从原始剖面(图 4a)可看到能量明显、连续性较好的同相轴,也有能量较弱的信号及少量噪声;缺失数据(图 4b)是对原始数据经人为删减40%地震道形成的;从采用本文方法恢复重建所得剖面(图 4c)上,可见同相轴信息完整,整体同相轴光滑、连续,充分地修复了缺失区域数据,且基本未引入噪声干扰,整体剖面重建结果较好。另外,该方法恢复重建的速度也较快。
|
图 4 叠后实际地震数据重建结果 (a)原始地震记录;(b)缺失40%地震记录;(c)使用本文方法重建记录 |
基于前人研究成果,本文根据DOST窗函数的可变性和较强的时频分析能力,改善压缩感知稀疏变换基的稀疏性,提出一种基于压缩感知技术的DOST重建方法,在提高计算效率的同时兼顾重建精度,无论针对弯曲或水平同相轴,都能得到较好的重建结果。对比基于DOST、FFT、Shearlet方法所得重建结果表明,本文方法(相比于其他两种稀疏变换法)同时具有收敛快、引入噪声少、重建精度高等特点。实际地震数据重建结果验证了本文方法的有效性和适用性。
| [1] |
李振春, 王姣, 孙苗苗, 等. 地震数据规则化重构方法策略[J]. 中国石油大学学报(自然科学版), 2018, 42(1): 40-49. LI Zhenchun, WANG Jiao, SUN Miaomiao, et al. Strategy of seismic data regularized reconstruction[J]. Journal of China University of Petroleum(Edition of Natural Science), 2018, 42(1): 40-49. DOI:10.3969/j.issn.1673-5005.2018.01.005 |
| [2] |
Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [3] |
宋维琪, 吴彩端. 利用压缩感知方法提高地震资料分辨率[J]. 石油地球物理勘探, 2017, 52(2): 214-219. SONG Weiqi, WU Caiduan. Seismic data resolution improvement based on compressed sensing[J]. Oil Geophysical Prospecting, 2017, 52(2): 214-219. |
| [4] |
Lustig M, Donoho D L, Santos J, et al. Compressed sensing MRI[J]. IEEE Signal Processing Magazine, 2008, 25(2): 72-82. DOI:10.1109/MSP.2007.914728 |
| [5] |
Oka A, Lampe L. A compressed sensing receiver for UWB impulse radio in bursty applications like wireless sensor networks[J]. Physical Communication, 2009, 30(14): 2802-2811. |
| [6] |
柳建新, 韩世礼, 马捷. 小波分析在地震资料去噪中的应用[J]. 地球物理学进展, 2006, 21(2): 541-545. LIU Jianxin, HAN Shili, MA Jie. Application of wavelet analysis in seismic data denoising[J]. Progress in Geophysics, 2006, 21(2): 541-545. DOI:10.3969/j.issn.1004-2903.2006.02.032 |
| [7] |
Morlet J, Arens G, Fourgeau E, et al. Wave propagation and sampling theory-Part Ⅱ:Sampling theory and complex waves[J]. Geophysics, 1982, 47(2): 222-236. DOI:10.1190/1.1441329 |
| [8] |
高建军, 陈小宏, 李景叶, 等. 基于非均匀Fourier变换的地震数据重建方法研究[J]. 地球物理学进展, 2009, 24(5): 1741-1747. GAO Jianjun, CHEN Xiaohong, Li Jingye, et al. Study on reconstruction of seismic data based on nonuniform Fourier transform[J]. Progress in Geophysics, 2009, 24(5): 1741-1747. DOI:10.3969/j.issn.1004-2903.2009.05.026 |
| [9] |
Choi H, Baraniuk R.Interpolation and denoising of nonuniformly sampled data using wavelet-domain processing[C].Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing, 1999, 3: 1645-1648.
|
| [10] |
Chui C K. An Introduction to Wavelets[M]. Elsevier, 2016.
|
| [11] |
温睿, 刘国昌, 冉扬. 压缩感知地震数据重建中的三个关键因素分析[J]. 石油地球物理勘探, 2018, 53(4): 682-693. WEN Rui, LIU Guochang, RAN Yang. Three key factors in seismic data reconstruction based on compressive sensing[J]. Oil Geophysical Prospecting, 2018, 53(4): 682-693. |
| [12] |
Herrmann F J, Hennenfent G. Non-parametric seismic data recovery with curvelet frames[J]. Geophysical Journal International, 2008, 173(1): 233-248. DOI:10.1111/j.1365-246X.2007.03698.x |
| [13] |
Yin W. Analysis and generalizations of the linearized bregman method[J]. SIAM Journal on Imaging Sciences, 2010, 3(4): 856-877. DOI:10.1137/090760350 |
| [14] |
Ma J, Plonka G. The curvelet transform[J]. IEEESignal Processing Magazine, 2010, 27(2): 118-133. DOI:10.1109/MSP.2009.935453 |
| [15] |
冯飞, 王征, 刘成明, 等. 基于Shearlet变换稀疏约束地震数据重建[J]. 石油物探, 2016, 55(5): 682-691. FENG Fei, WANG Zheng, LIU Chengming, et al. Seismic data reconstruction based on sparse constraint in the Shearlet domain[J]. Geophysical Prospecting for Petroleum, 2016, 55(5): 682-691. DOI:10.3969/j.issn.1000-1441.2016.05.007 |
| [16] |
张良, 韩立国, 许德鑫, 等. 基于压缩感知技术的Shearlet变换重建地震数据[J]. 石油地球物理勘探, 2017, 52(2): 220-225. ZHANG Liang, HAN Liguo, XU Dexin, et al. Seismic data reconstruction with Shearlet transform based on compressed sensing technology[J]. Oil Geophysical Prospecting, 2017, 52(2): 220-225. |
| [17] |
Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum:the S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. DOI:10.1109/78.492555 |
| [18] |
Stockwell R G. A basis for efficient representation of the S-transform[J]. Digital Signal Processing, 2007, 17(1): 371-393. DOI:10.1016/j.dsp.2006.04.006 |
| [19] |
杨晋吉, 王燚. 离散正交S变换在人脸识别中的应用研究[J]. 小型微型计算机系统, 2017, 38(1): 169-173. YANG Jinji, WANG Yi. Application research of discrete orthogonal S transform in face recognition[J]. Journal of Chinese Computer Systems, 2017, 38(1): 169-173. |
| [20] |
车彩玲, 赵庆生, 王旭平, 等. 基于快速离散正交S变换的电能质量扰动检测方法[J]. 科学技术与工程, 2017, 17(2): 57-62. CHE Cailing, ZHAO Qingsheng, WANG Xuping, et al. A method of power quality disturbance detection based on fast discret orthogonal S-transform[J]. Science Technology and Engineering, 2017, 17(2): 57-62. DOI:10.3969/j.issn.1671-1815.2017.02.010 |
| [21] |
曹鹏涛, 张敏, 李振春. 基于广义S变换及高斯平滑的自适应滤波去噪方法[J]. 石油地球物理勘探, 2018, 53(6): 1128-1136, 1187. CAO Pengtao, ZHANG Min, LI Zhenchun. An adaptive filtering denoising method based on generalized S-transform and Gaussian smoothing[J]. Oil Geophy-sical Prospecting, 2018, 53(6): 1128-1136, 1187. |
| [22] |
Yang P, Gao J, Chen W. On analysis-based two-step interpolation methods for randomly sampled seismic data[J]. Computers & Geosciences, 2013, 51(2): 449-461. |
| [23] |
周亚同, 王丽莉, 蒲青山. 压缩感知框架下基于K-奇异值分解字典学习的地震数据重建[J]. 石油地球物理勘探, 2014, 49(4): 652-660. ZHOU Yatong, WANG Lili, PU Qingshan. Seismic data reconstruction based on K-SVD dictionary learning under compressive sensing framework[J]. Oil Geophysical Prospecting, 2014, 49(4): 652-660. |
| [24] |
王本锋, 陈小宏, 李景叶, 等. POCS联合改进的Jitter采样理论曲波域地震数据重建[J]. 石油地球物理勘探, 2015, 50(1): 20-28. WANG Benfeng, CHEN Xiaohong, LI Jingye, et al. Seismic data reconstruction based on POCS and improved Jittered sampling in the curvelet domain[J]. Oil Geophysical Prospecting, 2015, 50(1): 20-28. |
| [25] |
李振春, 王华忠, 马在田. 共中心点道集偏移速度分析[J]. 石油物探, 2000, 39(1): 20-26. LI Zhenchun, WANG Huazhong, MA Zaitian. Migration velocity analysis of common midpoint gathers[J]. Geophysical Prospecting for Petroleum, 2000, 39(1): 20-26. DOI:10.3969/j.issn.1000-1441.2000.01.003 |



 张敏, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
张敏, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: