② 南方科技大学前沿与交叉科学研究院, 广东深圳 518055;
③ 南方科技大学地球与空间科学系, 广东深圳 518055
② Academy for Advanced Interdisciplinary Stu-dies, Southern University of Science and Technology, Shenzhen, Guangdong 518055, China;
③ Department of Earth and Space Sciences, Sou-thern University of Science and Technology, Shen-zhen, Guangdong 518055, China
重、磁、电单方法解决问题的局限性、观测数据的有限性以及数据存在的观测误差等诸多因素,造成了反演结果的多解性,影响了地质解释的可靠性。因此,综合利用重、磁、电等方法,从不同角度研究同一地质体,开展各种方法之间的联合反演与综合解释,降低多解性,成为众多学者的研究重点。
地震资料对中浅地层有很高的分辨率,但在复杂区对深层结构揭示不清,而重、磁、电资料可以为地震勘探提供重要的补充。利用已知的地震、地质、电测井等资料进行重、磁、电资料的约束反演是提高重、磁、电勘探分辨率的重要途径之一[1-10]。SEG(勘探地球物理学家学会)为此主办了多类关于数据联合反演的研讨会,并且在其他很多专题报告中,约束联合反演已成为一项提高分辨率的重要技术之一。Colombo等[11]通过建立密度、电阻率与速度的经验关系式,通过重、电、地震联合反演圈定了隐伏盐丘;De Stefano等[12]则提出了一种多种地球物理数据同时联合反演的新方法,提高了墨西哥湾地区地震偏移数据的质量;Zhdanov等[13]提出了基于Gramian约束的广义多种地球物理数据联合方法;陈华根等[14]研究了大地电磁(MT)与重力数据的模拟退火联合反演方法,取得了较好的效果;Liu等[15]提出了基于井数据和地震解释层位约束的三维重力反演方法,有效地提高了深部盐岩顶部构造的预测精度;李华东等[7]基于随机分布共网格单元模型的建模技术,利用密度、电阻率、磁性参数和速度等多种物性参数建立模型,通过引入正则化思想,实现了共网格条件下的重力、磁力、电法和地震资料的同步联合反演,较好地确定了物性界面及地质结构;陈晓等[10]提出了“多次建模,综合约束,分步反演”的多方法联合反演策略,并以大地电磁和地震数据联合反演为例,探讨了该框架在建立玄武岩模型中的适用性;潘豪杰等[16]提出在贝叶斯理论框架下基于非线性的简化三相方程和改进Archie公式的声波—电性数据联合反演方法,进行储层参数预测,有效降低因敏感性和噪声等问题产生的不确定性。
本文基于井—震约束的大地电磁与重力数据的人工鱼群联合反演,利用已知的测井数据、地震剖面、地质解释剖面等先验信息约束建模,引入人工鱼群的群智能反演算法,通过物性关系建立电阻率与密度之间联系,利用MPI编程环境对反演方法进行并行设计和编程实现,最后用模型数据和实测数据测试反演方法的正确性和可行性。
1 人工鱼群约束反演人工鱼群算法是一种群智能最优化算法。其基本思想是在一片水域中,鱼生存数目最多的地方一般就是该水域中富含营养物质最多的地方,数学上根据这个特点模仿鱼群的觅食行为、聚群行为和追尾行为,从而实现全局寻优。因此,人工鱼群算法主要包括以下四个步骤:模型选取、觅食行为、聚群行为、追尾行为,人工鱼群的约束反演主要通过指定模型参数变化空间来实现[17]。
1.1 约束模型选取假设人工鱼群反演模型矢量M的约束范围为[Mmin, Mmax],其模型参数可以是电阻率、密度或者厚度。在模型空间中随机产生初始模型,模拟人工鱼群的随机行为,并通过均匀概率分布产生第i条人工鱼的初始值
| $ \boldsymbol{M}_{i}^{0}=\boldsymbol{M}_{i}^{\min }+u_{i}\left(\boldsymbol{M}_{i}^{\max }-\boldsymbol{M}_{i}^{\min }\right) $ | (1) |
式中:Mimin和Mimax分别是模型参数Mi的取值下限和上限;ui为[0, 1]的随机数。由式(1)可以看出,Mi0在给定的约束模型空间[Mimin, Mimax]内变化,并且后续迭代的反演结果受式(1)的约束。
1.2 觅食行为觅食行为是鱼类的趋向食物的自然活动,鱼群一般通过视觉来感知水中的食物或者其浓度,进而选择趋向。对应于反演过程而言,就是寻找目标函数的极值位置。假设第i条人工鱼(即反演参数)的当前位置为Mit,在其视野范围内随机地选择一个位置Mij,有
| $ \boldsymbol{M}_{i}^{j}=\boldsymbol{M}_{i}^{t}+u_{1} \boldsymbol{V} $ | (2) |
式中:u1是[0, 1]的随机数;V为人工鱼的视野长度。如果位置Mij的目标值优于Mit的值,则人工鱼群按下式方向前进
| $ \boldsymbol{M}_{i}^{t+1}=\boldsymbol{M}_{i}^{t}+u_{2} S \frac{\boldsymbol{M}_{i}^{j}-\boldsymbol{M}_{i}^{t}}{\left\|\boldsymbol{M}_{i}^{i}-\boldsymbol{M}_{i}^{t}\right\|} $ | (3) |
式中:u2是[0, 1]的随机数;S为人工鱼群的觅食步长;Mit+1为移动后的位置。如果位置Mij的目标值劣于Mit的值,则重新随机地选择某种位置,继续判断是否满足前进条件。反复尝试Ntry次后,如果仍然不满足前进条件,则按照式(2)随机地移动一步。
1.3 聚群行为鱼在游动过程中会自然地聚集成群,目的是保证群体的生存及躲避危害。在人工鱼群方式下,对每条鱼制定以下原则进行聚群行为的模拟:一是尽量向鱼群的中心位置移动;二是避免过分拥挤。对于当前位置Mit,搜索当前邻域人工鱼的数量和中心位置Mc,如果鱼群中心有较多的食物并且不太拥挤,则向鱼群的中心位置移动,移动后的位置为
| $ \boldsymbol{M}_{i}^{t+1}=\boldsymbol{M}_{i}^{t}+u_{3} S \frac{\boldsymbol{M}_{\mathrm{c}}-\boldsymbol{M}_{i}^{t}}{\left\|\boldsymbol{M}_{\mathrm{c}}-\boldsymbol{M}_{i}^{t}\right\|} $ | (4) |
式中:
鱼群在游动过程中,当其中一条鱼或者几条鱼发现食物时,其附近的鱼会尾随快速游到食物地点,这就是人工鱼群的追尾行为。对于人工鱼i的当前位置Mit,计算当前视野邻域内的鱼数量以及视野内目标函数最优位置Mk,如果该鱼附近有较多的食物并且不太拥挤,则按下式向该鱼的位置移动
| $ \boldsymbol{M}_{i}^{t+1}=\boldsymbol{M}_{i}^{t}+u_{4} S \frac{\boldsymbol{M}_{\mathrm{k}}-\boldsymbol{M}_{i}^{t}}{\left\|\boldsymbol{M}_{\mathrm{k}}-\boldsymbol{M}_{i}^{t}\right\|} $ | (5) |
式中u4是[0, 1]的随机数。
2 二维电磁—重力数据并行约束联合反演本文基于电磁与重磁数据之间的关系,并利用已知的测井数据、地震解释剖面、地质解释剖面等先验信息约束建模,采用人工鱼群智能反演算法和MPI并行设计,实现MT—重力数据的并行约束联合反演。
二维MT—重力数据联合反演的目标函数为
| $ \left\{\begin{aligned} \Delta E_{\mathrm{joint}}=& \alpha \Delta E_{\mathrm{M}}+\beta \Delta E_{\mathrm{G}} \\ \Delta E_{\mathrm{M}}=& \sum\limits_{J=1}^{M_{\mathrm{s}}} \sum\limits_{I=1}^{M_{\mathrm{f}}}\left[\left(1-\frac{\rho_{I, J}^{\mathrm{TE}, \text { cal }}}{\rho_{I, J}^{\mathrm{TE}, \mathrm{obs}}}\right)^{2}+\left(1-\frac{\varphi_{I, J}^{\mathrm{TE}, \text { cal }}}{\varphi_{I, J}^{\mathrm{TE}, \mathrm{obs}}}\right)^{2}\right]+\\ & \sum\limits_{J=1}^{M_{\mathrm{s}}} \sum\limits_{I=1}^{M_{\mathrm{f}}}\left[\left(1-\frac{\rho_{I, J}^{\mathrm{TM}, \mathrm{cal}}}{\rho_{I, J}^{\mathrm{TM}, \mathrm{obs}}}\right)^{2}+\left(1-\frac{\varphi_{I, J}^{\mathrm{TM}, \mathrm{cal}}}{\varphi_{I, J}^{\mathrm{TM}, \mathrm{obs}}}\right)^{2}\right] \\ \Delta E_{\mathrm{G}}=& \sum\limits_{J=1}^{N_{\mathrm{s}}}\left(1-\frac{g_{J}^{\mathrm{cal}}}{g_{J}^{\mathrm{obs}}}\right)^{2} \end{aligned}\right. $ | (6) |
式中:α和β分别为大地电磁和重力反演目标函数的加权因子;下标“M”和“G”分别代表大地电磁和重力数据;上标“TE”和“TM”分别代表TE模式和TM模式;上标“cal”和“obs”分别代表计算值与观测值;Ms和Ns分别表示二维MT测点数和重力测点数;Mf为二维MT测点的频点数;ρ和φ分别代表视电阻率和相位;g代表重力值。
通过统计各个地层的密度、电阻率变化范围,建立层密度—电阻率之间的物性关系,在迭代反演过程可相互转换;分别计算大地电磁和重力的目标函数以及各自的加权因子α和β,获得联合反演的拟合差;再不断进行人工鱼群迭代反演,使目标函数达到期望值。联合反演过程中,要进行多次二维大地电磁和二维重力数据的正演计算,笔者利用MPI并行设计方法,分别对二维大地电磁和二维重力数据的正演模块进行并行计算,以期提高反演效率。
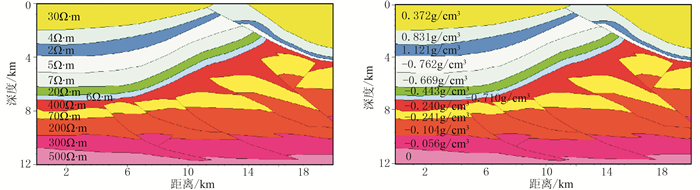
3 模型数据和实测数据试算 3.1 理论模型图 1所示为根据某实际地震解释剖面设计的一个复杂二维电阻率—密度模型。反演目的层的电阻率为400Ω·m、剩余密度为-0.024g/cm3、埋深为3000~8000m。目的是检验本文反演方法对埋藏深度大、深度变化范围也很大的层位是否能够有效识别。
|
图 1 复杂二维电阻率(左)与剩余密度(右)模型 |
二维MT和重力数据模拟的点距为200m,测点为99个,正演剖分网格均为115×111。MT数据采用二维有限差分进行正演,重力数据采用经典的二度体多边形正演算法。
对正演MT和重力数据分别进行二维单独反演和二维并行联合反演,以约束异常体的形态、反演异常体的电阻率和剩余密度。反演的模型空间变化范围为真实模型的±30%,最大迭代次数为30,人工鱼的数量为10,目标函数拟合终止条件是目标函数ΔE<1.0×10-6,MT和重力二维反演的模型剖分网格与正演相同,都为115×111。经过30次迭代反演之后,程序都到达最大迭代次数而正常结束。
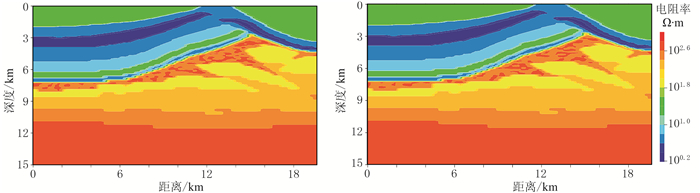
图 2为二维MT数据单独反演及MT—重力数据联合反演的电阻率剖面。由图可见,两种方法都较好地恢复了模型的真实值。图 3为二维MT数据单独反演及MT—重力数据联合反演的异常体电阻率分布柱状图。如果反演的电阻率异常值柱状分布越集中于实际值,说明反演的效果越好,因此通过图 3右可进一步分析、评价反演效果。从图 3可以看出,联合反演的电阻率柱状图的中心更为集中,并且中心值对应的最大数量大于300,而单独反演的最大数量约为200,说明联合反演结果更接近于真实值,反演效果亦更好。图 4为二维重力数据单独反演及MT—重力数据联合反演的剩余密度剖面,图 5是与之对应的剩余密度分布柱状图。从图 5可见,相对于较单独用重力数据进行反演,MT—重力数据联合反演的异常体剩余密度值分布中心更集中。
|
图 2 二维MT数据单独反演(左)及MT—重力数据联合反演(右)的电阻率剖面 |

|
图 3 二维MT数据单独反演(左)及MT—重力数据联合反演(右)的目的层电阻率柱状图 |

|
图 4 二维重力数据单独反演(左)及MT—重力数据联合反演(右)的剩余密度剖面 |

|
图 5 二维重力数据单独反演(左)及MT—重力数据联合反演(右)的目的层剩余密度柱状图 |
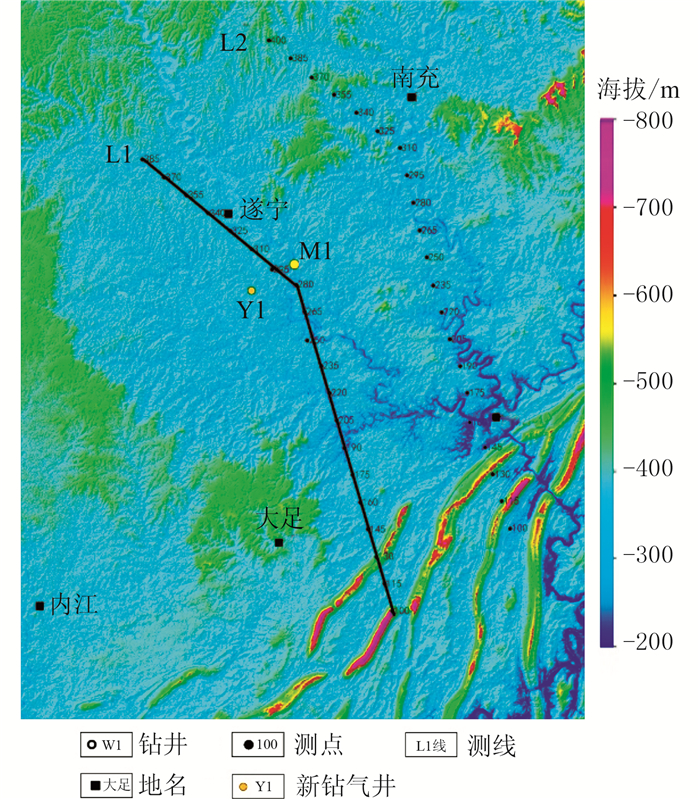
实测数据来自川中高石梯—龙女寺地区的大地电磁—重力勘探项目。以往的钻井及地震资料表明,川中地区震旦系油气的分布与深部裂谷的发育有一定关系[8]。为了进一步了解川中高石梯—龙女寺地区震旦系裂谷发育情况,在该区部署了重力和MT测线,重力测点与MT测点重合,图 6所示为测线分布图,本文以L1测线为例分析本文方法的效果。L1测线共有299个测点,点距约为500m,长度为161km。
|
图 6 研究区测线位置图 |
地层电阻率统计以区内及工区周边电阻率数据均较全的7口钻井资料为主。根据电阻率统计数据,研究区上三叠统以上地层呈低阻特征;下三叠统嘉陵江组—中三叠统雷口坡组为一套次高阻层;下三叠统飞仙关组—中二叠统呈低阻特征;下二叠统地层呈高阻特征;寒武系—奥陶系地层呈中—低阻特征;上震旦统呈高阻特征。统计川中地区各地层的电阻率和密度资料,发现研究区地层的密度与电阻率比较稳定,有一定的相关性。通过分层建立电阻率与密度的关系式,为MT与重力的联合反演提供物性关系的纽带。
对测线L1分别采用二维MT反演、二维重力反演和二维MT—重力联合反演。MT和重力反演的剖分网格大小都为318×121,MT数据参与反演的频点为19个,频率范围为0.001~320Hz。因为常规无旋转的TM数据反演结果与已知测井信息更加吻合,因此选择TM模式数据进行联合反演。利用测井和地震解释剖面进行建模约束,根据统计的地层电阻率和密度变化范围,确定各层的物性反演初值及变化范围;联合反演时,采用统计的地层电阻率—密度关系式。反演最大迭代次数为30,人工鱼的数量为10,目标函数拟合终止条件是ΔE<1.0×10-4,都采用10个CPU并行计算。经过30次迭代反演,结果都到达最大迭代次数而正常结束。
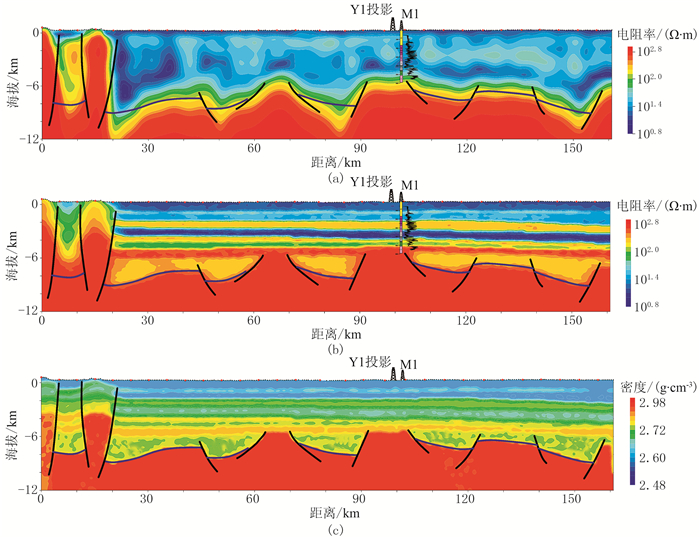
图 7为L1线常规二维MT反演、井震约束的二维MT—重力资料联合反演电阻率和密度剖面。距离该测线3km的东北方向有一钻井M1,其电阻率测井曲线如图 7所示。由图 7a可见,反演电阻率与M1井电阻率测井曲线一致性较好。基于该电阻率剖面,结合电测井、地震解释及物性资料,对地质层位以及深部裂谷进行了解释。常规的二维反演电阻率在幅值上与电测井有较大差异,且对深部薄层的分辨能力较差,因此需要联合地震和钻井资料,进行约束下的单独反演和联合反演,以提高重磁电勘探的分辨率。
|
图 7 L1线反演剖面 (a)常规方法二维电阻率反演剖面;(b)井震约束二维联合反演电阻率剖面;(c)井震约束二维联合反演密度剖面图中蓝线为解释的裂谷底,黑线为断层 |
图 7b为井震约束的二维MT与重力数据联合反演的电阻率剖面。由图可见,通过建模约束反演之后,电性层分布规律与电测井一致性很强,电阻率剖面对层位的刻画更加精细。在海拔-1km和-4km左右的两套高阻层连续性更好,与下伏地层的界面更清晰,裂谷形态在局部有微小的变化,电阻率也低于上覆和下伏地层,表明联合反演结果对深部地层电性刻画更精细。与MT数据的反演结果(图 7a)类似,联合反演的密度剖面(图 7c)上有四套高密度层,海拔-1km和-4km左右的两套高密度层横向连续性更好;海拔-6km以下裂谷的密度分布不均,密度为2.71~2.74g/cm3,符合裂谷的相对低密特征。
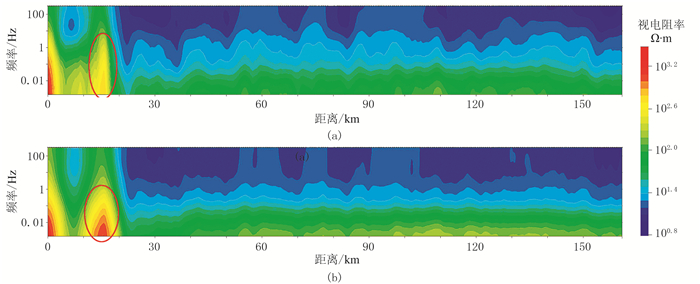
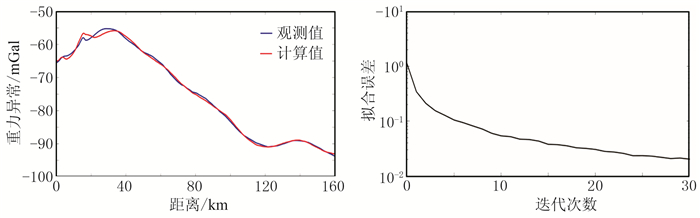
图 8为实测TM模式视电阻率剖面与联合反演拟合计算的TM视电阻率断面图。可以看出,总体上来说,联合反演剖面较好地拟合了实测数据,仅局部区域拟合效果还有待提高,比如剖面上10~20km段的中低频段(图中椭圆所示),一致性较差,还需进行精细的地质建模,调整约束参数范围。图 9为联合反演拟合计算与实测重力异常对比曲线,可见除了在5km~40km之间拟合略微欠缺,其他地方拟合程度较好。图 9为联合拟合差随反演迭代次数变化的对比图,联合反演的数据拟合差在30次迭代后达到0.0204,联合反演的拟合程度较好,说明反演结果比较可靠。
|
图 8 L1线实测TM模式视电阻率剖面(a)和联合反演拟合TM模式视电阻率剖面(b) |
|
图 9 实测及联合反演拟合的重力异常曲线对比(左)及拟合差曲线(右) |
2016年在研究区内新钻Y1井(图 6),该井日产115万方工业气流。Y1井临近L1测线的裂谷翼端,临近南华纪裂谷内断陷区,是油气的有利指向区。根据前述反演结果并结合测井和地震资料,综合推测此处为一级有利区,Y1井的试气结果证实了反演结果的可靠性。
4 结论本文提出了基于人工鱼群算法的非线性MT与重力数据的并行约束反演方法。理论模型计算结果证明了该方法的有效性;通过对实测资料应用本文方法进行反演,发现了川中深层裂谷及南华纪有利目标,解释结论得到后续钻井的证实。
(1) 根据测井、岩心和野外实测资料分析了研究区的地层电阻率和密度特征,并提出分层建立该工区电阻率与密度的关系式,为大地电磁与重力数据的联合反演提供物性关系的纽带。
(2) 对研究区的两条测线分别进行二维大地电磁反演和二维大地电磁—重力数据联合反演。结果表明,通过井震建模约束反演,电性层分布规律与电测井信息一致性很好,二维大地电磁与重力数据的联合反演对层位的刻画比大地电磁单独反演的结果更加精细,层位更加连续。
(3) 实际数据处理结果证实了本文提出的非线性约束联合反演有很强的实用性。
| [1] |
何展翔, 王永涛, 刘云祥, 等. 综合物探技术新进展及应用[J]. 石油地球物理勘探, 2005, 40(1): 108-112. HE Zhanxiang, WANG Yongtao, LIU Yunxiang, et al. New progress and application of integrative geophysical survey techniques[J]. Oil Geophysical Prospecting, 2005, 40(1): 108-112. DOI:10.3321/j.issn:1000-7210.2005.01.025 |
| [2] |
于鹏, 王家林, 吴健生, 等. 地球物理联合反演的研究现状和分析[J]. 勘探地球物理进展, 2006, 29(2): 87-93. YU Peng, WANG Jialing, WU Jiansheng, et al. Review and discussions on geophysical joint inversion[J]. Progress in Exploration Geophysics, 2006, 29(2): 87-93. |
| [3] |
Gallardo L A, Fontes S L, Meju M A, et al. Robust geo-physical integration through structure-coupled joint inversion and multispectral fusion of seismic reflection, magnetotelluric, magnetic, and gravity images:Example from Santos Basin, offshore Brazil[J]. Geophysics, 2012, 77(5): B237-B251. DOI:10.1190/geo2011-0394.1 |
| [4] |
Moorkamp M, Jegen M, Heincke B, et al. A frame-work for 3-D joint inversion of MT, gravity and seismic refraction data[J]. Geophysical Journal International, 2011, 184(1): 477-493. DOI:10.1111/j.1365-246X.2010.04856.x |
| [5] |
周丽芬, 谭捍东.大地电磁与地震数据交差梯度约束二维联合反演[C].第十届中国国际地球电磁学术讨论会论文集, 2011, 253-255. ZHOU Lifen, TAN Handong.Two-dimensional joint inversion of magnetotelluric and seismic data with cross gradient constraints[C].Proceedings of the 10th China International Geo-electromagnetic Induction Workshop, 2011, 253-255. |
| [6] |
Dell' A P, Colombo S, Ciurlo B, et al. CSEM data interpretation constrained by seismic and gravity data:An application in a complex geological setting[J]. First Break, 2012, 30(11): 43-52. |
| [7] |
李华东, 于鹏, 刘振友. 基于随机分布共网格模型的重磁电震联合反演技术及应用[J]. 石油地球物理勘探, 2015, 50(4): 742-748. LI Huadong, YU Peng, LIU Zhenyou. Joint inversion of gravity, magnetotelluric and seismic data based on common gridded model with random distributions[J]. Oil Geophysical Prospecting, 2015, 50(4): 742-748. |
| [8] |
石艳玲, 黄文辉, 魏强, 等. 电磁井震约束反演识别川中深层裂谷[J]. 石油地球物理勘探, 2016, 51(6): 1233-1240. SHI Yanling, HUANG Wenhui, WEI Qiang, et al. Deep rift identification with MT inversion constrained by shallow logging and seismic data[J]. Oil Geophysical Prospecting, 2016, 51(6): 1233-1240. |
| [9] |
Shi Y L, Hu Z Z, Huang W H, et al. The distribution of deep source rocks in the GS sag:joint MT-gravity modeling and constrained inversion[J]. Applied Geophysics, 2016, 13(3): 469-479. DOI:10.1007/s11770-016-0574-9 |
| [10] |
陈晓, 于鹏, 邓居智, 等. 地球物理联合反演新框架研究[J]. 石油地球物理勘探, 2017, 52(4): 851-858. CHEN Xiao, YU Peng, DENG Juzhi, et al. A new framework for geophysical joint inversion[J]. Oil Geophysical Prospecting, 2017, 52(4): 851-858. |
| [11] |
Colombo D, De Stefano M. Geophysical modeling via simultaneous joint inversion of seismic, gravity, and electromagnetic data:Application to prestack depth imaging[J]. The Leading Edge, 2007, 26(3): 326-331. DOI:10.1190/1.2715057 |
| [12] |
De Stefano M, Andreasi F G, Re S, et al. Multiple-domain, simultaneous joint inversion of geophysical data with application to subsalt imaging[J]. Geophysics, 2011, 76(3): R69--R80. DOI:10.1190/1.3554652 |
| [13] |
Zhdanov M S, Gribenko A, Wilson G. Generalized joint inversion of multimodal geophysical data using Gramian constraints[J]. Geophysical Research Letters, 2012, 39: L09301. |
| [14] |
陈华根, 李嘉虓, 吴健生, 等. MT-重力模拟退火联合反演研究[J]. 地球物理学报, 2012, 55(2): 663-670. CHEN Huagen, LI Jiaxiao, WU Jiansheng, et al. Study on simulated-annealing MT-gravity joint inversion[J]. Chinese Journal of Geophysics, 2012, 55(2): 663-670. |
| [15] |
Liu Y X.Application of a three-dimensional gravity inversion method constrained with density in complex areas[C].SEG Technical Program Expanded Abstracts, 2013, 32: 1156-1160.
|
| [16] |
潘豪杰, 张研, 李红兵, 等. 基于贝叶斯理论的天然气水合物储层弹性-电性数据联合反演[J]. 石油地球物理勘探, 2018, 53(3): 568-577. PAN Haojie, ZHANG Yan, LI Hongbing, et al. Joint inversion of elastic-electrical data for gas hydrate re-servoirs based on Bayesian theory[J]. Oil Geophysical Prospecting, 2018, 53(3): 568-577. |
| [17] |
胡祖志, 何展翔, 杨文采, 等. 大地电磁的人工鱼群最优化约束反演[J]. 地球物理学报, 2015, 58(7): 2578-2587. HU Zuzhi, HE Zhanxiang, YANG Wencai, et al. Constrained inversion of magnetotelluric data with the artificial fish swarm optimization method[J]. Chinese Journal of Geophysics, 2015, 58(7): 2578-2587. |



 胡祖志, 河北省涿州市范阳中路307号国际楼105室, 072751。Email:
胡祖志, 河北省涿州市范阳中路307号国际楼105室, 072751。Email: