大地电磁(Magnetotelluric,MT)勘探以天然电磁场为场源,通过测量地表相互正交的不同频率的电磁场分量,研究地球内部电性结构[1-3]。该方法具有探测深度大(可从地表至地下上千公里深度范围)、不需要人工场源、对低阻体敏感等特点,因而被广泛应用于深部地壳、地幔电性结构研究、油气资源普查、工程勘察、环境监测等领域[4-5]。
MT数据的反演研究经历了三个发展阶段。最早使用近似反演类方法,如Bostick反演[6]、大地电磁拟地震反演[7]、曲线对比法[8]等;随后发展了各种线性反演方法,如马奎特法[9]、广义逆矩阵法[10]、奥康姆法[11-12]、正则化法[13]等。由于MT反演是高度非线性的,线性反演方法容易陷入局部极小值,且初始模型的选择对反演结果影响很大[14],目前的反演研究转向非线性方法和仿生算法,如模拟退火法[15]、遗传算法[16]、人工神经网络[17]、粒子群算法[18-19]、人工鱼群算法[20]等。
布谷鸟搜索(Cuckoo search algorithm,CS)算法是受自然界中布谷鸟寄生育雏习性的启发而提出的,该算法采用莱维飞行模式更新个体,具有很强的全局搜索能力[21-23]。该算法一经提出,备受国内外学者的关注,并被不断改进以获得更好的优化效果。郑洪清[24]采用自适应的发现概率和步长,加快算法的收敛速度;李明等[25]提出一种结合差分进化算法的混合布谷鸟算法。
本文将粒子群算法中的全局最优解思想引入布谷鸟算法,加强算法的局部搜索能力;同时结合单纯形法,在每次迭代后,利用反射、扩张、压缩等手段改进较差的鸟巢,进一步提高算法的寻优精度。为了评价改进后算法对MT反演的有效性和稳定性,首先对三个典型模型的视电阻率和相位曲线进行联合反演试算,然后加入随机噪声分析算法的抗噪能力,最后反演了来自中国内蒙古的实测数据。
1 改进布谷鸟算法原理 1.1 基本布谷鸟算法自然界中布谷鸟不会筑巢,也不会孵化自己的卵,而是将卵产在其他鸟类的鸟巢中,由它们代为孵化。而其他鸟类不愿意孵化外来的卵,当它们发现外来的卵就会将其扔掉,有时甚至抛弃整个鸟巢,另筑新巢。为了不被发现,布谷鸟会根据自己的卵的形状和颜色选择宿主[26-28]。
布谷鸟算法规定一个布谷鸟只在一个鸟巢中产一个蛋,设总的鸟巢个数为n,用模型xi(i=1, 2, …,n)表示每个鸟巢的位置,其目标函数值表示鸟巢的优劣,每个模型xi中包括d个参数xij(j=1, 2, …, d),在这些参数范围内随机产生n个初始模型。
布谷鸟算法有两种方式更新鸟巢的位置:一是莱维飞行模式,另一种是随机搜索。
莱维飞行模型是模拟飞行动物觅食的过程,是一种随机游走的方式,其轨迹如图 1所示。在飞行过程中,大量的短距离搜索与偶尔的长距离跳跃交替出现,短距离搜索有利于提高算法的局部搜索能力,而偶尔的长距离跳跃使得优化算法不易陷入局部极值[29-30]。

|
图 1 莱维飞行轨迹示意图 |
莱维飞行公式为
| $ \boldsymbol{x}_{i}^{(t+1)}=\boldsymbol{x}_{i}^{(t)}+\alpha \boldsymbol{L}(\beta) $ | (1) |
式中:xi(t)和xi(t+1)分别表示第i个鸟巢在第t代和第t+1代的位置;α表示步长缩放因子,默认值为0.01;β为随机步长,通常取1.5;L(β)为莱维随机路径,其表达式为
| $ \boldsymbol{L}(\beta)=\frac{\phi \boldsymbol{u}}{|\boldsymbol{v}|^{1 / \beta}} $ | (2) |
式中:u、v是服从标准正态分布的随机变量;ϕ的取值为
| $ \phi=\left[\frac{\Gamma(1+\beta) \sin \frac{\pi \beta}{2}}{2^{\frac{\beta-1}{2}} \beta {\mathit{\Gamma}}\left(\frac{1+\beta}{2}\right)}\right]^{1 / \beta} $ | (3) |
其中Γ(·)是伽马函数。
另一种更新方式是对每个鸟巢都产生一个[0, 1]的随机数ε,与宿主发现布谷鸟鸟蛋的概率P做比较,通过下式判断是否产生新鸟巢
| $ \boldsymbol{x}_{i}^{(t+1)}=\boldsymbol{x}_{i}^{(t)}+\gamma H(P-\varepsilon)\left[\boldsymbol{x}_{j}^{(t)}-\boldsymbol{x}_{k}^{(t)}\right] $ | (4) |
式中:γ为[0, 1]的随机数;xi(t)、xj(t)、xk(t)为第t代的3个随机鸟巢的位置;H(·)为赫维赛德函数,当P-ε>0时,函数值为0,当P-ε<0时,函数值为1,当P-ε=0时,函数值为0.5。
1.2 改进的布谷鸟(ICS)算法由于采用莱维飞行更新个体,布谷鸟算法具有很强的探索能力,但开发能力稍显不足。本文借鉴粒子群中的全局最优解思想,对鸟巢位置的更新(式(1))进行改进
| $ \boldsymbol{x}_{i}^{(t+1)}=\boldsymbol{x}_{i}^{(t)}+\alpha \frac{\phi \boldsymbol{u}}{|\boldsymbol{v}|^{1 / \beta}}\left[\boldsymbol{x}_{i}^{(t)}-\boldsymbol{x}_{\text {best }}^{(i)}\right] $ | (5) |
式中xbest(t)表示第t代最优的鸟巢位置。
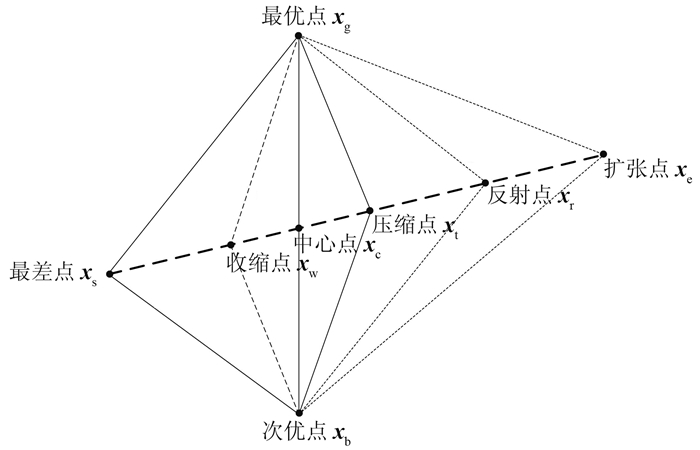
为了进一步提高布谷鸟算法的寻优精度,将单纯形法与布谷鸟算法结合。首先找出n个鸟巢中的最优位置、次优位置和最差位置,之后通过反射、压缩、扩张等操作改善较差的鸟巢,从而提高鸟巢的整体质量[31]。假设鸟巢的最优位置和次优位置分别为xg和xb,最优位置和次优位置的中心点为xc=$\frac{{{\boldsymbol{x}}_{\text{g}}}+{{\boldsymbol{x}}_{\text{b}}}}{2}$,最差位置为xs。各个操作过程描述如下。
反射操作:xr=xc+δr(xc-xs), 其中xr为反射点,反射系数δr通常取1.0。
扩张操作:xe=xc+δe(xr-xc), 其中xe为扩张点,扩张系数δe通常取2.0。
压缩操作:xt=xc+δt(xs-xc), 其中xt为压缩点,压缩系数δt通常取0.5。
收缩操作:xw=xc+δw(xs-xc), 其中xw为收缩点,收缩系数δw的取值一般等于压缩系数δt。
单纯形法(图 2)的计算步骤如下:
|
图 2 单纯形法结构示意图 |
(1) 通过比较各个鸟巢的目标函数值,得到最优鸟巢xg和次优鸟巢xb的目标函数值f(xg)和f(xb)。
(2) 找到最差鸟巢位置的目标函数值f(xs),对xs执行反射操作,得到反射点xr。
(3) 若f(xr)<f(xg),说明位置得到改善,继续执行扩张操作,得到扩张点xe;若f(xe)<f(xg), 则用xe代替xs,否则用xr代替xs。
(4) 若f(xr)>f(xs),说明位置变得更差,则执行压缩操作,得到压缩点xt; 若f(xt)<f(xs)则用xt代替xs。
(5) 若f(xg)<f(xr)<f(xs),执行收缩操作, 得到收缩点xw;若f(xw)<f(xs),则用xw代替xs,否则用xr代替xs。
1.3 算法测试为了检验改进算法的寻优性能,选择Ackely函数进行实验,主要测试算法的优化精度,并与基本布谷鸟算法进行对比。Ackely函数在(x1, x2, …, xd)=(0, 0, …, 0)处取最小值0,其中d为函数自变量的个数,本次实验d取6。此函数是典型的多极值函数[32],其表达式为
| $ \begin{array}{c} F=-20 \exp (-0.2 \sqrt{\frac{1}{d} \sum\limits_{i=1}^{d} x_{i}^{2}})- \\ \exp \left[\frac{1}{d} \sum\limits_{i=1}^{d} \cos \left(2 \pi x_{i}\right)\right]+20+\mathrm{e} \\ x_{i} \in[-32, 32] \end{array} $ | (6) |
分别应用ICS和CS算法对上述函数求取最小值,迭代次数为100次。表 1列出了两种算法的优化结果,每次结果均为6次计算结果的平均值。从表 1可以看出,改进后的算法在优化精度上有了明显的提高。
|
|
表 1 两种算法性能比较 |
为了检验ICS算法的有效性和稳定性,对三个典型地电模型进行反演试算。模型A为二层G型,模型B为三层H型,模型C为四层KH型,模型参数分别如表 2所示。在实际应用中,通常没有足够的信息估计地层的电阻率和厚度。为了更符合实际情况,使用较宽的模型搜索范围,规定搜索范围的下限和上限与真实值相差2倍以上。为了避免单次反演的偶然性,对每个模型都进行10次独立反演,并用这10次反演的平均值作为最终的反演结果。反演参数设置为:鸟巢个数为20,发现外来鸟蛋的最小概率为Pmin=0.1,最大概率为Pmax=0.8,最大迭代次数为200。
|
|
表 2 不同地电模型参数及反演搜索范围 |
MT反演是求解目标函数最小值的优化问题,由于视电阻率可以直观地反映介质的电阻率,因此对视电阻率数据进行反演的情况居多,而相位数据的反演则相对较少。本文同时对视电阻率和相位进行联合反演,目标函数公式为
| $ f=\frac{1}{2} \sum\limits_{i=1}^{N}\left(\frac{\rho_{\mathrm{cal}, i}-\rho_{\mathrm{obs}, i}}{\rho_{\mathrm{obs}, i}}\right)^{2}+\frac{1}{2} \sum\limits_{i=1}^{N}\left(\frac{\theta_{\mathrm{cal}, i}-\theta_{\mathrm{obs}, i}}{\theta_{\mathrm{obs}, i}}\right)^{2} $ | (7) |
式中:N为反演的频点数;ρcal, i和ρobs, i分别为第i个频率的视电阻率计算值和观测值;θcal, i和θobs, i分别为第i个频率的相位计算值和观测值。
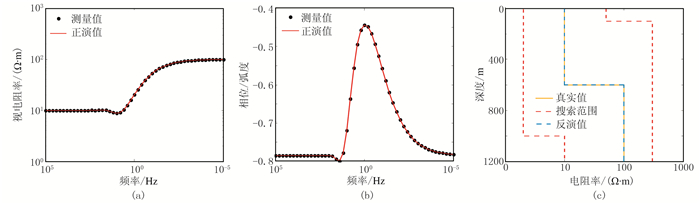
2.1 无噪声理论模型首先,应用ICS算法对无噪声的理论数据进行反演,三个模型的反演结果分别如表 3和图 3~图 5所示。由反演结果可以看出,使用较宽模型搜索范围时,反演的视电阻率和相位曲线与理论曲线基本重合。三个模型所有参数反演结果的最大相对误差分别为0、0、0.66%,即反演结果与模型十分吻合,各个模型的真实值均被ICS算法较准确地反演和重建。可见ICS算法可以对理论大地磁场数据进行精确反演。
|
|
表 3 模型A~模型C含噪与不含噪数据ICS法反演结果统计表 |
|
图 3 模型A不含噪声理论数据与反演结果对比 (a)视电阻率曲线;(b)相位曲线;(c)模型和反演结果及搜索范围 |
|
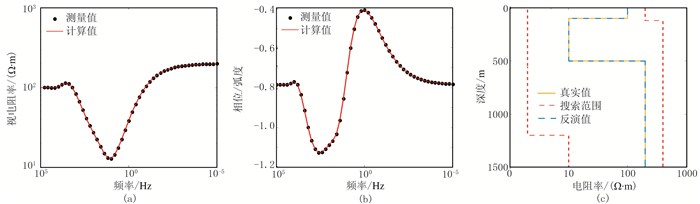
图 4 模型B不含噪声理论数据与反演结果对比 (a)视电阻率曲线;(b)相位曲线;(c)模型和反演结果及搜索范围 |
|
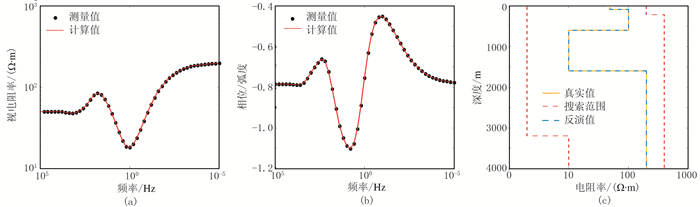
图 5 模型C不含噪声理论数据与反演结果对比 (a)视电阻率曲线;(b)相位曲线;(c)模型和反演结果及搜索范围 |
在野外采集MT数据时,不可避免地会接收到各种噪声干扰,这会导致反演算法的不稳定,可能会得到错误的反演结果,因此有必要对本文ICS算法的抗噪能力进行测试。在前面三种模型的理论视电阻率和相位数据中都加入10%的高斯随机噪声,使用ICS算法对含噪数据进行反演计算,反演结果见图 6~图 8。可以看出,与不含噪声相比,含噪数据的反演结果与真实模型之间存在一定偏差,三个模型中参数(电阻率或者厚度)最大相对误差分别增至2.05%、3.44%、5.33%,因此噪声对反演结果的准确性有一定影响。但是反演视电阻率和相位曲线依然能够很好地拟合理论曲线,计算的地层电阻率和厚度与实际模型基本吻合,说明ICS具有较好的抗噪性。
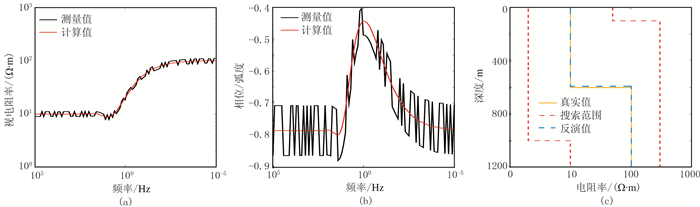
|
图 6 模型A含10%白噪声理论数据与反演结果对比 (a)视电阻率曲线;(b)相位曲线;(c)模型和反演结果及搜索范围 |
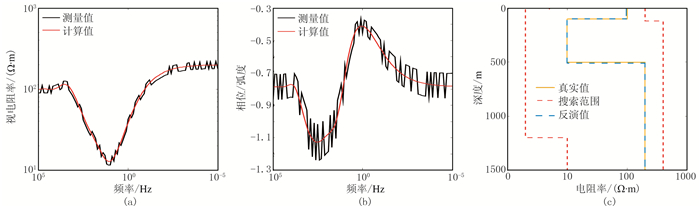
|
图 7 模型B含10%白噪声理论数据与反演结果对比 (a)视电阻率曲线;(b)相位曲线;(c)模型和反演结果及搜索范围 |
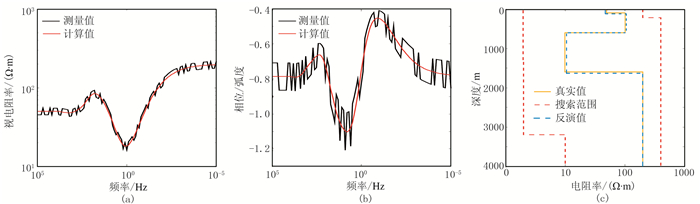
|
图 8 模型C含10%白噪声理论数据与反演结果对比 (a)视电阻率曲线;(b)相位曲线;(c)模型和反演结果及搜索范围 |
反演结果的稳定性和收敛性是评价算法的重要标准。利用ICS算法对每个模型都行了10次独立反演,反演结果中没有出现与真实模型相差很大的情况,即反演成功率为100%。
为了定量分析ICS算法的稳定性,统计了反演参数的相对误差和标准差。结果显示,对于无噪数据,模型的反演结果与真实值几乎完全一致,相对误差和标准差都趋近于零,说明反演结果准确可靠。对于含噪数据,地层厚度的相对误差最大不超过5.33%,标准差最大不超过32.08m,说明噪声在一定程度上影响了反演结果的精度,但所得解依然稳定,且与真实值相差不大,反演结果仍令人满意。
为了评价ICS算法的收敛性,以模型C为例,对反演过目标函数的收敛曲线进行分析。可以看出,无论含噪数据还是不含噪数据,目标函数在前20次迭代中快速收敛,随后逐渐收敛到零值(黑线)或某一常数(红线),这表明ICS算法完成了对最优解的搜索。由此可见,在无噪声和含10%噪声的情况下,ICS算法对MT数据的反演均具有良好的收敛性。
2.4 ICS与CS算法的对比分析为了进一步分析改进后算法的收敛性能,分别应用ICS和CS算法对模型C不含噪声的理论数据进行反演试算。使用表 2中的模型搜索范围,布谷鸟群个数为20,最大迭代次数为200。每种算法都进行10次独立反演,取其平均值作为最终的反演结果,反演结果如表 3和表 4所示。目标函数收敛曲线如图 9b所示。
|
|
表 4 模型C不含噪声数据CS法反演结果统计表 |

|
图 9 模型C反演目标函数收敛曲线 (a)含噪和不含噪数据ICS法收敛曲线;(b)不含噪数据的ICS法与CS法收敛过程对比 |
从图 9b可以看出,在200次迭代内,ICS比CS算法具有更好的收敛能力,且目标函数更趋近于零。为了定量分析,对ICS和CS算法反演结果的相对误差进行了统计(表 3和表 4),结果显示两种算法反演的最大相对误差分别为0.06%和1.13%,最大标准差分别为1.47m和16.82m,说明ICS反演更加稳定、反演结果的精度更高。在耗时方面,迭代反演200次CS算法用时21.227s,而ICS算法为22.674s,用时稍多,这是由于ICS算法中加入了单纯形法的反射、压缩、扩张操作,增加了反演时间,但增加时间并不太长,而在收敛性能和寻优精度上的提升效果更明显。
3 实测数据反演应用中国内蒙古某地的实测MT数据验证ICS算法的反演效果。测区内布设了8条测线,共130个测点,点距为500m。分别使用WinGlink软件中的OCCAM方法和本文的ICS算法对4号线第15个测点的数据进行反演。
图 10a为ICS和OCCAM方法反演得到的该测点地层电阻率。由图中可见,两种算法反演的电阻率变化趋势大致相同。从地表向下大致可以分为三个电性层:第一层为低阻层,电阻率仅十几欧姆米,厚度约为210m;第二层为次高阻层,电阻率为数十到上千欧姆米,厚度为2700m;第三层为高阻层,电阻率最大值达17600Ω·m。

|
图 10 内蒙古MT数据两种方法反演结果对比 (a)实测数据与反演模型视电阻率曲线;(b)电阻率反演结果 |
由图 10b可以看出,OCCAM和ICS反演模型的视电阻率曲线与实测数据都基本吻合,但是ICS反演结果与真实地层更加接近,即ICS算法反演结果拟合得更好。
4 结论本文将布谷鸟算法应用到MT数据反演中。通过引入粒子群中的全局最优解引导思想,提高算法的局部搜索能力,并结合单纯形法,进一步提高算法的寻优精度。首先采用无噪声和含10%噪声的理论数据对ICS算法的有效性和稳定性进行了试验;然后将ICS和CS算法进行比较,分析了改进前后布谷鸟算法的收敛性能;最后反演了来自内蒙古某地的实测MT数据。
理论和实测数据反演结果表明:
(1) ICS算法是一种性能优异的群智能优化算法,可以有效地对MT数据进行反演,且反演结果稳定、精度较高;
(2) 与传统的布谷鸟算法相比,ICS算法收敛能力更强、寻优精度更高,但反演用时稍多。
| [1] |
汤井田, 任政勇, 周聪. 浅部频率域电磁勘探方法综述[J]. 地球物理学报, 2015, 58(8): 2681-2705. TANG Jingtian, REN Zhengyong, ZHOU Cong. Frequency-domain electromagnetic methods for exploration of the shallow subsurface:A review[J]. Chinese Journal of Geophysics, 2015, 58(8): 2681-2705. |
| [2] |
叶高峰, 王辉, 郭泽秋. 长周期大地电磁测深数据采集及处理技术[J]. 地球物理学进展, 2013, 28(3): 1219-1226. YE Gaofeng, WANG Hui, GUO Zeqiu. Data acquisition and processing technology of long-period magnetotelluric[J]. Progress in Geophysics, 2013, 28(3): 1219-1226. |
| [3] |
魏文博. 我国大地电磁测深新进展及瞻望[J]. 地球物理学进展, 2002, 17(2): 245-254. WEI Wenbo. New advance and prospect of magnetotelluric sounding(MT) in China[J]. Progress in Geophysics, 2002, 17(2): 245-254. DOI:10.3969/j.issn.1004-2903.2002.02.009 |
| [4] |
闫永利, 马晓冰, 袁国平. 大地电磁法在阿苏卫填埋场地下水污染检测的应用研究[J]. 地球物理学报, 2007, 50(6): 1863-1868. YAN Yongli, MA Xiaobing, YUAN Guoping. Application of magnetotelluric method in groundwater pollution detection on Asuwei refuse sanitary landfill[J]. Chinese Journal of Geophysics, 2007, 50(6): 1863-1868. DOI:10.3321/j.issn:0001-5733.2007.06.029 |
| [5] |
陈理, 秦其明, 王楠. 低频电磁探测技术再煤层气富集区的应用[J]. 石油地球物理探, 2018, 53(5): 1095-1102. CHEN Li, QIN Qiming, WANG Nan. Application of low-frequency magnetotelluric detection in coalbed methane enrichment areas[J]. Oil Geophysical Prospecting, 2018, 53(5): 1095-1102. |
| [6] |
周虬. 一种简易的一维大地电磁测深反演方法-博斯蒂克法反演及其应用[J]. 石油地球物理勘探, 1985, 20(1): 80-88. ZHOU Qiu. A simple inversion of 1D magnetotelluric sounding curve:Bostick inversion method and application[J]. Oil Geophysical Prospecting, 1985, 20(1): 80-88. |
| [7] |
王家映. 大地电磁测深的拟地震解释法[J]. 石油地球物理勘探, 1985, 20(1): 66-79. WANG Jianying. The magnetotelluric interpretation simulation seismic method[J]. Oil Geophysical Prospecting, 1985, 20(1): 66-79. |
| [8] |
徐世浙, 刘斌. 大地电磁一维连续介质反演的曲线对比法[J]. 地球物理学报, 1995, 38(5): 676-682. XU ShiZhe, LIU Bin. The curve comparison method of MT inversion for one-dimensional continuous me-dium[J]. Chinese Journal of Geophysics, 1995, 38(5): 676-682. DOI:10.3321/j.issn:0001-5733.1995.05.015 |
| [9] |
冯思臣, 王绪本, 阮帅. 一维大地电磁测深几种反演算法的比较研究[J]. 石油地球物理勘探, 2004, 39(5): 594-599. FENG Sichen, WANG Xuben, RUAN Shuai. Comparison among several inversion algorithm of 1D MT[J]. Oil Geophysical Prospecting, 2004, 39(5): 594-599. DOI:10.3321/j.issn:1000-7210.2004.05.019 |
| [10] |
陈明生, 陈乐寿, 王天生. 用改进广义逆矩阵方法解释大地电磁测深及电测深资料[J]. 地球物理学报, 1983, 26(4): 390-400. CHEN Mingsheng, CHEN Leshou, WANG Tian-sheng. The interpretation of magnetotelluric and electric sounding data by modified generalized inversion matrix[J]. Chinese Journal of Geophysics, 1983, 26(4): 390-400. DOI:10.3321/j.issn:0001-5733.1983.04.009 |
| [11] |
Constable S C. Occam's inversion:A practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics, 1987, 52(3): 289-300. DOI:10.1190/1.1442303 |
| [12] |
吴小平, 徐果明. 大地电磁数据Occam反演改进[J]. 地球物理学报, 1998, 41(4): 547-553. WU Xiaoping, XU Guoming. Improvement of Occam inversion for MT data[J]. Chinese Journal of Geophysics, 1998, 41(4): 547-553. DOI:10.3321/j.issn:0001-5733.1998.04.013 |
| [13] |
陈小斌, 赵国泽, 汤吉. 大地电磁自适应正则化反演算法[J]. 地球物理学报, 2005, 48(4): 937-946. CHEN Xiaobin, ZHAO Guoze, TANG Ji. An adaptive regularized inversion algorithm for MT data[J]. Chinese Journal of Geophysics, 2005, 48(4): 937-946. DOI:10.3321/j.issn:0001-5733.2005.04.029 |
| [14] |
陈理, 秦其明, 王楠. 大地电磁测深正演和反演研究综述[J]. 北京大学学报(自然科学版), 2014, 50(5): 979-984. CHEN Li, QIN Qiming, WANG Nan. Review of the forward modeling and inversion in magnetotelluric sounding field[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2014, 50(5): 979-984. |
| [15] |
师学明, 王家映. 一维层状介质大地电磁模拟退火反演法[J]. 中国地质大学学报, 1998, 23(5): 542-546. SHI Xueming, WANG Jiaying. One-dimensional magnetotelluric sounding inversion using simulated annealing[J]. Journal of China University of Geosciences, 1998, 23(5): 542-546. |
| [16] |
师学明, 王家映, 张胜业. 多尺度逐次逼近遗传算法反演大地电磁资料[J]. 地球物理学报, 2000, 43(1): 122-130. SHI Xueming, Wang Jiaying, ZHANG Shengye. Multiscale genetic algorithm and its application in magnetotelluric sounding data inversion[J]. Chinese Journal of Geophysics, 2000, 43(1): 122-130. DOI:10.3321/j.issn:0001-5733.2000.01.015 |
| [17] |
王鹤, 蒋欢, 王亮. 大地电磁人工神经网络反演[J]. 中南大学学报(自然科学版), 2015, 46(5): 1707-1714. WANG He, JIANG Huan, WANG Liang. Magnetotelluric inversion using artificial neural network[J]. Journal of Central South University(Science and Technology Edition), 2015, 46(5): 1707-1714. |
| [18] |
韩瑞通, 王书明, 黄理善. 交叉粒子群算法在大地电磁反演中的应用[J]. 工程地球物理学报, 2009, 6(2): 223-228. HAN Ruitong, WANG Shuming, HUANG Lishan. The cross particle swarm optimization and its application in magnetotelluric inversion[J]. Chinese Journal of Engineering Geophysics, 2009, 6(2): 223-228. DOI:10.3969/j.issn.1672-7940.2009.02.018 |
| [19] |
师学明, 肖敏, 范建柯. 大地电磁阻尼粒子群优化反演研究[J]. 地球物理学报, 1998, 23(4): 1114-1120. SHI Xueming, XIAO Min, FAN Jianke. The damped PSO algorithm and its application for magnetotelluric sounding data inversion[J]. Chinese Journal of Geophysics, 1998, 23(5): 704-711. DOI:10.3321/j.issn:0001-5733.1998.05.014 |
| [20] |
胡祖志, 何展翔, 杨文采. 大地电磁的人工鱼群最优化约束反演[J]. 地球物理学报, 2015, 58(7): 2578-2587. HU Zuzhi, HE Zhanxiang, YANG Wencai. Constrained inversion of magnetotelluric data with the artificial fish swarm optimization method[J]. Chinese Journal of Geophysics, 2015, 58(7): 2578-2587. |
| [21] |
Zhang Y. Modified adaptive cuckoo search algorithm and formal description for global optimization[J]. In-ternational Journal of Computing Application in Technology, 2012, 44(2): 73-79. DOI:10.1504/IJCAT.2012.048675 |
| [22] |
陈乐, 龙文. 求解工程结构优化问题的改进布谷鸟搜索算法[J]. 计算机应用研究, 2014, 31(3): 679-683. CHEN Le, LONG Wen. Modified cuckoo search algorithm for solving engineering structural optimization problem[J]. Application Research of Computers, 2014, 31(3): 679-683. DOI:10.3969/j.issn.1001-3695.2014.03.009 |
| [23] |
吴炅, 周健勇. 整数规划的布谷鸟算法[J]. 数学理论与应用, 2013, 33(3): 99-106. WU Jiong, ZHOU Jianyong. Cuckoo search algorithm for solving integer programming[J]. Mathematical Theory and Application, 2013, 33(3): 99-106. |
| [24] |
郑洪清. 一种自适应步长的布谷鸟算法[J]. 计算机工程与应用, 2013, 49(10): 68-71. ZHENG Hongqing. Self-adaptive step cuckoo search algorithm[J]. Computer Engineering and Applications, 2013, 49(10): 68-71. DOI:10.3778/j.issn.1002-8331.1112-0292 |
| [25] |
李明, 曹德欣. 混合CS算法的DE算法[J]. 计算机工程与应用, 2013, 49(9): 57-60. LI Ming, CAO Dexin. Hybrid optimization algorithm of cuckoo search and DE[J]. Computer Engineering and Applications, 2013, 49(9): 57-60. DOI:10.3778/j.issn.1002-8331.1201-0110 |
| [26] |
Tiwari V. Face recognition based on cuckoo search algorithm[J]. Indian Journal of Computer Science and Engineering, 2012, 7(8): 401-405. |
| [27] |
Zhang Y W. Dynamic adaptation cuckoo search algorithm[J]. Control and Decision, 2014, 29(4): 617-622. |
| [28] |
兰少峰, 刘升. 布谷鸟搜索算法研究综述[J]. 计算机工程与设计, 2015, 36(4): 1063-1067. LAN Shaofeng, LIU Sheng. Overview of research on cuckoo search algorithm[J]. Computer Engineering and Design, 2015, 36(4): 1063-1067. |
| [29] |
Valian E. Improvement cuckoo search algorithm for global optimization[J]. International Journal Communication and Information Technology, 2011, 1(1): 31-44. |
| [30] |
胡欣欣. 求解函数优化问题的改进布谷鸟算法[J]. 计算机工程与设计, 2013, 34(10): 3639-3642. HU Xinxin. Improvement cuckoo search algorithm for function optimization problem[J]. Computer Engineering and Design, 2013, 34(10): 3639-3642. DOI:10.3969/j.issn.1000-7024.2013.10.053 |
| [31] |
莫愿斌, 马彦追, 郑巧燕. 单纯形法的改进萤火虫算法及其在非线性方程组求解中的应用[J]. 智能系统学报, 2014, 9(6): 747-754. MO Yuanbin, MA Yanzhui, ZHENG Qiaoyan. Improved firefly algorithm based on simplex method and its application in solving non-linear equation group[J]. CAAI Transactions on Intelligent System, 2014, 9(6): 747-754. |
| [32] |
蔡伟, 宋先海, 袁士川. 利用粒子群优化算法快速、稳定反演瑞雷波频散曲线[J]. 石油地球物理勘探, 2018, 53(1): 25-34. CAI Wei, SONG Xianhai, YUAN Shichuan. Fast and stable Rayleigh-wave dispersion-curve inversion based on particle swarm optimization[J]. Oil Geophysical Prospecting, 2018, 53(1): 25-34. |



 王书明, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院, 430074。Email:
王书明, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院, 430074。Email: