② 成都理工大学油气藏地质及开发工程国家重点实验室, 四川成都 610059;
③ 重庆三峡学院电子与信息工程学院, 重庆万州 404000
② State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Chengdu University of Technology, Chengdu, Sichuan 610059, China;
③ School of Electronic and Information Engineering, Chongqing Three Gorges University, Wanzhou, Chongqing 404000, China
裂缝型油气藏在碳酸盐岩、碎屑岩以及火山岩中广泛存在[1]。一般情况下,裂缝型油气藏都具有孔隙度低、裂缝带分布复杂及非均质性强等特点[2]。因此寻找裂缝型油气藏的关键在于确定致密岩层内的裂缝密度及分布范围。传统的岩心观测法虽然能准确地识别出裂缝发育带的位置等信息,但因岩心有限且仅能反映井眼附近区域,因此很难用该方法进行三维空间的裂缝带识别[3]。为此,越来越多的学者开始研究如何从地震波的响应特征中寻找裂缝带的分布及方位等信息。由于地震波传播到缝隙密度明显增大、并有一定延伸范围的岩体时,传播速度会明显降低,振幅、频率和相位等动力学特征也会发生明显变化[4]。所以各种基于地震资料的裂缝带刻画方法层出不穷,比如蚂蚁体追踪[5-6]、体曲率分析[7-8]、相干体分析[2, 9]和品质因子Q值属性[10-11]等。这些方法虽然各有所长,但单独使用时,结果常常存在不确定性及多解性[6]。因此,如何综合利用多种地震属性与井中裂缝发育状况之间的非线性对应关系是裂缝带预测中的一个难题。
很多学者已经证明机器学习算法能高效、准确地实现多属性的融合分类,是完成多属性分析的一种重要方法,其中最具代表性的机器学习算法有神经网络、支持向量机和随机森林(Random Forest)等。这些算法在水文气象学、医学和金融学等领域均有着广泛的应用[12-15]。近年来,机器学习算法应用于许多新的领域:如Chen等[16]在制造领域中利用人工神经网络集成方法估计模拟任务所需时间;李文秀等[17]应用近似支持向量机算法判别AVO类型;Asim等[18]在地学领域中应用随机森林算法预测地震活动情况;宋建国等[19]应用随机森林算法预测储层。考虑到这些机器学习算法中随机森林算法具有泛化误差小、抗干扰能力强、不易产生过拟合等特点[20],因此本文引入该算法对裂缝带进行综合预测。
首先从叠后地震资料出发,计算四种刻画裂缝带的地震属性数据体;然后从井旁道的各种地震属性中按照岩心中裂缝带的发育程度提取特征参数,建立地震属性与裂缝发育信息之间的对应关系;最后应用随机森林算法对裂缝带进行综合预测,从而减少单属性的多解性,实现对研究区裂缝带的自动识别。
1 随机森林算法的理论与实现方法 1.1 基本原理随机森林算法是Breiman在Bagging算法之后提出的另一种组合预测算法[21-22],它以决策树为基础,通过随机重复采样技术(Bootstrap技术[23])和节点随机分裂技术组建多棵决策树,最后组合大量决策树的预测结果并将其作为一个整体输出。通过多棵决策树进行集成学习,有效地克服了单棵决策树容易出现过拟合、分类精度较低等问题,并且有效地降低了学习系统的泛化误差。
随机森林算法是基于多棵决策树进行回归预测和分类预测的贪婪算法。它在每个内部节点中选择一个最优的属性(或最优值)进行分裂,分裂后的每个分支都有一个属性值与之相对应,样本的所属类别以沿此路径的每个叶节点为代表,如此递归构建决策树直到达到终止条件。根据Bootstrap方法随机地构建了一系列“自由生长”的决策树分类器{h(X, θk),k=1, 2, …, K},{θk, k=1, 2, …, K}为随机向量(通常服从独立分布),K表示森林中用于分类的决策树的数量。在自变量X给定的情况下,每棵决策树分类器依次参与判断,最后选取频次最高的类作为最后的最优分类结果。
随机森林的建模和预测机制是本文集成学习模型的思想来源,目的是获得较高和稳定的准确率。
1.2 算法实现为了提高裂缝发育带的预测精度,本文主要通过随机重复采样和随机特征选取两个随机性构造不同的随机森林决策树,主要步骤如下。
(1) 首先基于井旁道地震数据制作原始训练数据集,用Bootstrap重复采样方法有放回地随机抽取K个训练数据子集,这些子集的容量均与原始训练数据集一样,并由此构建K棵用于分类的决策树模型。
(2) 在生成每棵用于回归预测和分类预测的决策树模型的过程中,每个节点随机选取一部分输入变量的可能分割,再从中选取最优的分割进行分裂。这样可以降低随机森林中用于回归预测与分类预测的决策树之间的相关强度,提升集成系统的多样性和分类能力。
(3) 森林中每棵用于判别裂缝带发育状况的决策树最大限度地生长,不做任何剪裁。
(4) 集成多棵用于判别裂缝带发育信息的决策树构建随机森林分类器,然后利用该集成分类器对包含各种地震属性的大尺度地震数据进行分类,并统计森林中所有决策树的预测结果,选择在各棵决策树的分类结果中出现频次最高的作为最终的分类结果。
2 算法验证 2.1 实验模型利用川东北YL地区两组(17井和171井)测井数据验证随机森林分类算法的分类效果。分别在17井和171井油气储层裂缝发育、较发育和欠发育段选取声波时差(AC)、补偿中子(CNL)、密度(DEN)、自然伽马(GR)、深侧向电阻率(RD)、浅侧向电阻率(RS)和无铀伽马(KTH)等七种测井参数作为训练数据集(表 1)和预测数据集。
|
|
表 1 钻井裂缝识别训练数据集(部分) |
实验流程如图 1所示。

|
图 1 模型预测流程示意图 |
为了度量实验模型的分类性能,选择正确率评估随机森林算法的分类效果。正确率即为分类正确的样本数与样本总数的比值。
按照排列组合的方式,选取含有1,2,…,7种测井参数(以下简称属性)数据作为预测数据集。可用n维向量Xi=([xi]1, [xi]2, …, [xi]n),i=1, 2, …, 1409, n=1, 2, …, 7表示预测数据集,然后引入随机森林算法对这些预测数据集进行分类预测,分类结果见表 2。
|
|
表 2 模型评价结果 |
来自于裂缝欠发育带和裂缝发育带上的各个属性在数值上均有交集,因此仅使用单个属性进行分类预测,准确率较低。由表 2可见,当选择两种属性进行分类预测时的准确率相比一种属性显著增长。当所选属性增至4种后,再增加分类预测中预测数据集的属性种类,分类预测的正确率上升较为缓慢。如果分类预测所选属性种类太多,就会增加模型的复杂性并降低运算速度。从分类预测结果看,该测井数据制作的预测数据集使用4种属性进行分类预测时正确率达到95.03%,满足分类预测对正确率的要求。
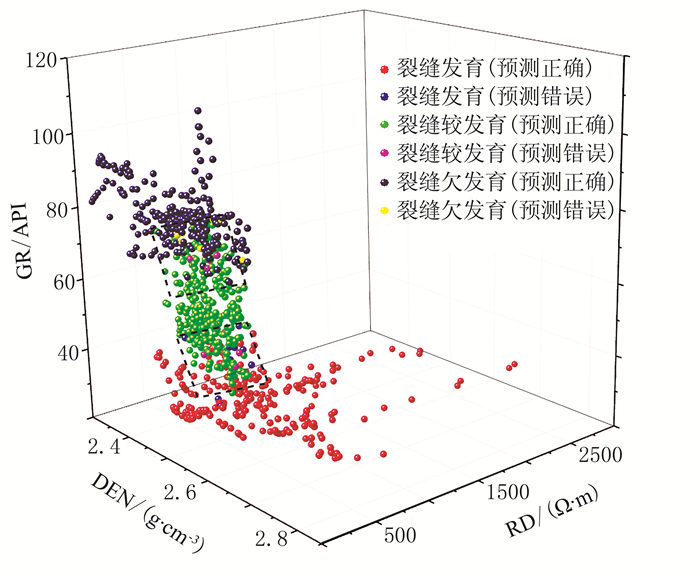
将包含密度、自然伽马、深侧向电阻率和无铀伽马4种属性参数的预测数据集引入随机森林算法,其中前三种属性参数交会图如图 2所示。得益于多种属性的参与,图中黑色虚线框内一部分原本互相混合的部分也能正确地进行分类。这说明随机森林算法的分类效果能够满足工程应用的要求。
|
图 2 模型测试结果DEN、RD和GR交会图 |
与测井数据相比,地震数据属于大尺度数据,这样的数据虽然很难识别单条裂缝,但对于大量裂缝组成的具有一定规模的裂缝发育带可能具有一定的识别能力。下面以YL地区须家河组须四段为例,检验随机森林算法对裂缝带的识别能力。
3.1 研究区概况YL地区主要目的层须四段具有“大面积含气、局部富集高产”的特点。该区六口井中,17井、171井和173井为高产井,172井、175井和176井为干井。单井日产量及测试段裂缝地震相类型见表 3。其中,第1类裂缝地震相对应通过大规模断裂所形成的裂缝通道;第2类对应通过较大规模断裂所形成的裂缝系统;第3类对应具有微断裂的裂缝系统;第4类对应细微裂缝;第5类对应基质。
|
|
表 3 单井日产量表 |
蚂蚁体、体曲率和相干体属性都可以在不同程度上反映断层及裂缝带信息,品质因子Q值在一定地震地质条件下也可表示储层内孔隙和裂缝发育特征。因此,将蚂蚁体、体曲率、相干体属性和品质因子Q值引入随机森林算法进行裂缝带的识别。
首先提取该工区内六口井井旁道地震属性并组成训练数据集;然后根据岩心裂缝的发育程度,将训练数据集分为裂缝发育、较发育以及欠发育等三类。
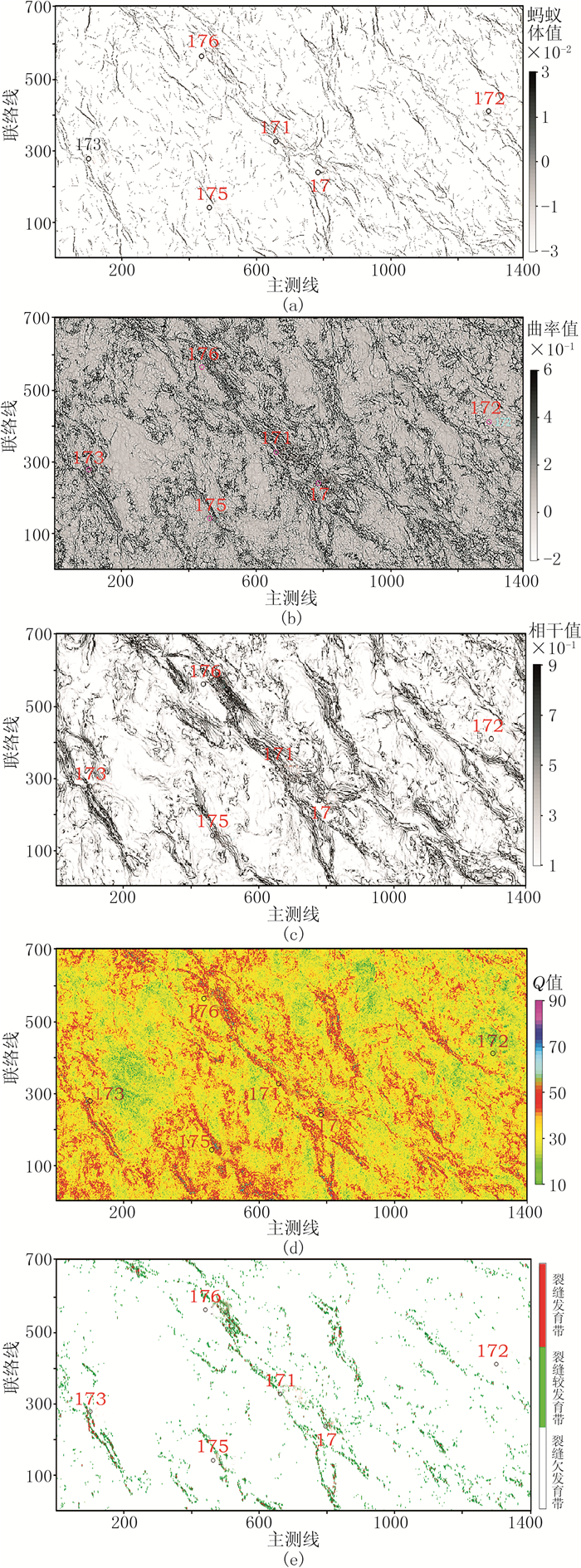
3.3 应用效果各种常规属性对于裂缝带的识别各有所长(图 3),但也都存在不足。蚂蚁体追踪算法通过检索地震数据不连续性完成断裂的追踪和识别。但由于它对地震资料品质要求较高,因此导致预测结果(图 3a)显示17井位于裂缝欠发育地区,而在该层不产气的172井和176井是否位于裂缝发育带上很难区分。体曲率属性中不仅显示裂缝信息,也凸显地层的起伏,因此较难区分裂缝发育信息。相干体属性通常只能用于定性分析,用于裂缝检测时尺度过大,因此常存在较大误差,所以其预测结果(图 3c)中175井及其附近区域的裂缝发育状况不太准确。品质因子Q值的大小虽然能反映裂缝发育情况,但它的求解同时也会受到储层含流体因素等的影响,导致了175井所处区域的裂缝预测结果出现了误差。因此,单属性预测结果反映裂缝特征存在不足,具有较强的多解性。
|
图 3 YL地区须四段不同属性裂缝发育预测结果 (a)蚂蚁体;(b)曲率属性;(c)相干属性;(d)Q值;(e)随机森林算法预测 |
针对上述问题,首先利用随机森林算法从训练数据集中随机选取2/3的训练数据用于构建600棵分类决策树。这些决策树通过对各属性的特征与岩心裂缝发育信息进行学习,有效地将两者结合起来,使得预测结果更有说服力。由随机森林算法预测的结果(图 3e)不仅能较为清晰地反映该地区须四段的大断裂,同时还准确地预测出了17井、171井和173井3口高产井及其附近区域的裂缝发育情况。预测结果显示3口高产井位于裂缝发育带上,172井、175井和176井位于裂缝欠发育地区。这与钻探结果吻合,说明利用随机森林算法进行裂缝带的综合预测能更准确地反映实际的裂缝发育情况。
4 结论本文将随机森林算法引入储层裂缝带预测中,得出以下结论。
(1) 随机森林算法对裂缝带进行预测时,用于裂缝预测的属性种类越多,其预测的准确率越高;但属性种类达到一定数量后,准确率上升较缓慢。因此,对裂缝带进行综合预测时可根据需要选择合适的地震属性数量。
(2) 随机森林算法将岩心裂缝发育信息与多种地震属性之间的非线性关系用于裂缝带的预测,克服了一些地震属性仅能在某些特定区域内取得一定效果的不足;同时也减弱了单属性带来的多解性问题。因此,其预测结果更加准确可靠,并具有较强的普适应用价值。
从川东北YL地区裂缝带的预测结果可以看出随机森林算法预测的准确性与可靠性均高于常规的单属性,证明了该算法在裂缝带预测中的适用性,同时也可将其推广到其他类似地区。
| [1] |
关宝文, 郭建明, 杨燕, 等. 油气储层裂缝预测方法及发展趋势[J]. 特种油气藏, 2014, 21(1): 12-17. GUAN Baowen, GUO Jianming, YANG Yan, et al. Methods of fracture prediction in oil & gas reservoirs and their development trend[J]. Special Oil & Gas Reservoirs, 2014, 21(1): 12-17. DOI:10.3969/j.issn.1006-6535.2014.01.003 |
| [2] |
张广智, 郑静静, 印兴耀. 基于Curvelet变换的多尺度性识别裂缝发育带[J]. 石油地球物理勘探, 2011, 46(5): 757-762. ZHANG Guangzhi, ZHENG Jingjing, YIN Xingyao. I-dentification technology of fracture zone and its strike based on the Curvelet transform[J]. Oil Geophysical Prospecting, 2011, 46(5): 757-762. |
| [3] |
董平川, 徐衍彬, 李飞, 等. 储层裂缝识别和预测方法[J]. 大庆石油地质与开发, 2010, 29(2): 5-12. DONG Pingchuan, XU Yanbin, LI Fei, et al. Reservoir crack identification and prediction method[J]. Petroleum Geology and Oilfield Development in Daqing, 2010, 29(2): 5-12. DOI:10.3969/J.ISSN.1000-3754.2010.02.002 |
| [4] |
贺振华, 黄德济, 文晓涛. 裂缝油气藏地球物理预测[M]. 四川成都: 四川科学技术出版社, 2007.
|
| [5] |
张瑞, 文晓涛, 李世凯, 等. 分频蚂蚁追踪在识别深层小断层中的应用[J]. 地球物理学进展, 2017, 32(1): 350-356. ZHANG Rui, WEN Xiaotao, LI Shikai, et al. Application of frequency division ant tracking in identifying deep small faults[J]. Progress in Geophysics, 2017, 32(1): 350-356. |
| [6] |
隆雨辰, 李俊, 王志章, 等. 综合蚂蚁体及曲率属性的断裂识别方法及应用[J]. 油气藏评价与开发, 2017, 7(4): 6-9. LONG Yuchen, LI Jun, WANG Zhizhang, et al. Fracture identification method and application of integra-ted ant body and curvature properties[J]. Reservoir Evaluation and Development, 2017, 7(4): 6-9. DOI:10.3969/j.issn.2095-1426.2017.04.002 |
| [7] |
王雷, 陈海清, 陈国文, 等. 应用曲率属性预测裂缝发育带及其产状[J]. 石油地球物理勘探, 2010, 45(6): 885-889. WANG Lei, CHEN Haiqing, CHEN Guowen, et al. Application of curvature attributes in predicting fracture-developed zone and its orientation[J]. Oil Geophysical Prospecting, 2010, 45(6): 885-889. |
| [8] |
胡宗全, 廖红伟, 刘人和. 分砂层地质曲率分析在裂缝预测中的应用[J]. 石油实验地质, 2002, 24(5): 450-454. HU Zongquan, LIAO Hongwei, LIU Renhe. Application of geological curvature analysis of sand layer in fracture prediction[J]. Petroleum Geology and Experi-mental, 2002, 24(5): 450-454. DOI:10.3969/j.issn.1001-6112.2002.05.013 |
| [9] |
覃天, 刘立峰. 多属性相干分析在预测储层裂缝发育带中的应用[J]. 石油天然气学报, 2008, 30(6): 254-257. QIN Tian, LIU Lifeng. Application of multi-attribute coherence analysis in predicting reservoir fracture zone[J]. Journal of Oil and Gas Technology, 2008, 30(6): 254-257. |
| [10] |
尹志恒, 魏建新, 狄帮让, 等. 利用Q值各向异性识别裂缝走向[J]. 石油地球物理勘探, 2011, 46(3): 429-433. YIN Zhiheng, WEI Jianxin, DI Bangrang, et al. Fracture orientation detection using Q anisotropy[J]. Oil Geophysical Prospecting, 2011, 46(3): 429-433. |
| [11] |
郝亚炬, 黄捍东, 文晓涛, 等. 广义S域Q值估计方法及其在油气检测中的应用[J]. 石油地球物理勘探, 2017, 52(5): 1059-1066. HAO Yaju, HUANG Handong, WEN Xiaotao, et al. Q estimation in the generalized S domain and its application in the hydrocarbon detection[J]. Oil Geophysical Prospecting, 2017, 52(5): 1059-1066. |
| [12] |
Alp M, Cigizoglu H K. Suspended sediment load si-mulation by two artificial neural network methods using hydrometeorological data[J]. Environmental Modelling & Software, 2007, 22(1): 2-13. |
| [13] |
Choi S, Jiang Z. Cardiac sound murmurs classification with autoregressive spectral analysis and multi-support vector machine technique[J]. Computers in Bio-logy & Medicine, 2010, 40(1): 8-20. |
| [14] |
Bahrammirzaee A. A comparative survey of artificial intelligence applications in finance:artificial neural networks, expert system and hybrid intelligent systems[J]. Neural Computing & Applications, 2010, 19(8): 1165-1195. |
| [15] |
Zou Z B, Peng H, Luo L K. The application of random forest in finance[J]. Applied Mechanics & Materials, 2015, 740(1): 947-951. |
| [16] |
Chen T, Wang Y C. Estimating simulation workload in cloud manufacturing using a classifying artificial neural network ensemble approach[J]. Robotics and Computer-Integrated Manufacturing, 2016, 38(2): 42-51. |
| [17] |
李文秀, 文晓涛, 李天, 等. 近似支持向量机的AVO类型判别[J]. 石油地球物理勘探, 2018, 53(5): 969-974. LI Wenxiu, WEN Xiaotao, LI Tian, et al. AVO types discrimination based on a proximal support vector machine[J]. Oil Geophysical Prospecting, 2018, 53(5): 969-974. |
| [18] |
Asim K M, Awais M, Martínez-Álvarez F, et al. Seismic activity prediction using computational intelligence techniques in northern Pakistan[J]. Acta Geophysica, 2017, 65(5): 919-930. DOI:10.1007/s11600-017-0082-1 |
| [19] |
宋建国, 杨璐, 高强山, 等. 强容噪性随机森林算法在地震储层预测中的应用[J]. 石油地球物理勘探, 2018, 53(5): 954-960. SONG Jianguo, YANG Lu, GAO Qiangshan, et al. Strong tolerance random forest algorithm in seismicreservoir prediction[J]. Oil Geophysical Prospecting, 2018, 53(5): 954-960. |
| [20] |
方匡南. 随机森林组合预测理论及其在金融中的应用[M]. 福建厦门: 厦门大学出版社, 2012.
|
| [21] |
Breiman L. Random Forests[J]. Machine Learning, 2001, 45(1): 5-32. DOI:10.1023/A:1010933404324 |
| [22] |
Breiman L. Bagging Predictors[J]. Machine Learning, 1996, 24(2): 123-140. |
| [23] |
Kushary D. Bootstrap methods and their application[J]. Technometrics, 2000, 42(2): 216-217. |



 何健, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院, 610059。Email:
何健, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院, 610059。Email: