2 中国石油大学(北京)CNPC物探重点实验室, 北京 102249;
3 中国石油大港油田勘探开发研究院, 天津 300280
2 CNPC Key Laboratory of Geophysical Exploration, China University of Petroleum(Beijing), Beijing 102249, China;
3 Research Institute of Exploration and Development, Dagang Oilfield Company, PetroChina, Tianjin 300280, China
尽管勘探地球物理领域对薄层的定义很多,不同观点之间也存在诸多争议,但1/4波长(λ)依然是应用最为广泛的薄层定义准则,这个厚度也称为地震极限分辨率[1-2]。提高地震分辨率的主要目标是展宽频带、压缩子波、减小干涉,由此缓解地震分辨率与薄层厚度之间的矛盾[3]。按照该思路,从现场地震数据采集到室内地震资料处理,发展了多种通过压缩子波提高地震分辨率的方法。尽管如此,现有地震数据的极限分辨率很难满足分辨10m以下目标储层的地质需求。
当薄层厚度小于极限分辨率时,一般采用地震属性进行薄层检测和估算。这一思路最早源于Kallweit等[4]和Widess[5]针对反射振幅和薄层厚度所开展的研究。随后,Robertson等[6]将瞬时频率引入到薄层厚度的估算中。Partyka等[7]基于薄层反射的陷频特性提出了谱分解薄层厚度估算方法。Liu等[8]采用楔形模型证实了瞬时峰值频率与薄层厚度的关系。
多年来,国内学者也持续开展了利用地震属性进行薄层分辨的研究。姚建阳[9]较早讨论了在频率域估算地层厚度的方法。刘建华等[10]将地震反射的波峰、波谷和零相位点应用到薄层厚度估算中,提出了基于反射波特征分析的薄层厚度估算方法。黄真萍等[11]和邵治龙等[12]提出了利用人工神经网络估算厚度的方法。柏冠军等[13]根据地震属性和薄层厚度的非线性关系,采用非线性反演估算薄层厚度。Sun等[14]给出了峰值频率和薄层厚度的解析关系,提高了利用峰值频率估算薄层厚度的精度。其后,王云专等[15]和高君等[16]完善了基于峰值频率的薄层厚度估算方法。但是,以上方法大多基于单砂体楔形模型。从理论上讲,仅适合于无限均匀介质中含有一套薄夹层的情况,不完全适合于薄互层情况下的薄层分析和厚度预测。Li等[17-20]根据薄互层地震反射特征开展了大量实验研究和理论分析,针对振幅和频率属性在薄互层砂体预测中的局限性,提出了利用零值振幅切片刻画薄互层结构的方法。
对于实际地质问题而言,很少有大套地层中沉积一套孤立薄层的情况,砂泥岩薄互层是更为广泛的薄层分布类型。对于砂泥岩薄互层而言,其地震响应是不同砂体反射在纵向上相互干涉的结果,薄互层的沉积结构决定了复合波的频率特征和振幅特征。由于缺乏针对砂泥岩薄互层的砂体厚度估算方法,地震资料解释人员经常使用基于单砂体楔形模型的地震属性分析方法对薄互层中某一层砂体的厚度进行估算和描述,这种做法存在薄互层应用对象和单砂体理论模型之间的结构性矛盾,不可避免地会产生较大的估算误差。实际上,对于砂泥岩薄互层而言,利用地震属性对其中某一层砂体进行厚度估算,无论在理论上还是在实践中都是十分困难的。相对而言,利用地震属性对砂泥岩薄互层中的砂岩累积厚度进行估算具有更加现实的可行性。
为减小由于地震属性与薄层厚度之间的非线性关系而引入的厚度估算误差,同时也为了克服单砂体理论模型与薄互层勘探对象之间的矛盾,本文提出了一种包含振幅和频率的复合地震属性。该属性不仅与地层厚度之间具有良好的线性映射关系,在一定程度上也适合于薄互层条件下砂体累积厚度的定量预测。
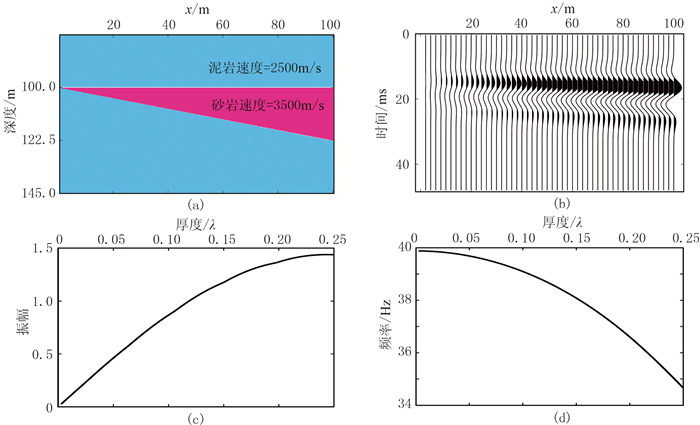
1 复合地震属性 1.1 振幅、频率与地层厚度的非线性关系尽管目前有多种利用振幅和频率属性对薄层厚度进行预测的方法,但这两种属性与厚度之间的关系大多源于对单砂体楔形模型地震反射的定量分析。图 1a为单砂体楔形地质模型, 图 1b是采用峰值频率30Hz雷克子波合成的地震记录,楔形模型的最大厚度为22.5m,约等于
|
图 1 单砂体楔形模型振幅、频率与砂体厚度的关系 (a)单砂体楔形模型;(b)合成地震记录;(c)最大振幅与砂体厚度的关系;(d)峰值频率与砂体厚度的关系 |
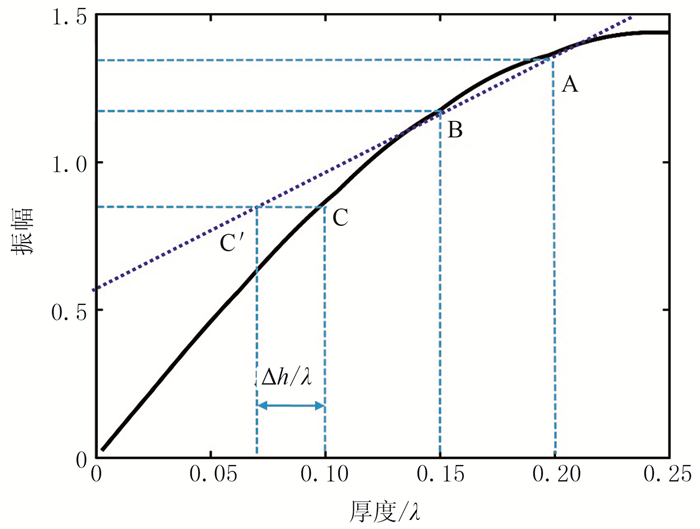
然而,尽管这两种属性与地层厚度之间存在较强的相关性,但并非理想的线性关系,当利用这种关系进行定量预测时,会产生一定的估算误差。图 2定量说明了这种非线性依赖关系引入的预测误差。假设从地震数据中得到A、B两点的振幅分别为1.370和1.176,且通过钻井数据得到了A点和B点的砂体厚度分别为0.20和0.15个波长,则由A、B两点构成的振幅与厚度的线性表达式为y=3.88x+0.594。基于该线性关系可以对其他位置的砂体厚度进行预测,假设被预测点C的振幅为0.867,则根据以上线性表达式预测的砂体厚度为0.07倍波长,而C点的实际厚度为0.1倍波长,预测误差约为30%。同理,频率与厚度的非线性关系也会产生类似的预测误差。
|
图 2 振幅与厚度函数关系的线性近似 |
振幅和频率与地层厚度的非线性关系降低了砂体厚度定量预测精度,为此,希望寻找一种由振幅和频率构成的复合地震属性,以期该复合地震属性与地层厚度之间具有更好的线性关系。为此,假设该复合地震属性的表达式为
| $ \gamma\left(a_{\mathrm{m}}, f_{\mathrm{m}}\right)=a_{\mathrm{m}} \mathrm{e}^{-\beta f_{\mathrm{m}}} $ | (1) |
式中:am为最大振幅;fm为峰值频率;β是待确定参量,为正实数。由表达式可以看出,该复合地震属性与振幅成正比,与频率成负相关,满足厚度预测的一般性要求。复合地震属性表达式中的β应该使得下面目标函数最小
| $ \operatorname{obj}(\beta)=\sum\limits_{h=0}^{\lambda / 4}\left\|\eta a_{\mathrm{m}}(h) \mathrm{e}^{-\beta f_{\mathrm{m}}(h)}-h\right\|_{2}^{2} $ | (2) |
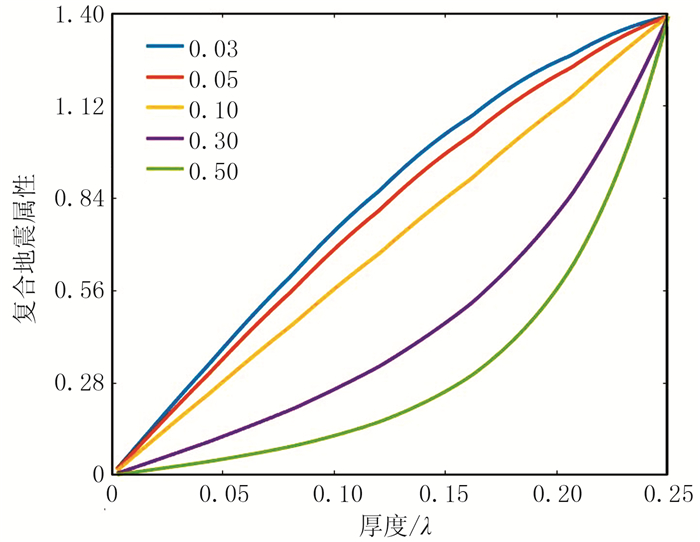
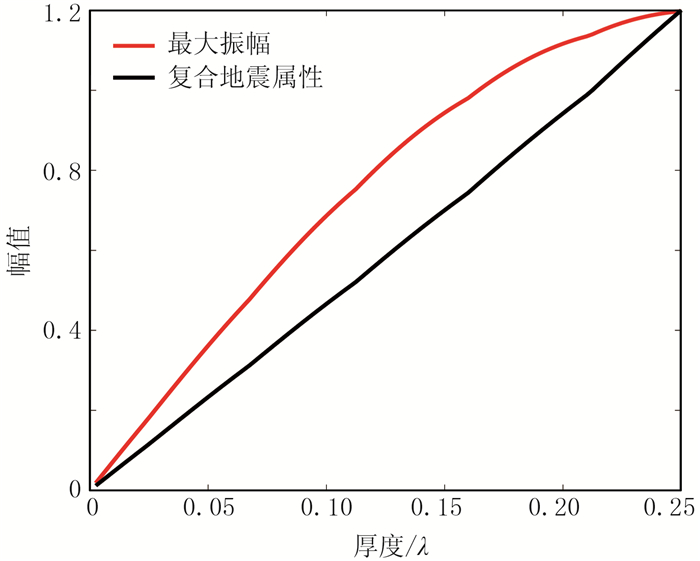
式中: h是薄层厚度;η是比例因子。式(2)属于简单的非线性最优化问题,可以采用模拟退火法求出该参数的最优解为β≈0.1。图 3给出了β取不同值时的模拟结果,为便于显示,将不同曲线乘上不同的比例因子η以便所有曲线在1/4波长位置具有相同的幅值。可以看出,当β=0.1时,复合地震属性与砂体厚度之间呈现较好的线性关系。图 4给出了β=0.1时,复合地震属性与砂体厚度及其最大振幅与砂体厚度的关系曲线。为便于两条曲线的对比,将复合地震属性乘上一个比例因子,使其在1/4波长厚度时的幅值与该处的最大反射振幅一致。两条曲线的对比凸显了复合地震属性与砂体厚度的线性关系。由此得到复合地震属性γ的一般表达式为
|
图 3 β取不同值时,复合地震属性与砂体厚度h的函数关系 |
|
图 4 复合地震属性与砂体厚度(黑色)及最大振幅与砂体厚度(红色)的函数关系对比 |
| $ \gamma=a_{\mathrm{m}} \mathrm{e}^{-0.1 f_{\mathrm{m}}} $ | (3) |
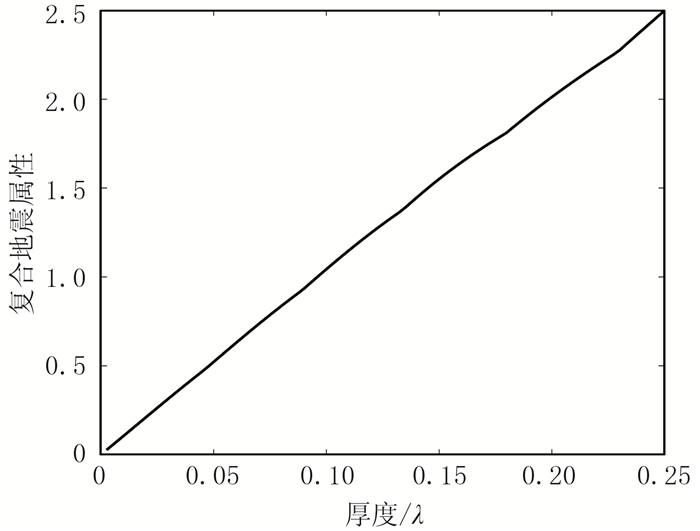
由于质心频率是某一频段内多个频率成分的统计结果,具有一定的统计效应,因此由地震记录确定薄层反射的质心频率较峰值频率更加稳定。另外,用于薄层解释的地震数据往往经历了反褶积和谱白化等高分辨率处理,不同频率成分在有效频带内近乎相等,其振幅谱更接近于辛克子波的频谱特征。再者,由于均方根振幅是某一时窗内多个样点的计算结果,较最大振幅具有更强的稳定性和抗噪性。为此,采用辛克子波代替雷克子波,采用质心频率代替峰值频率,采用均方根振幅代替最大振幅,重复上面的实验。图 5显示了采用低截频为5Hz、高截频为60Hz的辛克子波合成地震记录之后复合地震属性与砂体厚度的函数关系。可以看出,在上述情况下复合地震属性与砂体厚度之间依然具有很好的线性关系。
|
图 5 采用低截频5Hz、高截频60Hz的辛克子波时,复合地震属性与砂体厚度的函数关系 |
对于砂泥岩薄互层而言,利用地震属性估算的砂体厚度不可能是某一层砂体的厚度,往往是几套薄层砂体的累积厚度。下面利用薄互层模型开展应用复合地震属性估算砂体累计厚度的实验和分析。
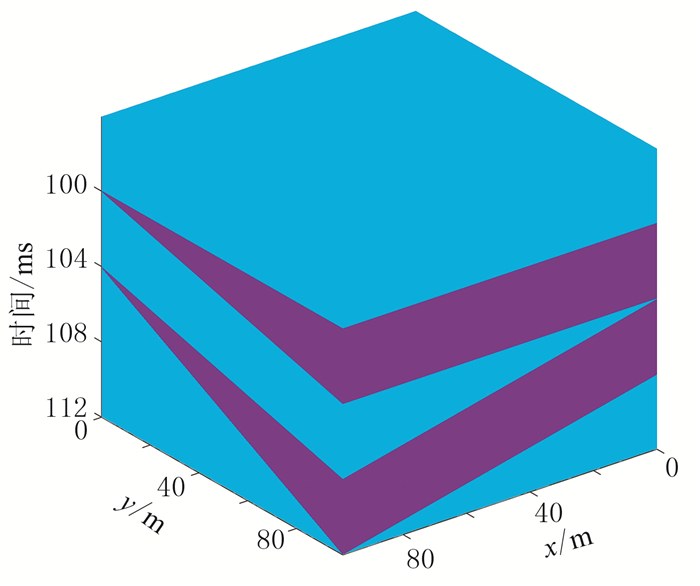
2.1 两套楔形砂体叠置构成的三维地质模型针对薄互层模型而言,目前还没有一套类似于单砂体楔形模型、广泛应用于薄互层地震反射特征分析的统一模型。为此,设计图 6所示的双楔形砂体叠置三维模型。之所以采用两个楔形砂体进行空间叠置,是因为该模型能够反映任意两套砂体空间叠置的厚度变化,可以作为两层砂体叠置的一般性模型。该模型由上、下两套楔形砂体和一套泥岩夹层构成,其中蓝色代表泥岩,速度为2500m/s;紫色代表砂岩,速度为3500m/s。单层砂岩最大厚度为14m,泥岩夹层最大厚度为10m。沿y方向砂岩累积厚度呈线性增加,但泥岩厚度不变;沿x方向泥岩厚度呈线性增加,但砂岩累积厚度不变。选择峰值频率为30Hz的雷克子波,利用褶积模型生成三维地震数据。其中,主测线方向平行于y轴,联络测线方向平行于x轴。
|
图 6 双楔形砂体叠置三维地质模型 |
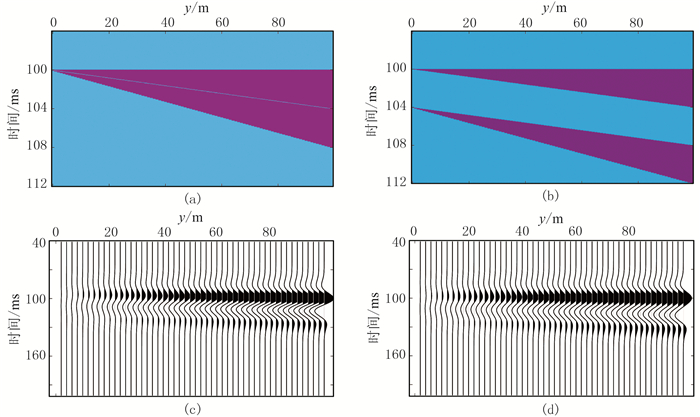
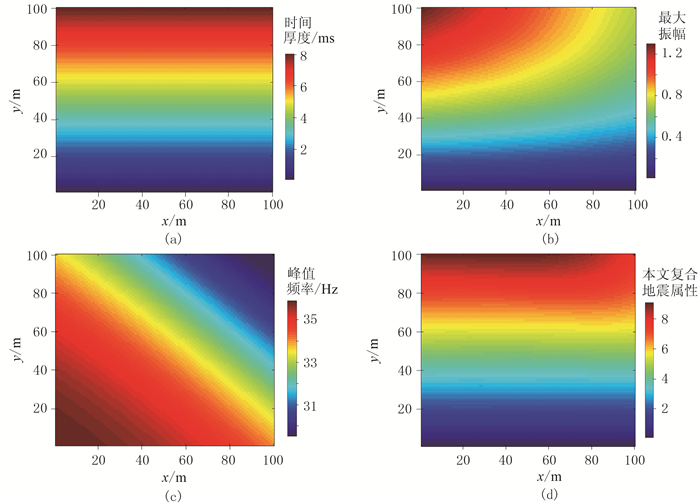
图 7显示了第一条主测线和最后一条主测线的地质模型及对应的合成记录,来自两个楔形砂体共四个反射界面的地震子波互相干涉形成一个复合波。从砂体累积厚度(图 8a)与最大振幅属性(图 8b)和峰值频率属性(图 8c)的对比可以看出,这两种地震属性都不能很好地反映砂体累积厚度的实际分布情况。本文提出的复合地震属性(图 8d)很好地反映了砂体累积厚度的空间分布情况。
|
图 7 双楔形砂体地质模型剖面及其合成记录 (a)第一条主测线地质模型剖面;(b)最后一条主测线地质模型剖面;(c)第一条主测线合成记录;(d)最后一条主测线合成记录 |
|
图 8 最大振幅、峰值频率和本文复合地震属性与砂体累积厚度的对比 (a)砂体累积厚度;(b)最大振幅切片;(c)峰值频率切片;(d)本文复合地震属性切片 |
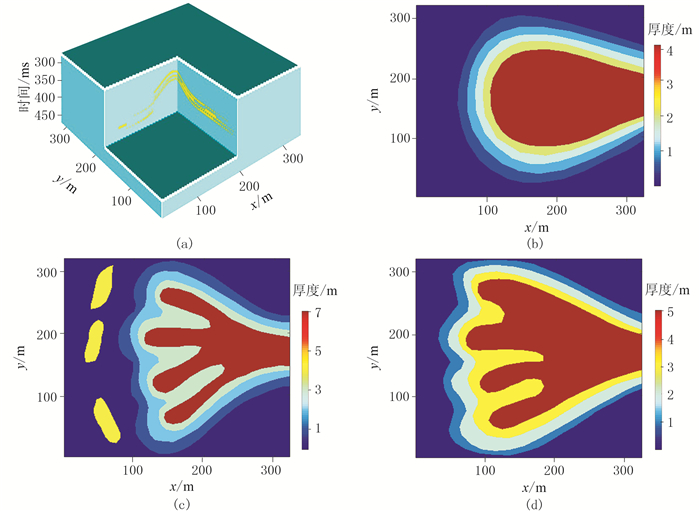
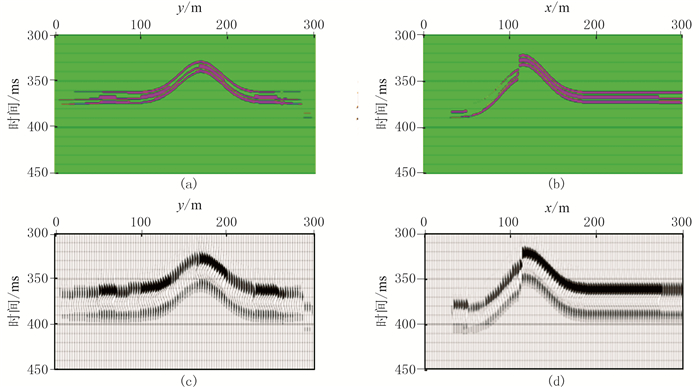
对于包含三层或三层以上砂体的薄互层,很难建立类似于单层和两层砂体那样的一般性简单模型,只能通过设计一些相对复杂的三维模型,对本文方法进行实验分析。为此,设计了一个相对复杂的薄互层地质模型。该模型包含上、中、下三套砂体,砂体之间包含两套泥岩夹层,三套砂体的最大累积厚度约为15m,泥岩夹层的平均厚度约为5m。图 9显示了该模型的三维结构及其上、中、下三套砂体的空间展布和厚度变化。使用峰值频率为27Hz的雷克子波合成地震记录,图 10展示了过模型中心的主测线和联络测线的地质剖面及其对应的地震剖面。可见三套砂体的地震反射相互干涉形成了反射特征空间变化的复合波。图 11是三套砂体的累积厚度及本文复合地震属性的对比情况,为便于对比,两幅图调整为相同幅值,并使用了相同的色标棒。
|
图 9 复杂薄互层地质模型及其三套砂体的空间展布和厚度变化 (a)地质模型;(b)第一套砂体厚度;(c)第二套砂体厚度;(d)第三套砂体厚度 |
|
图 10 过模型中心位置主测线Inline2150、联络测线Xline2150的地质剖面、地震剖面 (a)Inline2150地质剖面;(b)Xline2150的地质剖面;(c)Inline2150地震剖面;(d)Xline2150地震剖面 |
|
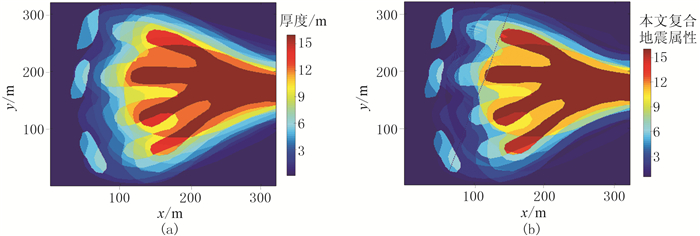
图 11 三套砂体累积厚度(a)和本文复合地震属性(b)平面图 |
可以看出,本文复合地震属性很好地反映了砂体累积厚度的空间变化,即使是砂体边界位置的细微变化在复合地震属性上也得到了清晰的展示和刻画。另外,最左面三套孤立砂体位置累积厚度变化也可通过复合地震属性很好地刻画。
3 实际资料应用利用本文复合地震属性对渤海湾某油田明化镇组砂泥岩薄互层地震数据进行测试、分析。研究区明化镇组为典型的陆相沉积,主要目的层由多套砂体叠置而成,单砂体最大厚度不超过6m,最小厚度约为2m。图 12分别是沿目的层提取的均方根振幅属性和本文复合地震属性。从宏观上看,两种地震属性所反映的砂体形态大致相同,但细节上两种地震属性所反映的砂体厚度变化在空间上存在较大差异,且本文复合地震属性所反映砂体边界更清晰。

|
图 12 目的层均方根振幅平面图(左)和本文复合地震属性平面图(右) |
为方便对比、分析地震属性与实际砂体厚度关系,分别对振幅属性和本文复合地震属性进行比例缩放处理,两种属性在G1井位置的幅值都设置为15.30。5口井的砂体累积厚度与两种属性的对应关系如表 1所示。
|
|
表 1 砂体累积厚度及对应的振幅和本文复合地震属性值 |
从图 12和表 1可见,若依据振幅属性,则G2井的砂体累计厚度要大于G3井和G5井,且G3井与G5井的砂体累计厚度比较接近。若依据本文复合地震属性,则G2井的砂体累计厚度要小于G3井,且G2井与G5井的砂体厚度比较接近。另外,若依据振幅属性,G2井和G5井位于砂体中心部位;如依据本文复合地震属性,G2井和G5井位于砂体边界附近。
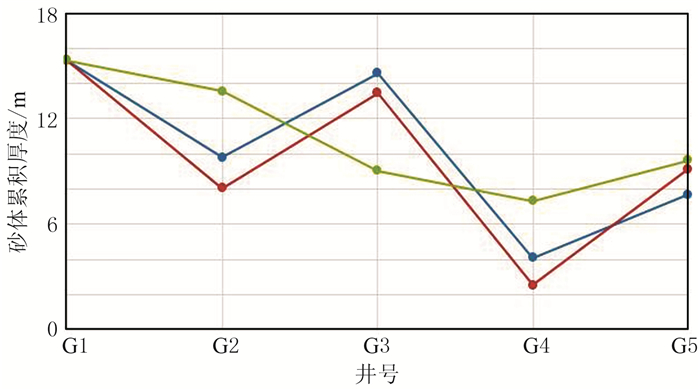
G3井的砂体累积厚度为14.6m,G2井的砂体累积厚度为9.8m,G1井与G3井的砂体厚度比较接近,两者都大于G2井的砂体厚度,这一点与本文复合地震属性所揭示的砂体厚度变化基本一致。图 13将振幅属性和本文复合地震属性与砂体累积厚度的关系进行了对比显示,本文复合地震属性较振幅属性更好地揭示了砂体累积厚度的空间变化。
|
图 13 砂体累积厚度(蓝色)与振幅属性(绿色)和本文复合地震属性(紫红色)关系对比 |
需要指出的是,尽管本文复合地震属性较振幅属性更好地反映了砂体累计厚度的实际变化情况,但G2井和G5井复合地震属性的相对关系与砂体累计厚度的相对关系并不一致。G5井的砂体累计厚度小于G2井,但其复合地震属性值却大于G2井。造成这种情况的原因很多,其中之一是本文方法把振幅、频率和复合地震属性的变化都归结为砂体厚度的变化,没有考虑砂体的非均质性及其流体性质差异对地震反射的影响,也没有考虑地震子波的横向变化对地震反射的影响。上述现象也许是本文方法的局限性。
4 结论和认识对于薄互层而言,从地震资料提取的振幅属性和频率属性既不能准确地反映某层砂体的厚度变化,也不能可靠地反映砂体累计厚度的空间变化。为此,本文提出了一种新的复合地震属性。就单砂体沉积地层而言,本文提出的复合地震属性与砂体厚度之间具有更好的线性函数关系,提高了单砂体厚度定量预测的准确性;就薄互层沉积地层而言,本文提出的复合地震属性与砂体累积厚度之间也具有较好的线性映射关系,可以对砂体累计厚度进行相对准确的估算和预测。由于实际应用中薄层多以互层的形式出现,因此本文提出的复合地震属性对于提高薄互层砂体累积厚度估算精度具有一定的应用潜力。
需要指出的是,就单砂体和两层砂体叠置的情况,本文提出的复合地震属性较振幅和频率两种单独属性具有更高的砂体厚度预测精度。但是,对于三层砂体以上的薄互层模型,尚缺乏严格的实验分析。另外,本文提出的复合地震属性及其相关结论主要依据模型数据的实验分析,尚缺乏严格的理论推导和数学证明。由于本文的实验方法和数学表达比较简单,该复合地震属性也很容易在实践中得到应用和验证,可在薄层特别是薄互层地震勘探中发挥作用。
| [1] |
李庆忠. 地震勘探分辨率与信噪比谱的关系[J]. 石油地球物理勘探, 2008, 43(2): 244-245. LI Qingzhong. Relationship between resolution of seismic exploration and spectrum of S/N ratio[J]. Oil Geophysical Prospecting, 2008, 43(2): 244-245. DOI:10.3321/j.issn:1000-7210.2008.02.024 |
| [2] |
云美厚, 丁伟. 地震分辨力新认识[J]. 石油地球物理勘探, 2005, 40(5): 603-608. YUN Meihou, DING Wei. New knowledge about seismic identifying capability[J]. Oil Geophysical Pro-specting, 2005, 40(5): 603-608. DOI:10.3321/j.issn:1000-7210.2005.05.022 |
| [3] |
李国发, 岳英, 熊金良, 等. 基于三维模型的薄互层振幅属性实验研究[J]. 石油地球物理勘探, 2011, 46(1): 115-120. LI Guofa, YUE Ying, XIONG Jinliang, et al. Experimental study on seismic amplitude attribute of thin interbed based on 3D model[J]. Oil Geophysical Pro-specting, 2011, 46(1): 115-120. |
| [4] |
Kallweit R S, Wood L C. The limits of resolution of zero-phase wavelets[J]. Geophysics, 1982, 47(7): 1035-1046. DOI:10.1190/1.1441367 |
| [5] |
Widess M B. Quantifying resolving power of seismic systems[J]. Geophysics, 1982, 47(8): 1160-1173. DOI:10.1190/1.1441379 |
| [6] |
Robertson J D, Nogami H H. Complex seismic trace analysis of thin beds[J]. Geophysics, 1984, 49(4): 344-352. DOI:10.1190/1.1441670 |
| [7] |
Partyka G, Gridley J, Lopez J. Interpretational applications of spectral decomposition in reservoir characterization[J]. The Leading Edge, 1999, 18(3): 353-360. DOI:10.1190/1.1438295 |
| [8] |
Liu J, Marfurt K J.Thin bed thickness prediction using peak instantaneous frequency[C].SEG Technical Program Expanded Abstracts, 2006, 25: 968-972.
|
| [9] |
姚建阳. 在频率域中求取薄地层的厚度[J]. 石油地球物理勘探, 1991, 26(5): 594-599. YAO Jianyang. Calculating thin-bed thickness in frequency domain[J]. Oil Geophysical Prospecting, 1991, 26(5): 594-599. |
| [10] |
刘建华, 刘天放, 李德春. 薄层厚度定量解释研究[J]. 物探与化探, 1997, 21(1): 24-28. LIU Jianhua, LIU Tianfang, LI Dechun. Quantitative interpretation of thin bed thickness[J]. Geophysical and Geochemical Exploration, 1997, 21(1): 24-28. |
| [11] |
黄真萍, 王晓华, 王云专. 薄层地震属性参数分析和厚度预测[J]. 石油物探, 1997, 36(3): 28-38. HUANG Zhenping, WANG Xiaohua, WANG Yunzhuan. Parameter analysis of seismic attribute and thickness prediction for thin bed[J]. Geophysical Prospecting for Petroleum, 1997, 36(3): 28-38. |
| [12] |
邵治龙, 尹成, 黄德济, 等. 用多参量法计算薄层和薄互层厚度[J]. 石油物探, 1997, 36(4): 93-98. SHAO Zhilong, YIN Cheng, HUANG Deji, et al. The calculation of thin bed and interbed thickness using multiparameter method[J]. Geophysical Prospecting for Petroleum, 1997, 36(4): 93-98. |
| [13] |
柏冠军, 吴汉宁, 赵希刚, 等. 地震资料预测薄层厚度方法研究与应用[J]. 地球物理学进展, 2006, 21(2): 554-558. BAI Guanjun, WU Hanning, ZHAO Xigang, et al. Research on prediction of thin bed thickness[J]. Progress in Geophysics, 2006, 21(2): 554-558. DOI:10.3969/j.issn.1004-2903.2006.02.034 |
| [14] |
Sun L P, Zheng X D, Li J S, et al. Thin-bed thickness calculation formula and its approximation using peak frequency[J]. Applied Geophysics, 2009, 6(3): 234-240. DOI:10.1007/s11770-009-0033-y |
| [15] |
王云专, 郭雪豹, 邢小林, 等. 薄层峰值频率特征分析[J]. 地球物理学进展, 2013, 28(5): 2515-2523. WANG Yunzhuan, GUO Xuebao, XING Xiaolin, et al. Analysis of peak frequency characteristics of thin bed[J]. Progress in Geophysics, 2013, 28(5): 2515-2523. |
| [16] |
高君, 曹思远, 吕雪雁, 等. 峰值频率法估算薄层厚度[J]. 地球物理学进展, 2018, 33(1): 204-210. GAO Jun, CAO Siyuan, LYU Xueyan, et al. Estimation of the thickness of thin layers using peak frequency method[J]. Progress in Geophysics, 2018, 33(1): 204-210. |
| [17] |
Li G F, Xiong J L, Zhou H, et al. Seismic reflection characteristics of fluvial sand and shale interbedded layers[J]. Applied Geophysics, 2008, 5(3): 219-229. DOI:10.1007/s11770-008-0025-3 |
| [18] |
李国发, 王艳仓, 熊金良. 地震波阻抗反演实验分析[J]. 石油地球物理勘探, 2010, 45(6): 868-872. LI Guofa, WANG Yancang, XIONG Jinliang. Experimental analysis on seismic impedance inversion[J]. Oil Geophysical Prospecting, 2010, 45(6): 868-872. |
| [19] |
Li G F, Qin D H, Peng G X. Experimental analysis and application of sparsity constrained deconvolution[J]. Applied Geophysics, 2013, 10(2): 191-200. DOI:10.1007/s11770-013-0377-1 |
| [20] |
Li G, Sacchi M D, Wang Y, et al. Characterization of interbedded thin beds using zero-crossing-time amplitude stratal slices[J]. Geophysics, 2015, 80(5): N23-N35. DOI:10.1190/geo2014-0608.1 |



 李皓, 北京市昌平区府学路18号中国石油大学(北京)CNPC物探重点实验室, 102249。Email:
李皓, 北京市昌平区府学路18号中国石油大学(北京)CNPC物探重点实验室, 102249。Email: