2 中国石化胜利油田分公司物探研究院, 山东东营 257022
2 Geophysical Research Institute, SINOPEC Shengli Oilfield, Dongying, Shandong 257022, China
东营凹陷纯化地区沙四段纯上与纯下亚段波阻抗差值大,两者的分界面为强波峰地震反射,横向连续性好,是该区地震反射标准层[1]。该强地震反射对下伏滩坝砂薄互层地震响应产生屏蔽作用,导致砂体识别困难,影响了油气勘探与开发。
不少学者提出了针对强地震反射层的目标处理技术。Mallat等[2]提出了匹配追踪算法;An等[3]分析了基于数据体的地震多子波分解技术;Wang[4]将匹配追踪算法应用于地震资料的时频分析,并提出了多道匹配算法;张军华等[5]将多子波分解与重构方法应用于强屏蔽层剥离,突出强屏蔽层下储层特征;张在金等[6]提出层位及子波约束匹配追踪方法,剥离煤层强反射,同时分析储层“低频伴影”;王大兴等[7]基于经验模态分解(EMD,Empirical Mode Decomposition)的最大能量法消除了强反射振幅;金成志等[8]基于地震沉积学理论提出了分析长、短旋回波形的方法去除强屏蔽的影响。
但是以上方法多存在分解过度的波形混杂现象和部分分量地球物理意义不明确的局限性。而变分模态分解(VMD,Variational Mode Decomposition)方法[9]具有很好的噪声鲁棒性,采样效应更小,可得到高分辨率的时频分布,能较好地缓解模态混叠现象。目前,VMD在地震勘探领域已被成功应用于面波压制、噪声去除、时频特征提取等方面[10]。
本文在前人研究基础上,针对纯化地区滩坝砂盖层频率低、能量强的特征,利用VMD方法分辨率高、能完备分解的优点,研发相关的算法与程序;设计模型测试、对比EMD与VMD方法消除强反射影响的效果;在实际资料应用中,强屏蔽层下滩坝砂弱反射得到有效增强。
1 滩坝砂地震反射特征纯化地区纯下亚段滩坝砂顶部与上覆低速油页岩、低阻泥岩之间存在稳定的地震反射界面T7,底部也存在一较强地震反射界面T7x。滩坝砂发育段为薄层或互层结构,由于顶部为连续强反射,砂岩地震反射特征多被掩盖,呈现出空白反射或表现为能量变化很小的弱反射,难以直接识别(图 1)。

|
图 1 东营凹陷沙四段滩坝砂储层地震反射特征 T7与T7x之间为滩坝砂储层, 粉色线为自然电位曲线 |
VMD方法由输入数据自适应驱动,动态迭代求解所构建的变分问题,以确定每个子信号的频率中心及频带宽度,从而完成稀疏表示,实现信号的频率剖分及各分量的有效分离。相比EMD[11]和局部均值分解(LMD,Local Mean Decomposition)[12]的经验式递归“筛分”模式,VMD是将信号分解过程转化为变分式非递归求解模式,频域上具有最优性,时域上具有整体性,相当于多个经典维纳滤波器的设计与求解[13]。
经VMD获得的一系列具有不同预估中心频率ωk的有限带宽信号被命名为本征模态函数(BIMF,Band-limited Intrinsic Mode Function)。构建的变分问题可解释为在各BIMF分量之和为原始输入信号的前提下,寻求k(分解得到的模态函数数量)个估计带宽之和最小值,具体实现步骤如下[9]。
(1) 将待寻求的模态函数uk进行希尔伯特变换,计算相关联的解析信号;再使用一个带预估中心频率的指数函数e-jωkt(j为虚数单位)进行解调处理,目的是将模态频谱搬移到相应的基频带上;对上述解调信号梯度值求取范数平方,估计各模态信号频带宽度。
(2) 构建约束变分数学问题可表示为
| $ \begin{array}{c} \min\limits_{\left\{u_{k}\right\}\left\{\omega_{k}\right\}}\left\{\left\|\partial_{t}\left\{\left[\delta(t)+\frac{\mathrm{j}}{\pi t}\right] * u_{k}(t)\right\} \mathrm{e}^{-\mathrm{j} \omega_{k} t}\right\|^{2}\right\} \\ \mathrm{s} . \mathrm{t} . \quad \sum u_{k}=f \end{array} $ | (1) |
式中:{uk}表示分解得到的各本征模态函数的集合;{ωk}表示各模态对应的中心频率集合;δ(t)为Dirac函数;t为时间;f为原始地震信号;“*”号表示褶积运算。
(3) 利用惩罚项系数α和拉格朗日乘法算子λ(t),将式(1)转变为非约束性变分问题
| $ \begin{array}{l} L\left(\left\{u_{k}\right\}, \left\{\omega_{k}\right\}, \lambda(t)\right) \\ \qquad \begin{aligned} =& \alpha \sum\limits_{k}\left\|\partial_{t}\left\{\left[\delta(t)+\frac{\mathrm{j}}{\pi t}\right] * u_{k}(t)\right\} \mathrm{e}^{-\mathrm{j} \omega_{k} t}\right\|^{2}+\\ &\left\|f(t)-\sum\limits_{k} u_{k}(t)\right\|^{2}+\left\langle\lambda(t), f(t)-\sum\limits_{k} u_{k}(t)\right\rangle \end{aligned} \end{array} $ | (2) |
式中:f(t)为待分解信号;L为增广拉格朗日函数;“〈〉”为内积运算符。
(4) 采用乘法算子交替方向法(ADMM,Alternate Direction Method of Multipliers)更迭上述变分问题的最优解。求取模态分量的迭代式可以表示为
| $ \hat{u}_{k}^{n+1}(\omega)=\frac{f(\omega)-\sum\limits_{i \neq k} \hat{u}_{i}(\omega)+\frac{\hat{\lambda}(\omega)}{2}}{1+2 \alpha_{k}\left|\omega-\omega_{k}\right|^{2}} $ | (3) |
同理,中心频率的更新表示为
| $ \omega_{k}^{n+1}=\frac{\int_{0}^{\infty} \omega\left|\hat{u}_{k}(\omega)\right|^{2} \mathrm{d} \omega}{\int_{0}^{\infty}\left|\hat{u}_{k}(\omega)\right|^{2} \mathrm{d} \omega} $ | (4) |
拉格朗日算子更新式为
| $ \hat{\lambda}^{n+1}(\omega)=\hat{\lambda}^{n}(\omega)+\tau\left[\hat{f}(\omega)-\sum\limits_{k} \hat{u}_{k}^{n+1}(\omega)\right] $ | (5) |
式中:
(5) 在频域内不断更新各模态与中心频率,当余量达到最初给定的判定精度后结束计算。对已分解得到的各模态信号进行逆傅里叶变换转换到时间域,最终得到各模态在时域的表示,完成VMD分解流程。
2.2 分解方法优化实际资料分解时,需要加时窗获取目标段地震信号。截取长度应根据标定确保包括强、弱信号的完整波形。为了减少端点效应引起的畸变,对时窗长度为T0的原信号x(t1)采用镜像延拓映射成2T0的闭合环形信号y(t2),这样能最大程度地避免频谱失真。延拓公式为
| $ y\left(t_{2}\right)=\left\{\begin{array}{lc} x\left(t_{1}\right): 0 \leqslant t_{1}<\frac{T_{0}}{2} & 0 \leqslant t_{2}<\frac{T_{0}}{2} \\ x\left(t_{1}\right): 0 \leqslant t_{1} \leqslant T_{0} & \frac{T_{0}}{2} \leqslant t_{2} \leqslant \frac{3 T_{0}}{2} \\ x\left(t_{1}\right): \frac{T_{0}}{2}<t_{1}<T_{0} & \frac{3 T_{0}}{2}<t_{2}<2 T_{0} \end{array}\right. $ | (6) |
式中:t1为原始信号的时间序列;t2为延拓后信号的时间系列。
VMD方法需要预设分解数,取值较大会造成过分解现象,取值较小会使得分解不够。由于各地震道相互独立,单道分析难免导致之后分解参数选择的不准确性和非唯一性,所以需要通过空间约束分析目标层段多道信号。因为滩坝砂体在横向上是非均匀分布的,连续性较差,在进行多道计算时,采用统一权值进行平均将会导致数据模糊,丢失有用信息,所以对于不同道数据应该分配不同权重。
本文以典型井所在道作为中心道,采用高斯加权算法求取地震平均道,完成地震频谱分析试验,利用频带高值数确定分解个数。加权公式为
| $ G=\frac{\sum\limits_{i}^{N} D_{i} \frac{1}{\sqrt{2 \pi} \sigma_{i}} \mathrm{e}^{\frac{-\left(D_{i}-\mu\right)^{2}}{2 σ_{i}^{2}}}}{N} $ | (7) |
式中:Di是原始输入的第i道数据;N是参与道数;σi是中心道与第i道数据的相关系数,作为尺度参数;μ是所有参与道数据的均值,作为位置参数;G是加权之后的平均道数据。
2.3 实现步骤针对强反射层与滩坝砂弱信号的共存问题,基本解决思路是剥离或削弱强反射盖层的能量,从而增强或凸显滩坝砂地震响应。本区滩坝砂盖层具有强振幅、连续性好、频率低等特征,因而VMD方法比较适用。具体实现步骤如下(图 2)。
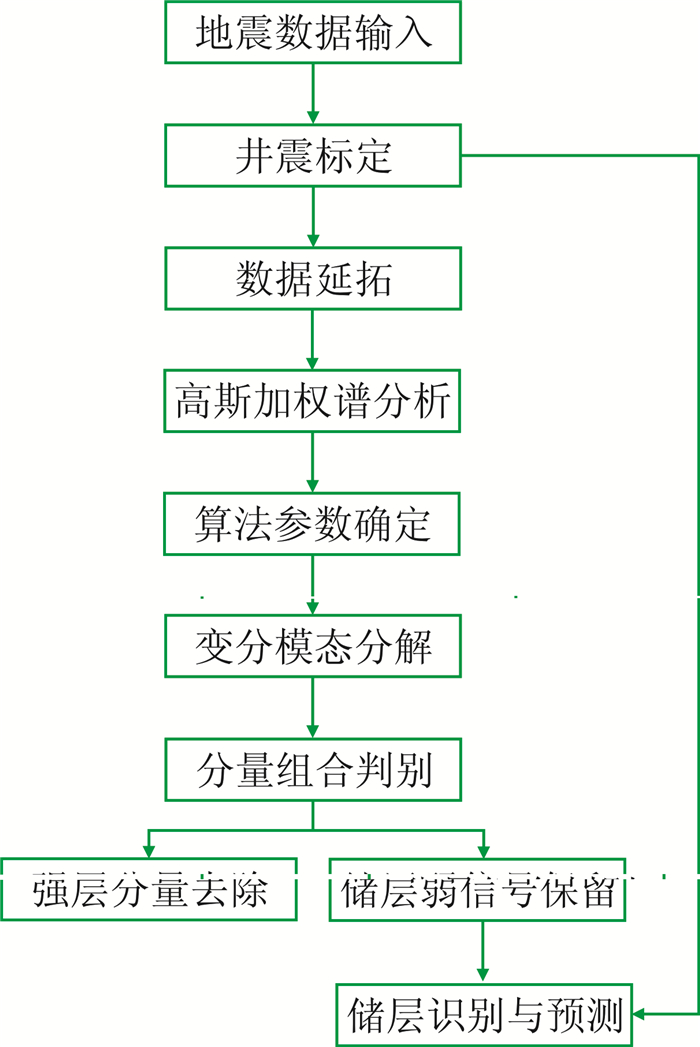
|
图 2 本文方法实现流程图 |
(1) 井震标定强反射层及其下部储层位置,确定时窗长度。
(2) 输入加窗后实际地震信号,对其进行镜像延拓,减少分解误差;再进行加权高斯谱分析,确定适合分解的模态频率及分解个数。
(3) 利用VMD技术分解地震数据,舍弃高能模态,组合优先模态,重构有效信号。
(4) 对重构后的数据体进行属性提取、储层预测与描述,最终得到强层信号压制、弱层信号凸显的储层预测结果。
3 模型测试为了验证方法的可行性,根据研究区实际地质情况设计模型。如图 3a所示,蓝色层段为围岩,速度为3200m/s;黑色段为油页岩,速度为2400m/s;中部橙色段为砂体,速度为3400m/s;下部灰色段为泥岩,速度为3550m/s。强信号层主要体现在上部与下部。计算反射系数并选用20Hz、25Hz、30Hz雷克子波分别与之褶积叠加,得到图 3b所示合成地震记录,采样间隔为1ms。
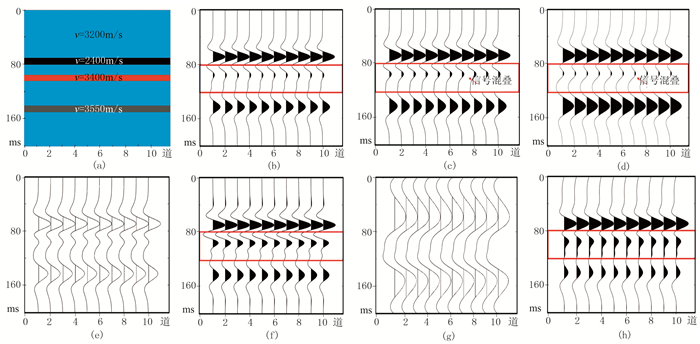
|
图 3 理论模型测试及效果对比 (a)地质模型;(b)合成地震记录;(c)惩罚系数为4000时VMD强(最大)分量记录;(d)惩罚系数为3000时VMD强(最大)分量记录;(e)惩罚系数2000时VMD强(最大)分量记录;(f)VMD压制强反射层后记录;(g)EMD强分量(最大)记录;(h)EMD压制强反射层后记录 |
VMD方法处理的核心是确定惩罚项系数与分解个数。其中,惩罚项系数α主要用于带宽限制,以确保数据保真,值过大或过小都可能影响收敛,导致惩罚失衡、引起混叠。图 3c、图 3d是将惩罚系数分别设为较大值4000和3000时的最大分量图,分解效果不理想,均存在不同程度的弱信号混叠。当惩罚系数为2000(图 3e),即采样频率的两倍值时,分解后的中心频率已收敛到设计频率附近。从图 3e可以看出分解的强层分量在时域内也能准确呈现。进一步试验表明,将惩罚系数设为采样频率的两倍时具有最好效果,此时混叠效应最弱。
本文模型中利用设计的主频数确定分解个数。分解个数设为3时,利用本文方法对模型记录分解后,将强反射分量(图 3e)去除,得到如图 3f所示重构结果,红框部分内弱反射信号较处理前变强,而原有层序结构不变。
本文还应用EMD方法进行了同模型对比试验。图 3g为最大分量,图 3h为利用EMD方法去除强分量后的剖面。可以看到,经过EMD后强层分量大体符合模型中的强层位置,波形存在强分量冗余。去除强反射后,弱信号层虽然得到了加强,但是波形记录中出现了不相干的反射轴(图 3h红框内)。这说明基于EMD方法处理时,各模态间存在有混杂现象,重构时产生了假的干涉成分。
4 应用效果本文利用T7反射层向上10ms、向下60ms时窗进行VMD,惩罚系数α设为采样频率的两倍。VMD分解数通过多道高斯加权谱确定,如图 4a截取了谱中相对振幅比在0.2以上的3个高峰值频率。图 4b展示了基于三分量VMD的模态中心频率,它们彼此没有重叠、有较好的区分度。但更多分量的分解会产生模态纠缠现象,不利于强反射层的表征。图 4c为五分量分解结果,不难看出,分量3与分量4很靠近,这会导致主频为25Hz左右的分量出现在多个模态中。
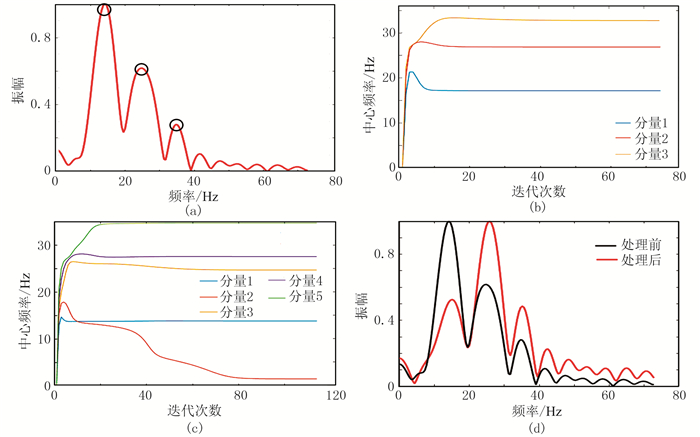
|
图 4 实际资料VMD分解模态个数的确定 (a)目标段频谱分析;(b)VMD三分量分解模态中心频率分布图;(c)VMD五分量分解模态中心频率分布图;(d)VMD三分量处理前后频谱对比 |
基于上述分析,确定了目标区滩坝砂数据采用三模态进行分解,第一模态对应强反射,进行压制,剩余分量进行全选重构,这样可以避免有效信息的遗失。处理前、后的频谱对比表明,弱反射对应的高频信息部分得到了相对增强(图 4d)。
图 5为实际过井地震剖面和应用本文VMD方法处理后的地震剖面对比。可以看到,滩坝砂弱反射得到了有效增强(虚线框),且与井旁左侧滩坝砂自然电位敏感测井曲线特征[14]对应关系也变好。

|
图 5 研究区连井地震剖面VMD处理前(a)、后(b)对比 粉色为自然电位曲线 |
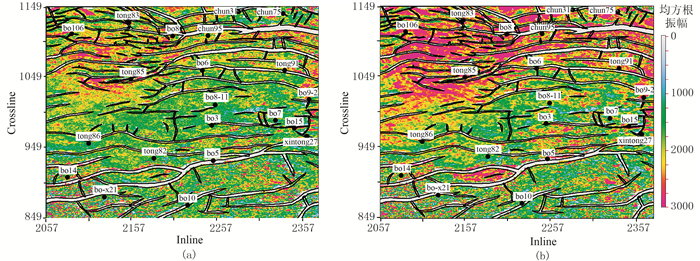
应用本文VMD方法处理前、后强反射层能量沿层属性(图 6)对比表明,处理后强反射能量(红色高值)得到了有效压制。由T7轴下部至17ms时窗内滩坝砂发育段均方根振幅属性(图 7)可见,强反射分量剥离后,滩坝砂能量得到增强。砂岩较厚的井(表 1)均方根振幅多处于高值区(红、黄色区域),较薄井处于高值和中值(绿色)区结合处,砂体不发育井多落在低值(偏蓝色)区域,且前后变化幅度不大。
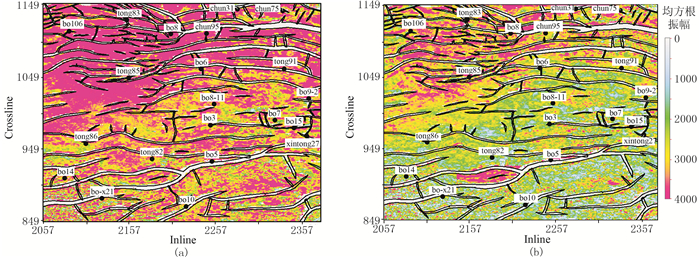
|
图 6 本文方法处理前(a)、后(b)强反射层能量沿层属性对比 |
|
图 7 本文方法处理前(a)、后(b)T7反射层下滩坝砂均方根振幅对比 |
|
|
表 1 钻井钻遇滩坝砂体厚度表 |
通过模型测试和实际资料应用,可以得出以下结论与认识。
(1) VMD方法具有分辨率高、分解完备、避免模态混叠效应等优点,适合于强屏蔽层下滩坝砂弱反射信号的增强。
(2) VMD处理的核心是确定惩罚项系数与分解个数。研究表明,采样频率的两倍可作为比较理想的惩罚参数,分解个数可以通过加权频谱的高值数确定。
(3) 对于强反射背景下薄滩坝砂层识别问题,减弱强反射干扰效应、增强下伏储层弱反射信号,再进行识别判定,是可行方法。
(4) 本文研究的滩坝砂强反射盖层去除能量主要是针对第一分量模态,如果地质体对应某个特殊模态,可以拓展本文方法,直接进行类似于分频处理的分模态方法。另外,加权变模态重构也值得进一步研究。
| [1] |
冯磊, 姜在兴, 田继军. 东营凹陷沙四上亚段层序地层格架研究[J]. 特种油气藏, 2009, 16(1): 16-19. FENG Lei, JIANG Zaixing, TIAN Jijun. Sequence stratigraphy framework of sub-Es4 up in Dongying Depression[J]. Special Oil and Gas Reservoirs, 2009, 16(1): 16-19. DOI:10.3969/j.issn.1006-6535.2009.01.004 |
| [2] |
Mallat S G, Zhang Z. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415. DOI:10.1109/78.258082 |
| [3] |
An P, Solutions G.Application of multi-wavelet seismic trace decomposition and reconstruction to seismic data interpretation and reservoir characterization[C].SEG Technical Program Expanded Abstracts, 2006, 25: 973.
|
| [4] |
Wang Y H. Multichannel matching pursuit for seismic trace decomposition[J]. Geophysics, 2010, 72(1): V61-V66. |
| [5] |
张军华, 刘振, 刘炳杨, 等. 强屏蔽层下弱反射储层特征分析及识别方法[J]. 特种油气藏, 2012, 19(1): 23-26. ZHANG Junhua, LIU Zhen, LIU Bingyang, et al. Analysis and identification of reservoir characteristics of weak reflectors under strong shielding layer[J]. Special Oil and Gas Reservoirs, 2012, 19(1): 23-26. DOI:10.3969/j.issn.1006-6535.2012.01.004 |
| [6] |
张在金, 张军华, 李军, 等. 煤系地层地震强反射剥离方法研究及低频伴影分析[J]. 石油地球物理勘探, 2016, 51(2): 376-383. ZHANG Zaijin, ZHANG Junhua, LI Jun, et al. A method for stripping coal seam strong reflection and low-frequency shadow analysis[J]. Oil Geophysical Prospecting, 2016, 51(2): 376-383. |
| [7] |
王大兴, 王永刚, 赵玉华, 等.一种地震强反射振幅消除方法在鄂尔多斯盆地的试验[C].SPG/SEG北京国际地球物理会议, 2016. WANG Daxing, WANG Yonggang, ZHAO Yuhua, et al.A strong seismic reflection amplitude suppressing method applied in the Ordos Basin[C].SPG/SEG Beijing International Geophysical Conference, 2016. |
| [8] |
金成志, 秦月霜. 利用长、短旋回波形分析法去除地震强屏蔽[J]. 石油地球物理勘探, 2017, 52(5): 1042-1048. JIN Chengzhi, QIN Yueshuang. Seismic strong shield removal based on the long and short cycle analysis[J]. Oil Geophysical Prospecting, 2017, 52(5): 1042-1048. |
| [9] |
Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. DOI:10.1109/TSP.2013.2288675 |
| [10] |
刘伟.高分辨率时频分析方法及其在储层预测中的应用研究[D].北京: 中国石油大学(北京), 2017. LIU Wei.Research on High-resolution Time-frequency Approaches and Applications in Reservoir Prediction[D].China University of Petroleum(Beijing), Beijing, 2017. http://cdmd.cnki.com.cn/Article/CDMD-11414-1018700113.htm |
| [11] |
Huang N E, Zheng S, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings Mathematical Physical & Engineering Sciences, 1998, 454(1971): 903-995. |
| [12] |
张雪冰, 刘财, 刘洋, 等. 基于局部均值分解的地震信号时频分解方法[J]. 吉林大学学报(地球科学版), 2017, 47(5): 234-243. ZHANG Xuebing, LIU Cai, LIU Yang, et al. Seismic data time-frequency decomposition based on local mean decomposition[J]. Journal of Jilin University(Earth Science Edition), 2017, 47(5): 234-243. |
| [13] |
于四伟.基于自适应稀疏反演的地震数据重构[D].黑龙江哈尔滨: 哈尔滨工业大学, 2017. YU Siwei.Seismic Data Reconstruction Based on Adaptive Sparse Inversion[D].Harbin Institude of Technology, Harbin, Heilongjiang, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10213-1017862666.htm |
| [14] |
刘磊, 朱博华, 刘显太, 等. 中国滩坝砂勘探现状与储层基本特征分析[J]. 特种油气藏, 2013, 20(5): 14-18. LIU Lei, ZHU Bohua, LIU Xiantai, et al. Exploration status and basic characteristics of beach-bar sand re-servoirs in China[J]. Special Oil and Gas Reservoirs, 2013, 20(5): 14-18. DOI:10.3969/j.issn.1006-6535.2013.05.003 |



 张军华, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
张军华, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: