2 中国地质大学(武汉)地球内部成像与探测实验室, 湖北武汉 430074;
3 浙江省交通规划设计研究院有限公司, 浙江杭州 310000;
4 华中科技大学物理学院基本物理测量教育部重点实验室, 湖北武汉 430074
2 Subsurface Imaging and Sensing Laboratory, China Unversity of Geosciences(Wuhan), Wuhan, Hubei 430074, China;
3 Zhejiang Provincial Institute of Communications Planning, Design and Research, Hangzhou, Zhejiang 310000, China;
4 MOE Key Laboratory of Fundamental Physical Quantities Measurements, School of Physics, Huazhong University of Science and Technology, Wuhan, Hubei 430074, China
面波沿自由表面(如土壤与空气之间界面、土壤与水之间界面)传播,瑞雷波和拉夫波是两种基本的面波类型。瑞雷波是由P波和S波耦合形成的[1],在半无限空间中,位于自由表面的粒子运动轨迹是沿逆时针方向旋转的椭圆,当瑞雷波传播到0.2倍波长的深度时,粒子运动轨迹由逆时针变为顺时针[2]。拉夫波的形成与层内多重SH波相互干涉有关[3],其粒子运动轨迹是水平的且垂直于波的传播方向。面波具有低速度、低频率、高振幅和频散等特点[4],高频面波方法即是依据这些特性而建立,且已被广泛应用于解决浅地表地球物理问题[5-6]。
面波在层状介质中具有多阶模态,按照数值由小到大分为基阶、一阶高阶和二阶高阶模式相速度等。高频面波方法通过提取和反演面波相速度频散曲线获得地下介质的横波速度[7-10]。由于高阶模式面波在高频段携带了比基阶模式波更多的能量,联合反演基阶和高阶模式瑞雷波(或拉夫波)相速度频散曲线可提高横波速度反演精度[11-13]。然而实际应用中,可能会因外在因素(如噪声干扰)使某些频段的瑞雷波(或拉夫波)频散数据缺失,导致单独反演瑞雷波或拉夫波相速度频散曲线得到的横波速度的精度较低[14]。这时,有必要同时考虑瑞雷波和拉夫波频散数据。Hamimu等[15]应用遗传算法联合反演基阶模式瑞雷波和拉夫波相速度频散曲线,明确指出瑞雷波和拉夫波联合反演法可有效提高横波速度的精度。然而这些研究均侧重于如何确定浅地表横波速度,并未细究面波相速度频散曲线的灵敏度对横波速度反演结果的影响。
面波相速度频散曲线的灵敏度分析可指导反演过程中选取合适的多模式和频段范围的面波相速度,从而保证稳定、可靠地反演横波速度[16]。Feng等[17]通过大量实验证明相同频率的多模式面波相速度对同一地层横波速度的灵敏度不同。基于Lai等[18]计算面波相速度偏导数的方法,Zeng等[19]指出相同模型内低频段的基阶模式瑞雷波相速度对半空间横波速度的灵敏度低于相同频段的基阶模式拉夫波相速度。
低速和高速夹层模型是浅地表物探中两种常见的速度非递增地质结构。其中低速夹层模型是指某一层的横波速度低于该层上覆地层中至少一层横波速度;高速夹层模型是指某一层的横波速度高于其下伏地层中至少一层横波速度。Liang等[20]发现瑞雷波的相速度对低速层下伏地层的横波速度不灵敏。在高速夹层模型中,相对于高速层的横波速度和层厚,基阶模式瑞雷波相速度频散曲线对高速层所在深度位置的改变更灵敏[21];Yin等[22]的模拟结果还证实基阶模式瑞雷波和拉夫波相速度频散曲线对高速层下伏地层的横波速度不灵敏。Shen等[23]研究认为随着速度异常层与邻层之间横波速度差异的增大,基阶模式瑞雷波和拉夫波相速度频散曲线关于速度异常层横波速度的灵敏度效应(高速层的低灵敏度和低速层的高灵敏度)会增强。
本文首先研究各模型参数的改变对多模式瑞雷波和拉夫波相速度频散曲线的影响;然后选取速度递增、低速夹层和高速夹层三种典型的水平层状模型,分别计算这些模型的不同模式瑞雷波和拉夫波相速度对于不同深度地层横波速度的灵敏度,探究不同模式瑞雷波和拉夫波相速度频散曲线对速度异常层横波速度的灵敏度,为面波反演获得高精度的横波速度提供理论指导。
1 方法原理 1.1 多模式瑞雷波和拉夫波相速度频散曲线计算对于水平层状模型,各频率的瑞雷波相速度可表示为四组模型参数(横波速度、密度、层厚、纵波速度)的函数[24]
| $ F_{\mathrm{R}}\left(f_{j}, c_{\mathrm{R} j}, \boldsymbol{v}_{\mathrm{S}}, \boldsymbol{v}_{\mathrm{P}}, \boldsymbol{\rho}, \boldsymbol{h}\right)=0 $ | (1) |
式中:FR是非线性的隐函数;j=1, 2, …, m,其中m为频率点的个数;fj代表第j个频率;cRj为第j个频率fj对应的瑞雷波的相速度;vS=(vS1, vS2, …, vSn)T代表横波速度的列向量,其中vSi为该向量的第i个元素,即第i层横波速度,i=1, 2, …, n,n是模型层数,上标“T”表示向量的转置;vP=(vP1, vP2, …, vPn)T是纵波速度的列向量,vPi为第i层的纵波速度;ρ=(ρ1, ρ2, …, ρn)T为密度向量,ρi表示第i层的密度;h=(h1, h2, …, hn)T表示层厚向量,hi是第i层的厚度。
拉夫波的产生要求在表层即覆盖层的下面存在一个高速层[25]。与瑞雷波不同,拉夫波的相速度与纵波速度无关[26],其表达式为
| $ F_{\mathrm{L}}\left(f_{j}, c_{\mathrm{L} j}, \boldsymbol{v}_{\mathrm{S}}, \boldsymbol{\rho}, \boldsymbol{h}\right)=0 $ | (2) |
式中cLj为第j个频率fj对应的拉夫波的相速度。
利用Knopoff算法计算某一频率的瑞雷波和拉夫波相速度[27]。假设共有m个频率,则将式(1)和式(2)分别改写成m个频散方程;再据二分法[28]对其求解,得到多模式瑞雷波和拉夫波相速度。
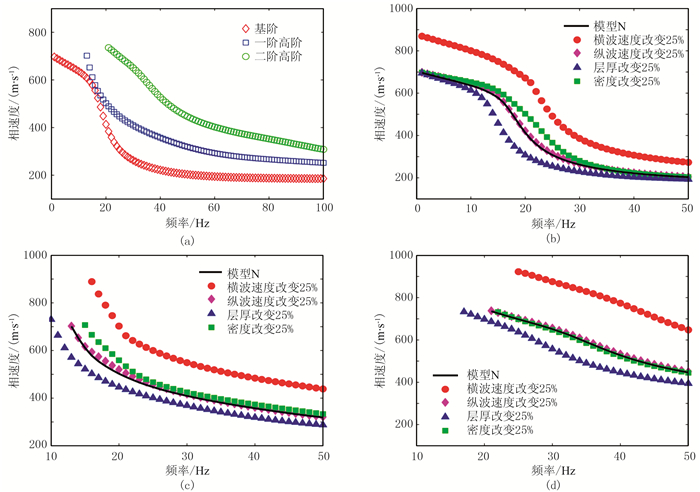
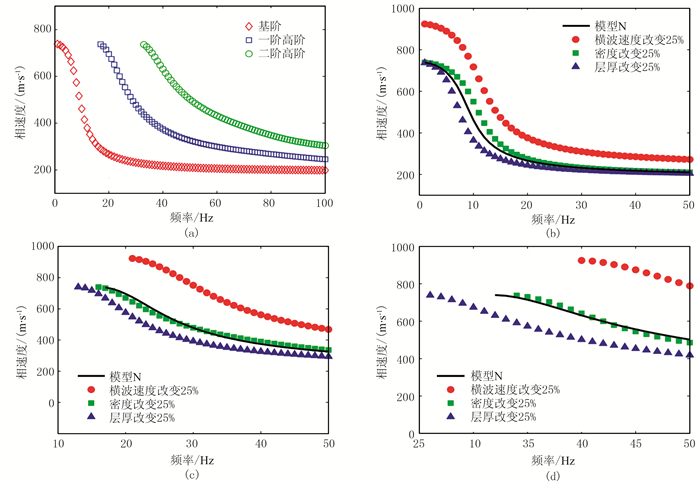
1.2 各模型参数的灵敏度分析由式(1)和式(2)可知,瑞雷波和拉夫波相速度皆与地下各层的横波速度、密度和层厚有关。此外,瑞雷波相速度亦与各层的纵波速度有关。但若某个参数对相速度频散曲线的影响小到一定程度,则可在反演过程中忽略该参数的影响。在1~50Hz频段内,分别将模型N(表 1,其中δ代表泊松比)中所有地层的横波速度、纵波速度和层厚增加25%,研讨横波速度、纵波速度和层厚的改变对不同模式瑞雷波和拉夫波相速度的影响。当讨论密度的改变对面波相速度的影响时,为了使密度的改变对面波相速度频散曲线的影响达到最大,这里将第1和第2层的密度同时减少25%,并将其他地层的密度增加25%(通常认为25%的密度变化近似于砂岩与页岩分界面、页岩与石灰岩分界面及砂砾与黏土分界面的变化幅度)(图 1和图 2)。
|
|
表 1 模型N的参数 |
|
|
表 4 模型L的参数 |
|
|
表 5 模型H的参数 |
|
图 1 模型N各参数的改变对多模式瑞雷波相速度频散曲线的影响 (a)基阶、一阶高阶和二阶高阶模式瑞雷波相速度频散曲线;(b)、(c)、(d)分别表示各模型参数(横波速度、纵波速度、密度、层厚)改变时正演得到的基阶、一阶高阶和二阶高阶模式瑞雷波相速度频散曲线 |
|
图 2 模型N各参数的改变对多模式拉夫波相速度频散曲线的影响 (a)基阶、一阶高阶和二阶高阶模式拉夫波相速度频散曲线;(b)、(c)、(d)分别表示各模型参数(横波速度、密度、层厚)改变时正演得到的基阶、一阶高阶和二阶高阶模式拉夫波相速度频散曲线 |
表 2总结了各模型参数的改变对1~50Hz频段内不同模式瑞雷波相速度频散曲线影响的平均值。当横波速度改变25%时,瑞雷波相速度频散曲线的平均相对变化最大(基阶、一阶高阶和二阶高阶模式的平均相对变化分别为39.65%、36.96%和41.52%);当层厚改变25%时,随着瑞雷波模式阶数的增加,层厚的影响增大(基阶、一阶、二阶对应的平均变化率为10.92%、11.04%和13.07%);相同幅度的密度变化对不同模式瑞雷波相速度频散曲线的影响较横波速度和层厚的影响明显降低(由低阶到高阶对应的平均变化率为5.92%、6.21%和0.65%);而相同幅度纵波速度变化对不同模式瑞雷波相速度频散曲线的影响在诸模型参数中最小(皆小于2%)。
|
|
表 2 模型参数改变25%时引起的1~50Hz频段的基阶、一阶高阶和二阶高阶瑞雷波相速度频散曲线的平均相对变化 |
由各模型参数改变25%时引起的不同模式拉夫波相速度频散曲线的平均相对变化(表 3)可知:当横波速度改变25%时,对拉夫波相速度频散曲线的影响随着面波模式阶数的增加而增大(由低阶到高阶对应的平均变化率为36.59%、49.97%和55.05%);同样幅度的密度改变引起的拉夫波相速度频散曲线的平均相对变化较小(由低阶到高阶依次为3.61%、3.07%和2.13%);当层厚改变25%时,对模式阶数越高的拉夫波相速度频散曲线的影响越显著,其中二阶高阶模式的平均变化率最大(18.76%)。
|
|
表 3 模型参数改变25%时引起的1~50Hz频段的基阶、一阶高阶和二阶高阶拉夫波相速度频散曲线的平均相对变化 |
根据以上分析,横波速度是影响瑞雷波和拉夫波相速度频散曲线变化的最主要参数,这也是反演瑞雷波或拉夫波相速度频散曲线可获得横波速度的根本原因。岩石密度改变25%导致瑞雷波和拉夫波相速度频散曲线的平均相对变化均小于7%;同时,纵波速度25%的改变引起的瑞雷波相速度频散曲线的平均相对变化小于2%。在实际反演应用中,由于获取精度大于25%的密度或纵波速度信息相对容易,因此可假定密度和纵波速度为已知。但地层层厚对面波相速度频散曲线的影响相对较大,使得反演面波相速度频散曲线估计层厚的可行性较强。为了减少解的非唯一性,可通过将地表以下地层细分为合理层数,使得反演过程中的层厚不再作为未知变量,则仅有横波速度为未知。然而,瑞雷波和拉夫波相速度频散曲线的反演是一个高度非线性的地球物理反演问题,为了得到精确的从表层到深层乃至半空间的横波速度,仍需深入研究多模式面波相速度频散曲线对各层横波速度变化的灵敏度。
利用雅可比矩阵对比分析多模式瑞雷波和拉夫波相速度频散曲线对各层横波速度改变的灵敏度[7]
| $ J_{\mathrm{S} i}=\left[\frac{\frac{\partial F}{\partial v_{\mathrm{S}l}}}{\frac{\partial F}{\partial c_{k j}}}\right] \quad i=1, 2, \cdots, n $ | (3) |
式中:c是相速度;k是面波的模式阶数(k=1、2、3, 分别对应基阶、一阶高阶、二阶高阶)。雅可比矩阵中各元素等价于第k阶模式瑞雷波或拉夫波相速度在某一特定频率fj时对第i层横波速度的偏导数。为简化计算,这里用有限差分代替求导,计算横波速度改变10%引起的相速度变化以获取偏导数。
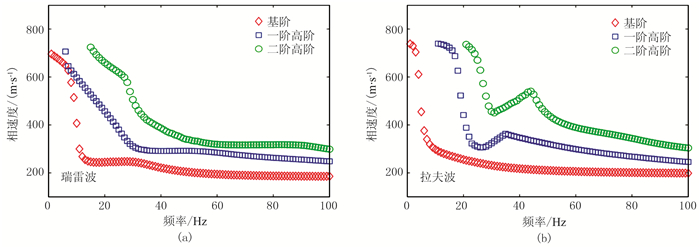
2 水平层状模型的面波相速度频散曲线的灵敏度分析 2.1 速度递增模型以表 1给出的模型N为研究对象,它是一个六层的速度递增模型(横波速度随深度递增,图 1a和图 2a)。无论是瑞雷波还是拉夫波,多模式面波相速度频散曲线的分布形态较规则;基阶模式瑞雷波和拉夫波相速度频散曲线在其高频段均趋近表层横波速度,在其低频段趋于半空间的横波速度。在16Hz处,瑞雷波相速度频散曲线呈现“模式接吻”(Mode-kissing)现象[12],即基阶与一阶高阶模式瑞雷波相速度的数值相近,这是由于多层模型的上覆(半空间以上)地层的等效代替层同半空间存在强的横波速度分界面造成的[29]。
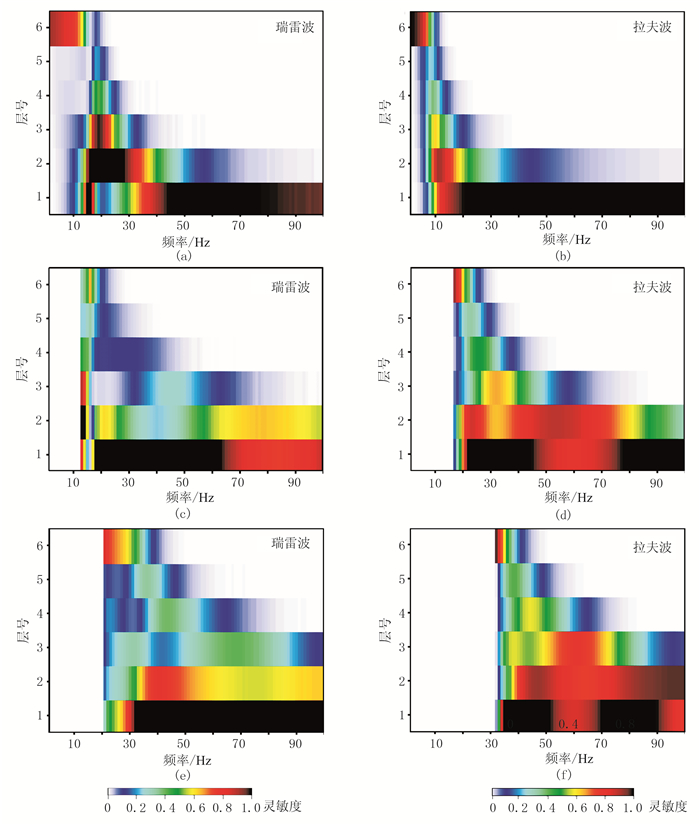
分别将模型N中各层的横波速度增加10%,然后计算多模式瑞雷波和拉夫波相速度频散曲线对应每个频率的相速度变化,得到模型N的基阶、一阶高阶和二阶高阶模式瑞雷波和拉夫波相速度频散曲线对各层横波速度变化的灵敏度(图 3)。
|
图 3 模型N的多模式瑞雷波和拉夫波相速度频散曲线的灵敏度分析 (a)、(c)、(e)对应基阶、一阶高阶和二阶高阶模式瑞雷波相速度频散曲线的灵敏度;(b)、(d)、(f)对应基阶、一阶高阶和二阶高阶模式拉夫波相速度频散曲线的灵敏度 |
从图 3可知,无论是瑞雷波还是拉夫波,面波相速度频散曲线对表层横波速度变化的灵敏频段占据了整个高频段;随着地层深度的增加,灵敏频段变得更为狭窄,表现为面波相速度的高频成分对表层横波速度的变化灵敏,而低频的面波相速度对深层和半空间横波速度的变化灵敏。
基阶模式瑞雷波相速度频散曲线对除表层外的各层横波速度的灵敏频段(图 3a)主要集中于10~25Hz频段,除表层外的各层灵敏度峰值均分布在18Hz附近;基阶模式拉夫波相速度对除表层外的各层横波速度的灵敏频段(图 3b)都集中于5~20Hz频段,且各层的灵敏度峰值分布在10Hz附近。当仅利用基阶模式瑞雷波和拉夫波相速度频散曲线进行反演时,能否准确地测量灵敏度峰值频段对应的基阶模式瑞雷波和拉夫波相速度频散曲线是获得准确横波速度的关键;同时由于灵敏度峰值集中,在灵敏度较小的频段内微小的数据扰动可能会影响反演的稳定性。
随着面波模式阶数的增加,高阶模式瑞雷波和拉夫波相速度频散曲线对各层横波速度的灵敏度峰值会向高频方向移动。一阶高阶模式瑞雷波和拉夫波相速度频散曲线对相同地层横波速度的高灵敏度的频段较宽(图 3c、图 3d),且灵敏度峰值分散;二阶高阶模式瑞雷波和拉夫波相速度频散曲线的灵敏度(图 3e、图 3f)具有相似的特点。由于高阶模式面波相速度频散曲线对横波速度的灵敏频段较宽,反演过程中高阶模式面波相速度频散曲线微小的扰动将不会导致反演横波速度结果大的改变。
依据相同模式瑞雷波和拉夫波相速度频散曲线关于同一地层横波速度有较大灵敏度的频段不同,可推知两种数据能够互为补充,因此联合利用瑞雷波和拉夫波相速度频散曲线进行反演,有助于获得高精度的横波速度。
2.2 低速夹层模型建立一个六层的低速夹层模型(表 4中模型L),即将速度递增模型(表 1中模型N)的第4层改为低速层,同时该层的纵波速度(由固定泊松比δ确定)和密度也进行相应改变,而其他参数不变。图 4为低速夹层模型正演计算的多模式瑞雷波和拉夫波的相速度频散曲线。基阶模式瑞雷波和拉夫波相速度频散曲线在其高频段趋近表层横波速度,而在其低频段趋近半空间的横波速度;在某些频段,瑞雷波和拉夫波相速度频散曲线随频率变化剧烈,这可能与低速层的存在有关[30]。
|
图 4 模型L的多模式瑞雷波(a)和拉夫波(b)的相速度频散曲线 |
通过计算模型L的多模式瑞雷波和拉夫波相速度频散曲线关于各层横波速度变化的灵敏度(图 5),可发现同速度递增模型(模型N)的瑞雷波与拉夫波的灵敏度分析结果类似,基阶、一阶高阶和二阶高阶模式瑞雷波和拉夫波相速度频散曲线关于相同地层横波速度具有高灵敏度频段的范围不同,对表层横波速度变化具有高灵敏度的频段主要集中在整个高频段;随着深度的增加,对各层横波速度变化的灵敏频段趋于低频,且更为狭窄。
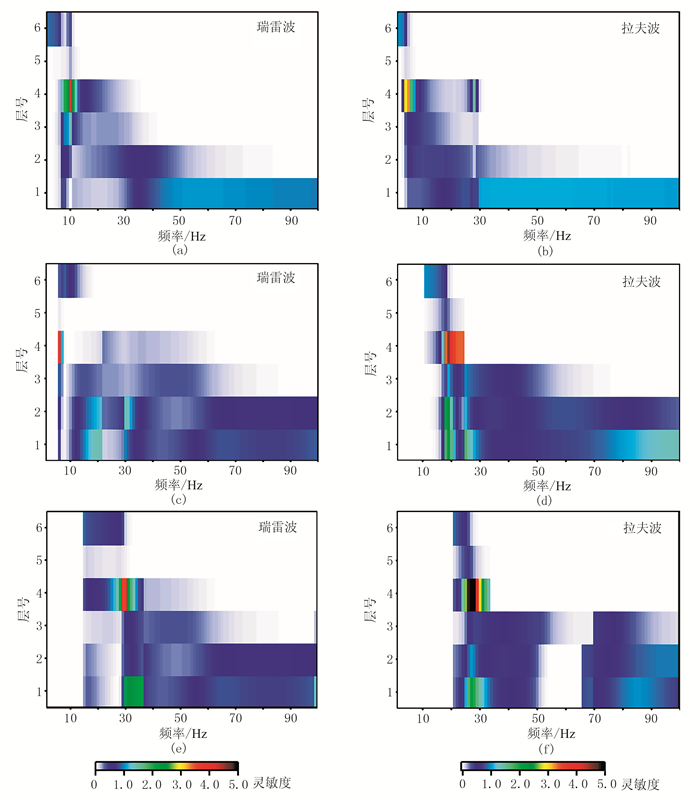
|
图 5 模型L的多模式瑞雷波和拉夫波相速度频散曲线的灵敏度分析 (a)、(c)、(e)对应基阶、一阶高阶和二阶高阶模式瑞雷波相速度频散曲线的灵敏度;(b)、(d)、(f)对应基阶、一阶高阶和二阶高阶模式拉夫波相速度频散曲线的灵敏度 |
基阶模式瑞雷波和拉夫波相速度频散曲线对低速层(第4层)横波速度的灵敏度最高(图 5a、图 5b),灵敏度的最大值分别为3.79和3.29;而低速层下伏地层(第5层和半空间)横波速度的灵敏度较低。出现这种现象的原因可解释为,当面波传播到低速层时,面波的大部分能量被“锁在”其中,仅有很少的能量能够穿透低速层下伏地层,从而导致面波相速度对低速层下伏地层的横波速度的改变不灵敏[31]。
相对于基阶模式波,高阶模式瑞雷波和拉夫波相速度频散曲线对第1、第2和第3层横波速度的灵敏频段更宽(图 5c、图 5f),因此加入高阶模式瑞雷波和拉夫波相速度频散曲线,有利于提高第1、第2和第3层的横波速度的反演精度。高阶模式瑞雷波和拉夫波相速度频散曲线对低速层横波速度的灵敏度高,但是对低速层下伏地层横波速度的灵敏度较低。
该结果说明低速层的横波速度能通过面波相速度频散曲线反演准确地确定,但低速层下伏地层的横波速度则具有较强不确定性,需慎重对待。
2.3 高速夹层模型建立一个六层的高速夹层模型(表 5中模型H),即将速度递增模型(表 1中模型N)的第4层改为高速层,同时该层对应的纵波速度(由固定泊松比δ确定)和密度也进行相应改变,其他参数不变。
在高速夹层模型中,多模式瑞雷波相速度频散曲线的分布形态与速度递增模型的相似(图 6a),出现“模式接吻”现象;而对于拉夫波,其低频段的高阶模式拉夫波相速度频散曲线呈现弯折现象(图 6b),该现象与高速层的存在有关[32]。
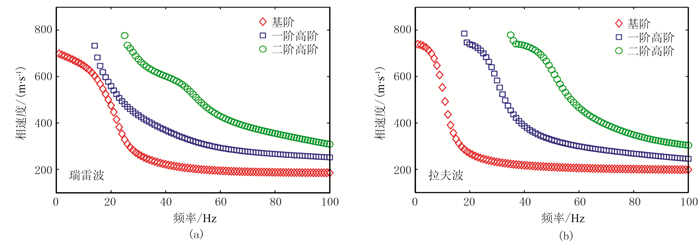
|
图 6 模型H的多模式瑞雷波(a)和拉夫波(b)的相速度频散曲线 |
通过计算模型H的多模式瑞雷波和拉夫波相速度频散曲线关于各层横波速度变化的灵敏度(图 7),可以看出,对于不同地层的横波速度,瑞雷波和拉夫波相速度频散曲线的灵敏频段范围不同。与速度递增模型(模型N)和低速夹层模型(模型L)类似,面波相速度频散曲线对表层横波速度变化的灵敏频段占据了整个高频段,表现为高频面波相速度对表层横波速度灵敏,而低频面波相速度对深层或半空间的横波速度灵敏。
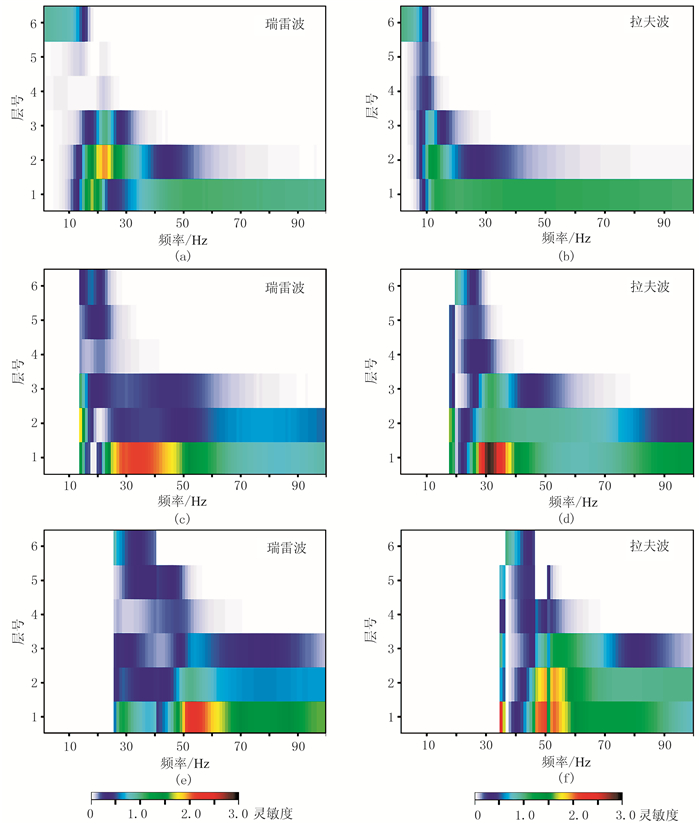
|
图 7 模型H的多模式瑞雷波(左)和拉夫波(右)相速度频散曲线的灵敏度分析 (a)、(c)、(e)对应基阶、一阶高阶和二阶高阶模式瑞雷波相速度频散曲线的灵敏度;(b)、(d)、(f)对应基阶、一阶高阶和二阶高阶模式拉夫波相速度频散曲线的灵敏度 |
相对于速度递增模型(模型N),基阶模式瑞雷波和拉夫波相速度频散曲线对高速层及其下伏地层横波速度的灵敏度均很低(图 7a、图 7b),这是因为当面波传播到高速层界面时,大部分能量会发生反射而非向下传播[33],导致面波对高速层及其更深地层横波速度的弱响应。相对于基阶模式波,由于相同地层中高阶模式波(图 7c、图 7f)的灵敏频段更宽且灵敏度峰值较高,因此高阶模式波的加入有利于获得更准确的高速夹层模型的横波速度。
比较相同模式瑞雷波和拉夫波相速度频散曲线的灵敏度,发现对于高速层及其下伏地层,相同模式的拉夫波比瑞雷波的灵敏度峰值更高。例如:在高速层(第4层)中,二阶高阶模式瑞雷波相速度频散曲线的灵敏度峰值为0.20,相同模式的拉夫波相速度频散曲线的灵敏度峰值为0.56;在高速层下伏地层(第5层)中,二阶高阶模式瑞雷波相速度频散曲线的灵敏度峰值为0.48,相同模式的拉夫波相速度频散曲线的灵敏度峰值为0.73;考虑在面波相速度频散曲线反演中给予这些灵敏度峰值点合适的权重,可提高高速层及其下伏地层的反演横波速度的精度。
2.4 讨论通过前面的研究,瑞雷波和拉夫波对高速层或速度(低速、高速)异常层下伏地层的灵敏度较低,低灵敏度会增加这些地层的横波速度反演的不确定度,因此有必要分析速度异常层对多模式瑞雷波和拉夫波相速度频散曲线的影响。图 8展示了基阶、一阶高阶、二阶高阶模式瑞雷波和拉夫波相速度频散曲线关于速度异常层(第4层)和速度异常层下伏地层(第5层)横波速度的灵敏度。
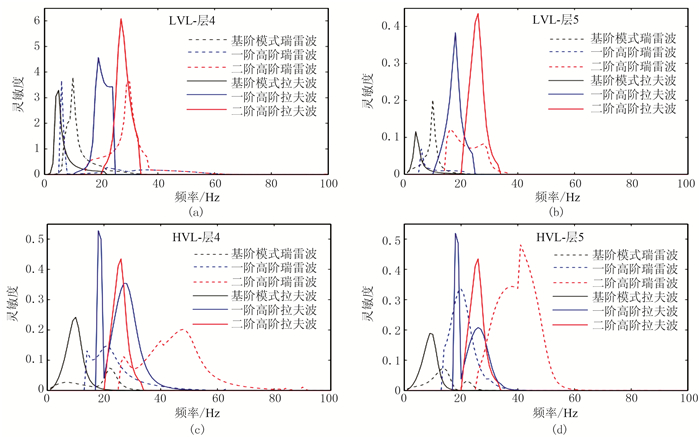
|
图 8 基阶、一阶高阶、二阶高阶模式瑞雷波和拉夫波相速度频散曲线对速度异常层及下伏地层横波速度的灵敏度分析 (a)低速层(LVL-层4);(b)低速层下伏地层(LVL-层5);(c)高速层(HVL-层4);(d)高速层下伏地层(HVL-层5) |
在低速夹层模型(模型L)中,低速层(第4层)的灵敏度峰值约为低速层下伏地层(第5层)灵敏度峰值的15倍(图 8a、图 8b),表明多模式瑞雷波和拉夫波相速度频散曲线的联合反演较容易获得低速层(第4层)的横波速度。对于低速层(第4层)及其下伏地层(第5层),相同模式拉夫波相速度频散曲线的高灵敏度频段比瑞雷波的更宽;同时,一阶高阶和二阶高阶模式拉夫波相速度频散曲线关于相同地层横波速度的灵敏度峰值比瑞雷波高。
在高速夹层模型(模型H)中,对于高速层(第4层)及其下伏地层(第5层),相同模式的拉夫波相速度频散曲线的灵敏频段低于瑞雷波的灵敏频段,且基阶和一阶高阶模式拉夫波相速度频散曲线关于高速层横波速度的灵敏度峰值高于相同模式的瑞雷波(图 8c、图 8d),因此拉夫波更利于重建低灵敏度的高速层和速度(低速、高速)异常层下伏地层的横波速度。
总之,相比于单一模式瑞雷波或拉夫波相速度频散曲线,联合反演多模式瑞雷波和拉夫波相速度频散曲线具有获取高精度横波速度的更大潜力。
3 结论针对水平层状模型,计算各模型参数(横波速度、纵波速度、密度和层厚)改变25%时多模式瑞雷波和拉夫波相速度频散曲线的平均相对变化,模拟结果证明:横波速度是影响多模式面波相速度频散曲线的最主要因素;相对于纵波速度和密度,层厚对多模式面波相速度频散曲线的影响较大,且随面波模式阶数增加,地层层厚的影响更显著。
利用面波相速度关于横波速度变化的雅可比矩阵探究多模式瑞雷波和拉夫波相速度频散曲线对速度递增模型、低速和高速夹层模型中各层横波速度变化的灵敏度。研究结果表明:
(1) 三种模型均表现为面波相速度频散曲线对横波速度变化的灵敏频段随深度而变化;无论是瑞雷波还是拉夫波,多模式面波相速度频散曲线对表层横波速度的灵敏频段主要集中于高频段;与其相反,随着深度递增,对深层横波速度的灵敏频段集中于低频且变窄。
(2) 在低速夹层模型中,基阶和高阶模式面波均表现为对低速层横波速度灵敏,然而对于低速层下伏地层的横波速度不灵敏。
(3) 在高速夹层模型中,多模式面波对高速层及其下伏地层横波速度的灵敏度较低。
(4) 相同模式拉夫波相速度频散曲线对速度(低速和高速)异常层的高灵敏度的频段比瑞雷波的更宽,且瑞雷波和拉夫波对速度异常层及下伏地层横波速度的灵敏度峰值存在差异,联合反演多模式瑞雷波和拉夫波相速度频散曲线有利于获得更精确的地下横波速度。
| [1] |
Strutt J W. On waves propagated along the plane surface of an elastic solid[J]. Proceedings of the London Mathematical Society, 1885, 17(1): 4-11. |
| [2] |
Sheriff R E. Encyclopedic Dictionary of Applied Geophysics (4th Edition)[M]. SEG, Tulsa, OK, 2002.
|
| [3] |
Bullen K E, Bolt B A. An Introduction to the Theory of Seismology[M]. Cambridge University Press, 1985.
|
| [4] |
Xia J, Miller R D, Xu Y, et al. High-frequency Rayleigh-wave method[J]. Journal of Earth Science, 2009, 20(3): 563-579. DOI:10.1007/s12583-009-0047-7 |
| [5] |
夏江海, 高伶俐, 潘雨迪, 等. 高频面波方法的若干新进展[J]. 地球物理学报, 2015, 58(8): 2591-2605. XIA Jianghai, GAO Lingli, PAN Yudi, et al. New findings in high-frequency surface wave method[J]. Chinese Journal of Geophysics, 2015, 58(8): 2591-2605. |
| [6] |
蔡伟, 宋先海, 袁士川, 等. 利用粒子群优化算法快速、稳定反演瑞雷波频散曲线[J]. 石油地球物理勘探, 2018, 53(1): 25-34. CAI Wei, SONG Xianhai, YUAN Shichuan, et al. Fast and stable Rayleigh-wave dispersion-curve inversion based on particle swarm optimization[J]. Oil Geophysical Prospecting, 2018, 53(1): 25-34. |
| [7] |
Xia J, Miller R D, Park C B. Estimation of near-surface shear-wave velocity by inversion of Rayleigh waves[J]. Geophysics, 1999, 64(3): 691-700. DOI:10.1190/1.1444578 |
| [8] |
邵广周, 李庆春. 联合应用τ-p变换法和相移法提取面波频散曲线[J]. 石油地球物理勘探, 2010, 45(6): 836-840. SHAO Guangzhou, LI Qingchun. Joint application of τ-p and phase-shift stacking method to extract ground wave dispersion curve[J]. Oil Geophysical Prospecting, 2010, 45(6): 836-840. |
| [9] |
李欣欣, 李庆春. 利用改进的F-K变换法提取瑞雷波的频散曲线[J]. 地球物理学进展, 2017, 32(1): 191-197. LI Xinxin, LI Qingchun. Rayleigh wave dispersion curve imaging using improved F-K transform approach[J]. Progress in Geophysics, 2017, 32(1): 191-197. |
| [10] |
姜福豪, 李培明, 张翊孟, 等. 多道面波频散分析在实际大炮数据中的应用[J]. 石油地球物理勘探, 2018, 53(1): 17-46. JIANG Fuhao, LI Peiming, ZHANG Yimeng, et al. Frequency dispersion analysis of MASW in real seismic data[J]. Oil Geophysical Prospecting, 2018, 53(1): 17-46. |
| [11] |
鲁来玉, 张碧星, 汪承灏. 基于瑞利波高阶模式反演的实验研究[J]. 地球物理学报, 2006, 49(4): 1082-1091. LU Laiyu, ZHANG Bixing, WANG Chenghao. Experi-ment and inversion studies on Rayleigh wave consi-dering higher modes[J]. Chinese Journal of Geophy-sics, 2006, 49(4): 1082-1091. DOI:10.3321/j.issn:0001-5733.2006.04.021 |
| [12] |
Xia J, Xu Y, Luo Y, et al. Advantages of using multichannel analysis of Love waves (MALW) to estimate near-surface shear-wave velocity[J]. Surveys in Geophy-sics, 2012, 33(5): 841-860. DOI:10.1007/s10712-012-9174-2 |
| [13] |
李子伟, 刘学伟. 空间假频对频率-波数域瑞利面波频散曲线反演的影响[J]. 石油地球物理勘探, 2013, 48(3): 395-402. LI Ziwei, LIU Xuewei. Effects of spatial aliasing on frequency-wavenumber domain inversion of Rayleigh-wave dispersion curve[J]. Oil Geophysical Pro-specting, 2013, 48(3): 395-402. |
| [14] |
艾东海.基于粒子群优化算法的瑞雷波非线性反演研究[D].湖北武汉: 中国地质大学(武汉), 2009. AI Donghai.Particle Swarm Optimization Algorithms for Nonlinear Inversion of Rayleigh-wave Dispersion Curves[D].China University of Geosciences(Wuhan), Wuhan, Hubei, 2009. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1661610 |
| [15] |
Hamimu L, Safani J, Nawawi M. Improving the accurate assessment of a shear-wave velocity reversal profile using joint inversion of the effective Rayleigh wave and multimode Love wave dispersion curves[J]. Near Surface Geophysics, 2011, 9(1): 1-14. DOI:10.3997/1873-0604.2010029 |
| [16] |
罗银河, 夏江海, 刘江平, 等. 基阶与高阶瑞利波联合反演研究[J]. 地球物理学报, 2008, 51(1): 242-249. LUO Yinhe, XIA Jianghai, LIU Jiangping, et al. Joint inversion of fundamental and higher mode Rayleigh waves[J]. Chinese Journal of Geophysics, 2008, 51(1): 242-249. DOI:10.3321/j.issn:0001-5733.2008.01.030 |
| [17] |
Feng S, Sugiyama T, Yamanaka H. Effectiveness of multi-mode surface wave inversion in shallow engineering site investigations[J]. Exploration Geophy-sics, 2005, 36(1): 26-33. DOI:10.1071/EG05026 |
| [18] |
Lai C G, Rix G J, Foti S, et al. Simultaneous measurement and inversion of surface wave dispersion and attenuation curves[J]. Soil Dynamics and Earthquake Engineering, 2002, 22(9): 923-930. |
| [19] |
Zeng C, Xia J, Liang Q, et al.Comparative analysis on sensitivities of Love and Rayleigh waves[C].SEG Technical Program Expanded Abstracts, 2007, 26: 1138-1141.
|
| [20] |
Liang Q, Chen C, Zeng C, et al. Inversion stability analysis of multimode Rayleigh-wave dispersion curves using low-velocity-layer models[J]. Near Surface Geophysics, 2008, 6(3): 157-165. DOI:10.3997/1873-0604.2007040 |
| [21] |
Jin X, Luke B and Lipinska-Kalita K.Surface-wave sensitivity to a high-velocity inclusion[C].Proceeding of the Symposium on the Application of Geophysics to Engineering and Environmental Problems (SAGEEP), Annual Meeting of the Environmental and Engineering Geophysical Society (EEGS), 2007, Denver, CO.
|
| [22] |
Yin X, Xia J, Shen C, et al. Comparative analysis on penetrating depth of high-frequency Rayleigh and Love waves[J]. Journal of Applied Geophysics, 2014, 111: 86-94. DOI:10.1016/j.jappgeo.2014.09.022 |
| [23] |
Shen C, Xu Y, Pan Y, et al. Sensitivities of phase-velocity dispersion curves of surface waves due to low-velocity-layer and high-velocity-layer models[J]. Journal of Applied Geophysics, 2016, 135: 367-374. DOI:10.1016/j.jappgeo.2016.10.017 |
| [24] |
Schwab F A, Knopoff L. Fast surface wave and free mode computations[J]. Methods in Computational Physics, 1972, 11(1): 87-180. |
| [25] |
Eslick R, Tsoflias G, Steeples D W. Field investigation of Love waves in near-surface seismology[J]. Geophysics, 2008, 73(3): G1-G6. DOI:10.1190/1.2901215 |
| [26] |
Aki K, Richards P G. Quantitative Seismology:Theory and Methods[M]. Freeman, San Francisco, 1980.
|
| [27] |
Schwab F A, Knopoff L. Surface-wave dispersion computations[J]. Bulletin of the Seismological Society of America, 1970, 60(2): 321-344. |
| [28] |
Preiss W H, Teukolsky S A, Vetterling W T, et al. Numerical Recipes in C++:The Art of Scientific Computing (2nd Edition)[M]. Cambridge University Press, Cambridge, 2002.
|
| [29] |
Gao L, Xia J, Pan Y, et al. Reason and condition for mode kissing in MASW method[J]. Pure and Applied Geophysics, 2016, 173(5): 1627-1638. DOI:10.1007/s00024-015-1208-5 |
| [30] |
邵广周, 李庆春, 吴华. 基于波场数值模拟的瑞利波频散曲线特征及各模式能量分布[J]. 石油地球物理勘探, 2015, 50(2): 306-315. SHAO Guangzhou, LI Qingchun, WU Hua. Characteristics of Rayleigh wave dispersion curve based on wave-field numerical simulation and energy distribution of each mode[J]. Oil Geophysical Prospecting, 2015, 50(2): 306-315. |
| [31] |
Calderón-Macías C, Luke B. Improved parameteriza-tion to invert Rayleigh-wave data for shallow profiles containing stiff inclusions[J]. Geophysics, 2006, 72(1): U1-U10. |
| [32] |
沈超.高频面波方法中的频散曲线自动拾取[D].湖北武汉: 中国地质大学(武汉), 2014. SHEN Chao.Automatic Picking Phase-velocity Dispersion Curves in High-frequency Surface Wave Method[D].China University of Geosciences(Wuhan), Wuhan, Hubei, 2014. |
| [33] |
Leslie D M, Evans B J.The effects of high-velocity layering on seismic wave propagation[C].SEG Technical Program Expanded Abstracts, 1999, 18: 1809.
|



 胥鸿睿, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球内部成像与探测实验室, 430074。Email:
胥鸿睿, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球内部成像与探测实验室, 430074。Email: