2 广州海洋地质调查局, 广东广州 510075
2 Guangzhou Marine Geological Survey, Guangzhou, Guangdong 510075, China
天然气水合物广泛分布于各大陆边缘海底和永久冻土带,是一种极具潜力的替换能源[1]。目前地震勘探是天然气水合物勘查的重要手段[2-4],通常含天然气水合物的沉积层具有较高的纵、横波速度[5-6],利用叠前地震反演技术可以获取纵、横波速度数据,再利用速度可预测沉积物中水合物的饱和度,进而估算其资源量[7-12]。然而在叠前反演中需要准确的纵、横波测井资料[13],但实际生产中由于各种原因往往缺乏横波信息,又由于天然气水合物既可作为固体骨架又可作为孔隙充填物存在于地层中[14],与油气储层区别较大,许多常规岩石物理模型不再适用,因此,为了获取水合物地层的纵横波速度,众多地球物理学者提出了水合物岩石物理经验公式和理论模型。Lee等[15]基于时间平均方程和Wood方程,提出了一个无物理意义的加权方程,根据水合物地层中三相体积百分含量,估算水合物地层的速度,该公式是经验公式,未考虑地层各组分的弹性模量;Helgerud等[16]和Dvorkin等[17]提出等效介质模型(EMT)计算干岩石体积模量和剪切模量,然后通过Gassmann方程计算饱含流体沉积物的体积模量和剪切模量,进而估算纵横速度,该方法常用于水合物饱和度的预测研究[8, 18-19]。Carcione等[20]基于Leclaire等[21]发展的三相孔隙介质理论,应用Biot型三相理论研究了水合物饱和度与纵横波速度的关系;Lee[22]对Biot-Gassmann方程进行了改进,提出了BGTL模型,高红艳等[23]利用该模型对南海神狐海区天然气水合物饱和度进行了估算,但其中Biot系数需根据Lee权重方程[15]和等效介质模型计算。宋海斌等[5]和孙春岩等[24]基于岩石物理模型和经验加权公式计算了水合物沉积层的纵波与横波速度,并分析了似海底反射层的AVA特征,但没有与实际数据进行对比,因而缺乏实际数据验证。潘豪杰等[25]分析了等效介质模型、改进的Biot-Gassmann模型以及简化的三相方程在同一赋存形态下预测饱和度的适用性,认为纵横波速度联合反演比单纵波预测的水合物饱和度更合理。张如伟等[26-27]结合等效介质模型和BISQ模型,模拟了海洋含水合物层的速度频散与衰减特征。刘洁等[6]利用等效介质模型对四相介质Wood方程进行了改进,把水合物看作固体骨架的一部分,计算水合物对岩石骨架速度的影响,并利用该方法计算了神狐海域水合物饱和度。
目前利用岩石物理模型进行水合物的饱和度预测和理论数值模拟的研究比较多,但利用实际常规测井资料进行水合物纵横波预测的研究还比较少。为此,在分析了矿物含量、孔隙度以及水合物饱和度对纵横波速度影响的基础上,本文基于等效介质模型,结合实际常规测井资料,以纵波速度、密度等常规测井资料为约束,建立了约束优化方程进行最优化参数反演,再利用反演出的参数进行横波速度和饱和度预测,与实际数据的对比验证了该方法横波速度预测的有效性。
1 基本原理 1.1 纵横波速度计算方法根据Gassmann方程,可以获得饱和流体沉积物的体积模量和剪切模量
| $ K_{\mathrm{sat}}=K_{\mathrm{ma}} \frac{\phi K_{\mathrm{dry}}-\frac{(1+\phi) K_{\mathrm{f}} K_{\mathrm{dry}}}{K_{\mathrm{ma}}}+K_{\mathrm{f}}}{(1-\phi) K_{\mathrm{f}}+\phi k_{\mathrm{ma}}-\frac{K_{\mathrm{f}} K_{\mathrm{dry}}}{K_{\mathrm{ma}}}} $ | (1) |
| $ G_{\mathrm{sat}}=G_{\mathrm{dry}} $ | (2) |
式中:Kma为沉积物骨架体积模量;Kf为孔隙流体体积模量;ϕ为孔隙度;Kdry和Gdry分别为干岩石的体积模量和剪切模量;Ksat和Gsat分别为饱含流体沉积物体积模量和剪切模量。在均匀各向同性弹性介质中,地震纵、横波速度分别为
| $ V_{\mathrm{P}}=\sqrt{\frac{K_{\mathrm{sat}}+\frac{4 G_{\mathrm{sat}}}{3}}{\rho_{\mathrm{sat}}}} $ | (3) |
| $ V_{\mathrm{S}}=\sqrt{\frac{G_{\mathrm{sat}}}{\rho_{\mathrm{sat}}}} $ | (4) |
式中ρsat为饱含流体的沉积物密度。上述公式中沉积物骨架体积模量Kma和孔隙流体体积模量Kf可分别由VRH混合模型和Wood公式求取。可见求取纵横波速度的关键是求取干岩体积模量Kdry和剪切模量Gdry。本文根据等效介质模型来求取干岩石的弹性模量。
1.2 等效介质模型等效介质模型是基于物理准则的岩石物理模型[16-17],适用于海底含天然气水合物非固结高孔隙度的松散沉积物的弹性波速度估算。该模型沉积物的干岩石弹性模量主要与孔隙度、骨架矿物的弹性模量和组分以及有效压力有关,饱含流体的弹性模量需要利用Gassmann方程进行计算,因此,最终的弹性波速度与矿物组分、孔隙度、有效压力、孔隙充填物的弹性性质以及孔隙充填物饱和度有关[5]。
水合物在地层中以固体形式存在,可将水合物地层的多种微观结构分两类进行处理,即分别将水合物看作孔隙充填物和岩石骨架[5, 14, 18, 28-29]:模型Ⅰ假设水合物是孔隙流体的一部分,并影响孔隙流体的体积模量;模型Ⅱ假设水合物是岩石骨架的一部分,水合物的存在降低了孔隙度,改变了骨架的弹性模量。
根据等效介质模型[5, 16-17],海洋沉积物的干岩石体积模量Kdry和剪切模量Gdry分别为
| $ K_{\mathrm{dry}}=\left\{\begin{array}{ll} \left(\frac{\frac{\phi}{\phi_{c}}}{K_{\mathrm{HM}}+\frac{4 G_{\mathrm{HM}}}{3}}+\frac{1-\frac{\phi}{\phi_{c}}}{K_{\mathrm{ma}}+\frac{4 G_{\mathrm{HM}}}{3}}\right)^{-1}-\frac{4 G_{\mathrm{HM}}}{3}\quad \phi < \phi_{\mathrm{c}}\\ \left(\frac{\frac{1-\phi}{1-\phi_{\mathrm{c}}}}{K_{\mathrm{HM}}+\frac{4 G_{\mathrm{HM}}}{3}}+\frac{\frac{\phi-\phi_{\mathrm{c}}}{4-\phi_{\mathrm{c}}}}{\frac{4 G_{\mathrm{HM}}}{3}}\right)^{-1}-\frac{4 G_{\mathrm{HM}}}{3} \quad \phi \geqslant \phi_{\mathrm{c}} \end{array}\right. $ | (5) |
| $ G_{\mathrm{dy}}=\left\{\begin{array}{ll} \left(\frac{\frac{\phi}{\phi_{\mathrm{c}}}}{G_{\mathrm{HM}}+Z}+\frac{1-\frac{\phi}{\phi_{\mathrm{c}}}}{G_{\mathrm{ma}}+Z}\right)^{-1}-Z & \phi<\phi_{\mathrm{c}} \\ \left[\frac{\frac{1-\phi}{1-\phi_{c}}}{G_{\mathrm{IH}}+Z}+\frac{\frac{\phi-\phi_{c}}{1-\phi_{c}}}{Z}\right]^{-1}-Z \quad \phi \geqslant \phi_{{\rm c}} \end{array}\right. $ | (6) |
式中
| $ Z=\frac{G_{\mathrm{HM}}}{6} \times \frac{9 K_{\mathrm{HM}}+8 G_{\mathrm{HM}}}{K_{\mathrm{HM}}+2 G_{\mathrm{HM}}} $ | (7) |
| $ \left\{\begin{array}{l} K_{\mathrm{HM}}=\left[\frac{n^{2}\left(1-\phi_{\mathrm{c}}\right)^{2} G_{\mathrm{ma}}^{2} P}{18 \pi^{2}(1-υ)^{2}}\right]^{\frac{1}{3}} \\ G_{\mathrm{HM}}=\frac{5-4 υ}{5(2-υ)}\left[\frac{3 n^{2}\left(1-\phi_{\mathrm{c}}\right)^{2} G_{\mathrm{ma}}^{2} P}{2 \pi^{2}(1-υ)^{2}}\right]^{\frac{1}{3}} \end{array}\right. $ | (8) |
其中:ϕc为临界孔隙度,取值范围为0.36~0.40[30];n为骨架颗粒接触点的平均数目,取值范围为8.0~9.5[31];P=(ρb-ρw)gD为有效压力,其中ρb为沉积物密度,ρw为海水密度,g为重力加速度,D为从海底起算的深度;Gma是沉积物骨架剪切模量;υ是沉积物骨架的泊松比,与岩石骨架弹性模量的关系为
| $ v=\frac{0.5\left(K_{\mathrm{ma}}-\frac{2 G_{\mathrm{ma}}}{3}\right)}{K_{\mathrm{ma}}+\frac{G_{\mathrm{ma}}}{3}} $ | (9) |
岩石骨架的弹性模量与其组成矿物的弹性模量有关,可根据Hill平均模型[32]计算。当水合物充填于孔隙中(模型Ⅰ)作为孔隙流体的一部分时,孔隙流体体积模量Kf是水的体积模量和水合物体积模量的等应力平均[33]
| $ K_{\mathrm{f}}=\left(\frac{S_{\mathrm{w}}}{K_{\mathrm{w}}}+\frac{1-S_{\mathrm{w}}}{K_{\mathrm{h}}}\right)^{-1} $ | (10) |
式中:Sw为含水饱和度;Kw和Kh分别为水和水合物的体积模量。
当水合物作为沉积骨架的一部分(模型Ⅱ)时,水合物的存在会降低孔隙度,并改变矿物骨架的各组分的体积百分含量。降低后的孔隙度
| $ \left\{\begin{array}{l} \tilde{f}_{i}=\frac{f_{i}(1-\phi)}{1-\tilde{\phi}} \\ \tilde{f}_{\mathrm{h}}=\frac{\phi S_{\mathrm{h}}}{1-\tilde{\phi}} \end{array}\right. $ | (11) |
式中fi为原矿物组分体积百分含量。根据式(11)分别重新计算出各种矿物和水合物的体积百分含量后,可再根据Hill平均模型重新计算出水合物作为沉积物骨架时矿物骨架的弹性模量。此种情况下孔隙流体为水或水和天然气,其体积模量为
| $ K_{\mathrm{f}}=\left(\frac{S_{\mathrm{w}}}{K_{\mathrm{w}}}+\frac{1-S_{\mathrm{w}}}{K_{\mathrm{g}}}\right)^{-1} $ | (12) |
式中Kg为天然气的体积模量。
当确定水合物的充填模式(模型Ⅰ或模型Ⅱ)后,即可计算出沉积物的骨架弹性模量、干岩石的弹性模量以及孔隙流体的弹性模量,然后利用Gassmann方程计算饱含流体岩石的体积模量和剪切模量,通过这些模量参数可以进一步计算纵波和横波速度。
2 纵横波速度预测误差分析利用等效介质模型进行纵横波速度预测,需要输入的参数有:沉积物骨架矿物组分的百分含量、体积模量、剪切模量、密度,流体的体积模量、密度、饱和度,孔隙度和临界孔隙度ϕc,骨架颗粒接触点的平均数目n。其中临界孔隙度ϕc和骨架颗粒接触点的平均数目n的取值只要在合理的范围内对计算结果影响就较小[16];沉积物骨架矿物组分的体积模量、剪切模量、密度和流体的体积模量、剪切模量、密度需要根据实验室岩石物理数据输入;矿物百分含量、孔隙度和饱和度数据可根据测井数据获得。由于实验室岩石物理数据相对较为准确,本文主要分析由于测井资料计算的矿物百分含量、孔隙度及饱和度数据对纵、横波速度的影响。
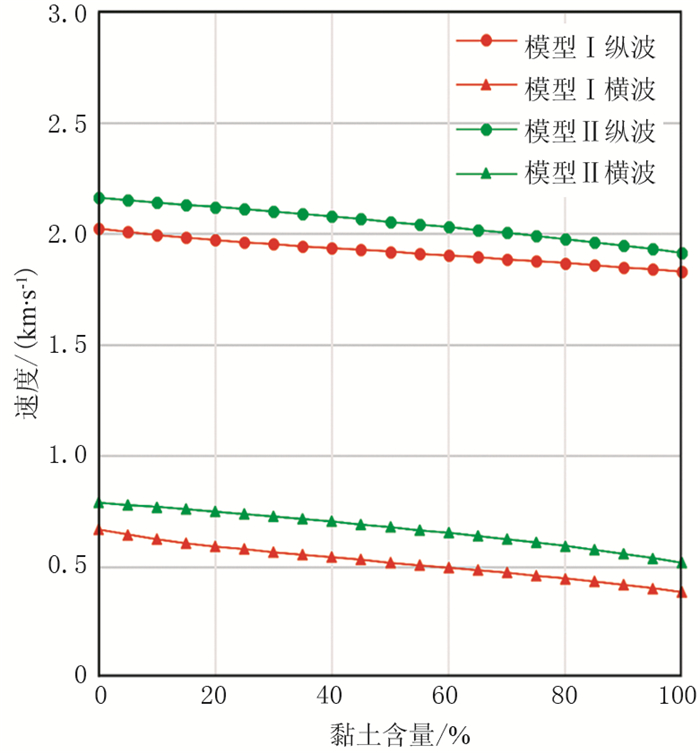
假设有效压力为10MPa,孔隙度为45%,水合物饱和度为40%,沉积物骨架主要由石英、方解石和黏土组成,不同矿物组分的弹性参数如表 1所示,方解石和石英的比例为18:82,黏土百分含量从0~100%变化,其纵、横波速度随黏土含量变化的计算结果如图 1所示。可以看出在水合物的两种充填模式下,纵、横波速度都随着黏土含量的增加而减少,水合物作为沉积物骨架(模型Ⅱ)时的纵、横波速度要高于水合物作为孔隙流体(模型Ⅰ)的纵、横波速度。
|
|
表 1 不同矿物成分弹性参数[34] |
|
图 1 纵、横波速度随黏土含量的变化曲线 |
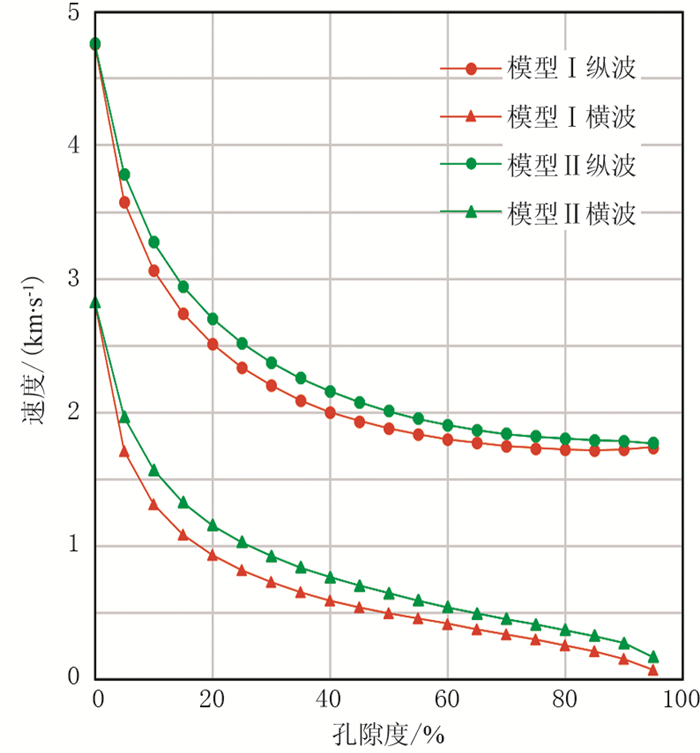
假定沉积物中黏土含量为40.0%、方解石为10.8%、石英为49.2%,水合物饱和度为40%,纵、横波速度随孔隙度变化的计算结果如图 2所示。可以看出,在两种充填模式下水合物沉积的纵横波速度随孔隙度的增大而减小,而且可以看出孔隙度对速度的影响要大于黏土含量。
|
图 2 纵、横波速度随孔隙度的变化曲线 |
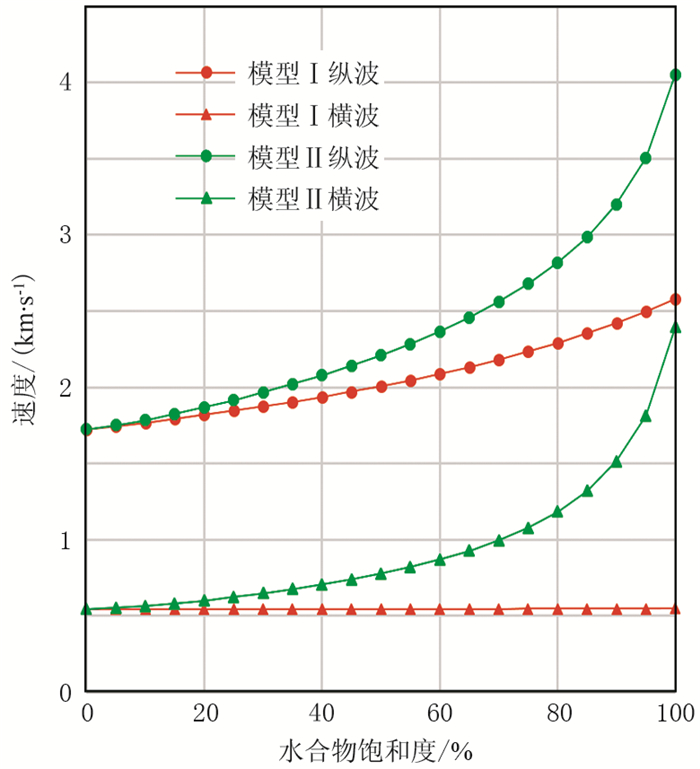
保持沉积物矿物含量不变,假设孔隙度为45%,分析水合物饱和度对纵横波速度的影响。图 3为纵、横波速度计算结果,在两种充填模式下水合物饱和度对纵波速度的影响都较大,纵波速度随水合物饱和度的增加而增加,而只有在水合物作为沉积物骨架时,水合物的饱和度才对横波速度有影响,在水合物作为孔隙流体时,对横波速度没有影响。同时可以看出,在水合物饱和度较低时,水合物无论作为孔隙流体还是沉积物骨架,其对纵、横波速度的影响一致,说明水合物饱和度较低时不受充填模式影响。
|
图 3 纵、横波速度随水合物饱和度的变化曲线 |
根据以上计算结果可知,对水合物地层的纵波速度影响较大的是孔隙度和水合物饱和度,而矿物组分影响相对较小。当水合物作为孔隙流体时,水合物饱和度不影响沉积物的横波速度,其影响因素主要为孔隙度;当水合物作为沉积物骨架时,横波速度的影响因素主要为孔隙度和水合物饱和度,矿物组分相对较小。由此可见,在估算水合物地层的纵横波速度时,孔隙度和水合物饱和度是关键参数。
3 实际数据计算根据等效介质模型理论,水合物既可作为孔隙充填物又可作为沉积物骨架,因此在估算水合物的纵横波速度时,需要进行水合物充填模式的分析。可利用测井解释的结果进行纵横波速度的初步估计,通过与实际纵横波测井数据对比来分析水合物的充填模式。
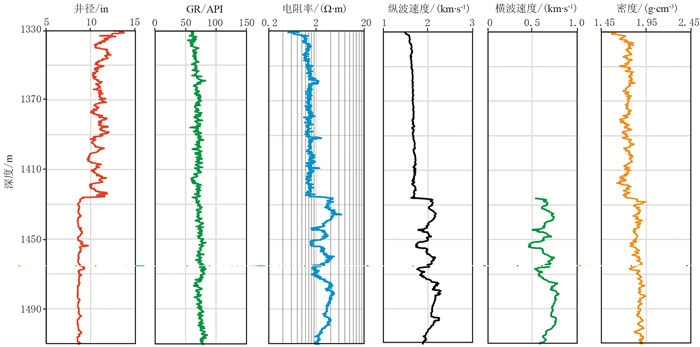
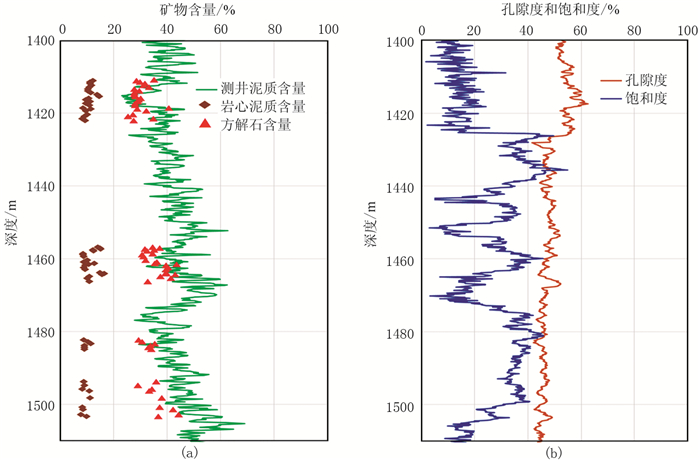
选取南海北部神狐海域W11井进行实际数据验证。该井资料较为齐全,具有较完整的测井数据以及岩心资料。图 4为该井的测井曲线,水合物主要发育在1425~1510m段,在水合物之上的地层,井径变化大,测井数据可能会受到影响;在含水合物地层,井径变化小,测井数据较为可靠。同时可以看出,水合物地层相对于上部地层具有较高的电阻率以及纵、横波速度,但密度和伽马曲线差异较小。
|
图 4 W11井测井曲线 |
根据分析,纵横波速度正演计算需要输入的参数主要有矿物组分、孔隙度、水合物饱和度和矿物的弹性模量。其中矿物的的弹性模量采用实验室岩石物理数据(表 1)。矿物组分根据测井解释和岩心分析资料获得,从该井岩心X射线衍射分析可知该区矿物组分主要由石英、方解石和黏土,且方解石含量比较稳定,约为10.8%;泥质含量通过伽马测井曲线解释,然后利用岩心结果标定(图 5a)得到,利用伽马测井计算的泥质含量比岩心资料分析的结果略微偏高,进行校正后就可获得较为准确的结果;其余矿物组分由石英组成。孔隙度通过密度测井计算获得。水合物饱和度利用电阻率测井根据阿尔奇公式[6, 19, 35]计算获得(图 5b)。
|
图 5 测井数据的解释结果 (a)矿物含量;(b)孔隙度和饱和度 |
利用矿物组分、孔隙度、水合物饱和度和沉积物的弹性模量数据,首先根据等效介质模型式(5)和式(6)计算出水合物在两种不同充填模式下干岩石的弹性模量,然后利用Gassmann方程计算出饱和流体沉积物的弹性模量,最后根据式(3)和式(4)分别计算出纵横波速度。
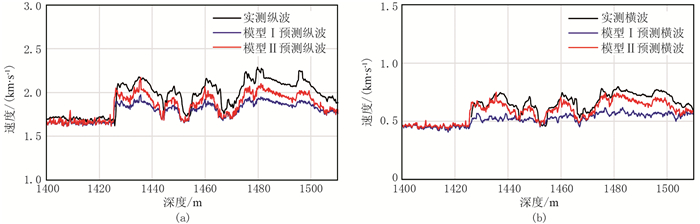
图 6为利用等效介质模型分别计算水合物作为孔隙流体充填(模型Ⅰ)和骨架支撑(模型Ⅱ)时的纵横波速度与实际测井纵横波速度的对比。结果显示,当水合物饱和度较低或者不含水合物时,两种充填模式下估算的纵横波速度比较接近,水合物的充填模式影响作用较小;当水合物饱和度较高时,水合物作为沉积物骨架支撑时计算的纵横波速度明显要比作为孔隙流体充填时要高,而且与实测数据更接近。由此可见,在该地区水合物饱和度较高时,水合物主要作为沉积物骨架存在于沉积物中。
|
图 6 估算的水合物纵、横波速度与实测数据对比 (a)纵波速度; (b)横波速度 |
根据分析可知,孔隙度和水合物饱和度对水合物地层的纵横波速度影响较大,而矿物组分影响相对较小。实际中,通过测井解释结合岩心资料就可获得相对准确的矿物组分含量。而对于孔隙度和水合物饱和度的测井解释结果,由于赋存水合物的沉积物埋藏浅,属于疏松未固结的地层,岩心资料容易松散,难以测量准确的孔隙度。其次由于压力以及温度的改变,岩心中的水合物容易发生分解,通过岩心资料也难以准确测量水合物的饱和度。因此孔隙度和饱和度难以通过岩心标定,存在较强的多解性,导致横波预测时也会存在较大误差。
为了解决这个问题,利用等效介质模型,根据最优化理论,构建一个约束优化函数,利用声波速度约束,寻找最优的孔隙度和饱和度数据,构建的约束优化函数[36]为
| $ \begin{array}{rl} \min & F\left(\phi, S_{\mathrm{h}}\right)=\left\|V_{\mathrm{P}}-V_{\mathrm{P}}^{\mathrm{est}}\right\| \\ & \quad \quad 满足 \phi>0, S_{\mathrm{h}}<100 \% \end{array} $ | (13) |
式中VPest为利用岩石物理模型估算的纵波速度。当利用等效介质模型估算的纵波速度与实测的纵波速度相接近或者满足收敛条件,并且其他参数也满足约束条件时,所计算的横波速度即为估算的横波速度。
采用信赖域算法[37-38]求解式(13)约束最优化问题。信赖域算法的基本原理是首先给定一个控制步长,以步长为半径,当前模型位置为中心,划定一个扰动区域,然后通过求解这个区域内与原问题近似模型的最优的校正量,最后根据目标函数的收敛情况决定是否接收扰动或进一步调节信赖域半径继续迭代。
信赖域算法的控制步长是通过求解信赖域子问题得到的,信赖域子问题形式为
| $ \min q_{k}(s)=\boldsymbol{d}_{k}^{\mathrm{T}} \boldsymbol{s}+\frac{1}{2} \boldsymbol{s}^{\mathrm{T}} \boldsymbol{H}_{k} \boldsymbol{s} \quad 满足~\|\boldsymbol{s}\|_{2} \leqslant R_{k} $ | (14) |
式中:dk为目标函数的梯度;s为优化校正量;Hk是目标函数的Hessian矩阵;Rk为信赖域半径。如果sk是信赖域子问题式(14)的解,则目标函数在第k步下降量为
| $ \Delta F_{k}=F\left(\boldsymbol{x}_{k}\right)-F\left(\boldsymbol{x}_{k}+\boldsymbol{s}_{k}\right) $ | (15) |
xk为第k步获得的中间解,信赖域子问题下降量为
| $ \Delta q_{k}=q(0)-q\left(\boldsymbol{s}_{k}\right) $ | (16) |
用
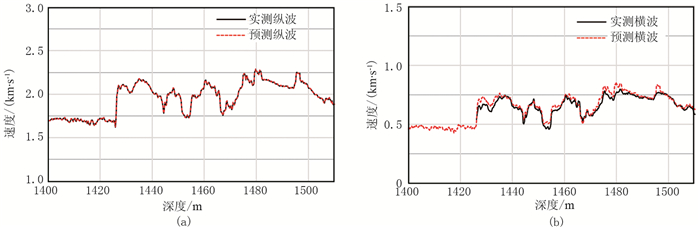
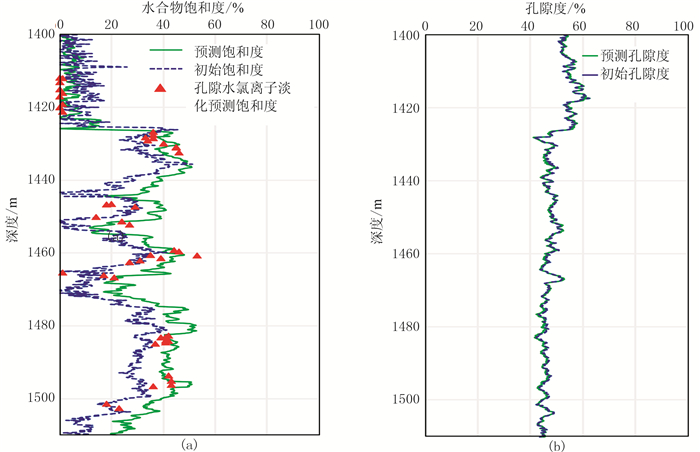
利用信赖域算法和神狐海域W11井的资料,根据构建的约束优化函数进行横波试算验证。初始输入数据如图 5所示,其中矿物组分作为确定值,孔隙度和饱和度数据作为优化参数,分别选择初始信赖域半径为0.01、0.10和0.50进行优化计算。结果表明不同的初始信赖域半径预测结果一致,仅在计算时间上略有差异。在相同的计算条件下,计算1220个样点数据的时间分别为5.0、4.9和5.2s。图 7a为估算与实测的纵波速度曲线对比,二者几乎完全重合;图 7b为估算与实测的横波速度曲线对比,两者的拟合度较高,说明本文方法预测的横波速度精度较高,能够满足实际应用需求。将反演优化得到的水合物饱和度和孔隙度与初始输入数据对比,结果如图 8所示。可以看出,孔隙度优化前、后变化较小,水合物饱和度变化相对较大,优化饱和度结果整体要高于初始饱和度。同时将饱和度结果与岩心孔隙水氯离子淡化估算的水合物饱和度进行对比[19](图 8a),两者吻合度相对较高,说明本文方法的参数优化正确。
|
图 7 最优化估算与实测速度曲线对比 (a)纵波;(b)横波 |
|
图 8 水合物饱和度和孔隙度预测结果 (a)水合物饱和度;(b)孔隙度 |
利用等效介质模型在含天然气水合物沉积地层中预测横波速度时需要考虑水合物充填模式的影响。从理论模拟结果来看,在水合物饱和度较低时,无论水合物作为孔隙充填物还是骨架,对纵横波速度的影响比较相似,此时水合物的充填模式影响较小。当水合物饱和度逐渐增加时,水合物的充填模式对沉积物的纵横波速度影响作用增强,水合物作为骨架支撑时,对沉积物的纵横波速度的影响较大;随水合物饱和度的增加而增加,但当水合物作为孔隙充填物时,水合物只影响纵波速度,而对横波速度没影响。
除水合物饱和度外,沉积物的孔隙度对纵横波速度的影响也较大,而矿物组分相对较低。因此,在构建约束优化函数时将矿物组分作为已知变量,而将饱和度和孔隙度作为优化变量,以寻找最优解。
利用信赖域算法求解了构建的约束优化问题,该算法具有收敛速度快、计算结果可靠的特点。神狐海域的钻井资料证实预测结果与实际资料相吻合,说明优化计算结果可靠,验证了方法正确性。
| [1] |
Makogon Y F, Holditch S A, Makogon T Y. Natural gas-hydrates:A potential energy source for the 21st century[J]. Journal of Petroleum Science & Enginee-ring, 2007, 56(1): 14-31. |
| [2] |
张光学, 张明, 杨胜雄, 等. 海洋天然气水合物地震检测技术及其应用[J]. 海洋地质与第四纪地质, 2011, 31(4): 51-58. ZHANG Guangxue, ZHANG Ming, YANG Sheng-xiong, et al. Application of seismic detecting technique to marine gas hydrate sea[J]. Marine Geology & Quaternary Geology, 2011, 31(4): 51-58. |
| [3] |
勾丽敏, 张金华, 王嘉玮. 海洋天然气水合物地震识别方法研究进展[J]. 地球物理学进展, 2017, 32(6): 2626-2635. GOU Limin, ZHANG Jinhua, WANG Jiawei. Progress in seismic identification approach of marine gas hydrate[J]. Progress in Geophysics, 2017, 32(6): 2626-2635. |
| [4] |
徐华宁, 杨胜雄, 郑晓东, 等. 南中国海神狐海域天然气水合物地震识别及分布特征[J]. 地球物理学报, 2010, 53(7): 1691-1698. XU Huaning, YANG Shengxiong, ZHENG Xiaodong, et al. Seismic identification of gas hydrate and its distribution in Shenhu area, South China Sea[J]. Chinese Journal of Geophysics, 2010, 53(7): 1691-1698. DOI:10.3969/j.issn.0001-5733.2010.07.020 |
| [5] |
宋海斌, Osamu M, 杨胜雄, 等. 含天然气水合物沉积物的岩石物性模型与似海底反射层的AVA特征[J]. 地球物理学报, 2002, 45(4): 546-556. SONG Haibin, Osamu M, YANG Shengxiong, et al. Physical property models of gas hydrate-bearing sediments and AVA character of bottom simulating re-flector[J]. Chinese Journal of Geophysics, 2002, 45(4): 546-556. DOI:10.3321/j.issn:0001-5733.2002.04.012 |
| [6] |
刘洁, 张建中, 孙运宝, 等. 南海神狐海域天然气水合物储层参数测井评价[J]. 天然气地球科学, 2017, 28(1): 164-172. LIU Jie, ZHANG Jianzhong, SUN Yunbao, et al. Gas hydrate reservoir parameter evaluation using logging data in the Shenhu area, South China Sea[J]. Natural Gas Geoscience, 2017, 28(1): 164-172. |
| [7] |
徐华宁, 张光学, 郑晓东, 等. 井震联合分析预测神狐海域天然气水合物可能的垂向分布[J]. 地球物理学报, 2014, 57(10): 3363-3372. XU Huaning, ZHANG Guangxue, ZHENG Xiao-dong, et al. Integrated analysis of well logs and seismic data to deduce the possible distribution in depth of gas hydrate in Shenhu Area, South China Sea[J]. Chinese Journal of Geophysics, 2014, 57(10): 3363-3372. DOI:10.6038/cjg20141023 |
| [8] |
Ghosh R, Sain K, Ojha M. Estimating the amount of gas-hydrate using effective medium theory:a case study in the blake ridge[J]. Marine Geophysical Researches, 2010, 31(1/2): 29-37. |
| [9] |
郭依群, 乔少华, 吕万军. 基于声波速度分析神狐海域水合物垂向分布特征[J]. 海洋地质前沿, 2011, 27(7): 7-12. GUO Yiqun, QIAO Shaohua, LYU Wanjun. Vertical distribution of gas hydrate in Shenhu area of the South China Sea based on acoustic velocity[J]. Marine Geology Frontiers, 2011, 27(7): 7-12. |
| [10] |
冯凯, 李敏锋, 刘竣川, 等. 天然气水合物和游离气层的弹性参数异常特征及其在饱和度估算中的应用[J]. 石油地球物理勘探, 2008, 43(4): 430-436. FENG Kai, LI Minfeng, LIU Junchuan, et al. Anomalous feature of elastic parameters in sediments with gas-hydrate and free gas and application in estimation of saturation[J]. Oil Geophysical Prospecting, 2008, 43(4): 430-436. DOI:10.3321/j.issn:1000-7210.2008.04.014 |
| [11] |
潘豪杰, 张研, 李红兵, 等. 基于贝叶斯理论的天然气水合物储层弹性-电性数据联合反演[J]. 石油地球物理勘探, 2018, 53(3): 568-577, 586. PAN Haojie, ZHANG Yan, LI Hongbing, et al. Joint inversion of elastic-electrical data for gas hydrate re-servoirs based on Bayesian theory[J]. Oil Geophysical Prospecting, 2018, 53(3): 568-577, 586. |
| [12] |
肖昆, 邹长春, 邓居智, 等. 利用声波测井估算裂缝型水合物储层水合物饱和度[J]. 石油地球物理勘探, 2017, 52(5): 1067-1076. XIAO Kun, ZOU Changchun, DENG Juzhi, et al. Gas hydrate saturation estimation in fractured reservoirs with acoustic logging[J]. Oil Geophysical Prospecting, 2017, 52(5): 1067-1076. |
| [13] |
凌东明, 杜启振, 田军, 等. 基于岩相约束的Xu-White模型线性化近似与反演[J]. 石油地球物理勘探, 2019, 54(3): 577-586. LING Dongming, Du Qizhen, Tian Jun, et al. The Xu-White model linearized approximation and inversion based on lithofacies constraint[J]. Oil Geophysical Prospecting, 2019, 54(3): 577-586. |
| [14] |
Ecker C, Dvorkin J, Nur A M. Estimating the amount of gas hydrate and free gas from marine seismic data[J]. Geophysics, 2000, 65(2): 565-573. DOI:10.1190/1.1444752 |
| [15] |
Lee M R, Hutchinson D R, Collett T S, et al. Seismic velocities for hydrate-bearing sediments using weighted equation[J]. Journal of Geophysical Research, 1996, 101(B9): 20347-22035. DOI:10.1029/96JB01886 |
| [16] |
Helgerud M B, Dvorkin J, Nur A, et al. Elastic-wave velocity in marine sediments with gas hydrates:Effective medium modeling[J]. Geophysical Research Letters, 1999, 26(13): 2021-2024. DOI:10.1029/1999GL900421 |
| [17] |
Dvorkin J, Prasad M, Sakai A, et al. Elasticity of marine sediments:Rock physics modeling[J]. Geophysical Research Letters, 1999, 26(12): 1781-1784. DOI:10.1029/1999GL900332 |
| [18] |
刘欣欣, 印兴耀, 栾锡武. 天然气水合物地层岩石物理模型构建[J]. 中国科学:地球科学, 2018, 48(9): 1248-1266. LIU Xinxin, YIN Xingyao, LUAN Xiwu. Seismic rock physical modelling for gas hydrate-bearing sediments[J]. Science China:Earth Sciences, 2018, 48(9): 1248-1266. |
| [19] |
郭依群, 杨胜雄, 梁金强, 等. 南海北部神狐海域高饱和度天然气水合物分布特征[J]. 地学前缘, 2017, 24(4): 24-31. GUO Yiqun, YANG Shengxiong, LIANG Jinjiang, et al. Characteristics of high gas hydrate distribution in the Shenhu area on the northern slope of the South China Sea[J]. Earth Science Frontiers, 2017, 24(4): 24-31. |
| [20] |
Carcione J M, Tinivella U. Bottom-simulating reflectors:Seismic velocities and AVO effects[J]. Geophy-sics, 2000, 65(1): 54-67. |
| [21] |
Leclaire P, Cohen-Ténoudji F, Aguirre-Puente J. Extension of Biot's theory of wave propagation to frozen porous media[J]. The Journal of the Acoustical Society of America, 1994, 96(6): 3753-3768. DOI:10.1121/1.411336 |
| [22] |
Lee M W. Modified Biot-Gassmann theory for calculating elastic velocities for unconsolidated and consolidated sediments[J]. Marine Geophysical Researches, 2002, 23(5/6): 403-412. DOI:10.1023/B:MARI.0000018195.75858.12 |
| [23] |
高红艳, 钟广法, 梁金强, 等. 应用改进的Biot-Gas-smann模型估算天然气水合物的饱和度[J]. 海洋地质与第四纪地质, 2012, 32(4): 83-89. GAO Hongyan, ZHONG Guangfa, LIANG Jinjiang, et al. Estimation of gas hydrate saturation with modified Biot-Gassmann theory:a case from Northern South China Sea[J]. Marine Geology & Quaternary Geology, 2012, 32(4): 83-89. |
| [24] |
孙春岩, 章明昱, 牛滨华, 等. 天然气水合物地震似海底反射现象AVO正演模型研究[J]. 现代地质, 2003, 17(3): 337-344. SUN Chunyan, ZHANG Mingyu, NIU Binhua, et al. Study of modeling seismic bottom simulating reflector for nature gas hydrate[J]. Geoscience, 2003, 17(3): 337-344. DOI:10.3969/j.issn.1000-8527.2003.03.016 |
| [25] |
潘豪杰, 刘堂晏, 邬龙, 等. 天然气水合物赋存形态识别及其饱和度预测[J]. 地球物理学进展, 2014, 29(4): 1735-1740. PAN Haojie, LIU Tangyan, WU Long, et al. Morphology identification and saturation estimation of gas hydrate[J]. Progress in Geophysics, 2014, 29(4): 1735-1740. |
| [26] |
张如伟, 李洪奇, 文鹏飞, 等. 海洋含水合物沉积层的速度频散与衰减特征分析[J]. 地球物理学报, 2016, 59(9): 3417-3427. ZHANG Ruwei, LI Hongji, WEN Pengfei, et al. The velocity dispersion and attenuation of marine hydrate bearing sediments[J]. Chinese Journal of Geophysics, 2016, 59(9): 3417-3427. |
| [27] |
张如伟, 张宝金, 黄捍东, 等. 天然气水合物沉积层的AVA特征[J]. 石油地球物理勘探, 2011, 46(4): 634-639. ZHANG Ruwei, ZHANG Baojin, HUANG Handong, et al. AVA characters on gas hydrate-bearing sedi-mentary[J]. Oil Geophysical Prospecting, 2011, 46(4): 634-639. |
| [28] |
Waite W F, Santamarina J C, Cortes D, et al. Physical properties of hydrate-bearing sediments[J]. Reviews of Geophysics, 2009, 47(4): 465-484. |
| [29] |
陈玉凤, 梁德青, 吴能友. 南海神狐海域水合物对岩心电阻率的影响[J]. 石油地球物理勘探, 2018, 53(6): 1241-1246. CHEN Yufeng, LIANG Deqing, WU Nengyou. Resistivity characteristics of core samples containing natural gas hydrate in Shenhu Area, the South China Sea[J]. Oil Geophysical Prospecting, 2018, 53(6): 1241-1246. |
| [30] |
Nur A, Mavko G, Dvorkin J, et al. Critical porosity:A key to relating physical properties to porosity in rocks[J]. The Leading Edge, 1998, 17(3): 357-362. DOI:10.1190/1.1437977 |
| [31] |
Murphy W F.Effects of Microstructure and Pore Fluids on the Acoustic Properties of Granular Materials[D].Stanford University, Dissertation, 1982.
|
| [32] |
Hill R. The elastic behavior of a crystalline aggregate[J]. Proceedings of the Physical Society, 1952, 65(5): 349-354. DOI:10.1088/0370-1298/65/5/307 |
| [33] |
张秉铭, 刘致水, 刘俊州, 等. 富有机质泥页岩岩石物理横波速度预测方法研究[J]. 石油物探, 2018, 57(5): 658-667. ZHANG Bingming, LIU Zhishui, LIU Junzhou, et al. A new S-wave velocity estimation method for organic-enriched shale[J]. Geophysical Prospecting for Petroleum, 2018, 57(5): 658-667. DOI:10.3969/j.issn.1000-1441.2018.05.004 |
| [34] |
Lee M W. Elastic velocities of partially gas-saturated unconsolidated sediments[J]. Marine and Petroleum Geology, 2004, 21(6): 641-650. DOI:10.1016/j.marpetgeo.2003.12.004 |
| [35] |
王秀娟, 吴时国, 刘学伟, 等. 基于电阻率测井的天然气水合物饱和度估算及估算精度分析[J]. 现代地质, 2010, 24(5): 993-999. WANG Xiujuan, WU Shiguo, LIU Xuewei, et al. Estimation of gas hydrate saturation based on resistivity logging and analysis of estimation error[J]. Geoscience, 2010, 24(5): 993-999. DOI:10.3969/j.issn.1000-8527.2010.05.022 |
| [36] |
Branch M A, Coleman T F, Li Y Y. A subspace, interior, and conjugate gradient method for large-scale bound-constrained minimization problems[J]. SIAM Journal on Scientific Computing, 1999, 21(1): 1-23. DOI:10.1137/S1064827595289108 |
| [37] |
林恬, 孟小红, 张致付. 基于约束最小二乘与信赖域的储层参数反演方法[J]. 地球物理学报, 2017, 60(10): 3969-3983. LIN Tian, MENG Xiaohong, ZHANG Zhifu. The petrophysical parameter inversion method based on constrained least squares and trust region approach[J]. Chinese Journal of Geophysics, 2017, 60(10): 3969-3983. DOI:10.6038/cjg20171024 |
| [38] |
潘克家, 汤井田, 杜华坤, 等. 轴对称地层中高分辨率阵列侧向测井信赖域反演法[J]. 地球物理学报, 2016, 59(8): 3110-3120. PAN Kejia, TANG Jingtian, DU Huakun, et al. Trust region inversion algorithm of high-resolution array lateral logging in axisymmetric formation[J]. Chinese Journal of Geophysics, 2016, 59(8): 3110-3120. |



 孟大江, 广东省广州市黄埔区广海路188号海洋地质办公楼广州海洋地质调查局资料处理研究所, 510075。Email:
孟大江, 广东省广州市黄埔区广海路188号海洋地质办公楼广州海洋地质调查局资料处理研究所, 510075。Email: