页岩气水平井布设和碳酸盐岩缝洞储层预测等对地震资料深度域成像精度提出了更高的要求[1-4]。地下介质普遍呈各向异性[5-9],传统的各向同性叠前深度偏移成像结果与真实界面深度不符。为了消除这种井震误差,VTI各向异性叠前深度偏移技术得到了广泛的使用[10-18]。但VTI介质假设地层产状水平,与实际情况不符。TTI各向异性处理在参数提取和偏移的过程中充分考虑了地层的倾角和方位角信息,与实际情况更接近,因而反射界面归位更准确[19]。目前TTI各向异性参数建模与叠前深度偏移技术已逐渐成为了主流的处理手段。本文对传统的TTI各向异性参数建模结果分析发现,在地层厚度变化剧烈的情况下,反演得到的vP0和δ会出现畸变,vP0和δ体的取值明显与地层厚度的变化相关。为了避免这种不合理现象,本文提出了一种优化的TTI各向异性参数提取方法。
通过基于δ的井震误差插值方法将地层厚度信息引入各向异性参数反演流程,使反演结果更加精确。
1 传统TTI各向异性建模方法TI介质中不同方向上传播的地震波速度与各向异性参数之间的关系[5]为
| $ v_{\mathrm{P}}(\theta)=v_{\mathrm{P0}}\left(1+\delta \sin ^{2} \theta \cos ^{2} \theta+\varepsilon \sin ^{4} \theta\right) $ | (1) |
式中:vP0、δ和ε为各向异性参数;θ为传播方向与各向异性介质对称轴之间的夹角。由式(1)可知,当波以中、小角度入射时,波速主要由vP0和δ决定。在实际地震勘探中,大多数入射角都处于中、小角度范围,通过各向同性网格层析反演得到的速度是沿中小角度传播的速度的综合体现。在实际生产中,δ一般取正值,此时各向同性层速度viso一般大于vP0。所以各向同性深度偏移的成像深度一般会大于实际地层深度,并且随着深度的增加,井震误差会逐渐增大。在层析反演迭代过程中,随着各向异性参数(vP0和δ)精度的提高,井震深度误差会逐渐消失。
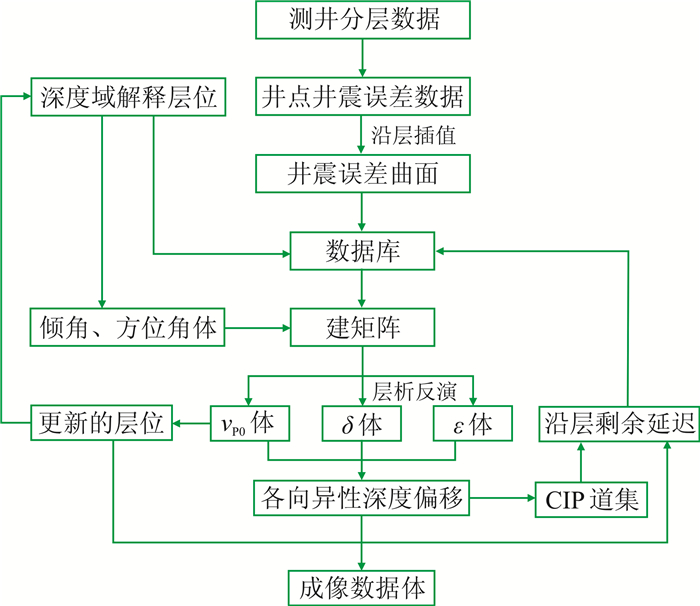
1.1 传统TTI各向异性建模流程传统的TTI各向异性建模流程如图 1所示,总体上采取先反演vP0和δ,再单独反演ε的思路。其详细步骤如下。
|
图 1 传统的TTI各向异性建模流程 |
(1) 输入各向同性深度域解释层位,并提取地层倾角和方位角,得到倾角、方位角属性体。
(2) 输入测井分层数据(Marker),并求取其与深度域解释层位之间的深度误差(Mistie)。
(3) 根据井位处的井震误差,沿层插值,求出整个工区范围内每层的井震误差。
(4) 将井震误差数据、深度域解释层位和各向同性深度域速度汇总至数据库并与倾角、方位角属性体结合,建立网格层析反演矩阵。
(5) 假设ε=δ,通过网格层析反演得到vP0、δ和ε体。
(6) 用vP0和δ更新解释层位的深度,并与井Marker值做对比。若井与地震分层信息还存在误差,则回到第二步,开始迭代。井信息与地震分层完全匹配后,利用倾角、方位角属性体、vP0、δ和ε体进行TTI各向异性叠前深度偏移,得到共成像点(CIP)道集。若CIP道集未被拉平,则转到步骤(8)。
(7) 在CIP道集上沿层拾取剩余延迟,将剩余延迟信息、深度域层位与各向异性参数模型输入到层析反演模块中,更新ε体。
(8) 利用更新后的各向异性参数模型进行TTI各向异性深度偏移,判断CIP道集是否拉平。若未拉平,则重复步骤(7)。若同相轴被拉平则输出最终的成像数据体。
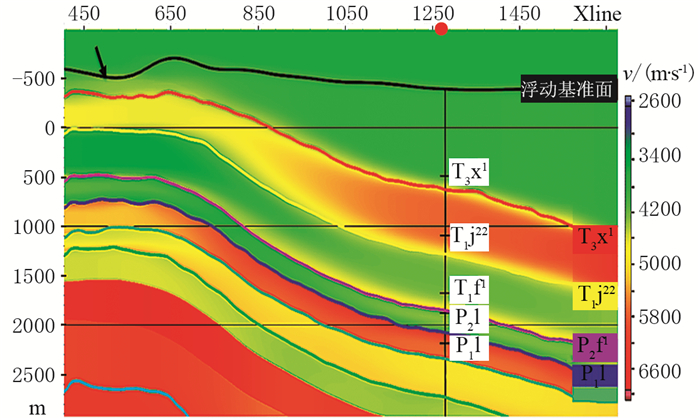
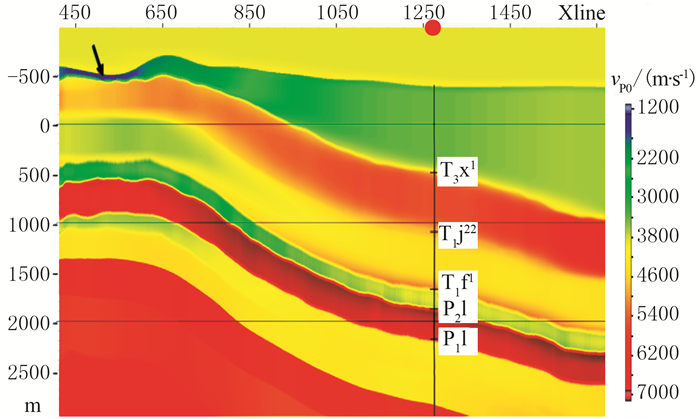
1.2 井震误差插值方法的缺陷各向异性参数建模流程中对井点位置的井震误差进行插值是非常重要的一步,因为井数据信息是求取各向异性参数的关键。然而井的分布一般比较稀疏,这就需要对井点位置的井震误差进行插值来预测其他位置的深度误差,从而求得全工区范围内的各向异性参数。但这种插值方法未考虑地层厚度变化对参数提取结果的影响。图 2为威远X三维工区过井线的各向同性深度域层速度、解释层位和测井分层的叠合显示。可以看到测井分层的第一层(须家河组底,红色曲线)与浮动基准面(黑色曲线)间的厚度较大,但由于地层上倾,该层最薄处仅有158m(黑色箭头所示),并且此处附近没有井信息。图 3为传统流程提取的vP0体,可以看到在地层变薄处,第一层的vP0出现异常,最小仅有1200m/s(黑色箭头所示),并且vP0的横向变化与层厚明显相关。分析认为,这是传统TTI各向异性建模流程中对井震误差直接插值造成的。井位处的井震误差为-137.8m,这是波经过1018m厚的各向异性地层时产生的深度误差。而对井震误差的直接插值使得地层最薄处的井震误差也约为-130m,但此处地层厚度仅为158m,导致后续反演出的各向异性参数出现异常。因此层析反演求取各向异性参数时要综合考虑地层厚度和井震误差,所以在对井震误差插值时也应该引入层厚信息。
|
图 2 各向同性深度域层速度、解释层位和测井分层的叠合 |
|
图 3 传统流程提取的TTI各向异性参数vP0剖面 |
在井震深度误差信息插值过程中加入层厚信息可以通过求取井震误差与层厚的比值实现。井震误差只存在于井位处,而层厚信息存在于整个工区。因此,首先提取出井位处的层厚信息,求出井位处每层的井震误差与层厚的比值(Scale)。以须家河组底界面为例,工区内六口井的相关信息如表 1所示。然后选用合适的插值方式对Scale进行插值,如最小曲率法插值或克里金插值方法。最后用Scale面与层厚曲面相乘得到井震误差曲面。此时的井震误差曲面中同时含有了井震误差和层厚的趋势信息,并且在井位处井震误差曲面的取值与实际值相等。
|
|
表 1 须家河组底的井震误差、层厚和Scale信息 |
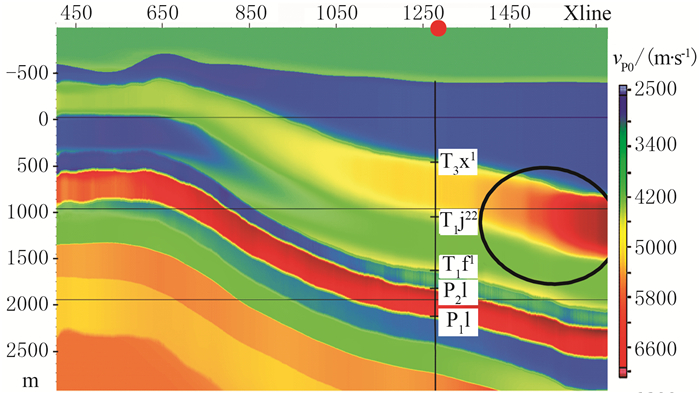
利用基于层厚的插值方法得到的井震误差曲面反演各向异性vP0参数模型,结果如图 4所示。可以看到图 4中第一层层厚变薄处的vP0没有出现畸变,并且速度的取值也未随层厚变化。但第二层(嘉陵江二段)的大号端(黑色圆圈处)速度出现异常。经过反演后速度取值变大,最大处取值超过7500m/s。这是由于基于层厚的插值方法仅考虑本层的厚度。但在第一层厚度变化剧烈而第二层厚度变化较小时,上一层的厚度变化也会对该层的井震误差取值产生影响。所以在对井震误差进行插值时不仅要考虑本层的层厚信息,还要考虑上一层的厚度或井震误差信息。
|
图 4 基于层厚插值方法反演的各向异性参数vP0剖面 |
经过分析可知,对井震误差进行插值本质上是为了求取各向异性参数变化的趋势,合理的做法是将各向异性参数的取值引入到插值过程中。δ的估算公式[20-22]为
| $ \delta^{i}=\frac{1}{2}\left[\left(\frac{D_{\mathrm{S}}^{i}}{D_{\mathrm{w}}^{i}}\right)^{2}-1\right] $ | (2) |
式中:DSi为各向同性深度偏移获得的第i层厚度;DWi为第i层实际厚度。实际地层厚度可由测井分层深度求出,即
| $ D_{\mathrm{w}}^{i}=H_{\mathrm{w}}^{i}-H_{\mathrm{w}}^{i-1} $ | (3) |
式中HWi-1和HWi分别为第i层顶、底测井分层深度。井位分层与地震解释层位的深度关系为
| $ H_{\mathrm{w}}^{i}=H_{\mathrm{S}}^{i}+M_{\mathrm{S}}^{i} $ | (4) |
式中:HSi为地震解释深度;MSi为井震误差。将式(3)和式(4)代入式(2),可得
| $ \delta^{i}=\frac{1}{2\left(1+\frac{M_{\mathrm{S}}^{i}-M_{\mathrm{S}}^{i-1}}{D_{\mathrm{S}}^{i}}\right)^{2}}-\frac{1}{2} $ | (5) |
由式(5)可知,δ随位置的变化仅与
| $ M_{\mathrm{S}}^{i}=S_{\delta}^{i} D_{\mathrm{S}}^{i}+M_{\mathrm{S}}^{i-1} $ | (6) |
值得注意的是,沿层厚插值方法的插值对象是
图 5为基于δ的井震误差插值流程,总体思路是自上而下逐层求取井震误差曲面,并将该层的井震误差输入到下一层的求取过程中。将此流程引入TTI各向异性建模流程中则可形成优化的TTI各向异性参数建模流程。

|
图 5 基于δ的井震误差插值流程 |
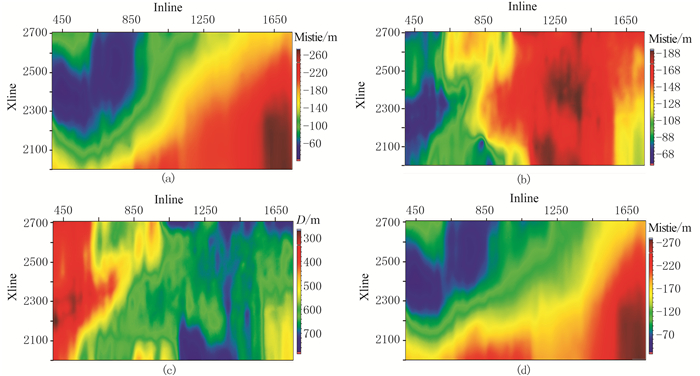
表 2为井位处第二层(嘉陵江组二段)底的井震误差(MT1j22)、层厚(DT1j22)、上一层的井震误差(MT3x1)及计算得到的SδT1j22信息。对SδT1j22进行插值,并代入式(6)可以得到MT1j22曲面。图 6a为基于δ插值计算的MT1j22,图 6b为基于层厚插值计算的MT1j22。可见,基于层厚插值结果的趋势仅与该层的层厚(图 6c)和井间的井震误差变化相关。而基于δ插值结果的趋势是层厚、井间的井震误差变化和上一层的井震误差(图 6d)综合作用的结果。
|
|
表 2 井位处的T1j22层参数 |
|
图 6 基于不同参数插值的效果效果分析 (a)基于δ插值的T1j22层Mistie曲面;(b)基于层厚插值的T1j22层Mistie曲面;(c)T1j22层厚度;(d)基于δ插值的T3x1层Mistie曲面 |
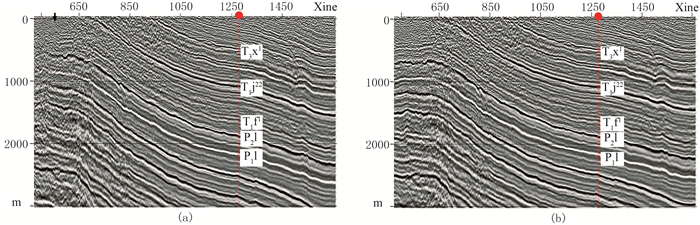
图 7为优化的TTI各向异性参数建模流程反演的各向异性vP0参数模型,可见图 4黑色圆圈中的第二层速度异常已被消除。此外,层内的速度取值也更为均匀(如黑色箭头所指的层)。此时,层内速度的变化仅与各向同性层速度趋势以及井间井震误差趋势相关,而与该层以及上覆层的厚度无关。因此优化的各向异性参数建模方法得到的模型更为精确、可靠。图 8为使用传统和优化后流程得到的偏移剖面。箭头所指处为传统流程vP0模型出现畸变的位置(图 2)。传统流程得到的各向异性参数模型受地层厚度变化趋势的影响,其偏移剖面虽然在井位处与钻井吻合,但地层产状并不合理。优化后的流程在求取各向异性参数模型时使用了基于δ的插值方法,有效避免了层厚对各向异性参数取值的影响,所以其偏移剖面的地层产状更为可靠。

|
图 7 基于δ的插值方法反演的各向异性参数vP0剖面 |
|
图 8 传统(a)和优化后流程(b)各向异性参数偏移剖面 |
各向异性参数建模流程中对井震误差的插值是一个关键的步骤。传统各向异性参数建模流程中,由于插值方法的缺陷,在地层厚度突变时会造成各向异性参数的畸变,并且在通常情况下,传统流程得到的各向异性参数模型取值与地层厚度有明显的相关性。本文提出了一种基于δ的井震误差插值方法,并将该方法引入各向异性参数建模流程中,实现了各向异性参数建模方法的优化。实际资料处理结果表明,该优化各向异性参数建模方法可以有效避免地层厚度突变带来的各向异性参数畸变问题,并且其模型取值与地层厚度变化无关,因而更为精确、合理。
| [1] |
罗鑫, 匡建超, 瞿子易, 等. 济阳拗陷埕北306-桩海10下古生界缝洞型储层横向预测[J]. 石油地球物理勘探, 2010, 45(4): 571-576. LUO Xin, KUANG Jianchao, QU Ziyi, et al. Lateral prediction of Lower Paleozoic fractured-vuggy reservoir in Chengbei 306-Zhuanghai 10 area[J]. Oil Geophysical Prospecting, 2010, 45(4): 571-576. |
| [2] |
李凡异, 狄帮让, 魏建新, 等. 溶洞体宽度对偏移剖面反射振幅影响的定量研究[J]. 岩性油气藏, 2016, 28(5): 113-116. LI Fanyi, DI Bangrang, WEI Jianxin, et al. Quantitative study of the effect of cavern width on reflection amplitude of migration section[J]. Lithologic Reservoirs, 2016, 28(5): 113-116. DOI:10.3969/j.issn.1673-8926.2016.05.014 |
| [3] |
王卫, 王佳琦, 古茜. 井震联合构建三维地质导向模型关键技术研究[J]. 录井工程, 2018, 29(2): 27-31. WANG Wei, WANG Jiaqi, GU Xi. Research on key technologies of joint construction of three-dimensional geological guidance model by well and seismology[J]. Mud Logging Engineering, 2018, 29(2): 27-31. DOI:10.3969/j.issn.1672-9803.2018.02.007 |
| [4] |
郭伟. 四川威远区块页岩气水平井产量差异分析[J]. 科学技术与工程, 2018, 18(1): 228-233. GUO Wei. Differetiation analysis on shale gas production of the horizontal wells in Sichuan Weiyuan Block[J]. Science Technology and Engineering, 2018, 18(1): 228-233. DOI:10.3969/j.issn.1671-1815.2018.01.040 |
| [5] |
Thomsen L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [6] |
Isaac J H, Lawton D C. Image mispositioning due to dipping TI media:A physical seismic modeling study[J]. Geophysics, 1999, 64(4): 1230-1238. DOI:10.1190/1.1444629 |
| [7] |
谢剑勇, 魏建新, 狄帮让, 等. 页岩各向异性参数间关系及其影响因素分析[J]. 石油地球物理勘探, 2015, 50(6): 1141-1145. XIE Jianyong, WEI Jianxin, DI Bangrang, et al. Correlation of shale anisotropic parameters and their influence factors[J]. Oil Geophysical Prospecting, 2015, 50(6): 1141-1145. |
| [8] |
韩冰凯, 顾汉明, 刘少勇. TI介质带限射线束传播及偏移方法[J]. 石油地球物理勘探, 2018, 53(2): 297-303, 310. HAN Bingkai, GU Hanming, LIU Shaoyong. Band-limited beam propagation and migration in TI media[J]. Oil Geophysical Prospecting, 2018, 53(2): 297-303, 310. |
| [9] |
刘财, 邓馨卉, 郭智奇, 等. 基于岩石物理的页岩储层各向异性表征[J]. 石油地球物理勘探, 2018, 53(2): 339-346. LIU Cai, DENG Xinhui, GUO Zhiqi, et al. Shale reservoir anisotropic characterization based on rock physics[J]. Oil Geophysical Prospecting, 2018, 53(2): 339-346. |
| [10] |
刁文川, 刘哲生, 蔡希玲, 等. 浅述地震各向异性[J]. 石油地球物理勘探, 2007, 42(增刊): 106-110, 123. DIAO Wenchuan, LIU Zhesheng, CAI Xiling, et al. Brief talk about seismic anisotrpy[J]. Oil Geophysical Prospecting, 2007, 42(S): 106-110, 123. |
| [11] |
赵玲芝, 王克斌, 戴晓云. VTI各向异性叠前深度偏移技术应用研究——以JZ工区三维地震资料处理为例[J]. 石油地球物理勘探, 2011, 50(2): 201-205. ZHAO Lingzhi, WANG Kebin, DAI Xiaoyun. Application of VTI anisotropic pre-stack depth migration technique for 3D seismic data processing in JZ area[J]. Oil Geophysical Prospecting, 2011, 50(2): 201-205. |
| [12] |
刘瑞合, 赵金玉, 印兴耀, 等. VTI介质各向异性参数层析反演策略与应用[J]. 石油地球物理勘探, 2017, 52(3): 484-490. LIU Ruihe, ZHAO Jinyu, YIN Xingyao, et al. Strategy of anisotropic parameter tomography inversion in VTI medium[J]. Oil Geophysical Prospecting, 2017, 52(3): 484-490. |
| [13] |
朱峰, 黄建平, 李振春. 黏声VTI介质傅里叶有限差分叠前深度偏移[J]. 石油地球物理勘探, 2017, 52(5): 956-966. ZHU Feng, HUANG Jianping, LI Zhenchun. FFD prestack depth migration for viscoacoustic VTI medium[J]. Oil Geophysical Prospecting, 2017, 52(5): 956-966. |
| [14] |
韩建光, 王赟, 张晓波, 等. VTI介质高斯束叠前深度偏移[J]. 石油地球物理勘探, 2015, 50(2): 267-273. HAN Jianguang, WANG Yun, ZHANG Xiaobo, et al. Gaussian beam prestack depth migration in VTI media[J]. Oil Geophysical Prospecting, 2015, 50(2): 267-273. |
| [15] |
张洪宙, 王彦飞. VTI介质迭代正则化偏移反演算法[J]. 石油地球物理勘探, 2014, 49(6): 1083-1090. ZHANG Hongzhou, WANG Yanfei. Iterative regula-rization migration inversion in VTI media[J]. Oil Geophysical Prospecting, 2014, 49(6): 1083-1090. |
| [16] |
王琦, 李庆春, 王芷琪. VTI介质起伏界面混合网格旅行时线性插值计算方法[J]. 石油地球物理勘探, 2018, 53(6): 1175-1187. WANG Qi, LI Qingchun, WANG Zhiqi. A linear tra-veltime interpolation method with hybrid meshes for VTI medium under rugged interface conditions[J]. Oil Geophysical Prospecting, 2018, 53(6): 1175-1187. |
| [17] |
张凯, 陈军屹, 祝佰航, 等. 基于程函方程的VTI介质初至波走时层析反演[J]. 石油地球物理勘探, 2018, 53(6): 1218-1226. ZHANG Kai, CHEN Junyi, ZHU Baihang, et al. First break traveltime tomographic imaging based on the eikonal equation in VTI medium[J]. Oil Geophysical Prospecting, 2018, 53(6): 1218-1226. |
| [18] |
肖建恩, 李振春, 张凯, 等. TI介质角度域高斯束逆时偏移方法[J]. 石油地球物理勘探, 2019, 54(5): 1067-1074. XIAO Jian'en, LI Zhenchun, ZHANG Kai, et al. Angle-domain reverse time migration with Gaussian beams for TI media[J]. Oil Geophysical Prospecting, 2019, 54(5): 1067-1074. |
| [19] |
王伟国, 熊水金, 徐华宁, 等. TTI介质各向异性伪谱法逆时偏移[J]. 石油地球物理勘探, 2012, 47(4): 566-572. WANG Weiguo, XIONG Shuijin, XU Huaning, et al. Reverse-time migration using pseudo-spectral method for tilted TI media[J]. Oil Geophysical Prospecting, 2012, 47(4): 566-572. |
| [20] |
刘茂诚. 一个各向异性速度分析应用实例[J]. 石油地球物理勘探, 2010, 45(4): 525-529. LIU Maocheng. An application case study for anisotropic velocity analysis[J]. Oil Geophysical Prospecting, 2010, 45(4): 525-529. |
| [21] |
韩令贺, 胡自多, 冯会元, 等. 井震联合网格层析各向异性速度建模研究及应用[J]. 岩性油气藏, 2018, 30(4): 91-97. HAN Linghe, HU Ziduo, FENG Huiyuan, et al. Grid tomography based on well-to-seismic integration in anisotropic velocity modeling and its application[J]. Lithologic Reservoirs, 2018, 30(4): 91-97. |
| [22] |
裴云龙, 王立歆, 邬达理, 等. 井控各向异性速度建模技术在YKL地区的应用[J]. 石油物探, 2017, 56(3): 390-399. PEI Yunlong, WANG Lixin, WU Dali, et al. The application of well-controlled anisotropy velocity mode-ling in YKL region[J]. Geophysical Prospecting for Petroleum, 2017, 56(3): 390-399. DOI:10.3969/j.issn.1000-1441.2017.03.009 |



 杨宗青, 四川省成都市天府新区华阳大道一段216号东方地球物理公司西南物探研究院处理一室, 610000。Email:
杨宗青, 四川省成都市天府新区华阳大道一段216号东方地球物理公司西南物探研究院处理一室, 610000。Email: