② 海洋石油勘探国家工程实验室, 北京 100028
② National Engineering Laboratory for Offshore Oil Exploration, Beijing 100028, China
宽频地震资料频带宽、子波旁瓣小,有利于深部复杂构造、小圈闭的成像[1-2],能为解释及反演提供更可靠、更优质的基础地震数据[3]。近年来海上宽频地震勘探技术在深水区取得了较大的进展,但是在浅水区进展缓慢,尤其像渤海平均水深不超过30m的浅水海域,变深度缆宽频采集难以实施,只有通过常规采集、宽频处理才有可能实现这一目的。对于浅水区,地震资料不但受到鬼波的影响,还受到浅水多次波的影响,浅水多次波引起的陷频效应甚至大于鬼波影响,因此要实现浅水资料宽频处理必须去除鬼波及浅水多次波的影响。
针对拖缆资料的鬼波压制方法较多,例如在偏移过程中实现鬼波的压制方法[4-6]、基于Bootstrap的鬼波压制方法[7]、混合范数联合反褶积的鬼波压制方法[8]、基于逆散射级数的鬼波压制方法[9]、τ-p域鬼波压制方法[10]、基于格林函数理论的鬼波压制方法[11]、基于波场延拓和反演的鬼波压制方法[12]、基于波场外推和阈值截断的鬼波压制方法[13]、基于最小平方残差的鬼波压制方法[14]、基于子波处理的鬼波压制技术[15]等。相对于深水海域环境下的鬼波,浅水资料不同炮检距、不同目的层反射波所产生的鬼波入射角变化范围更大,即浅水海域条件下的鬼波时空变更加剧烈。
浅水环境下产生的多次波阶数通常较高,并覆盖整个地震剖面,因此在有效压制鬼波的同时需要较好地压制浅水多次波。目前浅水多次波压制技术较多,如:基于多道预测的浅水多次波压制技术(SWD)[16]、基于水层模型驱动的浅水多次波压制技术(MWD)[17]、基于τ-p域水体驱动的浅水多次波压制技术[18-19]、基于克希霍夫衍射理论的浅水多次波压制技术[20]、基于交替分裂Bregman迭代算法多道预测反褶积的浅水多次波压制技术[21]等。其中模型驱动的方法应用最广,但需要较为准确的海底模型。通常通过对海底进行深度域成像或者通过近道叠加自相关拾取浅水多次波周期建立海底深度模型,利用该模型进行浅水多次波预测及压制。但对于像渤海这样平均水深不超过30m的浅水海域,且采集时近炮检距数据缺失,海底基本无法成像,海底模型难以建立。另外,近道叠加对浅水多次波的周期改变严重,利用近道叠加自相关计算的海底模型精度不高、浅水多次波压制效果不佳。
目前针对深水区变深度缆采集资料的宽频处理关键技术[22-24]及常规采集资料宽频处理关键技术[25-26]建立了相对比较完整的技术体系及流程,针对浅水区的宽频处理关键技术研究相对较少,且多集中在近百米水深的浅水区[24, 27];针对像渤海这样平均水深不超过30m的浅水海域条件下的宽频地震资料处理研究就更少。
本文针对渤海海域鬼波时空变剧烈的问题,研究了τ-p域自适应参数估计的鬼波压制技术、有效解决鬼波时空变剧烈及枪深、缆深、海面不恒定的问题;针对渤海海域海底模型难以建立、浅水多次波压制困难的问题,研究了τ-p域自适应海底深度估计的浅水多次波压制技术。将本文研究的两项关键技术与常规处理相结合,实现了渤海海域浅水资料宽频处理的目的。
1 τ-p域自适应参数估计的鬼波压制技术 1.1 τ-p域鬼波压制原理为了方便,仅以电缆鬼波为例说明τ-p域鬼波压制方法。鬼波是有效波(上行波)被接收后继续向上传播经过海面反射(下行波)被再次接收。地震数据经过τ-p变换后,同一个p参数对应着具有相同传播角度的平面波,沿τ轴上、下行波的延迟时固定不变。
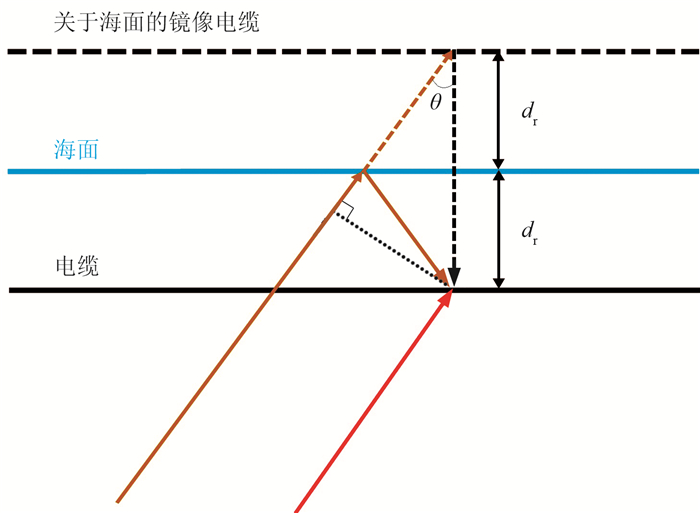
如图 1所示,在τ-p域,电缆接收到的上、下行波的延迟时间Δtrg可以表示为
|
图 1 鬼波产生示意图 |
| $ \Delta {t_{rg}} = \frac{{2{d_r}\cos \theta }}{v} $ | (1) |
式中:θ为平面波传播方向与垂直方向的夹角;v为海水速度,通常约为1500m/s;dr为电缆沉放深度。从式(1)可见,上、下行波的延迟时间随入射角变化。对于浅水资料,不同炮检距、不同反射目的层的θ变化范围更广,即鬼波时空变更加剧烈,因此在时空域很难对鬼波进行有效压制。
根据τ-p变换与平面波射线参数的关系,有
| $ p=\frac{\sin \theta}{v} $ | (2) |
式(1)可写为
| $ \Delta t_{\mathrm{rg}}=\frac{2 d_{\mathrm{r}} \sqrt{1-p^{2} v^{2}}}{v} $ | (3) |
在τ-p域接收到的全波场地震数据可以表示为
| $ D_{\mathrm{rg}}\left(p, d_{r}, \tau\right)=S\left(p, d_{r}, \tau\right)+r_{\mathrm{p}} S\left(p, d_{r}, \tau-\Delta t_{r g}\right) $ | (4) |
式中:S(p,dr,τ)为有效反射波数据;rp为海面反射系数。将式(4)对τ进行傅里叶变换,可得
| $ {D_{{\rm{rg}}}}\left( {p, {d_{\rm{r}}}, \omega } \right) = S\left( {p, {d_{\rm{r}}}, \omega } \right)\left[ {1 + {r_{\rm{p}}}\exp \left( { - {\rm{i}}\omega \Delta {t_{{\rm{rg}}}}} \right)} \right] $ | (5) |
式中ω为角频率。如果能准确求取鬼波上、下行波延迟时间Δtrg和海面反射系数rp,就可以获得不含鬼波的地震数据
| $ S\left( {p, {d_r}, \omega } \right) = \frac{{{D_{{\rm{rg}}}}\left( {p, {d_r}, \omega } \right)}}{{1 + {r_{\rm{p}}}\exp \left( { - i\omega \Delta {t_{{\rm{rg}}}}} \right)}} $ | (6) |
在实际鬼波压制过程中,通常从导航文件获取的震源深度ds、电缆沉放深度dr不准确,实际海面反射系数rp是个大于-1的未知数,因此如何较为准确地求取ds、dr、rp是压制鬼波的关键环节。
1.2 τ-p域鬼波参数自适应估计由式(6)可知,若能获得鬼波压制后的有效反射波数据,则鬼波可以由原始数据减去有效反射数据获得。当鬼波压制参数正确时,获取的有效波与鬼波能量之和应该达到最小化,因此可以通过有效波与鬼波能量之和的最优化问题获取ds、dr、rp,实现鬼波参数的自适应估计。
由于实际海面反射系数通常接近-1,且变化相对较小,因此先进行震源及电缆深度的估计。在这两个参数估计的过程中假设海面反射系数恒定为-1。当这两参数估计完成后,再利用这两个参数进行海面反射系数的估计。
对于同一炮地震数据,电缆沉放深度dr是随着炮检距变化而变化的,因此每一射线参数p对应的电缆深度可以通过下式的最优化问题求解,即
| $ \begin{array}{l} \min :E = {\left| {{D_{{\rm{rg}}}}\left( {p, {d_{\rm{r}}}, \omega } \right) - S\left( {p, {d_{\rm{r}}}, \omega } \right)} \right|^2} + \\ {\left| {S\left( {p, {d_{\rm{r}}}, \omega } \right)} \right|^2} \end{array} $ | (7) |
同样,震源沉放深度ds和海面反射系数rp可以用类似的方法进行求解。
在获得震源沉放深度ds、电缆沉放深度dr和海面反射系数rp后,就可以利用式(6)在τ-p域分别进行震源鬼波、电缆鬼波的压制,然后进行τ-p反变换即可得到鬼波压制后的炮集数据。
2 τ-p域自适应海底深度估计的浅水多次波压制技术 2.1 τ-p域浅水多次波压制原理在浅水区,经过τ-p变化后,地震数据可以看作平面波,可以利用射线参数p确定传播方向。在p相同的情况下,有效波与水层多次波之间沿着τ轴的时间延迟具有周期性。在τ-p域,有效波通过延拓可以预测出水层一阶多次波,一阶多次波通过延拓预测出二阶水层多次波,…,n-1阶多次波预测出n阶多次波。
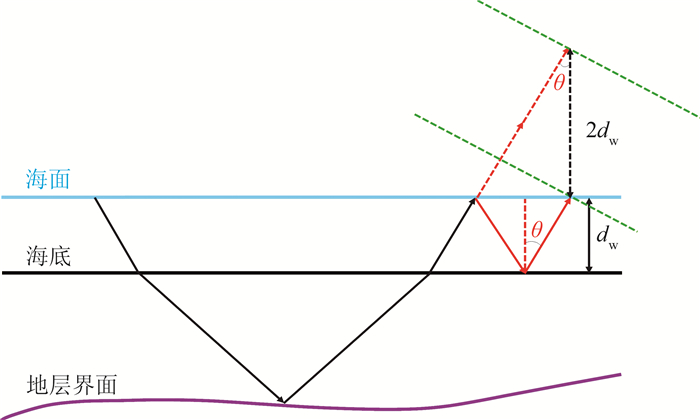
如图 2所示,在τ-p域水层多次波与有效波的时差Δtm可表示为
|
图 2 水层多次波与有效波传播示意图 |
| $ \Delta {t_{\rm{m}}} = \frac{{2{d_{\rm{w}}}\cos \theta }}{v} $ | (8) |
式中dw为海底深度。对比式(1)与式(8),可见二者形式完全相同,只是将电缆深度替换为海底深度。
在τ-p域进行波场延拓后,就可以预测出水层多次波,通过自适应匹配相减则可将水层多次波进行压制,再进行τ-p反变换后就获得水层多次波压制后的炮集数据。
2.2 自适应海底深度估计由式(8)可知,如果海底深度dw已知,就可以在τ-p域进行波场延拓获得多次波模型。对于相对较深的浅水海域,通过对海底进行深度域成像,就可以获得海底深度dw。但是对于像渤海这样平均水深不超过30m的海域,由于近炮检距数据的缺失,海底深度很难通过成像获得;而近道叠加自相关获得的浅水多次波周期被改变,建立的海水深度模型精度不高。为此,本文提出了一种在τ-p域进行自适应海底深度估计的方法。
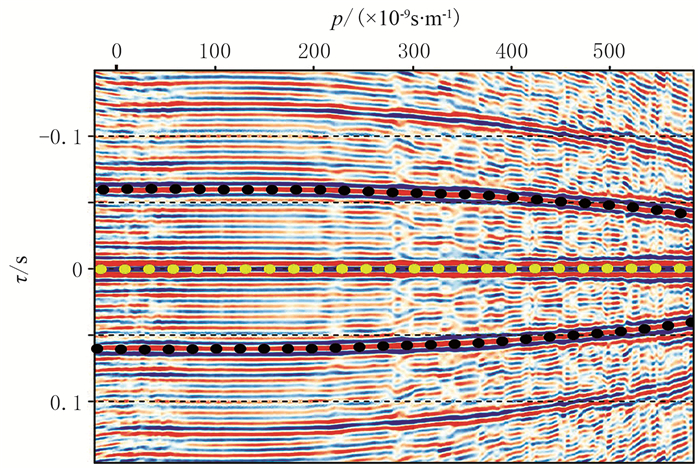
由于炮集在τ-p域浅水多次波与一次波具有很好的周期性,因此在τ-p域浅水多次波与一次波具有很好的相关性。通过在τ-p域进行自相关,相关能量最强的为零延迟自相关,相关能量次强且与零延迟自相关极性相反的即为浅水多次波的周期,通过该周期可以获得海底深度模型。如图 3所示,τ=0对应的峰值为一次波自相关的能量,即图中黄色圆点所标示的位置,黑色圆点虚线所标示位置所对应的时间即为一阶多次波在τ-p域的周期。
|
图 3 τ-p域炮集自相关浅水多次波周期示意图 |
为了提高计算海水深度的稳定性,拾取不同p参数下的浅水多次波周期,计算海底深度及平均海水速度
| $ \begin{array}{l} \left\{ \begin{array}{l} \Delta {t_1} = \frac{{2{d_{\rm w}}\sqrt {1 - p_1^2v_w^2} }}{{{v_w}}}\\ \Delta {t_2} = \frac{{2{d_{\rm w}}\sqrt {1 - p_2^2v_w^2} }}{{{v_w}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ \Delta {t_n} = \frac{{2{d_{\rm w}}\sqrt {1 - p_n^2v_w^2} }}{{{v_w}}} \end{array} \right.\\ \;\;\;\;\;\;\;\;\; \end{array} $ | (9) |
式中:Δti为在射线参数pi下拾取的浅水多次波周期;dw为海底深度;vw为平均海水速度。通过求解超定方程组式(9)可以获得海底深度dw及平均海水速度vw,从而在τ-p域实现浅水多次波的预测及压制。
3 实际资料应用为了验证本文方法的正确性及实用性,应用渤海M工区实际常规水平拖缆采集数据进行测试。实际数据炮间距为25m,道间距为12.5m,采样率为2ms,震源沉放深度为5m,电缆沉放深度为6m,工区平均水深约为27m。理论上震源鬼波的陷频点为0、150Hz,电缆鬼波的陷频点为0、125Hz,浅水多次波的陷频点为27.7Hz的整数倍。
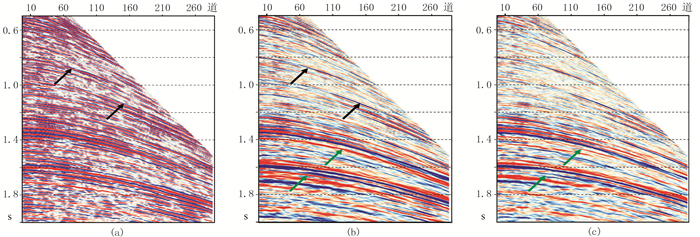
图 4为实际炮集鬼波、浅水多次波压制前、后的对比。其中图 4a为原始输入炮集记录;图 4b为在图 4a的基础上应用本文方法进行电缆和震源鬼波压制后的炮集,与图 4a相比,相位更为单一(黑色箭头所示);图 4c为在图 4b数据的基础上进行浅水多次波压制后的炮集,其中绿色箭头所指为浅水多次波压制前、后的效果对比。
|
图 4 实际地震炮集鬼波、多次波压制结果 (a)原始炮集;(b)震源、电缆鬼波压制后的炮集;(c)浅水多次波压制后的炮集 |
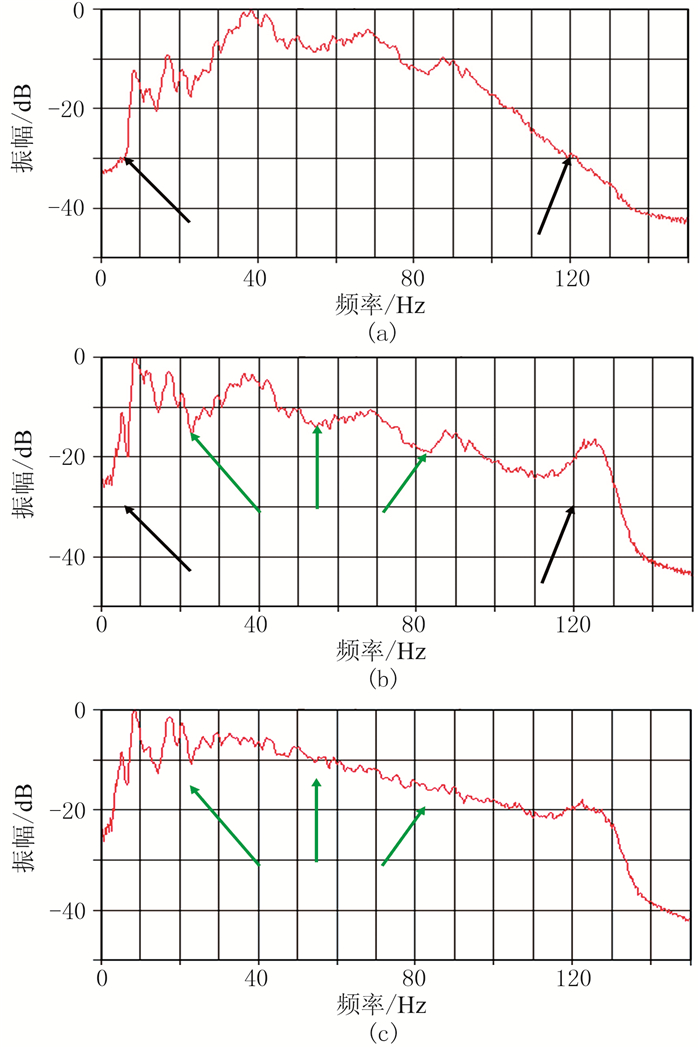
图 5为图 4炮集的频谱,可见:震源及电缆鬼波压制后,地震资料的频谱得到了明显的拓宽,尤其低频成分(< 20Hz)得到了很好的恢复,高频端(>100Hz)也略有提升(黑色箭头所示);浅水多次波压制后,消除了由浅水多次波引起的陷频现象(绿色箭头所示);压制鬼波、浅水多次波后,地震资料的频谱更加光滑。
|
图 5 炮集鬼波、多次波压制前、后频谱对比 (a)原始炮集;(b)震源、电缆鬼波压制后;(c)浅水多次波压制后 |
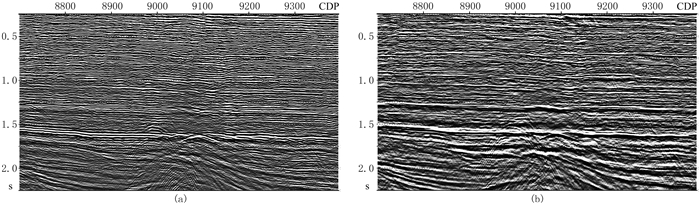
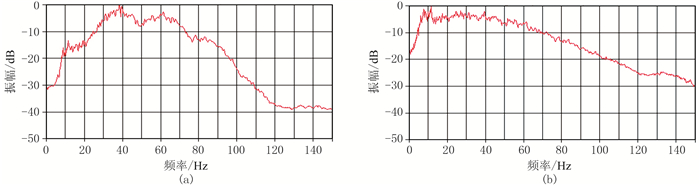
图 6为鬼波、浅水多次波压制前、后叠加剖面的对比,可见鬼波、浅水多次波压制后波组特征更加清楚,相位更为单一。图 7为图 6叠加剖面频谱,可见鬼波、浅水多次波压制后,低频得到了明显的拓展,以-10dB作为标准,低频端由25Hz拓展到5Hz。
|
图 6 鬼波、多次波压制前(a)、后(b)叠加剖面对比 |
|
图 7 鬼波、多次波压制前(a)、后(b)叠加剖面频谱对比 |
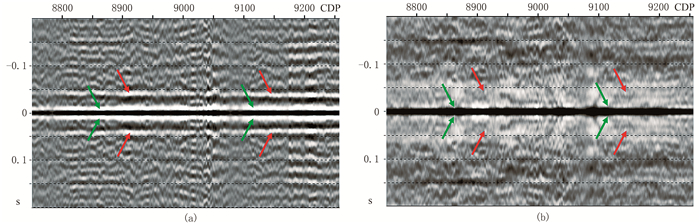
图 8为图 6叠加剖面自相关谱,可见:鬼波得到有效压制,子波旁瓣(绿色箭头所示)明显减小;浅水多次波得到有效压制,明显减少了剖面中周期性重复出现的同向轴(红色箭头所示)。
|
图 8 鬼波、多次波压制前(a)、后(b)叠加剖面自相关谱对比 |
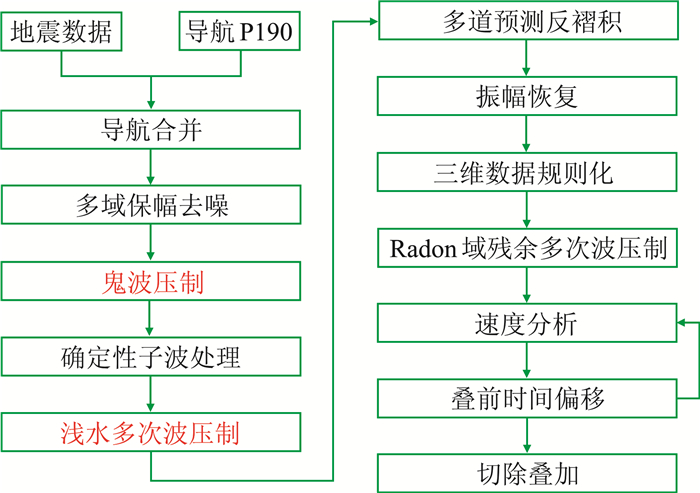
图 9为在渤海M实际工区的宽频处理技术流程,其中红色字体所示为本文研究的浅水宽频处理关键技术。图 10a为利用常规处理流程(不包含图 9中红色字体所示的两项技术)获得的叠前时间偏移剖面,图 10b为本文宽频处理流程获得的叠前时间偏移剖面。对比可见,宽频处理流程在浅层能明显提升地震资料的分辨率,在中浅层低频信息更加丰富,波组特征更加清楚。
|
图 9 渤海海域水平拖缆宽频处理流程 |

|
图 10 常规(a)与本文宽频(b)处理流程时间偏移剖面对比 |
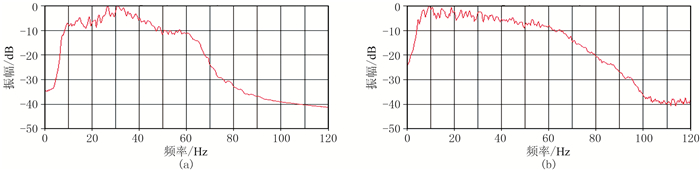
图 11为图 10时间偏移剖面频谱对比,可见宽频处理后地震资料的低、高频能量都得到了一定程度的拓展,消除了由浅水多次波引起的陷频现象,频谱更加饱满、光滑。
|
图 11 叠前时间偏移剖面频谱对比 (a)常规处理流程;(b)本文宽频处理流程 |
处理实践表明,在像渤海这样的浅水海域,宽频处理仍然能提升地震资料的品质,为老资料挖潜提供了一条可能的处理方向。
4 结论(1) 本文针对浅水海域鬼波时空变剧烈的问题,提出了一种基于τ-p域自适应参数估计的平缆鬼波压制技术;针对浅水海域海底模型难以建立的问题,提出了一种τ-p域自适应海底深度估计的浅水多次波压制技术。
(2) 将本文研究的关键技术与常规处理技术相结合,形成了浅水海域水平拖缆宽频处理技术流程,在渤海实际数据处理中取得了一定的应用效果,验证了本文所提出方法及技术流程的合理性及正确性。
(3) 本文主要针对像渤海这样浅水海域水平拖缆资料的鬼波、浅水多次波压制技术进行了研究,并未考虑大地的吸收衰减作用,为了取得更好的应用效果,针对宽频资料的吸收衰减补偿技术有待进一步研究。
| [1] |
Soubaras R.Deghosting by joint deconvolution of a migration and a mirror migration[C].SEG Technical Program Expanded Abstracts, 2010, 29: 3406-3410.
|
| [2] |
Rebert T, Rablon R, Vidal N, et al.Improving pre-salt imaging with variable-depth streamer data[C].SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [3] |
Soubaras R, Lafet Y.Variable-depth streamer acquisition: broadband data for imaging and inversion[C].SEG Technical Program Expanded Abstracts, 2011, 30: 2364-2368.
|
| [4] |
Zhang Y, Roberts G, Khalil A.Compensating for source and receiver ghost effects in reverse time migration[C].SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [5] |
Sun W B, Zhang J M, Zhu Z Y, et al.Application of RTM with deghosting on deepwater seismic data[C].SEG Technical Program Expanded Abstracts, 2016, 35: 4409-4413.
|
| [6] |
吴娟, 白敏, 张华. 基于高斯束偏移的鬼波压制[J]. 石油地球物理勘探, 2018, 53(3): 443-448. WU Juan, BAI Min, ZHANG Hua. Deghosting with Gauss beam migration[J]. Oil Geophysical Prospecting, 2018, 53(3): 443-448. |
| [7] |
Wang P, Peng C.Premigration deghosting for marine towed streamer data using a bootstrap approach[C].SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [8] |
Zhang Z G, Ji J, Wang B.Joint deconvolution with hybrid norm and its applications to flat cable images and pre-migration data[C].SEG Technical Program Expanded Abstracts, 2013, 32: 4241-4245.
|
| [9] |
王芳芳, 李景叶, 陈小宏. 基于逆散射级数法的鬼波压制方法[J]. 地球物理学报, 2013, 56(5): 1628-1636. WANG Fangfang, LI Jingye, CHEN Xiaohong. De-ghosting method based on inverse scattering series[J]. Chinese Journal of Geophysics, 2013, 56(5): 1628-1636. |
| [10] |
Masoomzadeh H, Woodburn N.Broadband processing of conventional streamer data-optimized de-ghosting in the tau-p domain[C].Extended Abstracts of 75th EAGE Conference & Exhibition, 2013, Th-08-14.
|
| [11] |
李洪建, 韩立国, 巩向博, 等. 基于格林函数理论的波场预测和鬼波压制方法[J]. 地球物理学报, 2016, 59(3): 1113-1124. LI Hongjian, Han Liguo, Gong Xiangbo, et al. A wavefiled predicition and ghost suppression method based on Green function theory[J]. Chinese Journal of Geophysics, 2016, 59(3): 1113-1124. |
| [12] |
王建花, 王艳冬, 刘国昌. 基于波场延拓和反演的变深度缆地震数据鬼波压制方法[J]. 石油地球物理勘探, 2017, 52(5): 885-893. WANG Jianhua, WANG Yandong, LIU Guochang. A deghosting method on variable-depth streamer data based on wavefield extrapolation and inversion[J]. Oil Geophysical Prospecting, 2017, 52(5): 885-893. |
| [13] |
马继涛, 王艳冬, 陈小宏, 等. 基于波场外推和阈值截断的鬼波压制方法[J]. 石油地球物理勘探, 2018, 53(2): 227-235. MA Jitao, WANG Yandong, CHEN Xiaohong, et al. A ghost suppression method based on wavefield extra-polation and threshold truncation[J]. Oil Geophysical Prospecting, 2018, 53(2): 227-235. |
| [14] |
张威, 韩立国, 李洪建, 等. 基于LSMR算法的斜缆数据鬼波压制方法[J]. 石油地球物理勘探, 2017, 52(3): 434-441. ZHANG Wei, HAN Liguo, LI Hongjian, et al. De-ghosting of variable-depth streamer data based on LSMR[J]. Oil Geophysical Prospecting, 2017, 52(3): 434-441. |
| [15] |
陈宝书, 陶杰, 李松康, 等. 基于确定性子波处理的鬼波压制方法[J]. 中国海上油气, 2017, 29(1): 39-45. CHEN Baoshu, TAO Jie, LI Songkang, et al. Degho-sting method based on deterministic wavelet proce-ssing[J]. China Offshore Oil and Gas, 2017, 29(1): 39-45. |
| [16] |
Barry K, Yang K L, Zhou J, et al. Shallow water demultiple[J]. ASEG-Advanced Systems Engineering Group, 2010(2): 2-5. |
| [17] |
Wang P, Jin H Z, Xu S, et al.Model-based water-layer demultiple[C].SEG Technical Program Expanded Abstracts, 2011, 30: 3551-3555.
|
| [18] |
冯全雄, 王彦春, 李三福, 等. τ-p域水体模型驱动压制浅水区水层多次波[J]. 石油地球物理勘探, 2015, 50(1): 41-47. FENG Quanxiong, WANG Yanchun, LI Sanfu, et al. Model-driving shallow-water-layer multiple attention in τ-p domain[J]. Oil Geophysical Prospecting, 2015, 50(1): 41-47. |
| [19] |
张连群, 陈宝书, 李松康, 等. 白云凹陷陆架-陆坡区多次波压制技术[J]. 石油地球物理勘探, 2018, 53(2): 236-242. ZHANG Lianqun, CHEN Baoshu, LI Songkang, et al. Multiple suppression in continental shelf and slope areas of Baiyun Depression[J]. Oil Geophysical Prospecting, 2018, 53(2): 236-242. |
| [20] |
宋建国, 姜梦奇, 杨宇. 基于克希霍夫衍射理论的水层多次波预测方法[J]. 地球物理学进展, 2016, 31(5): 2133-2138. SONG Jianguo, JIANG Mengqi, YANG Yu. Water-layer multiple prediction method based on Kirchhoff diffraction theory[J]. Progress in Geophysics, 2016, 31(5): 2133-2138. |
| [21] |
李钟晓, 李振春. 基于交替分裂Bregman迭代算法的鲁棒多道预测反褶积方法[J]. 石油地球物理勘探, 2017, 52(4): 678-688. LI Zhongxiao, LI Zhenchun. Robust multichannel predictive deconvolution based on the alternating split Bregman iteration algorithm[J]. Oil Geophysical Prospecting, 2017, 52(4): 678-688. |
| [22] |
许志强, 李添才, 王用军, 等. 倾斜电缆地震资料处理关键技术及其效果分析[J]. 中国海上油气, 2015, 27(6): 10-18. XU Zhiqiang, LI Tiancai, WANG Yongjun, et al. Key technology for slant streamer seismic data processing and its application analysis[J]. China Offshore Oil and Gas, 2015, 27(6): 10-18. |
| [23] |
Wang Y D, Wang J H, Wang X L, et al.Broadband processing key technology research and application on slant streamer[C].CPS/SEG International Geophysical Conference, 2018, 135-138.
|
| [24] |
张振波, 李东方. 斜缆宽频地震勘探技术在珠江口盆地的应用[J]. 石油地球物理勘探, 2014, 49(3): 451-456. ZHANG Zhenbo, LI Dongfang. Variable-depth strea-mer seismic acquisition and processing in Pearl River Mouth Basin[J]. Oil Geophysical Prospecting, 2014, 49(3): 451-456. |
| [25] |
郭建卿, 丁在宇, 王者武, 等.拖缆资料宽频处理关键技术及应用效果[C].中国石油学会2017年物探技术研讨会论文集, 2017, 24-28.
|
| [26] |
Xie L B, Guo J Q, Zhang R H, et al.An integrated broadband processing method for conventional flat tow-stremear data[C].CPS/SEG 2018 Beijing International Geophysical Conference, 2018, 142-145.
|
| [27] |
仝中飞, 陈宝书, 李松康, 等.三维水平拖缆地震资料宽频处理技术应用研究[C].中国石油学会2017年物探技术研讨会论文集, 2017, 704-708.
|



 王艳冬, 北京市朝阳区太阳宫南街6号院海油大厦A座1005室, 100028。Email:
王艳冬, 北京市朝阳区太阳宫南街6号院海油大厦A座1005室, 100028。Email: