② 中原经济区煤层(页岩)气河南省协同创新中心, 河南焦作 454000;
③ 中国石油集团东方地球物理公司大庆物探一公司, 黑龙江大庆 163357
② Collaborative Innovation Center of Coalbed Methane and Shale Gas for Central Plains Econo-mic Region, Jiaozuo, Henan 454000, China;
③ Daqing Branch, BGP Inc., CNPC, Daqing, Heilongjiang 163357, China
随着地震勘探的不断深入,它所面临的近地表地震地质条件越来越复杂。因此,对复杂近地表介质的非均匀性、各向异性、非完全弹性特性及其对地震勘探的影响的研究备受关注。为了提高地震勘探精度,着力消除近地表地层的影响已成为现今地震数据采集、处理的重要内容。
研究表明[1-2]:与深部地层介质的吸收衰减效应相比,近地表介质对地震波高频成分的吸收衰减是降低地震资料分辨率的重要因素之一;地表介质对地震波高频成分的吸收约占地层吸收总量的80%。依据李庆忠[3]构建的新生界华北盆地与中生界松辽及二连盆地经典吸收模型,经笔者初步估算,3s以上地层近地表地震波衰减分贝数占总衰减分贝数的变化范围大致是15%~40%,且探测深度越小,近地表衰减占总衰减的比例越大。
对于沙漠地区,尤其是巨厚沙丘地表区,人们普遍认同近地表对地震波的吸收非常强烈。宋智强等[4]指出:对于60Hz以上的地震波,当它穿过80m厚的沙丘时,地震波衰减大于38dB,能量相对损失可超过90%。但由于沙漠区勘探目标层深度普遍较大,笔者认同近地表衰减分贝数占总衰减分贝数的最大占比不超过80%的上限值[1]。对于勘探深度在6000m以内的情形,初略估算近地表衰减所占比例应低于60%。
由此可见,近地表介质吸收衰减补偿处理已成为高分辨率地震勘探成败的关键,其核心是构建精确近地表Q模型,而近地表Q值估算方法的合理选用无疑是近地表衰减Q模型构建的基础。
目前近地表Q值估算在算法理论上并无明显创新,基本上沿用已有的相对成熟的算法理论,且尤以经典的谱比法应用居多。不过因实施Q值估算基础数据来源不同,使Q值估算呈现出自身独有的特点。总体而言,可用于求取近地表Q值的基本途径主要包括岩石样本测定及利用微测井、大炮初至、面波勘探和小折射等现场实测地震数据的直接估算或反演成像。因资料来源不同,Q值估算或反演结果参差不齐,从而造成了研究和应用中的困惑,甚至出现了一些错误的理解和认识。
本文基于调研文献成果,重点对现今常用近地表Q值估算方法进行梳理、总结。主要从岩石样本实验测试和地层原位测量两个方面对Q值测量方法进行分类研究,着重阐述各种方法的实现过程、应用条件、优缺点及发展前景,以期为Q值测试和估算方法的合理利用及近地表Q模型的构建等提供借鉴和指导,更好促进相关方法技术的发展与应用。
需要指出的是,由于地震波吸收衰减理论方法及补偿技术飞速发展,相关文献资料层出不穷,不胜枚举。评述中难免会挂一漏万,但旨在抛砖引玉。
1 Q值估算方法概述迄今为止,可用于地层Q值估算或反演成像的方法有很多。表 1按算法原理的不同对Q值估算方法进行了初步分类,并给出了相关代表性方法[5-6]。由于本文论述的重点在于不同来源数据近地表Q值估算方法的差异性和互补性,尽管表 1对于Q值估算方法理论的总结可能不够全面,但足以满足后续论述的需要。下面仅就近地表Q值估算中现今常用的谱比法、质心频移法及波场模拟反演、层析反演等部分算法的基本原理做简要概述。
|
|
表 1 地层品质因子Q值估算方法分类 |
以井中观测为例,对于深度分别为hi和hi+1的相邻两道记录,若对应信号振幅谱分别为Si(f)和Si+1(f),在常Q值假设条件下,利用Futterman吸收衰减模型[7],该相邻两道的振幅谱比对数可表示为
| $ \ln \frac{{{S_{i + 1}}\left( f \right)}}{{{S_i}\left( f \right)}} = \ln \frac{{{G_{i + 1}}{P_{i + 1}}}}{{{G_i}{P_i}}} - \frac{{{\rm{ \mathsf{ π} }}\Delta {h_i}}}{{QV}}f $ | (1) |
或用时差表示为
| $ \ln \frac{{{S_{i + 1}}\left( f \right)}}{{{S_i}\left( f \right)}} = \ln \frac{{{G_{i + 1}}{P_{i + 1}}}}{{{G_i}{P_i}}} - \frac{{{\rm{ \mathsf{ π} }}\Delta {t_i}}}{Q}f $ | (2) |
式中:Gi表示几何扩散效应;Pi表示透射损失;V为地层速度;Δhi=hi+1-hi为相邻两道记录深度间隔;Δti=ti+1-ti为相邻两道记录初至波旅行时差。
式(1)和式(2)即为谱比法(SR)估算Q值的理论基础。应用中通过对谱比对数值和频率的线性回归分析可求取拟合曲线斜率p,则品质因子为
| $ Q = - \frac{{{\rm{ \mathsf{ π} }}\Delta {h_i}}}{{pV}} = - \frac{{{\rm{ \mathsf{ π} }}\Delta {t_i}}}{p} $ | (3) |
由式(3)可见,谱比法Q值估算的精度由速度估算误差和初至时间拾取误差决定。特别是当深度间隔很小时,初至时间拾取误差对Q值估算的影响非常大,往往会造成Q值估算结果的剧烈波动。此外,当记录中存在噪声时,也会造成振幅谱的波动,进而降低谱比对数值的精度,最终导致Q值估算结果的不稳定。
Quan等[8]提出质心频移法(CFS)新算法,定义信号振幅谱S(f)的质心频率fs和方差σs2为
| $ {f_{\rm{s}}} = \frac{{\int_0^\infty {fS\left( f \right){\rm{d}}f} }}{{\int_0^\infty {S\left( f \right){\rm{d}}f} }} $ | (4) |
| $ \sigma _{\rm{S}}^2 = \frac{{\int_0^\infty {\left( {f - {f_{\rm{s}}}} \right)S\left( f \right){\rm{d}}f} }}{{\int_0^\infty S (f){\rm{d}}f}} $ | (5) |
假设入射波频谱为高斯频谱,经理论推导可得
| $ \left\{ {\begin{array}{*{20}{l}} {{\alpha _{0i}} = \frac{1}{{\sigma _i^2}}\frac{{\Delta {f_i}}}{{\Delta {h_i}}}}\\ {{Q_i} = \frac{{\rm{ \mathsf{ π} }}}{{{\alpha _0}{V_i}}}} \end{array}} \right. $ | (6) |
式中:α0i为相应深度间隔Δhi的衰减系数;Δfi=fi-fi+1为深度hi与hi+1两道记录振幅谱的质心频率差;σi2为深度hi处记录振幅谱的方差;Qi为相应深度间隔品质因子;Vi为间隔层速度;
从式(4)~式(6)不难看出,因质心频率和方差的求取利用了振幅谱的全频段积分,使质心频移法Q值估算具有较好的抗噪性。
高静怀等[9]借鉴质心频移法的基本思想,在假定震源子波近似为Ricker子波的前提条件下,给出了峰值频移法,同样可获得较好的Q值估算效果。但需指出的是,不论是质心频移法还是峰值频移法,二者最大的限制都在于实际地震波频谱是否满足高斯子波或Ricker子波的假设前提。
为了降低噪声对Q值估算的影响,Wang等[10]基于谱比法原理,通过积分运算,提出了对数谱面积差(LSAD)Q值估算新方法。它在给定频段[fL,fH]内,定义任意第i道记录相对于第1道记录的对数谱面积差为
| $ \Delta {A_{{\rm{a}}i}} = \int_{{f_{\rm{L}}}}^{{f_{\rm{H}}}} {\ln {S_i}\left( f \right){\rm{d}}f} - \int_{{f_{\rm{L}}}}^{{f_{\rm{H}}}} {\ln {S_1}\left( f \right){\rm{d}}f} $ | (7) |
若预先对资料做几何扩散校正,则相应第1道与第i道之间的地层平均品质因子Qai的估算表达式可写为
| $ {Q_{{\rm{a}}i}} = \frac{{\Delta {T_i}}}{{\Delta {A_{{\rm{a}}i}} + \int_{{f_{\rm{L}}}}^{{f_{\rm{H}}}} {\ln } \left( {\prod\limits_{j = 2}^{i - 1} {{P_j}} } \right){\rm{d}}f}}\int_{{f_{\rm{L}}}}^{{f_{\rm{H}}}} {{\rm{ \mathsf{ π} }}f{\rm{d}}f} $ | (8) |
式中:ΔTi为第1道到第i道记录的旅行时差;Pj为第j个界面的透射系数,可利用垂直入射透射系数公式近似由各层段速度计算获得。
进一步,当已知第i和第i+1测点的Qai和Qai+1时,相应第i层段的品质因子可由下式给出
| $ \frac{1}{{{Q_i}}} = \frac{{\frac{{\Delta {T_{i + 1}}}}{{{Q_{{\rm{a}}i + 1}}}} - \frac{{\Delta {T_i}}}{{{Q_{{\rm{a}}i}}}}}}{{\Delta {T_{i + 1}} - \Delta {T_i}}} $ | (9) |
与谱比法和质心频移法相比,对数谱面积差法不论是在Q值估算的抗噪性还是稳定性方面均具有明显优势。但迄今为止,尚未见该方法在近地表Q值估算中的具体应用。
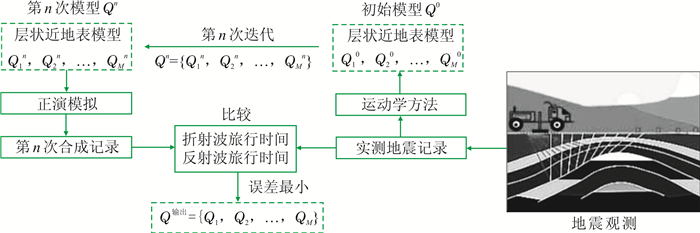
1.2 波传播模拟法Q反演EI Yadari等[11]基于黏弹性声波方程频率域有限差分正演模拟方法提出一种波传播模拟法近地表衰减品质因子估算方法。该方法在模型速度、密度及厚度已确定的前提下,采用剥层法思想,从浅到深逐层不断修改模型参数Q值,实施黏弹性正演模拟,然后对比合成记录与实测记录反射波与折射波能量的一致性,使其逐步逼近或达到某一门槛值,则模型参数即为相应地层的估算Q值。具体算法流程如图 1所示。
|
图 1 波传播模拟法近地表Q值反演流程图(据EI Yadari等[11]整理) |
由图 1可见,该方法实现过程较为复杂,计算量大,Q值估算结果受子波、地表地形、模型结构、速度、厚度等多种因素的影响。不过,随着计算机技术的发展,特别是并行与多进程运算技术的出现,计算效率得到极大提高,相关商业软件已基本实现了工业化应用。
1.3 Q值层析反演目前Q值层析反演技术基本成熟,相关商业软件已实现工业化应用。如中国石油集团东方地球物理公司的GeoEast地震数据处理解释一体化软件系统中的Q值反演模块,就是采用Q层析反演获取Q场。Q值层析反演一般有两种途径。一是基于射线理论,采用速度层析相同的算法原理,通过拾取初至波旅行时间和振幅,构建目标函数,再借助联立迭代重构技术实现速度与Q值联合层析反演。另一种途径是以前述直接Q值估算法基本公式(如谱比法、频移法等)为基础构建目标函数,进而实现层析反演。下面分别简述两类算法原理。
Brzostowski等[12]假定三维地震记录初至波振幅的几何扩散与散射效应已被消除,且非弹性衰减较小,则相应射线路径(ray)k的旅行时间tk和观测振幅Ak可近似表示为
| $ {t_k} = \int_{\left( {{\rm{ray}}} \right)k} {{v^{ - 1}}\left( {x,y,z} \right){\rm{d}}s} $ | (10) |
| $ {A_k} = {A_{\rm{s}}}\exp \left\{ { - \left[ {\frac{\omega }{2}\int_{{{\left( {{\rm{ray}}} \right)}_k}} {\frac{{{\rm{d}}s}}{{Q\left( {x,y,z} \right)v\left( {x,y,z} \right)}}} } \right]} \right\} $ | (11) |
式中:As为震源振幅;ω为角频率;v为速度。对于确定的频率f,依据谱比法原理,式(11)可改写为
| $ - \ln \left( {\frac{{{A_k}}}{{{A_{\rm{s}}}}}} \right) = {\rm{ \mathsf{ π} }}f\int_{{{\left( {{\rm{ray}}} \right)}_k}} {\frac{{{\rm{d}}s}}{{Q\left( {x,y,z} \right)v\left( {x,y,z} \right)}}} $ | (12) |
式(10)和式(12)共同构成速度与Q联合层析反演基本公式。具体实现过程中,利用上述二式同步反演获得速度v(x,y,z)和p(x,y,z)=Q(x,y,z)v(x,y,z)的空间分布,进一步换算可得Q(x,y,z)分布。显然,该方法中Q值成像的精度受制于速度成像精度,因此取得可靠的速度分布成像是获取最佳Q值成像效果的前提。
Xin等[13]基于三维叠前深度偏移数据提出三维叠前成像Q反演法,其核心原理仍为谱比法。将三维空间网格化,则三维叠前成像Q反演公式为
| $ {Q_{ijk}} = \frac{{{\rm{ \mathsf{ π} }}{f_{ijk}}{l_{ijk}}}}{{\ln \left( {\frac{{{A_0}}}{{{A_{ijk}}}}} \right){v_{ijk}}}} $ | (13) |
式中:A0为某层反射波参考振幅,可视为未遭吸收衰减影响的振幅或源振幅;A为相应层反射衰减振幅;l为波传播距离;ijk代表某一特定网格单元。
对于某一共成像点道集内所有反射层和炮检距,Q成像反演公式可改写为
| $ \mathit{\boldsymbol{Fm}} = \mathit{\boldsymbol{a}} $ | (14) |
式中:F为Frechet导数矩阵;m为包括Q在内的衰减扰动向量;a为包含对数振幅比的向量。
具体实施中,假定已拾取某一层位数据,则利用层位上某一未受衰减异常影响位置的参考平均振幅构成同一层位各点的振幅比图。波传播的射线路径为从层位拾取点到地面观测点的路径。当射线穿过网格单元时,记录射线通过每个单元的传播距离,则来自该拾取点的信息形成矩阵F的一行或向量a中的一个元素。对于多个拾取点,不同炮检距和不同层位信息的增加将成为矩阵F中的多行或向量a中的多个元素。最后,利用诸如最小二乘共轭梯度法等标准算法即可求解矩阵方程(式(14)),获得m值及相关Q值。
Li等[14]依据谱比法原理,针对井地联合采集多道地震记录构建了层析反演算法。就算法理论看,与Xin等[13]给出的算法在本质上大同小异。其他类似的近地表Q值层析反演法参阅文献[15-17]。
此外,张剑锋等[18]基于海上拖缆或地面接收反射地震资料,提出了一种叠前三维Q值场建模方法:将叠前黏弹性偏移成像与Q值扫描等相结合率先获得不同深度等效Q值场,类似于前述平均Q值;再采用与式(9)相同方式由等效Q值获得层Q值场。与前述成像方法相比,该方法实现过程较为复杂。限于篇幅,具体算法理论不赘述。
2 近地表Q值估算方法分类针对现有近地表Q值测定、观测及估算方法特点的不同,对其进行初步分类(表 2)。
|
|
表 2 近地表品质因子Q值估算方法分类 |
由表 2可见,近地表Q值的测试与估算主要有两条途径:①通过近地表岩石现场采样,再在室内借助不同方法技术实施实验测试以估算岩样Q值;②在不破坏原有岩石或地层的基础上,直接对原状地层进行现场原位观测,然后借助一定技术手段,针对观测数据实施Q值估算。根据两类测试或观测方法特点的最大差别,前者可统称为岩石样本测试Q值估算或“小样”Q测试,后者则可统称为地层原位测量Q值估算,或形象地称为“大样”Q值测量。
对于岩石“小样”Q值测试方法而言,按照室内具体测试方法技术的不同,可将其进一步细分为应力—应变法、驻波法和行波法三类。三种方法测量频率明显不同,其中应力—应变法测量频率低,最贴近地震勘探的频率范围;行波法测量频率最高;驻波法测量频率基本介于二者之间。
对于地层原位测量Q值估算方法而言,按照观测数据来源不同,可将其细分为地面观测(包括:面波勘探、大炮面波、大炮初至波、小折射初至波)、微测井以及井地联合观测或多数据源联合反演三大类。此类方法测试频率与地震勘探基本一致,估算结果通常可直接用于地震波衰减特性分析和补偿处理应用,但纵向分辨率存在较大差异。
3 岩石样本测试Q值估算方法岩石样本Q值实验测试方法主要有基于应力—应变测试理论的静态、准静态和动态测量法及基于样本振动和波传播理论的动态测量法(包括动态谐振法和动态脉冲法)两大类(表 2)。
3.1 应力—应变法应力—应变法Q测试技术,也称为应力—应变曲线法[19]。按照应力加载方式的不同可分为经典应力—应变法和交变应力—应变法。该方法基于内摩擦理论定义品质因子,通过对岩石样本缓慢的循环应力加载—卸载实验,测定不同应力条件下岩石变形所产生的应变值,从而可得到对应加载和卸载过程的两条应力—应变曲线。理论上应力—应变曲线所围成的面积代表了应变能。两条应力—应变曲线所围成的面积之差代表了经过一个循环应力加载—卸载过程所消耗的能量ΔW,而加载过程中应力—应变曲线所围成的面积代表了岩石应变达到极大时所贮存的应变能W(图 2)。

|
图 2 循环加载实验确定岩石内摩擦特性示意图[19] |
基于内摩擦理论,通常定义损耗比ΔW/W以表征岩石的内摩擦特性。损耗比与1/Q成正比,有
| $ \frac{1}{Q} = \frac{{\Delta W}}{{2{\rm{ \mathsf{ π} }}W}} $ | (15) |
式(15)为Q值的基本定义式[20]。地震勘探中有时也将1/Q称为耗散率或耗散因子。该方法最大的优点是整个测量过程不需要对内摩擦机制做任何假设。存在的主要问题是测量结果依赖于应力变化幅度、循环速度和样本过往受力作用历史等。
当采用交变应力(如正弦波形或三角波形)实施加载测试时,对应每一频率取一个周期进行密集采样,并求取同一时间周期应力与应变峰值偏移样点数(反映相位差)即可计算Q值,有[19, 21]
| $ Q = \frac{n}{{2{\rm{ \mathsf{ π} }}\Delta M}} $ | (16) |
式中:n为一个周期总采样点数;ΔM为应力与应变峰值偏移点数。
需要指出的是,用正弦波和用三角波两种方式加载所获得的Q值与频率关系很相似,并且三角波加载所测得的Q值普遍高于用正弦波加载测得的Q值。究其原因在于,正弦波循环加载大大降低了岩石的强度,三角波则对岩石强度降低较少。
Tisato等[21]研发了一种宽带衰减器(Broad Band Attenuation Vessel,BBAV),它通过对样本加载正弦周期应力,然后测量样本体应变的周期变化,并采用经典应力—应变曲线法相同的原理通过数值积分计算一个应力—应变周期内所包围的面积,获得耗散能和储能值,进而由式(15)估算Q值。此外,也可通过对应力、应变测试数据的正弦函数拟合或借助于傅里叶变换两种途径求取应力与应变之间的相位差ϕ,由下式求取Q值,有
| $ {Q^{ - 1}} = \tan \phi $ | (17) |
BBAV测试系统克服了经典应力—应变法测试困难、效率低下等不足,可在0~25MPa不同围压及不同饱和度条件下实现频率范围为0.01~100Hz的样本衰减特性测量和Q值求取。若岩样满足线性时不变条件,则当相移小于0.1(Q>10)时,采用正弦函数拟合法和数值积分求面积方法求取的Q值基本一致,差异一般小于5%;若岩样满足非线性变化条件,则基于面积法的Q值估算方法因不受应变状态的影响,Q值测量精度更高。现有的各种交变应力—应变测试仪器测量原理与BBAV大同小异,均可实现不同压力条件下的Q值测试,且测量频率上限可扩展到约1kHz。
童立红等[22]基于非线性弹性理论,由动应力—应变关系及应变波传播波动方程出发,推导了由入射应变波和透射应变波幅值的比值计算岩石衰减系数以及由透射谐波应变幅值和入射应变幅值平方的比值计算岩石非线性系数的基本公式,发明了一种联合测定、计算岩石衰减系数及非线性系数的方法。其测量频率可达几千赫兹,且要求准确求取应力波基阶和二次谐波的振幅。
总体而言,经典应力—应变法相对较成熟,但测试难度大,效率低,且测量所得静态测试结果与地震波传播的动态特性不匹配,直接用于地震勘探存在一定差异性。交变应力—应变法克服了经典应力—应变法诸多缺点和不足,测试方法技术已基本成熟。目前可实现不同温压条件下岩石样本的弹性模量和衰减特性测试,但测试效率仍较低,且可变温度范围多在100℃以下。超低频测量通常为静态或准静态测量,测量结果与经典应力—应变法类似不适用于地震勘探。加载频率处于30Hz以下的测试研究在公路工程应用较多,且已被列入公路工程质量评价规范。其大多测量道路的弹性模量或对比分析动静态测试结果,对于衰减特性的测量关注较少。对于地震勘探而言,交变应力—应变法可实现与地震频率相一致的岩石样本弹性模量和衰减测量。因应力波与地震波具有内在本质的一致性,因此基于中低频交变应力—应变法的动态测量结果,可较好地反映岩石样本的中低频衰减特性,且可直接用于地震勘探。正因如此,在沉寂多年后,随着测试仪器和工艺的不断改进,目前该方法已成为地震勘探岩石样本Q值测试的新宠,备受业界推崇,呈现出良好的发展与应用前景。
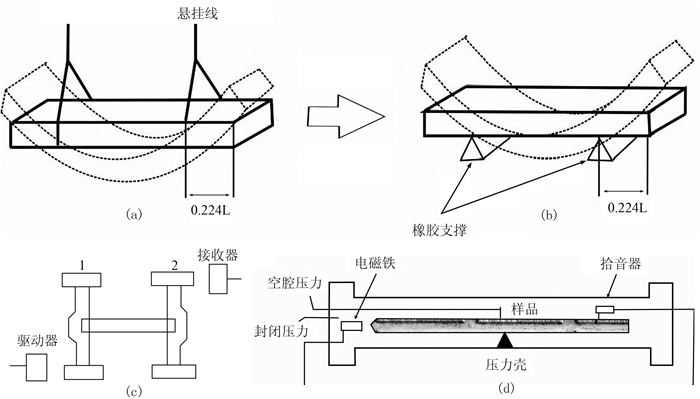
3.2 驻波振动法[23-28]所谓驻波是指具有相同频率、相同振幅且振动方向相同的两列简谐波在同一直线上沿相反方向等速传播时,二者相互叠加干涉所形成的一种波动现象。驻波法Q测量主要是测量样本(通常加工成圆柱状、棱柱状或矩形截面板状)在激振外力作用下发生弯曲振动(测量纵波品质因子)或扭转振动(测量横波品质因子)及其与样本端面反射振动相互干涉形成的驻波振幅变化,因此,该方法称为驻波振动法或动态谐振法[23-24]。其独特优点在于可用较低的频率(一般为1~10kHz)测试获得相对较高精度的Q值。按照样本激振后观测方法和原理的不同,驻波法可分为自由振动法和强迫振动法两种,且尤以强迫振动法应用最广。因测量样本一般要求加工成柱状或杆状,通常形象地称此类方法为共振杆法或谐振杆法。
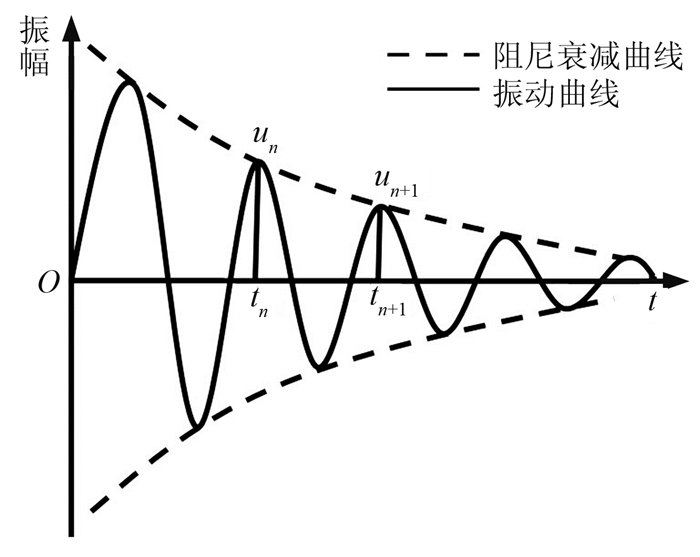
3.2.1 自由振动法[28-29]自由振动法也称为自由振动阻尼衰减法,是测量岩石样本激振产生的机械振动振幅随时间的衰减变化。测量过程中,首先需激振岩石样本,并通过调节激振频率让岩石样本处于谐振状态,使接收驻波振动信号幅值到达最大值。然后终止激振,让岩石样本处于自由振动状态。此时,因内摩擦作用岩石样本振动能量不断损耗、振幅随时间逐渐减小,相应振动曲线见图 3中黑色实线。然后利用不同周期振动信号极大振幅点的连线(振动信号外包络线)确定样本阻尼自由振动衰减曲线(图 3中黑色虚线)。此过程可借助于希尔伯特变换通过求取瞬时振幅实现。进一步,利用图 3所示阻尼衰减曲线相继两个周期自由振动信号的振幅比值,依据内摩擦理论即可求取样本Q值。设相继两个自由振动振幅分别为un和un+1,则岩石样本固有衰减的Q值计算公式为[28]
| $ Q = \frac{{\rm{ \mathsf{ π} }}}{\delta } = {\rm{ \mathsf{ π} }}\ln \left( {\frac{{{u_{n + 1}}}}{{{u_n}}}} \right) $ | (18) |
|
图 3 阻尼自由振动衰减曲线示意图[19] |
上式表明,通过测量相继两个周期自由振动的振幅比值,即可很容易地求取样本Q值。
最经典的自由振动Q值测试系统为单摆实验系统(图 4),其主要由岩石棒和很高惯性的质量系统组成。岩石棒经高力矩惯性质量系统激发谐振,在一个很短的时间周期内达到共振,然后,在两个相继准周期下测量衰减振幅,利用式(18)即可求得Q值。
应用中难以准确确定相邻两个周期的振幅值,因此常用做法是在阻尼衰减曲线上以不小于一个周期为前提任意选取两个时间点t1和t2的振幅值u1和u2,则Q值可由下式计算
| $ Q = {\rm{ \mathsf{ π} }}{f_0}\Delta t\ln \left( {\frac{{{u_1}}}{{{u_2}}}} \right) $ | (19) |
式中:f0为岩石样本阻尼自由振动频率;Δt=t2-t1,为任意两个时间点的差值。
目前,自由振动法大多采用与强迫振动法相同的装置类型测量样本达到谐振时的自由振荡过程,单摆法的测量与应用基本上被淘汰。
吴志刚等[30]针对传统自由振动衰减测试中因激振器与受试样本连接造成的附加刚度问题,据电磁学原理设计了可实现样本与激振器自由分离的激振杆,当试件(样本)处于自由衰减状态时,激振器可从测试系统轻松剥离,确保衰减测量准确性。
3.2.2 强迫振动法[19, 26, 29, 31]强迫振动法也称为共振法、谐振法、动态谐振法、共振棒(杆)法、谐振曲线法等。主要是利用岩石棒(杆、板)的强迫振动所形成的驻波谐振效应,通过测量驻波谐振振幅随频率变化的谐振曲线求取岩石样本Q值的一种测量方法,可实现纵、横波Q值的测量。
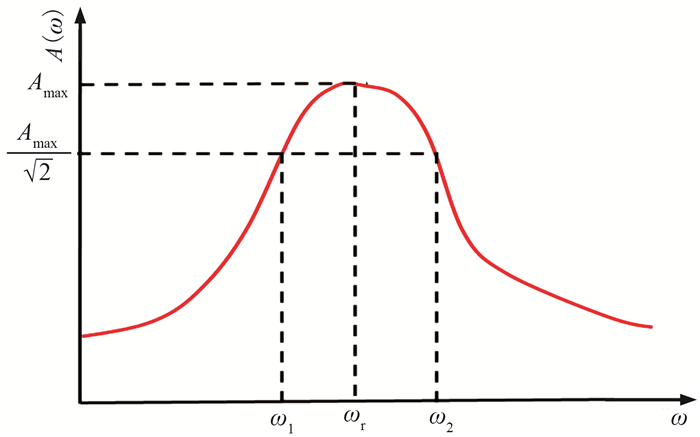
通常利用外源以基波或谐波频率在岩石样本中激发产生驻波。当岩石棒(杆)发生驻波共振或谐振时,利用共振或谐振频率ωr与谐振曲线(即驻波谐振振幅谱曲线,图 5)半功率点频率范围Δω的比值即可估算岩石样本Q值。具体计算公式如下[19, 23]
| $ \frac{1}{Q} = \frac{{{\omega _2} - {\omega _1}}}{{{\omega _{\rm{r}}}}} = \frac{{\Delta \omega }}{{{\omega _{\rm{r}}}}} $ | (20) |
|
图 5 驻波谐振曲线示意图[19] |
按照目前驻波法Q值测试常用实验装置设计结构不同,大致可将其划分为悬线法[29, 31]、单或双支撑点法[26, 28, 32]等(图 6)。
悬线法Q测量装置出现最早,整体设计较为简单,不过实用中样本调平困难,测量效率较低。双橡胶支撑点法和双转体固定悬线法均是对传统悬线的改进。森本喜隆等[32]用双橡胶柱替换双悬线支撑样本,并将整个测量装置放置在一个大的操作平台上,因而易于调平样本,测量更便捷。双转体固定悬线法设计思路更加巧妙,其测量系统由两个可调整的转动体组成,岩石样品通过固定在转动体顶底的垂直细钢丝被固定在两个转动体之间,当转动体1被激励时,产生绕铜丝的微小振动,进而引起岩石样本的弯曲振动,并将振动传递给转动体2被记录下来。该方法无需调平等操作,应用更方便。单支撑点法是Winkler[28, 34]设计开发的全新实验装置,它较好地克服了驻波法难以在复杂介质环境(如考虑温度、围压的影响等)中实施测量的不足,可实现不同温压条件的Q值测量,适用性更强,测量效率更高。需要指出的是,上述所有实验装置均可用于自由振动测量。
由于驻波法测量结果主要为扩张波和扭转(剪切,S)波的衰减。而地震波主要为体积压缩和剪切形变诱发的压缩波(P波)和剪切波(S波),因此,基于驻波法得到的结论一般难以直接应用于现场行波。为此,Winkler[28.34]在线性和弱衰减假设条件下,推导了驻波衰减与行波衰减品质因子之间的相互关系,有
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\left( {1 - \sigma } \right)\left( {1 - 2\sigma } \right)}}{{{Q_{\rm{P}}}}} = \left( {1 + \frac{\sigma }{{{Q_{\rm{E}}}}}} \right) - \frac{{2\sigma \left( {2 - \sigma } \right)}}{{{Q_{\rm{S}}}}}}\\ {\frac{{1 + \sigma }}{{{Q_{\rm{K}}}}} = \frac{{3\left( {1 - \sigma } \right)}}{{{Q_{\rm{P}}}}} - \frac{{2\left( {1 - 2\sigma } \right)}}{{{Q_{\rm{S}}}}}}\\ {\frac{{1 - 2\sigma }}{{{Q_{\rm{K}}}}} = \frac{3}{{{Q_{\rm{E}}}}} - \frac{{2\left( {\sigma + 1} \right)}}{{{Q_{\rm{S}}}}}} \end{array}} \right. $ | (21) |
如果0≤σ≤0.5,则有
| $ {Q_{\rm{K}}} > {Q_{\rm{P}}} > {Q_{\rm{E}}} > {Q_{\rm{S}}} $ | (22) |
| $ {Q_{\rm{K}}} = {Q_{\rm{P}}} = {Q_{\rm{E}}} = {Q_{\rm{S}}} $ | (23) |
| $ 或\;{Q_{\rm{K}}} < {Q_{\rm{P}}} < {Q_{\rm{E}}} < {Q_{\rm{S}}} $ | (24) |
式中:σ为泊松比;QP为压缩波品质因子;QE为扩张波品质因子;QS为剪切波品质因子;QK为体积压缩波品质因子。
对于式(22)~式(24),仅当泊松比在一定范围内,相应弹性模量方程才成立。
总体而言,驻波法可适用于较低频率的Q值测定,且Q值估算精度较高,但因其测量原理与地震波传播理论不同,通常无法直接用于地震勘探。此外,当测量环境条件较复杂(如考虑温度、压力变化的影响)时,测量往往难以实现。正因如此,驻波法在地震勘探岩石样本测试研究和应用中具有很大局限性。
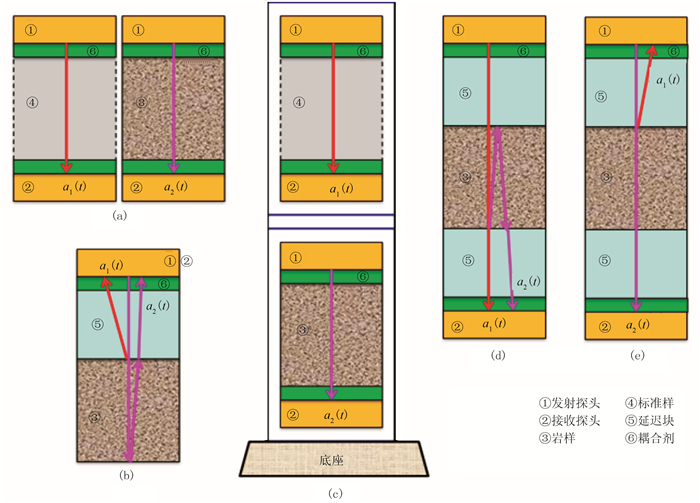
3.3 行波法行波法也称为动态脉冲法,是基于平面波假设和常Q模型假设,通过测量求取岩石样本中超声脉冲波传播的衰减谱,进而采用谱比法换算求取Q值。目前常用测试法主要有脉冲透射波法[19]、脉冲反射波法[27, 32]及改进法[24, 28, 34](图 7)。
经典脉冲透射波法[19](图 7a)实施过程中,首先需要将标准样(或称为参考样本)和待测岩样加工成相同几何形状和相同体积。通常标准样采用可视为无衰减的高Q值(Q=50000)铝样。然后,采用同一测试系统分两次先后对标准样和待测岩样实施透射波传播测量。最后,拾取脉冲波在待测岩样中的传播时间,并将测量所得透射脉冲信号做频谱分析获得振幅谱,进一步,利用前述谱比法原理即可直接换算得到待测岩样的Q值。该方法因需要重复两次测量,所以测量效率较低,且受两次测量环境的变化影响较大。为此,一种新的同步脉冲透射波测试新方法被提出[24](图 7c)。其将标准样和岩样加载到同一测试系统,在相同温压条件下,一次测量可同时获得标准样和岩样的透射波脉冲波信号,不仅大大提高了测量效率,而且避免了经典脉冲透射波法逐次测量可能出现的测量环境变化问题。不过,该方法要求两组测试探头的材料、谐振频率等必须要一致。
经典反射波法测试[27, 32](图 7b)过程中只需要一个探头,该探头既是发射探头,也是接收探头。为了获得岩样顶面的反射波,通常在岩样上部叠合一个截面尺度与岩样大小相同且Q值足够大的延迟块(也称为缓冲块),通常采用铝块或有机玻璃块。岩样底面为自由界面或者增加一个缓冲块。这样通过测量岩样顶、底面反射脉冲,采用与透射波法类似的处理方法,由谱比法即可换算得到岩样Q值。图 7d和图 7e是在经典透射波和反射波测试方法基础上发展的部分改进方法[23-24, 34],笔者分别将其称为透射—反射波法和反射—透射波法。其Q值测试的基本原理相同,在此不再赘述。
最后,需要指出的是不论是透射波法还是反射波法,在Q值测量过程中脉冲波传播振幅的变化除了受到样本本身固有衰减特性的影响外,还会受到几何扩散、界面反射、透射以及岩石内部非均匀散射等多种因素的影响,因此,测试过程中设法消除固有衰减外的其他因素对波传播振幅影响是关键。谱比法可在一定程度上减少或降低几何扩散、界面反射、透射等因素的影响,因而在超声波Q值测试中被广泛应用。
总体而言,超声波Q值测试技术基本成熟,一般可实现不同温压条件下的岩石样本弹性模量和衰减特性的高效测试,且Q值测试结果相对较稳定。因测量原理与地震波传播原理相同,且易于实现,是目前应用最广且最为成熟的方法之一。与前两种测试方法相比,超声波测试频率远远高于地震勘探频率,是三类样本测试方法中测量频率最高的方法。正因如此,当地层品质因子不满足常Q假设条件或存在频散时,超声实验Q值测试结果将无法直接用于地震勘探。
4 地层原位测量Q估算方法地层原位测量Q估算主要是利用地面测量数据和微测井观测数据估算或反演近地表Q值。地面测量数据通常包括常规地面地震观测数据(俗称大炮记录)、专门用于近地表结构调查的浅层折射波数据(俗称小折射)以及工程地震中的面波勘探数据等。因测量数据频率与地震勘探基本一致,Q值估算结果可直接用于地震波衰减特性分析和补偿处理应用。不同来源数据Q值估算结果的纵向分辨率和空间采样率存在较大差异。下面按照地面观测法和微测井法两大类分别阐述其方法原理。
4.1 地面观测法对于不同来源的地面观测数据,按照可用于近地表Q值估算的地震波特点划分为:面波、初至直达波、初至折射波和浅层反射波。因初至直达波和初至折射波Q值估算原理具有同一性,可将其合并分析,并统称为初至波法。下面分别就面波法和初至波法Q值估算方法原理加以阐述。利用反射波数据反演估算地层Q值的研究尽管很多,但大多集中在深层,真正用于近地表Q值建模的研究则很少[11]。参见4.3节详述,此处略。
4.1.1 面波法目前,面波法在近地表地层结构和速度分析方面已取得较好的应用,并已成为工程勘查的重要技术手段之一。基于面波法数据的衰减研究和Q值估算最早始于天然地震和工程勘查中,在地震勘探中的研究和应用才刚刚起步,尚处于初级阶段。面波法Q值估算主要是利用瑞雷面波和勒夫波的衰减特性估算地层纵横波Q值,且尤以瑞雷面波的应用居多[35-44]。对近地表Q值估算而言,瑞雷面波数据可由面波勘探获得,也可通过常规地面地震勘探资料获得,如大炮记录中的面波干扰信息。至于勒夫波通常多见于井间地震数据或煤矿井下槽波地震勘探数据中。
瑞雷波沿着自由地表传播时,通常具有高能量、低速度和低频率的特点[39, 42]。在均匀介质中,瑞雷波一般呈指数规律衰减,相速度与频率无关,不存在频散现象。在非均匀介质中,瑞雷波具有频散特性,不同频率的谐波成分传播相速度不同,进而会造成面波波形随传播距离的变化,而且面波频散与介质的层状结构有直接的联系,这为利用面波估算近地表属性参数提供了基础。Mitchell[35]利用层状地质模型通过反演瑞雷波衰减系数研究了北美洲上地壳Q的结构。刘学伟等[41, 43]把风化层视为黏弹性介质,用面波反演风化层Q值。胡家富等[44]根据瑞雷波的群速度和相速度频散反演剪切波速度,同时计算基阶瑞雷波振幅谱,并利用线性回归得到衰减系数的频散曲线。裴江云等[45]利用面波衰减Q模型反演近地表Q值,并通过反Q滤波提高地震资料的分辨率。在常Q模型假设[46]和Q值为深度函数的层状模型假设[35]前提下,Xia等[36-39]推导了瑞雷波衰减系数与纵、横波Q值之间的关系,探讨了反演瑞雷波衰减系数的可行性,并利用高频振幅信息求得近地表Q值。在其专著[40]中对利用面波信息估算Q值进行了系统总结和阐述。理想情形下,用高频(≥2Hz)瑞雷面波可估算近地表 30m深度范围内Q值[40, 42]。具体反演算法如下。
在平面波假设条件下,瑞雷波随传播距离呈指数衰减[37, 40],与前述Futterman吸收衰减模型相一致。因此基于谱比法原理可由任意两道面波记录谱求取瑞雷波频域衰减系数αR(f),有
| $ {\alpha _{\rm{R}}}\left( f \right) = - \frac{{\ln \left[ {\left| {\frac{{W\left( {x + {\rm{d}}x,f} \right)}}{{W\left( {x,f} \right)}}} \right|\sqrt {\frac{{x + {\rm{d}}x}}{x}} } \right]}}{{{\rm{d}}x}} $ | (25) |
式中:W为瑞雷波振幅谱;x为炮检距;dx为相邻两检波器间距。
在层状介质假设条件下,瑞雷波衰减系数和纵横波耗散因子之间的关系可表示为[37, 40]
| $ {\alpha _{\rm{R}}}\left( f \right) = \frac{{{\rm{ \mathsf{ π} }}f}}{{C_{\rm{R}}^2\left( f \right)}}\left[ {\sum\limits_{i = 1}^n {{P_i}\left( f \right)Q_{{{\rm{P}}_i}}^{ - 1}} + \sum\limits_{i = 1}^n {{S_i}\left( f \right)Q_{{{\rm{S}}_i}}^{ - 1}} } \right] $ | (26) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {{S_i}\left( f \right) = {V_{{{\rm{S}}_i}}}\frac{{\partial {C_{\rm{R}}}\left( f \right)}}{{\partial {V_{{{\rm{S}}_i}}}}}}\\ {{P_i}\left( f \right) = {V_{{{\rm{P}}_i}}}\frac{{\partial {C_{\rm{R}}}\left( f \right)}}{{\partial {V_{{{\rm{P}}_i}}}}}} \end{array}} \right. $ | (27) |
式中:CR(f)为瑞雷波相速度;n为层状介质模型的层数;VPi、VSi分别为第i层的纵、横波速度;QPi-1、QSi-1分别为第i层的纵、横波耗散因子。
式(26)反映了瑞雷波衰减系数相对于QPi-1、QSi-1的变化率,控制了瑞雷波的衰减系数对QPi-1、QSi-1的灵敏度。式(25)和式(26)共同构成了由面波衰减估算纵横波Q值的基本公式。
具体计算中,首先需确定速度频散曲线CR(f)。目前常用速度频散曲线确定方法主要有面波谱分析法(SASW)和多道面波分析法(MASW)。前者是在频率域通过计算两道检波器之间的相位差提取频散曲线,计算效率和精度均较低。后者则是采用带阻尼的广义线性迭代反演从多道地震数据中提取频散曲线和反演横波速度,不仅能够较好地压制噪声,而且计算精度较高。
夏江海等研究表明[37, 40],在已知瑞雷波相速度和表层介质纵、横波速度的前提下,联立式(25)、式(26)可反演近地表的纵波和横波的耗散因子或品质因子。但是此反演算法稳定性较差,仅当VS/VP>0.45时,方可获得有效Qp反演,且反演误差近似为衰减系数误差的1.0~1.5倍。为了提高反演算法稳定性,在式(26)中引入阻尼系数,则反演方程可由如下带阻尼矩阵方程描述,有
| $ \left( {\mathit{\boldsymbol{A}} + \lambda \mathit{\boldsymbol{I}}} \right)\bar X = \bar B\;\;\;\;{x_i} > 0 $ | (28) |
式中:I为酋矩阵;λ为阻尼系数;X为待反演品质因子;为衰减系数;A为与速度频散有关的系数矩阵。
此外,何洋洋等[46]提出了利用单炮瑞雷面波记录借助于多道面波分析、拉东变换以及模拟退火反演算法理论估算近地表Q值的新方法。因专利书中并未给出Q值估算的实际成果,具体效果如何尚有待进一步验证。
对于勒夫波,其与瑞雷波最大的不同是衰减系数与P波速度无关,仅与剪切波速度有关,且频散曲线较为简单[38]。利用勒夫波衰减系数反演耗散因子的表达式较瑞雷波衰减系数参数更少,表达式更简洁,减少了反演的非唯一性,因此,反演结果较瑞雷波更稳定。然而,由于P波能量和随机噪声的影响使衰减系数求取存在较大误差,通过衰减系数反演横波Q值仍然难以获得较高的精度。
综上所述,尽管理论上采用面波法可同时估算纵、横波Q值,但因面波数据处理、信息提取及高精度频散曲线和衰减系数求取方法等尚待完善,整体而言,Q值估算精度还较低,相关算法理论还有待深入研究和不断完善。此外,由于来自自由地表面波的趋肤效应,面波法探测深度有限,仅可反映自由地表附近有限深度地层的衰减特性。
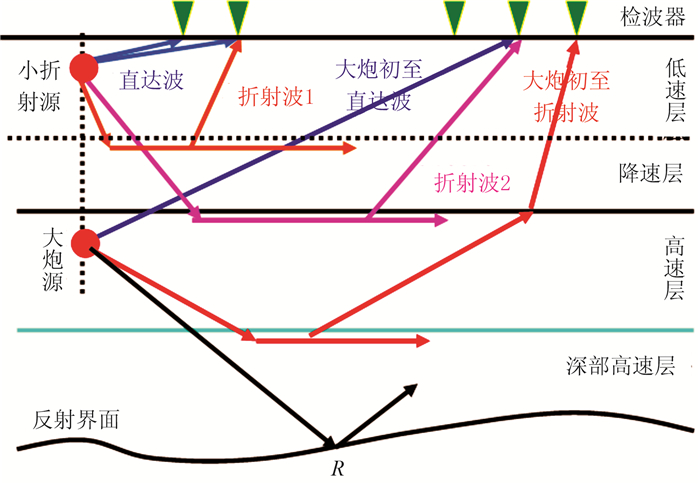
4.1.2 初至波法初至波法主要利用大炮记录或浅层折射(即小折射)记录中的初至直达波和折射波的振幅或能量差异等信息,基于谱比法或质心频移法等算法直接估算近地表地层平均Q值,或通过层析成像算法反演确定近地表Q值的空间分布[11, 47-48]。两种波Q值估算结果的唯一差异是探测深度不同。大炮采集通常在潜水面以下高速层中以炸药激发[40, 42, 49],而小折射采集则多采用浅坑炸药激发(坑深一般不大于0.5m)或重锤敲击激发,因激发深度不同,大炮记录初至波与小折射初至波传播路径截然不同(图 8),因而所反映的近地表衰减特性也不完全相同。
|
图 8 小折射与大炮初至波射线路径示意图 |
由图 8可见,对于小折射而言,基于初至直达波的Q值主要反映低速层的衰减特性;基于降速层的初至折射波1的Q值主要反映降速层的衰减特性;基于高速层的初至折射波2的Q值主要反映高速层的衰减特性。相比较而言,基于炸药震源大炮记录的初至直达波的Q值主要反映低、降速层及部分高速层衰减的平均效应,相应初至折射波则来自于近地表高速层之下的深部高速地层,因此,从严格意义上来讲,基于大炮初至折射波的Q值已不再反映通常意义下的近地表衰减特性。这一点很容易被研究者忽略,错误地认为大炮初至折射波反映的是近地表高速层的衰减特性。不过,当采用可控源激发时,因震源点位于地面,相应大炮记录初至波与小折射初至波均可较好地反映近地表衰减特性。
Jeng等[50]采用VAKIMPAK机械震源和7kg重锤震源分别激发,道间距为2.0m的24道三分量检波器短排列实施二维地面观测。通过拾取初至直达波,在假定Q与频率相关的前提下,采用谱比法(式(2))依次由具有不同频率和不同道间时差的谱比对数值估算近地表纵、横波Q值,较好地验证了测区内近地表Q值与频率相关这一论断。
Brzostowski等[12]基于俄克拉荷马州东南部奥基塔前缘逆冲带三维地面观测数据,通过拾取初至波旅行时间和振幅,采用速度与Q值联合反演方法,成功实现了近地表速度和Q层析成像,且成像结果与近地表地质情况吻合。Gao等[51]利用鄂尔多斯黄土塬区大炮初至波信息,采用速度与Q值联合反演方法获得了近地表黄土层Q值的良好成像,进一步采用基于波动方程的衰减补偿实现了近地表吸收衰减的稳健补偿。
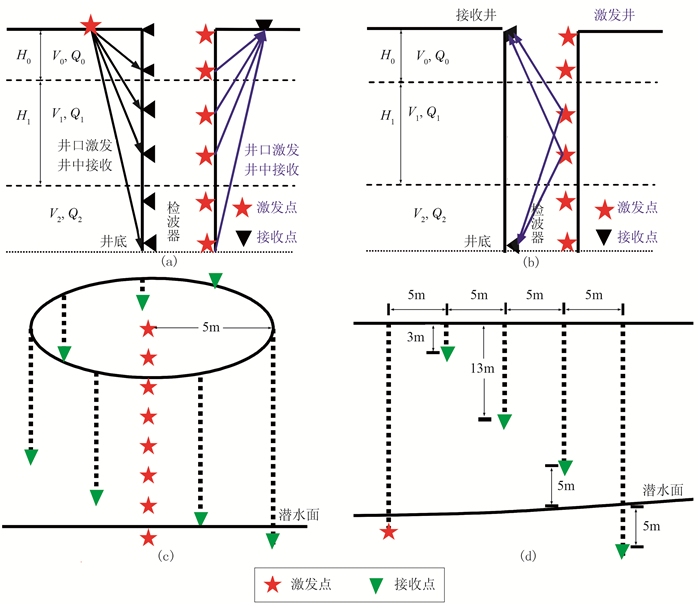
4.2 微测井法作为近地表结构调查最常用方法之一,微测井具有施工简单、地表适应能力强、应用范围广和测量精度高等诸多优点。早期微测井主要用于近地表结构调查和速度分层,直到高分辨率地震勘探出现,逐渐利用微测井资料估算近地表衰减特性。按照微测井观测系统的不同,笔者将微测井分为单井微测井[2, 52-53]、双井微测井[54]、多井微测井[2, 55]和井地联合微测井[14, 56-57],如图 9所示。
单井微测井是目前应用最多的微测井观测方式,其常用观测系统主要有井中激发—井口或地面接收[2, 52]、井口激发—井中接收[53, 58](图 9a)两种类型,在钻井条件便利、激发条件较好、地表平坦的平原区大多采用前一种类型。实际施工中通常在井口周围呈扇形排列或十字交叉状排列布设一定数量检波器,以便获得更丰富的试验区微测井信息。对于诸如山地等激发条件较差、钻井困难的探区,往往采用井口激发—井中接收观测系统。在某些特殊情况下,为了进行数据对比分析,两种观测模式可交替或同时采用。
双井微测井和多井微测井主要针对复杂近地表结构调查或者专门为某一特殊目的而设计。以多井微测井为例,其大多用于复杂近地表衰减特性的精细研究。就现场观测方式而言,双井微测井类似于井间地震,通常在一口井中依次激发,在另一口井中多道接收(图 9b)。多井微测井常用观测模式有圆形排列观测[14, 55]和直线排列观测[2]两种模式。前者通常由位于潜水面之下的井底位置向上每隔一定深度依次激发,然后以炮井井口为圆心,有限长度为半径,沿圆弧等间距布设若干深度渐变的接收井,并在井底布设检波器接收(图 9c)。杜增利等[55]称此为补偿微测井。后者则是利用地面地震勘探的炮井在潜水面以下单点激发,从炮井向外沿测线方向以较小的间距,按一定的间距钻若干不同深度接收井,并在井底分别埋置检波器接收(图 9d)。石战结等[2]称此为大炮震源微测井。两种模式均要求必须保证在低、降速层的顶、底部均有接收点。这类观测系统的优点是能根据需要得到整个低降速层不同深度的地震记录,记录的信噪比高;缺点是要通过钻井方式埋置检波器,在钻井过程中钻井液或钻头压力对地层原有弹性特性的改造不可避免。
井地联合微测井目前常见观测系统是在图 9所示单井和多井微测井观测系统基础上增加了地面直线排列[14, 56-57]。其突出优点是可实现井地观测数据的互补。考虑到其Q值估算所涉及地震波场的多样性,将在后文4.3节加以详述。
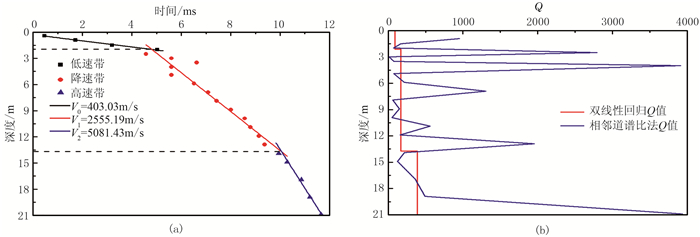
目前,基于微测井资料实施Q估算多采用谱比法和频移法以及Q-V经验公式法等,且以单井微测井近地表衰减Q值估算应用居多。云美厚等[59]以微测井速度解释成果为基础,借助于Q-V经验公式近似估算Q值,对比、分析了川东北碳酸盐岩裸露区近地表不同岩性出露区段衰减特性差异。张光德等[60]针对柴达木盆地三湖地区盐岩区的勘探实际,利用谱模拟谱比法由微测井数据估算了近地表Q值。李伟娜等[58]针对传统的相邻道谱比法Q值估算稳定性差、精度低等问题,提出了基于速度分层约束的非相邻道双线性回归稳定Q值估算新方法。该方法可获得与近地表速度分层相一致的较为稳定的、地质意义明确的近地表Q估算值,且对于各种微测井观测系统均具较好适应性。图 10为川东北实测微测井数据近地表速度分析结果以及传统相邻道谱比法与非相邻道双线性回归新方法Q值估算结果的比较。显然,新方法Q值估算结果更稳定且与速度分层具有良好的一致性,地质意义更明确。
|
图 10 川东北实测微测井数据近地表速度分析(a)与Q值估算结果(b)[58] |
于承业等[54]通过双井微测井观测,由地面和井底检波器接收的初至波信号峰值频率利用峰值频率频移法获得了较好的近地表Q估算。杜增利等[55]以塔里木和准噶尔盆地试验区为靶区,基于多井微测井圆形观测模式(图 9c)采用谱比法和上升时间法估算地表疏松沙层的Q值,揭示了在100m深度范围内,沙层Q值分布范围为7~25。石战结等[2]利用多井微测井直线观测模式(图 9d),研究西部大沙漠区近地表地震波衰减规律,较好地克服了常规单井微测井Q值估算的不足,实现了近地表巨厚沙层对地震波的吸收衰减的有效补偿。
需要指出的是,在近地表品质因子“大样”测试方法中,当实测资料品质较好时,基于微测井资料的Q值估算精度最高。通常影响微测井Q值估算精度的主要原因有四个。①因钻井破坏作用导致井壁附近浅层介质的压实程度和湿度改变,进而可能会改变浅层介质速度与Q值。②因检波器埋置条件和耦合效应的差异导致所接收初至波波形和振幅差异。对于井中接收微测井,井壁的光滑程度直接影响井中检波器的耦合效果,特别是对于检波器与井壁的耦合影响尤为显著,采用井底检波器接收耦合效果相对要好一点。③因不同深度激发条件(岩性、耦合性)差异导致激发子波波形、能量、频宽及主频等差异。对于井中激发微测井,激发是主要影响因素,其次为接收因素;对于井中接收微测井而言,检波器与井壁的耦合效应是最大影响因素,其次才是激发因素。④品质因子和旅行时间随射线路径变化导致基于常Q模型的Q值估算方法适应性变差。由此可见,利用微测井数据估算Q值,设法降低或消除上述各因素的影响是保证估算精度的关键。
总体而言,基于微测井数据的近地表Q值估算是目前估算精度较高、应用最广的方法之一[54, 61]。相关商业软件已基本实现了工业化应用。与单井微测井相比,双井微测井、多井微测井以及井地联合微测井因实施工艺繁杂、勘探成本高,主要用于复杂近地表衰减特性的分析研究。
4.3 联合Q值估算与反演随着复杂近地表地震勘探工作量的不断增加及地震勘探对分辨率的要求不断提高,对复杂近地表地层结构和吸收衰减特性的精细建模要求也越来越迫切。为此,将微测井Q值估算的纵向高分辨率与地面观测Q值估算的横向高密度相结合,采用井地联合观测数据或多源多波场数据估算和反演近地表Q值,构建精细近地表Q模型已成为当前研究的主旋律。前者被称为井地联合Q值估算,后者则可称为多源多波场联合Q值反演或层析成像。二者统称为联合Q值估算与反演。分述如下。
4.3.1 井地联合Q值估算井地联合Q值估算主要是利用微测井纵向Q值分层能力强以及地面观测横向Q值采样密度大的优点构建精细近地表Q模型。目前主要有两种实现途径:一是通过设计专门的井地联合微测井观测系统,并基于实测数据实现精细近地表Q值估算;一是利用单独测量的微测井和地面大炮初至波数据分别实施Q值估算,然后通过两种Q值估算结果的数据融合构建精细近地表Q值空变模型,进而用于衰减补偿处理以提高地震资料分辨率。
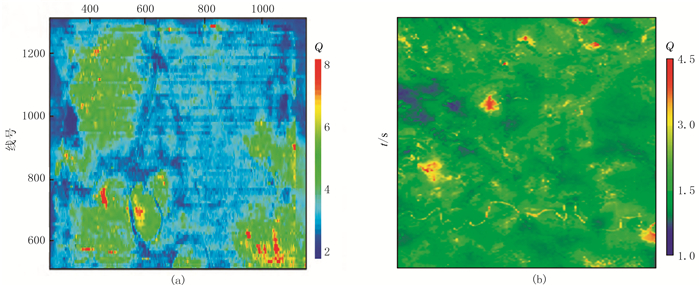
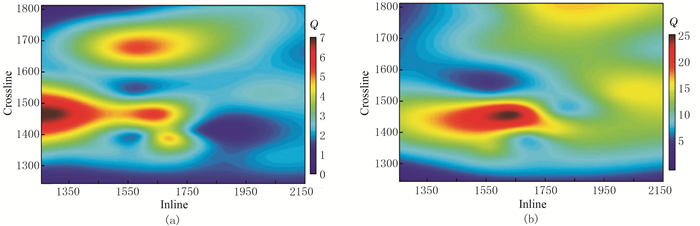
翟桐立等[56]以大港油田的沧东凹陷孔店工区为靶区,按照2km×2km的网格在工区内多点均匀布设地面短排列井地一体化观测系统,并利用谱比法对实测数据实施Q值估算,然后通过区内多点Q值估算值内插获得全区近地表Q模型(图 11)。进一步利用此估算结果实施近地表吸收衰减补偿处理,较好地提高了叠加剖面的分辨率。
|
图 11 近地表低速层(a)和降速层(b)Q值平面分布[56] |
陈志德等[49]利用大炮初至波振幅的相对变化求取各检波点的相对Q值,再用基于微测井资料的质心频移法估算的绝对Q值对其标定,进而可获得精度较高的空变近地表Q模型(图 12a)。实际应用和反Q滤波处理表明补偿效果明显,与常规处理成果相比,在保持地震低频成分的前提下可展宽频带10Hz以上。宋吉杰等[57]采用同样的研究思路实现了塔北浮土区可靠近地表Q模型的构建。不同之处是为了提高调查点Q值估算精度,其在直线排列多井微测井观测系统(图 9d)基础上,通过延长地面排列设计了多井微测井和地面直线排列相结合的新型井地联合微测井观测系统,以此实现调查点的精细Q值估算。然后基于大炮记录炮检点初至波数据统计、反演全区相对Q值,进一步运用信息融合策略由调查点精细Q值约束相对Q值,构建精确的近地表Q模型(图 12b)。经叠前补偿处理,目的层的地震反射波频带展宽超过20Hz,极大地提高了地震资料分辨率。不过需要指出的是,文中将高速层激发、地面远排列道接收的直达波称为折射波是不当的,具体原因见图 8大炮初至直达波。
Li等[14]在图 9c所示微测井圆形观测系统基础上,沿地面测线方向增加了一条过微测井中心点的测线,从而构建了井地联合微测井观测系统。进一步采用前述谱比法层析反演算法对实测数据实施了近地表Q值空间分布的反演成像。经合成地震记录数据和大庆油田实测数据的试用表明,该方法Q值估算结果具有较好的稳定性和可靠性。
4.3.2 多源多波场联合Q值反演所谓多源多波场联合Q值反演主要是指将多种来源数据(如面波勘探、小折射、大炮记录、微测井等)的多种波场(如纵、横波或直达波、折射波、反射波、面波等)观测数据共同作为基础数据实施联合Q值反演成像。随着计算机技术的发展,特别是并行与多进程运算技术的出现,极大提高了基于波传播模拟和层析成像等反演算法的计算效率,相关软件技术日趋成熟并投入商业应用,但是,不论是纵横波联合反演还是井地联合反演大多用于深层储层反演成像[14-17, 62]。在近地表速度建模和衰减研究中常见大炮初至反演、微测井初至波反演等单一数据源或单一波场的反演,真正基于多种数据源或多种波场类型的联合近地表Q值反演与建模研究则很少。现有近地表联合反演大多以初至波(初至直达波、折射波)反演最为普遍,将浅层反射波用于近地表结构调查或衰减同样很少。EI Yadari等[11]基于波传播模拟法开展了反射波法近地表Q值估算方法探索,受计算方法和计算效率等影响,仅仅较准确地估算了第一层介质的Q值。随着各种反演成像算法和软件工业化应用程度的提高,基于多源多波场联合Q值反演构建精细近地表Q模型无疑具有良好发展前景。特别是随着多波多分量观测技术在近地表调查中的推广应用,开展纵、横波观测数据联合解释与反演方法研究较单分量、单一波场的分析更具有实际意义。
5 近地表Q值估算法对不同地表结构类型的实用性分析对于不同的近地表结构类型,相应近地表结构调查方法各不相同。因此,可用于近地表Q值估算的方法也不尽相同。鉴于中国陆上近地表结构类型的多样性,下面针对部分常见近地表结构类型就前述各种Q值估算方法的实用性做粗略分析(表 3)。
|
|
表 3 不同近地表结构类型近地表Q值估算方法实用性初步评价 |
由表 3可见,对于平原区,现有近地表Q值估算方法均具有相对较好的实用性,且各种近地表Q值估算方法的应用效果均优于其他三种表层结构类型。对于沙漠区,基于地面观测的面波、初至波Q值估算与反演是实施近地表Q值估算的最佳途径。尽管基于微测井,特别是多井微测井用于沙漠区近地表Q值估算不乏一些成功案例[2, 55, 61],但由于沙漠区成井不宜,故基于微测井实施近地表Q值估算尽管可用,但并非普遍实用的方法。与沙漠区相比黄土塬区和山地岩石区相对容易获得钻孔取样,故三大类岩石样本测试方法均可用于Q值估算,部分因地层岩石破碎无法取样的情况除外。在地表相对平坦区,基于面波法以及小折射和大炮初至波有望获得较为理想的近地表Q值估算。在地表起伏变化区,微测井是获得近地表Q值估算的最佳途径。因山区钻井成本高,实施多井微测井Q值估算尽管可行,但不实用。需要指出的是,近地表Q值精确估算的主要目的在于衰减补偿处理,以提高地震资料的分辨率。但对于沙漠区、黄土塬区以及山地碳酸盐岩裸露区等极低信噪比地区,尽管低信噪比成因多样,或因激发能量不足、或因表层衰减严重、或因干扰波发育,或者是多种因素的叠加。总之,对于此类地区勘探的重点是大力提升激发能量,全方位消除和压制噪声,进而提高资料的构造成像质量,甚至可不惜牺牲分辨率换取信噪比。,
6 问题与展望综上所述,尽管可用于估算近地表Q值的方法很多,但就Q值估算或反演结果的精度和稳定性而言,仍存在明显的不足,在近地表衰减补偿处理中的实际应用效果也参差不齐。下面就目前近地表Q值反演估算中存在的问题以及未来可能的发展方向进行初步概述。
(1) Q值测试及反演估算精度整体偏低,因此,设法提高近地表Q值反演估算精度仍然是未来研究和发展的主旋律。
现有Q值反演估算方法大多是基于常Q模型,即Q值与频率无关这一衰减机制实现的。事实上,所谓“常Q”一般仅仅是对一个不太宽的频带而言的,对于不同的频率范围,即使是对同一块样品所测Q值也常常是不同的。因计算所采用的模型本身具有极大的近似性,不论是岩石物理实验测试还是地层原位测量,Q值反演法估算精度整体上偏低,即使是对于普遍认为测量精度最高的岩石物理测试结果,Q值测量的相对误差依然非常大,一般为10%~20%[5]。由此不难想象,基于地层原位测量数据的Q值反演精度将更加令人堪忧。通常认为利用微测井数据可准确求取地层Q值,实际情形是由于上、下行波场的干涉效应、短程微屈多次反射波以及透射损失等对频谱的影响,造成利用理论上纯直达下行波(地面激发—井中接收)或上行波(井中激发—地面观测)求取Q值时,反演估算误差依然会高达一倍以上。若采用实测数据经波场分离后的上、下行波估算Q值,再加上时间拾取误差以及噪声干扰的影响,Q值估算误差将会达到难以容忍的程度[11, 53, 58]。因此,设法提高Q值估算精度将会是未来研究的重中之重。开展Q值估算新方法、新技术探索研究,寻求更加可靠、稳定的Q值估算与反演方法依然任重道远。那么,如何来提高近地表Q值反演估算精度呢?笔者认为可从以下几个方面加以深入研究。
1) 重视近地表衰减方法理论的改进与完善。目前,可用于描述地层介质吸收衰减特性的基本理论有很多,诸如黏弹性介质理论、双相介质理论、喷射流理论等。不同的理论是基于不同的假设条件提出的,基于不同理论的分析结果具有明显的差异性,Q估算或反演结果也不同。由于近地表地层介质的复杂性和特殊性,单纯利用单一衰减机制或理论很难完全合理地描述其衰减特性。因此,在现有衰减理论基础上,如何实现多种理论的相互融合与完美统一,构建能够更加准确描述近地表吸收衰减特性的新理论,为近地表衰减定量分析奠定基础,对于优化反演算法无疑具有重要的意义,这将是衰减理论研究的重要发展方向之一。
2) 寻求最佳反演方法。现有的反演估算方法大多是基于经典的平面波传播理论和Futtman模型给出,方法的抗噪性、稳定性、灵敏度等还存在很大不足。因此,应重视多种算法的互补融合以克服单一算法的局限性。从长远来看,基于现场实测数据的全波场Q值层析成像,特别是考虑地形起伏变化的全波场层析反演算法研究,可能对提高反演精度具有积极的意义。换言之,基于多源多波场信息的Q值联合反演研究值得进一步深入。
3) 重视波场分离和有效波提取方法研究。由于地震波场的干涉效应以及各种噪声的影响,不论是微测井数据,还是地面测量数据都不同程度受到续至波场和噪声的影响,因此,寻求最佳的波场分离方法和有效信息提取方法,是改善近地表Q值估算结果的重要环节。特别是利用大炮面波信息反演近地表Q值时,准确的面波资料获取无疑是保障Q值估算精度的根本。
4) 应重视浅层地震记录数据偏振特性的研究和校正。以常规单分量垂直检波器接收为例,通常当炮检距小于目的层埋深一半时,来自目的层的反射波近似垂直地表出射,此时垂直检波器接收信号以反射纵波为主,相应记录可视为纵波记录。但是,对于浅层初至波或浅层反射波而言,不论是在小折射记录中的折射波、还是大炮记录中的初至直达波、折射波或反射波,远炮检距道出射角均很大,因纵波偏振方向严重偏离垂直方向而造成的记录纵波能量变化是不可忽略的。在这种情况下,利用相关记录研究或分析近地表速度变化是可行的,若用于研究衰减效应或反演Q值时就必须要注意考虑是否需要进行偏振校正。
5) 应分区域、分类型研究近地表吸收衰减参数检测的影响因素及工艺流程。纵观中国的陆上近地表结构类型,主要包括第四系沉积形成的平原区、巨厚沉积且干燥的黄土塬冲沟区、山地岩石区、呈现连续介质特征的沙漠区、沉积地层与火山岩互层区等多种近地表结构类型。近地表结构类型与特征不同,相应近地表结构调查方法与参数表征方法也不尽相同,甚至可以说是千差万别。为此,分区域研究不同类型近地表结构特征条件下不同近地表调查方法的影响因素,评估对近地表参数检测的影响程度等。与此同时,开展工艺流程的研究,针对性地通过工艺流程的改进与完善有效消除不同区域、不同类型近地表结构吸收衰减参数检测的影响,持续提升参数检测及建场精度。
(2) 表层松散介质Q值测试、测量研究和创新不足,探索松散介质Q值测试技术应予以重视。
近地表由于地层风化作用的影响,大多为未固结成岩的疏松介质或破碎岩石,特别是沙漠区、砾石覆盖区等完整取样基本上是不可能的。那么,如何在不改变松散介质特性的前提下,对其开展岩石样本测试,就必须要在测试方法技术上寻求突破。目前,相关研究还很少,杨凯[63]曾将来自塔里木和准噶尔盆地的松散沙样放在特制密闭容器内,模拟不同深度地质条件,实施了不同压力和不同含水量的沙层速度与品质因子Q值的超声测试,尽管取得了一定的测试结果,但这种模拟松散介质是否能够真实反映沙层的客观实际尚无法验证。孟祥梅等[64]针对海底松散沉积物,设计制造了一个长和宽端面分别装有两组声发射与接收探头的长方形沉积物箱,可实现声波速度与衰减系数联合测量。本质上与文献[63]的测试装置大同小异。此外,专利报告中关于几何扩散损失的理论表述欠合理,对沉积物箱几何尺度大小及其对测量结果的影响等也未加以明确说明,实际应用效果无法判定。笔者认为,借鉴测井原理,开展表层原位“小样”测试方法技术研究和仪器开发值得去尝试。
就现场观测方法而言,针对近地表地质结构特点,开展包括微测井、小折射以及浅层反射波法在内的井地联合多波观测技术研究,充分利用包含面波、初至波甚至反射波信息在内的全波场信息实现近地表Q值的联合反演,以避免估算结果的多解性,获得近地表Q值精细的空间分布。或者在最佳波场分离技术研究基础上,充分利用大炮记录中的初至波(直达波、反射波)以及面波等信息,实现近地表Q值多波联合估算与层析反演,以实现Q值的相对稳定估算,这些构想将有可能成为现有条件下改善Q值估算精度的根本出路。
(3) 品质因子估算精度定量评价方法缺失。探索可作为Q值评价标准的高精度Q值测试、测量方法值得重视。
众所周知,地震速度反演结果的好坏可通过与速度测井资料的对比分析进行客观地评价。但是对于Q值反演结果而言,迄今为止没有哪一种方法可获得准确的Q值并作为衡量或评价其他方法估算精度或可靠性的判据。这正是为什么目前大多数关于Q值估算的算法研究论文中很少进行对比法Q值预测精度定量评价的主要原因。目前常用评价方法主要有基于方法过程每一步统计误差的自我评价、基于模型分析结果的评价以及基于Q补偿处理效果的间接、定性评价。可以说,这些评价方法仅是一种权宜之计,并不能对实测数据Q值反演结果的可靠性作出客观准确的评定。因此,寻求可作为Q值评价标准的高精度Q值测试、测量方法值得去探索和研究。对于深层储层Q反演而言,开展Q值测井技术研究,利用全波声波测井记录直接估算纵、横波Q值,得到Q值随深度变化曲线,并以此作为Q值评价的基础不失为一个可行的途径。但是对于近地表Q反演而言,是否引入浅层全波列测井实施Q反演,或基于测井原理开发更加便捷的近地表原位Q测试技术值得人们去尝试和探索。
一般来说,全地层Q值大致可分为三个层段,即500m以下的油气勘探层段、0~50m(最大为200m)的近地表层段以及200(或50)~500m的中间层段。之所以选取500m作为分界点主要是考虑到500m是目前VSP测井的上限。这样一来,500m以下可通过全波列测井或VSP等方法获得相对高精度Q值。对于近地表层段,理论上,基于微测井的Q值估算应该是高精度的。事实上,由于震源、检波器耦合等多种因素影响,实际反演Q值精度尚难以作为Q值精度评价的标准。至于采用浅层全波列测井求取近地表Q值,测井仪器能否有效耦合推靠井壁,测量结果能否获得满意的Q值估算效果目前尚无法定论。此外,实际生产中一般只有电测井和放射性测井偶有从地面开始的全井段测量,声波全波列测井很少从地面开始测量,煤田勘探中最浅观测深度也大多起始于基岩顶面,第四系地层声波测井纵向分层效果并不理想,这也是一个不容忽视的现实问题。
(4) 关于不同来源数据估算Q值的同一性与可比性研究不足。开展不同数据源Q值测试及估算结果的关联性研究值得探讨。
由于地震波衰减机制的复杂性,以及不同观测方式的差异性,使得影响地震波衰减的因素呈现出多样性,进而导致不同方法估算Q值的同一性或可比性较差。因此,尝试并构建不同来源反演估算数据的关联模式,以实现不同数据的优势互补和充分利用无疑具有重要的现实意义。
研究表明[50],近地表衰减或Q值是随频率变化的,即存在衰减频散效应。而现有的Q值估算均是基于常Q假设获得的。从岩石样本测试、到微测井,再到地面观测,由于观测数据存在频率差异,源于不同数据源的Q值估算结果是否具有同一性,是否具有频散特性,其关联模式是怎样的,如何实现不同数据源Q值估算结果的互补利用,等等,这些问题均值得进一步探索和研究。
(5) 关于面波法Q值反演方法的研究和应用不足。
对煤、油气地震勘探而言,面波法Q值估算不失为一个全新的近地表Q值估算方法。利用面波频散效应,不仅可估算近地表 30m范围内地层的横波Q值,而且在条件有利的情况下也可实现纵波Q值的有效估算。常规地震勘探拥有丰富的面波信息,但目前的研究和应用还几乎是一片空白。因此,如何充分利用常规勘探记录中的面波信息,使其变废为宝,更好地服务于高分辨率地震勘探的需要,无疑将会成为地震勘探的福音。
(6) 应重视近地表横波Q值估算方法研究,着力提高近地表横波衰减建模的精度。
随着多波多分量地震勘探技术的进步和推广应用,对近地表横波速度和衰减建模的要求也日益提高。由于横波速度受孔隙流体影响很小,这使横波速度变化较纵波对地层岩性变化更敏感也更稳定。换言之,利用横波速度构建近地表结构模型更可靠。与此同时,分析近地表纵横波的吸收衰减和波前扩散效应不仅有利于深层目的层反射波和转换波真实动力学特性的恢复,而且有利于通过补偿处理提高转换波地震资料的分辨率。正因如此,随着三分量检波器在常规地震勘探以及近地表结构调查中应用的不断推广应用,近地表横波速度建模以及横波衰减研究已引起业界的广泛重视。
目前,除利用岩石样本测试和面波法等手段可估算近地表横波衰减和Q值外,类似纵波近地表调查方法的横波或纵横波联合观测系统(如横波微测井[65]、横波小折射[66]以及多波多分量观测[67]等)均可用于横波衰减研究。现有的横波数据采集主要有两种模式:①基于炸药震源激发,三分量检波器接收,实施纵横波联合数据采集;②基于横波震源激发(多采用SH波源),横波检波器接收,实施纯横波数据采集。就已发表文献看,目前关于近地表横波速度建模的相关研究相对较多,而关于横波衰减,特别是Q估算的研究,尽管在算法理论上与纵波一致,但因横波信息提取、偏振处理等多方面问题,实施近地表横波Q值估算和反演还存在很大不足,相关研究还有待进一步完善和提高。
最后,需要强调的是,陆上复杂多变的近地表结构类型与不同区域的近地表结构特征、多种存在差异的影响因素交织在一起,加上所选用的检测方法及手段的多样性,使得陆上近地表结构参数检测技术的研发一直在路上,因此更需要一种科学与宽容的研究态度。
| [1] |
王建民, 陈树民, 苏茂鑫, 等. 近地表高频补偿技术在三维地震勘探中的应用研究[J]. 地球物理学报, 2007, 50(6): 1837-1843. WANG Jianmin, CHEN Shumin, SU Maoxin, et al. A study of the near surface high-frequency compensation technology in 3-D seismic exploration[J]. Chinese Journal of Geophysics, 2007, 50(6): 1837-1843. DOI:10.3321/j.issn:0001-5733.2007.06.026 |
| [2] |
石战结, 田钢. 西部大沙漠区近地表地震波衰减及高频补偿技术研究[J]. 石油地球物理勘探, 2007, 42(4): 392-395. SHI Zhanjie, TIAN Gang. Technique of attenuation of near-surface seismic wave and high-frequency compensation in western large desert area[J]. Oil Geophysical Prospecting, 2007, 42(4): 392-395. DOI:10.3321/j.issn:1000-7210.2007.04.006 |
| [3] |
李庆忠. 走向精确勘探的道路——高分辨率地震勘探系统工程剖析[M]. 北京: 石油工业出版社, 1994: 41-44.
|
| [4] |
宋智强, 刘斌, 陈吴金, 等. 沙漠区表层Q值求取及补偿方法研究[J]. 油气藏评价与开发, 2013, 3(4): 8-11. SONG Zhiqiang, LIU Bin, CHEN Wujin, et al. Research on calculating and compensation methods of Q value in desert area surface[J]. Reservoir Evaluation and Development, 2013, 3(4): 8-11. DOI:10.3969/j.issn.2095-1426.2013.04.002 |
| [5] |
云美厚, 党鹏飞, 李伟娜, 等. 地层品质因子Q值地震反演问题剖析[J]. 石油地球物理勘探, 2017, 52(1): 189-198. YUN Meihou, DANG Pengfei, LI Weina, et al. On issues of formation quality factor Q inversion[J]. Oil Geophysical Prospecting, 2017, 52(1): 189-198. |
| [6] |
Tonn R. Comparison of seven methods for the computation of Q[J]. Physics of the Earth and Planetary Interiors, 1989, 55(3-4): 259-268. DOI:10.1016/0031-9201(89)90074-5 |
| [7] |
Futterman W I. Dispersive body waves[J]. Journal of Geophysical Research, 1962, 67(13): 5279-5291. DOI:10.1029/JZ067i013p05279 |
| [8] |
Quan Y, Harris J M. Seismic attenuation tomography using the frequency shift method[J]. Geophysics, 1997, 62(3): 895-905. DOI:10.1190/1.1444197 |
| [9] |
高静怀, 杨森林. 利用零偏移VSP资料估计介质品质因子方法研究[J]. 地球物理学报, 2007, 50(4): 1198-1209. GAO Jinghuai, YANG Senlin. On the method of quality factors estimation from zero-offset VSP data[J]. Chinese Journal of Geophysics, 2007, 50(4): 1198-1209. DOI:10.3321/j.issn:0001-5733.2007.04.029 |
| [10] |
Wang S, Yang D, Li J, et al. Q factor estimation based on the method of logarithmic spectral area difference[J]. Geophysics, 2015, 80(6): V157-V171. DOI:10.1190/geo2014-0257.1 |
| [11] |
EI Yadari N, Ernst F, Mulder W. Near-surface atte-nuation estimation using wave-propagation modeling[J]. Geophysics, 2008, 73(6): 563-572. |
| [12] |
Brzostowski M A, McMechan G A. 3-D tomographic imaging of near-surface seismic velocity and attenuation[J]. Geophysics, 1992, 57(3): 396-403. DOI:10.1190/1.1443254 |
| [13] |
Xin K and Hung B.3-D tomographic Q inversion for compensating frequency dependent attenuation and dispersion[C].SEG Technical Program Expanded Abstracts, 2009, 28: 4014-4018.
|
| [14] |
Li G, Zheng H, Zhu W, et al. Tomographic inversion of near-surface Q factor by combining surface and cross-hole seismic surveys[J]. Applied Geophysics, 2016, 13(1): 93-102. DOI:10.1007/s11770-016-0544-2 |
| [15] |
于倩倩, 李振春, 张敏, 等. 谱比法地震衰减层析反演方法研究[J]. CT理论与应用研究, 2017, 26(5): 533-541. YU Qianqian, LI Zhenchun, ZHANG Min, et al. The study of seismic attenuation tomography inversion based on spectrum ratio method[J]. CT Theory and Applications, 2017, 26(5): 533-541. |
| [16] |
Cavalca M, Moore I, Zhang L, et al.Ray-based tomography for Q estimation and Q compensation in complex media[C].SEG Technical Program Expanded Abstracts, 2011, 30: 3989-3993.
|
| [17] |
赵连锋, 王卫民, 姚振兴. 逐次线性化衰减层析成像方法研究[J]. 地球物理学报, 2004, 47(4): 691-696. ZHAO Lianfeng, WANG Weimin, YAO Zhenxing. Seismic attenuation tomography using the successive linearization method[J]. Chinese Journal of Geophy-sics, 2004, 47(4): 691-696. DOI:10.3321/j.issn:0001-5733.2004.04.021 |
| [18] |
张剑锋, 刘伟, 王进, 等.基于地面接收的反射地震资料的Q值场建模方法[P].CN106443786A, 2017-02-22.
|
| [19] |
陈颙, 黄庭芳, 刘恩儒. 岩石物理学[M]. 安徽合肥: 中国科学技术大学出版社, 2009.
|
| [20] |
云美厚, 聂岩, 李运肖, 等. 地层品质因子的几种定义及相互关系[J]. 石油地球物理勘探, 2013, 48(5): 816-823. YUN Meihou, NIE Yan, LI Yunxiao, et al. Definition and mutual relationship of several quality factors[J]. Oil Geophysical Prospeting, 2013, 48(5): 816-823. |
| [21] |
Tisato N, Madonna C. Attenuation at low frequencies in partially saturated rocks:Measurements and description of a new apparatus[J]. Journal of Applied Geophysics, 2012, 86(3): 44-53. |
| [22] |
童立红, 丁海滨, 于洋, 等.一种测定及计算岩石衰减系数及非线性系数的方法[P].CN109283079A, 2019-01-29.
|
| [23] |
陈颙. 地壳岩石的力学性能——理论基础与实验方法[M]. 北京: 地震出版社, 1988.
|
| [24] |
伍向阳, 陈祖安, 魏建新. 一种测量岩石声波速度和衰减谱的技术[J]. 岩石力学与工程学报, 2000, 19(增刊): 895-898. WU Xiangyang, CHEN Zu'an, WEI Jianxin. A technique for measuring ultrasonic velocity and attenuation spectra[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(S): 895-898. |
| [25] |
马丽云, 赵建华, 戴飒, 等. 单轴压缩下大理岩的Q值与频率关系的研究[J]. 地球物理学报, 1990, 33(6): 689-693. MA Liyun, ZHAO Jianhua, DAI Sa, et al. Study of quality factor Q as a function of frequencies under uniaxial pressure in Lai Yang marble[J]. Acta Geophysica Sinica, 1990, 33(6): 689-693. DOI:10.3321/j.issn:0001-5733.1990.06.008 |
| [26] |
Peselnick L, Outerbridge W F. Internal friction in shear and shear modulus of Solehofen limestone over a frequency range of 10 cycles per second[J]. Journal of Geophysical Research, 1961, 66(2): 581-588. DOI:10.1029/JZ066i002p00581 |
| [27] |
Winkler K W, Nur A. Seismic attenuation:Effects of pore fluids and frictional sliding[J]. Geophysics, 1982, 47(1): 1-15. DOI:10.1190/1.1441276 |
| [28] |
Winkler K W. Dispersion analysis of velocity and a-ttenuation in Berea sandstone[J]. Journal of Geophy-sical Research, 1985, 90(B8): 6793-6800. DOI:10.1029/JB090iB08p06793 |
| [29] |
马丽云, 戴飒, 孙达江, 等. 微机系统在谐振法测量岩石Q值中的应用[J]. 地震地磁观测与研究, 1990, 11(1): 31-32, 68. MA Liyun, DAI Sa, SUN Dajiang, et al. Application of PC system in the measurement of rock Q by resonant method[J]. Seismological and Geomagnetic Observation and Research, 1990, 11(1): 31-32, 68. |
| [30] |
吴志刚, 孙玉凯, 杨超.一种用于非线性结构地面共振衰减试验的激振杆[P].CN108827569A, 2018-11-16.
|
| [31] |
万明浩, 秦顺亭, 起凤梧, 等. 岩石物理性质及其在石油勘探中的应用[M]. 北京: 地质出版社, 1994: 20-44.
|
| [32] |
森本喜隆, 等. 利用非接触谐振法的纵向弹性模量和切变弹性模量测定装置[J]. 国外计量, 1991(6): 12-15. |
| [33] |
席道瑛, 邱文亮, 程经毅, 等. 饱和多孔岩石的衰减与孔隙率和饱和度的关系[J]. 石油地球物理勘探, 1997, 32(2): 196-201. XI Daoying, QIU Wenliang, CHENG Jingyi, et al. Relation between attenuation and porosity or saturation of rock[J]. Oil Geophysical Prospecting, 1997, 32(2): 196-201. |
| [34] |
Winkler K W.The Effects of Pore Fluids and Frictional Sliding on Seismic Attenuation[D].Stanford University, California, USA, 1979.
|
| [35] |
Mitchell B J. Regional Rayleigh wave attenuation in North America[J]. Journal of Geophysical Research, 1975, 80(35): 4904-4916. DOI:10.1029/JB080i035p04904 |
| [36] |
Xia J, Miller R D, Park C B, et al. Determining Q of near-surface materials from Rayleigh waves[J]. Journal of Applied Geophysics, 2002, 51(2-4): 121-129. DOI:10.1016/S0926-9851(02)00228-8 |
| [37] |
Xia J, Xu Y, Miller R D, et al. Estimation of near-surface quality factors by constrained inversion of Rayleigh-wave attenuation coefficients[J]. Journal of Applied Geophysics, 2012, 82: 137-144. DOI:10.1016/j.jappgeo.2012.03.003 |
| [38] |
Xia J, Yin X, Xu Y. Feasibility of determining Q of near-surface materials from Love waves[J]. Journal of Applied Geophysics, 2013, 95: 47-52. DOI:10.1016/j.jappgeo.2013.05.007 |
| [39] |
Xia J. Estimation of near-surface shear-wave velocities and quality factors using multichannel analysis of surface-wave methods[J]. Journal of Applied Geophysics, 2014, 103: 140-151. DOI:10.1016/j.jappgeo.2014.01.016 |
| [40] |
夏江海. 高频面波方法[M]. 湖北武汉: 中国地质大学出版社, 2015: 131-147.
|
| [41] |
刘学伟, 邰圣宏, 何樵登. 用面波反演风化层的Q值[J]. 石油物探, 1996, 35(2): 89-95. LIU Xuewei, TAI Shenghong, HE Qiaodeng. Inversion of quality factor Q for weathered layer using surface waves compensating seismic wave absorption in weathered layer to increase resolution[J]. Geophysical Prospecting for Petroleum, 1996, 35(2): 89-95. |
| [42] |
杨天春, 何继善. 层状介质中瑞利波频散特性[M]. 湖南长沙: 中南大学出版社, 2013.
|
| [43] |
刘学伟, 邰圣宏, 何樵登. 一种考虑噪音干扰的地表风化层Q值反演方法[J]. 石油地球物理勘探, 1996, 31(3): 367-373. LIU Xuewei, TAI Shenghong, HE Qiaodeng. Weathered layer Q-value inversion method with consideration of noise[J]. Oil Geophysical Prospecting, 1996, 31(3): 367-373. |
| [44] |
胡家富, 苏有锦. 用面波估计浅土层的品质因子[J]. 地震学报, 1997, 21(4): 433-438. HU Jiafu, SU Youjin. Estimation of the quality factor in shallow soil using surface waves[J]. Acta Seismological Sinica, 1997, 21(4): 433-438. |
| [45] |
裴江云, 陈树民, 刘振宽, 等. 近地表Q值求取及振幅补偿[J]. 地球物理学进展, 2001, 16(4): 18-22. PEI Jiangyun, CHEN Shumin, LIU Zhenkuan, et al. Near-surface Q value extraction and amplitude compensation[J]. Progress in Geophysics, 2001, 16(4): 18-22. DOI:10.3969/j.issn.1004-2903.2001.04.004 |
| [46] |
何洋洋, 朱振宇, 张金淼, 等.一种复杂介质近地表地层Q值的估计方法[P].CN105652319A, 2016-06-08.
|
| [47] |
Johnston D H, Toksǒez M N. Ultrasonic P and S wave attenuation in dry and saturated rocks under pressure[J]. Journal of Geophysical Research, 1980, 85(B2): 925-936. DOI:10.1029/JB085iB02p00925 |
| [48] |
严又生, 宜明理, 魏新, 等. 井间地震速度和Q值联合层析成像及应用[J]. 石油地球物理勘探, 2001, 36(1): 9-17. YAN Yousheng, YI Mingli, WEI Xin, et al. Joint tomographic imaging for cross-hole seismic velocity and Q value[J]. Oil Geophysical Prospecting, 2001, 36(1): 9-17. DOI:10.3321/j.issn:1000-7210.2001.01.002 |
| [49] |
陈志德, 王成, 刘国友, 等. 近地表Q值模型建立方法及其地震叠前补偿应用[J]. 石油学报, 2015, 36(2): 188-196. CHEN Zhide, WANG Cheng, LIU Guoyou, et al. Modeling method of near-surface Q value and its seismic pre-stack compensation application[J]. Acta Petrolei Sinica, 2015, 36(2): 188-196. |
| [50] |
Jeng Y, Tsai J Y, Chen S H. An improved method of determining near-surface Q[J]. Geophysics, 1999, 64(5): 1608-1617. DOI:10.1190/1.1444665 |
| [51] |
Gao L D, Wang D X, Liu X L, et al. Study on calculation and compensation method of surface Q in loess plateau[J]. CPS/SEG Beijing 2018 International Geophysical Conference & Exposition, 2018, 219-223. |
| [52] |
徐峰, 尹成, 李忠, 等. 井中激发地表接收的近地表结构调查方法[J]. 石油物探, 2009, 48(3): 294-298. XU Feng, YIN Cheng, LI Zhong, et al. Investigation method for near-surface structure with shot in hole and received at surface[J]. Geophysical Prospecting for Petroleum, 2009, 48(3): 294-298. |
| [53] |
张志锋, 刘胜, 杨继友, 等. 表层多波模型调查方法[J]. 石油物探, 2012, 51(3): 257-263. ZHANG Zhifeng, LIU Sheng, YANG Jiyou, et al. Surface layer structure multi-wave investigation method[J]. Geophysical Prospecting for Petroleum, 2012, 51(3): 257-263. DOI:10.3969/j.issn.1000-1441.2012.03.008 |
| [54] |
于承业, 周志才. 利用双井微测井资料估算近地表Q值[J]. 石油地球物理勘探, 2011, 46(1): 89-92. YU Chengye, ZHOU Zhicai. Estimation of near-surface Q value based on the datasets of the uphole survey in double hole[J]. Oil Geophysical Prospecting, 2011, 46(1): 89-92. |
| [55] |
杜增利, 施泽进, 徐峰, 等. 近地表疏松介质吸收补偿的数学模拟研究[J]. 西南石油大学学报, 2007, 29(1): 44-46. DU Zhengli, SHI Zejin, XU Feng, et al. The mathematical modeling of absorption compensation in loose medium at surface[J]. Journal of Sourthwest Petroleum University, 2007, 29(1): 44-46. DOI:10.3863/j.issn.1674-5086.2007.01.014 |
| [56] |
翟桐立, 马雄, 彭雪梅, 等. 基于井地一体化测量的近地表品质因子Q值估算与应用[J]. 石油物探, 2018, 57(5): 685-690. ZHAI Tongli, MA Xiong, PENG Xuemei, et al. Near-surface Q factor measurements by combining surface and cross-hole seismic surveys[J]. Geophysical Prospecting for Petroleum, 2018, 57(5): 685-690. DOI:10.3969/j.issn.1000-1441.2018.05.007 |
| [57] |
宋吉杰, 禹金营, 王成, 等. 近地表介质Q估计及其在塔河北部油田的应[J]. 石油物探, 2018, 57(3): 436-442. SONG Jijie, YU Jinying, WANG Cheng, et al. Q estimation for near-surface media and its application in the northern Tahe oilfield, China[J]. Geophysical Prospecting for Petroleum, 2018, 57(3): 436-442. DOI:10.3969/j.issn.1000-1441.2018.03.013 |
| [58] |
李伟娜, 云美厚, 党鹏飞, 等. 基于微测井资料的双线性回归稳定Q估计[J]. 石油物探, 2017, 56(4): 483-490. LI Weina, YUN Meihou, DANG Pengfei, et al. Stability Q estimation by dual linear regression based on uphole survey data[J]. Geophysical Prospecting for Petroleum, 2017, 56(4): 483-490. DOI:10.3969/j.issn.1000-1441.2017.04.003 |
| [59] |
云美厚, 曹文明, 聂岩, 等. 碳酸盐岩裸露区近地表地震波衰减特性初探[J]. 石油物探, 2012, 51(5): 425-430. YUN Meihou, CAO Wenming, NIE Yan, et al. Preliminary study on the attenuation characteristics of seismic wave propagation in near surface layers of carbonate outcropped area[J]. Geophysical Prospecting for Petroleum, 2012, 51(5): 425-430. DOI:10.3969/j.issn.1000-1441.2012.05.001 |
| [60] |
张光德, 刘斌, 张志林, 等. 柴达木盆地三湖地区盐岩区表层调查方法研究[J]. 石油物探, 2013, 52(2): 195-200. ZHANG Guangde, LIU Bin, ZHANG Zhilin, et al. Surface investigation of salt beds in Sanhu Area, Qaidam Basin[J]. Geophysical Prospecting for Petro-leum, 2013, 52(2): 195-200. DOI:10.3969/j.issn.1000-1441.2013.02.012 |
| [61] |
杜增利, 施泽进, 田军, 等. 新疆沙漠地区低降速带品质因子计算[J]. 大庆石油学院学报, 2006, 30(6): 20-23, 27. DU Zengli, SHI Zejin, TIAN Jun, et al. Calculation of quality factor of LVL in Tarim basin[J]. Journal of Daqing Petroleum Institute, 2006, 30(6): 20-23, 27. |
| [62] |
Gebretsadik E.Geologically and Well-log Constrained Quality Factor(Q) Analysis for Seismic Reservoir Characterization[D].University of Oklahoma, 2005, 91-126.
|
| [63] |
杨凯.沙漠地区低降速带地震波的传播特征与衰减补偿方法研究[D].同济大学, 2004, 29-33. YANG Kai.Study on Propagation Characteristics and Attenuation Compensation of Seismic Waves in Low-velocity Zone in Desert Area[D].Tongji University, 2004, 29-33. |
| [64] |
孟祥梅, 王景强, 阚光明, 等.沉积物声速和声衰减测量装置及方法[P]. CN108956781A, 2018-12-07.
|
| [65] |
胡中平, 吴永检, 褚晓喆, 等. 纵横波浅层折射和纵横波微测井方法联合应用研究[J]. 石油物探, 1998, 37(1): 89-94. HU Zhongping, WU Yongjian, CHU Xiaozhe, et al. Joint application of shallow refraction and microlog methods for both P-wave and S-wave[J]. Geophysical Prospecting for Petroleum, 1998, 37(1): 89-94. |
| [66] |
段云卿, 皮金云, 刘冰, 等. 三分量小折射表层调查研究[J]. 石油地球物理勘探, 2008, 43(6): 652-655. DUAN Yunqing, PI Jinyun, LIU Bing, et al. Study on near-suface by 3-component(3-C)shallow refraction[J]. Oil Geophysical Prospecting, 2008, 43(6): 652-655. DOI:10.3321/j.issn:1000-7210.2008.06.007 |
| [67] |
李晓明, 陈双全, 李向阳. 利用多分量地震数据反演近地表横波速度[J]. 石油地球物理勘探, 2012, 47(4): 532-536. LI Xiaoming, CHEN Shuangquan, LI Xiangyang. An inversion method for near-surface shear-wave velocity using multi-component seismic data[J]. Oil Geophysical Prospecting, 2012, 47(4): 532-536. |



 云美厚, 河南省焦作市高新区世纪路2001号河南理工大学资源环境学院, 454000。Email:
云美厚, 河南省焦作市高新区世纪路2001号河南理工大学资源环境学院, 454000。Email: