重力归一化总梯度法由前苏联学者Березкин[1]于1967年提出,因其先对重力异常进行向下解析延拓,再计算归一化总梯度而得名。它是一种利用高精度重力异常确定场源、断裂位置及密度界面的方法。肖一鸣[2]首次将该方法引入中国,给出了利用泰勒级数展开计算重力归一化总梯度的方法,并探讨了影响该方法应用效果的因素,如谐波数、随机噪声、测线长度等。随后该方法在中国得到了广泛应用。肖一鸣等[3]将该方法成功应用于油气勘探;王家林等[4]利用该方法分析断层和密度分界面;吴燕冈等[5]提出将重力归一化总梯度与相位叠置处理,用于确定深大断裂的空间位置;张凤旭等[6-7]利用Hilbert变换改进重力归一化总梯度法,并提出在位场转换的向下延拓和求导过程中分别引入圆滑滤波因子,提高了该方法的分辨率、可靠性和稳定性,增大了延拓深度;肖鹏飞等[8]利用向下延拓的迭代算法替代波数域的直接向下延拓算子,提高了重力归一化总梯度法的稳定性;张凤琴等[9]采用DCT变换计算重力归一化总梯度,增加了下延深度;王彦国等[10]和郭灿灿等[11]提出了基于泰勒级数迭代法的快速稳定向下延拓的重力归一化总梯度法;苏超等[12]对归一化函数的分母计算几何平均,提高了重力归一化总梯度法的抗噪能力;王选平等[13]将正则化因子引入重力场的下延计算,提出了利用正则化方法计算重力归一化总梯度的方法;王彦国等[14]提出基于幂次平均的离散归一化总梯度法,可以有效识别叠加场源的位置信息。由此可见,对重力归一化总梯度法的改进主要集中在向下延拓和求导这两步计算过程,其稳定性和精度直接影响重力归一化总梯度法的稳定性和精度。
张冲等[15-17]针对向下延拓问题,提出了基于求解微分方程的Adams-Bashforth公式法和基于Simpson求积公式的Milne法。前者下延深度能达到5倍点距,后者甚至可超过10倍点距。Milne法利用观测面上的重力垂向一阶导数、向上延拓不同高度的重力场和重力垂向一阶导数求解下延深度的重力场。向下延拓Milne法具有下延深度大、相对误差小的特点,能获得稳定准确的结果。但该方法需要计算垂向导数,且求导的精度直接影响向下延拓的精度。
早在2001年,Fedi等[18]基于重力位的二阶导数在场源外满足拉普拉斯方程的原理,提出了对随机噪声有压制作用的积分垂向二阶导数法(Integrated Second Vertical Derivative, ISVD)。之后,崔瑞华等[19]将该方法引入中国,首先对重力异常积分,计算得到重力位,然后计算重力位的水平二阶导数,最后根据拉普拉斯方程计算重力异常的垂向一阶导数。相对于常规的波数域求垂向导数的方法,ISVD法由于进行了积分运算,对随机噪声有抑制作用,因而更稳定。
本文将这两种稳定算法,即向下延拓Milne法和ISVD法引入重力归一化总梯度的计算,通过理论模型试算和实际资料处理,验证了方法的有效性。
1 方法原理 1.1 重力归一化总梯度法的基本原理以重力剖面观测数据为例,归一化总梯度的表达式[2]为
| $ {G^{\rm{H}}}(x, z) = \frac{{\sqrt {V_{zx}^2(x, z) + V_{zz}^2(x, z)} }}{{\frac{1}{M}\sum\limits_{i = 1}^M {\sqrt {V_{zx}^2\left( {{x_i}, z} \right) + V_{zz}^2\left( {{x_i}, z} \right)} } }} $ | (1) |
式中:GH(x, z)为计算点(x, z)处的重力归一化总梯度值;M为重力剖面上的测点总数;Vzx(x, z)和Vzz(x, z)为计算点的重力位二阶偏导数,同时也是计算点(x, z)处重力异常沿x方向和z方向的一阶偏导数。
1.2 向下延拓Milne法的基本原理重力场向下延拓四阶Milne公式[15]为
| $ \begin{array}{c}{V_{z}\left(x, z_{h}\right)=V_{z}\left(x, z_{-3 h}\right)+\frac{4 h}{3}\left[2 V_{z z}\left(x, z_{-2 h}\right)-\right.} \\ {\left.V_{z z}\left(x, z_{-h}\right)+2 V_{z z}\left(x, z_{0}\right)\right]}\end{array} $ | (2) |
式中:h为向下延拓深度;Vz(x, zh)表示由观测面z0向下延拓h深度的重力场;Vz(x, z-3h)表示由观测面向上延拓3h高度的重力场;Vzz(x, z-h)和Vzz(x, z-2h)分别表示由观测面向上延拓h和2h高度的重力垂向一阶导数;Vzz(x, z0)表示观测面上的重力垂向一阶导数。由式(2)可知,计算下延重力场时需要利用向上延拓所得到的重力场及其垂向一阶导数。
这里选择在波数域中进行向上延拓。向上延拓是一种稳定算法,对高波数成分(包括噪声)有压制作用。将观测面上的重力异常向上延拓nh高度的表达式为
| $ \widetilde{V}_{z}\left(u, z_{-n h}\right)=\widetilde{V}_{z}\left(u, z_{0}\right) \mathrm{e}^{-2 \pi n h \sqrt{u^{2}}} $ | (3) |
式中:
式(2)右端涉及向上延拓和垂向导数两个计算过程,其中向上延拓具有压制随机噪声的作用,而垂向求导有提高分辨率的作用,因此该算法比较稳定,也具有较高的精度。根据张冲等[15]的理论模型试验结果,下延超过5倍以上点距深度时,Milne法的计算误差显著低于积分迭代法和传统波数域向下延拓方法,即使下延10倍点距时,下延结果也不会发散。
式(2)中的Vzz(x, z-2h)和Vzz(x, z-h)是重力场经过向上延拓后再计算其垂向一阶导数,因而对随机噪声不敏感;Vzz(x, z0)是观测面的重力垂向一阶导数,一般情况下,它是由观测面上的重力异常直接求垂向导数所得,因此受随机噪声影响最大。故本文选择对噪声有一定压制作用的垂向导数算法,即ISVD法。
1.3 ISVD法的基本原理二度体引起的重力位二阶导数,在场源外满足拉普拉斯方程
| $ V_{x x}+V_{x}=0 $ | (4) |
式中:Vxx表示重力位的x方向二阶导数;Vzz表示重力位的垂向二阶导数。通常实测数据是重力异常,为了获得重力位,可先在波数域对重力异常Vz积分得到重力位V
| $ \widetilde{V}=\frac{1}{2 \pi \sqrt{u^{2}}} \widetilde{V}_{z} $ | (5) |
式中:
| $ V_{x(0)}=\frac{1}{2 \Delta x}\left(V_{(1)}-V_{(-1)}\right) $ | (6) |
式中:Vx(0)表示三点滑动窗口内中心点重力位的水平一阶导数;V(1)和V(-1)分别表示滑动窗口右端点和左端点的重力位;Δx表示点距。将第一次使用式(6)计算得到的Vx再次代入式(6),可求得重力位V在x方向的二阶导数Vxx。最后将Vxx代入式(4)即得到重力异常垂向一阶导数Vzz。由于该方法先进行积分运算,在一定程度上平滑了重力异常中的随机噪声。值得注意的是,该方法并不能完全抑制数据中的非随机噪声,例如浅层地质体引起的干扰。当重力异常中含有“毛刺”等明显干扰时,建议先去除高波数的干扰成分,然后再做后续处理。
1.4 基于向下延拓Milne法的重力归一化总梯度法的实现步骤① 以向下延拓深度h为例,利用式(3)在波数域对观测剖面上重力异常的波谱
② 根据式(5),在波数域对
③ 将第①步和第②步计算得到的结果代入式(2),求出下延深度为h的重力异常Vz(x, zh)。
④ 再利用第②步方法,计算Vz(x, zh)的垂向一阶导数Vzz(x, zh),并应用式(6)直接在空间域计算Vz(x, zh)沿x方向的一阶导数Vzx(x, zh)。
⑤ 将Vzz(x, zh)和Vzx(x, zh)代入式(1)计算GH(x, zh)。
⑥ 修改下延深度,重复以上步骤,获得不同深度的重力归一化总梯度值。
⑦ 最后绘制GH(x, z)等值线剖面,极大值点即是异常体的中心位置。
2 理论模型实验设计一个无限长水平圆柱体模型,剩余密度为-0.5×103kg/m3,中心位置为x=100m、z=25m,观测剖面长度为200m,测量点距为1m,共201个观测点。计算该模型的重力异常,分别利用本文方法和基于泰勒级数展开的重力归一化总梯度法计算其中心位置,结果如图 1所示。
|
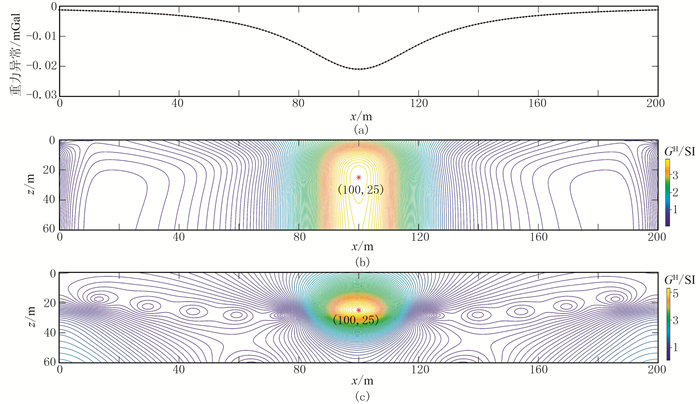
图 1 无限长水平圆柱体理论模型不同方法重力归一化总梯度计算结果 (a)理论重力异常曲线;(b)本文方法;(c)泰勒级数展开 |
由图 1可知,采用两种不同的重力归一化总梯度法,其极大值点(图 1b和图 1c中的红色圆点)均能准确地指示出水平圆柱体模型的中心位置,说明这两种方法处理理论模型数据的效果较好。
实测重力数据中通常包含区域场和随机误差。为检验该方法的抗干扰能力,对模型数据加入5%的随机噪声和一阶趋势背景场,处理结果如图 2所示。
|
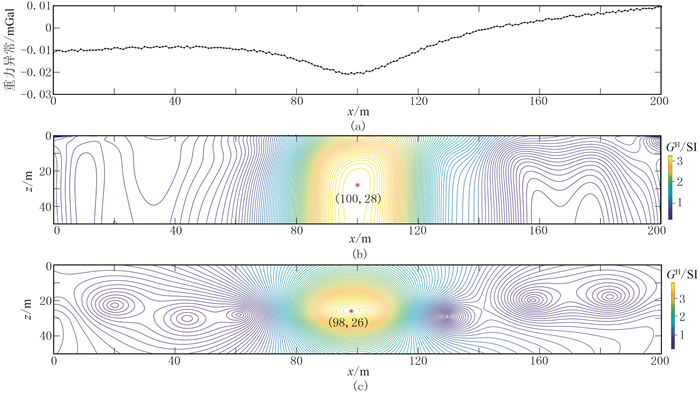
图 2 对含5%噪声和一阶趋势背景场的理论模型数据利用不同方法得到的重力归一化总梯度剖面 (a)重力异常曲线;(b)本文方法;(c)泰勒级数展开 |
由图 2可知,基于向下延拓Milne法的重力归一化总梯度法所得到的模型中心位置为x=100m、z=28m(图 2b),与理论坐标位置相比,计算结果偏深3m,水平位置无偏移,说明随机噪声和背景场仍然对该方法有一定的影响。同样,基于泰勒级数展开的重力归一化总梯度法也受影响,计算埋深偏大1m,水平位置向左偏移2m(图 2c)。对比图 2b与图 2c可见,后者出现很多等值线圈闭。在实际资料处理中,这些虚假异常圈闭容易引起对真实场源位置的误判。引起这些圈闭的原因是基于泰勒级数展开的重力归一化总梯度法在计算过程中放大了高波数信号。相比而言,基于向下延拓Milne法的重力归一化总梯度法在一定程度上压制了高波数噪声,计算结果稳定,虚假异常圈闭相对较少。
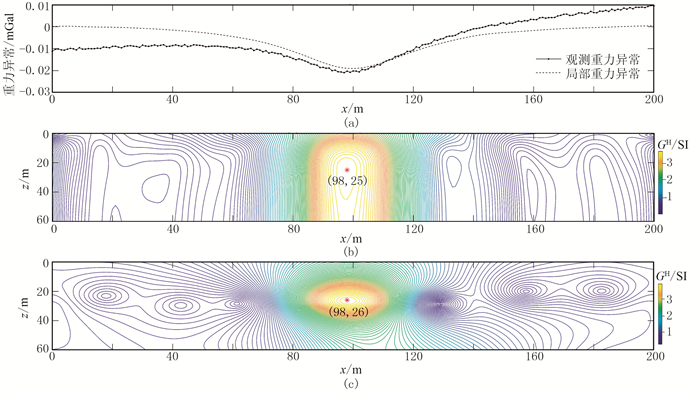
选取图 2a剖面两端的数据(0~20m及180~200m)进行一阶多项式拟合,用拟合值作为区域异常;再用重力异常减去区域异常得到局部异常,并对其进行圆滑滤波处理,得到图 3a中虚线所示的异常曲线;最后分别用基于向下延拓Milne法的重力归一化总梯度法和基于泰勒级数展开的重力归一化总梯度法得到图 3b和图 3c所示结果。由图 3b可见,计算得到的模型中心位置为x=98m、z=25m,中心埋深与理论模型一致,水平方向有2m的左向偏移;由图 3c可见,计算得到的模型中心位置为x=98m、z=26m,中心埋深比实位置偏大1m,水平方向向左偏移2m。这两种方法均出现水平位置的偏差,分析应该与区域背景场分离不彻底有关,因为分离后的局部重力异常的极小值也有微小的左向偏移。
|
图 3 对局部重力异常采用不同方法得到的重力归一化总梯度剖面 (a)局部重力异常曲线;(b)本文方法;(c)泰勒级数展开 |
由模型试验可知,利用本文方法计算重力归一化总梯度具有中心埋深计算准确、虚假异常圈闭相对较少等优点;但若应用于含噪、含背景场干扰的重力数据处理时,需要进行背景场的剥离和去噪处理,这样才能得出比较准确的场源中心位置。
3 实测重力剖面数据应用将本文方法应用于辽宁省葫芦岛市杨家杖子镇经济技术开发区黑鱼沟A矿洞的实测重力剖面数据。A矿洞位于黑鱼沟西山寒武系下方,是铅锌矿开采矿洞。矿洞断面为马蹄形,水平延伸近50m,可近似为一个无限长的水平圆柱体。矿洞中心埋深为5m,高和宽均约2m。在地面采集重力数据,重力观测剖面垂直于矿洞走向。
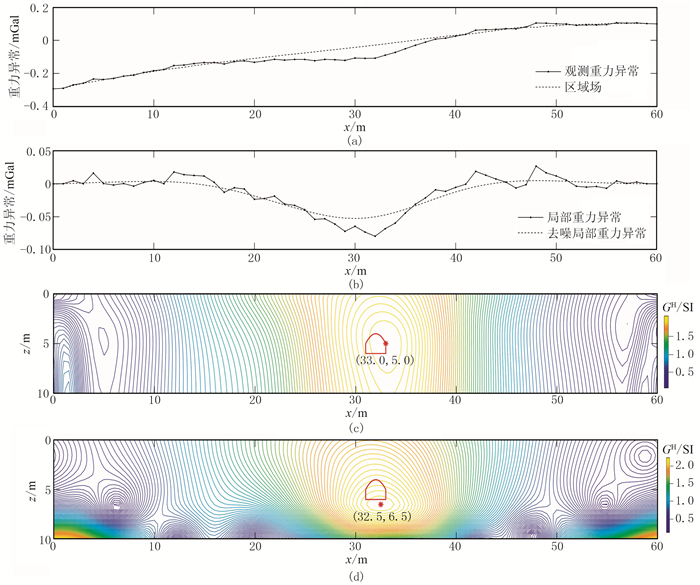
观测布格重力异常如图 4a中的实线所示。首先对该数据进行异常分离,这里采用非线性滤波分离区域(背景)场(图 4a中虚线);去掉背景场后的局部重力异常如图 4b中实线所示,可见局部重力异常含有明显的高波数干扰成分,故对其进行去噪处理。选用多次圆滑方法压制随机噪声,去噪后的结果如图 4b中的虚线所示,对其分别利用本文方法和基于泰勒级数展开得到如图 4c和图 4d所示的重力归一化总梯度剖面。对比图 4c与图 4d可见,根据本文方法计算结果解释的矿洞深度与实际情况基本一致,而根据图 4d解释的矿洞埋深较真实位置偏大1.5m。对比其他方法计算的该矿洞中心埋深(5.0~5.6m)[22-25]可以证实,本文方法处理结果的准确度较高。
|
图 4 实测重力数据计算结果对比 (a)实测布格重力异常和分离的区域(背景)场;(b)局部重力异常(实线)及去噪后的局部重力异常(虚线);(c)本文方法得到的重力归一化总梯度剖面;(d)基于泰勒级数展开的重力归一化总梯度剖面图中红色马 蹄形实线为矿洞位置,红色圆点为重力归一化总梯度剖面中极大值点(即矿洞的中心点) |
理论模型和实际数据计算结果表明,基于向下延拓Milne法的重力归一化总梯度法具有算法稳定、准确性较高的优点。相对于其他重力归一化总梯度法,不需要设置最佳谐波数、正则化参数及迭代次数等参数,减少了数据处理中参数选取引入的误差。但原始重力数据中的随机噪声和背景场对本方法有一定的影响,故在实际应用中需首先进行区域场的分离和去噪处理。
| [1] |
Березкин B M著; 陆克, 刘文锦, 焦恩富译.物探数据的总梯度解释法[M].北京: 地质出版社, 1994.
|
| [2] |
肖一鸣. 重力归一化总梯度法[J]. 石油地球物理勘探, 1981, 16(3): 47-56. XIAO Yiming. The normalized total gradient method of gravity[J]. Oil Geophysical Prospecting, 1981, 16(3): 47-56. |
| [3] |
肖一鸣, 张林祥. 重力归一化总梯度法在寻找油气中的应用[J]. 石油地球物理勘探, 1984, 19(3): 247-254. XIAO Yiming, ZHANG Linxiang. The application of total gradient of gravity in funding oil-gas[J]. Oil Geophysical Prospecting, 1984, 19(3): 247-254. |
| [4] |
王家林, 王一新, 万明浩, 等. 用重力归一化总梯度法确定密度界面[J]. 石油地球物理勘探, 1987, 22(6): 684-692. WANG Jialin, WANG Yixin, WAN Minghao, et al. The determination of density interface using the normalized total gravity gradient method[J]. Oil Geophysical Prospecting, 1987, 22(6): 684-692. |
| [5] |
吴燕冈, 单汝俭, 周富祥, 等. 重力归一化总梯度及其相位的叠置方法研究[J]. 世界地质, 1996, 15(3): 84-90. WU Yangang, SHAN Rujian, ZHOU Fuxiang, et al. A study of appending of total gradient of gravity and its phase[J]. Global Geology, 1996, 15(3): 84-90. |
| [6] |
张凤旭, 孟令顺, 张凤琴, 等. 利用Hilbert变换计算重力归一化总梯度[J]. 地球物理学报, 2005, 48(3): 704-709. ZHANG Fengxu, MENG Lingshun, ZHANG Fengqin, et al. Calculating normalized full gradient of gravity anomaly using Hilbert transform[J]. Chinese Journal of Geophysics, 2005, 48(3): 704-709. DOI:10.3321/j.issn:0001-5733.2005.03.031 |
| [7] |
张凤旭, 孟令顺, 张凤琴, 等. 波数域重力归一化总梯度法中的圆滑滤波因子[J]. 物探与化探, 2005, 29(3): 248-252. ZHANG Fengxu, MENG Lingshun, ZHANG Fengqin, et al. A study of smoothing filter operator for normalized full gradient of gravity anomaly in wave-number domain[J]. Geophysical and Geochemical Exploration, 2005, 29(3): 248-252. DOI:10.3969/j.issn.1000-8918.2005.03.016 |
| [8] |
肖鹏飞, 李明, 徐世浙, 等. 重力归一化总梯度的稳定解法[J]. 石油地球物理勘探, 2006, 41(5): 596-600. XIAO Pengfei, LI Ming, XU Shizhe, et al. Stable solution of normalized total gravity gradient[J]. Oil Geophysical Prospecting, 2006, 41(5): 596-600. DOI:10.3321/j.issn:1000-7210.2006.05.021 |
| [9] |
张凤琴, 张凤旭, 刘财, 等. 利用DCT法计算重力归一化总梯度[J]. 吉林大学学报(地球科学版), 2007, 34(4): 804-808. ZHANG Fengqin, ZHANG Fengxu, LIU Cai, et al. Using DCT to calculate normalized full gradient of gravity anomalies[J]. Journal of Jilin University (Earth Science Edition), 2007, 34(4): 804-808. |
| [10] |
王彦国, 张凤旭, 王祝文, 等. 位场向下延拓的泰勒级数迭代法[J]. 石油地球物理勘探, 2011, 46(4): 657-662. WANG Yanguo, ZHANG Fengxu, WANG Zhuwen, et al. Taylor series iteration for downward continuation of potential fields[J]. Oil Geophysical Prospecting, 2011, 46(4): 657-662. |
| [11] |
郭灿灿, 张凤旭, 王彦国, 等. 基于泰勒级数迭代的重力归一化总梯度[J]. 世界地质, 2012, 31(4): 824-830. GUO Cancan, ZHANG Fengxu, WANG Yanguo, et al. Calculating normalized full gradient of gravity anomalies using Taylor series iteration[J]. Global Geo-logy, 2012, 31(4): 824-830. DOI:10.3969/j.issn.1004-5589.2012.04.026 |
| [12] |
苏超, 杜晓娟, 马国庆, 等. 几何平均重力归一化总梯度在山东招远金矿采空区的应用[J]. 世界地质, 2014, 33(4): 889-894. SU Chao, DU Xiaojuan, MA Guoqing, et al. Application of normalized full gradient method with geome-tric mean in mined-out area of Zhaoyuan gold deposit in Shandong[J]. Global Geology, 2014, 33(4): 889-894. DOI:10.3969/j.issn.1004-5589.2014.04.017 |
| [13] |
王选平, 张凤旭, 王彦国, 等. 利用正则化方法计算重力归一化总梯度[J]. 世界地质, 2014, 33(1): 221-226. WANG Xuanping, ZHANG Fengxu, WANG Yanguo, et al. Calculating normalized full gradient of gravity anomalies using regularization method[J]. Global Geo-logy, 2014, 33(1): 221-226. DOI:10.3969/j.issn.1004-5589.2014.01.024 |
| [14] |
王彦国, 吴姿颖, 邓居智, 等. 基于幂次平均的离散归一化总梯度法[J]. 石油地球物理勘探, 2018, 53(6): 1351-1364. WANG Yanguo, WU Ziying, DENG Juzhi, et al. Discretization of normalized total gradient based on power mean[J]. Oil Geophysical Prospecting, 2018, 53(6): 1351-1364. |
| [15] |
张冲, 黄大年, 刘杰. 重力场向下延拓Milne法[J]. 地球物理学报, 2017, 60(11): 4212-4220. ZHANG Chong, HUANG Danian, LIU Jie. Milne method for downward continuation of gravity filed[J]. Chinese Journal of Geophysics, 2017, 60(11): 4212-4220. DOI:10.6038/cjg20171109 |
| [16] |
Zhang C, Lu Q T, Yan J Y, et al. Numerical solutions of the mean-value theorem:New methods for downward continuation of potential fields[J]. Geophysical Research Letters, 2018, 45(8): 3461-3470. DOI:10.1002/2018GL076995 |
| [17] |
张冲.重磁位场数据空间重构及层状介质反演研究[D].吉林长春: 吉林大学, 2017. ZHANG Chong.The Study of Data Space Reconstruction and Layered Medium Inversion of Gravity and Magnetic Fields[D].Jilin University, Changchun, Jilin, 2017. |
| [18] |
Fedi M, Florio G. Detection of potential fields source boundaries by Enhanced Horizontal Derivative me-thod[J]. Geophysical Prospecting, 2001, 49(1): 40-58. DOI:10.1046/j.1365-2478.2001.00235.x |
| [19] |
崔瑞华, 谷社峰, 李成立. 位场垂向导数的稳定算法[J]. 物探化探计算技术, 2009, 31(5): 426-430. CUI Ruihua, GU Shefeng, LI Chengli. A stable algorithm for calculating the vertical derivatives of potential field[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2009, 31(5): 426-430. DOI:10.3969/j.issn.1001-1749.2009.05.005 |
| [20] |
焦新华, 吴燕岗. 重力与磁法勘探[M]. 北京: 地质出版社, 2009.
|
| [21] |
罗孝宽, 郭绍雍. 应用地球物理教程——重力磁法[M]. 北京: 地质出版社, 1991.
|
| [22] |
石甲强, 肖锋, 唐振, 等. 梯级化方法在重力场源深度计算中的应用[J]. 工程地球物理学报, 2018, 15(1): 32-38. SHI Jiaqiang, XIAO Feng, TANG Zhen, et al. The application of terracing method to the calculation of gravity anomaly source depth[J]. Chinese Journal of Engineering Geophysics, 2018, 15(1): 32-38. DOI:10.3969/j.issn.1672-7940.2018.01.005 |
| [23] |
赵国兴, 吴燕冈, 王凤刚, 等. 基于窗口数据的重力相关成像[J]. 世界地质, 2016, 35(3): 858-864. ZHAO Guoxing, WU Yangang, WANG Fenggang, et al. Gravity correlation imaging based on window data[J]. Global Geology, 2016, 35(3): 858-864. DOI:10.3969/j.issn.1004-5589.2016.03.027 |
| [24] |
田明阳, 吴燕冈, 张爽, 等. 基于重力及重力梯度数据的位场偏移成像[J]. 世界地质, 2018, 37(1): 218-223. TIAN Mingyang, WU Yangang, ZHANG Shuang, et al. Potential field migration for imaging based on gravity and gravity gradient data[J]. Global Geology, 2018, 37(1): 218-223. DOI:10.3969/j.issn.1004-5589.2018.01.019 |
| [25] |
张爽, 唐振, 李禄, 等. 利用重力异常和垂向-阶导数的特征点求水平圆柱体中心埋深[J]. 工程地球物理学报, 2017, 14(6): 710-715. ZHANG Shuang, TANG Zhen, LI Lu, et al. Calculate the central depth of horizontal cylinder by feature points of gravity anomaly and first vertical derivative[J]. Chinese Journal of Engineering Geophysics, 2017, 14(6): 710-715. DOI:10.3969/j.issn.1672-7940.2017.06.012 |



 肖锋, 吉林省长春市西民主大街938号吉林大学(朝阳校区)地球探测科学与技术学院, 130026。Email:
肖锋, 吉林省长春市西民主大街938号吉林大学(朝阳校区)地球探测科学与技术学院, 130026。Email: