② 中南大学地球科学与信息物理学院, 湖南长沙 410083;
③ 中国能源建设集团广东省电力设计研究院有限公司, 广东广州 510663;
④ 桂林理工大学地球科学学院, 广西桂林 541004;
⑤ 东方地球物理公司大庆物探一公司, 黑龙江大庆 163357
② School of Geosciences and Info-physics, Central South University, Changsha, Hunan 410083, China;
③ Guangdong Electric Power Design Institute, China Energy Engineering Group CO., Guangzhou, Guangdong 510663, China;
④ College of Earth Sciences, Guilin University of Technology, Guilin, Guangxi 541004, China;
⑤ No. 1 Daqing Geophysical Exploration Company of BGP, CNPC, Daqing, Heilongjiang 163357, China
任意复杂条件下的重力异常的高效、高精度数值模拟,在重力异常反演成像及人机交互解释、建模中至关重要。目前重力异常的正演方法按照求解域的不同一般分为空间域和波数域两类。
在空间域正演中,Hubbert[1]给出了二度体重力异常线积分公式;Talwani等[2]推导了截面为多边形的常密度二度体重力异常解析式,并指出对于任意二度体都可以用该模型逼近;Rao[3]推导了截面为矩形、密度随深度呈二次变化的重力异常解析表达式。后来关于截面为多边形、物性连续变化的二度体重力异常解析式的计算方法取得了较大进展[4-8]。李明等[9]采用级数展开计算了重力垂直一次导数;徐世浙[10]在二维重力场垂直分量及梯度张量的正演计算中引入了有限单元法;姜效典等[11]利用样条插值函数计算了变密度地质体重力异常;金刚燮等[12]利用等参数有限元的高斯数值积分实现了复杂形体重力异常正演;Reeder等[13]提出一种采用卷积算子提高二度体重力异常计算效率的有限元方法;Ren等[14]提出了一种基于非结构化网格的重磁正演快速多极子算法,很好地解决了复杂边界和几何形状情况下重磁异常的正演问题;肖宝泽等[15]采用均匀多边形截面二度体重力异常公式实现了复杂模型的重力异常数值模拟。
在波数域正演中,Sharma等[16]给出了任意断层面倾角的断层重力场的波数域表达式;Rao等[17]推导一个截面为等腰三角形的二度体模型的波数域表达式;Bhattacharyya等[18]推导了任意二度体的重力异常场波数域表达式;在此基础上,Pedersen[19]首次推导了以三角形组合作为其截面形状的二度体重力异常波数域表达式,并分析了在波数域如何以简单方式建模,从而解决波数域反演中的一些问题;吴宣志[20]将均质物性的任意二度体模型推广至密度随深度呈线性或指数变化的模型;柴玉璞[21]运用偏移抽样方法提高了反傅里叶变换数值精度;Tontini等[22]实现了重力异常波数域正演,并研究了快速傅里叶变换(FFT)扩边法与误差的关系;Wu等[23]利用Gauss-FFT提高了反傅里叶变换的数值精度,降低了FFT引起的强制周期化、边界震荡效应等影响;商宇航等[24]推导了双曲线密度模型的波数域重力异常表达式。
空间域方法数值模拟精度高,网格剖分灵活,但计算大量位置点的异常场数据时,速度较慢。相对空间域方法,波数域方法速度较快,但精度相对较低,且垂向网格等间隔采样不利于模拟复杂地形或复杂模型。为了兼顾数值模拟的精度与效率,充分利用空间域方法和波数域方法的优势,本文针对任意形状、任意密度分布的二度体重力异常计算效率低的问题,提出一种空间—波数混合域二度体重力异常正演方法。该方法对空间域引力位满足的二维偏微分方程沿水平方向进行一维傅里叶变换,把空间域引力位满足的二维偏微分方程转化为不同波数相互独立的一维常微分方程,将一个复杂问题分解为多个小问题。该方法实现了不同波数之间常微分方程相互独立,具有高度并行性。该方法在垂向上为空间域,便于浅层网格剖分适当加密,深层网格剖分适当稀疏,有利于适应复杂地形的模拟,兼顾了计算精度与计算效率;采用有限单元法求解不同波数满足的常微分方程,并充分利用追赶法求解定带宽线性方程组的高效性,进一步提高了计算效率。
1 理论方法 1.1 控制方程引力位满足二维泊松方程[25]
| $ {\nabla ^2}U\left( {x,z} \right) = - 4{\rm{ \mathsf{ π} }}G\Delta \tilde \rho \left( {x,z} \right) $ | (1) |
式中:U为引力位;G为万有引力常数;Δρ为异常体剩余密度;(x, z)表示空间任意一点坐标。
对式(1)沿x方向进行一维傅里叶变换,得到
| $ \frac{{{\partial ^2}\tilde U\left( {k,z} \right)}}{{\partial {z^2}}} - {k^2}\tilde U\left( {k,z} \right) = - 4{\rm{ \mathsf{ π} }}G\Delta \tilde \rho \left( {k,z} \right) $ | (2) |
式中:k为波数;
特别地,当k=0时,空间—波数混合域引力位满足常微分方程
| $ \frac{{{\partial ^2}\tilde U\left( {0,z} \right)}}{{\partial {z^2}}} = - 4{\rm{ \mathsf{ π} }}G\Delta \tilde \rho \left( {0,z} \right) $ | (3) |
在无源区域,式(2)的通解为
| $ \tilde U = A{{\rm{e}}^{kz}} + B{{\rm{e}}^{ - kz}} $ | (4) |
式中A和B为任意常数。在笛卡尔坐标系中,令坐标轴z向下为正,模型的上边界z=zmin,下边界z=zmax,如图 1所示。则上、下边界条件为
| $ \left\{ {\begin{array}{*{20}{l}} {{{\left. {\frac{{\partial \tilde U}}{{\partial z}}} \right|}_{z = {z_{\min }}}} = k\tilde U}\\ {{{\left. {\frac{{\partial \tilde U}}{{\partial z}}} \right|}_{z = {z_{\max }}}} = - k\tilde U} \end{array}} \right. $ | (5) |

|
图 1 二度体模型上、下边界示意图 |
在无源区域,可以通过频率域求导得到重力场和重力梯度张量。空间域重力场g、重力梯度张量T与引力位分别为
| $ \mathit{\boldsymbol{g}} = \left[ {\begin{array}{*{20}{l}} {{g_x}}\\ {{g_z}} \end{array}} \right] = - \left[ {\begin{array}{*{20}{l}} {\frac{{\partial U}}{{\partial x}}}\\ {\frac{{\partial U}}{{\partial z}}} \end{array}} \right] $ | (6) |
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{l}} {{g_{xx}}}&{{g_{xz}}}\\ {{g_{zx}}}&{{g_{zz}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {\frac{{\partial {g_x}}}{{\partial x}}}&{\frac{{\partial {g_x}}}{{\partial z}}}\\ {\frac{{\partial {g_z}}}{{\partial x}}}&{\frac{{\partial {g_z}}}{{\partial z}}} \end{array}} \right] $ | (7) |
由式(6)可得空间—波数混合域引力位与重力场的关系式
| $ \mathit{\boldsymbol{\tilde g}} = \left[ {\begin{array}{*{20}{c}} {{{\tilde g}_x}}\\ {{{\tilde g}_z}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - {\rm{i}}k\tilde U}\\ {k\tilde U} \end{array}} \right] $ | (8) |
式中
由式(7)可得空间—波数混合域引力位与重力梯度张量的关系式
| $ \mathit{\boldsymbol{\tilde T}} = \left[ {\begin{array}{*{20}{l}} {{{\tilde g}_{xx}}}&{{{\tilde g}_{xz}}}\\ {{{\tilde g}_{zx}}}&{{{\tilde g}_{zz}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{k^2}\tilde U}&{k\left( { - {\rm{i}}k\tilde U} \right)}\\ { - {\rm{i}}k\left( {k\tilde U} \right)}&{ - {k^2}\tilde U} \end{array}} \right] $ | (9) |
式中
在有源区域,重力场和重力梯度张量,即异常体内部的
式(2)为引力位在空间—波数混合域满足的常微分方程,本文采用基于二次插值的一维有限单元法对其进行数值模拟。该方法一方面能实现复杂模型和复杂地形的高精度模拟,另一方面在一维条件下利用追赶法可实现对角线性方程组(五对角)的高效、高精度求解。
联立式(2)与式(5)可得空间—波数混合域引力位的边值问题
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\partial ^2}\tilde U}}{{\partial {z^2}}} - {k^2}\tilde U = - 4{\rm{ \mathsf{ π} }}G\Delta \tilde \rho \left( {k,z} \right)}\\ {{{\left. {\frac{{\partial \tilde U}}{{\partial z}}} \right|}_{z = {z_{\min }}}} = k\tilde U}\\ {{{\left. {\frac{{\partial \tilde U}}{{\partial z}}} \right|}_{z = {z_{\max }}}} = - k\tilde U} \end{array}} \right. $ | (10) |
基于变分原理[25]构造泛函,可得到与边值问题(式(10))等价的变分问题
| $ \left\{ \begin{array}{l} F\left( {\tilde U} \right) = \int_{{z_{\min }}}^{{z_{\max }}} {\left[ {{{\left( {\frac{{\partial \tilde U}}{{\partial z}}} \right)}^2} + {{\left( {k\tilde U} \right)}^2} + 8{\rm{ \mathsf{ π} }}G\Delta \tilde \rho k\tilde U} \right]{\rm{d}}z} + \\ \;\;\;\;\;\;\;\;\;\;\;\;k\left( {k\tilde U_{{z_{\max }}}^2 + k\tilde U_{{z_{\min }}}^2} \right)\\ {\rm{ { δ} }}F\left( {k\tilde U} \right) = 0 \end{array} \right. $ | (11) |
在如图 1所示的笛卡尔坐标系中,沿z方向进行单元剖分。在每个单元内,采用二次插值函数,即空间—波数混合域引力位
| $ F\left( {\tilde U} \right) = {\mathit{\boldsymbol{u}}^{\rm{T}}}\mathit{\boldsymbol{Ku}} - 2{\mathit{\boldsymbol{u}}^{\rm{T}}}\mathit{\boldsymbol{P}} $ | (12) |
式中:u为由某个波数在z方向各个节点的引力位
对F(
| $ {\rm{ { δ} }}F\left( {\tilde U} \right) = {\rm{ { δ} }}{\mathit{\boldsymbol{u}}^{\rm{T}}}\left( {2\mathit{\boldsymbol{Ku}} - 2\mathit{\boldsymbol{P}}} \right) = 0 $ | (13) |
由于δu≠0,故
| $ \mathit{\boldsymbol{Ku}} = \mathit{\boldsymbol{P}} $ | (14) |
对该五对角线性方程组(式(14))的求解参见文献[26]。通过重力场、重力梯度张量与引力位之间的关系式(式(6)和式(7)),得到空间—波数混合域的重力场和重力梯度张量,采用Gauss-FFT对空间波数混合域引力位、场及梯度张量进行反变换,可得到空间域的引力位、重力场和重力梯度张量。
3 数值试验为验证本文算法的正确性及可靠性,分别设计了截面为矩形的常密度和变密度二度体模型及任意密度分布的Teplow模型[13]。最后,对本文算法的计算效率随网格剖分大小的变化规律进行了统计分析。以下算法均利用Fortran95语言编程串行计算实现,笔记本电脑配置为:CPU-Inter Core i4-4790,主频为4.0GHz,内存为32GB。
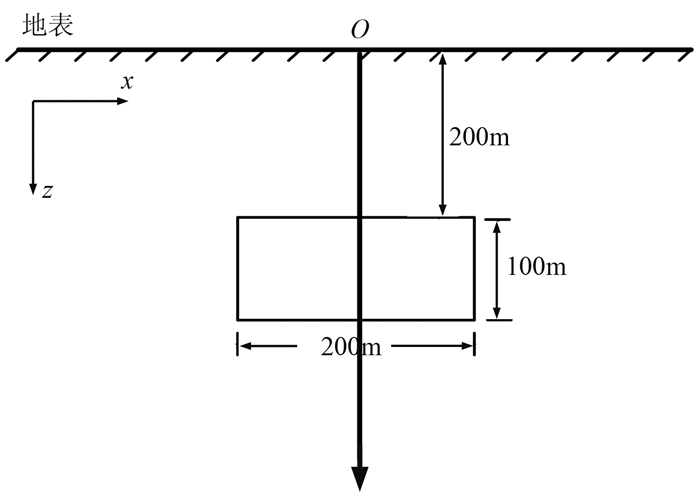
3.1 常密度二度体模型设计如图 2所示的截面为矩形的常密度二度体模型。研究区域为:x方向[-500m,500m],z方向[0,500m]。网格数为200×100,水平和垂向采样间隔均为5m。异常体范围沿x方向为[-100m,100m],z方向为[200m,300m],异常体剩余密度为100kg/m3。重力异常及梯度张量的解析解[27]和数值解及与地面位置各观测点的相对误差分别如图 3、图 4所示。
|
图 2 二度体常密度模型示意图 |
|
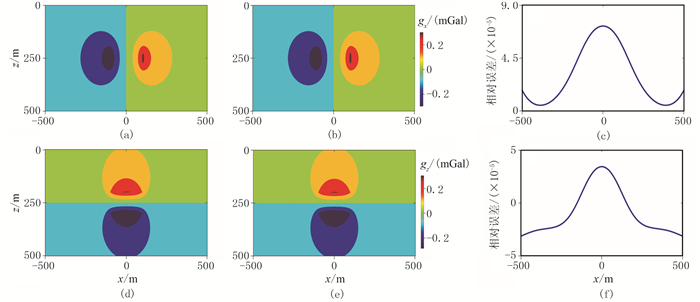
图 3 常密度模型重力场解析解和数值解以及相对误差 (a)重力异常x分量解析解; (b)重力异常x分量数值解; (c)地表处相对误差;(d)重力异常解析解; (e)重力异常数值解; (f)地表处相对误差 |

|
图 4 常密度模型重力梯度张量解析解与数值解以及地面位置的相对误差 (a)重力异常垂向梯度解析解; (b)重力异常垂向梯度数值解; (c)图a与图b相对误差;(d)重力异常水平梯度解析解; (e)重力异常水平梯度数值解; (f)图d与图e相对误差 |
从图 3可以看出,重力场x分量的数值解与解析解吻合度较高,地面位置的最大相对误差小于1.0×10-4。从图 4可以看出,重力梯度张量的数值解与解析解吻合较好,地面各观测点的重力梯度z分量在零值点附近相对误差最大,约为2.0×10-3,这是零值点附近数值计算误差大引起的,在其他位置相对误差均小于1.0×10-3。综合图 3和图 4可以看出,重力场和重力梯度张量的相对误差较小,验证了本文算法的正确性和高精度。
3.2 变密度二度体模型设计一个截面为矩形的变密度二度体模型,研究区域为:x方向[-500m,500m],z方向[0, 500m]。网格数为200×100,水平和垂向采样间隔均为5m。异常体沿x方向范围为[-100m,100m],z方向为[150m,300m]。异常体的密度随深度的关系为
| $ \rho \left( z \right) = 1.54 + 0.24z - 0.035{z^2}\;\;\;\;\;150 \le z \le 300 $ |
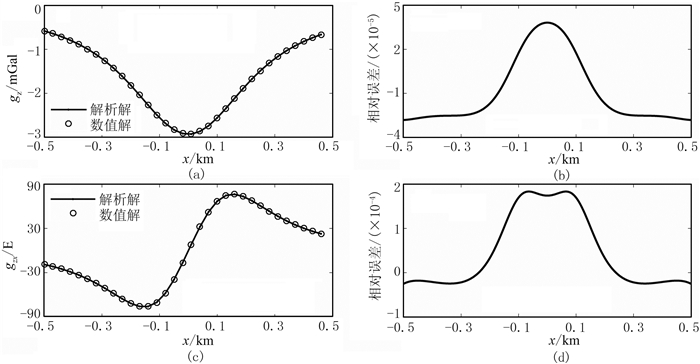
当z=0时(即地面),重力异常和梯度张量解析解[27]及相对误差如图 5所示。可以看出,数值解与解析解形态十分吻合,重力异常和重力梯度张量的相对误差均小于2.0×10-4,与常密度模型计算结果相比,变密度模型的计算结果精度更高。说明本文算法更适用于变密度二度体模型的重力异常数值模拟。
|
图 5 变密度模型重力异常及重力梯度张量解析解与数值解以及z=0处的相对误差 (a)重力异常解析解和数值解; (b)z=0处重力异常相对误差; (c)重力异常水平梯度解析解和数值解;(d)z=0处重力异常水平梯度相对误差 |
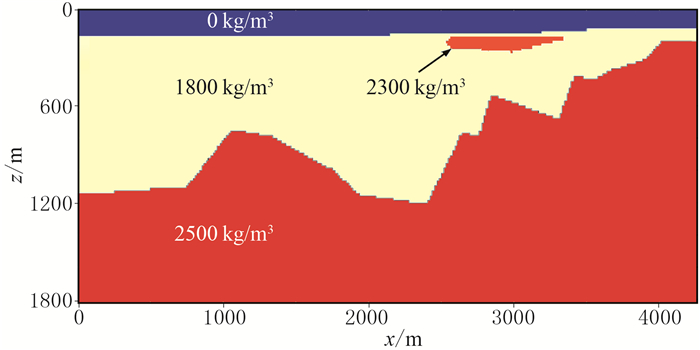
为了进一步检验本文算法对任意形状截面、任意密度分布情况下二度体重力异常计算的适应性,引入Reeder等[13]的Teplow密度分布模型(图 6)。研究区域范围为:x方向[0,4268.3m],z方向为[0,1829.3m],剖分网格数为994×743。
|
图 6 Teplow密度分布模型[13] |
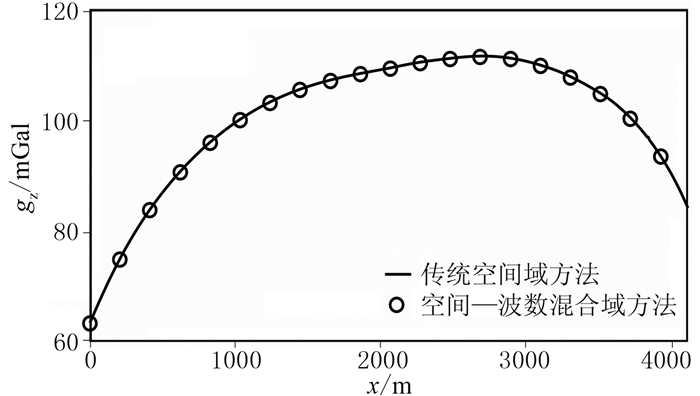
采用本文算法计算地面位置的重力异常,结果如图 7所示。由图可知,传统空间域累加算法[27]与本文算法的计算结果吻合很好,表明本文算法能够计算复杂密度分布情况下的重力异常,且精度较高。
|
图 7 Teplow密度模型不同方法计算的重力异常曲线 |
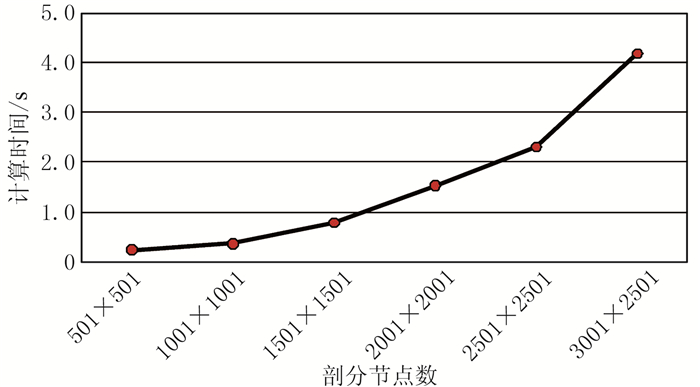
计算效率是评价数值模拟方法好坏的一个重要指标。图 8给出了本文方法的计算时间随网格剖分数目变化的曲线。可以看出,计算时间随着网格剖分数目的大小呈近似线性增长。当网格剖分数目为500×500时,即251001个节点,采用本文算法计算整个剖面耗时约0.24s,采用传统空间域累加算法计算地面501个节点需耗时38.73s[27],表明本文算法计算效率更高。
|
图 8 本文方法计算时间随网格剖分节点数的变化曲线 |
本文提出了一种高效、高精度的空间—波数混合域二度体重力异常正演方法。设计了二度体模型开展数值试验,通过对比数值解与解析解验证了本文方法的正确性和可靠性。通过计算Teplow密度分布模型重力异常,表明了该算法对任意密度分布的二度体模型具有很好的适应性。数值算例结果表明,本文算法具有较高的计算精度和计算效率,为计算任意复杂形体的重力异常提供了一种新途径,对提高二度体重力异常反演成像的效率具有现实意义。
附录A求解文中变分问题(式(11))时,需将整个区域的单元积分分解为各个单元的积分之和,则式(11)变为
| $ \begin{array}{l} F\left( {\tilde U} \right) = \sum {\int_q {{{\left( {\frac{{\partial \left( {\tilde U} \right)}}{{\partial z}}} \right)}^2}} {\rm{d}}z} + \sum {\int_q {{{\left( {k\tilde U} \right)}^2}} {\rm{d}}z} + \\ \;\;\;\;\;2\sum {\int_q {\tilde J\tilde U{\rm{d}}z} } + k\tilde U_{{z_{\max }}}^2 + k\tilde U_{{z_{\min }}}^2 \end{array} $ | (A-1) |
其中
| $ \tilde J\left( {k,z} \right) = 4{\rm{ \mathsf{ π} }}G\Delta \tilde \rho $ | (A-2) |
令
| $ \left. {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{N}} = {{\left( {{N_j},{N_p},{N_m}} \right)}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{u}}_q} = {{\left( {{u_j},{u_p},{u_m}} \right)}^{\rm{T}}}} \end{array}} \right\} $ | (A-3) |
式中:j、m分别为单元两端节点坐标;p为单元中点坐标。有
| $ \mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{N}}^{\rm{T}}}{\mathit{\boldsymbol{u}}_q} = \mathit{\boldsymbol{u}}_q^{\rm{T}}\mathit{\boldsymbol{N}} $ | (A-4) |
式(A-1)中第一项单元积分为
| $ \begin{array}{*{20}{c}} {\int_q {\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial z}}\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial z}}{\rm{d}}z} = \mathit{\boldsymbol{u}}_q^{\rm{T}}\left( {\int_q {\frac{{\partial \mathit{\boldsymbol{N}}}}{{\partial z}}\frac{{\partial {\mathit{\boldsymbol{N}}^{\rm{T}}}}}{{\partial z}}{\rm{d}}z} } \right){\mathit{\boldsymbol{u}}_q}}\\ { = \mathit{\boldsymbol{u}}_q^{\rm{T}}{\mathit{\boldsymbol{K}}_{1q}}{\mathit{\boldsymbol{u}}_q}} \end{array} $ | (A-5) |
其中
| $ {\mathit{\boldsymbol{K}}_{1q}} = \int_q {\frac{{\partial \mathit{\boldsymbol{N}}}}{{\partial z}}\frac{{\partial {\mathit{\boldsymbol{N}}^{\rm{T}}}}}{{\partial z}}{\rm{d}}z} = \frac{1}{{3l}}\left[ {\begin{array}{*{20}{c}} 7&{ - 8}&1\\ { - 8}&{16}&{ - 8}\\ 1&{ - 8}&7 \end{array}} \right] $ | (A-6) |
式中l为单元长度。
式(A-1)中第二项单元积分为
| $ \int_q {{k^2}{\mathit{\boldsymbol{u}}^2}{\rm{d}}z} = \mathit{\boldsymbol{u}}_q^{\rm{T}}\left( {\int_q {{k^2}\mathit{\boldsymbol{N}}{\mathit{\boldsymbol{N}}^{\rm{T}}}{\rm{d}}z} } \right){\mathit{\boldsymbol{u}}_q} = \mathit{\boldsymbol{u}}_q^{\rm{T}}{\mathit{\boldsymbol{K}}_{2q}}{\mathit{\boldsymbol{u}}_q} $ | (A-7) |
其中
| $ {\mathit{\boldsymbol{K}}_{2q}} = \int_q {{k^2}\mathit{\boldsymbol{N}}{\mathit{\boldsymbol{N}}^{\rm{T}}}{\rm{d}}z} = \frac{{l{k^2}}}{{30}}\left[ {\begin{array}{*{20}{c}} 4&2&{ - 1}\\ 2&{16}&2\\ { - 1}&2&4 \end{array}} \right] $ | (A-8) |
式(A-1)中第三项单元积分为
| $ 2\int_q {\tilde J\mathit{\boldsymbol{u}}{\rm{d}}z} = 2\int_q {{j_{az}}u{\rm{d}}z} $ | (A-9) |
利用形函数将jaz表示为
| $ {j_{az}} = {j_{azj}}{N_j} + {j_{azp}}{N_p} + {j_{azm}}{N_m} = {\mathit{\boldsymbol{N}}^{\rm{T}}}\mathit{\boldsymbol{s}}{\mathit{\boldsymbol{z}}_q} = \mathit{\boldsymbol{sz}}_q^{\rm{T}}\mathit{\boldsymbol{N}} $ | (A-10) |
其中
| $ \mathit{\boldsymbol{s}}{\mathit{\boldsymbol{z}}_q} = {\left( {{j_{azj}},{j_{azp}},{j_{azm}}} \right)^{\rm{T}}} $ | (A-11) |
则式(A-9)中的单元积分为
| $ \int_q {{j_{az}}\mathit{\boldsymbol{u}}{\rm{d}}z} = \mathit{\boldsymbol{u}}_q^{\rm{T}}\left( {\int_q {\mathit{\boldsymbol{N}}{\mathit{\boldsymbol{N}}^{\rm{T}}}{\rm{d}}z} } \right)\mathit{\boldsymbol{s}}{\mathit{\boldsymbol{z}}_q} = \mathit{\boldsymbol{u}}_q^{\rm{T}}{\mathit{\boldsymbol{P}}_{1q}}\mathit{\boldsymbol{s}}{\mathit{\boldsymbol{z}}_q} $ | (A-12) |
其中
| $ {\mathit{\boldsymbol{P}}_{1q}} = \int_q {\mathit{\boldsymbol{N}}{\mathit{\boldsymbol{N}}^{\rm{T}}}{\rm{d}}z} = \frac{l}{{30}}\left( {\begin{array}{*{20}{c}} 4&2&{ - 1}\\ 2&{16}&2\\ { - 1}&2&4 \end{array}} \right) $ | (A-13) |
式(A-1)中z=zmin、z=zmax分别为第一个和最后一个节点,可将其分别扩展成
| $ \left\{ {\begin{array}{*{20}{l}} {ku_{{z_{\min }}}^2 = {\mathit{\boldsymbol{u}}^{\rm{T}}}{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{u}}}\\ {ku_{{z_{\max }}}^2 = {\mathit{\boldsymbol{u}}^{\rm{T}}}{\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{u}}} \end{array}} \right. $ | (A-14) |
其中
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} k&{}&{}&{}\\ {}&0&{}&{}\\ {}&{}& \ddots &{}\\ {}&{}&{}&0 \end{array}} \right]\\ {\mathit{\boldsymbol{B}}_2} = \left[ {\begin{array}{*{20}{c}} 0&{}&{}&{}\\ {}& \ddots &{}&{}\\ {}&{}&0&{}\\ {}&{}&{}&k \end{array}} \right] \end{array} \right. $ | (A-15) |
综上,可将式(A-1)表示为
| $ F\left( \mathit{\boldsymbol{u}} \right) = {\mathit{\boldsymbol{u}}^{\rm{T}}}\mathit{\boldsymbol{Ku}} - 2{\mathit{\boldsymbol{u}}^{\rm{T}}}\mathit{\boldsymbol{P}} $ | (A-16) |
| [1] |
Hubbert M K. A line-integral method of computing the gravimetric effects of two-dimensional masses[J]. Geophysics, 1948, 13(2): 215-225. DOI:10.1190/1.1437395 |
| [2] |
Talwani M, Worzel J L, Landisman M. Rapid gravity computations for two-dimensional bodies with application to the Mendocino submarine fracture zone[J]. Journal of Geophysical Research, 1959, 64(1): 49-59. DOI:10.1029/JZ064i001p00049 |
| [3] |
Rao D B. Modelling of sedimentary basins from gravity anomalies with variable density contrast[J]. Geophysical Journal International, 1986, 84(1): 207-212. DOI:10.1111/j.1365-246X.1986.tb04353.x |
| [4] |
Murthy I V R, Rao D B. Gravity anomalies of two-dimensional bodies of irregular cross-section with density contrast varying with depth[J]. Geophysics, 1979, 44(9): 1525-1530. DOI:10.1190/1.1441023 |
| [5] |
Pan J. Gravity anomalies of irregularly shaped two-dimensional bodies with constant horizontal density gradient[J]. Geophysics, 1989, 54(4): 528-530. DOI:10.1190/1.1442680 |
| [6] |
Kwok Y K. Contour integrals for gravity computation of horizontal 212-D bodies with variable density[J]. Applied Mathematical Modelling, 1991, 15(2): 98-103. DOI:10.1016/0307-904X(91)90017-J |
| [7] |
Zhou X B. Analytic solution of the gravity anomaly of irregular 2D masses with density contrast varying as a 2D polynomial function[J]. Geophysics, 2010, 75(2): I11-I19. DOI:10.1190/1.3294699 |
| [8] |
D'Urso M G. The gravity anomaly of a 2D polygonal body having density contrast given by polynomial functions[J]. Surveys in Geophysics, 2015, 36(3): 391-425. DOI:10.1007/s10712-015-9317-3 |
| [9] |
李明, 王宜昌. 重力垂直一次导数的计算及应用[J]. 石油地球物理勘探, 1983, 18(2): 167-173. LI Ming, WANG Yichang. The computation and application of vertical first derivative of gravity[J]. Oil Geophysical Prospecting, 1983, 18(2): 167-173. |
| [10] |
徐世浙. 用有限元法计算二维重力场垂直分量及重力位二阶导数[J]. 石油地球物理勘探, 1984, 19(5): 468-476. XU Shizhe. Calculation of vertical component of 2D gravitational field and second derivative of gravitational potential by finite element method[J]. Oil Geophysical Prospecting, 1984, 19(5): 468-476. |
| [11] |
姜效典, 王硕儒. 计算变密度任意形状地质体重力异常的B样条函数法[J]. 石油地球物理勘探, 1990, 25(3): 362-373. JIANG Xiaodian, WANG Shuoru. B spline function method for calculating gravity field of density-variable source body with arbitrary shape[J]. Oil Geophysical Prospecting, 1990, 25(3): 362-373. |
| [12] |
金钢燮, 胡祥云, 超敬来, 等. 复杂形体重磁异常的等参数有限元积分算法研究[J]. 石油地球物理勘探, 2009, 44(2): 231-239. KIM Kangsop, HU Xiangyun, CHO Gyonglae, et al. Study on isoparametric finite-element integral algorithm of gravity and magnetic anomaly for body with complex shape[J]. Oil Geophysical Prospecting, 2009, 44(2): 231-239. DOI:10.3321/j.issn:1000-7210.2009.02.019 |
| [13] |
Reeder K, Louie J, Kent G, et al.Efficient 2D finite element gravity modeling using convolution[C].SEG Technical Program Expanded Abstracts, 2014, 33: 1254-1258.
|
| [14] |
Ren Z Y, Tang J T, Kalscheuer T, et al. Fast 3-D large-scale gravity and magnetic modeling using unstructured grids and an adaptive multilevel fast multipole method[J]. Journal of Geophysical Research:Solid Earth, 2017, 122(1): 79-109. DOI:10.1002/2016JB012987 |
| [15] |
林宝泽, 肖锋, 王明常. 二维重力数据径向反演及应用[J]. 石油地球物理勘探, 2018, 53(2): 403-409. LIN Baoze, XIAO Feng, WANG Mingchang. 2D gra-vity data radial inversion[J]. Oil Geophysical Prospecting, 2018, 53(2): 403-409. |
| [16] |
Sharma B, Geldart L P. Analysis of gravity anomalies of two-dimensional faults using Fourier transforms[J]. Geophysical Prospecting, 1968, 16(1): 77-93. DOI:10.1111/j.1365-2478.1968.tb01961.x |
| [17] |
Rao K G C, Avasthi D N. Analysis of the Fourier spectrum of the gravity effect due to two-dimensional triangular prism[J]. Geophysical Prospecting, 1973, 21(3): 526-542. DOI:10.1111/j.1365-2478.1973.tb00043.x |
| [18] |
Bhattacharyya B K, Leu L K. Spectral analysis of gravity and magnetic anomalies due to 2-dimensional structures[J]. Geophysics, 1975, 40(6): 993-1013. DOI:10.1190/1.1440593 |
| [19] |
Pedersen L B. A statistical analysis of potential fields using a vertical circular cylinder and a dike[J]. Geophysics, 1978, 43(5): 943-953. DOI:10.1190/1.1440875 |
| [20] |
吴宣志. 三度体位场波谱的正演计算[J]. 地球物理学报, 1983, 26(2): 177-187. WU Xuanzhi. The computation of spectrum of potential field due to 3-D arbitrary bodies[J]. Chinese Journal of Geophysics, 1983, 26(2): 177-187. DOI:10.3321/j.issn:0001-5733.1983.02.009 |
| [21] |
柴玉璞. 偏移抽样理论及其应用[M]. 北京: 石油工业出版社, 1997.
|
| [22] |
Tontini F C, Cocchi L, Carmisciano C. Rapid 3-D forward model of fields with application to the Palinuro Seamount gravity anomaly[J]. Journal of Geophysical Research:Solid Earth, 2009, 114(B2): 1205-1222. |
| [23] |
Wu L Y, Tian G. High-precision Fourier forward mode-ling of potential field[J]. Geophysics, 2014, 79(5). |
| [24] |
商宇航, 邰振华, 秦涛. 基于双曲线密度模型的频率域界面反演[J]. 石油地球物理勘探, 2018, 53(4): 858-864. SHANG Yuhang, TAI Zhenhua, QIN Tao. Interface inversion in the frequency domain based on the hyperbolic density model[J]. Oil Geophysical Prospecting, 2018, 53(4): 858-864. |
| [25] |
徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994.
|
| [26] |
徐士良. FORTRAN常用算法程序集[M]. 北京: 清华大学社出版社, 1995.
|
| [27] |
Blakely R J. Potential Theory in Gravity and Magnetic Applications[M]. London: Cambridge University Press, 1996.
|



 王旭龙, 湖南省长沙市岳麓区中南大学地球科学与信息物理学院, 410083。Email:
王旭龙, 湖南省长沙市岳麓区中南大学地球科学与信息物理学院, 410083。Email: