② 成都理工大学信息科学与技术学院, 四川成都 610059
② College of Information Science and Technology, Chengdu University of Technology, Chengdu, Sichuan 610059, China
时间域航空电磁法(Airborne Time-domain Electromagnetic Method, ATEM)利用飞机上搭载的发射线圈向地下发送一次脉冲磁场(一次场),地下的地质体由一次场激发出感应涡流,产生随时间变化的感应场(二次场),同时使用飞机上搭载的接收线圈采集从地下返回的电磁信号,通过分析采集到的电磁信号,探测地下地质体[1]。ATEM具有良好的灵活性和机动性,勘查速度快、成本相对较低,受地形、地貌条件的影响较小等优势,能够应用于油气[2]和矿产资源勘探[3]、水文地质调查[4]以及环境监测[5-6]等领域。由于ATEM数据量巨大,且二维[7]和三维反演[8-10]需要大量的计算时间,因此很少应用于实际工程。一维反演因其计算量相对较小,在实际的ATEM数据处理和解释中有着广泛的应用[4-5]。
ATEM数据是全时连续采集,数据密度大,测点间距小,在大部分地质环境中,尤其是沉积环境下,相邻测点间的反演结果应具有较强的横向连续性。传统的一维反演方法,如Occam反演[5, 11]、自适应正则化反演[12-13]、阻尼特征参数反演[14]等只考虑单个测点的情况,既使通过选取合理的初始值对反演进行优化[15],其反演结果的横向连续性也较差。为此,Auken等[16]在反演直流电法数据时利用相邻测点间的横向粗糙度对模型进行约束(Laterally constrained inversion, LCI),获得了较好的反演结果;此外,Auken等[17]还应用LCI对古河道模型的瞬变电磁数据进行反演,并与一维单点反演结果进行对比,结果表明LCI可以在一定程度上提高反演分辨率,同时还能抑制数据噪声的影响。Vallee等[18]将横向约束应用于ATEM数据,并详细地讨论了横向约束中一阶导数约束和二阶导数约束对反演结果的影响。为了突出层参数横向连续的重要性,蔡晶等[19]引入加权横向约束的概念。然而,由于LCI同时对多个测点进行计算, 随着测点数的增多,模型参数的数量也随之增加,导致了计算时间急剧增加。Siemon等[20]对频率域航空电磁数据进行反演,并讨论了LCI模型参数的数量与计算时间之间的关系:当模型参数数量超过1000时,反演时间会急剧增加。Yu等[21]用前一个测点的反演结果作为先验信息约束当前测点,以此保证反演结果在横向上的连续性。但是这种横向先验信息约束很大程度上依赖于前一个测点的反演结果,因此反演结果具有明显的方向性。
ATEM勘探中,单条测线的测点数量从几千到几万不等,数据量巨大,因此对整条测线上所有测点同时进行计算,会耗费大量的时间。为了减少计算时间和提高反演精度,本文对整条测线上的测点进行分段计算,对每一段同时使用横向和垂向粗糙度约束以确保反演结果的连续性,段与段之间使用Yu等[21]提出的横向先验信息进行约束,确保反演结果在段间的连续性。
本文首先详细阐述这种横向分段组合约束反演的实现方案,然后使用模拟数据和实测数据对本文反演方案进行测试,最后分析上述三种约束对反演结果的影响,验证了本文反演方案的实用性和有效性。
1 反演方法 1.1 数据拟合ATEM数据反演通过不断调整迭代模型或迭代模型参数m,使正演响应g(m)与观测数据dobs实现最佳拟合。将观测数据通过一阶泰勒级数展开,建立模型参数与观测数据之间的线性逼近关系[16, 22]
| $ {\mathit{\boldsymbol{d}}_{{\rm{obs}}}} \cong \mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{m}} \right) + \mathit{\boldsymbol{G}}\left( {{\mathit{\boldsymbol{m}}_{{\rm{true}}}} - \mathit{\boldsymbol{m}}} \right) $ | (1) |
式中:mtrue表示真实模型数据;G是雅可比矩阵,其第u行、第v列元素为
| $ {G_{u,v}} = \frac{{\partial {d_u}}}{{\partial {m_v}}} $ | (2) |
式中:du表示第u个正演响应数据;mv表示第v个模型参数。令
| $ {\rm{ { δ} }}\mathit{\boldsymbol{m}} = {\mathit{\boldsymbol{m}}_{{\rm{trve}}}} - \mathit{\boldsymbol{m}} $ | (3) |
| $ {\rm{ { δ} }}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} = {\mathit{\boldsymbol{d}}_{{\rm{obs}}}} - \mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{m}} \right) $ | (4) |
则式(1)变为
| $ \mathit{\boldsymbol{G}}{\rm{ { δ} }}\mathit{\boldsymbol{m}} - {\rm{ { δ} }}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} = {\mathit{\boldsymbol{e}}_{{\rm{obs}}}} $ | (5) |
式中eobs为截断误差。本文采用阻尼最小二乘法对式(5)进行求解。由于只考虑了数据拟合误差函数,因此反演结果具有多解性。为此,除了拟合误差函数,还需对模型进行约束,以降低反演的多解性。
1.2 横向粗糙度约束假设地质模型在横向上的电性特征变化较平缓,为了保证反演结果在横向上具有较好的连续性,需要施加横向粗糙度约束[16]
| $ {\mathit{\boldsymbol{R}}_{1{\rm{s}}}}{\mathit{\boldsymbol{m}}_{{\rm{true}}}} = {\mathit{\boldsymbol{e}}_{{\rm{ls}}}} $ | (6) |
式中:els表示模型参数在横向上的误差,其值越小,代表模型在横向方向上越光滑;Rls是模型的横向约束矩阵。将式(6)的左、右两边同时减去Rlsm,得到
| $ {\mathit{\boldsymbol{R}}_{1{\rm{s}}}}{\mathit{\boldsymbol{m}}_{{\rm{true}}}} - {\mathit{\boldsymbol{R}}_{1{\rm{s}}}}\mathit{\boldsymbol{m}} = - {\mathit{\boldsymbol{R}}_{1{\rm{s}}}}\mathit{\boldsymbol{m}} + {\mathit{\boldsymbol{e}}_{{\rm{ls}}}} $ | (7) |
则有
| $ {\mathit{\boldsymbol{R}}_{{\rm{ls}}}}{\rm{ { δ} }}\mathit{\boldsymbol{m}} + {\mathit{\boldsymbol{R}}_{{\rm{ls}}}}\mathit{\boldsymbol{m}} = {\mathit{\boldsymbol{e}}_{{\rm{ls}}}} $ | (8) |
横向约束矩阵Rls采用模型在横向上的一阶差分矩阵,即在横向相邻的两模型参数间使用一阶差分,其他位置均为0
| $ \begin{array}{l} {\mathit{\boldsymbol{R}}_{{\rm{ls}}}} = \\ {\left[ {\begin{array}{*{20}{c}} 1&0& \cdots &0&{ - 1}&0& \cdots &0&0&0\\ 0&1&0& \cdots &0&{ - 1}&0& \cdots &0&0\\ \vdots &{}&{}&{}&{}& \vdots &{}&{}&{}& \vdots \\ 0&0&0& \cdots &0&1&0& \cdots &0&{ - 1} \end{array}} \right]_{{S_1} \times {T_1}}} \end{array} $ | (9) |
式中:S1=(M-1)N; T1=MN。其中M为测点个数,N为模型层数。
1.3 横向先验信息约束横向先验信息约束是将前一个点的反演结果作为先验信息约束当前点的反演[21]。先验信息约束假设模型与先验信息的差距尽可能小,即
| $ {\mathit{\boldsymbol{m}}_{{\rm{true}}}} = {\mathit{\boldsymbol{m}}_{{\rm{prior}}}} + {\mathit{\boldsymbol{e}}_{{\rm{lp}}}} $ | (10) |
式中:mprior为模型的先验信息,本文指上一段最后一个测点的反演结果;elp是模型与先验信息的误差,elp越小,代表模型与先验信息越接近。将式(10)左、右两边同时减去m,有
| $ {\mathit{\boldsymbol{m}}_{{\rm{true}}}} - \mathit{\boldsymbol{m}} = {\mathit{\boldsymbol{m}}_{{\rm{prior}}}} - \mathit{\boldsymbol{m}} + {\mathit{\boldsymbol{e}}_{{\rm{lp}}}} $ | (11) |
得到
| $ {\rm{ { δ} }}\mathit{\boldsymbol{m}} = {\mathit{\boldsymbol{m}}_{{\rm{prior }}}} - \mathit{\boldsymbol{m}} + {\mathit{\boldsymbol{e}}_{{\rm{lp}}}} $ | (12) |
垂向粗糙度约束[23]能使模型在垂直方向上具有较好的连续性。其推导过程与横向约束一样,因此与式(8)类似,即
| $ {\mathit{\boldsymbol{R}}_{{\rm{vs}}}}{\rm{ { δ} }}\mathit{\boldsymbol{m}} + {\mathit{\boldsymbol{R}}_{{\rm{vs}}}}\mathit{\boldsymbol{m}} = {\mathit{\boldsymbol{e}}_{{\rm{vs}}}} $ | (13) |
式中下标“VS”代表垂直方向,各变量的含义与式(8)相同。与式(9)类似,Rvs的取值为
| $ {\mathit{\boldsymbol{R}}_{{\rm{vs}}}} = {\left[ {\begin{array}{*{20}{c}} 1&{ - 1}&{}&{}&{}&{}&{}&{}\\ {}& \ddots & \ddots &{}&{}&{}&{}&{}\\ {}&{}&1&{ - 1}&{}&{}&{}&{}\\ {}&{}&{}&{}&1&{ - 1}&{}&{}\\ {}&{}&{}&{}&{}& \ddots & \ddots &{}\\ {}&{}&{}&{}&{}&{}&1&{ - 1} \end{array}} \right]_{{S_2} \times {T_2}}} $ | (14) |
式中S2=MN, T2=M(N-1)。
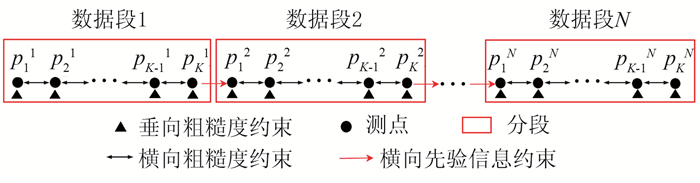
1.5 横向分段组合约束反演为了减少计算时间,提高反演精度,本文提出横向分段组合约束反演方案(图 1)。首先将整条测线上的测点分为N段,每段由K个测点组成,图 1中的pij表示位于第j段的第i个测点;然后在段内相邻测点pij和pi+1j之间使用横向粗糙度约束,保证反演结果横向上的连续性;在段与段之间使用横向先验信息约束,确保各段间的连续性,即使用测点pKj的反演结果作为先验信息,对测点p1j+1进行约束;同时对每个测点pij施加垂向粗糙度约束,保证反演结果垂向上的连续性;最后依次对每段数据进行反演。
|
图 1 横向分段组合约束反演示意图 |
根据图 1中的横向分段组合约束反演的计算策略,将数据拟合方程(式(5))、横向粗糙度约束方程(式(8))、横向先验信息约束方程(式(12))以及垂向粗糙度约束方程(式(13))联合,可以得到总的反演方程
| $ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{G}}\\ {{\mathit{\boldsymbol{R}}_{{\rm{ls}}}}}\\ {{\mathit{\boldsymbol{R}}_{{\rm{vs}}}}}\\ \mathit{\boldsymbol{I}} \end{array}} \right]{\rm{ { δ} }}\mathit{\boldsymbol{m}} - \left[ {\begin{array}{*{20}{c}} {{\rm{ { δ} }}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}}}\\ { - {\mathit{\boldsymbol{R}}_{{\rm{ls}}}}\mathit{\boldsymbol{m}}}\\ { - {\mathit{\boldsymbol{R}}_{{\rm{vs}}}}\mathit{\boldsymbol{m}}}\\ {{\mathit{\boldsymbol{m}}_{{\rm{prior}}}} - \mathit{\boldsymbol{m}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_{{\rm{obs}}}}}\\ {{\mathit{\boldsymbol{e}}_{{\rm{ls}}}}}\\ {{\mathit{\boldsymbol{e}}_{{\rm{vs}}}}}\\ {{\mathit{\boldsymbol{e}}_{{\rm{lp}}}}} \end{array}} \right] $ | (15) |
令
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{G'}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{G}}&{}&{}&0\\ {}&{{\mathit{\boldsymbol{R}}_{{\rm{ls}}}}}&{}&{}\\ {}&{}&{{\mathit{\boldsymbol{R}}_{{\rm{vs}}}}}&{}\\ 0&{}&{}&\mathit{\boldsymbol{I}} \end{array}} \right]\\ {\rm{ { δ} }}\mathit{\boldsymbol{d'}} = \left[ {\begin{array}{*{20}{c}} {{\rm{ { δ} }}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}}}\\ { - {\mathit{\boldsymbol{R}}_{{\rm{ls}}}}\mathit{\boldsymbol{m}}}\\ { - {\mathit{\boldsymbol{R}}_{{\rm{vs}}}}\mathit{\boldsymbol{m}}}\\ {{\mathit{\boldsymbol{m}}_{{\rm{prior}}}} - \mathit{\boldsymbol{m}}} \end{array}} \right] \end{array} \right. $ | (16a) |
| $ \mathit{\boldsymbol{e'}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_{{\rm{obs}}}}}\\ {{\mathit{\boldsymbol{e}}_{{\rm{ls}}}}}\\ {{\mathit{\boldsymbol{e}}_{{\rm{vs}}}}}\\ {{\mathit{\boldsymbol{e}}_{{\rm{lp}}}}} \end{array}} \right] $ | (16b) |
则式(15)可以写为
| $ \mathit{\boldsymbol{G'}}{\rm{ { δ} }}\mathit{\boldsymbol{m}} - {\rm{ { δ} }}\mathit{\boldsymbol{d'}} = \mathit{\boldsymbol{e'}} $ | (17) |
根据文献[24], 式(17)的解为
| $ {\rm{ { δ} }}{\mathit{\boldsymbol{m}}_{{\rm{est}}}} = {\left[ {{{\left( {\mathit{\boldsymbol{G'}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{WG'}}} \right]^{ - 1}}{\left( {\mathit{\boldsymbol{G'}}} \right)^{\rm{T}}}\mathit{\boldsymbol{W}}{\rm{ { δ} }}\mathit{\boldsymbol{d'}} $ | (18) |
式中W为模型参数和数据项的权值矩阵,可以写成
| $ \mathit{\boldsymbol{W}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{W}}_{{\rm{obs}}}}}&{}&{}&{}\\ {}&{{\mathit{\boldsymbol{W}}_{{\rm{ls}}}}}&{}&{}\\ {}&{}&{{\mathit{\boldsymbol{W}}_{{\rm{vs}}}}}&{}\\ {}&{}&{}&{{\mathit{\boldsymbol{W}}_{{\rm{lp}}}}} \end{array}} \right] $ | (19) |
其中Wobs、Wls、Wvs和Wlp均为对角加权矩阵,Wobs为数据项的加权矩阵,Wls为模型项的横向约束加权矩阵,Wvs为模型项的垂向约束加权矩阵,Wlp为先验模型的加权矩阵。为了使式(18)解更稳定,引入阻尼因子,将其改为迭代形式
| $ {\mathit{\boldsymbol{m}}_{n + 1}} = {\mathit{\boldsymbol{m}}_n} + {\left( {\mathit{\boldsymbol{G'}}_n^{\rm{T}}\mathit{\boldsymbol{W}}{{\mathit{\boldsymbol{G'}}}_n} + {\lambda _n}\mathit{\boldsymbol{I}}} \right)^{ - 1}}{\left( {{{\mathit{\boldsymbol{G'}}}_n}} \right)^{\rm{T}}}\mathit{\boldsymbol{W}}\delta {{\mathit{\boldsymbol{d'}}}_n} $ | (20) |
式中:λn为第n次迭代的阻尼因子,求解方法见文献[25];mn为第n次迭代的模型参数。将式(16)和式(19)代入式(20),有
| $ \begin{array}{l} {\mathit{\boldsymbol{m}}_{n + 1}} = {\mathit{\boldsymbol{m}}_n} + \left( {\mathit{\boldsymbol{G}}_{{\rm{obs}}}^{\rm{T}}{\mathit{\boldsymbol{W}}_{{\rm{obs}}}}{\mathit{\boldsymbol{G}}_{{\rm{obs}}}} + \mathit{\boldsymbol{R}}_{{\rm{ls}}}^{\rm{T}}{\mathit{\boldsymbol{W}}_{{\rm{ls}}}}{\mathit{\boldsymbol{R}}_{{\rm{ls}}}} + } \right.\\ \;\;\;\;\;\;\;\;\;{\left. {\mathit{\boldsymbol{R}}_{{\rm{vs}}}^{\rm{T}}{\mathit{\boldsymbol{W}}_{{\rm{vs}}}}{\mathit{\boldsymbol{R}}_{{\rm{vs}}}} + {\mathit{\boldsymbol{W}}_{{\rm{lp}}}} + {\lambda _{\rm{n}}}\mathit{\boldsymbol{I}}} \right)^{ - 1}} \times \\ \;\;\;\;\;\;\;\;\;\left\{ {\mathit{\boldsymbol{G}}_{{\rm{obs}}}^{\rm{T}}{\mathit{\boldsymbol{W}}_{{\rm{obs}}}}\left[ {{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} - \mathit{\boldsymbol{g}}\left( {{\mathit{\boldsymbol{m}}_n}} \right)} \right] + {\boldsymbol{R}}_{{\rm{ls}}}^{\rm{T}}{{\boldsymbol{W}}_{{\rm{ls}}}}\left( { - {{\boldsymbol{R}}_{{\rm{ls}}}}{{\boldsymbol{m}}_n}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\left. {\mathit{\boldsymbol{R}}_{{\rm{vs}}}^{\rm{T}}{\mathit{\boldsymbol{W}}_{{\rm{vs}}}}\left( { - {\mathit{\boldsymbol{R}}_{{\rm{vs}}}}{\mathit{\boldsymbol{m}}_n}} \right) + {\mathit{\boldsymbol{W}}_{{\rm{lp}}}}\left( {{\mathit{\boldsymbol{m}}_{{\rm{prior}}}} - {\mathit{\boldsymbol{m}}_n}} \right)} \right\} \end{array} $ | (21) |
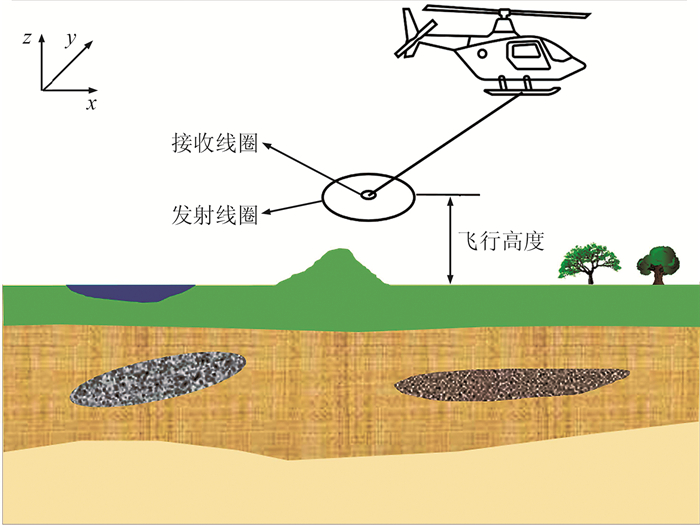
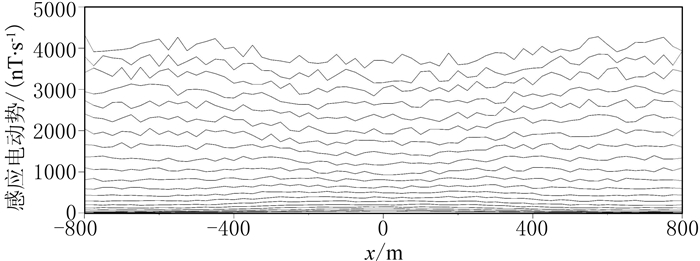
为了验证该方法的有效性,本文使用2.5维正演程序[26]模拟ATEM响应数据。ATEM数据采集系统见图 2,发射和接收系统主要参数为:发射线圈面积为123.9m2,匝数为5;发射基频为25Hz,发射波形为三角波,上升沿时长为1.5ms,下降沿时长为1.50ms,峰值电流为300A;接收和发射线圈离地高度均为30m。理论模型包括3层:第1层的厚度为40m,电阻率为100Ω·m;第2层电阻率为5Ω·m,两边厚度为40m,中间厚度为100m,在中间位置有一宽度大约为200m、厚度逐渐变化的区域;第3层是基底,电阻率为100Ω·m。测线长度为1600m,测点间距为25m,测点个数为65。在测量发射电流关断后0.04~4.00ms时间段内按照对数等间距抽取21道的感应电动势(图 3)。为了尽量接近实测数据,对模拟的电磁响应数据添加5%的高斯白噪声。
|
图 2 航空电磁采集系统示意图 |
|
图 3 理论模型的模拟电磁响应曲线 图中曲线从上到下分别对应衰减早期到晚期的感应电动势 |
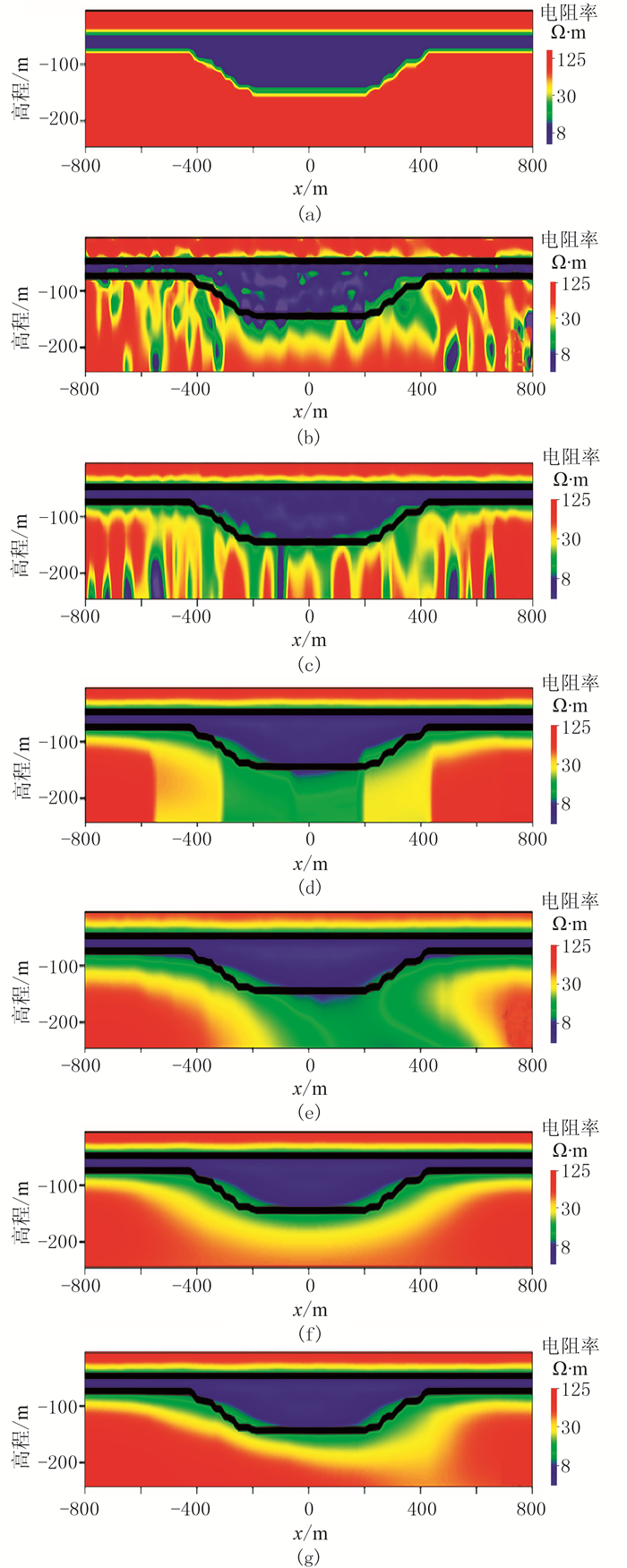
反演初始模型是电阻率为100Ω·m的均匀半空间,共26层,每层厚度均为10m。图 4b~图 4g为不同方法的反演结果,其中图 4b~图 4d和图 4g采取分段反演方法,即测线上的所有测点分为7段,前6段的测点数均为10,最后一段的测点个数为5,而图 4e采用单测点依次反演,图 4f则是所有测点同时反演。表 1为不同反演方法的计算时间及反演结果与理论模型的均方根误差。本文所用的计算平台CPU型号为E3-1505M(8核),内存为16GB。
|
图 4 模型数据反演结果 (a)理论模型; (b)无约束分段反演; (c)垂向粗糙度约束分段反演; (d)垂向和横向粗糙度约束分段反演; (e)垂向粗糙度约束和横向先验信息约束单点反演; (f)垂向和横向粗糙度约束反演; (g)横向分段组合约束反演 图中黑线为理论模型界面 |
|
|
表 1 理论模型不同反演方法计算时间及均方根误差(RMSE) |
从图 4b~图 4d、图 4g可以看出:无约束的分段反演结果(图 4b)整体效果较差,边界模糊,中间部位电阻率值波动较大。进行了垂向粗糙度约束(图 4c)的反演结果得到了一定的改善,中间部位基本连成一块,但是横向连续性依然不理想。图 4d在图 4c的基础上增加了横向粗糙度约束,可见反演结果在横向上的连续性得到了改善,但是由于段与段之间没有进行横向约束,反演结果出现了分块现象。图 4g是在图 4d的基础上在段与段之间增加了横向先验信息约束,其结果与图 4a中的理论模型比较接近。对比图 4d与图 4g可以发现,横向先验信息约束可以消除由分段引起的反演结果的分块现象,提高反演的精度。
结合表 1可以发现,在ATEM数据反演中,增加适当的约束可在提高反演结果准确性的同时减少计算时间。
对比图 4e与图 4g可以看出:图 4e整体连续性较好,但由于采用前一个测点的反演结果作为当前测点的先验信息来保持模型在横向上的连续性,这只是单向约束,导致反演结果具有明显的方向性,因而与图 4a中理论模型相差较大;图 4g的横向分段组合约束反演是在段与段之间采用单向的横向先验信息约束,而在段内采用双向约束的横向粗糙度约束,因此,反演结果受单向横向先验信息约束的影响较小,没有出现类似于图 4e中明显的方向性。因此,图 4e虽计算时间较少(表 1),但是反演结果的异常体的边界不准确,误差较大;图 4g的计算时间稍长,但是反演精度较高,能真实地反映地下介质的电性分布特征。
对比图 4f与图 4g可以看出,二者与理论模型(图 4a)较为接近,边界轮廓比较清晰,整体的连续性也较好。图 4f的计算时间是图 4g的近80倍,且误差也稍大。因此,横向分段组合约束反演可以在确保反演精度的同时大幅度减少计算时间。
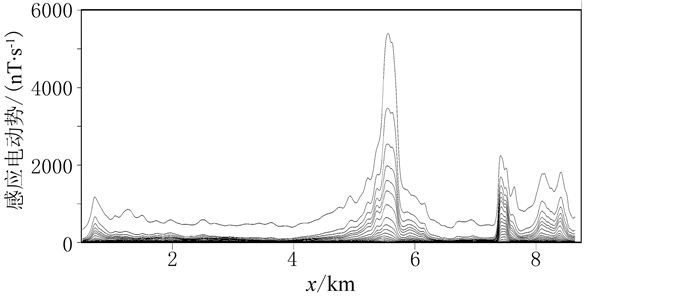
2.2 实测数据反演为了验证该横向分段组合约束反演方案的实用性,对美国地质调查局(USGS)网站上公开的野外ATEM勘探数据(图 5)[27]进行反演。
|
图 5 实测电磁响应曲线 |
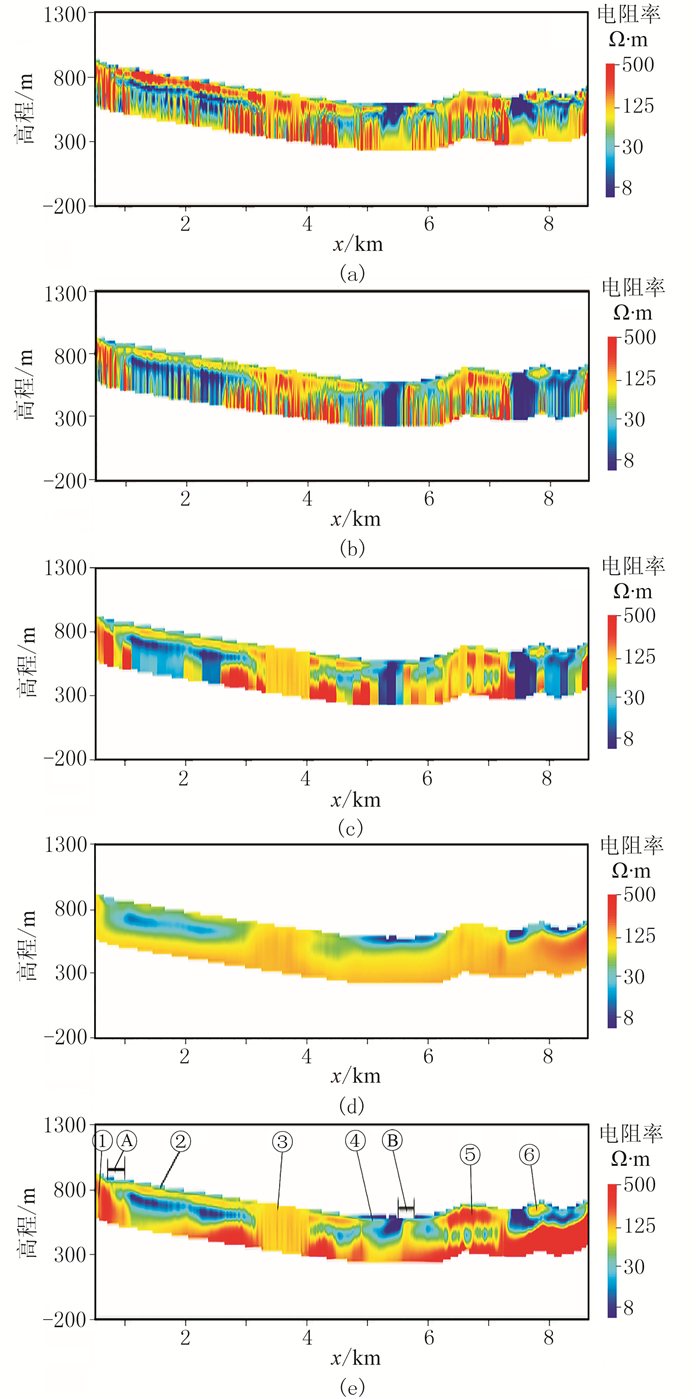
每10个测点分为一段,反演结果见图 6。对比图 6a~图 6d可以发现,无约束的反演结果(图 6a)整体连续性较差,仅能够反应地质体的大致位置,边界较模糊;增加了垂向约束的反演结果(图 6b)在垂直方向上的连续性增强,但是地质体的形状和轮廓仍然较为模糊,且第三层的反演效果不佳;增加了横向粗糙度约束的反演结果(图 6c)的整体连续性增加,但是分段导致相邻段之间的反演结果差别较大,不能很好地突出地质体的边界和轮廓;图 6d整体较光滑,但是地质体的位置和形状不能很好地得到反映;横向分段组合约束的反演结果(图 6e)所反映的地质体位置、形状和边界较清晰。
|
图 6 实测数据不同方式的反演结果 (a)无约束的分段反演结果; (b)垂向粗糙度约束的分段反演结果; (c)垂向和横向粗糙度约束的分段反演结果; (d)垂向粗糙度约束和横向先验信息约束的单点反演结果; (e)横向分段组合约束反演的反演结果 |
(1) 图中①处存在着一条山脉,分布着大量的基性火成岩,其电阻率大于1000Ω·m,与反演结果基本一致;
(2) 图 6e中①、②之间的A处存在断层, 而图 6e中的电阻率在①、②之间的断层A处的左右对比明显,能够很好地展现出断层的垂向变化;
(3) 图中的②、③、④位于盆地中,其中②处的表层是由松散砂砾石组成的冲积扇沉积物,电阻率为80~150Ω·m, 反演结果能够很好地体现,③位于露头花岗岩附近,图中这个位置也呈现较高电阻率,④处富含粘土,具有较低的电阻率;
(4) 图中的⑤处位于盆地边缘,主要由长英质火山岩组成,其电性与花岗岩相近,即具有较高的电阻率,与反演剖面结果一致;
(5) 图中B处存在一个横切的断裂带,这可能是导致⑤处内部电阻率等值线不连续的原因;
(6) 图中⑥处表层黄色位置为长英质火山岩,具有较高的电阻率。蓝色位置由较新的中等冲积扇沉积物组成,主要包含分选不良、致密的胶结砂和砾石,具有较低的电阻率(< 10Ω·m)。
由此可见,实测ATEM数据反演所得到的构造、断层及地质体的位置、形状和边界较清晰,反演结果与实际的地质资料吻合较好,说明本文提出的反演策略可有效地应用于实测ATEM数据的反演。
3 结论本文将垂向粗糙度约束、横向粗糙度约束以及横向先验信息约束三者相结合,对ATEM数据进行分段反演。模拟数据和实际数据的反演结果说明:
(1) 适当的约束条件可提高ATEM数据反演结果的准确性,同时也能减少计算时间;
(2) 横向先验信息约束可消除由分段引起的段间不连续现象;
(3) 横向粗糙度约束能有效地降低由横向先验信息约束引起的方向性。
| [1] |
殷长春, 黄威, 贲放. 时间域航空电磁系统瞬变全时响应正演模拟[J]. 地球物理学报, 2013, 56(9): 3153-3162. YIN Changchun, HUANG Wei, BEN Fang. The full-time electromagnetic modeling for time-domain airborne electromagnetic systems[J]. Chinese Journal of Geophysics, 2013, 56(9): 3153-3162. |
| [2] |
Pfaffhuber A A, Monstad S, Rudd J. Airborne electro-magnetic hydrocarbon mapping in Mozambique[J]. Exploration Geophysics, 2009, 40(3): 237-245. DOI:10.1071/EG09011 |
| [3] |
Smith R.Airborne electromagnetic methods: applications to minerals, water and hydrocarbon exploration[C].CSEG 2010 Distinguished Lecture, 2010, 7-10.
|
| [4] |
Siemon B, Christiansen A V, Auken E. A review of helicopter-borne electromagnetic methods for groundwater exploration[J]. Near Surface Geophysics, 2009, 7(5-6): 629-646. DOI:10.3997/1873-0604.2009043 |
| [5] |
Vallee M A, Smith R S. Application of Occam's in-version to airborne time-domain electromagnetics[J]. The Leading Edge, 2009, 28(3): 284-287. DOI:10.1190/1.3104071 |
| [6] |
Viezzoli A, Auken E, Munday T. Spatially constrained inversion for quasi 3D modelling of airborne electromagnetic data:an application for environmental assessment in the lower Murray region of South Australia[J]. Exploration Geophysics, 2009, 40(1): 173-183. |
| [7] |
Wolfgram P, Sattel D, Christensen N B. Approximate 2D inversion of AEM data[J]. Exploration Geophy-sics, 2003, 34(2): 29-33. |
| [8] |
Cox L H, Wilson G A, Zhdanov M S. 3D inversion of airborne electromagnetic data[J]. Geophysics, 2012, 77(4): 59-69. DOI:10.1190/geo2011-0370.1 |
| [9] |
Haber E, Schwarzbach C. Parallel inversion of large-scale airborne time-domain electromagnetic data with multiple OcTree meshes[J]. Inverse Problem, 2014, 30(5): 1-28. |
| [10] |
Yang D, Oldenbuurg D W, Haber E. 3-D inversion of airborne electromagnetic data parallelized and accele-rated by local mesh and adaptive soundings[J]. Geophysical Journal International, 2014, 196(3): 1492-1507. DOI:10.1093/gji/ggt465 |
| [11] |
Constable S C, Parker R L, Constable C G. Occam's inversion:a practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics, 1987, 52(3): 289-300. DOI:10.1190/1.1442303 |
| [12] |
陈小斌, 赵国泽, 汤吉, 等. 大地电磁自适应正则化反演算法[J]. 地球物理学报, 2005, 48(4): 937-946. CHEN Xiaobin, ZHAO Guoze, TANG Ji, et al. An adaptive regularized inversion algorithm for magnetotelluric data[J]. Chinese Journal of Geophysics, 2005, 48(4): 937-946. DOI:10.3321/j.issn:0001-5733.2005.04.029 |
| [13] |
毛立峰, 王绪本, 陈斌. 直升机航空瞬变电磁自适应正则化一维反演方法研究[J]. 地球物理学进展, 2011, 26(1): 300-305. MAO Lifeng, WANG Xuben, CHEN Bin. Study on an adaptive regularized 1D inversion method of helicopter TEM data[J]. Progress in Geophysics, 2011, 26(1): 300-305. DOI:10.3969/j.issn.1004-2903.2011.01.035 |
| [14] |
罗勇, 陆从德, 王宇航. 时间域航空瞬变电磁一维阻尼特征参数反演方法[J]. 地球物理学进展, 2014, 29(6): 2723-2729. LUO Yong, LU Congde, WANG Yuhang. 1D inversion method based on damped eigen parameter for airborne time domain electromagnetic data[J]. Progress in Geophysics, 2014, 29(6): 2723-2729. |
| [15] |
昌彦君, 肖明顺, 武毅. 瞬变电磁数据一维反演的初值选取研究[J]. 石油地球物理勘探, 2010, 45(2): 295-298. CHANG Yanjun, XIAO Mingshun, WU Yi. Studies on initial parameter selection of one-dimensional inversion for transient electromagnetic data[J]. Oil Geo-physical Prospecting, 2010, 45(2): 295-298. |
| [16] |
Auken E, Christiansen A V. Layered and laterally con-strained 2D inversion of resistivity data[J]. Geophy-sics, 2004, 69(3): 752-761. |
| [17] |
Auken E, Christiansen A V, Jacobsen L H. A resolution study of buried valleys using laterally constrained inversion of TEM data[J]. Journal of Applied Geophysics, 2008, 65(1): 10-20. DOI:10.1016/j.jappgeo.2008.03.003 |
| [18] |
Vallee M A, Smith R S. Inversion of airborne time-domain electromagnetic data to a 1D structure using la-teral constraints[J]. Near Surface Geophysics, 2009, 7(1): 63-71. DOI:10.3997/1873-0604.2008035 |
| [19] |
蔡晶, 齐彦福, 殷长春, 等. 频率域航空电磁数据的加权横向约束反演[J]. 地球物理学报, 2014, 57(1): 953-960. CAI Jing, QI Yanfu, YIN Changchun, et al. Weighted laterally-constrained inversion of frequency-domain airborne EM data[J]. Chinese Journal of Geophysics, 2014, 57(1): 953-960. |
| [20] |
Siemon B, Auken E, Christiansen A V. Laterally con-strained inversion of helicopter-borne frequency-do-main electromagnetic data[J]. Journal of Applied Geo-physics, 2009, 67(3): 259-268. DOI:10.1016/j.jappgeo.2007.11.003 |
| [21] |
Yu X D, Wang X B, Lu C D, et al. A combining regu-larization strategy for inversion of airborne time-domain electromagnetic data[J]. Journal of Applied Geo-physics, 2018, 155(1): 110-121. |
| [22] |
Jupp D L B, Vozoff K. Stable iterative methods for the inversion of geophysical data[J]. Geophysical Journal of the Royal Astronomical Society, 1975, 42(3): 957-976. |
| [23] |
Farquharson C G and Oldenburg D W. Non-linear inversion using general measures of data misfit and model structure[J]. Geophysical Journal Internatio-nal, 1998, 134(1): 213-227. DOI:10.1046/j.1365-246x.1998.00555.x |
| [24] |
Menke W. Geophysical Data Analysis:Discrete In-verse Theory[M]. New York: Academic Press Inc, 1989.
|
| [25] |
Marquart D. An algorithm for least squares estimation of nonlinear parameters[J]. Journal of the Society for Industrial and Applied Mathematics, 1963, 11(2): 431-441. DOI:10.1137/0111030 |
| [26] |
Wilson G A, Raiche A P, Sugeng F. 2.2.5D inversion of airborne electromagnetic data[J]. Exploration Geophysics, 2006, 37(4): 363-371. DOI:10.1071/EG06363 |
| [27] |
Bedrosian P A, Ball L B, Bloss B R.Airborne electromagnetic data and processing within Leach Lake Basin, Fort Irwin, California[R].US Geological Survey Open File Report 2013-1024, 2014, 1-20.https://doi.org/10.3133/ofr20131024G.
|



 陆从德, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院, 610059。Email:
陆从德, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院, 610059。Email: