② 中国石油华北油田第五采油厂, 河北辛集 052360;
③ 中国石油集团渤海钻探工程有限公司第二录井分公司, 河北任丘 062552
② No. 5 Oil Production Plant, Huabei Oilfield Company, PetroChina, Xinji, Hebei 052360, China;
③ Logging Branch 2, Bohai Drilling Engineering Company Limited, CNPC, Renqiu, Hebei 062552, China
相关系数是一种定量描述两组随机变量的统计学相关性的指标。相关系数的计算方法有很多种,其中比较经典的有Pearson[1]、Spearman[2]和Kendall[3]等相关系数法。这些计算方法都有其适用范围: Pearson相关系数适用于二元高斯分布;Spearman和Kendall相关系数适用于非线性分布[4]。虽然计算过程不同,但是以上三种相关系数有相似性,它们都可以抽象为广义相关系数[5],即通过比较数组中的每个数对以确定两组数据整体间的相关程度。
相关系数在油气勘探中应用最多的是数据优选,如利用有效性开展属性优选[6-7]、地球化学取样中的多自由度分析[8]、烃源岩的预测[9]等。同时,还有学者将相关系数应用到多种数据的联合预测[10]和磁法勘探的低纬度化极算法[11]中。
在地球物理学中应用相关系数的基本原理是不同地球物理参数的同源性[12],即在一片区域观测的不同类型的物理量(重、磁、电、震、测井数据等)是同一套地质体的不同响应。所以,研究不同数据的相关性的大小有助于优选出与地质体有关的变量,从而揭示地质体与观测量之间关系的规律。
在油气勘探领域,变量常受多种因素影响,因而两组变量的相关情况比较复杂。为了尽量减少影响,可以选择计算地理位置较近点(两组特定变量)的相关性。当两个取样点的地理位置较近时,它们受同一因素影响的可能性更高,因此比较地理位置较近的样点更有助于控制变量数目。为了研究数据在空间分布上的特征,本文在广义相关系数的基础上,引入空间权重的概念,在比较每组数据时加入与空间距离有关的权重改进比较结果。在空间数据学中,有应用类似的权重计算空间自相关的方法,比如Moran自相关[13]和Geary自相关[14],前者经过宋马林等[15]改进也可以应用到非网格型数据的相关计算中。
如果将广义相关系数看作一种全局相关系数,那么这种距离权重改进的相关系数则是一种局部相关系数。本文将详细说明局部相关系数的原理及其性质,并利用模拟数据和实际数据检验该相关系数的应用效果。
1 原理假设有两组随机变量X和Y,它们各自经历了n次独立观测。Xi和Yi表示第i次观测值,(xi, yi)是第i次观测的大地坐标。
1.1 广义相关系数Pearson、Spearman、Kendall相关系数都可以抽象为以下计算模式[4, 16]
| $ {\mathit{\Gamma}}_{\mathrm{D}}=\frac{\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n} a_{i j} b_{i j}}{\left(\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n} a_{i j}^{2} \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n} b_{i j}^{2}\right)^{\frac{1}{2}}} $ | (1) |
如果aij=Xj-Xi、bij=Yj-Yi,式(1)为Pearson相关系数计算公式;
如果aij=Pj-Pi、bij=Qj-Qi,P为X在本组变量中的序次,Q为Y在本组变量中的序次,此时式(1)为Spearman相关系数计算公式;
如果aij=sgn(Xj-Xi)、bij=sgn(Yj-Yi), sgn(·)表示符号函数,此时式(1)为Kendall相关系数计算公式。
式(1)说明了这三种相关系数的计算方法都可以看成是比较随机变量中的每一组数对后再求和的形式。每组数对的比较都会给计算结果贡献一个值,最后求和是为了得到各个数对的比较结果的整体趋势。
广义相关系数的取值范围为[-1, 1]。当相关系数的绝对值越大,说明两组随机变量的相关性越强。符号为正时称为正相关,即一组变量随着另一组变量的增大而增大;符号为负时称为负相关,即一组变量随着另一组变量的增大而减小。
1.2 距离权重如果应用具地理意义的距离权重,需要符合“地理上距离越近的事物关联性越强”[17]这一条地理学第一定律,即权重矩阵与数对之间的距离为负相关,也说是说,两点间的距离越近,权重越大。这里仅讨论一种比较简单的距离权重选取方式
| $ \lambda_{i j}=\left\{\begin{array}{ll}{1} & {d_{i j} <\sigma} \\ {0} & 其他情况\end{array}\right. $ | (2) |
| $ d_{i j}=\sqrt{\left(x_{j}-x_{i}\right)^{2}+\left(y_{j}-y_{i}\right)^{2}} $ | (3) |
式中:λij为距离权重,值域为[0, 1];dij为i与j点之间的距离;σ为搜索半径(距离阈值)。式(2)、式(3)表明,只比较两点之间的距离小于一定值的点,且在这个距离范围内赋予各点等权重。
1.3 距离权重改进的Pearson相关系数若计算两组数据在空间上的相关情况,需将空间(距离)权重引入到相关计算中。以Pearson相关系数为模板
| $ I=\frac{\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n}\left(X_{j}-X_{i}\right)\left(Y_{j}-Y_{i}\right)}{\left[\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n}\left(X_{j}-X_{i}\right)^{2} \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n}\left(Y_{j}-Y_{i}\right)^{2}\right]^{\frac{1}{2}}} $ | (4) |
将Pearson相关系数结合空间权重推广到空间内
| $ \begin{array}{l}{I^{\prime}=} \\ {\qquad \frac{\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n} \lambda_{i j}^{(X)}\left(X_{j}-X_{i}\right) \lambda_{i j}^{(Y)}\left(Y_{j}-Y_{i}\right)}{\left\{\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n}\left[\lambda_{i j}^{(X)}\left(X_{j}-X_{i}\right)\right]^{2} \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n}\left[\lambda_{i j}^{(Y)}\left(Y_{j}-Y_{i}\right)\right]^{2}\right\}^{\frac{1}{2}}}}\end{array} $ | (5) |
式(4)为Pearson相关系数,该式通过比较数据中的每组数对,再累加求和,从而体现数据的整体趋势(单调性)。
式(4)的核心是(Xj-Xi)(Yj-Yi),即比较数据中任意一个数对的X变量和Y变量,并将其结果相乘。如果数对(Xj-Xi)与(Yj-Yi)异号,则说明X较大值对应Y的较小值(或X较小值对应Y的较大值);如果数对(Xj-Xi)与(Yj-Yi)同号,则说明X的较大值对应Y的较大值(或X的较小值对应Y的较小值)。分子通过两次求和计算以统计数据中每组数对的符号异、同性。如果这组数据具有单调性,则每组数对的比较结果(Xj-Xi)(Yj-Yi)出现同一种符号的数量多,此时累加求和的结果的绝对值就大。而当(Xj-Xi)(Yj-Yi)出现不同符号的数量越多时,则累加求和的结果越接近0。
式(4)的分母可以看作是这组数据的(Xj-Xi)与(Yj-Yi)分别求均方根、再相乘的形式。分母并不影响式(4)的符号,只是将分子的结果进行归一化。
通过(Xj-Xi)(Yj-Yi)可以看出,Pearson相关系数只比较了数据中的X和Y变量,但没有考虑不同数据的取样的位置。
为了将取样点的位置引入式(4)中,在比较这组数对X与Y变量的同时,比较两个数据取样点的距离大小,即1.2节中的距离权重。将(Xj-Xi)×(Yj-Yi)变为λij(X)(Xj-Xi)λij(Y)(Yj-Yi),用距离权重修正(Xj-Xi)(Yj-Yi)的结果。
式(5)中的λij(X)表示X随机变量中第i个数据到第j个数据的距离权重,λij(Y)表示Y随机变量中第i个数据到第j个数据的距离权重。在一般情况下,数据采集的地理位置只有一组,所以λij(X)=λij(Y)。如果研究比较复杂的问题,可以令λij(X)≠λij(Y),即X和Y有不同的距离权重。
式(5)表示,在比较每组数对时,将其结果乘以相应的距离权重,最后再求和计算。权重的取值总为正,它只改变每组比较结果的取值大小,而不改变符号。需要注意的是虽然权重不影响每组数对的符号,但是最后的汇总结果的符号会受权重影响。
式(5)的取值范围为[-1, 1]。由于距离权重的各向同性,可以将加权后的数据比较看成两组新数据做比较,所以式(5)的取值范围和Pearson相关系数的取值范围相同。当距离权重全部相同时,式(5)退化为Pearson相关系数计算公式(式(4))。
1.4 局部相关系数Pearson相关系数不考虑数据取样点远近,比较全部数据的X与Y变量的相关性;而距离权重改进的相关系数突出了距离较近的取样点的X与Y变量的相关性,针对每个样点来说,比较了该样点附近的样点。因此,在空间上Pearson相关系数是平等考虑所有样点的“全局相关系数”,而距离加权的相关系数是一种突出局部相关性的“局部相关变量”。
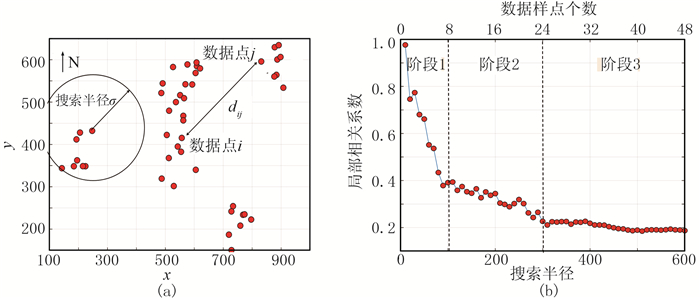
1.5 距离—相关性频谱局部相关系数虽然能体现距离较近样点的相关性(图 1a),但是需要人工确定搜索半径。搜索半径决定了样点的个数,因此在很大程度上影响了局部相关系数的大小。
|
图 1 取样点位置(a)及局部相关性频谱(b) 数据来源于表 1 |
|
|
表 1 模拟数据 |
为了解决人工选择搜索半径的困难,可以将搜索半径作为一个变化值,并以固定步长为增量,计算该组数据样点之间最小距离到最大距离内所有搜索半径的局部相关系数。将每个搜索半径对应其局部相关系数做成一张折线图,这张图即为距离—相关性频谱(图 1b)。
通过距离—相关性频谱图,所有搜索半径下的局部相关系数得以展示。然后可以通过分析折线图挖掘两组数据被距离关系掩盖的相关性,并研究在不同尺度下两组数据相关性的变化规律。
综上所述,距离权重改进前、后的相关系数主要不同之处有:改进前相关系数是所有样点都参与计算,每个数对对结果的影响相同,最终结果为一个数值;而距离权重改进后相关系数计算时,距离较近的数对对结果的影响大,体现最终结果的是距离—相关性频谱图,反映的是很少样点的相关性。
2 模拟数据测试为了测试改进后相关系数的效果,应用二维模拟数据(表 1)进行检验。
该模拟数据的目的是体现局部相关系数的重要性。由于Pearson相关系数在计算时对每个数据的采样点赋予相等权重,而且最后的结果也仅是一个取值范围[-1, 1]的数值。这就使得可能在小范围内存在相关性的两组数据被大范围内的非相关性掩盖。
该模拟数据由周期函数加随机噪声构成,模仿在空间上周期出现的数据,如地质构造、井距与产量关系等类似数据。
表 1中x与y是地理位置,X与Y变量无单位。距离权重选用式(2)。图 1a展示了数据取样点的地理位置,图 1b为采用不同的搜索半径得到的局部相关系数的折线图。这种研究空间内相关性变化趋势的曲线类似于克里金插值中用到的变差函数[18],也是一种距离和某种属性的距离频谱。
根据斜率,图 1b中的曲线可以大致分为三个阶段:第一阶段,搜索半径从0到100,曲线的下降速度快,这说明这组模拟数据在小范围内相关关系不稳定,随着数据点个数的增多,相关性快速降低;第二阶段,搜索半径从100到300,曲线下降速度变慢,这说明在中等范围内可以维持一定的相关性;第三阶段,搜索半径从300到600,曲线较为平缓,这说明在大范围内数据呈现稳定的相关性,相关系数随着半径的变大不会出现较大的变化。当包含全部样点时,曲线收敛为Pearson相关系数。
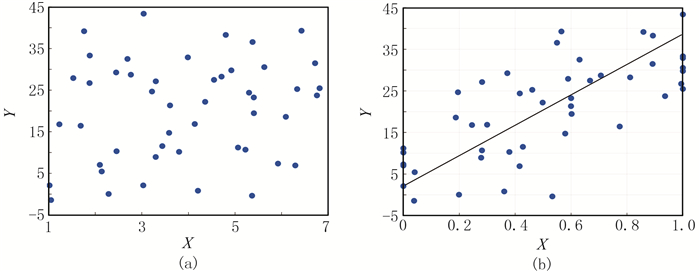
局部相关和全局相关的差别可以通过图 2说明。图 2a是全局相关视角下X与Y两变量的交会图,从中很难发现X与Y变量的相关性。利用相同的两组数据,先通过数据点的空间位置对数据进行分组(以距离100为阈值),将距离较近的样点分为一组;再将X变量在每组内归一化,最后再制做与Y变量的交会图,即可得到图 2b。该图为局部相关视角下的交会图,可以清楚地发现两组变量的相关性。从相关系数上来看,搜索半径为100的局部相关系数为0.4;而未改进的Pearson(全局)相关系数为0.21,可见全局相关系数掩盖了数据的局部相关性。
|
图 2 全局相关与局部相关比较
(a)全局相关系数视角下的交会图;(b)局部相关系数视角下的交会图 数据来源于表 1 |
实际资料来自沁水盆地南部某区块,有若干生产井,三维地震勘探覆盖全区。山西组3号煤层为主要产气层之一,由北东向南西方向逐渐变薄;顶板泥岩较为发育,煤层气封存条件较好;煤层主要受燕山期和喜山期运动影响而发育裂缝,该煤层的产气量受裂缝和煤的厚度影响较大。
表 2为该区块井点的数据资料,井位坐标相对位置关系见图 3。日产气量为统计的实际信息。方位各向异性由叠前地震数据计算而得,煤厚度由储层参数反演而得,应力由叠后地震数据根据构造和速度场计算而得。通过方位各向异性、厚度和应力三种数据的筛选与融合以获得和日产气量相关性较高的融合数据。
|
|
表 2 山西组3号煤层井点数据 |

|
图 3 沁水盆地南部某区块山西组3号煤层属性及其与日产气量的局部相关性频谱 (a)方位各向异性平面图;(b)方位各向异性与日产气量的局部相关性频谱;(c)煤厚度(预测)平面图;(d)煤厚度与日产气量的局部相关性频谱;(e)应力属性平面图;(f)应力属性与日产气量的局部相关性频谱 |
首先,计算方位各向异性(图 3a)、厚度(图 3c)和应力(图 3e)三组数据和日产气量的全局相关系数。方位各向异性的全局相关系数为0.28;煤厚度的全局相关系数为0.53;应力的全局相关系数为-0.52。从全局相关系数看,应该选用煤厚度与应力融合以预测日产气量,图 4c为其融合结果。

|
图 4 煤层厚度与应力属性空间频率滤波后融合属性及其与日产气量的局部相关性频谱 本文改进相关方法筛选的融合平面图(a)及其与日产气量的局部相关性频谱(b);Pearson相关方法筛选的融合平面图(c)及其与日产气量的局部相关性频谱(d) |
下面介绍用距离权重改进后的Pearson相关系数方法优选数据。
图 3b是方位各向异性与日产气量的局部相关频谱。方位各向异性是一种微裂缝(煤层中的割理缝)的指示标志。因为较大的比表面积和较小的孔隙度,一般认为割理缝有利于煤层气的储存。从图 3b可以看出,在使用小搜索半径时,日产气量与方位各向异性有比较弱的负相关性;而当搜索半径比较大时,这两组数据又有比较弱的正相关性,这一点与前人的认识相符。因为两组数据的较弱的相关性,所以不用方位各向异性进行下一步的预测工作。
从图 3d可以看出,在考察邻近某口井一定范围内的井时,也就是在小范围内,原生煤厚度与日产气量的相关性不明显。但如果从整体上考察,原生煤厚度与日产气量的相关性达到了0.5以上。
从图 3f可以看出,当搜索半径在10个点左右时,局部相关系数为0.26;当搜索半径较大时,全局相关系数为-0.52。这种现象说明,应力和产气量在小范围内正相关,应力越大对产气有利;但在大范围内为负相关,应力越大越不利于产气。这种现象的原因可能是,在小尺度下应力越大越容易形成小规模裂隙,此时有利于煤层气赋存;而在大范围内,应力越大越容易形成大规模裂缝,会导致煤层气逸散,此时不利于煤层气的赋存[19]。
以上三种地球物理参数和产气量的距离加权相关性研究结果表明,这三种地球物理参数各有其特点。应力在小尺度范围与产气量相关性好,而原生煤厚度在大尺度范围与产气量相关性强。因此在应用属性融合进行产气预测时,可以使用不同尺度的空间滤波,取应力的较高频部分(局部特征)和煤层厚度的较低频部分(背景场)进行融合,以达到最好的效果。这种分尺度研究数据的方法,陈文浩等[20]在变差函数的估算中曾经应用。
图 4a展示了用改进优选方法的融合平面图。从图 4b可以看出融合后在搜索半径为12时即可到达0.3的相关程度,而且在大搜索半径上仍然保持较高的相关程度。与应用未改进方法优选再融合的结果图 4c、图 4d比较,利用本文方法优选指导融合的结果在各个尺度上的相关性均优于按Pearson相关方法指导的融合结果。通过其他开发井进行检验,本文方法的结果的产气量吻合率更高。
4 结论(1) 距离权重改进的相关系数具有计算两组变量局部空间相关性的作用,可以用于挖掘被距离关系掩盖的相关性。
(2) 在选择空间权重的函数类型之后,多数情况下并不清楚数据在多大的搜索半径内具有相关性。如果搜索半径是一个固定值,则其对应的局部相关系数仅代表在这个搜索范围内的相关系数。因此,把搜索半径当成一个自变量,计算不同搜索半径下的相关性,并以折线图(距离-相关性频谱)表示。通过折线图的变化特征可以分析这两组变量在空间分布下的相关性。
(3) 局部相关变量和距离-相关性频谱具有指导数据优选和数据融合的作用。
| [1] |
Pearson K. Note on regression and inheritance in the case of two parents[J]. Proceedings of the Royal Society of London, 1895, 58(1): 240-242. |
| [2] |
Spearman C. "Footrule" for measuring correlation[J]. British Journal of Psychology, 1906, 2(1): 89-108. |
| [3] |
Kendall M G. A new measure of rank correlation[J]. Biometrika, 1938, 30(1/2): 81-93. DOI:10.2307/2332226 |
| [4] |
徐维超. 相关系数研究综述[J]. 广东工业大学学报, 2012, 29(3): 12-17. XU Weichao. A review on correlation coefficients[J]. Journal of Guangdong University of Technology, 2012, 29(3): 12-17. DOI:10.3969/j.issn.1007-7162.2012.03.002 |
| [5] |
Daniels H E. The relation between measures of correlation in the universe of sample permutations[J]. Bio-metrika, 1944, 33(2): 129-135. |
| [6] |
倪逸, 杨慧珠, 郭玲萱, 等. 储层油气预测中地震属性优选问题探讨[J]. 石油地球物理勘探, 1999, 34(6): 614-626. NI Yi, YANG Huizhu, GUO Lingxuan, et al. Optimization problem of seismic attributes in hydrocarbon reservoir prediction[J]. Oil Geophysical Prospecting, 1999, 34(6): 614-626. DOI:10.3321/j.issn:1000-7210.1999.06.002 |
| [7] |
Schultz P S, Ronen S, Hattori M, et al. Seismic-guided estimation of log properties (Part 1:A data-driven interpretation methodology)[J]. The Leading Edge, 1994, 13(5): 305-310. DOI:10.1190/1.1437020 |
| [8] |
张金震, 鞠霞, 张起, 等. 地质找矿中相关系数的等效性比较及应用[J]. 地质科技情报, 2017, 36(3): 306-314. ZHANG Jinzhen, JU Xia, ZHANG Qi, et al. Comparisons and applications of correlation coefficient equivalence in geological prospecting[J]. Geological Science and Technology Information, 2017, 36(3): 306-314. |
| [9] |
季少聪, 杨香华, 朱红涛, 等. 下刚果盆地A区块Madingo组烃源岩TOC含量的地球物理定量预测[J]. 石油地球物理勘探, 2018, 53(2): 369-380. JI Shaocong, YANG Xianghua, ZHU Hongtao, et al. Geophysical quantitative prediction of TOC content in source rocks of Madingo Formation in Block A, Lower Congo Basin[J]. Oil Geophysical Prospecting, 2018, 53(2): 369-380. |
| [10] |
殷长春, 孙思源, 高秀鹤, 等. 基于局部相关性约束的三维大地电磁数据和重力数据的联合反演[J]. 地球物理学报, 2018, 61(1): 358-367. YIN Changchun, SUN Siyuan, GAO Xiuhe, et al. 3Djoint inversion of magnetotelluric and gravity data based on local correlation constraints[J]. Chinese Journal of Geophysics, 2018, 61(1): 358-367. |
| [11] |
张琪, 张英堂, 李志宁, 等. 改进的低纬度化极稳定算法[J]. 石油地球物理勘探, 2018, 53(3): 606-616. ZHANG Qi, ZHANG Yingtang, LI Zhining, et al. An improved stable algorithm of the reduction-to-the-pole at low latitudes[J]. Oil Geophysical Prospecting, 2018, 53(3): 606-616. |
| [12] |
王珺璐, 冯兵, 杨万军, 等. 非震物化探找油方法优选组合研究——以鄂尔多斯盆地为例[J]. 物探与化探, 2014, 38(6): 1159-1163. WANG Junlu, FENG Bing, YANG Wanjun, et al. The optimized combination of non-seismic geophysical and geochemical exploration methods in the prospecting for oil:A case study of Ordos Basin[J]. Geophysical and Geochemical Exploration, 2014, 38(6): 1159-1163. |
| [13] |
Moran A P. Notes on continuous stochastic phenomena[J]. Biometrika, 1950, 37(1/2): 17-23. DOI:10.2307/2332142 |
| [14] |
Geary R C. The contiguity ratio and statistical mapping[J]. The Incorporated Statistician, 1954, 5(3): 115-146. DOI:10.2307/2986645 |
| [15] |
宋马林, 王舒鸿, 汝慧萍. 一种新的考虑时间和空间的相关系数及其算例[J]. 数量经济技术经济研究, 2010, 27(7): 142-152. SONG Malin, WANG Shuhong, RU Huiping. A new correlation coefficient considering space-time factors and its illustration[J]. The Journal of Quantitative & Technical Economics, 2010, 27(7): 142-152. |
| [16] |
Kendall M G.Rank Correlation Methods[M].Griffin, London, 1990.
|
| [17] |
Tobler W R. A computer movie simulating urban growth in the Detroit region[J]. Economic Geography, 1970, 46(S): 234-240. |
| [18] |
Matheron G. Principles of geostatistics[J]. Economic Geology, 1963, 58(8): 1246-1266. DOI:10.2113/gsecongeo.58.8.1246 |
| [19] |
潘仁芳, 金吉能. 断层和裂缝尺度识别的地球物理方法探讨[J]. 长江大学学报(自然科学版), 2011, 8(3): 16-18. PAN Renfang, JIN Jineng. Geophysical method for recognizing faults and fracture sizes[J]. Journal of Yangtze University (Natural Science Edition), 2011, 8(3): 16-18. |
| [20] |
陈文浩, 王志章, 刘月田, 等. 储层随机模拟中的多尺度变差函数估算方法[J]. 石油地球物理勘探, 2019, 54(1): 154-163. CHEN Wenhao, WANG Zhizhang, LIU Yuetian, et al. Multi-scale horizontal variogramestimation in re-servoir stochastic simulation[J]. Oil Geophysical Prospecting, 2019, 54(1): 154-163. |



 韩晟, 河北省任丘市建设中路1号华北油田勘探开发研究院, 062550。Email:
韩晟, 河北省任丘市建设中路1号华北油田勘探开发研究院, 062550。Email: