② 长江大学地球物理与石油资源学院, 湖北武汉 430100;
③ 中国石油大学(华东), 山东青岛 266580;
④ 中国石化江苏油田分公司, 江苏扬州 225009;
⑤ 东方地球物理公司西南物探分公司, 四川成都 610213;
⑥ 东方地球物理公司研究院大港分院, 天津 300280
② College of Geophysics and Petroleum Resources, Yangtze University, Wuhan, Hubei 430100, China;
③ School of Geosciences, China University of Petroleum(East China), Qingdao, Shandong 266580, China;
④ Jiangsu Oilfield Branch Co., SINOPC, Yangzhou, Jiangsu 225009, China;
⑤ Southwest Branch, BGP Inc., CNPC, Chengdu, Sichuan 610213, China;
⑥ Dagang Branch, GRI, BGP Inc., CNPC, Tianjin 300280, China
随着油气勘探、开发的不断深入,重点目标逐渐转为隐蔽油气藏,其中岩性油气藏显得尤为重要。地球物理反演是岩性油气藏勘探的主要手段之一[1]。一般情况下,叠后地震资料反演只能得到纵波阻抗(ZP),但由于不同岩性的纵波阻抗区间存在重叠,所以利用纵波阻抗单参数识别岩性存在局限性。而叠前地震资料反演能够得到更多反映地下岩石物理性质的参数,因此得到广泛应用。
1987年,Smith等[2]首次提出流体因子概念。之后,众多学者基于不同目的提出了各种流体因子。Goodway等[3]提出拉梅参数交会法识别岩性及流体。在考虑多孔流体饱和岩石的前提下,Russell等[4]总结前人的观点,将Biot-Gassmann方程流体因子项改写为纵、横波阻抗(ZS)加权形式,并对比了加权因子取值不同时储层流体的识别能力。宁忠华等[5]基于横波不在流体中传播的前提,采用纵波阻抗和横波阻抗高次方加权组合,形成高灵敏度流体识别因子(HSFIF)。Al-Dabagh等[6]展示了Kρ(体积模量与密度乘积)和λρ(拉梅常数与密度乘积)的对比效果,并说明利用Kρ检测流体的优越性。许翠霞等[7]针对致密含气砂岩孔隙度较低、不同流体引起储层与盖层波阻抗差异较小的问题,提出了一种适合致密含气砂岩预测的敏感参数λ/VS(拉梅常数/横波速度),其识别气层能力优于λρ和VP/VS(纵波速度/横波速度)。Sharma等[8]提出了一个新的属性Eρ(杨氏模量和密度的乘积),该因子既可以预测岩性,在页岩气勘探中也可以预测岩石脆性参数,拓宽了叠前地震资料的应用,并说明Kρ-Eρ比Kρ-μρ(剪切模量与密度乘积)更容易区分岩性和流体。
上述关于岩石脆性预测、岩性区分及流体识别的敏感因子都是在叠前三参数(纵波速度、横波速度、密度)反演基础上通过二次计算得到的。为了提高敏感识别因子提取精度,许多学者研究叠前地震反演方法与敏感识别因子直接提取理论。Fatti[9]利用Gardner速度与密度关系式,将Aki-Richards AVO近似式的纵、横波速度及密度转换为纵、横波阻抗、密度的反射系数之和。Gray[10]将Aki-Richards近似式进行重排,得到了包含岩石的拉梅常数、体积模量、密度的AVO近似式。Russell等[11]根据Biot-Gassmann饱和孔隙介质理论,通过去除干岩石属性增强流体敏感性,建立了流体因子f,为减少二次计算误差积累推导了包含该流体因子的AVO近似式。Zong等[12]考虑到密度反演的不稳定性,建立了预测页岩脆性的杨氏模量、泊松比、密度三项AVO近似式。弹性阻抗概念的提出[13]与发展[14]为利用AVO近似式直接提取各种敏感识别因子提供了技术手段。印兴耀等[15]兼顾常规弹性波阻抗反演的高抗噪性和流体因子f识别流体的直观性,形成了直接提取Russell流体因子叠前弹性阻抗反演方法。考虑到Russell等[11]提出的流体因子敏感性,印兴耀等[16]推导了密度与包含流体因子乘积(ρf)和纵波阻抗的AVO近似式,并详细说明了适合深层储层流体识别的两项弹性阻抗直接反演Russell流体因子的方法,直接计算敏感识别因子的效果明显优于间接计算。杨培杰等[17]在贝叶斯理论框架下,提出了一种流体因子直接提取的新方法,具有更高的分辨率、更高的精度。张丰麒等[18]在基追踪分解算法实现叠前AVA稀疏层反演时,考虑了弹性参数之间的相关性,并引入低频软约束项补偿反演的低频信息,使反演结果具有更高的稳定性与垂向分辨率。
大量文献证明敏感识别因子已成功用于岩性、流体、岩石脆性等的预测,而且在一般情况下敏感识别因子随研究地区和对象不同而不同。利用敏感识别因子预测储层涉及两个关键问题:一是针对具体研究工区和对象如何建立敏感识别因子;二是如何实现敏感识别因子的直接提取。本文以苏北盆地黄珏地区浅层的砂岩储层为例,提出一套建立和直接提取砂岩敏感识别因子的方法。
黄珏地区浅层砂岩纵、横波速度相对较高,密度较低。针对该特点,首先利用交会图分析砂岩分布特征,生成敏感砂岩岩性识别因子;然后,根据砂、泥岩模型,据Goodway等[3]提出的方法计算各个因子敏感系数,定量评价各个因子区分不同岩性的能力;同时,运用不同岩性速度与密度的拟合关系式分析岩性敏感识别因子特点,进而推导敏感识别因子的AVO近似方程,讨论其精度;为提高反演结果的稳定性与精度,引入低频软约束项补偿反演的低频信息,结合Downton的参数协方差矩阵特征分解去相关思路,建立直接提取敏感识别因子的目标函数,并通过求解目标函数,直接提取敏感识别因子;最后,通过实际的应用效果说明该方法的可行性。
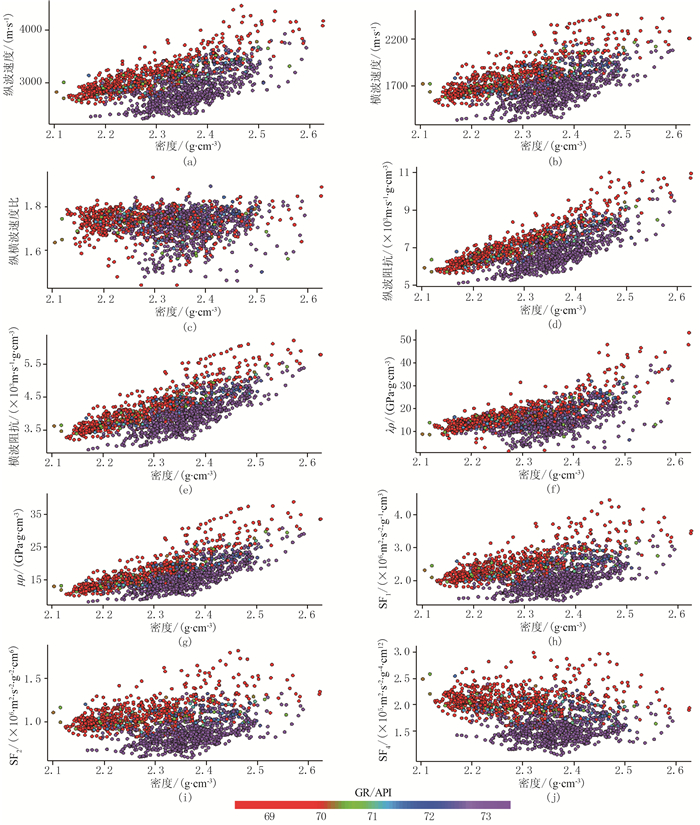
1 砂岩敏感识别因子的建立苏北盆地黄珏地区新生界三垛组具有良好的油气勘探前景,但到目前为止,储层分布仍未查明。为此,针对该区砂岩储层开展地球物理识别方法研究。首先根据测井数据分析砂岩岩性特征;然后再根据砂岩岩性特点寻找砂岩敏感识别因子。由图l可见,砂岩纵、横波速度相对较高,密度相对较低;纵横波速度无法识别砂岩。为此,本文设计增强砂岩异常的敏感识别因子
| $ {\rm{S}}{{\rm{F}}_4} = {V_{\rm{P}}}\frac{{{V_{\rm{S}}}}}{{{\rho ^4}}} $ | (1) |
式中:VP、VS分别为砂岩纵、横波速度;ρ为密度。由于密度低、纵横波速度高,这样可以增大砂岩与泥岩的差异,进而更好地识别砂岩。与常用的弹性参数对比表明(图 1),本文提出的SF4可以较好地区分砂岩和泥岩。纵波阻抗、横波阻抗、λρ、μρ等因子都是乘积组合形式,在数值上易出现重叠性。
|
图 1 各岩石物理参数与密度交会图 (a)纵波速度;(b)横波速度;(c)纵横波速度比;(d)纵波阻抗; (e)横波阻抗;(f)λρ;(g)μρ;(h) 红色对应砂岩,紫色对应泥岩。图 2色标同 |
另外,通过统计砂、泥岩纵、横波速度与密度资料,计算了14种不同因子识别能力
| $ \begin{array}{*{20}{c}} {R = \frac{1}{2}\left( {\frac{{\left| {{\rm{Attribut}}{{\rm{e}}_1} - {\rm{Attribut}}{{\rm{e}}_2}} \right|}}{{{\rm{Attribut}}{{\rm{e}}_1}}} + } \right.}\\ {\left. {\frac{{\left| {{\rm{Attribut}}{{\rm{e}}_1} - {\rm{Attribut}}{{\rm{e}}_2}} \right|}}{{{\rm{Attribut}}{{\rm{e}}_2}}}} \right)} \end{array} $ | (2) |
式中Attribute1、Attribute2分别表示两种不同岩性弹性参数值。计算结果(表 1)表明,相对最敏感的砂岩识别因子为SF4。
|
|
表 1 砂岩和泥岩的14种识别因子 |
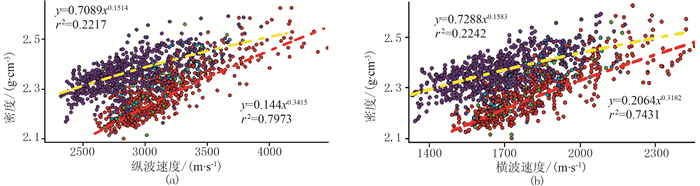
利用测井曲线,按照岩性拟合密度与纵、横波速度幂指数关系式(图 2、表 2)可以进一步说明SF4的优势。根据拟合关系求得不同岩性纵、横波速度拟合曲线的交点
|
图 2 砂、泥岩密度与纵(a)、横(b)波速度关系r为相关系数 |
|
|
表 2 密度与纵、横波速度三者间的拟合公式 |
| $ \frac{{{\rho _{砂}}}}{{{\rho _{泥}}}} = \frac{{0.144}}{{0.7098}}V_{\rm{P}}^{0.3415 - 0.1514} = 1 $ | (3) |
| $ \frac{{{{\rm{ \mathsf{ ρ} }}_{砂}}}}{{{{\rm{ \mathsf{ ρ} }}_{泥}}}} = \frac{{0.2064}}{{0.7288}}{\rm{V}}_{\rm{P}}^{0.3182 - 0.1583} = 1 $ | (4) |
可得交点位置VP=4408m/s、VS=2657m/s。当VP < 4408m/s、VS < 2657m/s时,ρ砂/ρ泥 < 1,由此可得出该区浅层砂岩密度小于泥岩。由于浅层的砂岩速度大于泥岩,因此通过密度与速度定量拟合关系进一步说明了本文建立的SF4具有更高的岩性识别能力。
2 砂岩敏感识别因子AVO近似式推导应用砂岩敏感识别因子AVO近似式,可以避免二次计算SF4参数产生的累计误差,下面给出其推导步骤。
2.1 公式推导Aki-Richards AVO近似式[19]为
| $ \begin{array}{*{20}{c}} {R\left( \theta \right) = \frac{{\Delta {V_{\rm{P}}}}}{{2{V_{\rm{P}}}}}{{\sec }^2}\theta - 4\frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}}\gamma _{{\rm{sat}}}^2{{\sin }^2}\theta + }\\ {\left( {1 - 4\gamma _{{\rm{sat}}}^2{{\sin }^2}\theta } \right)\frac{{\Delta \rho }}{{2\rho }}} \end{array} $ | (5) |
式中:γsat、θ分别为饱和岩石的横波与纵波速度比、入射角;ΔVP、2VS、Δρ分别为界面两侧纵波、横波和密度变化量。
Aki-Richards近似式由三项简化的反射系数构成。反射系数与纵波阻抗、横波阻抗有相同的数学形式,如纵波速度、横波速度和密度的反射系数定义为
| $ {R_{{V_{\rm{P}}}}} = \frac{{{V_{{\rm{P}}2}} - {V_{{\rm{Pl}}}}}}{{{V_{{\rm{P}}2}} + {V_{{\rm{Pl}}}}}} = \frac{1}{2}\frac{{\Delta {V_{\rm{P}}}}}{{{V_{\rm{P}}}}} $ | (6) |
| $ {R_{{V_{\rm{S}}}}} = \frac{{{V_{{\rm{S}}2}} - {V_{{\rm{S}}1}}}}{{{V_{{\rm{S}}2}} + {V_{{\rm{S}}1}}}} = \frac{1}{2}\frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}} $ | (7) |
| $ {V_\rho } = \frac{{{\rho _2} - {\rho _1}}}{{{\rho _2} + {\rho _1}}} = \frac{1}{2}\frac{{\Delta \rho }}{\rho } $ | (8) |
式中:RVP、RVS、Rρ分别为纵、横波速度及密度的反射系数;VPi、VSi、ρi(i=1, 2,分别表示上、下层介质)分别为介质的纵、横波速度及密度。
不同学者研究目的不同,对不同的地球物理量进行微分,建立与Aki-Richards参数之间的关系,最后得到不同AVO的近似形式
| $ \begin{array}{l} \left| {\begin{array}{*{20}{c}} {{R_{{I_{\rm{P}}}}}}\\ {{R_{{I_{\rm{S}}}}}}\\ {{R_\gamma }}\\ {{R_v}}\\ {{R_K}}\\ {{R_\lambda }}\\ {{R_\mu }}\\ {{R_f}}\\ {{R_{\rho f}}} \end{array}} \right| = \left| {\begin{array}{*{20}{c}} 1&0&1\\ 0&1&1\\ { - 1}&1&0\\ {\frac{1}{{\frac{3}{2} - \gamma _{{\rm{sat}}}^2 - \frac{1}{{2\gamma _{{\rm{sat}}}^2}}}}}&{\frac{{ - 1}}{{\frac{3}{2} - \gamma _{{\rm{sat}}}^2 - \frac{1}{{2\gamma _{{\rm{sat}}}^2}}}}}&0\\ {\frac{6}{{3 - 4\gamma _{{\rm{sat}}}^2}}}&{ - \frac{{8\gamma _{{\rm{sat}}}^2}}{{3 - 4\gamma _{{\rm{sat}}}^2}}}&1\\ {\frac{2}{{1 - 2\gamma _{{\rm{sat}}}^2}}}&{ - \frac{{4\gamma _{{\rm{sat}}}^2}}{{1 - 2\gamma _{{\rm{sat}}}^2}}}&1\\ 0&2&1\\ {\frac{{2\gamma _{{\rm{sat}}}^2}}{{\gamma _{{\rm{sat}}}^2 - \gamma _{{\rm{dry}}}^2}}}&{ - \frac{{2\gamma _{{\rm{dry}}}^2}}{{\gamma _{{\rm{sat}}}^2 - \gamma _{{\rm{dry}}}^2}}}&1\\ {\frac{{2\gamma _{{\rm{sat}}}^2}}{{\gamma _{{\rm{sat}}}^2 - \gamma _{{\rm{dry}}}^2}}}&{ - \frac{{2\gamma _{{\rm{dry}}}^2}}{{\gamma _{{\rm{sat}}}^2 - \gamma _{{\rm{dry}}}^2}}}&2 \end{array}} \right| \times \\ \;\;\;\;\;\;\;\;\;\;\left| {\begin{array}{*{20}{c}} {{R_{{V_{\rm{P}}}}}}\\ {{R_{{V_{\rm{S}}}}}}\\ {{R_\rho }} \end{array}} \right| \end{array} $ | (9) |
式中:RIP、RIS分别为纵、横波阻抗反射系数;Rγ为纵横波速比反射系数;Rυ为泊松比反射系数;RK为体积模量反射系数;Rλ、Rμ分别为拉梅常数反射系数;Rf为Russell等[11]根据Biot-Gassmann饱和孔隙介质理论提出的识别饱和岩石与干岩石属性的流体因子f反射系数;Rρf为Russell等[4]将Biot-Gassmann方程流体因子项改写的纵、横波阻抗加权形式(ρf)反射系数,且
| $ \left\{ \begin{array}{l} {R_{{I_{\rm{P}}}}} = \frac{1}{2}\frac{{\Delta {I_{\rm{P}}}}}{{{I_{\rm{P}}}}}\\ {R_{{I_{\rm{S}}}}} = \frac{1}{2}\frac{{\Delta {I_{\rm{S}}}}}{{{I_{\rm{S}}}}}\\ {R_\gamma } = \frac{1}{2}\frac{{\Delta \gamma }}{\gamma }\\ {R_v} = \frac{1}{2}\frac{{\Delta v}}{v}\\ {R_K} = \frac{1}{2}\frac{{\Delta K}}{K}\\ {R_\lambda } = \frac{1}{2}\frac{{\Delta \lambda }}{\lambda };\\ {R_\mu } = \frac{1}{2}\frac{{\Delta \mu }}{\mu }\\ {R_f} = \frac{1}{2}\frac{{\Delta f}}{f}\\ {R_{\rho f}} = \frac{1}{2}\frac{{\Delta \left( {\rho f} \right)}}{{\rho f}} \end{array} \right. $ | (10) |
式中:IP、IS、γ、υ、K、λ、μ和ΔIP、ΔIS、Δγ、Δυ、ΔK、Δλ、Δμ分别表示纵波阻抗、横波阻抗、纵横波速度比、泊松比、体积模量、拉梅弹性参数和上、下层介质弹性参数的差值;f、ρf和Δf、Δ(ρf)分别为Russell[4, 11]提出的流体因子和相应的流体因子上、下层介质的差值。
对SF4(式(1))全微分可得
| $ \Delta {\rm{S}}{{\rm{F}}_4} = \frac{{{V_{\rm{S}}}}}{{{\rho ^4}}}\Delta {V_{\rm{P}}} + \frac{{{V_{\rm{P}}}}}{{{\rho ^4}}}\Delta {V_{\rm{S}}} - 4\frac{{{V_{\rm{P}}}{V_{\rm{S}}}}}{{{\rho ^5}}}\Delta \rho $ | (11) |
两边除以SF4得
| $ \frac{{\Delta {\rm{S}}{{\rm{F}}_4}}}{{{\rm{S}}{{\rm{F}}_4}}} = \frac{{\Delta {V_{\rm{P}}}}}{{{V_{\rm{P}}}}} + \frac{{\Delta {V_{\rm{S}}}}}{{{V_{\rm{S}}}}} - 4\frac{{\Delta \rho }}{\rho } $ | (12) |
由式(12)可得到砂岩敏感识别因子反射系数与纵、横波速度、密度反射系数之间的关系
| $ {R_{{\rm{S}}{{\rm{F}}_4}}} = {R_{{V_{\rm{P}}}}} + {R_{{V_{\rm{S}}}}} - 4{R_\rho } $ | (13) |
由式(9)可组合出砂岩敏感识别因子、剪切模量与密度反射系数组合的AVO近似式
| $ \left[ {\begin{array}{*{20}{l}} {{R_{{\rm{SF}}}}}\\ {{R_\mu }}\\ {{R_\rho }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&1&{ - 4}\\ 0&2&1\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{R_{{V_{\rm{P}}}}}}\\ {{R_{{V_{\rm{S}}}}}}\\ {{R_\rho }} \end{array}} \right] $ | (14) |
将系数矩阵求逆代入Aki-Richards近似式(式(5)),可得包含砂岩敏感识别因子、剪切模量与密度AVO近似式
| $ \begin{array}{l} R\left( \theta \right) = \frac{1}{2}\frac{{\Delta {\rm{SF}}}}{{{\rm{SF}}}}{\sec ^2}\theta - \frac{1}{4}\left( {{{\sec }^2}\theta + 8\gamma _{{\rm{sat}}}^2\theta } \right)\frac{{\Delta \mu }}{\mu } + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{1}{4}\left( {9{{\sec }^2}\theta + 2} \right)\frac{{\Delta \rho }}{\rho } \end{array} $ | (15) |
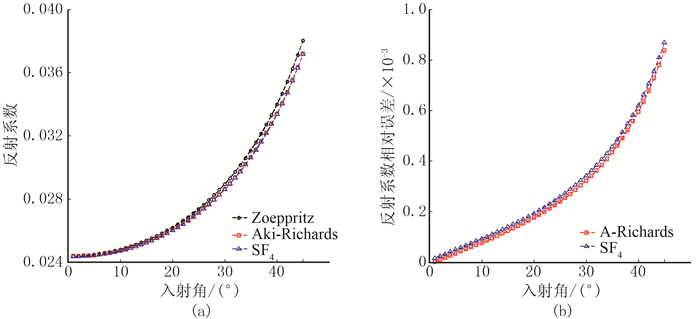
据表 1参数建立模型,采用精确Zeoppritz方程、Aki-Richards近似式、SF4近似式(式(15))计算模型界面的反射系数(图 3a)及其相对误差(图 3b)。在θ≤45°范围内,SF4与Aki-Richards近似式计算结果非常接近,都能逼近Zeoppritz方程。另外,两个近似式与Zeoppritz方程计算结果误差随入射角增大而增大,但在地震波小角度入射时, 误差为10-3数量级,即误差在地震勘探允许的范围内。因此,从叠前角度道集资料中利用SF4 AVO近似式反演SF4进行砂岩的识别是可行的。
|
图 3 反射系数精度对比 (a)模型界面的反射系数;(b)反射系数相对误差 |
应用上述方法,需要对弹性参数进行去相关性处理。
考虑地下n+1层介质、3个角度入射情况,利用式(15)计算地下地层各界面反射系数矩阵形式
| $ \left[ {\begin{array}{*{20}{c}} {r_1^1}\\ \vdots \\ {r_1^n}\\ {r_2^1}\\ \vdots \\ {r_2^n}\\ {r_3^1}\\ \vdots \\ {r_3^n} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {a_1^1}&{}&0&{b_1^1}&{}&0&{c_1^1}&{}&0\\ {}& \ddots &{}&{}& \ddots &{}&{}& \ddots &{}\\ 0&{}&{a_1^n}&0&{}&{b_1^n}&0&{}&{c_1^n}\\ {a_2^1}&{}&0&{b_2^1}&{}&0&{c_2^1}&{}&0\\ {}& \ddots &{}&{}& \ddots &{}&{}& \ddots &{}\\ 0&{}&{a_2^n}&0&{}&{b_2^n}&0&{}&{c_2^n}\\ {a_3^1}&{}&0&{b_3^1}&{}&0&{c_3^1}&{}&0\\ {}& \ddots &{}&{}& \ddots &{}&{}& \ddots &{}\\ 0&{}&{a_3^n}&0&{}&{b_3^n}&0&{}&{c_3^n} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {R_{{\rm{SF}}}^1}\\ \vdots \\ {R_{{\rm{SF}}}^n}\\ {R_\mu ^1}\\ \vdots \\ {R_\mu ^n}\\ {r_\rho ^1}\\ \vdots \\ {r_\rho ^n} \end{array}} \right] $ | (16) |
式中:rθk为入射角为θ的第k界面的反射系数;RSFk、Rμk、Rρk、aθk、bθk、cθk分别为砂岩敏感识别因子、剪切模量与密度反射系数及其相应系数。
将式(16)进一步简化为分块矩阵,并代入子波矩阵得
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{d}}_1}}\\ {{\mathit{\boldsymbol{d}}_2}}\\ {{\mathit{\boldsymbol{d}}_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{A}}_1}}&{\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{B}}_1}}&{\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{C}}_1}}\\ {\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{A}}_2}}&{\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{B}}_2}}&{\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{C}}_2}}\\ {\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{A}}_3}}&{\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{B}}_3}}&{\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{C}}_3}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{{\rm{SF}}}}}\\ {{\mathit{\boldsymbol{R}}_\mu }}\\ {{\mathit{\boldsymbol{R}}_\rho }} \end{array}} \right] $ | (17) |
式中:dθ为入射角为θ时叠前角度道集向量;W为子波矩阵;Aθ、Bθ、Cθ为斜对角矩阵;RSF、Rμ、dρ为砂岩敏感识别因子、剪切模量与密度反射系数向量。
式(17)可简写为
| $ {\mathit{\boldsymbol{d}}_{3n \times 1}} = {\mathit{\boldsymbol{G}}_{3n \times 3n}} \cdot {\mathit{\boldsymbol{R}}_{3n \times 1}} $ | (18) |
由于式(15)中三参数SF4、μ和ρ之间是统计相关的,因此需要应用三者之间的协方差矩阵对参数进行去相关处理。根据Downton思路[20],将待反演的参数之间的协方差矩阵CR表示为
| $ {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{R}}} = \left[ {\begin{array}{*{20}{c}} {\sigma _{{R_{{\rm{SF}}}}}^2}&{{\sigma _{{R_{{\rm{SF}}}}{R_\mu }}}}&{{\sigma _{{R_{{\rm{SF}}}}{R_\rho }}}}\\ {{\sigma _{{R_{{\rm{SF}}}}{R_\mu }}}}&{\sigma _{{R_\mu }}^2}&{{\sigma _{{R_\mu }{R_\rho }}}}\\ {{\sigma _{{R_{{\rm{SF}}}}{R_\rho }}}}&{{\sigma _{{R_\mu }{R_\rho }}}}&{\sigma _{{R_\rho }}^2} \end{array}} \right] $ | (19) |
式中:σRSF2、σRμ2、σRρ2分别为SF4、μ、ρ反射系数的方差;σRSFRμ、σRSFRμ、σRμRρ分别为SF4、μ、ρ反射系数之间的协方差。由于该矩阵为实对称矩阵,则可将其奇异值分解为
| $ {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{R}}} = \mathit{\boldsymbol{v}}\Sigma {\mathit{\boldsymbol{v}}^{\rm{T}}} = \mathit{\boldsymbol{v}}\left[ {\begin{array}{*{20}{c}} {{\sigma _1}}&0&0\\ 0&{{\sigma _2}}&0\\ 0&0&{{\sigma _3}} \end{array}} \right]{\mathit{\boldsymbol{v}}^{\rm{T}}} $ | (20) |
式中σi、v分别为协方差矩阵的特征值及特征向量矩阵,即
将式(20)中单个界面协方差矩阵特征向量的逆扩展n个界面
| $ {\left[ {\begin{array}{*{20}{c}} {{v_{11}}}&{}&0&{{v_{12}}}&{}&0&{{v_{13}}}&{}&0\\ {}& \ddots &{}&{}& \ddots &{}&{}& \ddots &{}\\ 0&{}&{{v_{11}}}&0&{}&{{v_{12}}}&0&{}&{{v_{13}}}\\ {{v_{21}}}&{}&0&{{v_{22}}}&{}&0&{{v_{23}}}&{}&0\\ {}& \ddots &{}&{}& \ddots &{}&{}& \ddots &{}\\ 0&{}&{{v_{21}}}&0&{}&{{v_{22}}}&0&{}&{{v_{23}}}\\ {{v_{31}}}&{}&0&{{v_{32}}}&{}&0&{{v_{33}}}&{}&0\\ {}& \ddots &{}&{}& \ddots &{}&{}& \ddots &{}\\ 0&{}&{{v_{31}}}&0&{}&{{v_{32}}}&0&{}&{{v_{33}}} \end{array}} \right]_{3n \times 3n}} $ | (21) |
对式(18)做如下变换
| $ {\mathit{\boldsymbol{d}}_{3n \times 1}} = \mathit{\boldsymbol{G'R'}} $ | (22) |
其中
经过变换后的参数协方差矩阵
| $ {\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{R'}}}} = \left[ {\begin{array}{*{20}{c}} {{\sigma _1}}&0&0\\ 0&{{\sigma _2}}&0\\ 0&0&{{\sigma _3}} \end{array}} \right] $ | (23) |
从上式可以看出,非对角线上的元素均为零,说明经过变换后的参数之间是相互独立的。
4 贝叶斯反演方程的建立与模型测试为提高叠前反演精度,可以采用基于贝叶斯理论框架的概率化反演方法直接估算该因子。
4.1 贝叶斯反演方程的建立贝叶斯公式反演模型参数基本原理为
| $ p\left( {\mathit{\boldsymbol{m}}\left| \mathit{\boldsymbol{d}} \right.} \right) = \frac{{p\left( {\mathit{\boldsymbol{d}}\left| \mathit{\boldsymbol{m}} \right.} \right)p\left( \mathit{\boldsymbol{m}} \right)}}{{p\left( \mathit{\boldsymbol{d}} \right)}} $ | (24) |
式中:m为待反演的模型参数;d为叠前角度道集数据;p(m|d)称为似然函数,是在观测数据d下模型m的后验概率密度函数,用于表示正演记录与实际观察数据之差;p(m)是模型m的先验概率密度函数;p(d)为模型的全模型空间的概率,其数值一般取常数。
假设叠前角度道集数据中的噪声信息服从Gauss分布,反演参数服从Cauchy分布,可得待反演参数后验概率密度分布为
| $ \begin{array}{l} p\left( {\mathit{\boldsymbol{R'}}\left| \mathit{\boldsymbol{d}} \right.} \right) \propto \prod\limits_{i = 1}^N {\left[ {\frac{1}{{1 + \frac{{\mathit{\boldsymbol{R'}}}}{{\sigma _{\rm{m}}^2}}}}} \right]} \times \\ \;\;\;\;\;\;\;\;\exp \left[ {\frac{{ - {{\left( {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{G'R'}}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{G'R'}}} \right)}}{{2\sigma _{\rm{n}}^2}}} \right] \end{array} $ | (25) |
式中:σn2为叠前角度道集与正演记录的噪声方差;σm2为模型反射系数的方差。
对式(25)取对数,并求取最大后验概率,可得反演初步目标函数
| $ \left( {{{\mathit{\boldsymbol{G'}}}^{\rm{T}}}\mathit{\boldsymbol{G'}} + \varepsilon \mathit{\boldsymbol{Q}}} \right)\mathit{\boldsymbol{R'}} = {{\mathit{\boldsymbol{G'}}}^{\rm{T}}}\mathit{\boldsymbol{d}} $ | (26) |
式中:
| $ \mathit{\boldsymbol{Q}} = {\rm{diag}}\left[ {\frac{1}{{1 + \frac{{\mathit{\boldsymbol{R}}_1^2}}{{\sigma _{\rm{m}}^2}}}},\frac{1}{{1 + \frac{{\mathit{\boldsymbol{R}}_2^2}}{{\sigma _{\rm{m}}^2}}}}, \cdots ,\frac{1}{{1 + \frac{{\mathit{\boldsymbol{R}}_M^2}}{{\sigma _{\rm{m}}^2}}}}} \right] $ | (27) |
式中M为地震数据的采样点数。
由于地震数据缺失低频成分,因此需要用约束条件才能获取阻抗的唯一的、稳定的解。以砂岩敏感识别因子为例,令RSF为砂岩敏感识别因子反射系数,在界面上、下岩石物理性质差别不大的假设前提下
| $ {R_{{\rm{SF}}}}\left( t \right) \approx \frac{{{\rm{dSF}}\left( t \right)}}{{2{\rm{SF}}\left( t \right)}} \approx \frac{{\partial \ln \left[ {{\rm{SF}}\left( t \right)} \right]}}{{2\partial t}} $ | (28) |
对时间积分,可得砂岩相对敏感识别因子
| $ \int_{{t_0}}^t {{R_{{\rm{SF}}}}\left( \tau \right){\rm{d}}\tau } = \frac{1}{2}\ln \frac{{{\rm{SF}}\left( t \right)}}{{{\rm{SF}}\left( {{t_0}} \right)}} $ | (29) |
式中SF(t0)为砂岩初始敏感识别因子。该式就是将砂岩敏感识别因子与砂岩敏感识别因子反射系数联系起来的基本公式。同理,其他两个参数
| $ \left\{ {\begin{array}{*{20}{l}} {\int_{{t_0}}^t {{R_\mu }\left( \tau \right){\rm{d}}\tau } = \frac{1}{2}\ln \frac{{\mu \left( t \right)}}{{\mu \left( {{t_0}} \right)}}}\\ {\int_{{t_0}}^t {{R_\rho }\left( \tau \right){\rm{d}}\tau } = \frac{1}{2}\ln \frac{{\rho \left( t \right)}}{{\rho \left( {{t_0}} \right)}}} \end{array}} \right. $ | (30) |
则可定义新的目标函数
| $ \begin{array}{l} F\left( {\mathit{\boldsymbol{R'}}} \right) = {F_{\rm{G}}}\left( {\mathit{\boldsymbol{R'}}} \right) + {F_{{\rm{Cauchy}}}}\left( {\mathit{\boldsymbol{R'}}} \right) + F\left( {{{\mathit{\boldsymbol{R'}}}_{{\rm{SF}}}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{F}}\left( {{{\mathit{\boldsymbol{R'}}}_\mu }} \right) + F\left( {{{\mathit{\boldsymbol{R'}}}_\rho }} \right) \end{array} $ | (31) |
其中
| $ {F_{\rm{G}}}\left( {\mathit{\boldsymbol{R'}}} \right) = {\left( {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{G'R'}}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{G'R'}}} \right) $ |
| $ {F_{{\rm{Cauchy}}}}\left( {\mathit{\boldsymbol{R'}}} \right) = 2\sigma _{\rm{n}}^2\sum\limits_{i = 1}^M {\ln } \frac{{1 + {{\mathit{\boldsymbol{R'}}}_i}}}{{\sigma _{\rm{m}}^2}} $ |
| $ F\left( {{{\mathit{\boldsymbol{R'}}}_{{\rm{SF}}}}} \right) = {\lambda _{{\rm{SF}}}}{\left( {{\mathit{\boldsymbol{\xi }}_{{\rm{SF}}}} - {{\mathit{\boldsymbol{C'}}}_{{\rm{SF}}}}{{\mathit{\boldsymbol{R'}}}_{{\rm{SF}}}}} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{\xi }}_{{\rm{SF}}}} - {{\mathit{\boldsymbol{C'}}}_{{\rm{SF}}}}{{\mathit{\boldsymbol{R'}}}_{{\rm{SF}}}}} \right) $ |
| $ {\rm{F}}\left( {{{\mathit{\boldsymbol{R'}}}_\mu }} \right) = {\lambda _\mu }{\left( {{\mathit{\boldsymbol{\xi }}_\mu } - {{\mathit{\boldsymbol{C'}}}_\mu }{{\mathit{\boldsymbol{R'}}}_\mu }} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{\xi }}_\mu } - {{\mathit{\boldsymbol{C'}}}_\mu }{{\mathit{\boldsymbol{R'}}}_\mu }} \right) $ |
| $ F\left( {{{\mathit{\boldsymbol{R'}}}_\rho }} \right) = {\lambda _\rho }{\left( {{\mathit{\boldsymbol{\xi }}_\rho } - {{\mathit{\boldsymbol{C'}}}_\rho }{{\mathit{\boldsymbol{R'}}}_\rho }} \right)^{\rm{T}}}\left( {{\mathit{\boldsymbol{\xi }}_\rho } - {{\mathit{\boldsymbol{C'}}}_\rho }{{\mathit{\boldsymbol{R'}}}_\rho }} \right) $ |
根据前述参数去相关性,可得
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{C}}_X^\prime = {\mathit{\boldsymbol{C}}_X}\mathit{\boldsymbol{V}}}\\ {\mathit{\boldsymbol{R}}_X^\prime = {\mathit{\boldsymbol{V}}^{ - 1}}{\mathit{\boldsymbol{R}}_X}}\\ {{\mathit{\boldsymbol{C}}_X} = \int_{{t_0}}^t {\rm{d}} \tau }\\ {{R_X}\left( {{t_i}} \right) = \frac{{X\left( {{t_i}} \right) + X\left( {{t_{t - 1}}} \right)}}{{X\left( {{t_i}} \right) - X\left( {{t_{t - 1}}} \right)}}}\\ {{\xi _X} = \frac{1}{2}\ln \frac{{X(t)}}{{X\left( {{t_0}} \right)}}} \end{array}} \right. $ | (32) |
式中X取值为砂岩敏感识别因子、剪切模量与密度。
将式(30)目标函数取极小值,可得
| $ \begin{array}{l} {{\mathit{\boldsymbol{C'}}}^{\rm{T}}}\mathit{\boldsymbol{d}} + \mathit{\boldsymbol{C'}}_{{\rm{SF}}}^{\rm{T}}{\mathit{\boldsymbol{\xi }}_{{\rm{SF}}}} + \mathit{\boldsymbol{C'}}_\mu ^{\rm{T}}{\mathit{\boldsymbol{\xi }}_\mu } + \mathit{\boldsymbol{C'}}_\rho ^{\rm{T}}{\mathit{\boldsymbol{\xi }}_\rho }\\ \;\;\;\; = \left( {{{\mathit{\boldsymbol{G'}}}^{\rm{T}}}\mathit{\boldsymbol{G'}} + \varepsilon \mathit{\boldsymbol{Q}} + {\lambda _{{\rm{SF}}}}\mathit{\boldsymbol{C'}}_{{\rm{SF}}}^{\rm{T}}{{\mathit{\boldsymbol{C'}}}_{{\rm{SF}}}} + } \right.\\ \;\;\;\;\;\;\;\left. {{\lambda _\mu }\mathit{\boldsymbol{C'}}_\mu ^{\rm{T}}{{\mathit{\boldsymbol{C'}}}_\mu } + {\lambda _\rho }\mathit{\boldsymbol{C'}}_\rho ^{\rm{T}}{{\mathit{\boldsymbol{C'}}}_\rho }} \right)\mathit{\boldsymbol{R'}} \end{array} $ | (33) |
式中:G′TG′是用来约束模型数据合成记录与实测地震数据的相似程度;εQ用来约束模型数据的稀疏程度;λSFC′SFT C′SF、λμC′μTC′μ、λρC′ρTC′ρ为用来约束反演结果的趋势。对于以上弱非线性问题,可采用迭代重加权最小二乘法对目标函数求解。
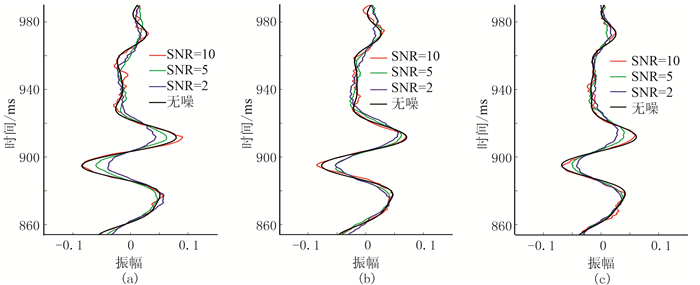
4.2 模型测试为了验证式(15)直接反演砂岩敏感识别因子的优越性,根据从A1井实际测得的纵、横波速度和密度曲线,利用褶积模型计算得到AVO合成记录,然后分别加入噪声,部分叠加得到近、中、远道三个不同信噪比的叠加道集(图 4)。为了分析、对比直接与间接反演弹性参数效果,在不同噪声情况下,分别采用间接与直接反演两种方法得到SF4、μ、ρ(图 5)。所谓间接反演方法,即利用Fatti[9]AVO近似式为核函数从叠前道集中反演出纵、横波阻抗,然后再间接计算所需弹性参数。直接反演方法,即利用式(15)为核函数从叠前道集中反演,直接反演一步得到所需弹性参数。通过分析可得如下观点。
|
图 4 AVO正演记录角度道集叠加 (a)近道;(b)中道;(c)远道 |
|
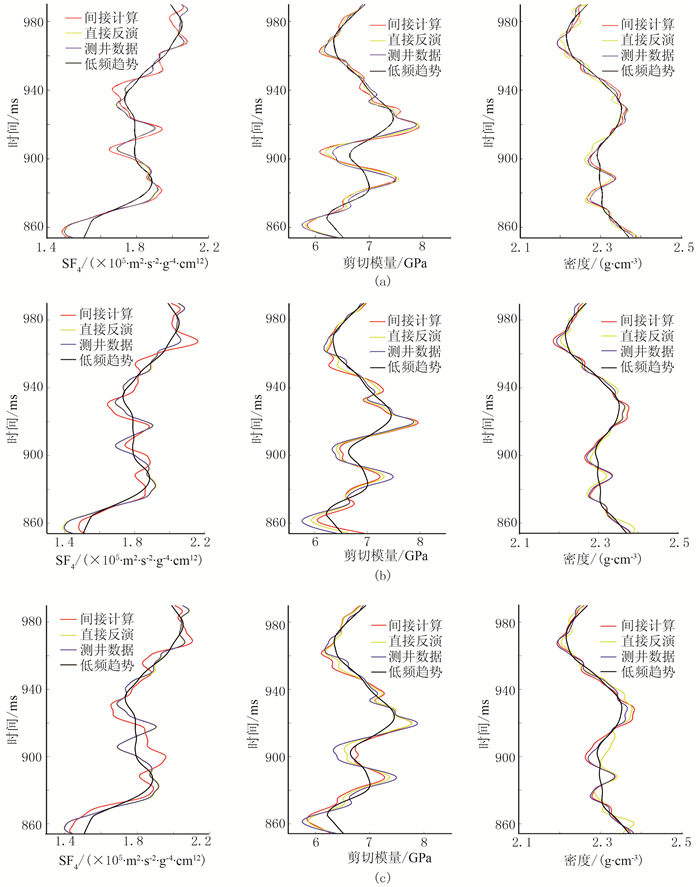
图 5 信噪比为10(a)、5(b)及2(c)的情况下各弹性参数反演结果 |
(1) 不同信噪比情况下,直接反演的SF4效果明显优于间接计算。地震资料信噪比为10以上时,直接与间接计算结果效果差别不大;信噪比为5甚至为2时,间接计算结果虽然大体趋势与测井数据基本吻合,但是细节上差别较大,而直接计算结果总体趋势与细节上都和测井数据吻合较好,其原因主要在于信噪比较低的地震记录间接反演时引入了累计误差。
(2) 直接反演的密度效果低于间接计算,其原因主要为间接计算时采用的Fatti AVO近似式组成的方程组系数矩阵条件数相对较小,而直接计算时采用的式(15)组成方程组系数矩阵条件数相对较大,使密度反演不够准确,这也是该方法的缺点。据前文分析认为敏感识别因子SF4直接计算效果明显优于间接计算。
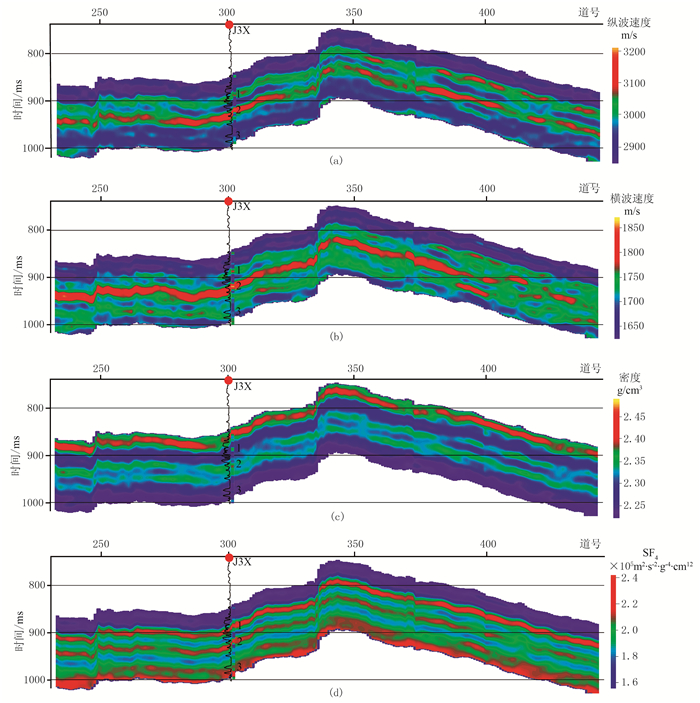
5 应用效果应用本文方法对苏北盆地黄珏地区新生界三垛组砂岩进行识别。图 6a~6c为以Fatti[9]近似式为核函数从叠前道集中直接反演的纵波速度、密度、纵波阻抗反演剖面,图 6d为以式(15)为核函数从叠前道集中直接反演的SF4。图 6中测井曲线为岩性曲线(自然电位曲线SP),井位置处为原始测井数据计算的相应的弹性参数。根据SP异常,该井段大致划分三个砂层组(黑框位置),特征如下:
|
图 6 过J3X井叠前地震数据反演剖面 (a)纵波速度;(b)横波速度;(c)密度;(d)SF4 |
(1) 1砂层组纵、横波速度相对较高,密度相对较低,利用常规的纵、横波速度剖面不能很好识别,砂岩与泥岩速度大小重叠较为严重,而SF4剖面异常明显,该因子利用了砂岩弹性参数特点,放大了该类砂岩弹性参数异常;
(2) 2砂组纵、横波速度最高,密度相对较低,利用常规的纵、横波速度剖面能很好地识别,计算的SF4异常也很明显;
(3) 3砂层组纵、横波速度相对较低,密度最低,常规的纵、横波速度剖面不能识别该类砂岩,砂岩与泥岩速度基本一样,而SF4剖面异常明显,原因也在于该因子纵、横波速度与密度参数增大了异常。
综上所述,在叠前地震资料信噪比不高、砂岩速度略大于泥岩速度、而砂岩密度略低于泥岩密度的情况下,应用直接反演砂岩敏感识别因子SF4能够减少间接计算的误差累积,相对常规弹性参数具有更高的砂岩识别能力。
6 结论针对苏北盆地黄珏地区浅层叠前地震资料信噪比不高、砂岩速度略大于泥岩速度、而砂岩密度略低于泥岩情况下,提出了一套建立并直接提取砂岩敏感识别因子SF4的技术,该技术有以下特点。
(1) 避免了常规岩性识别因子大部分是速度与密度乘积的形式而造成的砂、泥岩数值区间重叠,提高了砂岩的识别精度。
(2) 地震资料信噪比较高时,直接与间接计算敏感识别因子效果差别不大,但是对于叠前地震资料信噪比较低情况下,直接反演敏感识别因子效果优于间接计算。
| [1] |
撒利明, 杨午阳. 非线性拟测井曲线反演在油藏监测中的应用及展望[J]. 石油地球物理勘探, 2017, 52(2): 402-410. SA Liming YANG Wuyang, YANG Wuyang. Application and prospect of nonlinear time-lapse pseudo log parameter inversion in reservoir monitoring[J]. Oil Geophysical Prospecting, 2017, 52(2): 402-410. |
| [2] |
Smith G C, Gidlow P M. Weighted stacking for rock property estimation and detection of gas[J]. Geophy-sical Prospecting, 1987, 35(9): 992-1014. |
| [3] |
Goodway B, Chen T, Downton J.Improved AVO fluid detection and lithology discrimination using Lamé petrophysical parameters; "λρ", "μρ", & "λ/μ fluid stack", from P and S inversions[C].SEG Technical Program Expanded Abstracts, 1997, 16: 183-186.
|
| [4] |
Russell B H, Hedlin K, Hilterman F J, et al. Fluidproperty discrimination with AVO:A Biot-Gassmann perspective[J]. Geophysics, 2003, 68(1): 29-39. DOI:10.1190/1.1543192 |
| [5] |
宁忠华, 贺振华, 黄德济. 基于地震资料的高灵敏度流体识别因子[J]. 石油物探, 2006, 45(3): 239-241. NING Zhonghua, HE Zhenhua, HUANG Deji. High sensitive fluid identification based on seismic data[J]. Geophysical Prospecting for Petroleum, 2006, 45(3): 239-241. |
| [6] |
Al-Dabagh H H, Alkhafaf S. Comparison of Kρ and λρ in clastic rocks:A test on two wells with different reservoir-quality stacked sands from West Africa[J]. The Leading Edge, 2011, 30(9): 986-994. DOI:10.1190/1.3640520 |
| [7] |
许翠霞, 马朋善, 赖令彬, 等. 致密砂岩含气性敏感参数--以松辽盆地英台气田营城组为例[J]. 石油勘探与开发, 2014, 41(6): 712-716. XU Cuixia, MA Pengshan, LAI Lingbin, et al. Sensitivity parameters of tight sand gas:A case study of Lower Cretaceous Yingcheng Formation of Yingtai gas field in Songliao Basin, NE China[J]. Petroleum Exploration & Development, 2014, 41(6): 778-783. |
| [8] |
Sharma R K, Chopra S. Determination of lithology and brittleness of rocks with a new attribute[J]. The Leading Edge, 2015, 34(5): 554-564. DOI:10.1190/tle34050554.1 |
| [9] |
Fatti J L. Detection of gas in sandstone reservoirs using AVO analysis:A 3-D seismic case history using the Geostack technique[J]. Geophysics, 1994, 59(9): 1362-1376. DOI:10.1190/1.1443695 |
| [10] |
Gray D.Bridging the gap: Using AVO to detect changes in fundamental elastic constants[C].SEG Technical Program Expanded Abstracts, 1999, 18: 852-855.
|
| [11] |
Russell B H, Gray D, Hampson D P. Linearized AVO and poroelasticity[J]. Geophysics, 2011, 76(3): C19-C29. DOI:10.1190/1.3555082 |
| [12] |
Zong Z, Yin X, Wu G. Elastic impedance parameterization and inversion with Young's modulus and Poisson's ratio[J]. Geophysics, 2013, 78(6): N35-N42. DOI:10.1190/geo2012-0529.1 |
| [13] |
Connolly P. Elastic impedance[J]. The Leading Edge, 1999, 18(4): 438-452. DOI:10.1190/1.1438307 |
| [14] |
王保丽, 印兴耀, 张繁昌. 基于Gray近似的弹性波阻抗方程及反演[J]. 石油地球物理勘探, 2007, 42(4): 435-439. WANG Baoli, YIN Xingyao, ZHANG Fanchang. Gray approximation-based elastic wave impedance equation and inversion[J]. Oil Geophysical Prospecting, 2007, 42(4): 435-439. DOI:10.3321/j.issn:1000-7210.2007.04.014 |
| [15] |
印兴耀, 张世鑫, 张繁昌, 等. 利用基于Russell近似的弹性波阻抗反演进行储层描述和流体识别[J]. 石油地球物理勘探, 2010, 45(3): 373-380. YIN Xingyao, ZHANG Shixin, ZHANG Fanchang, et al. Utilizing Russell approximation-based elastic wave impedance inversion to conduct reservoir description and fluid identification[J]. Oil Geophysical Prospecting, 2010, 45(3): 373-380. |
| [16] |
印兴耀, 张世鑫, 张峰. 针对深层流体识别的两项弹性阻抗反演与Russell流体因子直接估算方法研究[J]. 地球物理学报, 2013, 56(7): 2378-2390. YIN Xingyao, ZHANG Shixin, ZHANG Feng. Two-term elastic impedance inversion and Russell fluid factor direct estimation method for deep reservoir fluid identification[J]. Chinese Journal of Geophysics, 2013, 56(7): 2378-2390. |
| [17] |
杨培杰, 董兆丽, 刘昌毅, 等. 敏感流体因子定量分析与直接提取[J]. 石油地球物理勘探, 2016, 51(1): 158-164. YANG Peijie, DONG Zhaoli, LIU Changyi, et al. Sensitive fluid factor extraction and analysis[J]. Oil Geophysical Prospecting, 2016, 51(1): 158-164. |
| [18] |
张丰麒, 金之钧, 盛秀杰, 等. 基于低频软约束的叠前AVA稀疏层反演[J]. 石油地球物理勘探, 2017, 52(4): 770-782. ZHANG Fengqi, JIN Zhijun, SHENG Xiujie, et al. AVA sparse layer inversion with the soft-low frequency constraint[J]. Oil Geophysical Prospecting, 2017, 52(4): 770-782. |
| [19] |
Aki K, Richards P G.Quantitative Seismology[M].University Science Books, Sausalito, California, 2002, 141-153.
|
| [20] |
Downton J E.Seismic Parameter Estimation from AVO Inversion[D].University of Calgary, Calgary, 2005.
|



 高刚 湖北省武汉市蔡甸区蔡甸街大学路111号长江大学油气资源与勘探技术教育部重点实验室, 430100。Email:
高刚 湖北省武汉市蔡甸区蔡甸街大学路111号长江大学油气资源与勘探技术教育部重点实验室, 430100。Email: